Refined 2D and Exact 3D Shell Models for the Free Vibration Analysis of Single- and Double-Walled Carbon Nanotubes
Abstract
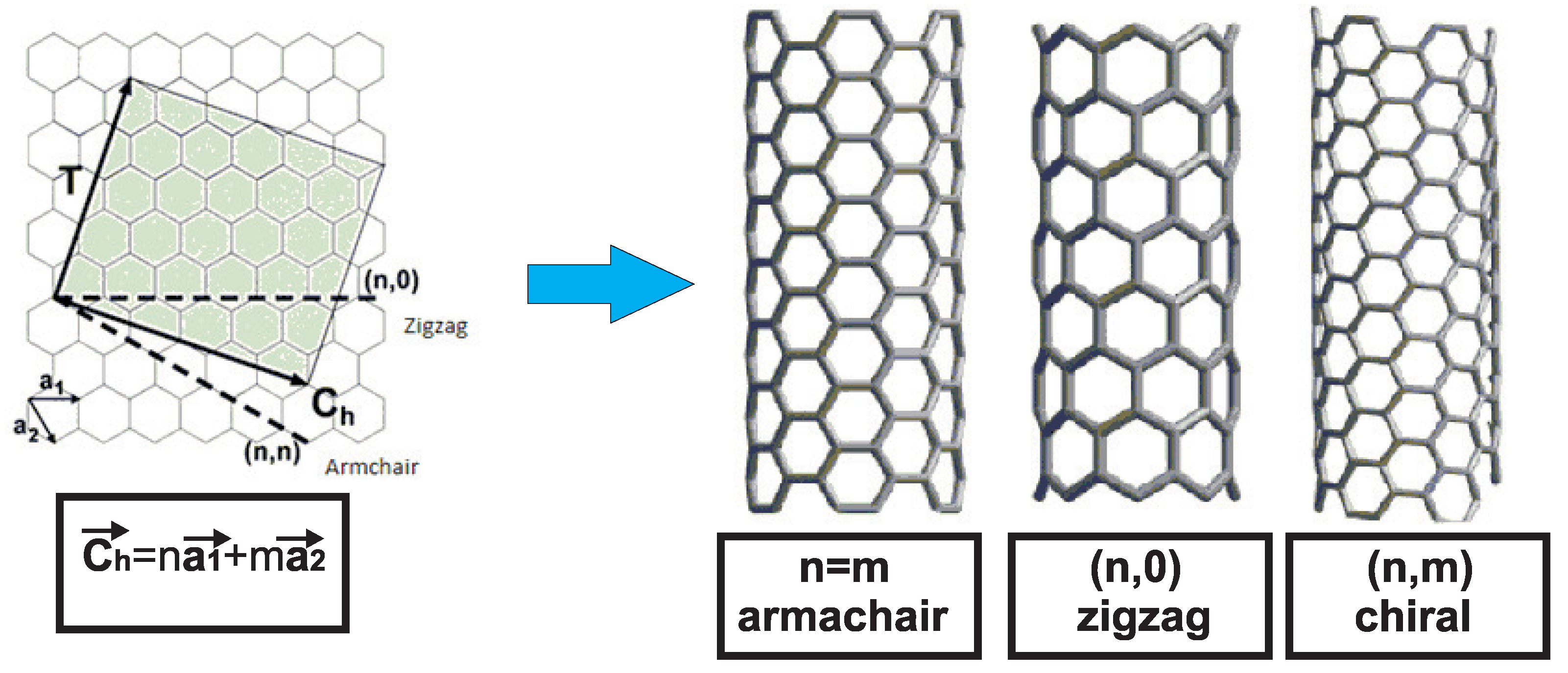
:1. Introduction
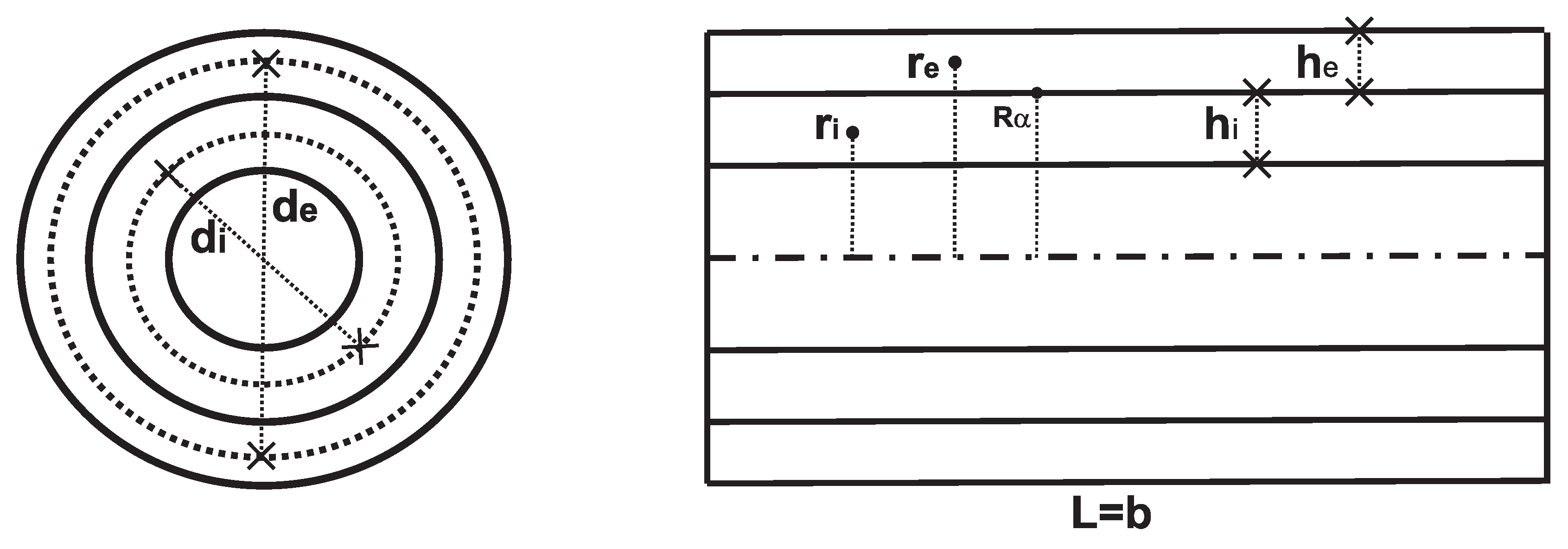
2. 3D Exact Shell Model

3. 2D GDQ Shell Models
4. Results and Discussion
4.1. Preliminary Assessment
| mode (p,q) | 3D Exact | RM-GDQ | ESL-GDQ | EBM [20,39] | TBM [20] |
|---|---|---|---|---|---|
| L/de = 5 | |||||
| I (2,1) | 9.3481 | 9.3672 | 9.3480 | - | - |
| I (2,2) | 32.917 | 32.941 | 32.907 | - | - |
| I (2,3) | 63.917 | 63.683 | 63.685 | - | - |
| L/de = 10 | |||||
| I (2,1) | 9.7295 | 9.7525 | 9.7290 | 9.8696 | 9.7443 |
| I (2,2) | 37.392 | 37.469 | 37.392 | 39.478 | 36.841 |
| I (2,3) | 79.361 | 79.483 | 79.358 | 88.826 | 57.450 |
| L/de = 20 | |||||
| I (2,1) | 9.8356 | 9.8584 | 9.8337 | 9.8696 | 9.8381 |
| I (2,2) | 38.918 | 39.010 | 38.916 | 39.478 | 38.964 |
| I (2,3) | 86.072 | 86.264 | 86.070 | 88.826 | 85.748 |
| L/de = 50 | |||||
| I (2,1) | 9.8638 | 9.8888 | 9.8638 | 9.8696 | 9.8645 |
| I (2,2) | 39.392 | 39.485 | 39.386 | 39.478 | 39.398 |
| I (2,3) | 88.375 | 88.583 | 88.363 | 88.826 | 88.415 |
| L/de = 100 | |||||
| I (2,1) | 9.8487 | 9.8932 | 9.8682 | - | - |
| I (2,2) | 39.488 | 39.555 | 39.455 | - | - |
| I (2,3) | 88.752 | 88.934 | 88.710 | - | - |
4.2. Benchmarks
| SWCNT (n,m) | (5,5) | (10,0) | (8,4) |
|---|---|---|---|
| r(nm) | 0.338 | 0.390 | 0.413 |
| n. atoms | 1040 | 1200 | 1200 |
| Armachair (5,5) | |||
|---|---|---|---|
| mode (p,q) | 3D Exact | RM-GDQ | ESL-GDQ |
| L/r = 20 | |||
| I (2,1) | 215.0 | 215.0 | 215.0 |
| I (2,2) | 791.7 | 791.8 | 791.7 |
| I (2,3) | 1595 | 1595 | 1595 |
| L/r = 25 | |||
| I (2,1) | 139.1 | 139.1 | 139.2 |
| I (2,2) | 526.2 | 526.2 | 526.2 |
| I (2,3) | 1093 | 1093 | 1093 |
| L/r = 30 | |||
| I (2,1) | 97.23 | 97.24 | 97.23 |
| I (2,2) | 373.5 | 373.5 | 373.5 |
| I (2,3) | 791.7 | 791.8 | 791.7 |
| L/r = 35 | |||
| I (2,1) | 71.70 | 71.71 | 71.70 |
| I (2,2) | 278.2 | 278.3 | 278.2 |
| I (2,3) | 597.9 | 597.9 | 597.9 |
| Zigzag (10,0) | |||
|---|---|---|---|
| mode (p,q) | 3D Exact | RM-GDQ | ESL-GDQ |
| L/r = 20 | |||
| I (2,1) | 186.0 | 186.0 | 186.0 |
| I (2,2) | 684.9 | 684.9 | 684.9 |
| I (2,3) | 1380 | 1380 | 1380 |
| L/r = 25 | |||
| I (2,1) | 120.4 | 120.4 | 120.4 |
| I (2,2) | 455.2 | 455.2 | 455.2 |
| I (2,3) | 945.7 | 945.7 | 945.7 |
| L/r = 30 | |||
| I (2,1) | 84.12 | 84.12 | 84.12 |
| I (2,2) | 323.1 | 323.2 | 323.1 |
| I (2,3) | 684.9 | 685.0 | 684.9 |
| L/r = 35 | |||
| I (2,1) | 62.04 | 62.04 | 62.04 |
| I (2,2) | 240.7 | 240.7 | 240.7 |
| I (2,3) | 517.2 | 517.2 | 517.2 |
| General Chirality (8,4) | |||
|---|---|---|---|
| mode (p,q) | 3D Exact | RM-GDQ | ESL-GDQ |
| L/r = 20 | |||
| I (2,1) | 175.5 | 175.6 | 175.5 |
| I (2,2) | 646.4 | 646.4 | 646.4 |
| I (2,3) | 1302 | 1302 | 1302 |
| L/r = 25 | |||
| I (2,1) | 113.6 | 113.6 | 113.6 |
| I (2,2) | 429.6 | 429.6 | 429.6 |
| I (2,3) | 892.4 | 892.5 | 892.4 |
| L/r = 30 | |||
| I (2,1) | 79.39 | 79.39 | 79.39 |
| I (2,2) | 305.0 | 305.0 | 305.0 |
| I (2,3) | 646.4 | 646.4 | 646.4 |
| L/r = 35 | |||
| I (2,1) | 58.55 | 58.55 | 58.55 |
| I (2,2) | 227.2 | 227.2 | 227.2 |
| I (2,3) | 488.1 | 488.1 | 488.1 |

| Nanotube 1 | ||||
|---|---|---|---|---|
| Mode (p,q) | 3D Exact | 3DvdW Exact | ESL-GDQ | LW-GDQ |
| L/de = 5 | ||||
| I (2,1) | 277.4 | 270.8 | 277.4 | 277.4 |
| I (2,2) | 946.2 | 892.3 | 946.2 | 946.2 |
| I (2,3) | 1785 | 1628 | 1785 | 1785 |
| L/de = 10 | ||||
| I (2,1) | 73.12 | 72.64 | 73.12 | 73.12 |
| I (2,2) | 277.4 | 270.8 | 277.4 | 277.4 |
| I (2,3) | 579.4 | 554.3 | 579.4 | 579.4 |
| L/de = 15 | ||||
| I (2,1) | 32.85 | 32.76 | 32.85 | 32.85 |
| I (2,2) | 128.1 | 126.6 | 128.1 | 128.1 |
| I (2,3) | 277.4 | 270.8 | 277.4 | 277.4 |
| L/de = 30 | ||||
| I (2,1) | 8.266 | 8.266 | 8.266 | 8.266 |
| I (2,2) | 32.85 | 32.76 | 32.85 | 32.85 |
| I (2,3) | 73.12 | 72.64 | 73.12 | 73.12 |
| L/de = 50 | ||||
| I (2,1) | 2.980 | 2.980 | 2.980 | 2.980 |
| I (2,2) | 11.89 | 11.89 | 11.89 | 11.89 |
| I (2,3) | 26.65 | 26.60 | 26.65 | 26.65 |

| Nanotube 2 | ||||
|---|---|---|---|---|
| Mode (p,q) | 3D Exact | 3DvdW Exact | ESL-GDQ | LW-GDQ |
| L/de = 5 | ||||
| I (2,1) | 106.5 | 106.2 | 106.5 | 106.5 |
| I (2,2) | 347.7 | 346.1 | 347.7 | 347.7 |
| I (2,3) | 629.9 | 624.2 | 629.9 | 629.9 |
| L/de = 10 | ||||
| I (2,1) | 28.55 | 28.54 | 28.55 | 28.55 |
| I (2,2) | 106.5 | 106.2 | 106.5 | 106.5 |
| I (2,3) | 217.6 | 216.1 | 217.6 | 217.6 |
| L/de = 15 | ||||
| I (2,1) | 12.88 | 12.87 | 12.88 | 12.88 |
| I (2,2) | 49.79 | 49.74 | 49.79 | 49.79 |
| I (2,3) | 106.5 | 106.2 | 106.5 | 106.5 |
| L/de = 30 | ||||
| I (2,1) | 3.248 | 3.248 | 3.248 | 3.248 |
| I (2,2) | 12.88 | 12.87 | 12.88 | 12.88 |
| I (2,3) | 28.55 | 28.53 | 28.55 | 28.55 |
| L/de = 50 | ||||
| I (2,1) | 1.172 | 1.171 | 1.172 | 1.172 |
| I (2,2) | 4.671 | 4.671 | 4.671 | 4.671 |
| I (2,3) | 10.45 | 10.45 | 10.45 | 10.45 |
| Nanotube 3 | ||||
|---|---|---|---|---|
| Mode (p,q) | 3D Exact | 3DvdW Exact | ESL-GDQ | LW-GDQ |
| L/de = 5 | ||||
| I (2,1) | 71.74 | 71.70 | 71.74 | 71.74 |
| I (2,2) | 231.5 | 231.3 | 231.5 | 231.5 |
| I (2,3) | 414.6 | 414.4 | 414.6 | 414.6 |
| L/de = 10 | ||||
| I (2,1) | 19.34 | 19.33 | 19.34 | 19.34 |
| I (2,2) | 71.74 | 71.70 | 71.74 | 71.74 |
| I (2,3) | 145.8 | 145.6 | 145.8 | 145.8 |
| L/de = 15 | ||||
| I (2,1) | 8.729 | 8.729 | 8.729 | 8.729 |
| I (2,2) | 33.67 | 33.66 | 33.67 | 33.67 |
| I (2,3) | 71.74 | 71.70 | 71.74 | 71.74 |
| L/de = 30 | ||||
| I (2,1) | 2.203 | 2.203 | 2.203 | 2.203 |
| I (2,2) | 8.729 | 8.729 | 8.729 | 8.729 |
| I (2,3) | 19.34 | 19.33 | 19.34 | 19.34 |
| L/de = 50 | ||||
| I (2,1) | 0.7949 | 0.7946 | 0.7949 | 0.7949 |
| I (2,2) | 3.168 | 3.168 | 3.168 | 3.168 |
| I (2,3) | 7.088 | 7.087 | 7.088 | 7.088 |
| Nanotube 4 | ||||
|---|---|---|---|---|
| mode (p,q) | 3D exact | 3DvdW exact | ESL-GDQ | LW-GDQ |
| L/de = 5 | ||||
| I (2,1) | 51.79 | 51.78 | 51.79 | 51.79 |
| I (2,2) | 166.1 | 166.1 | 166.1 | 166.1 |
| I (2,3) | 295.6 | 295.6 | 295.6 | 295.6 |
| L/de = 10 | ||||
| I (2,1) | 14.00 | 14.00 | 14.00 | 14.00 |
| I (2,2) | 51.79 | 51.78 | 51.79 | 51.79 |
| I (2,3) | 104.9 | 104.9 | 104.9 | 104.9 |
| L/de = 15 | ||||
| I (2,1) | 6.323 | 6.323 | 6.323 | 6.323 |
| I (2,2) | 24.35 | 24.35 | 24.35 | 24.35 |
| I (2,3) | 51.79 | 51.78 | 51.79 | 51.79 |
| L/de = 30 | ||||
| I (2,1) | 1.597 | 1.597 | 1.597 | 1.597 |
| I (2,2) | 6.323 | 6.323 | 6.323 | 6.323 |
| I (2,3) | 14.00 | 14.00 | 14.00 | 14.00 |
| L/de = 50 | ||||
| I (2,1) | 0.5761 | 0.5761 | 0.5761 | 0.5761 |
| I (2,2) | 2.296 | 2.296 | 2.296 | 2.296 |
| I (2,3) | 5.135 | 5.135 | 5.135 | 5.135 |
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Valavala, P.K.; Odegard, G.M. Modeling techniques for determination of mechanical properties of polymer nanocomposites. Rev. Adv. Mater. Sci. 2005, 9, 34–44. [Google Scholar]
- Rouainia, G.; Djeghaba, K. Evaluation of Young’s modulus of single walled carbon nanotube (SWNT) reinforced concrete composite. J. Eng. Appl. Sci. 2008, 3, 504–515. [Google Scholar]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhang, L.C. A critical assessment of the elastic properties and effective wall thickness of single-walled carbon nanotubes. Nanotechnology 2008, 19, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Qian, D.; Wagner, G.J.; Liu, W.K.; Yu, M.F.; Ruoff, R.S. Mechanics of carbon nanotubes. Appl. Mech. Rev. 2002, 55, 495–533. [Google Scholar] [CrossRef]
- Chen, X.; Cao, G. A structural mechanics study of single-walled carbon nanotubes generalized from atomistic simulation. Nanotechnology 2006, 17, 1004–1015. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.G.; Liew, K.M.; Wang, Q. Modeling of vibrations of carbon nanotubes. Procedia Eng. 2012, 31, 343–347. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Arash, B. Vibrations of single- and double-walled carbon nanotubes with layerwise boundary conditions: A molecular dynamics study. Curr. Appl. Phys. 2012, 12, 707–711. [Google Scholar] [CrossRef]
- Chowdhury, R.; Adhikari, S.; Wang, C.Y.; Scarpa, F. A molecular mechanics approach for the vibration of single-walled carbon nanotubes. Comput. Mater. Sci. 2010, 48, 730–735. [Google Scholar] [CrossRef]
- Das, S.L.; Mandal, T.; Gupta, S.S. Inextensional vibration of zig-zag single-walled carbon nanotubes using nonlocal elasticity theories. Int. J. Solids Struct. 2013, 50, 2792–2797. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, C.M.; Tan, V.B.C. Assessment of Timoshenko beam models for vibrational behavior of single-walled carbon nanotubes using molecular dynamics. Adv. Appl. Math. Mech. 2009, 1, 89–106. [Google Scholar]
- Sinnott, S.S.; Mao, Z.; Lee, K.-H. Computational studies of molecular diffusion through carbon nanotube based membranes. Comput. Model. Eng. Sci. 2002, 3, 589–600. [Google Scholar]
- Brenner, D.W.; Shenderova, O.A.; Areshkin, D.A.; Schall, J.D.; Frankland, S.-J.V. Atomic modeling of carbon-based nanostructures as a tool for developing new materials and technologies. Comput. Model. Eng. Sci. 2002, 3, 643–674. [Google Scholar]
- Yang, L.; Han, J.; Anantram, M.P.; Jaffe, R.L. Bonding geometry and bandgap changes of carbon nanotubes under uniaxial and torsional strain. Comput. Model. Eng. Sci. 2002, 3, 675–686. [Google Scholar]
- Namilae, S.; Chandra, U.; Srinivasan, A.; Chandra, N. Effect of interface modification on the mechanical behavior of carbon nanotube reinforced composites using parallel molecular dynamics simulations. Comput. Model. Eng. Sci. 2007, 22, 189–202. [Google Scholar]
- Arghavan, S.; Singh, A.V. On the vibrations of single-walled carbon nanotubes. J Sound Vib. 2011, 330, 3102–3122. [Google Scholar] [CrossRef]
- Gupta, A.; Sharma, S.C.; Harsha, S.P. Vibration analysis of carbon nanotubes based mass sensor using different boundary conditions. Int. J. Mech. Sci. 2012, 2, 8–12. [Google Scholar]
- Mir, M.; Hosseini, A.; Majzoobi, G.H. A numerical study of vibrational properties of single-walled carbon nanotubes. Comput. Mater. Sci. 2008, 43, 540–548. [Google Scholar] [CrossRef]
- Yan, Y.; Shi, G.; Zhao, P. Frequency study of single-walled carbon nanotubes based on a space-frame model with flexible connections. J. Comput. 2011, 6, 1125–1130. [Google Scholar] [CrossRef]
- Aydogdu, M. Axial vibration of the nanorods with the non local continuum rod model. Phys. E 2009, 41, 861–864. [Google Scholar] [CrossRef]
- Yan, J.W.; Liew, K.M.; He, L.H. Free vibration analysis of single-walled carbon nanotubes using a higher-order gradient theory. J Sound Vib. 2013, 332, 3740–3755. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhang, L.C. A critical assessment of the elastic properties and effective wall thickness of single-walled carbon nanotubes. Nanotechnology 2008, 19, 1–5. [Google Scholar]
- Wang, C.Y.; Zhang, L.C. An elastic shell model for characterizing single-walled carbon nanotubes. Nanotechnology 2008, 19, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Vodenitcharova, T.; Zhang, L.C. Effective wall thickness of a single-walled carbon nanotube. Phys. Rev. B 2003, 68, 1–4. [Google Scholar] [CrossRef]
- Odegard, G.M.; Gates, T.S.; Nicholson, L.M.; Wise, K.E. Equivalent-continuum modeling of nano-structured materials. Compos. Sci. Technol. 2002, 62, 1869–1880. [Google Scholar] [CrossRef]
- Lee, U.; Oh, H. Evaluation of the structural properties of single-walled carbon nanotubes using a dynamic continuum modeling method. Mech. Adv. Mater. Struct. 2008, 15, 79–87. [Google Scholar] [CrossRef]
- Zhang, L.C. On the mechanics of single-walled carbon nanotubes. J. Mater. Process. Technol. 2009, 209, 4223–4228. [Google Scholar] [CrossRef]
- Araújo dos Santos, J.V. Effective elastic moduli evaluation of single walled carbon nanotubes using flexural vibrations. Mech. Adv. Mater. Struct. 2011, 18, 262–271. [Google Scholar] [CrossRef]
- Azrar, A.; Azrar, L.; Aljinaidi, A.A. Length scale effect analysis on vibration behavior of single walled carbon nanotubes with arbitrary boundary conditions. Rev. Mec. Appl. Theor. 2011, 2, 475–485. [Google Scholar]
- Benzair, A.; Tounsi, A.; Besseghier, A.; Heireche, H.; Moulay, N.; Boumia, L. The thermal effect on vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. J. Phys. D Appl. Phys. 2011, 41, 1–10. [Google Scholar] [CrossRef]
- Demir, C.; Civalek, O.; Akgöz, B. Free vibration analysis of carbon nanotubes based on shear deformable beam theory by discrete singular convolution technique. Math. Comput. Appl. 2010, 15, 57–65. [Google Scholar]
- Foda, M.A. Steady state vibration analysis and mitigation of single-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comput. Mater. Sci. 2013, 71, 38–46. [Google Scholar] [CrossRef]
- Horng, T.L. Transverse vibration analysis of single-walled carbon nanotubes embedded in an elastic medium using Bernoulli-Fourier method. J. Surf. Eng. Mater. Adv. Technol. 2012, 2, 203–209. [Google Scholar] [CrossRef]
- Ming, L.; Huiming, Z. Small scale effect on thermal vibration of single-walled carbon nanotubes with nonlocal boundary condition. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 2729–2733. [Google Scholar]
- Swain, A.; Roy, T.; Nanda, P.K. Vibration behaviour of single walled carbon nanotube using finite element. Int. J. Theor. Appl. Res. Mech. Eng. 2013, 2, 129–133. [Google Scholar]
- Wang, B.; Deng, Z.C.; Zhang, K. Nonlinear vibration of embedded single-walled carbon nanotube with geometrical imperfection under harmonic load based on nonlocal Timoshenko beam theory. Appl. Math. Mech. 2013, 34, 269–280. [Google Scholar] [CrossRef]
- Wang, B.L.; Wang, K.F. Vibration analysis of embedded nanotubes using nonlocal continuum theory. Compos. B Eng. 2013, 47, 96–101. [Google Scholar] [CrossRef]
- Soltani, P.; Kassaei, A.; Taherian, M.M.; Farshidianfar, A. Vibration of wavy single-walled carbon nanotubes based on nonlocal Euler-Bernoulli and Timoshenko models. Int. J. Adv. Struct. Eng. 2012, 4, 1–10. [Google Scholar] [CrossRef]
- Simsek, M. Vibration analysis of a single-walled carbon nanotube under action of a moving harmonic load based on nonlocal elasticity theory. Phys. E 2010, 43, 182–191. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Phys. E 2009, 41, 1232–1239. [Google Scholar] [CrossRef]
- Aydogdu, M. A general non local beam theory: Its application to nanobeam bending, buckling and vibration. Phys. E 2009, 41, 1651–1655. [Google Scholar] [CrossRef]
- Aydogdu, M. Vibration of multi-walled carbon nanotubes by generalized shear deformation theory. Int. J. Mech. Sci. 2008, 50, 837–844. [Google Scholar] [CrossRef]
- Khosrozadeh, A.; Hajabasi, M.A. Free vibration of embedded double-walled carbon nanotubes considering nonlinear interlayer van der Waals forces. Appl. Math. Model. 2012, 36, 997–1007. [Google Scholar] [CrossRef]
- Fang, B.; Zhen, Y.-X.; Zhang, C.-P.; Tang, Y. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Appl. Math. Model. 2013, 37, 1096–1107. [Google Scholar] [CrossRef]
- Natsuki, T.; Ni, Q.-Q.; Endo, M. Analysis of the vibration characteristics of double-walled carbon nanotubes. Carbon 2008, 46, 1570–1573. [Google Scholar] [CrossRef]
- Kiani, K. Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subjected to axial load using nonlocal shear deformable beam theories. Int. J. Mech. Sci. 2013, 68, 16–34. [Google Scholar] [CrossRef]
- Aydogdu, M. Longitudinal wave propagation in multiwalled carbon nanotubes. Compos. Struct. 2014, 107, 578–584. [Google Scholar] [CrossRef]
- de Borbón, F.; Ambrosini, D. On the influence of van der Waals coefficient on the transverse vibration of double walled carbon nanotubes. Comput. Mater. Sci. 2012, 65, 504–508. [Google Scholar] [CrossRef]
- Chang, T.-P. Stochastic FEM on nonlinear vibration of fluid-loaded double-walled carbon nanotubes subjected to a moving load based on nonlocal elasticity theory. Compos. B Eng. 2013, 54, 391–399. [Google Scholar] [CrossRef]
- Benguediab, S.; Tounsi, A.; Zidour, M.; Semmah, A. Chirality and scale effects on mechanical buckling properties of zigzag double-walled carbon nanotubes. Compos. B Eng. 2014, 57, 21–24. [Google Scholar] [CrossRef]
- Brischetto, S. A continuum elastic three-dimensional model for natural frequencies of single-walled carbon nanotubes. Compos. B Eng. 2014, 61, 222–228. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhang, L.C. An elastic shell model for characterizing single-walled carbon nanotubes. Nanotechnology 2008, 19, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Alibeigloo, A.; Shaban, M. Free vibration analysis of carbon nanotubes by using three-dimensional theory of elasticity. Acta Mech. 2013, 224, 1415–1427. [Google Scholar] [CrossRef]
- Mikhasev, M. On localized modes of free vibrations of single-walled carbon nanotubes embedded in nonhomogeneous elastic medium. Z. Angew. Math. Mech. 2013, 1–12. [Google Scholar] [CrossRef]
- Silvestre, N.; Wang, C.M.; Zhang, Y.Y.; Xiang, Y. Sanders shell model for buckling of single-walled carbon nanotubes with small aspect ratio. Compos. Struct. 2011, 93, 1683–1691. [Google Scholar] [CrossRef]
- Strozzi, M.; Manevitch, L.I.; Pellicano, F.; Smirnov, V.V.; Shepelev, D.S. Low-frequency linear vibrations of single-walled carbon nanotubes: Analytical and numerical models. J Sound Vib. 2014, 333, 2936–2957. [Google Scholar] [CrossRef] [Green Version]
- Liew, K.M.; Wang, Q. Analysis of wave propagation in carbon nanotubes via elastic shell theories. Int. J. Eng. Sci. 2007, 45, 227–241. [Google Scholar] [CrossRef]
- Cinefra, M.; Carrera, E.; Brischetto, S. Refined shell models for the vibration analysis of multiwalled carbon nanotubes. Mech. Adv. Mater. Struct. 2011, 18, 476–483. [Google Scholar] [CrossRef]
- Brischetto, S. A Continuum shell model including van derWaals interaction for free vibrations of double-walled carbon nanotubes. Comput. Model. Eng. Sci. 2015, 104, 305–327. [Google Scholar]
- Dong, K.; Zhu, S.Q.; Wang, X. Wave propagation in multiwall carbon nanotubes embedded in a matrix material. Compos. Struct. 2008, 82, 1–9. [Google Scholar] [CrossRef]
- Li, R.; Kardomateas, G.A. Vibration characteristics of multiwalled carbon nanotubes embedded in elastic media by a nonlocal elastic shell model. J. Appl. Mech. 2007, 74, 1087–1094. [Google Scholar] [CrossRef]
- Yao, X.; Han, Q. Torsional buckling and postbuckling equilibrium path of double-walled carbon nanotubes. Compos. Sci. Technol. 2008, 68, 113–120. [Google Scholar] [CrossRef]
- He, X.Q.; Kitipornchai, S.; Wang, C.M.; Liew, K.M. Modeling of van der Waals force for infinitesimal deformation of multi-walled carbon nanotubes treated as cylindrical shells. Int. J. Solids Struct. 2005, 42, 6032–6047. [Google Scholar] [CrossRef]
- Han, Q.; Lu, G.; Dai, L. Bending instability of an embedded double-walled carbon nanotube based on Winkler and van der Waals models. Compos. Sci. Technol. 2005, 65, 1337–1346. [Google Scholar] [CrossRef]
- Hoseinzadeh, M.S.; Khadem, S.E. Thermoelastic vibration and damping analysis of double-walled carbon nanotubes based on shell theory. Phys. E 2011, 43, 1146–1154. [Google Scholar] [CrossRef]
- Brischetto, S. Exact elasticity solution for natural frequencies of functionally graded simply-supported structures. Comput. Model. Eng. 2013, 95, 391–430. [Google Scholar]
- Brischetto, S. An exact 3D solution for free vibrations of multilayered cross-ply composite and sandwich plates and shells. Int. J. Appl. Mech. 2014, 6, 1–42. [Google Scholar] [CrossRef]
- Brischetto, S. Three-dimensional exact free vibration analysis of spherical, cylindrical, and flat one-layered panels. Shock Vib. 2014, 2014, 1–29. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Exact 3D solutions and finite element 2D models for free vibration analysis of plates and cylinders. Curved Layer. Struct. 2014, 1, 59–92. [Google Scholar] [CrossRef]
- Messina, A. Three Dimensional Free Vibration Analysis of Cross-Ply Laminated Plates through 2D and Exact Models. In Proceedings of the 3rd International Conference on Integrity, Reliability and Failure, Porto, Portugal, 20–24 July 2009.
- Soldatos, K.P.; Ye, J. Axisymmetric static and dynamic analysis of laminated hollow cylinders composed of monoclinic elastic layers. J Sound Vib. 1995, 184, 245–259. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Fantuzzi, N. General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels. Compos. Struct. 2013, 104, 94–117. [Google Scholar] [CrossRef]
- Tornabene, F. General higher order layer-wise theory for free vibrations of doubly-curved laminated composite shells and panels. Mech. Adv. Mater. Struct. 2015, in press. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories. Compos. B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The local GDQ method applied to general higher-order theories of doubly-curved laminated composite shells and panels: The free vibration analysis. Compos. Struct. 2014, 116, 637–660. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Reddy, J.N. Winkler-Pasternak foundation effect on the static and dynamic analyses of laminated doubly-curved and degenerate shells and panels. Compos. B Eng. 2014, 57, 269–296. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Ferreira, A.J.M. Radial basis function method applied to doubly-curved laminated composite shells and panels with a general higher-order equivalent single layer theory. Compos. B Eng. 2013, 55, 642–659. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. General higher-order shear deformation theories for the free vibration analysis of completely doubly-curved laminated shells and panels. Compos. Struct. 2013, 95, 639–666. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Accurate inter-laminar recovery for plates and doubly-curved shells with variable radii of curvature using layer-wise theories. Compos. Struct. 2015, 124, 368–393. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67. [Google Scholar] [CrossRef]
- Tornabene, F.; Brischetto, S.; Fantuzzi, N.; Viola, E. Numerical and exact models for free vibration analysis of cylindrical and spherical shell panels. Compos. B Eng. 2015, 81, 231–250. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Nali, P. Plates and Shells for Smart Structures: Classical and Advanced Theories for Modeling and Analysis; John Wiley & Sons, Ltd.: New Delhi, India, 2011. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brischetto, S.; Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Refined 2D and Exact 3D Shell Models for the Free Vibration Analysis of Single- and Double-Walled Carbon Nanotubes. Technologies 2015, 3, 259-284. https://doi.org/10.3390/technologies3040259
Brischetto S, Tornabene F, Fantuzzi N, Bacciocchi M. Refined 2D and Exact 3D Shell Models for the Free Vibration Analysis of Single- and Double-Walled Carbon Nanotubes. Technologies. 2015; 3(4):259-284. https://doi.org/10.3390/technologies3040259
Chicago/Turabian StyleBrischetto, Salvatore, Francesco Tornabene, Nicholas Fantuzzi, and Michele Bacciocchi. 2015. "Refined 2D and Exact 3D Shell Models for the Free Vibration Analysis of Single- and Double-Walled Carbon Nanotubes" Technologies 3, no. 4: 259-284. https://doi.org/10.3390/technologies3040259
APA StyleBrischetto, S., Tornabene, F., Fantuzzi, N., & Bacciocchi, M. (2015). Refined 2D and Exact 3D Shell Models for the Free Vibration Analysis of Single- and Double-Walled Carbon Nanotubes. Technologies, 3(4), 259-284. https://doi.org/10.3390/technologies3040259









