Human Activities Recognition Based on Neuro-Fuzzy Finite State Machine

Abstract

Human activity recognition and modelling comprise an area of research interest that has been tackled by many researchers. The application of different machine learning techniques including regression analysis, deep learning neural networks, and fuzzy rule-based models has already been investigated. In this paper, a novel method based on Fuzzy Finite State Machine (FFSM) integrated with the learning capabilities of Neural Networks (NNs) is proposed to represent human activities in an intelligent environment. The proposed approach, called Neuro-Fuzzy Finite State Machine (N-FFSM), is able to learn the parameters of a rule-based fuzzy system, which processes the numerical input/output data gathered from the sensors and/or human experts’ knowledge. Generating fuzzy rules that represent the transition between states leads to assigning a degree of transition from one state to another. Experimental results are presented to demonstrate the effectiveness of the proposed method. The model is tested and evaluated using a dataset collected from a real home environment. The results show the effectiveness of using this method for modelling the activities of daily living based on ambient sensory datasets. The performance of the proposed method is compared with the standard NNs and FFSM techniques.

1. Introduction

Monitoring and recognising human activities in an indoor environment (home or office) are studied within the general topic of Ambient Intelligence (AmI) [1,2]. Human activities can be sensed using unobtrusive sensors such as Passive Infrared (PIR) sensors and images/videos captured using cameras [3]. Attention has predominantly been focused on data collected by unobtrusive sensors, which are more acceptable by users [4]. The analysis of the captured data can be used to optimise energy consumption, address health and safety concerns, or lead to an improved level of the residences’ comfort and living quality [5].

In order to recognise human activities based on low-level sensory information, different modelling techniques are investigated. One of the promising techniques in modelling and recognising human activities is based on the Finite State Machine (FSM) [6]. The classic FSM is employed to represent the states and the functionality of transitions between different states (here, the activities). However, considering the uncertainties incorporated in human activities, a fusion of fuzzy logic with FSM allows a more powerful tool to model the dynamic processes that may change over time [6,7,8]. Considering the uncertainty involved in the collected data that represent human activities, it is argued that the Fuzzy Finite State Machine (FFSM) is a suitable technique to deal with large uncertain data collected from real-world environments. Furthermore, the system can assign a degree of truth to the occurrence of each activity.

In an FFSM model, the transitions between states are triggered by fuzzy variables instead of crisp values. This provides an accurate model supported by a reasoning mechanism represented with a degree of truth related to each state transition. Thus, the system can be in more than one state at any time based on the membership values or degree of belonging to each state [5,6]. Readers are referred to [9] for the theoretical definition of the FFSM with some recent developments reported in [10,11].

The research reported in this paper is part of the on-going research works in our research group to support the independent living and enhance the quality of life for elderly residents. The aim of the research reported in this paper is to develop a model representing the Activities of Daily Living (ADL). The work could be easily expanded to include Activities of Daily Working (ADW) if required. Once the human activities are modelled, an individual profile for each user (house residence or office worker) can be created to adjust automatically his/her environment (residence-places/work-spaces) conditions according to the user’s preferences [3,5]. Recognising a user’s activity leads to predicting what that person is going to do next. The predicting process might be made on the basis of the person’s behavioural pattern repeatedly observed in the past. By understanding the human behavioural patterns, the future activities can be predicted. Once the predicted activities are identified, many different aspects of human lifestyle can be improved; e.g., safety, security, and energy saving. For instance, in the case of ADW, the environmental conditions of the workspace such as the heating system, ambient light, and turning on/off the computers could be adjusted based on the prediction of the worker’s arriving and leaving times. In this case, the energy consumption can be reduced and the workers’ comfortability will be increased. It should be mentioned that activity prediction is beyond the scope of this paper. In this paper, a learning method to create the FFSM rules is proposed, which allows the model to generate automatically the rules based on the numerical information gathered from the sensors and the knowledge gathered from human experts. The rules represent the probabilistic transitions between the states, whereas the states themselves are still defined based on the experts’ knowledge.

This paper is an extension of the authors’ research work in developing an FFSM used for Human Activity Recognition (HAR) based on the data gathered from low-level ambient sensors [12]. Employing FFSMs to model the HAR is justified mainly due to their capabilities in modelling and recognising the uncertainties in human behaviour. The original approach is extended in this paper by integrating the learning capabilities of Neural Networks (NNs) to generate the fuzzy rules that govern the fuzzy states’ transitions. Moreover, experts’ knowledge is used to identify the number of sates, the number of linguistic labels associated with each input, and the general structure of the rules.

The rest of this paper is organised as follows: after a review of the literature in Section 2, the methodologies are presented in Section 3, including FFSM and the proposed human activity modelling using the Neuro-Fuzzy Finite State Machine (N-FFSM). In Section 4, a human activity recognition case study is detailed, including the experimental results, followed by the discussion of the results in Section 5. The pertinent conclusions are drawn in Section 6.

2. Literature Review

Modelling human activities in an indoor environment is a challenging task, as humans behave with great uncertainty within their living and working places. Many research works have been conducted to monitor and analyse the activities of people using many different machine learning techniques including genetic-fuzzy FSM [13], dynamic Bayesian network modelling [14], echo-state neural networks [15], and regression models [16]. In [5], it was shown that the ADW in an AmI environment can be modelled using the FFSM technique by means of sequential events based on a dataset collected from a real smart office environment. Although the authors have presented the human activities by fuzzy states, they faced difficulties in generating fuzzy rules solely based on experts’ knowledge.

The researchers in [2,17,18] investigated different ways in which human behaviour can be detected and modelled using the Markov Model (MM) and the Hidden Markov Model (HMM). Their experiments were based on the data collected from some wearable sensors and cameras, with a focus on using the Hierarchical Context Hidden Markov Model (HC-HMM) from video streams. In [19], the authors presented a novel approach for monitoring people’s behaviour using an indoor localisation system based on the stigmergy technique. They suggested that a further work is required to implement the same concepts for enhancing the system’s ability to monitor human behaviour. This enhancement can be processed after training the system using a dataset collected from a real environment. A relatively new research work [4] presented a new model based on the Markov Modulated Poisson Process (MMPP) that promises to come up with a model to represent multi-visitor recognition with more accuracy. In [20], a framework was proposed to integrate temporal and spatial contextual information to determine the wellness of an elderly person living alone in a home environment.

The swarm intelligence method was used in [19] to monitor an elderly person’s activities via indoor position-based stigmergy. Other evolutionary computing and machine learning techniques based on MMPP are similarly employed to enhance human activity monitoring accuracy. Some works used a dataset collected by a smartphone’s accelerometer [4,21]. Hybrid computational techniques, such as data mining [22], pattern recognition, and human activity profiling using Convolutional Neural Network (CNN) [23], are also used in the context of ADL and ADW in order to divide the monitored human behaviours into activities and preferences [7].

Many published papers addressed the issue of modelling human behaviour using wearable sensors [24,25]. Developing activity recognition systems using the smartphones’ built-in accelerometer together with employing CNNs to model the activities was addressed in some recent publications [26,27]. In [28], the authors proposed a novel way of implementing the task of recognition by using probabilistic graphical models such as Bayesian Network (BN) and Dynamic Bayesian Network (DBN). These techniques are widely used in different domains including speech recognition and bio-sequence analysis [28]. Furthermore, they used the proposed DBN to recognise the current pair of activity-object and predict the most probable task based on the features extracted from RGB Depth (RGB-D) raw data. This information was then used to make the human-robot cooperation more efficient.

In [29], the authors proposed a sequential meta-cognitive learning algorithm for a Neuro-Fuzzy Inference System (McFIS) to develop a classifier for human actions recognition based on a video sequence. They used a four-layer NN to determine the number of rules and their corresponding parameters. The motion features were used for each action by extracting the accumulated motion information over a small time window. The results obtained from this work indicate superior performance of the McFIS classifier compared to the standard Support Vector Machine (SVM). The developed system uses a Neuro-Fuzzy Inference System for HAR. Based on the literature review conducted for this research, a gap is identified where NN learning could be integrated with FFSM.

3. Methodology

In this section, first the fuzzy finite state machine is introduced, then a proposed enhancement is introduced that is able to implement a learning method using neural networks.

3.1. Fuzzy Finite State Machine

A Fuzzy Finite State Machine (FFSM) [30,31] is an extended version of the classical Finite State Machine (FSM), in which a computation model can simulate the sequence of events in a dynamic process. The FSM computation is based on a model made of one or more states. Only one single state of this machine can be active at a time. The machine performs different actions, by transiting from one state to another, triggered by fixed values. By adding the fuzziness aspect to the state transitions, the states are not only triggered by binary values, but also by means of fuzzy variables. Moreover, the states could be represented by fuzzy variables as well [5,13,30]. However, in some FFSM applications, it is assumed that states are still defined as fixed values, whereas the fuzzy values are to be used to control the state transitions [32]. In both approaches, the system is not necessarily in one state at the same time [30], i.e., fuzzy membership values are associated with the states at each time [31].

In an FFSM, the state variables are shown as a set of linguistic variables $S=\{s_1,s_2,\dots ,s_n\}$ where n is the number of states. For a non-sequential system at time t, the FFSM state is represented as a state vector $S(t)$ (as opposed to the scalar state of the FSM). When the system evolves in time, the next state is represented as a vector $S(t+1)$.

FFSM is defined as a tuple $\left(S(t),U(t),f,Y(t),g\right)$, where $S(t)=[s_1(t),s_2(t),\dots ,s_n(t)]$ is the state vector, $U(t)=[u_1(t),u_2(t),\dots ,u_k(t)]$ is the input vector to the system, with k being the number of input variables, $Y(t)=[y_1(t),y_2(t),\dots y_p(t)]$ is the vector of output variables with p being the number of output variables, f is the function that calculates the next state at time t, and g is the function that calculates the output vector Y at time t [5,6,13]. Considering the complexity of our modelling cases, it may be impossible to identify analytically the functions f and g.

In a general time-invariant model, the FFSM’s states and outputs are therefore expressed [5,13] as:

$$S(t+1)=f\left(S(t),U(t)\right)$$

(1)

$$Y(t)=g\left(S(t),U(t)\right)$$

(2)

More details about each of these elements are provided below:

• Fuzzy state $(S(t)$) is a vector representing the system’s states at time t. Each individual state at time t $s_i(t);i=1\dots n$ is a numerical value that is in fact the membership grade (between 0 and 1) given to each linguistic variable $s_i$ within the set of FFSM’s states (S).
• Input vector $(U(t))$ represents the values associated with the linguistic variables that are generally obtained after a fuzzification process of sensors’ data, a combination of different signals, or any other calculation of numerical data. The fuzzification process, which is designed based on experts’ view, translates the numerical input values into a set of membership grades given to each linguistic label, which defines all the acceptable values. The labels that are associated with the input $u_i$ are represented as $A_{u_i}=\{A_{u_i}^1,A_{u_i}^2,\dots ,A_{u_i}^{k_i}\}$, where $k_i$ is the number of associated linguistic labels [6].
• Output vector $(Y(t))$ is the output vector consisting of crisp values associated with each output, which are calculated based on the current state of the system $S(t)$ and the input vector $(U(t))$.
• Output function $(g)$ is the output function that is used to calculate the value of output vector $Y(t)$, at each time instant t.
• Transition function $(f)$ is the state transition function that is used to calculate the next state vector $S(t+1)$, at each time instant. The transition function f controls the allowed transitions between the defined relevant states in the system. f is defined as a set of fuzzy rules. There are different ways to define the rules; e.g., using human experts’ knowledge [5] or learning from the numerical input-output data by applying machine learning algorithms [32,33,34]. A combination of these approaches can also be implemented to have one framework that contains the rules that were generated by learning from the numerical data and those assigned by the human experts’ knowledge [34].

Figure 1 illustrates the system states and transition mechanism between two exemplary states $s_i$ and $s_j$. The transition mechanism from $s_i$ to $s_j$ is represented by the following general fuzzy rule:

$$R_{ij}\mathbf{:}\mathbf{IF}(S(t)\mathbf{is}{s}_i)\mathbf{AND}{H}_{ij}\mathbf{THEN}S(t+1)\mathbf{is}{s}_j$$

The antecedent part of the rule is a combination of two terms: The first term, $(S(t)$ is $s_i)$, is used to determine if the state $s_i$ is an activated state in time instant t. The second term of the antecedent part is $H_{ij}$, which represents all constraints imposed on the input variables that are required to either remain in state $s_i$ (when, $i=j$) or change to state $s_j$, e.g., $H_{ij}=(u_1(t)$ is $A_{u1}^3)$ AND $(u_2(t)$ is $A_{u2}^4$ OR $A_{u2}^2)$. The consequent part of the given rule is $S(t+1)$ is $s_j$, which determines the next value of the state vector $S(t+1)$ for being in state $s_j$. The linguistic variables of the consequent part are considered as being singletons, i.e., all elements of the $S(t)$ vector are zero, except for the $j^{\mathrm{th}}$ element, which is 1 [13].

For the $k^{\mathrm{th}}$ rule, a t-norm method (e.g., minimum) is used to calculate the rule’s firing degree $w_k$. For a rule-base consisting of $\kappa$ rules, the next value of the state vector $S(t+1)$ is the weighted average utilising the firing degree of each rule, defined as:

$$S(t+1)=\frac{{\sum }_{k=1}^{\kappa }{w}_k.S(t)}{{\sum }_{k=1}^{\kappa }{w}_k}if\sum _{k=1}^{\kappa }{w}_k\ne 0$$

(3)

$$S(t+1)=S(t)if\sum _{k=1}^{\kappa }{w}_k=0$$

(4)

The expression above is considered as an inference process that is applied to a set of fuzzy rules where the linguistic variables of the consequent part are singletons. Readers are referred to [5,13,35] for more information about FFSM. More details about the transition function element based on fuzzy rules are explained in the next section.

3.2. Neuro-Fuzzy Finite State Machine

A common approach in incorporating learning capabilities into the fuzzy systems is based on the combination of fuzzy systems and Artificial Neural Networks (ANNs), also known as Neural Networks (NNs), leading to a well-known hybrid system called a neuro-fuzzy system [36]. Fuzzy rules are generally based on the numerical data rather than experts’ knowledge [37]. In this section, the fusion framework between FFSM and NNs is explained.

Figure 2 illustrates the schematic diagram of the proposed Neuro-Fuzzy Finite State Machine (N-FFSM). The proposed N-FFSM model can automatically generate the fuzzy rules representing the state transitions. In this approach, the experts are also allowed to introduce their own knowledge over the whole system by defining the system states and specifying the general structure of the fuzzy rules representing the state transitions. The fuzzy rules and the associated linguistic labels to each input are automatically derived by the neuro-fuzzy rule-based system. Therefore, it is possible to construct the Membership Functions (MFs) associated with the linguistic label used in the fuzzy rules.

The N-FFSM system is considered as an adaptive network, which is functionally equivalent to the fuzzy systems in terms of representing the fuzzy rules linguistically with the capabilities of neural learning. This network is comprised of nodes (neurons) identifying specific functions gathered in layers. The final output of these layers is able to construct a network generating the fuzzy rules.

Based on the explanation given in the proceeding sections, a new model is proposed to generate automatically the rules representing the transition based on learning from the sensors’ data.

4. Case Study

Modelling the ADL for a single user living within a smart home environment is represented as a case study in this section. The N-FFSM approach introduced earlier is applied to the data gathered from a smart home environment representing the activities of the occupant. The fuzzy rules are automatically generated based on the data gathered from the sensors.

4.1. Human Activity Recognition

Recognising the human activities based on data gathered from some low-level sensors comprises some challenges. They are:

• Recognising concurrent or simultaneous activities: By nature, several activities can be undertaken by a single user at the same time [38]. For example, people can read a book while they are watching TV or eating. In this case, it is not necessary to know which activity started first; that means the existence of concurrent activities when an activity (e.g., eating) starts while the other activity is already started (e.g., reading a book). A specialised approach is required to recognise these non-sequential behaviours.
• Recognising interleaved activities: In real life, a certain activity can be interrupted by another activity [8]. For example, while the current activity of an office worker is recorded as “computer activity”, a visitor comes to the office. In this case, the first activity is paused for the period of the second activity’s duration before the previous activity is resumed.
• Recognising multiple residents: In many situations, more than one user is present in the environment at the same time. It is even harder than the previous scenarios to recognise parallel activities for multiple people living/working together in the same place. Different statistical measurements are provided in this research area, but it is still considered as a challenge [16].

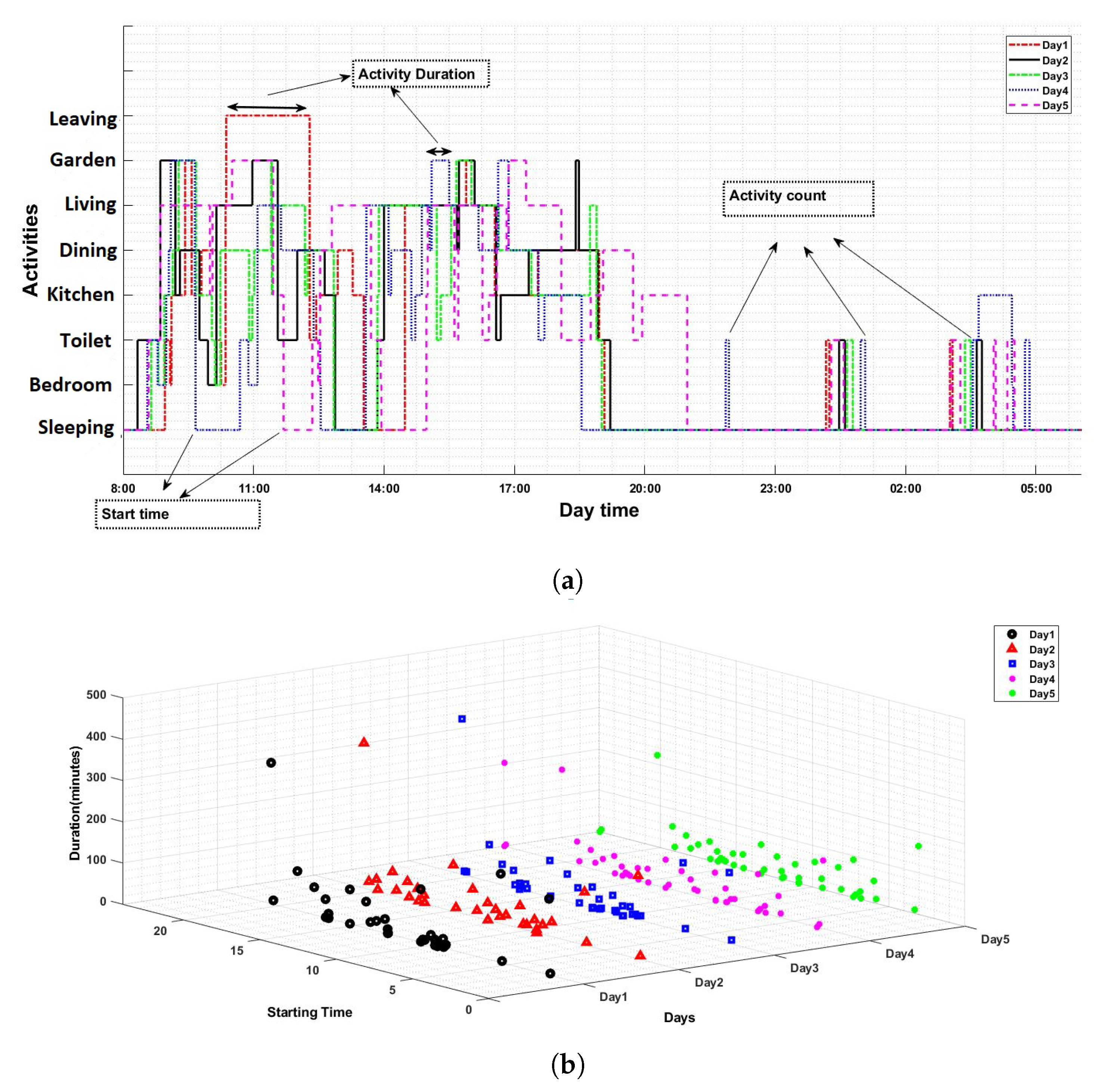
4.2. Data Collection System

The experiment was conducted at the Smart Home facilities within Nottingham Trent University. A floor plan of the house is shown in Figure 3. The list of sensors embedded in the environment that were used for this experiment is also provided in

Table 1. List of sensors used in the experiment that can measure different conditions and activities (* denotes the unused sensors in this research).

Sensors	Sensors’ Quantity	Used for
Passive Infrared Red (PIR)	6	Detecting the movement and occupancy
On/off door switches	2	Detecting when doors are open
Mat pressure sensor	1	Measuring bed occupancy
Electricity usage sensors	2	Plugs measuring electricity consumption
		usage, e.g., microwave and kettle.
* Indoor temperature sensors	5	Measuring ambient temperature
* Humidity sensors	5	Measuring ambient humidity
* Outdoor temperature sensors	1	Measuring outside temperature
* Light intensity sensors	6	Measuring ambient light intensity

. A set of data was collected from this environment.

Figure 4 shows a sample of the collected binary data from PIR sensors. Each data record from the sensors contained the information presented as a triple $(t,a_{on},a_{off})$, where t is the timestamp of the action or activity, and $a_{on}$ and $a_{off}$ are the sensor status at the time instant t, represented as a binary data (1 or 0). The information involved in the raw data is used to extract the required features for the input variables.

4.3. System States’ Definition

As explained in Section 3, each state represents an activity. Multiple activities could be associated with one room. Based on the available experts’ knowledge, eight different states were defined representing eight distinguishable activities. This is easily represented by means of the proposed state diagram illustrated in Figure 5. These eight states are defined as follows:

• $s_1$: The sleeping state represents sleeping activity either during the night or while taking a nap during the daytime. Intuitively, the collected starting time and the duration of this activity could vary depending on the day of the week, even for the same user. Furthermore, the state can be interrupted by other activities such as going to the toilet, etc.
• $s_2$: The bedroom state is used to represent the other duties in the bedroom except for the sleeping activity.
• $s_3$: The toilet state represents the times when the user is using the toilet.
• $s_4$: The kitchen state is where the user spends time in the kitchen to prepare food or to clean.
• $s_5$: The dining room state usually comes after the kitchen state, when the user stays in the dining room to eat the prepared meal.
• $s_6$: The living room state corresponds to the time spent in the living room to watch TV or other social activities.
• $s_7$: The garden state is used when the user uses the back door to go to the garden.
• $s_8$: The leaving home state becomes active when the individual leaves the home from the front door. This can be for any duties away from the home such as shopping. This state might occur regularly at a certain time (in the case of the individual having a daily job) or irregularly (in the case of shopping and social visiting).

4.4. Input Variables’ Definition

Once the data have been collected from all sensors, three features are extracted to be used as the inputs to the proposed N-FFSM system. The input variable vector is $U=[u_1,u_2,u_3]$. $u_1$ represents activity start time; $u_2$ denotes the duration of each activity, which is represented in minutes; $u_3$ is the activity count, which defines a number that represents how many times the activity was sensed per day. Each input variable is fuzzified to translate the numerical data to their relevant linguistic values. These values are represented as fuzzy Membership Functions (MFs).

The linguistic labels for each input variable are shown in Figure 6, as explained below:

• For input variable $u_1$, five linguistic labels are used, which represent five activity start times during a day, as: $\{E{M}_{u_1},M_{u_1},A{F}_{u_1},E{V}_{u_1},N{I}_{u_1}\}$. $EM$ is Early Morning; M is Morning; $AF$ is Afternoon; $EV$ is Evening; and $NI$ is Night. Therefore, $A_{u_1}=\{A_{u_1}^1,A_{u_1}^2,A_{u_1}^3,A_{u_1}^4,A_{u_1}^5\}$, where $A=\{EM,M,AF,EV,NI\}$.
• For input variable $u_2$, this input variable has five linguistic labels, as well, which represent five different periods of time for the activity duration as: $\{V{S}_{u_2},S{H}_{u_2},M{E}_{u_2},L{O}_{u_2},VL{O}_{u_2}\}$. $VS$ is Very Short; $SH$ is Short; $ME$ is Medium; $LO$ is Long; and $VLO$ is Very Long. Therefore, $A_{u_2}=\{A_{u_2}^1,A_{u_2}^2,A_{u_2}^3,A_{u_2}^4,A_{u_2}^5\}$, where $A=\{VS,SH,ME,LO,VLO\}$.
• For input variable $u_3$, only three linguistic labels are used, which represent three different usage levels, as: $\{H{U}_{u_3},M{U}_{u_3},R{U}_{u_3}\}$. $HU$ is Heavy Usage; $MU$ is Medium usage; and $RU$ is Rare Usage. Therefore, $A_{u_3}=\{A_{u_3}^1,A_{u_3}^2,A_{u_3}^3\}$, where $A=\{RU,MU,HU\}$.

4.5. Transition Function Definition

In order to control the transitions between the system’s states, a set of fuzzy rules is required. From the state diagram shown in Figure 5, the required rules that can define the transitions between the system states are determined. The rules have the following structure:

$$\mathbf{IF}(S(t)\mathbf{is}{s}_1)\mathbf{AND}{H}_{12}\mathbf{THEN}S(t+1)\mathbf{is}{s}_2$$

$$\mathbf{IF}(S(t)\mathbf{is}{s}_2)\mathbf{AND}{H}_{23}\mathbf{THEN}S(t+1)\mathbf{is}{s}_3$$

$$\mathbf{IF}(S(t)\mathbf{is}{s}_3)\mathbf{AND}{H}_{34}\mathbf{THEN}S(t+1)\mathbf{is}{s}_4$$

$$\dots \dots \dots \dots \dots \dots \dots \dots \dots$$

$$\mathbf{IF}(S(t)\mathbf{is}{s}_5)\mathbf{AND}{H}_{57}\mathbf{THEN}S(t+1)\mathbf{is}{s}_7$$

It should be noted that there are limitations in the transition between states. For example, when the user is in the sleeping state $(S_1)$, the system can go to the bedroom state $S_2$. However, while the user is in the bedroom state $(S_2)$, the model only allows going to the toilet state $S_3$, kitchen state $S_4$, or leaving home state $S_8$. These limitations are enforced by the physical layout of the house shown in Figure 3. The state transitions are governed by the fuzzy rules, which are generated by means of NNs based on the data gathered from sensors.

4.6. Output Definition

For this specific system model, the output vector Y is the result of states’ activation or the membership degrees given to each state, i.e., $Y(t)=S(t)$.

4.7. Results

Based on the information provided in the previous section, an N-FFSM model was implemented to model the Activities of Daily Living (ADL) for a single user in a smart home environment. A sample of ADL data for five days is illustrated in Figure 7. A multilevel activity graph is illustrated in Figure 7a, and a scattered plot of the same data is shown in Figure 7b. This section presents the obtained results of the conducted experiments.

Datasets representing human activities are often imbalanced where some activities appear much more frequently than others. It is evident that if the dominant activity is recognised with a high level of performance, the overall level of accuracy is high, even if all other activities are not well recognised [39]. Therefore, we did a cross-validation for each activity over the whole model.

Table 2. Accuracy, recall, and precision for each activity obtained based on the proposed N-FFSM method.

Activities	Accuracy	Recall	Precision
(1) Sleeping	85.7	84.1	81.8
(2) Bedroom	93.9	93.3	96.8
(3) Toilet	87.5	86.4	100
(4) Kitchen	100	99.1	90.5
(5) Dining room	100	97.8	100
(6) Living room	100	98.3	100
(7) Garden	100	90.9	100
(8) Leaving home	100	95.2	100

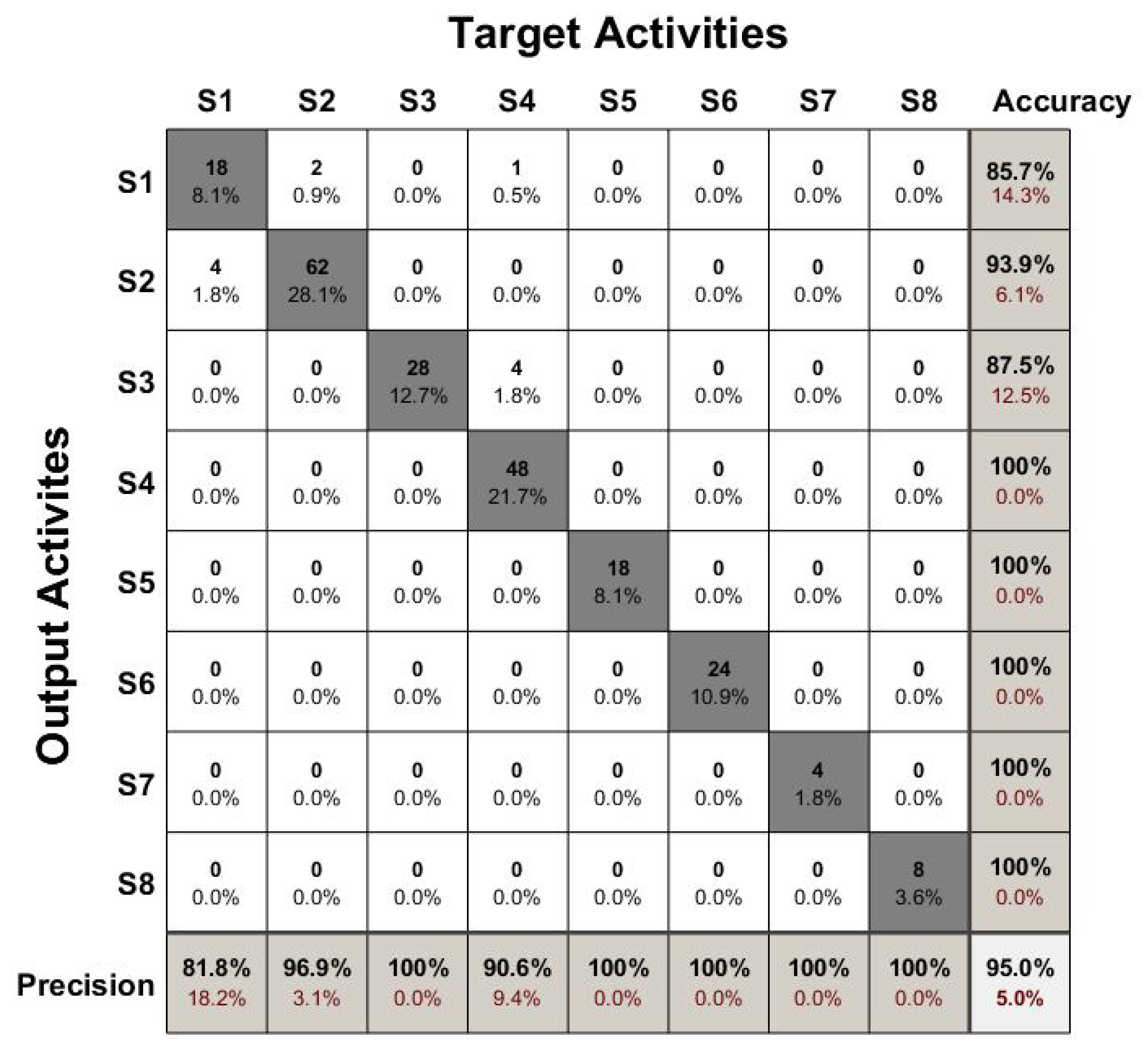
shows the recall (known as sensitivity), precision, and accuracy obtained by using the N-FFSM model for each activity. Moreover, a confusion matrix plot representing the precision and accuracy scores over the whole model, as well as for each activity is illustrated in Figure 8. The information given in the confusion matrix is explained as follows:

• The rows and columns represent the output activities and target activities, respectively. The activities are identified as $s_1,s2,\dots ,s_8$.
• The diagonal cells from the upper left to the lower right indicate activities that are correctly recognised.
• The off-diagonal cells represent the incorrectly-recognised activities.
• The right-most column shows the accuracy of each activity.
• The last row at the bottom shows the precision for each activity.
• The bottom right cell represents the accuracy over the whole model.

The expressions that were used to calculate accuracy, precision, and recall are given below:

$$Accuracy=\frac{1}{N}\sum _{i=1}^{C}t{p}_i$$

(5)

$$Precision=\frac{1}{C}\sum _{i=1}^C\frac{t{p}_i}{t{p}_i+f{p}_i}$$

(6)

$$Recall=\frac{1}{C}\sum _{i=1}^C\frac{t{p}_i}{t{p}_i+f{n}_i}$$

(7)

where N is the total number of events $N=t{p}_i+t{n}_i+f{p}_i+f{n}_i$ for $i^{\mathrm{th}}$ activity in the source data. $t{p}_i$, $t{n}_i$, $f{n}_i$, and $f{p}_i$ are the number of true positives, true negative, false negatives, and false positives of the $i^{\mathrm{th}}$ activity, respectively. C is the number of activities for which their accuracy, recall, and precision are calculated. For this study, $t{p}_i,t{n}_i,f{p}_i$ and $f{n}_i$ were defined as follows:

-

True positive $(t{p}_i)$: the case when $i^{\mathrm{th}}$ activity is correctly recognised as being the $i^{\mathrm{th}}$ activity.

-

True negative $(t{n}_i)$: the case when all the other activities are correctly recognised as being not the $i^{\mathrm{th}}$ activity.

-

False positive $(f{p}_i)$: the case when all the other activities are incorrectly recognised as being the $i^{\mathrm{th}}$ activity.

-

False negative $(f{n}_i)$: the case when the $i^{\mathrm{th}}$ activity is incorrectly recognised as being not the $i^{\mathrm{th}}$ activity.

4.8. Comparison with Existing Modelling Techniques

In order to evaluate the proposed method, we compared the performance of the proposed N-FFSM with some existing methodologies. The dataset mentioned earlier was applied to a classical FFSM and standard NNs, and the results were compared with the proposed N-FFSM. The FFSM contained eight states representing the same eight activities mentioned earlier. The state transitions were controlled by fuzzy rules that were generated based on the experts’ knowledge only. Accuracy, recall, and precision of models based on FFSM and NNs are shown in

Table 3. Accuracy, recall, and precision for each activity obtained based on FFSM.

Activities	Accuracy	Recall	Precision
(1) Sleeping	38.4	37.8	100
(2) Bedroom	24.2	24.0	66.6
(3) Toilet	75	74.0	31.5
(4) Kitchen	40.7	40.4	27.5
(5) Dining room	100	98.9	81.8
(6) Living room	0	0	NaN
(7) Garden	100	83.3	100
(8) Leaving home	0	0	NaN

and

Table 4. Accuracy, recall, and precision for each activity obtained based on NNs.

Activities	Accuracy	Recall	Precision
(1) Sleeping	100	98.4	76.4
(2) Bedroom	89.1	88.7	100
(3) Toilet	93.7	92.5	93.7
(4) Kitchen	85.7	85.1	88.8
(5) Dining room	70	69.3	77.7
(6) Living room	100	95.2	66.6
(7) Garden	NaN	0	0
(8) Leaving home	100	95.2	100

respectively.

5. Discussion

Considering the results obtained from our experiments, this section discusses three different aspects related to the proposed model: i.e., accuracy, interpretability, and the importance of using experts’ knowledge.

• Accuracy: The results illustrated in Table 2 show that the N-FFSM model exhibited a high accuracy, recall, and precision when its performance was tested for each activity separately. The results presented in

  Table 5. Overall accuracy, recall, and precision obtained based on the N-FFSM, FFSM, and NN methods.

  Activities	Accuracy	Recall	Precision
  N-FFSM (proposed)	95.2%	93.18%	96.16%
  NNs model	78.72%	78.81%	75.44%
  FFSM model	46.61%	44.84%	NaN

  show the overall activity recognition performance when it was compared with the existing FFSM and NNs in terms of accuracy, recall, and precision. According to the achieved results, the N-FFSM model was considerably better at ADL recognition based on data gathered from low-level ambient sensors. Furthermore, it can be seen how the N-FFSM model was able to follow the proper sequence of states with the correct state activation degree.
• Interpretability discussion: From the interpretability point of view, the most commonly-used approaches in human activity recognition research works have been NNs and HMMs. These models are considered as black-box approaches because of the complexity of understanding their underlying concepts. This complexity increases when a large number of input and output variables are used. Nevertheless, the proposed N-FFSM model is described linguistically using eight linguistic states representing eight different activities, as well as fuzzy rules associated with the linguistic inputs.
• The importance of using human experts’ knowledge: In order to achieve a robust model for representing human activities, the advantages of using experts’ knowledge with the learning capabilities in NNs can be integrated with the N-FFSM model. Designing an FFSM only based on the linguistic information assigned by human experts is not enough for a successful human activity recognition model. On the other hand, information derived from the gathered sensor data is not usually enough to achieve a high-performance model. Experts’ knowledge was used to define the fuzzy rules, as well as distinguishing the system’s current state(s). This allowed obtaining a linguistic description of the ADL, i.e., the final set of fuzzy rules that control the transition between states.

6. Conclusions

This paper has presented a practical application of utilising FFSM to model and recognise human activities using NNs and human experts’ knowledge. The principal elements of the FFSM were explained in detail, as well as the developed NN learning technique for generating the fuzzy rules and MFs associated with the linguistic labels in the inputs and outputs of the FFSM. Experts’ knowledge can still be used to define the system’s states and the general structure of the state transitions. Experimental results were presented to demonstrate the effectiveness of the proposed method. The advantage of the proposed system is that it integrates the experts’ knowledge with the information derived from the automatic learning process. The results obtained from the proposed N-FFSM model show that human activities could be modelled/learned with a high degree of accuracy based on the data gathered from low-level sensors.