High Throughput Implementation of the Keccak Hash Function Using the Nios-II Processor †
Abstract
:1. Introduction
- We designed the Keccak core solution for all the output lengths of the algorithm (224, 256, 384, and 512).
- We researched on the optimization strategy for the throughput and efficiency of all output lengths of the Keccak algorithm (SHA-3).
- We performed extensive analysis and compared the throughput and efficiency of our proposed method with other similar methods.
- For the first time, to the best of our knowledge, we provide extensive estimation of performance and power analysis for all the output lengths for the SHA-3 algorithm.
2. Related Work
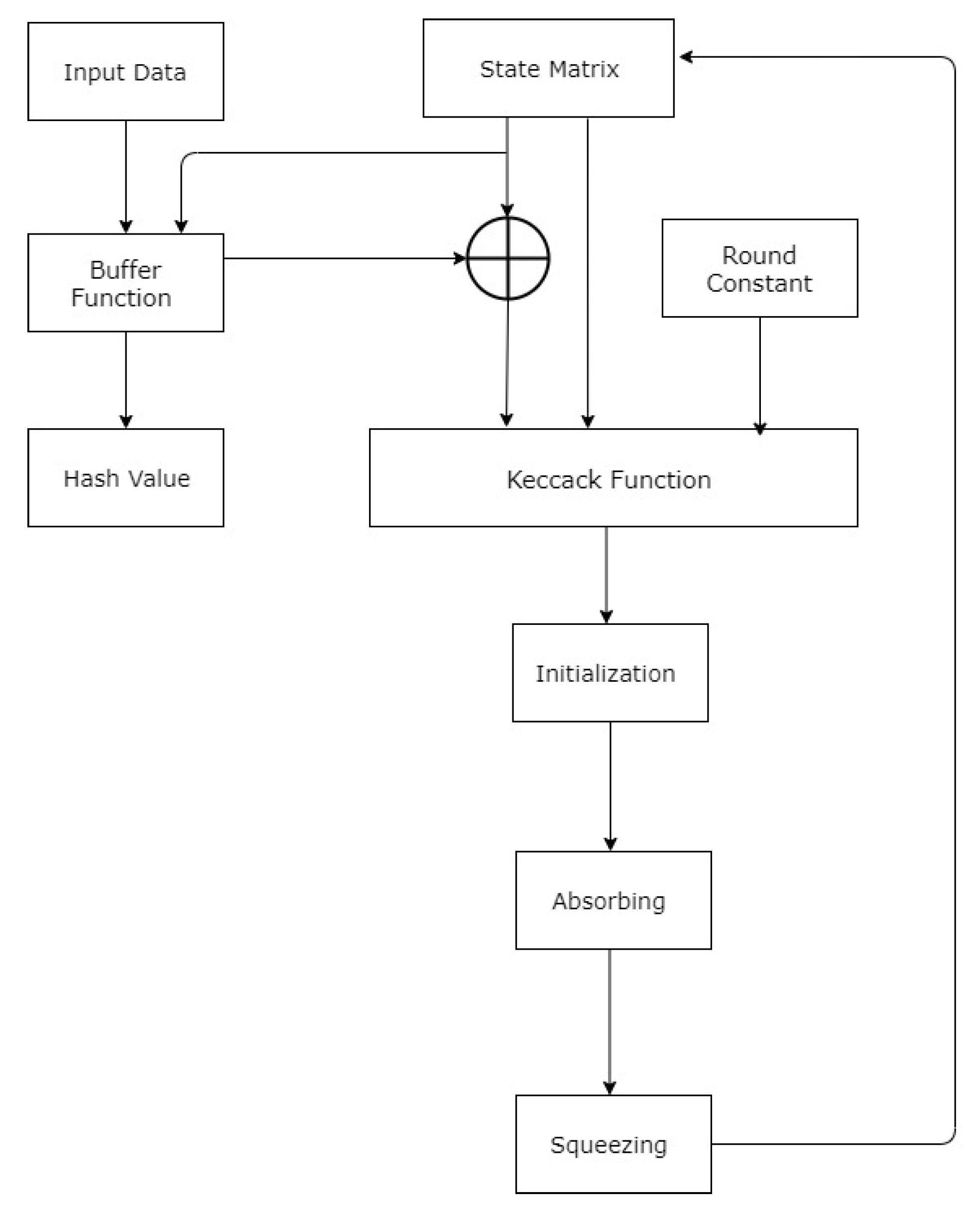
3. Keccak Hash Function
4. Implementation
4.1. Nios II Embedded Processor
4.2. Floating Point Hardware 2
4.3. System Integration
- S1 for instance choice
- S2 for main computing
- S3 for hash computing
- S4 for rounds
- S5 for last round
5. Experimental Results
5.1. Synthesis Report
5.2. Throughput and Efficiency Results
5.3. Power Analysis EPE
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SHA | Secure Hash Algorithm |
| NIST | National Institute of Standards and Technology |
| VHDL | Very High Speed Integrated Circuit Hardware Description Language |
| FPGA | Field-Programmable Gate Array |
| FPH | Floating Point Hardware |
| Gbps | Gigabits per second |
| HMAC | Hashed Message Authentication Code |
| SET | Secure Electronic Transactions |
| PKI | Public Key Infrastructure |
| IP | Intellectual Property |
| DSP | Digital Signal Processing |
| LUTs | lookup tables |
| GPU | Graphics Processing Unit |
| Mbps | Megabits per second |
| GB | Gigabytes |
| RC | Round Constant |
| CPU | Central Processing Unit |
| ASIC | Application-Specific Integrated Circuit |
| GHz | Gigahertz |
| DDR4 | Double Data Rate 4 |
| SDRAM | Synchronous Dynamic Random-Access Memory |
| SO-DIMM | Small Outline Dual In-line Memory Module |
| MHz | Megahertz |
| FSM | Finite-State Machine |
| PIO | Parallel Input Output |
| JTAG | Joint Test Action Group |
| UART | Universal Asynchronous Receiver Transmitter |
| PLL | Phase Locked Loop |
| USB | Universal Serial Bus |
| ALM | Adaptive Logic Module |
| C | Celsius |
| W | Watt |
| EPE | Early Power Estimators |
References
- Turner, J.M. The keyed-hash message authentication code (HMAC). In Federal Information Processing Standards Publication; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008; pp. 191–198. [Google Scholar]
- Dang, Q. Recommendation for Applications Using Approved Hash Algorithms; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008. [Google Scholar]
- Jarupunphol, P.; Buathong, W. Secure Electronic Transactions (SET): A case of secure system project failures. Int. J. Eng. Technol. 2013, 5, 278. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, D.R.; Hu, V.C.; Polk, W.T.; Chang, S.J. Introduction to Public Key Technology and the Federal PKI Infrastructure; Technical Report for National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Loshin, P. IPv6: Theory, Protocol, and Practice; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Thomas, S. SSL and TLS Essentials; Wiley: Hoboken, NJ, USA, 2000; p. 3. [Google Scholar]
- Wang, X.; Yin, Y.L.; Yu, H. Finding Collisions in the Full SHA-1; Springer: Berlin/Heidelberger, Germany, 2005; pp. 17–36. [Google Scholar]
- Radack, S. Secure Hash Standard: Updated Specifications Approved and Issued as Federal Information Processing Standard (FIPS) 180-4; Technical Report for National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012. [Google Scholar]
- Dworkin, M.J. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; Technical Report for National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Sideris, A.; Sanida, T.; Dasygenis, M. Hardware Acceleration of SHA-256 Algorithm Using NIOS-II Processor. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 1–4. [Google Scholar]
- Kitsos, P.; Sklavos, N. On the hardware implementation efficiency of SHA-3 candidates. In Proceedings of the 2010 17th IEEE International Conference on Electronics, Circuits and Systems, Athens, Greece, 12–15 December 2010; pp. 1240–1243. [Google Scholar]
- Mestiri, H.; Kahri, F.; Bedoui, M.; Bouallegue, B.; Machhout, M. High throughput pipelined hardware implementation of the KECCAK hash function. In Proceedings of the 2016 International Symposium on Signal, Image, Video and Communications (ISIVC), Tunis, Tunisia, 21–23 November 2016; pp. 282–286. [Google Scholar]
- Baldwin, B.; Byrne, A.; Lu, L.; Hamilton, M.; Hanley, N.; O’Neill, M.; Marnane, W.P. FPGA implementations of the round two SHA-3 candidates. In Proceedings of the 2010 International Conference on Field Programmable Logic and Applications, Milano, Italy, 31 August–2 September 2010; pp. 400–407. [Google Scholar]
- Akin, A.; Aysu, A.; Ulusel, O.C.; Savaş, E. Efficient hardware implementations of high throughput SHA-3 candidates keccak, luffa and black midnight wish for single-and multi-message hashing. In Proceedings of the 3rd International Conference on Security of Information and Networks, Rostov-on-Don, Russia, 7–11 September 2010; pp. 168–177. [Google Scholar]
- Kerckhof, S.; Durvaux, F.; Veyrat-Charvillon, N.; Regazzoni, F.; de Dormale, G.M.; Standaert, F.X. Compact FPGA implementations of the five SHA-3 finalists. In Proceedings of the International Conference on Smart Card Research and Advanced Applications, Athens, Greece, 12–15 December 2010; pp. 217–233. [Google Scholar]
- Jararweh, Y.; Tawalbeh, H.; Moh’d, A. Hardware performance evaluation of SHA-3 candidate algorithms. J. Inf. Secur. 2012, 3. [Google Scholar] [CrossRef] [Green Version]
- Provelengios, G.; Kitsos, P.; Sklavos, N.; Koulamas, C. FPGA-based design approaches of keccak hash function. In Proceedings of the 2012 15th Euromicro Conference on Digital System Design, Izmir, Turkey, 5–8 September 2012; pp. 648–653. [Google Scholar]
- Jungk, B. Evaluation of compact FPGA implementations for all SHA-3 finalists. In Proceedings of the Third SHA-3 Candidate Conference, Washington, DC, USA, 22–23 March 2012. [Google Scholar]
- Pereira, F.D.; Ordonez, E.D.M.; Sakai, I.D.; de Souza, A.M. Exploiting Parallelism on Keccak: FPGA and GPU comparison. Parallel Cloud Comput. 2013, 2, 1–6. [Google Scholar]
- Bertoni, G.; Daemen, J.; Peeters, M.; Van Assche, G. Cryptographic Sponges Functions. Available online: http://sponge.noekeon.org/CSF-0.1.pdf (accessed on 5 February 2020).
- Bertoni, G.; Daemen, J.; Peeters, M.; Assche, G. The keccak reference. Submiss. NIST Round 3 2011, 13, 14–15. [Google Scholar]
- Intel®FPGA. Nios® II Processors for FPGAs. Available online: https://www.intel.com/content/www/us/en/products/programmable/processor/nios-ii.html (accessed on 5 February 2020).
- Intel®FPGA. Overview of the Floating Point Hardware 2 Component. Available online: https://www.intel.com/content/www/us/en/programmable/documentation/cru1439932898327.html#shd1506201174145 (accessed on 5 February 2020).
- Terasic. All FPGA Main Boards-Arria 10-DE5a-Net-DDR4. Available online: https://www.terasic.com.tw/cgi-bin/page/archive.pl?Language=English&No=1108 (accessed on 5 February 2020).
- CSDITL-NIST. Example Values—Cryptographic Standards and Guidelines. Available online: https://csrc.nist.gov/projects/cryptographic-standards-and-guidelines/example-values (accessed on 5 February 2020).
- Intel®FPGA. Early Power Estimator for Intel® Arria® 10 FPGAs User Guide. Available online: https://www.intel.com/content/dam/www/programmable/us/en/pdfs/literature/ug/ug-01164.pdf (accessed on 5 February 2020).






| RC[0] | 0x0000000000000001 | RC[8] | 0x000000000000008A | RC[16] | 0x8000000000008002 |
| RC[1] | 0x0000000000008082 | RC[9] | 0x0000000000000088 | RC[17] | 0x8000000000000080 |
| RC[2] | 0x800000000000808A | RC[10] | 0x0000000080008009 | RC[18] | 0x000000000000800A |
| RC[3] | 0x8000000080008000 | RC[11] | 0x000000008000000A | RC[19] | 0x800000008000000A |
| RC[4] | 0x000000000000808B | RC[12] | 0x000000008000808B | RC[20] | 0x8000000080008081 |
| RC[5] | 0x0000000080000001 | RC[13] | 0x800000000000008B | RC[21] | 0x8000000000008080 |
| RC[6] | 0x8000000080008081 | RC[14] | 0x8000000000008089 | RC[22] | 0x0000000080000001 |
| RC[7] | 0x8000000000008009 | RC[15] | 0x8000000000008003 | RC[23] | 0x8000000080008008 |
| Instance | Output Size d | Rate r-Block Size | Capacity c |
|---|---|---|---|
| SHA3-224(M) | 224 | 1152 | 448 |
| SHA3-256(M) | 256 | 1088 | 512 |
| SHA3-384(M) | 384 | 832 | 768 |
| SHA3-512(M) | 512 | 576 | 1024 |
| Floating Point Hardware 2 Component (altera_nios_custom_instr_floating_point_2) | |
|---|---|
| Combinatorial Custom Instruction (altera_nios_custom_instr_floating_point_2_combi) | Multi-Cycle Custom Instruction (altera_nios_custom_instr_floating_point_2_multi) |
| minimum maximum compare negate absolute | add subtract multiply divide square root convert |
| Parameters | Values |
|---|---|
| Family | Intel Arria® 10 GX FPGA |
| Device | 10AX115N2F45E1SG |
| Memory | 2 × 4 GB DDR4 SO-DIMM 2400 MHz SDRAM |
| System Clock Frequency | 50 MHz Oscillator |
| Items | Without Custom Instruction | With Floating Point Hardware 2 |
|---|---|---|
| Logic use (in ALMs) | 11,102/427,200 * (3%) | 12,020/427,200 * (4%) |
| Total registers | 24,519 | 24,568 |
| Total pins | 370/992 * (37%) | 372/992 * (38%) |
| Total block memory bits | 1,501,453/55,562,240 * (3%) | 1,504,301/55,562,240 * (3%) |
| Total DSP Blocks | 3/1518 * (<1%) | 7/1518 * (<1%) |
| Total PLLs | 7/112 * (6%) | 7/112 * (6%) |
| Design | Proposed Design without Custom Instruction | Proposed Design with FPH2 | |
|---|---|---|---|
| Area (Slices) | 2776 | 3005 | |
| Throughput (Gbps) | r = 1152 | 29.525 | 33.216 |
| r= 1088 | 27.885 | 31.370 | |
| r= 832 | 21.323 | 23.989 | |
| r= 576 | 14.762 | 16.608 | |
| Efficiency (Mbps/Slices) | r= 1152 | 10.63 | 11.05 |
| r= 1088 | 10.04 | 10.43 | |
| r= 832 | 7.68 | 7.98 | |
| r= 576 | 5.31 | 5.52 | |
| Design | FPGA | Frequency (MHz) | Area (Slices) | Throughput (Gbps) | |||
|---|---|---|---|---|---|---|---|
| r = 1152 | r = 1088 | r = 832 | r = 576 | ||||
| Kitsos P. et al. (2010) [11] | - | 215 | 4745 | - | 11.9 | - | - |
| Mestiri H. et al. (2016) [12] | Virtex-5 | 317.11 | 4793 | - | - | - | 12.68 |
| Jararweh Y. et al. (2012) [16] | Virtex-5 | 271 | 1414 | - | 12.28 | - | - |
| Provelengios G. et al. (2012) [17] | Virtex-5 | 285 | 2573 | - | - | - | 5.70 |
| Kerckhof S. et al. (2011) [15] | Virtex-6 | 285 | 188 | - | - | - | 0.077 |
| Jungk B. (2012) [18] | Virtex-6 | 197 | 397 | - | 1.071 | - | - |
| Baldwin B. et al. (2010) [13] | Virtex-5 | 189 | 1117 | 5.915 | 6.263 | 8.190 | 8.518 |
| Pereira F. et al. (2013) [19] | Virtex-5 | 452 | 3117 | - | - | - | 7.70 |
| Akin A. et al. (2010) [14] | Virtex-4 | 509 | 4356 | - | 22.33 | - | - |
| Proposed design with FPH2 | Arria 10 GX | 692 | 3005 | 33.216 | 31.370 | 23.989 | 16.608 |
| Design | FPGA | Frequency (MHz) | Area (Slices) | Efficiency (Mbps/Slices) | |||
|---|---|---|---|---|---|---|---|
| r = 1152 | r = 1088 | r = 832 | r = 576 | ||||
| Kitsos P. et al. (2010) [11] | - | 215 | 4745 | - | 2.50 | - | - |
| Mestiri H. et al. (2016) [12] | Virtex-5 | 317.11 | 4793 | - | - | - | 2.71 |
| Jararweh Y. et al. (2012) [16] | Virtex-5 | 271 | 1414 | - | 8.68 | - | - |
| Provelengios G. et al. (2012) [17] | Virtex-5 | 285 | 2573 | - | - | - | 2.21 |
| Kerckhof S. et al. (2011) [15] | Virtex-6 | 285 | 188 | - | - | - | 0.41 |
| Jungk B. (2012) [18] | Virtex-6 | 197 | 397 | - | 2.69 | - | - |
| Baldwin B. et al. (2010) [13] | Virtex-5 | 189 | 1117 | 3.00 | 3.17 | 4.15 | 4.32 |
| Pereira F. et al. (2013) [19] | Virtex-5 | 452 | 3117 | - | - | - | 2,47 |
| Akin A. et al. (2010) [14] | Virtex-4 | 509 | 4356 | - | 5.13 | - | - |
| Proposed design with FPH2 | Arria 10 GX | 692 | 3005 | 11.05 | 10.43 | 7.98 | 5.52 |
| Thermal Analysis | Thermal Power (W) | ||
|---|---|---|---|
| Junction Temp, TJ (°C) | 22.1 | HPS | 0.018 |
| Maximum Allowed TA (°C) | 95.8 | PSTATIC | 0.766 |
| TOTAL (W) | 0.784 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sideris, A.; Sanida, T.; Dasygenis, M. High Throughput Implementation of the Keccak Hash Function Using the Nios-II Processor. Technologies 2020, 8, 15. https://doi.org/10.3390/technologies8010015
Sideris A, Sanida T, Dasygenis M. High Throughput Implementation of the Keccak Hash Function Using the Nios-II Processor. Technologies. 2020; 8(1):15. https://doi.org/10.3390/technologies8010015
Chicago/Turabian StyleSideris, Argyrios, Theodora Sanida, and Minas Dasygenis. 2020. "High Throughput Implementation of the Keccak Hash Function Using the Nios-II Processor" Technologies 8, no. 1: 15. https://doi.org/10.3390/technologies8010015
APA StyleSideris, A., Sanida, T., & Dasygenis, M. (2020). High Throughput Implementation of the Keccak Hash Function Using the Nios-II Processor. Technologies, 8(1), 15. https://doi.org/10.3390/technologies8010015







