1. Introduction
Deep neural networks (DNN) have emerged as a means to tackle complex problems such as image classification and speech recognition. The success of DNNs is attributed to the big data availability, the easy access to enormous computational power and the introduction of novel algorithms that have substantially improved the effectiveness of the training and inference [
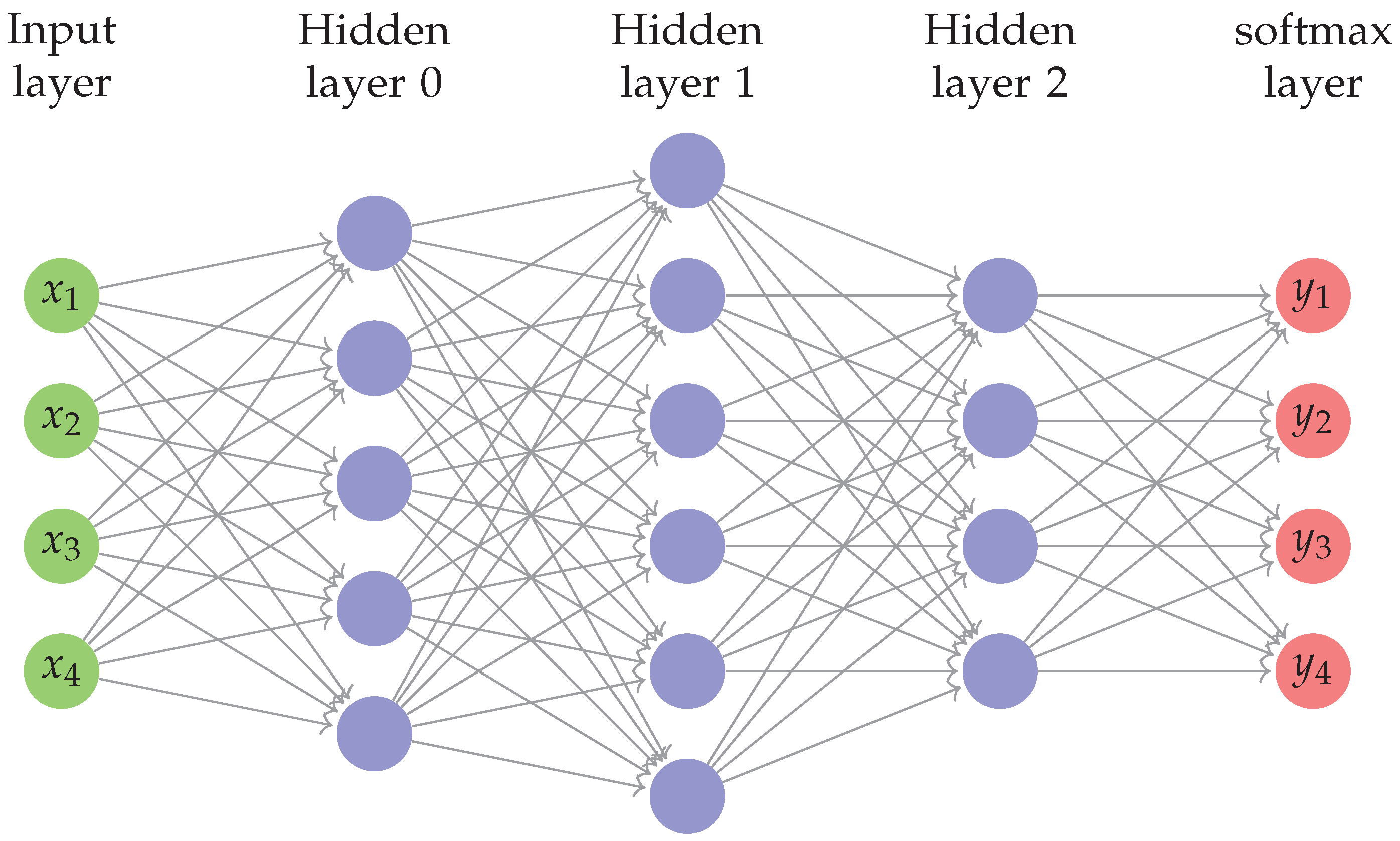
1]. A DNN is defined as a neural network (NN) which contains more than one hidden layer. In the literature, a graph is used to represent a DNN, with a set of nodes in each layer, as shown in
Figure 1. The nodes at each layer are connected to the nodes of the subsequent layer. Each node performs processing including the computation of an activation function [
2]. The extremely large number of nodes at each layer impels the training procedure to require extensive computational resources.
A class of DNNs are the convolutional neural networks (CNNs) [
2]. CNNs offer high accuracy in computer-vision problems such as face recognition and video processing [
3] and have been adopted in many modern applications. A typical CNN consists of several layers, each one of which can be convolutional, pooling, or normalization with the last one to be a non-linear activation function. A common choice for normalization layers is usually the softmax function as shown in
Figure 1. To cope with increased computational load, several FPGA accelerators have been proposed and have demonstrated that convolutional layers exhibit the largest hardware complexity in a CNN [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]. In addition to CNNs, hardware accelerators for RNNs and LSTMs have also been investigated [
16,
17,
18]. In order to implement a CNN in hardware, the softmax layer should also be implemented with low complexity. Furthermore, the hidden layers of a DNN can use the softmax function when the model is designed to choose one among several different options for some internal variable [
2]. In particular, neural turing machines (NTM) [
19] and differentiable neural computer (DNC) [
20] use softmax layers within the neural network. Moreover, softmax is incorporated in attention mechanisms, an application of which is machine translation [
21]. Furthermore, both hardware [
22,
23,
24,
25,
26,
27,
28] and memory-optimized software [
29,
30] implementations of the softmax function have been proposed. This paper, extending previous work published in MOCAST2019 [
31], proposes a simplified architecture for a softmax-like function, the hardware implementation of which is based on a proposed approximation which exploits the statistical structure of the vectors processed by the softmax layers in various CNNs. Compared to the previous work [
31], this paper uses a large set of known CNNs, and performs extensive and fair experiments to study the impact of the applied optimizations in terms of the achieved accuracy. Moreover the architecture in [
31] is further elaborated and generalized by taking into account the requirements of the targeted application. Finally, the proposed architecture is compared with various softmax hardware implementations. In order for the softmax-like function to be implemented efficiently in hardware, the approximation requirements are relaxed.
The remainder of the paper is organized as follows.
Section 2 revisits the softmax activation function.
Section 3 describes the proposed algorithm and
Section 4 offers a quantitative analysis of the proposed architecture.
Section 5 discusses the hardware complexity of the proposed scheme based on synthesis results. Finally, conclusions are summarized in
Section 6.
3. Proposed Softmax Architecture
Equation (
15) involves the distance of the maximum component from the remainder of the components of a vector. As
, the differences in
s increase and
. On the contrary, as
the differences in
s are eliminated. Based on this observation, a simplifying approximation can be obtained, as follows. The third term in the right hand side of (
16),
, can be roughly approximated by 0. Hence, (
16) is approximated by
Furthermore, this simplification substantially reduces hardware complexity as described below. From (
17), it follows that
Theorem 1. Let and be the decisions obtained by (1) and (18), respectively. Then . Proof. Due to the softmax definition, it holds that
For the case of the proposed function (
18), it holds that
From (
20) and (
22), it is derived that
. Hence,
. □
Corollary 1. It holds that
Proof. Proof is trivial and is omitted. □
Theorem 1 states that the proposed softmax-like function and the actual softmax function always derive the same decisions. The proposed softmax-like approximation is based on the idea that the softmax function is used during training to target an output
by using maximum-log likelihood [
2]. Hence, if the correct answer has already the maximum input value to the softmax function then
will roughly alter the output decision due to the exponent function used in term
. In general,
, since the sequence
cannot be denoted as a probability density function. For models where the normalization function is required to be a pdf, a modified approach can be followed, as detailed below.
According to the second approach, from (
11) and (
12) it follows:
with
, where
are chosen to be the top
maximum values of
. For the quantity
, it holds
, with
being the remainder values of the vector
, i.e.,
.
A second approximation is performed as
From (
26)–(
28), it derives that
Equation (
30) uses parameter
which defines the number of additional terms used. By properly selecting
, then it holds that
and (
30) approximates pdf better than (
18). This is derived from the fact that in a real life CNN, the
maximum values are those that contribute to the computation of the softmax since all the remainder values are close to zero.
Lemma 1. It holds when
Proof. By definition, it holds that when
then
, since the
maximum value
is identified as the maximum
. Hence, by substituting
in (
30), it derives that
□
From a hardware perspective, (
18) and (
30) can be performed by the same circuit which implements the exponential function. The contributions of the paper are as follows. Firstly, the quantity
is eliminated from (
16), implying that the target application requires decision making. Secondly, further mathematical manipulations are proposed to be applied to (
30), in order to approximate the outputs as pdf i.e., probabilities that sum to one. Thirdly, the circuit for the evaluation of
is simplified, since
and
Figure 2 depicts the various building blocks of the proposed architecture. More specifically, the proposed architecture is comprised of the block which computes the maximum
, i.e.,
. The particular computation is performed by a tree which generates the maximum by comparing the elements by two, as shown in
Figure 3. The depicted tree structure generates
,
. Notation
denotes the maximum of
and
, while
denotes the maximum of
and
. The same architecture is used to compute the top
maximum values of
s. For example,
,
,
and
are the top four maximum values and
is the maximum.
Subsequently,
is subtracted from all the component values
as dictated by (
17). The subtraction is performed through adders, denoted as
in
Figure 2, using two’s complement representation for the input negative values
. The obtained differences, also represented in two’s complement, are used as inputs to a LUT, which performs the proposed simplified
operation of (
18), to compute the final vector
as shown in
Figure 2a. Additional
terms are added and subsequently each output
through (
30) generates the final value for the softmax-like layer output as shown in
Figure 2b. For the hardware implementation of the
function, an LUT is adopted the input of which is
. The LUT size increases on the larger range of
. Our proposed hardware implementation is simpler than other exponential implementations which propose CORDIC transformations [
32], use floating-point representation [
33], or LUTs [
34]. In (
33), the
values are restricted to the range
and the derived LUT size significantly diminishes and leads to simplified hardware implementation. Furthermore, no conversion from the logarithmic to the linear domain is required, since
represents the final classification layer.
The next section quantitatively investigates the validity and usefulness of employing , in terms of the approximation error.
4. Quantitative Analysis of Introduced Error
This section quantitatively verifies the applicability of the approximation introduced in
Section 2, for certain applications, by means of a series of Examples.
In order to quantify the error introduced by the proposed architecture, the mean square error (MSE) is evaluated as
where
and
are the expected and the actually evaluated softmax output, respectively.
As an illustrative example, denoted as Example 1,
Figure 4 depicts the histograms of component values in test vectors used as inputs to the proposed architecture, selected to have specific properties detailed below. The corresponding parameters are evaluated by using the proposed architecture for the case of a 10-bit fixed-point representation, where 5 bits are used for the integer and 5 bits are allocated to the fractional part. More specifically, the vector in
Figure 4a contains
values, for which it holds that
,
and
. For this case the softmax values obtained by (
1) are
From a CNN perspective, the softmax layer output generates similar values, where possibilities are all around 3%, and hence classification or decision cannot be made with high confidence. By using (
18), the modified softmax values are
The statistical structure of the vector is characterized by the quantity
of (
15). The estimated
dictates that the particular vector is not suitable as an alternative to softmax input in terms of CNN performance, i.e., the obtained classification is performed with low confidence. Hence although the proposed approximation in (
18) demonstrates large differences when compared to (
1), neither is applicable in CNN terms.
Consider the following Example 2. The component values for vector
in Example 2 are
the histogram of which is shown in
Figure 4b. In this case, the statistical structure of the vector demonstrates
and
. The feature of vector
in Example 2 is that it contains three large different component values close to each other, namely
and all other components are smaller than 1. The softmax output in (
1) for the values in the particular
are
By using the proposed approximation (
18), the obtained modified softmax values are
Equations (
41) and (
42) show that the proposed architecture chooses component
with value 1 while the actual probability is 0.7675. This means that the introduced error of
can be negligible depending on the application, dictated by
.
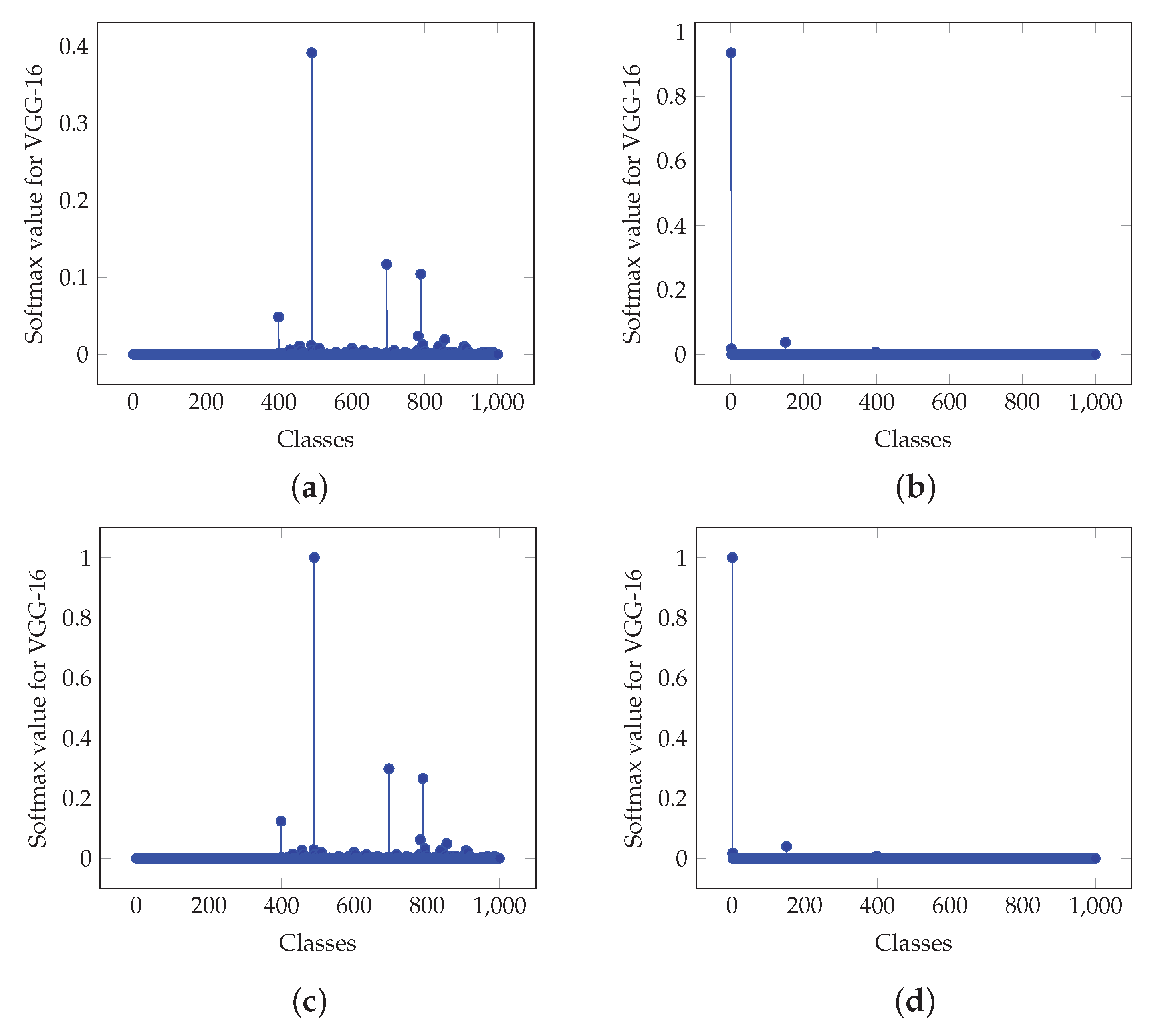
In the following, tests using vectors obtained from real CNN applications are considered. More specifically, in an example shown in
Figure 5, the vectors are obtained from image and digit classification applications. In particular,
Figure 5a,b depict the values used as input to the final softmax layer, generated during a single inference for a VGG-16 imagenet image classification network for 1000 classes and a custom net for MNIST digit classification for 10 classes. Quantity
can be used to determine whether the proposed architecture is appropriate for application on vector
before evaluating the MSE. It is noted that
for the example of
Figure 5a and
for the example of
Figure 5b are of the orders of
and
, respectively which renders them as negligible.
Subsequently, the proposed method is applied on the ResNet-50 [
35], VGG-16, VGG-19 [
36], InceptionV3 [
37] and MobileNetV2 [
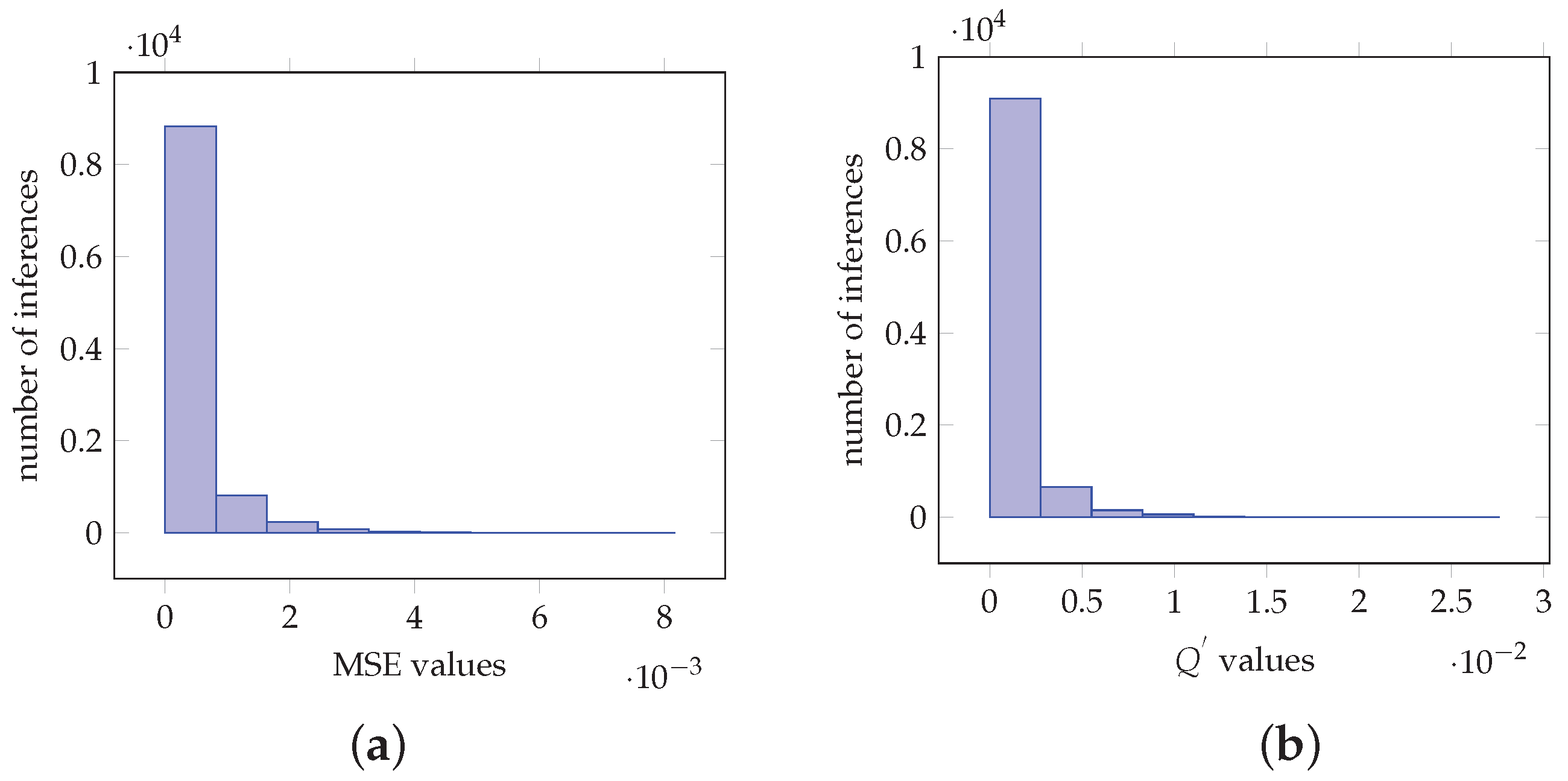
38] CNNs, for 1000 classes with 10000 inferences of a custom image data set. In particular, for the case of ResNet-50,
Figure 6a,b depict the histograms of the MSE and
values, respectively. More specifically,
Figure 6a demonstrates that the MSE values are of magnitude
with 8828 of the values be in the interval
. Furthermore,
Figure 6b shows that the
values are of magnitude
with 9096 of them be in the interval
. Furthermore,
Table 1a–e depict actual softmax and the proposed method softmax-like values obtained by executing inference on the CNN models for six custom images. The values are sorted from left to right with the maximum value on the left side. Furthermore, the inferences
and
denote the same custom image as input to the model. More specifically,
Table 1a demonstrates values from six inferences for the ResNet-50 model. It is shown that for the case of inference
the maximum obtained values are
and
, for
and
, respectively. Other values are
,
,
,
and
,
,
,
, respectively. Hence, as shown by colorally 1, the maximum takes the value ‘1’ and the remainder of the values follow the values obtained by the actual softmax function. Similar analysis can be obtained for all the inferences
and
for each one of the CNNs. Furthermore, the same class is outputted from the CNN in both cases for each inference.
For the case of VGG-16,
Figure 7a depicts the histogram of the MSE values. It is shown that the values are of magnitude
and 8616 are in the interval
.
Figure 7b demonstrates histogram for the
values with magnitude of
and more than 8978 values are in the interval
.
Table 1b demonstrates that in the case of the
and
inference the top values are 0.51182884 and 1, respectively. The second top values are 0.18920843 and 0.369140625, respectively. In this case, the decision is made with a confidence of 0.51182884 for the actual softmax value and 1 for the softmax-like value. Furthermore, the second top value is 0.369140625 which is not negligible when compared to 1 and hence denotes that the selected class is of low confidence. The same conclusion derives for the case of the actual softmax value. Furthermore, for the case of
and
inferences, the values obtained by
Figure 8b are close to the actual pdf softmax outputs. In particular, for the
and
cases, the top 5 values are 0.747070313, 0.10941570, 0.065981410, 0.018329350, 0.012467328 and 0.747070313, 0.110351563, 0.06640625, 0.017578125, 0.01171875, respectively. It is shown that values are similar. Hence, depending the application, an alternative architecture, as shown in
Figure 2b can be used to generate pdf softmax values as outputs.
Moreover,
Figure 8a,b depict graphically the values for the actual softmax and the proposed softmax-like output for inferences A and B, respectively, for the case of the VGG-16 CNN for the output classification. Furthermore,
Figure 8c–f depict values for the architectures in
Figure 2a,b, respectively. It is shown that in the case of
Figure 2a, the values demonstrate a similar structure. In case of
Figure 2b, values are similar to the actual softmax outputs.
Similar analysis can be performed for the case of VGG-19. In particular,
Figure 9a demonstrates that MSE is of magnitude
and 8351 of which are in the interval
. In
Figure 9b 8380 values are in the interval
. For the case of InceptionV3, histograms in
Figure 10a,b demonstrate MSE and
values the 9194 and 9463 of which are in the intervals
and
, respectively. For the MobileNetV2 network,
Figure 11a,b demonstrate MSE and
values the 8990 and 9103 of which are in the intervals
and
, respectively. Furthermore,
Table 1c–e derive similar conclusions as in the case of VGG-16.
In general, in all cases identical output decisions are obtained for the actual softmax and the softmax-like output layer for each one of the CNNs.
Considering the impact of the data wordlegth representation, let
denote the fixed-point representation of a number with
integral and
fractional bits.
Figure 12a,b depict histograms for the MSE values obtained for the case of 1000 inferences by the VGG-16 CNN. It is shown that the case
demonstrates the smaller MSE values. The reason for this is that the maximum value of the inputs in the softmax layer is 56 for all the 1000 inferences, and hence the value of 6 for the integral part is sufficient.
Summarizing, it is shown that the proposed architecture suits well for the final stage of a CNN network as an alternative to implementing the softmax layer stage, since the MSE is negligible. Next, the proposed architecture is implemented in hardware and compared with published counterparts.
5. Hardware Implementation Results
This section describes implementation results obtained by synthesizing the proposed architecture outlined in
Figure 2. Among several authors reporting results on CNN accelerators, [
22,
23,
24] have recently published works focusing on hardware implementation of the softmax function. In particular, in [
23], a study based on stochastic computation is presented. Geng et al. provide a framework for the design and optimization of softmax implementation in hardware [
26]. They also discuss operand bit-width minimization, taking into account application accuracy constraints. Du et al. propose a hardware architecture that derives the softmax function without a divider [
25]. The appproach relies on an equivalent softmax expression which requires natural logarithms and exponentials. They provide detailed evaluation of the impact of the particular implementation on several benchmarks. Li et al. describe a 16-bit fixed-point hardware implementation of the softmax function [
27]. They use a combination of look-up tables and multi-segment linear approximations for the approximation of exponentials and a radix-4 Booth–Wallace-based 6-stage pipeline multiplier and modified shift-compare divider.
In [
24], the architecture demonstrates LUT-based computations that add complexity and exhibits 444,858
m
area complexity by using 65-nm standard-cell library. For the same library the architecture in [
25] reports 640,000
m
area complexity with 0.8
w power consumption at a 500 MHz clock frequency. The architecture in [
28] reports 104,526
m
area complexity with 4.24
w power consumption at a 1 GHz clock frequency. The proposed architecture in [
26] demonstrates power consumption and area complexity of 1.8
w and 3000
m
, respectively at a 500 MHz clock frequency with UMC 65 nm standard cell library. In [
27], it is reported 3.3 GHz and 34,348
m
frequency and area complexity at 45 nm technology node. Yuan [
22] presented an architecture for implementing the softmax layer. Nevertheless there is no discussion of the implementation of the LUTs and there are no synthesis results. Our proposed softmax-like function differs from the actual softmax function due to the approximation of the quantity
, as discussed in
Section 3. In particular, (
18) approximates the softmax output as a decision making application and not as a pdf function. The proposed softmax-like function in (30) approximates outputs as pdf function, depending on the number of
terms used. As
, (30)
actual softmax function. The hardware complexity reduction derives from the fact that a limited number,
, of
s contribute to the computation of the softmax function. Summarizing, we compare both architectures depicted in
Figure 2a,b with [
22] to quantify the impact of
on the hardware complexity.
Section 4 shows that the softmax-like function suits well in a CNN. For a fair comparison we have implemented and synthesized both architectures, our proposed and [
22], by using a 90 nm 1.0 V CMOS standard-cell library with Synopsys Design Compiler [
39].
Figure 13 depicts the architecture obtained from synthesis where the various building blocks, namely maximum evaluation, subtractor and the simplified exponential LUTs that perform in parallel, are shown. Furthermore registers have been added at the circuits inputs and outputs for applying the delay constraints. Detailed results are depicted in
Table 2a–c for the proposed softmax-like of
Figure 2a, the [
22] and the proposed softmax-like of
Figure 2b layer with size 10, respectively. Furthermore, results are plotted graphically in
Figure 14a,b where area vs. delay and power vs. delay are depicted, respectively. Results demonstrate that substantially area savings are achieved with no delay penalty. More specifically, for a 4 ns delay constraint the area complexity is 25,597
m
and 43,576
m
in case of architectures in
Figure 2b and [
22], respectively. For the case where the pdf output is not significant, the area complexity reduction can be 17,293
m
for the architecture on
Figure 2a. Summarizing, depending on the application and the design constraints there is a trade-off between the additional
terms used for the evaluation of the softmax output. As we increase the value of the parameter
, then the actual softmax value is better approximated while hardware complexity increases. When
, then the hardware complexity is minimized while softmax output approximation diverges.