1. Introduction
Functionally graded materials (FGMs) are advanced composites designed and fabricated in a way that their physical and mechanical properties spatially vary in their structures. An overview of manufacturing methods for FGMs, their applications and future challenges, based on the available literature over 30 years, has been recently published by Saleh et al., in [
1].
Due to the continuous variation in material properties, many problems related to the material discontinuities of conventional composite material (stress concentrations, residual stresses, delamination phenomena and damage growth) can be significantly reduced and high permeance requirements ensured [
2,
3,
4].
In most cases, functionally graded materials are made of a combination of metal and ceramic to offer a wide range of applications for various equipment subject to extreme thermo-mechanical stresses [
5,
6,
7,
8,
9,
10,
11,
12,
13].
Recent studies have also shown that, by managing some fabrication parameters during the manufacture of FGMs, different kinds of porosity distributions can be fabricated inside their structure to further improve the physical and mechanical characteristics of the material [
14,
15,
16,
17,
18]. For example, the results of the investigations reported in [
19,
20,
21,
22] have highlighted the benefits of cellular metals and metal foams inside the structure of micro/nano-scale systems (MEMS/NEMS) in terms of electrical conductivity, thermal transport and energy absorption.
Various simple models have been widely adopted by many researchers to describe the interaction of the nano-beam with its foundation for a wide range of engineering applications. However, to the best of our knowledge, the analyses of the mechanical behavior of porous nano-beams resting on elastic foundations are rather rare and the available results are limited to FG nano-beams without porosities [
23,
24,
25,
26,
27].
As is well-known, the mechanical response of nanostructures made of functionally graded materials is strongly size-dependent and therefore the small-scale effects on the mechanical behavior of FG nanostructures must be considered [
28,
29,
30,
31,
32].
In order to overcome the enormous costs and computation times of molecular dynamics (MD) simulations, and the difficulties to conduct experimental investigations at the nanoscale, the size-dependent effects on the static and dynamic characteristics of small-scaled structural systems may be accurately captured by the so-called scale-dependent continuum mechanics-based theories, including the strain gradient theory of elasticity [
33,
34] and Eringen’s nonlocal elasticity theory [
35,
36,
37]. In the first theory, the material response at a point of a continuum is assumed to be dependent on both the strain and the strain gradients of different orders, while, in the second one, the output field at a point of a continuum is assumed to be the integral convolution between the elastic source field and a suitable averaging kernel.
In the framework of nonlocal elasticity, the basic integral constitutive law is the strain-driven Eringen’s integral model (EIM), which was recommended, for the first time, by Peddieson [
38] to analyze the mechanical behavior of nanoscale structures. For unbounded continua, when considering the bi-exponential nonlocal kernel function, due to tacit fulfillment of the vanishing boundary conditions at infinity, the integral strain-driven theory (EIM) can be replaced with the well-known differential type theory (EDM), by which it is much easier to model small-scale phenomena in nanostructures than with the corresponding integral formulation.
Recently, it was shown that the nonlocal differential-based and integral-based theories of elasticity models may be not equivalent to each other for boundary condition problems, since adequate higher-order homogeneous constitutive boundary conditions have to be prescribed.
Consequently, for bounded nanostructures, the strain-driven purely nonlocal elastic problems defined on bounded domains are mathematically ill-posed due to the incompatibility between the higher-order constitutive boundary conditions and equilibrium requirements (e.g., the paradox of a cantilever nano-beam subject to a transverse concentrated load at the free end) [
39].
The ill-posed problem related to the pure nonlocal model may be circumvented by adopting the Eringen local-nonlocal mixture constitutive model [
37] or by using coupled theories, such as the nonlocal strain gradient theory [
40] and the combination of pure nonlocal theory with the surface theory of elasticity [
41]. For example, some recent applications of the theories mentioned above are addressed in [
42,
43,
44].
Furthermore, these difficulties can be overcome by adopting the stress-driven nonlocal integral model (SDM) recently proposed by Romano and Barretta [
45], in which the roles of stress and elastic strain fields are swapped with respect to the strain-driven model. In addition, in this case, for a class of bi-exponential kernels, the integral form of the constitutive equations is shown to be mathematically equivalent to differential equations subjected to some higher order constitutive boundary conditions.
The stress-driven nonlocal theory of elasticity has been widely respected by the scientific community and has been successfully applied to investigate size-dependent behavior of elastic nano-beams [
46,
47,
48,
49,
50,
51,
52,
53,
54] with bounded structural domains. In particular, closed form solutions for stress-driven integral models [
55] have been provided for cantilever, simply supported, clamped-pinned and fully-clamped FG nano-beams subject to different load conditions.
Recently, the authors of this paper examined the nonlinear vibration behavior of geometrically imperfect functionally graded nano-beams on the basis of both the stress-driven nonlocal integral model (SDM) and the strain-driven model (EDM), especially in the presence of an axial pretension force [
56].
In the present paper, the nonlinear free vibration of a metal-ceramic functionally graded Bernoulli–Euler nano-beam, resting on a Winkler elastic foundation, is examined taking into account von Kármán type nonlinearity and initial geometric imperfection. In particular, small scale effects are considered by using the stress-driven nonlocal elasticity. The equation of motion is determined by Hamilton’s principle and simplified by Galerkin’s method. The first order Hamiltonian approach [
57] was then employed to solve the nonlinear vibrations problem.
In order to show the efficiency and accuracy of the proposed approach, several comparisons with existing models in the literature are performed. Finally, the effects of initial geometric imperfection, the gradient index coefficient, the porosity volume fraction and the Winkler elastic foundation coefficient on nonlinear fundamental frequencies of porous FG simply supported nano-beams are presented and discussed.
2. Functionally Graded Porous Material
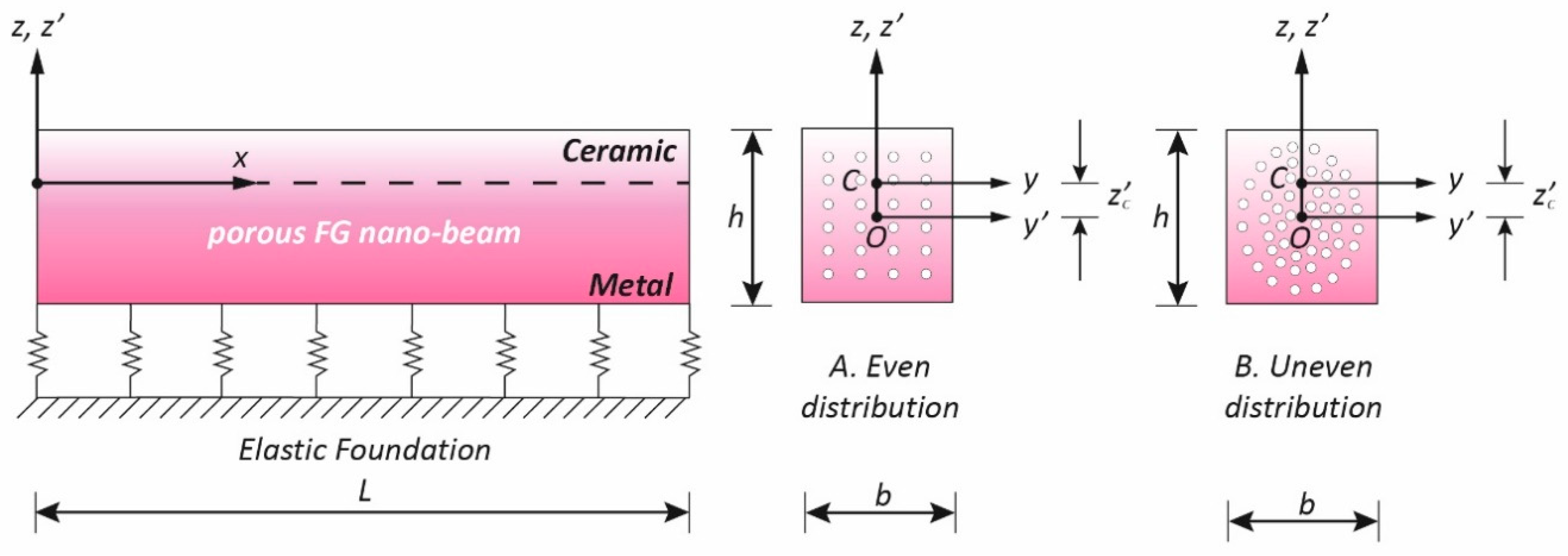
We consider a Bernoulli–Euler straight nano-beam, with length “
L”, thickness “
h” and width “
b”, resting on a Winkler foundation, and denote by
y’ and
z’ the principal axes of geometric inertia of its rectangular cross-section (Σ), originating at the geometric center O (
Figure 1).
The nano-beam is supposed to be made of a functionally graded (FG) material, composed of a mixture of metal and ceramic, whose distribution spatially varies from the bottom (z’ = −h/2) to the top (z’ = +h/2) surface. In this investigation, the top surface is ceramic-rich, whereas the bottom surface is metal-rich.
The nano-beam structure is assumed to have porosities inside the FG material generated during the manufacturing process of the two constituents. In particular, the porous FG nano-beam is assumed to have two kinds of porosity distributions across the thickness of the beam (
Figure 1): in the first scenario, the porosity is evenly distributed among the metal and ceramic with widespread porosities; in the second scenario (uneven distribution), the porosities are distributed around the central area of the cross section of the FG nano-beam and tend to vanish both on the top surface (ceramic-rich) and on the bottom surface (metal-rich) of the nano-beam.
By denoting with
k (
k ≥ 0) the gradient index of the FG material, and with
ζ the porosity volume fraction (
ζ ≪ 1), in the case of an even distribution of porosity, the effective material properties, here described by the mass density,
(
z’), and by Young’s modulus,
E(
z’), can be formulated by the following power-laws [
58]:
where
c,
m and
Ec,
Em are the material densities and the Euler–Young moduli of ceramic and metal, respectively.
In the second scenario (uneven distribution of the porosity), the previous expressions are modified as follows
As is well-known, in order to remove bending–stretching coupling caused by FG material variation, it is convenient to take as reference for the evaluation of the previous effective materials properties (Equations (1)–(4)) the elastic center C, whose position is shifted from the geometric center O of the following quantity
Accordingly, in the new elastic Cartesian reference system at elastic center C,
z =
z’−
and
y =
y’ (
Figure 1).
Moreover, determination of the bending stiffness,
, and the axial stiffness,
, of the FG porous nano-beam is useful in the subsequent relations. The first quantity is defined by the second moment of elastic area, weighted with the scalar field of the Euler–Young moduli, about the y axis (
), and is evaluated considering the bending abscissa z originating at C. Similarly, the axial stiffness is defined by the elastic cross-sectional area weighted with the scalar field of the Euler–Young moduli
Moreover, the effective cross-sectional mass,
, and rotatory inertia,
, can be determined employing the previously introduced effective material density
By substituting Equations (2) and (4) into Equation (5), we obtain the following coordinate of the elastic center C for the two distributions of porosity considered here
Utilizing the expressions of the effective Euler–Young modulus introduced above for the two scenarios of porosity distribution taken into account (Equations (2) and (4)), bending stiffness, axial stiffness, cross-sectional mass and rotatory inertia can be determined as follows
where
Iy’ =
bh3/12 is the second geometric moment of area of the cross-section about the y’ axis about the geometric center and
A =
bh is the cross-sectional area.
If the porosity volume fraction ζ → 0, it is inferred from Equations (11)–(18) that, as k → 0 and k → ∞, the aforementioned material quantities approach the corresponding material quantities of pure ceramic and pure metal, respectively.
In this work, the nano-beam material is assumed to be made of silicon nitride-stainless steel (Si3N4-SuS3O4), whose properties are listed in the following
Table 1 [
59,
60].
Figure 2 shows the effect of the gradient index of the porous FG material (
) on the dimensionless position of the elastic center C (
of the rectangular cross section of the nano-beam.
Firstly, it can be noted that the dimensionless distance
increases as the gradient index
increases, with a maximum attained at a value of
*, which depends on the value of
; note that for
*, the distance
tends to vanish for
→ ∞. From
Figure 2, one can also note that the curves corresponding to the second type of porosity distribution exhibit less of an increase than those of the first scenario of porosity.
Variations of the dimensionless axial stiffness (
and dimensionless bending stiffness (
) of the porous FG nano-beam, in terms of the gradient index, are reported in
Figure 3, varying the porosity volume fraction of the material. As can be observed, the increase in the gradient index, as well as in the value of the porosity volume fraction, causes a decrease of the axial and bending stiffness of porous FG nano-beams, for both the two kinds of porosity distribution considered.
In particular, for each assigned value of the dashed lines, corresponding to the uneven distributions of porosity, always have a greater value than the continuous ones, which correspond to the even distribution.
Figure 4 show the variations of the dimensionless cross-sectional mass (
) and rotatory inertia (
of the gradient index, respectively, varying the porosity volume fraction. From these graphs, one finds that
and
increase with increasing
and with decreasing
.
The variations of the Euler–Young modulus across the thickness of a nano-beam are illustrated in
Figure 5A, assuming
equal to zero and varying
in the set {0, 0.3, 0.5, 1, 3, 5, → ∞}. As was to be expected, when
= 0, the FG material reduces to pure ceramic (
E =
Ec = 322.3 GPa) while, on the contrary, for
→ ∞, the material properties tend to pure metal (
E =
Em = 207.8 GPa).
The variations of the Euler–Young modulus through the thickness of the nano-beam cross section, assuming
= 0.2, are illustrated in
Figure 5B,C for even and uneven porosity distributions, respectively. As can be noted, the curves of the variation of
E relative to the even distribution (
Figure 5B) have the same behavior of those illustrated in
Figure 5A, corresponding to a non-porous material, but with a decrease in the values of Young’s moduli. Finally,
Figure 5C shows that the maximum of Euler–Young’s modulus for the uneven distribution of porosity is reached at the top and bottom of the cross section and decreases in the direction of the middle zone.
3. Governing Equation
Using the Bernoulli–Euler theory, the displacement components
and
along
x,
y and
z directions, respectively, at any point of the nano-beam, can be written as
where
and
are the axial and transverse displacements of the elastic center C at time
t, respectively;
is the rotation of the cross section about the
y-axis, and
is the initial assigned geometric imperfection in the transverse direction [
61].
On the basis of the nonlinear Von-Kármán assumptions, with small strains and moderate rotation, the nonlinear strain–displacement relation may be written as [
62]
As is well-known, the nonlinear equations of motion can be obtained using Hamilton’s principle:
where the expression of
(kinetic energy),
(strain energy) and
(work done by external forces) are given in the following.
The variation of kinetic energy
is
The expression for the variation of the strain energy
is
where the stress resultants
and
introduced in Equation (25) are defined as:
The expression of the virtual work of the external force
can be expressed by
where
and
are the axial and the transverse vertical distributed loads, respectively, and
is the Winkler elastic foundation coefficient.
By substituting the expressions of
,
, and
into Hamilton’s principle (Equation (23)), performing integration-by-parts with respect to
t as well as
x to relieve the generalized displacements
,
and
of any differentiations, and using the fundamental lemma of differential calculus, we obtain the following equations of motion:
The boundary conditions involve specifying one element of each of the following three pairs:
5. Convergence and Comparison Study
Some numerical examples are presented in this paragraph to validate the accuracy and reliability of the proposed approach. In the first comparison example (
Table 2) geometrical nonlinearity, initial imperfection and the elastic foundation coefficient are neglected in order to compare the results obtained with the present approach. The comparison, in terms of linear dimensionless natural frequencies of homogeneous simply-supported (S-S) and clamped-clamped (C-C) FG nano-beams, is made with the results of Apuzzo et al., who in [
55] obtained results while varying the dimensionless nonlocal parameter
in the set {0.00
+, 0.01, 0.03, 0.05, 0.1}.
In the second comparison study (
Table 3), the present approach is compared with the model of Mahmoudpou et al., [
59] for homogenous S-S and C-C nano-beams resting on an elastic foundation with
, and assuming that
and
are equal to zero.
The third example (
Table 4) concerns the evaluation of the ratios between the local nonlinear frequency (
ωNL) and the local linear one (
ωL), for a perfect simply-supported homogeneous nano-beams, varying the dimensionless amplitude of the nonlinear oscillator
, and neglecting the elastic foundation coefficient. The results obtained with the present approach are compared with the results of Singh et al., [
63], based on the Ritz–Galerkin method (RGM), and with those of Mahmoudpou et al., [
59], based on the first-order homotopy analysis method (HAM).
Finally, in
Table 5 and
Table 6 the values of the nonlocal nonlinear dimensionless frequencies, evaluated with the present approach varying the dimensionless amplitude of the nonlinear oscillator
in the set {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6}, are summarized and compared with the results by Mahmoudpou et al., in [
59] for two values of the elastic foundation coefficient: 50 and 100.
From these comparison studies, the accuracy of the Hamiltonian approach to nonlinear oscillators here employed is validated.