A Novel Ensemble Machine Learning Approach for Bioarchaeological Sex Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Missing Data
“approximating a data set as a product of two low dimensional factors by minimizing an objective function. The objective will consist of a loss function on the approximation error together with regularization of the low dimensional factors. With these extensions of PCA, the resulting low rank representation of the data set still produces a low dimensional embedding of the data set, as in PCA”[43] (p. 3)
2.3. Ensemble Machine Learning
2.4. Evaluating Model Performance
3. Results
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buikstra, J.E.; Ubelaker, D.H. Standards for Data Collection from Human Skeletal Remains; Arkansas Archaeological Survey: Fayetteville, AR, USA, 1994. [Google Scholar]
- Garvin, H.M.; Ruff, C.B. Sexual dimorphism in skeletal browridge and chin morphologies determined using a new quantitative method. Am. J. Phys. Anthr. 2012, 147, 661–670. [Google Scholar] [CrossRef]
- Krishan, K.; Chatterjee, P.M.; Kanchan, T.; Kaur, S.; Baryah, N.; Singh, R.K. A review of sex estimation techniques during examination of skeletal remains in forensic anthropology casework. Forensic Sci. Int. 2016, 261, e1–e165. [Google Scholar] [CrossRef]
- Slemenda, C.W.; Reister, T.K.; Hui, S.L.; Miller, J.Z.; Christian, J.C.; Johnston, C.C. Inluences on skeletal mineralization in children and adolescents: Evidence for varying effects of sexual maturation and physical activity. J. Pediatr. 1994, 125, 201–207. [Google Scholar] [CrossRef]
- Wang, Y. Is Obesity Associated with Early Sexual Maturation? A Comparison of the Association in American Boys Versus Girls. Pediatrics 2002, 110, 903–910. [Google Scholar] [CrossRef] [Green Version]
- Weiss, K.M. On the systematic bias in skeletal sexing. Am. J. Phys. Anthr. 1972, 37, 239–249. [Google Scholar] [CrossRef] [Green Version]
- Sutter, R.C. Nonmetric Subadult Skeletal Sexing Traits: I. A Blind Test of the Accuracy of Eight Previously Proposed Methods Using Prehistoric Known-Sex Mummies from Northern Chile. J. Forensic Sci. 2003, 48, 927–935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konigsberg, L.W.; Algee-Hewitt, B.F.B.; Steadman, D.W. Estimation and evidence in forensic anthropology: Sex and race. Am. J. Phys. Anthr. 2009, 139, 77–90. [Google Scholar] [CrossRef]
- Jackes, M. Representativeness and bias in archaeological skeletal samples. In Social Bioarchaeology; Agarwal, S.C., Glencross, B.A., Eds.; Wiley-Blackwell: West Sussex, UK, 2011; pp. 107–145. [Google Scholar]
- Sierp, I.; Henneberg, M. The Difficulty of Sexing Skeletons from Unknown Populations. J. Anthr. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Irurita Olivares, J.; Alemán Aguilera, I. Validation of the sex estimation method elaborated by Schutkowski in the Granada Osteological Collection of identified infant and young children: Analysis of the controversy between the different ways of analyzing and interpreting the results. Int. J. Leg. Med. 2016, 130, 1623–1632. [Google Scholar] [CrossRef]
- Sjøvold, T. A report on the heritability of some cranial measurements and non-metric traits. In Multivariate Statistical Methods in Physical Anthropology; Van Vark, G.H., Howells, W.W., Eds.; Reidel Publishing Company: Dordrecht, The Netherlands, 1984; pp. 223–246. [Google Scholar]
- Devor, E.J. Transmission of human cranial dimensions. J. Craniofac. Genet. Dev. Biol. 1987, 7, 95–106. [Google Scholar]
- Roseman, C.C. Detecting interregionally diversifying natural selection on modern human cranial form by using matched molecular and morphometric data. Proc. Natl. Acad. Sci. USA 2004, 101, 12824–12829. [Google Scholar] [CrossRef] [Green Version]
- Roseman, C.C.; Weaver, T.D. Multivariate apportionment of global human craniometric diversity. Am. J. Phys. Anthr. 2004, 125, 257–263. [Google Scholar] [CrossRef]
- Carson, E.A. Maximum likelihood estimation of human craniometric heritabilities. Am. J. Phys. Anthr. 2006, 131, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Witherspoon, D.J.; Wooding, S.; Rogers, A.R.; Marchani, E.E.; Watkins, W.S.; Batzer, M.A.; Jorde, L.B. Genetic similarities within and between human populations. Genetics 2007, 176, 351–359. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Abadías, N.; Esparza, M.; Sjøvold, T.; González-José, R.; Santos, M.; Hernández, M. Heritability of human cranial dimensions: Comparing the evolvability of different cranial regions. J. Anat. 2009, 214, 19–35. [Google Scholar] [CrossRef] [PubMed]
- Strauss, A.; Hubbe, M. Craniometric Similarities Within and between Human Populations in Comparison with Neutral Genetic Markers. Hum. Biol. 2010, 82, 315–330. [Google Scholar] [CrossRef] [PubMed]
- Herrera, B.; Hanihara, T.; Godde, K. Comparability of multiple data types from the Bering Strait region: Cranial and dental metrics and nonmetrics, mtDNA, and Y-Chromosome DNA. Am. J. Phys. Anthr. 2014, 54, 334–348. [Google Scholar] [CrossRef] [PubMed]
- Buikstra, J.E.; Frankenberg, S.R.; Konigsberg, L.W. Skeletal biological distance studies in American Physical Anthropology: Recent trends. Am. J. Phys. Anthr. 1990, 82, 1–7. [Google Scholar] [CrossRef]
- Cunningham, S.J. Machine learning applications in anthropology: Automated discovery over kinship structures. Comput. Humanit. 1996, 30, 401–406. [Google Scholar] [CrossRef]
- Bell, S.; Jantz, R. Neural network classification of skeletal remains. In Archaeological Inormatics: Pushing the Envelope; Burenhult, G., Ed.; Archaeopress: Oxford, UK, 2001; pp. 205–212. [Google Scholar]
- Hefner, J.T.; Ousley, S.D. Statistical Classification Methods for Estimating Ancestry Using Morphoscopic Traits. J. Forensic Sci. 2014, 59, 883–890. [Google Scholar] [CrossRef]
- Czibula, G.; Ionescu, V.S.; Miholca, D.L.; Mircea, I.G. Machine learning-based approaches for predicting stature from archaeological skeletal remains using long bone lengths. J. Archaeol. Sci. 2016, 69, 85–99. [Google Scholar] [CrossRef]
- Ionescu, V.S.; Teletin, M.; Voiculescu, E.M. Machine learning techniques for age at death estimation from long bone lengths. In Proceedings of the 2016 IEEE 11th International Symposium on Applied Computational Intelligence and Inormatics (SACI), Timisoara, Romania, 12–14 May 2016; pp. 457–462. [Google Scholar]
- Ionescu, V.S.; Czibula, G.; Teletin, M. Supervised Learning Techniques for Body Mass Estimation in Bioarchaeology. In Soft Computing Applications—Advances in Intelligent Systems and Computing 634; Balas, V., Jain, L., Balas, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Miholca, D.L.; Czibula, G.; Mircea, I.G.; Czibula, I.G. Machine learning based approaches for sex identification in bioarchaeology. In Proceedings of the 18th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 24–27 September 2016; pp. 311–314. [Google Scholar]
- Pink, C.M. Forensic Ancestry Assessment Using Cranial Nonmetric Traits Traditionally Applied to Biological Distance Studies. In Biological Distance Analysis–Forensic and Bioarchaeological Perspectives; Pilloud, M.A., Hefner, J.T., Eds.; Academic Press: San Diego, CA, USA, 2016; pp. 213–230. [Google Scholar]
- Porto, F.P.; Lima, L.N.C.; Flores, M.R.P.; Valsecchi, A.; Ibanez, O.; Palhares, C.E.M.; de Barros Vidal, F. Automatic cephalometric landmarks detection on frontal faces: An approach based on supervised learning techniques. Digit. Investig. 2019, 30, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Ortiz, A.G.; Costa, C.; Silva, R.H.A.; Biazevic, M.G.H.; Michel-Crosato, E. Sex estimation: Anatomical references on panoramic radiographs using machine learning. Forensic Imaging 2020, 20, 200356. [Google Scholar] [CrossRef]
- Kenyhercz, M.W.; Passalacqua, N.V. Missing Data Imputation Methods and Their Performance with Biodistance Analyses. In Biological Distance Analysis–Forensic and Bioarchaeological Perspectives; Pilloud, M.A., Hefner, J.T., Eds.; Academic Press: San Diego, CA, USA, 2016; pp. 181–194. [Google Scholar]
- Muzzall, E.; Kennedy, C.J.; Culich, A. Ensemble Machine Learning for Sex Prediction of a Worldwide Craniometric Dataset, Poster Presented at the Berkeley Institute for Data Science Data Science Faire. Available online: https://github.com/EastBayEv/Ensemble-machine-learning-for-sex-prediction-of-a-worldwide-craniometric-dataset (accessed on 7 July 2020).
- Scozzari, R.; Cruciani, F.; Pangrazio, A.; Santolamazza, P.; Vona, G.; Moral, P.; Latini, V.; Varesi, L.; Memmi, M.M.; Romano, V.; et al. Human Y-chromosome variation in the Western Mediterranean area: Implications for the peopling of the region. Hum. Immunol. 2001, 62, 871–884. [Google Scholar] [CrossRef] [Green Version]
- Coppa, A.; Cucina, A.; Lucci, M.; Mancinelli, D.; Vargiu, R. Origins and spread of agriculture in Italy: A nonmetric dental analysis. Am. J. Phys. Anthr. 2007, 133, 918–930. [Google Scholar] [CrossRef]
- Muttoni, G.; Scardia, G.; Kent, D.V.; Swisher, C.C.; Manzi, G. Pleistocene magnetochronology of early hominin sites at Ceprano and Fontana Ranuccio, Italy. Earth Planet Sci. Lett. 2009, 286, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Fu, Q.; Rudan, P.; Pääbo, S.; Krause, J. Complete Mitochondrial Genomes Reveal Neolithic Expansion into Europe. PLoS ONE 2012, 7, e32473. [Google Scholar] [CrossRef] [Green Version]
- Ghirotto, S.; Tassi, F.; Fumagalli, E.; Colonna, V.; Sandionigi, A.; Lari, M.; Vai, S.; Petiti, E.; Corti, G.; Rizzi, E.; et al. Origins and Evolution of the Etruscans’ mtDNA. PLoS ONE 2013, 8, e55519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muzzall, E.; Coppa, A. Temporal and Spatial Biological Kinship Variation at Campovalano and Alfedena in Iron Age Central Italy. In Bioarcheology of Frontiers and Borderlands; Tica, C., Martin, D.L., Eds.; University Press of Florida: Gainesville, FL, USA, 2019; pp. 107–132. [Google Scholar]
- Coppa, A.; Macchiarelli, R. The maxillary dentition of the Iron-Age population of Alfedena (Middle-Adriatic Area, Italy). J. Hum. Evol. 1982, 11, 219–235. [Google Scholar] [CrossRef]
- Bondioli, L.; Corruccini, R.S.; Macchiarelli, R. Familial segregation in the Iron Age community of Alfedena, Abruzzo, Italy, based on osteodental trait analysis. Am. J. Phys. Anthr. 1986, 71, 393–400. [Google Scholar] [CrossRef]
- Hillson, S.; FitzGerald, C.; Flinn, H. Alternative dental measurements: Proposals and relationships with other measurements. Am. J. Phys. Anthr. 2006, 126, 413–426. [Google Scholar] [CrossRef]
- Udell, M.; Horn, C.; Zadeh, R.; Boyd, S. Generalized Low Rank Models. Found. Trends Mach. Learn. 2016, 9, 1–118. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Breiman, L. Statistical Modeling: The Two Cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Welling, M. Are ML and Statistics Complimentary? Roundtable Discussion at the 6th IMS-ISBA Meeting on Data Science in the Next 50 Years; University of Amsterdam: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Turing, A.M. Computing Machinery and Intelligence. Mind 1950, 59, 433–460. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 207–226. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In Lecture Notes in Computer Science 1857; Goos, G., Hartmanis, J., van Leeuwen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Van der Laan, M.J.; Polley, E.C.; Hubbard, A.E. Super Learner. Stat. Appl. Genet. Mol. Biol. 2007, 6, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Polley, E.C.; van der Laan, M.J. Super Learner in Prediction, UC Berkeley Division of Biostatistics Working Paper Series Paper 266. Available online: https://biostats.bepress.com/ucbbiostat/paper266 (accessed on 8 September 2020).
- Efron, B.; Gong, G. A Leisurely Look at the Bootstrap, the Jackknife, and Cross-Validation. Am. Stat. 1982, 37, 36–48. [Google Scholar] [CrossRef]
- Dobson, A.J. An Introduction to Generalized Linear Models; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wright, N.; Ziegler, A. ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. A Short Introduction to Boosting. J. Jpn. Soc. Art. Int. 1999, 14, 1–14. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Xgboost: Extreme Gradient Boosting, R Package, 2019, Version 0.90.0.2. Available online: https://CRAN.R-project.org/package=xgboost (accessed on 26 September 2020).
- Kennedy, C. Guide to SuperLearner. 2017. Available online: https://cran.r-project.org/web/packages/SuperLearner/vignettes/Guide-to-SuperLearner.html (accessed on 26 September 2020).
- Lantz, B. Machine Learning with R.; Packt Publishing: Birmingham, UK, 2015. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Polley, E.; LeDell, E.; Kennedy, C.; van der Laan, M. SuperLearner: Super Learner Prediction, R Package Version 2.0-26. 2019. Available online: https://CRAN.R-project.org/package=SuperLearner (accessed on 21 November 2020).
- Kennedy, C. Ck37r: Chris Kennedy’s R Toolkit, R Package Version 1.0.3. 2020. Available online: https://github.com/ck37/ck37r (accessed on 10 March 2020).
- Taubadel, N.V.C. Revisiting the homoiology hypothesis: The impact of phenotypic plasticity on the reconstruction of human population history from craniometric data. J. Hum. Evol. 2009, 57, 179–190. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Chipman, H.A.; George, E.I.; McCulloch, R.E. BART: Bayesian additive regression trees. Ann. Appl. Stat. 2010, 1, 266–298. [Google Scholar] [CrossRef]
- Chollet, F.; Allaire, J.J. Deep Learning with R.; Manning: New York, NY, USA, 2017. [Google Scholar]

| Location | Time Period | Male | Female |
|---|---|---|---|
| Alfedena Arboreto | 600–400 BCE | 9 | 10 |
| Alfedena Campo Consolino | 600–400 BCE | 61 | 19 |
| Alfedena Scavi Mariani | 600–400 BCE | 37 | 28 |
| Alfedena Sergi Museum | 600–400 BCE | 19 | 13 |
| Campovalano Iron Age | 750–200 BCE | 89 | 77 |
| Campovalano St. Peter | 9–11th C. CE | 25 | 33 |
| Total | 240 | 180 |
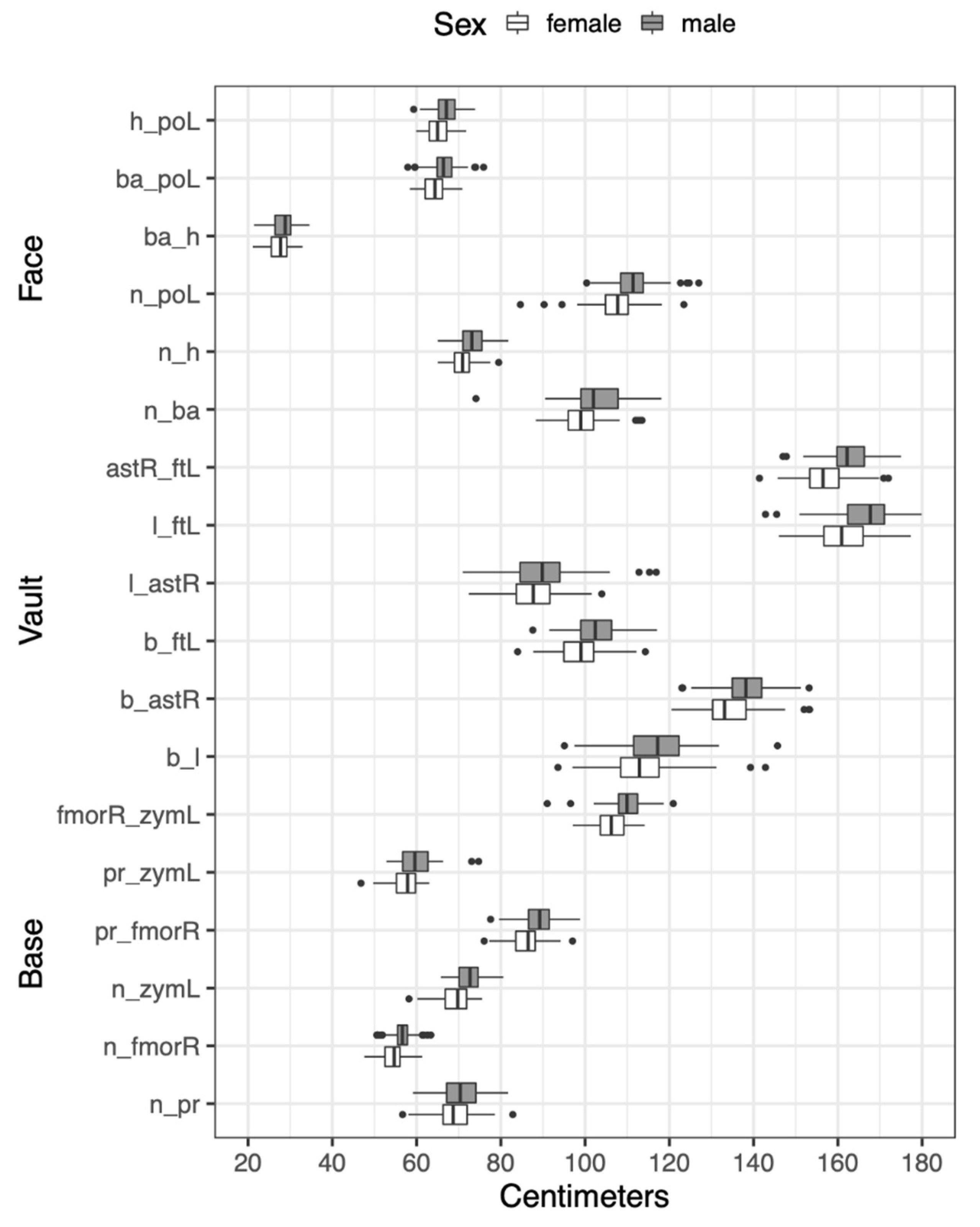
| Face | Definition |
|---|---|
| Nasion (n) | The intersection of the naso-frontal suture in the midsagittal plane |
| Prosthion (pr) | The location of the anteriorly located portion of the anterior surface of the alveolar process at the most anterior point of the alveolar process |
| Right frontomalare | The location where the zygomaticofrontal suture intersects the orbital margin |
| orbitale (fmorR) | |
| Left zygomaxillare (zymL) | The most inferior and anterior location on the zygomaticomaxillary suture |
| Vault | |
| Bregma (b) | The landmark where the sagittal and coronal sutures meet in the midsagittal plane. In cases where the sagittal suture deflects laterally, an estimation must be made of the location in the midsagittal plane |
| Lambda (l) | The landmark where the left and right lambdoidal sutures intersect the sagittal suture. The landmark must be estimated when the suture intersection is obliterated, or where strongly serrated sutures are present |
| Right Asterion (astR) | The juncture of the lambdoid, parietomastoid, and occipitomastoid sutures |
| Left Frontotemporale | The most medial and anterior point on the superior temporal line on the frontal bone |
| (ftL) | |
| Base | |
| Nasion (n) | The intersection of the naso-frontal suture in the midsagittal plane |
| Basion (ba) | The inner border where the anterior portion of the foramen magnum is intersected by the midsagittal plane |
| Hormion (h) | The juncture of the sphenoid and vomer bones in the midsagittal plane |
| Left Porion (poL) | The most superior point on the external margin of the external auditory meatus |
| Bony Region | Measurement | Proportion Missing Male | Proportion Missing Female |
|---|---|---|---|
| Face | n_pr | 63 | 67 |
| n_fmorR | 54 | 58 | |
| n_zymL | 57 | 65 | |
| pr_fmorR | 63 | 68 | |
| pr_zymL | 63 | 69 | |
| fmorR_zymL | 63 | 71 | |
| Vault | b_l | 38 | 47 |
| b_astR | 38 | 46 | |
| b_ftL | 42 | 51 | |
| l_astR | 37 | 44 | |
| l_ftL | 44 | 54 | |
| astR_ftL | 46 | 54 | |
| Base | n_ba | 61 | 66 |
| n_h | 63 | 68 | |
| n_poL | 53 | 61 | |
| ba_h | 65 | 69 | |
| ba_poL | 57 | 62 | |
| h_poL | 61 | 66 | |
| Dentition | XC | 59 | 69 |
| P3 | 53 | 63 | |
| P4 | 50 | 66 | |
| M1 | 49 | 46 | |
| M2 | 53 | 53 |
| Algorithm | Description | Reference |
|---|---|---|
| Logistic regression | Logistic regression models the relationships between the outcome variable (male/female sex) and the predictor variables. It computes the probability that the Y variable (sex) belongs to one of the two binary classes. | Dobson, 1990 [54] |
| Lasso | Lasso (least absolute shrinkage and selection operator) is a form of penalized regression (L1) that produces a sparse solution to remove predictor variables from the model that are not related to the outcome. | Friedman et al.,. 2010 [55] |
| Decision tree | A decision tree is a relatively simple tree-based method that gauges the probability of classifying the outcome based on the predictor variables before splitting a given decision node a certain number of times until there are no longer enough observations to split. | Breiman et al., 1984 [56] |
| Ranger (random forest) | Ranger is a decorrelated random forest ensemble classifier method that uses the average of multiple bootstrapped decision tree models for classification. Unlike single decision tree models that use all predictors at each split, random forests use only a random subsample of the total predictors for each split in each tree. | Breiman, 2001 [57]; Wright and Ziegler, 2017 [58] |
| Xgboost | A gradient boosted tree is another tree-based method that fits a tree to the residuals of the previous tree in succession. It downweights easily predicted cases but upweights those that it cannot predict. This continues over many iterations so that weak trees are “boosted” into strong ones. | Freund and Schapire, 1999 [59]; Chen et al.,. 2019 [60] |
| SuperLearner | The SuperLearner algorithm is an optimal weighted ensemble average that improves predictor construction and is flexible in that it can perform well on different data distributions and protects against overfitting through external cross-validation. Individual algorithm weights can be investigated to see which ones contribute most to the ensemble. | van der Laan et al., 2007 [51]; Kennedy, 2017 [61] |
| Mean of Y | The mean of Y (dependent variable) is the benchmark algorithm based only on the mean. This is a very simple prediction so the more complex algorithms should perform better than this one. It should not be the best single-performing algorithm and should have a low weight in the weighted-average ensemble. If it is the best performing algorithm something is likely wrong. | Polley and van der Laan, 2010 [52] |
| DiscreteSL | The discrete SuperLearner is the single best performing algorithm(s) as identified by the SuperLearner. Alternatively, this might also correspond to the combination of best performing algorithms at different cross-validation folds, in which case the DiscreteSL AUC-ROC will not be identical to that of a single algorithm. | Polley and van der Laan, 2010 [52] |
| Bony Region | Algorithm | AUC-ROC | Standard Error | Confidence Interval (Lower) | Confidence Interval (Upper) |
|---|---|---|---|---|---|
| Face | Mean of Y | 0.5000 | 0.0493 | 0.4034 | 0.5966 |
| Decision tree | 0.8069 | 0.0259 | 0.7562 | 0.8577 | |
| Xgboost | 0.8998 | 0.0152 | 0.8701 | 0.9295 | |
| Lasso | 0.9042 | 0.0161 | 0.8727 | 0.9357 | |
| Logistic regression | 0.9088 | 0.0157 | 0.8781 | 0.9395 | |
| Ranger | 0.9306 | 0.0122 | 0.9066 | 0.9545 | |
| DiscreteSL | 0.9306 | 0.0122 | 0.9066 | 0.9545 | |
| SuperLearner | 0.9426 | 0.0111 | 0.9208 | 0.9644 | |
| Vault | Mean of Y | 0.5000 | 0.0493 | 0.4034 | 0.5966 |
| Logistic regression | 0.8458 | 0.0200 | 0.8067 | 0.8850 | |
| Lasso | 0.8486 | 0.0198 | 0.8099 | 0.8873 | |
| Xgboost | 0.8690 | 0.0188 | 0.8322 | 0.9058 | |
| Decision tree | 0.8998 | 0.0218 | 0.8570 | 0.9425 | |
| DiscreteSL | 0.9030 | 0.0164 | 0.8709 | 0.9351 | |
| Ranger | 0.9065 | 0.0158 | 0.8756 | 0.9374 | |
| SuperLearner | 0.9116 | 0.0147 | 0.8827 | 0.9404 | |
| Base | Mean of Y | 0.5000 | 0.0493 | 0.4034 | 0.5966 |
| Logistic regression | 0.7667 | 0.0238 | 0.7201 | 0.8132 | |
| Lasso | 0.7685 | 0.0238 | 0.7219 | 0.8152 | |
| Decision tree | 0.7986 | 0.0248 | 0.7500 | 0.8472 | |
| Xgboost | 0.8646 | 0.0177 | 0.8298 | 0.8993 | |
| Ranger | 0.9051 | 0.0146 | 0.8764 | 0.9338 | |
| DiscreteSL | 0.9051 | 0.0146 | 0.8764 | 0.9338 | |
| SuperLearner | 0.9060 | 0.0146 | 0.8774 | 0.9347 | |
| Cranial | Mean of Y | 0.5000 | 0.0493 | 0.4034 | 0.5966 |
| Decision tree | 0.9125 | 0.0189 | 0.8754 | 0.9496 | |
| Lasso | 0.9236 | 0.0138 | 0.8966 | 0.9506 | |
| Logistic regression | 0.9282 | 0.0128 | 0.9032 | 0.9533 | |
| Xgboost | 0.9306 | 0.0128 | 0.9054 | 0.9557 | |
| Ranger | 0.9519 | 0.0103 | 0.9317 | 0.9720 | |
| DiscreteSL | 0.9519 | 0.0103 | 0.9317 | 0.9720 | |
| SuperLearner | 0.9644 | 0.0084 | 0.9480 | 0.9807 | |
| Dental | Mean of Y | 0.5000 | 0.0493 | 0.4034 | 0.5966 |
| Decision tree | 0.6537 | 0.0280 | 0.5989 | 0.7086 | |
| Xgboost | 0.6551 | 0.0270 | 0.6021 | 0.7081 | |
| Ranger | 0.7171 | 0.0250 | 0.6680 | 0.7662 | |
| DiscreteSL | 0.7213 | 0.0256 | 0.6711 | 0.7715 | |
| Lasso | 0.7412 | 0.0250 | 0.6921 | 0.7903 | |
| Logistic regression | 0.7417 | 0.0252 | 0.6924 | 0.7910 | |
| SuperLearner | 0.7421 | 0.0248 | 0.6935 | 0.7908 | |
| Combined craniodental | Mean of Y | 0.5000 | 0.0493 | 0.4034 | 0.5966 |
| Decision tree | 0.9060 | 0.0196 | 0.8675 | 0.9445 | |
| Xgboost | 0.9375 | 0.0116 | 0.9148 | 0.9602 | |
| Logistic regression | 0.9426 | 0.0111 | 0.9209 | 0.9643 | |
| Lasso | 0.9528 | 0.0104 | 0.9324 | 0.9731 | |
| Ranger | 0.9549 | 0.0100 | 0.9353 | 0.9745 | |
| DiscreteSL | 0.9549 | 0.0100 | 0.9353 | 0.9745 | |
| SuperLearner | 0.9722 | 0.0070 | 0.9585 | 0.9860 |
| Bony Region | Algorithm | Mean (Contribution to Ensemble) | Standard Deviation | Min | Max |
|---|---|---|---|---|---|
| Face | Ranger | 0.4634 | 0.1058 | 0.2389 | 0.6044 |
| Logistic regression | 0.4193 | 0.0373 | 0.3262 | 0.4779 | |
| Xgboost | 0.1159 | 0.0928 | 0.0000 | 0.3199 | |
| Lasso | 0.0013 | 0.0059 | 0.0000 | 0.0263 | |
| Decision tree | 0.0001 | 0.0004 | 0.0000 | 0.0017 | |
| Mean of Y | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Vault | Ranger | 0.5004 | 0.1205 | 0.1910 | 0.7078 |
| Decision tree | 0.3234 | 0.0935 | 0.1591 | 0.5442 | |
| Logistic regression | 0.1412 | 0.0520 | 0.0556 | 0.2234 | |
| Xgboost | 0.0350 | 0.0561 | 0.0000 | 0.1483 | |
| Mean of Y | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Lasso | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Base | Ranger | 0.8878 | 0.0701 | 0.7068 | 0.9811 |
| Logistic regression | 0.0758 | 0.0259 | 0.0189 | 0.1264 | |
| Xgboost | 0.0364 | 0.0590 | 0.0000 | 0.2168 | |
| Mean of Y | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Lasso | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Decision tree | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Crania | Ranger | 0.4610 | 0.1162 | 0.2750 | 0.6789 |
| Logistic regression | 0.1940 | 0.0859 | 0.0299 | 0.3193 | |
| Lasso | 0.1411 | 0.0753 | 0.0380 | 0.2882 | |
| Decision tree | 0.1267 | 0.1028 | 0.0000 | 0.3101 | |
| Xgboost | 0.0772 | 0.0826 | 0.0000 | 0.2452 | |
| Mean of Y | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Dental | Logistic regression | 0.5591 | 0.0608 | 0.4472 | 0.6747 |
| Ranger | 0.3582 | 0.0953 | 0.1797 | 0.5286 | |
| Decision tree | 0.0747 | 0.0719 | 0.0000 | 0.2339 | |
| Xgboost | 0.0080 | 0.0160 | 0.0000 | 0.0573 | |
| Mean of Y | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Lasso | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Combined craniodental | Lasso | 0.4522 | 0.0918 | 0.2598 | 0.6602 |
| Ranger | 0.1734 | 0.1048 | 0.0000 | 0.3853 | |
| Xgboost | 0.1700 | 0.0739 | 0.0416 | 0.2906 | |
| Logistic regression | 0.1319 | 0.0892 | 0.0000 | 0.3308 | |
| Decision tree | 0.0726 | 0.0755 | 0.0000 | 0.1891 | |
| Mean of Y | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzzall, E. A Novel Ensemble Machine Learning Approach for Bioarchaeological Sex Prediction. Technologies 2021, 9, 23. https://doi.org/10.3390/technologies9020023
Muzzall E. A Novel Ensemble Machine Learning Approach for Bioarchaeological Sex Prediction. Technologies. 2021; 9(2):23. https://doi.org/10.3390/technologies9020023
Chicago/Turabian StyleMuzzall, Evan. 2021. "A Novel Ensemble Machine Learning Approach for Bioarchaeological Sex Prediction" Technologies 9, no. 2: 23. https://doi.org/10.3390/technologies9020023
APA StyleMuzzall, E. (2021). A Novel Ensemble Machine Learning Approach for Bioarchaeological Sex Prediction. Technologies, 9(2), 23. https://doi.org/10.3390/technologies9020023






