Macroprudential and Monetary Policy Interactions and Coordination in South Africa: Evidence from Business and Financial Cycle Synchronisation
Abstract
:1. Introduction
2. Literature on Conceptual and Empirical Matters
3. Database and Methodology
3.1. Database and Data Modifications
3.2. Composite Financial Cycle Index Development Approach
3.3. Model Specification for the Interactions of MaPP and MP
3.3.1. Conditional Correlations MGARCH Models
Constant Conditional Correlation Model
Dynamic Conditional Correlations Model
Asymmetric Generalised Dynamic Conditional Correlations
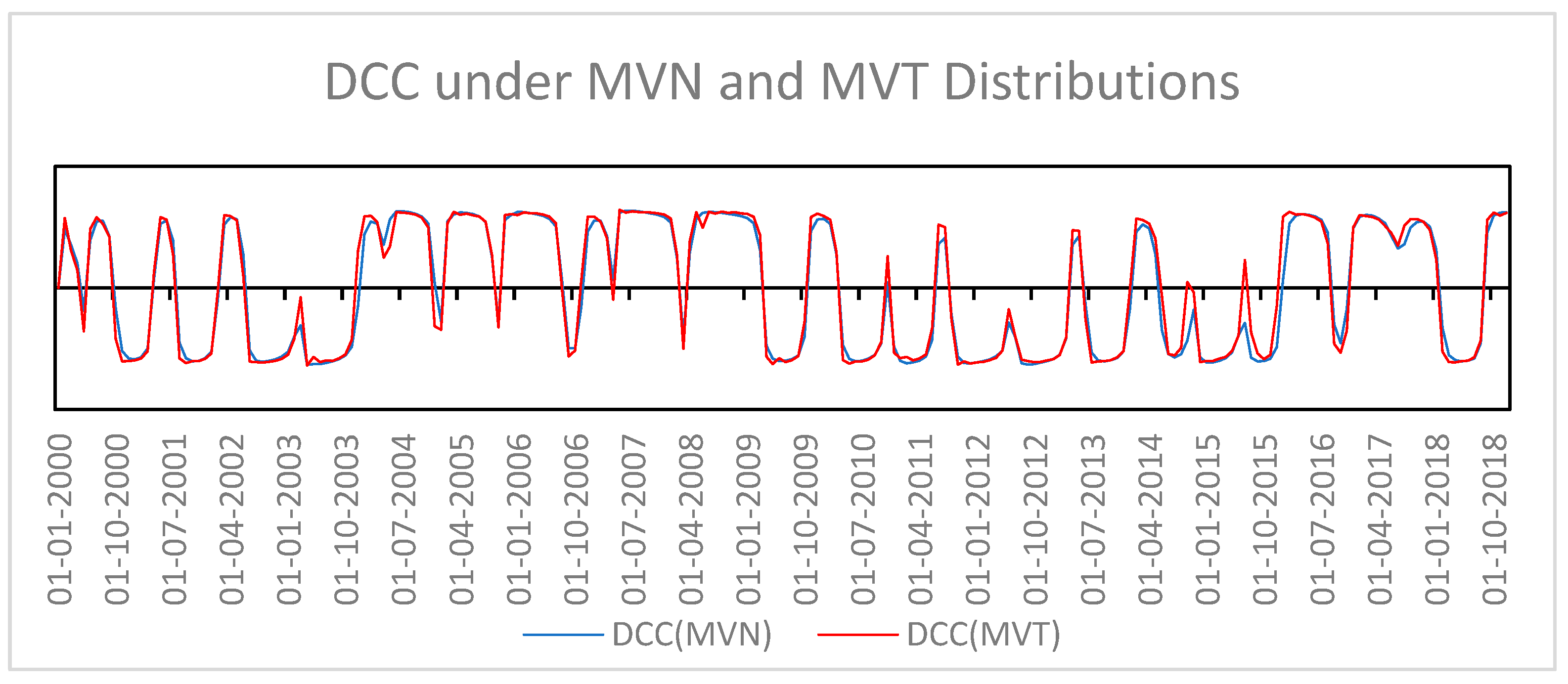
3.3.2. Chosen Models and Estimation Process
4. Estimation Results and Analysis
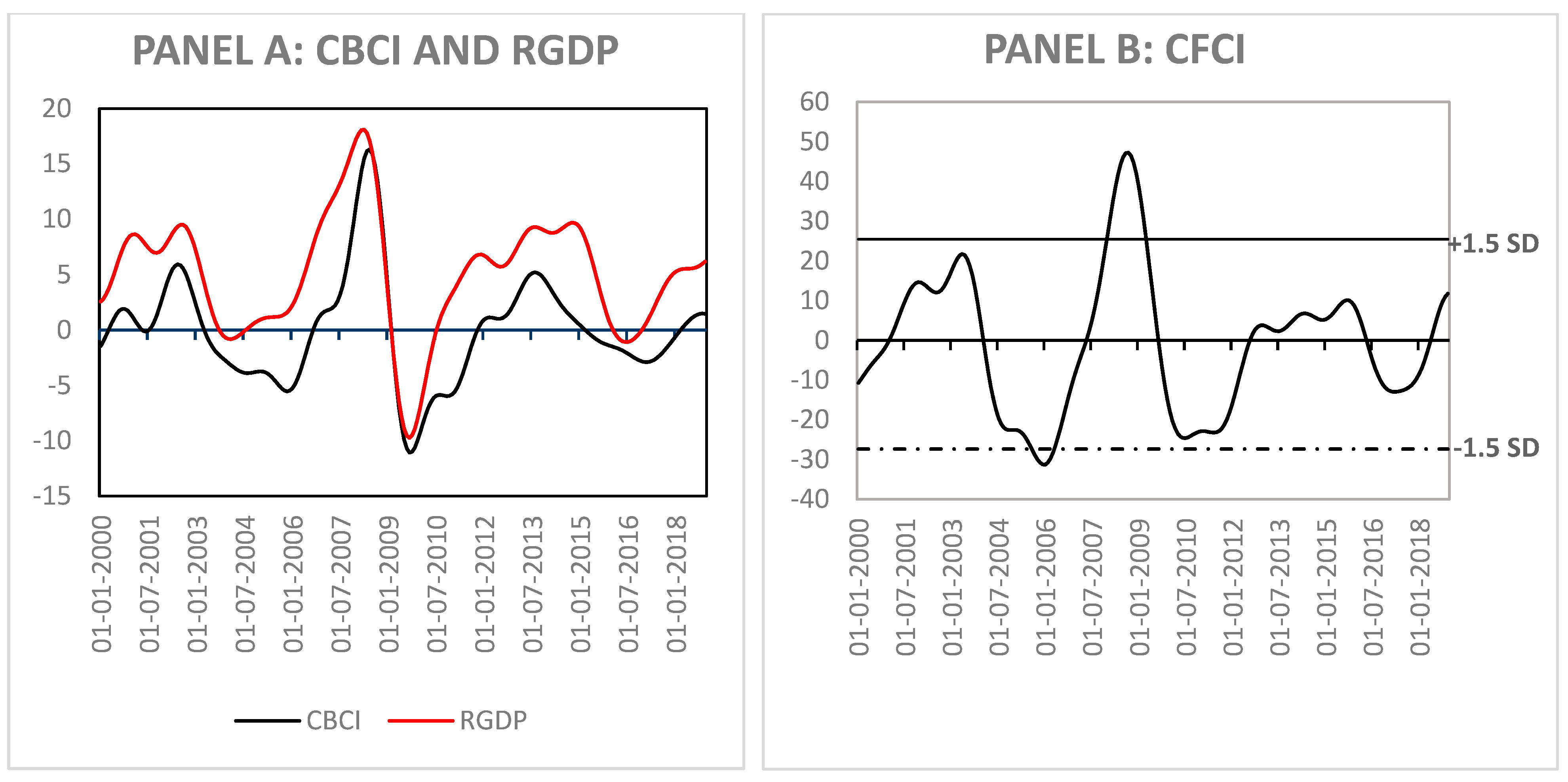
4.1. Results on the Measurement of Composite Indices
4.1.1. First Step: DFM and PCA
4.1.2. Second Step: Markov Switching Dynamic Regression Model
4.2. Results on the Interactions between MaPP and MP
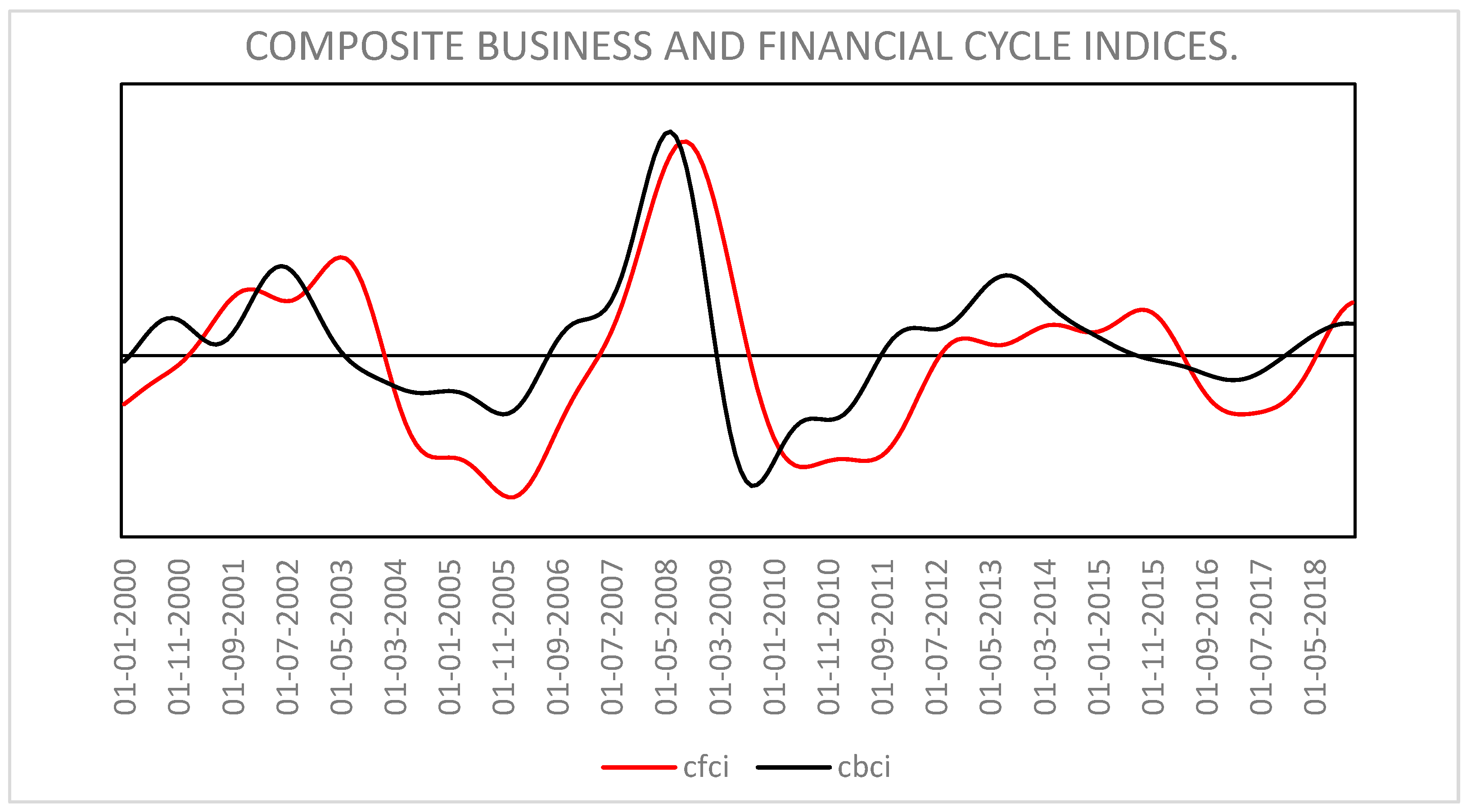
4.2.1. Graphical Illustration of the Interactions between CBCI and CFCI
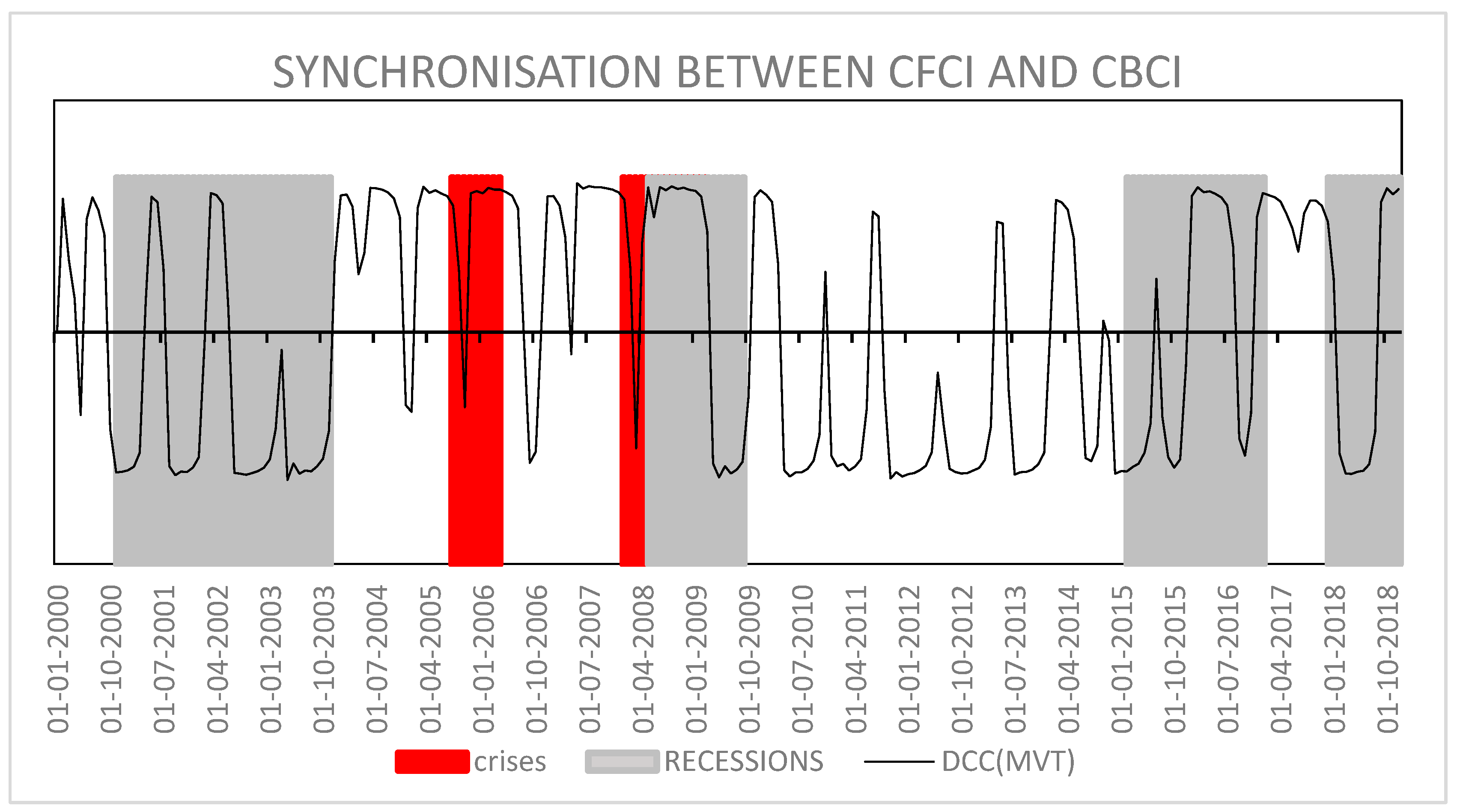
4.2.2. Synchronisation between CFCI and CBCI
4.2.3. Interactions between MaPP and MP and Their Coordination
4.2.4. Discussion of Findings
5. Conclusions and Recommendations
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| List of Indicators Used to Describe Composite Business Cycle Index | |
|---|---|
| SARB Selected Monthly release | WHOLESALE SALES |
| SARB Selected Monthly release | RETAIL SALES |
| SARB Selected Monthly release | NEW PASS VEHICLE |
| SARB Selected Monthly release | Real estate loans |
| SARB Selected Monthly release | IP-Total M |
| SARB Selected Monthly release | IP-food and beverages |
| SARB Selected Monthly release | IP-Raw Material |
| SARB Selected Monthly release | IP-textiles, Leather, |
| SARB Selected Monthly release | IP-wood and paper |
| SARB Selected Monthly release | IP-Equipment |
| SARB Selected Monthly release | IP-Durable Material |
| SARB Selected Monthly release | IP-Fuels |
| SARB Selected Monthly release | Building Plans Pd |
| SARB Selected Monthly release | Real Eff EX |
| SARB Selected Monthly release | M0 |
| SARB Selected Monthly release | M1 |
| SARB Selected Monthly release | M2 |
| SARB Selected Monthly release | SA/ US dollar |
| SARB Selected Monthly release | SA/British pound |
| SARB Selected Monthly release | SA/Euro |
| SARB Selected Monthly release | SA/Japanese yen |
| SARB Selected Monthly release | Reserves of commercial Banks |
| SARB Selected Monthly release | Total Loans |
| SARB Selected Monthly release | Total Credit Ext |
| SARB Selected Monthly release | PPI-ALL GROUPS |
| SARB Selected Monthly release | PPI-INTERMEDIATE |
| SARB Selected Monthly release | PPI-CRUDE OILS |
| SARB Selected Monthly release | PPI-MANUFACTURING |
| SARB Selected Monthly release | PPI-METAL PRODS |
| SARB Selected Monthly release | PPI-METALS PPI-FOOD |
| SARB Selected Monthly release | CPI-ALL ITEMS |
| SARB Selected Monthly release | CPI-APPAREL |
| SARB Selected Monthly release | CPI-TRANSPORT |
| SARB Selected Monthly release | CPI-MEDICAL C |
| SARB Selected Monthly release | CPI-COMMODITY |
| SARB Selected Monthly release | CPI-DURABLES |
| SARB Selected Monthly release | CPI-SERVICES |
| SARB Selected Monthly release | CPI-ALL ITEMS LF |
| SARB Selected Monthly release | CPI-ALL ITEMS LS |
| SARB Selected Monthly release | CPI-ALL ITEMS LMC |
| SARB Selected Monthly release | Treasury Bills |
| SARB Selected Monthly release | 5 Year Gvnt Bonds |
| SARB Selected Monthly release | 10-year Gvnt Bonds |
| SARB Selected Monthly release | All Share Prices |
| SARB Selected Monthly release | Gvnt Debt |
| SARB Selected Monthly release | Gold Reserves |
| SARB Selected Monthly release | Total Exports |
| SARB Selected Monthly release | Total Imports |
| SARB Selected Monthly release | Budget Balance |
| SARB Selected Monthly release | Liquidation of Co |
| SARB Selected Monthly release | Total Credit to PS |
| SARB Selected Monthly release | Prime lending rate |
| SARB Selected Monthly release | investments |
| SARB Selected Monthly release | Gvnt Exp |
| SARB Selected Monthly release | Total Mining |
| SARB Selected Monthly release | Manufacturing |
| SARB Selected Monthly release | Comp Leading |
| SARB Selected Monthly release | Comp Coincident |
| SARB Selected Monthly release | Comp Lagging |
| SARB Selected Monthly release | Interest rates |
| SARB Selected Monthly release | total reserves |
| SARB Selected Monthly release | OECD Indicator for SA |
| SARB Selected Monthly release | Employment-Manu |
| SARB Selected Monthly release | Employment-Cons |
| SARB Selected Monthly release | Employment-Service |
| SARB Selected Monthly release | unemp-15–24 |
| SARB Selected Monthly release | Gvnt Final consumption |
| SARB Selected Monthly release | unemp 25–54 |
| SARB Selected Monthly release | unemp 55–64 |
| SARB Selected Monthly release | employment-industry |
| SARB Selected Monthly release | employment-Agriculture |
| SARB Selected Monthly release | GDP Growth |
| SARB Selected Monthly release | Household Debt |
| SARB Selected Monthly release | Real GDP |
| SARB Selected Monthly release | Gross Domestic EXP |
| SARB Selected Monthly release | Final Cons HH |
| SARB Selected Monthly release | Final Cons GVNT |
| SARB Selected Monthly release | Gross Fixed CF |
| SARB Selected Monthly release | Foreign Direct Inv |
References
- Adrian, Tobias, and Nellie Liang. 2016. Monetary Policy, Financial Conditions, and Financial Stability. Available online: https://www.newyorkfed.org/medialibrary/media/research/staff_reports/sr690.pdf (accessed on 18 September 2023).
- Adrian, Tobias, Arturo Estrella, and Hyun Song Shin. 2010. Monetary Cycles, Financial Cycles and the Business Cycle (1 January 2010). FRB of New York Staff Report No. 421. New York: FRB of New York. [Google Scholar] [CrossRef]
- Agénor, Pierre-Richard, Koray Alper, and Luiz Pereira da Silva. 2013. Capital regulation, monetary policy and financial stability. International Journal of Central Banking 9: 193–238. [Google Scholar]
- Agur, Itai. 2019. Monetary and macroprudential policy coordination among multiple equilibria. Journal of International Money and Finance 96: 192–209. [Google Scholar] [CrossRef]
- Ahmed, Jameel, Sajid M. Chaudhry, and Stefan Straetmans. 2018. Business and financial cycles in the Eurozone: Synchronization or decoupling. The Manchester School 86: 358–89. [Google Scholar] [CrossRef]
- Akar, Cüneyt. 2016. Analyzing the Synchronization between the Financial and Business Cycles in Turkey. Journal of Review on Global Economics 5: 25–35. Available online: https://ssrn.com/abstract=2913550 (accessed on 18 September 2023). [CrossRef]
- Artis, Mike, Hans-Martin Krolzig, and Juan Toro. 2004. The European business cycle. Oxford Economic Papers 56: 1–44. [Google Scholar] [CrossRef]
- Billio, Monica, and Anna Petronevich. 2017. Dynamical Interaction between Financial and Business Cycles (15 October 2017). University Ca’ Foscari of Venice, Department of Economics Research Paper Series No. 24/WP/2014; Venezia: University Ca’ Foscari of Venice. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. The Review of Economics and Statistics 72: 498–505. Available online: https://public.econ.duke.edu/~boller/Published_Papers/restat_90.pdf (accessed on 18 September 2022). [CrossRef]
- Borio, Claudio. 2014a. Monetary Policy and Financial Stability: What Role in Prevention and Recovery? Available online: https://www.bis.org/publ/work440.htm (accessed on 18 September 2022).
- Borio, Claudio. 2014b. The financial cycle and macroeconomics: What have we learnt? Journal of Banking & Finance 45: 182–98. [Google Scholar]
- Borio, Claudio, Craig Furfine, and Philip Lowe. 2001. Procyclicality of the financial system and financial stability: Issues and policy options. BIS Papers 1: 1–57. [Google Scholar]
- Bosch, Adél, and Franz Ruch. 2013. An Alternative Business Cycle Dating Procedure for South Africa. South African Journal of Economics 81: 491–516. [Google Scholar] [CrossRef]
- Bosch, Adél, and Steven F. Koch. 2020. The South African financial cycle and its relation to household deleveraging. South African Journal of Economics 88: 145–73. [Google Scholar] [CrossRef]
- Cagliarini, Adam, and Fiona Price. 2017. Exploring the Link between the Macroeconomic and Financial Cycles. In Monetary Policy and Financial Stability in a World of Low Interest Rates; Edited by Jonathan Hambur and John Simon. Reserve Bank of Australia. Available online: https://www.rba.gov.au/publications/confs/2017/pdf/rba-conference-volume-2017-cagliarini-price.pdf (accessed on 18 September 2023).
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Chorafas, Dimitris N. 2015. Financial cycles. In Financial Cycles: Sovereigns, Bankers, and Stress Tests. New York: Palgrave Macmillan US, pp. 1–24. Available online: https://link.springer.com/chapter/10.1057/9781137497987_1 (accessed on 18 September 2022).
- Choudhry, Taufiq, Fotios I. Papadimitriou, and Sarosh Shabi. 2016. Stock market volatility and business cycle: Evidence from linear and nonlinear causality tests. Journal of Banking & Finance 66: 89–101. [Google Scholar]
- Claessens, Stijn. 2013. Interactions between Monetary and Macroprudential Policies in an Interconnected World. Paper presented at Bank of Thailand-IMF Conference on Monetary Policy in an Interconnected World, Bangkok, Thailand, November 1–2; vol. 31. Available online: https://www.bcu.gub.uy/Comunicaciones/DCI_Interno/Claessens%20-%20Interactions%20between%20Monetary%20and%20Macroprudential%20Policies%20in%20an%20Interconnected%20World.pdf (accessed on 18 September 2022).
- Claessens, Stijn, M. Ayhan Kose, and Marco E. Terrones. 2011. Financial cycles: What? how? when? In NBER International Seminar on Macroeconomics. Chicago: University of Chicago Press, vol. 7, pp. 303–44. [Google Scholar]
- Claessens, Stijn, M. Ayhan Kose, and Marco E. Terrones. 2012. How do business and financial cycles interact? Journal of International Economics 87: 178–90. [Google Scholar] [CrossRef]
- Comrey, Andrew L., and Howard B. Lee. 2013. A First Course in Factor Analysis. New York: Psychology Press. [Google Scholar] [CrossRef]
- Constâncio, Vítor, Inês Cabral, Carsten Detken, John Fell, Jérôme Henry, Paul Hiebert, Sujit Kapadia, Sergio Nicoletti Altimar, Fatima Pires, and Carmelo Salleo. 2019. Macroprudential Policy at the ECB: Institutional Framework, Strategy, Analytical Tools and Policies. Strategy, Analytical Tools and Policies (July). Available online: https://www.ecb.europa.eu/pub/pdf/scpops/ecb.op227~971b0a4996.en.pdf (accessed on 18 September 2022).
- de Paoli, Bianca, and Matthias Paustian. 2017. Coordinating monetary and macroprudential policies. Journal of Money, Credit and Banking 49: 319–49. [Google Scholar] [CrossRef]
- Doz, Catherine, and Anna Petronevich. 2016. Dating business cycle turning points for the french economy: An MS-DFM approach. In Dynamic Factor Models. Bingley: Emerald Group Publishing Limited, pp. 481–538. [Google Scholar] [CrossRef]
- Drehmann, Mathias, Claudio Borio, and Konstantinos Tsatsaronis. 2012. Characterising the Financial Cycle: Don’t Lose Sight of the Medium Term! (June 1). BIS Working Paper No. 380. Available online: https://ssrn.com/abstract=2084835 (accessed on 18 September 2022).
- Dunstan, Ashley. 2014. The interaction between monetary and macro-prudential policy. Reserve Bank of New Zealand Bulletin 77: 15–25. [Google Scholar]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Farrell, Greg, and Esti Kemp. 2020. Measuring the financial cycle in South Africa. South African Journal of Economics 88: 123–44. [Google Scholar] [CrossRef]
- Frait, Jan, and Zlatuše Komárková. 2010. Financial stability, systemic risk and macroprudential policy. Financial Stability Report 2011: 96–111. [Google Scholar]
- Frait, Jan, Simona Malovaná, and Vladimír Tomšík. 2014. The interaction of monetary and macroprudential policies in the pursuit of the central bank’s primary objectives. CNB Financial Stability Report 2015: 110–20. [Google Scholar]
- Gächter, Martin, Aleksandra Riedl, and Doris Ritzberger-Grünwald. 2012. Business cycle synchronization in the euro area and the impact of the financial crisis. Monetary Policy & the Economy 2: 33–60. [Google Scholar]
- Ghalanos, Alexios. 2019. The RMGARCH Models: Background and Properties. Version 1.3-0. Available online: https://mran.microsoft.com (accessed on 19 June 2021).
- Gogas, Periklis, and George Kothroulas. 2009. Two Speed Europe and Business Cycle Synchronization in the European Union: The Effect of the Common Currency. MPRA Paper. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/13909 (accessed on 18 September 2022).
- Gökalp, Bekir Tamer, and Xingkai Yu. 2018. Do the Business Cycles and Financial Cycles Move Together in Turkey? Journal of Advances in Economics and Finance 3: 19–26. [Google Scholar] [CrossRef]
- Hamilton, James D. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica: Journal of the Econometric Society 57: 357–84. [Google Scholar] [CrossRef]
- Hodula, Martin, Jan Janků, and Lukáš Pfeifer. 2023. Macro-prudential policies to contain the effect of structural risks on financial downturns. Journal of Policy Modeling. [Google Scholar] [CrossRef]
- Hollander, Hylton, and Dawie Van Lill. 2019. A Review of the South African Reserve Bank’s Financial Stability Policies. Working Papers 11/2019, Stellenbosch University, Department of Economics. Available online: https://ideas.repec.org/p/sza/wpaper/wpapers325.html (accessed on 18 September 2022).
- Jeantheau, Thierry. 1998. Strong consistency of estimators for multivariate ARCH models. Econometric Theory 14: 70–86. [Google Scholar] [CrossRef]
- Kim, Chang-Jin. 1994. Dynamic linear models with Markov-switching. Journal of Econometrics 60: 1–22. [Google Scholar] [CrossRef]
- Kim, Myung-Jig, and Ji-Sung Yoo. 1995. New index of coincident indicators: A multivariate Markov switching factor model approach. Journal of Monetary Economics 36: 607–30. [Google Scholar] [CrossRef]
- Kokores, Ioanna. 2015. Lean-against-the-wind monetary policy: The post-crisis shift in the literature. SPOUDAI Journal of Economics and Business 65: 66–99. [Google Scholar]
- Kose, M. Ayhan, Christopher Otrok, and Eswar Prasad. 2012. Global Business Cycles: Convergence or Decoupling? International Economic Review 53: 511–38. Available online: http://www.jstor.org/stable/23251597 (accessed on 18 September 2023). [CrossRef]
- Krznar, Ivo. 2011. Identifying Recession and Expansion Periods in Croatia. CNB Istraživanja. Available online: https://www.hnb.hr/repec/hnb/wpaper/pdf/w-029.pdf (accessed on 18 September 2023).
- Krznar, Ivo, and Troy D. Matheson. 2017. Financial and Business Cycles in Brazil. International Monetary Fund. Available online: https://www.imf.org/en/Publications/WP/Issues/2017/01/24/Financial-and-Business-Cycles-in-Brazil-44577 (accessed on 18 September 2023).
- Leamer, Edward E. 2007. Housing is the Business Cycle. No. w13428. Kansas City: Federal Reserve Bank of Kansas City, pp. 149–233. [Google Scholar]
- Liu, Guangling, and Thabang Molise. 2020. The optimal monetary and macroprudential policies for the South African economy. South African Journal of Economics 88: 368–404. [Google Scholar] [CrossRef]
- Ma, Yong, and Jinglan Zhang. 2016. Financial cycle, business cycle and monetary policy: Evidence from four major economies. International Journal of Finance & Economics 21: 502–27. [Google Scholar]
- Malovana, Simona, and Jan Frait. 2017. Monetary policy and macroprudential policy: Rivals or teammates? Journal of Financial Stability 32: 1–16. [Google Scholar] [CrossRef]
- Malovaná, Simona, Martin Hodula, Zuzana Gric, and Josef Bajzík. 2023. Macroprudential policy in central banks: Integrated or separate? Survey among academics and central bankers. Journal of Financial Stability 65: 101107. [Google Scholar] [CrossRef]
- Metcalfe, Les. 1994. International policy co-ordination and public management reform. International Review of Administrative Sciences 60: 271–90. [Google Scholar] [CrossRef]
- Mink, Mark, Jan P. A. M. Jacobs, and Jakob de Haan. 2007. Measuring Synchronicity and Co-Movement of Business Cycles with an Application to the Euro Area. CESifo Working Paper, No. 2112. Munich: Center for Economic Studies and ifo Institute (CESifo). Available online: http://hdl.handle.net/10419/26157 (accessed on 18 September 2023).
- Nzimande, Ntokozo Patrick, and Harold Ngalawa. 2016. Is There a SADC Business Cycle? Evidence from a Dynamic Factor Model. Economic Research Southern Africa. Available online: https://policycommons.net/artifacts/2120725/is-there-a-sadc-business-cycle-evidence-from-a-dynamic-factor-model/2876023/ (accessed on 20 September 2022).
- Oman, William. 2019. The synchronization of business cycles and financial cycles in the euro area. International Journal of Central Banking 15: 327–62. [Google Scholar]
- Pan, Haifeng, and Dingsheng Zhang. 2020. Coordination Effects and Optimal Policy Choices of Macroprudential Policy and Monetary Policy. Complexity 2020: 1–11. [Google Scholar] [CrossRef]
- Pineda, Emilio, Paul Anthony Cashin, and Yan Sun. 2009. Assessing Exchange Rate Competitiveness in the Eastern Caribbean Currency Union. Available online: https://www.imf.org/external/pubs/ft/wp/2009/wp0978.pdf (accessed on 18 September 2023).
- Rünstler, Gerhard, and Marente Vlekke. 2015. Business and Financial Cycles: An Unobserved Components Models Perspective. European Central Bank. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=R%C3%BCnstler%2C+Gerhard%2C+and+Marente+Vlekke.+%22Business+and+financial+cycles%3A+an+unobserved+components+models+perspective.%22+European+Central+Bank+%282015%29.+&btnG= (accessed on 18 September 2023).
- Sala-Rios, Mercè, Teresa Torres-Solé, and Mariona Farré-Perdiguer. 2016. Credit and business cycles’ relationship: Evidence from Spain. Portuguese Economic Journal 15: 149–71. [Google Scholar] [CrossRef]
- Savva, Christos S., Kyriakos C. Neanidis, and Denise R. Osborn. 2010. Business cycle synchronization of the euro area with the new and negotiating member countries. International Journal of Finance & Economics 15: 288–306. [Google Scholar]
- Seo, Joo Hwan, Sung Yong Park, and Larry Yu. 2009. The analysis of the relationships of Korean outbound tourism demand: Jeju Island and three international destinations. Tourism Management 30: 530–43. [Google Scholar] [CrossRef]
- Smets, Frank. 2018. Financial stability and monetary policy: How closely interlinked? International Journal of Central Banking 10: 263–300. [Google Scholar]
- South African Reserve Bank. 2016. A New Macroprudential Policy Framework for South Africa. Pretoria: Financial Stability Department. Available online: https://www.resbank.co.za/content/dam/sarb/what-we-do/financial-stability/A%20new%20macroprudential%20policy%20framework%20for%20South%20Africa.pdf (accessed on 18 September 2023).
- Spencer, Grant. 2014. Coordination of Monetary Policy and Macro-Prudential Policy. In Speech Delivered to Credit Suisse Asian Investment Conference in Hong Kong. Available online: https://www.rbnz.govt.nz/hub/publications/speech/2014/speech2014-03-27 (accessed on 18 September 2023).
- Stock, James H., and Mark W. Watson. 2003. Forecasting output and inflation: The role of asset prices. Journal of economic literature 41: 788–829. [Google Scholar] [CrossRef]
- Svensson, Lars E. O. 2018. Monetary policy and macroprudential policy: Different and separate? Canadian Journal of Economics/Revue Canadienne D’économique 51: 802–27. [Google Scholar] [CrossRef]
- Tse, Yiu Kuen, and Albert K. C. Tsui. 2002. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. Journal of Business & Economic Statistics 20: 351–62. [Google Scholar]
- Tsiakas, Ilias, and Haibin Zhang. 2023. On the direction of causality between business and financial cycles. Journal of Risk and Financial Management 16: 430. [Google Scholar] [CrossRef]
- Venter, Johann Christoffel. 2009. Business Cycles in South Africa during the Period 1999 to 2007. Pretoria: South African Reserve Bank. Available online: https://www.resbank.co.za/content/dam/sarb/publications/quarterly-bulletins/quarterly-bulletin-publications/2009/4051/Article---Business-cycles-in-South-Africa-during-the-period-1999-to-2007.pdf (accessed on 18 September 2023).
- Vermeulen, Cobus, A. Bosch, J. Rossouw, and F. Joubert. 2017. From the business cycle to the output cycle: Predicting South African economic activity. Studies in Economics and Econometrics 41: 111–33. [Google Scholar] [CrossRef]

| Variable | Abreviation | Description | Source |
|---|---|---|---|
| Real Broad effective exchange rate | RBEER | RBEER is a measure of value of the currency against a weighted average of several foreign currencies divided by a price deflator or index of cost (Pineda et al. 2009). | South African Reserve Bank |
| House Prices | HP | HP is measured by the Residential Property Price Index showing indices of residential property prices over time. | Bank for International Settlements |
| All Share Price Index | ASP | ASP is the total share price for all share on the JSE. | South African Reserve Bank |
| Long-term Government bond yields | LTGBY | LTGBY represents long-term interest rates exceeding 10 years | South African Reserve Bank |
| 10-year Government bond yields | GB10Y | GB10Y represents long-term interest rates equal to 10 years | South African Reserve Bank |
| 5-year Government bond yields | GB5Y | GB5Y represents short-term interest rates less than 10 years | South African Reserve Bank |
| Total credit to the private Non-Financial sector | TCPFS | TCPFS is provided by domestic banks, all other sectors of the economy and non-residents. | OECD, Reserve Bank of St Louis |
| Nominal effective exchange rate | NEER | NEER is calculated as geometric weighted averages of bilateral exchange rates. | OECD, Reserve Bank of St Louis |
| Treasury Bill Rate | TBILL | TBILL is a short-term debt obligation of the central government | South African Reserve Bank |
| The three measures of money in South Africa | M1, M2 and M3 | Narrow Measure, Intermediate measure, Broad measure | South African Reserve Bank |
| Interbank Lending rate | ILR | ILR is the rate charged on short-term loans between South African banks | OECD, Reserve Bank of St Louis |
| CBCI | CFCI | ||
|---|---|---|---|
| Peaks | Troughs | Peaks | Troughs |
| March 2003 | March 2004 | May 2003 | January 2006 |
| August 2008 | July 2010 | September 2008 | June 2011 |
| DCC (MVN) | ADCC (MVN) | DCC (MVT) | ADCC (MVT) | |
|---|---|---|---|---|
| 0.731 *** | 0.731 *** | 0.854 *** | 0.855 *** | |
| 0.198 *** | 0.198 ** | 0.060 * | 0.060 * | |
| - | 0 | - | 0 | |
| - | - | 50.000 *** | 50.000 *** | |
| 752.70 | 752.70 | 766.01 | 767.34 |
| Level 8: Establishing central priorities desynchronization between BCs and FCs |
| Level 7: Setting limits on policy actions desynchronization between BCs and FCs |
| Level 6: Arbitration of policy differences desynchronization between BCs and FCs |
| Level 5: Search for agreement among MaPP and MP desynchronization between BCs and FCs |
| Level 4: Avoid divergences among MaPP and MP 0%―39% synchronization between BCs and FCs |
| Level 3: Consultation and feedback between MaPP and MP 40%―59% synchronization between BCs and FCs |
| Level 2: Communication between each other (MaPP and MP) 60%―79% synchronization between BCs and FCs |
| Level 1: Independent decision-making by MaPP and MP 80%―100% synchronization between BCs and FCs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyati, M.C.; Muzindutsi, P.-F.; Tipoy, C.K. Macroprudential and Monetary Policy Interactions and Coordination in South Africa: Evidence from Business and Financial Cycle Synchronisation. Economies 2023, 11, 272. https://doi.org/10.3390/economies11110272
Nyati MC, Muzindutsi P-F, Tipoy CK. Macroprudential and Monetary Policy Interactions and Coordination in South Africa: Evidence from Business and Financial Cycle Synchronisation. Economies. 2023; 11(11):272. https://doi.org/10.3390/economies11110272
Chicago/Turabian StyleNyati, Malibongwe Cyprian, Paul-Francois Muzindutsi, and Christian Kakese Tipoy. 2023. "Macroprudential and Monetary Policy Interactions and Coordination in South Africa: Evidence from Business and Financial Cycle Synchronisation" Economies 11, no. 11: 272. https://doi.org/10.3390/economies11110272






