Public R&D and Growth: A dynamic Panel Vector-Error-Correction Model Analysis for 14 OECD Countries
Abstract
:1. Introduction
2. Economic and Econometric Approaches of the Literature to Public R&D Analysis
2.1. Direct Effects of Public R&D in the Traditional Standard Approach
2.2. Indirect Effects of Public R&D in an Endogenous Growth Approach
2.3. Direct and Indirect Effects of Public R&D in VECMs
2.4. Choices in Panel Data Econometrics
- (i)
- Cointegration tests show the relation for the pairs of variables mentioned above; three of the five pairs have no panel cointegration, and therefore, we go from five pairs to four triples of variables that do have cointegration6 and are estimated using cointegrating regression methods, FMOLS and DOLS:
- GDP–productivity;
- Productivity–private R&D–public R&D;
- Private R&D–public R&D–foreign private R&D;
- Public R&D–foreign private R&D–foreign public R&D.
- (ii)
- We use a vector-error-correction model with these four cointegrating equations from group mean versions of DOLS and FMOLS estimations with cross-section fixed effects and, in the differenced part, fixed effects and slope homogeneity in the regression coefficients and the adjustment coefficients. This a restricted version of the panel VECM suggested in the econometric literature (Hsiao 2022, chp. 5.3.2.1). It allows us to run simulations of shock effects going through all six equations for growth of the endogenous GDP, productivity and four R&D variables mentioned above (see Section 4).7 We find positive direct and indirect effects of public R&D on productivity in the long-term relations obtained via DOLS and FMOLS and also through the shocks on the public R&D equation.
3. Data
4. Econometric Methods
4.1. Unit Roots in the Presence of Cross-Section Dependence
4.2. Cointegration Testing Linked to VECMs and Residual-Based Tests
4.3. A VECM with Fixed Effects, Slope Homogeneity in Differenced Terms and Adjustment Coefficients and Long-Term Growth Relations from DOLS and FMOLS
5. Estimation Results from Dynamic Modeling
5.1. Unit Roots Results
5.2. Panel Cointegration Results
5.3. Results for a Two-Stage VECM with Long-Term Relations from DOLS and FMOLS Estimates
6. Public and Private R&D Changes
6.1. Effects from Enhancing Public R&D
6.2. Effects from Enhancing Domestic Private R&D, Foreign Private and Public R&D
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Variable | Bai/Ng (a): No Unit Root | Bai/Ng (b): No Unit Root | No. of No-Unit Roots in CIPS Test (Table 2) |
|---|---|---|---|
| LGDP | No country | AUT | 1 (DEU) |
| LTH07 | DEU, JPN | DEU, JPN | 1 (DEU) |
| LBERDST | AUT, BEL, DEU, FIN | AUT, BEL, DNK, ESP, FIN, ITA, NLD, SWE | 4 (AUT, ESP, NLD, USA) |
| LPUBST | All but … (c) | FIN, GBR, ITA, PRT, SWE | 5 (DEU, DNK, ITA, PRT, SWE) |
| LFPUBST | DEU | No country | 0 |
| LFBERDST | AUT, DEU, DNK, ITA, JPN, NLD, NOR, SWE | BEL, GBR, ITA | 2 (GBR, ITA) |
| Equation Country | D(LGDP) | D(LOG(TH07)) | D(LBERDST) | D(LPUBST) | D(LFBERDST) | D(LFPUBST) |
|---|---|---|---|---|---|---|
| AUT | R2: 0.299 | 0.115 | 0.696 | 0.827 | 0.894 | 0.94 |
| (b): −0.316 | −0.664 | 0.428 | 0.675 | 0.8 | 0.888 | |
| DW:2.31 | 2.04 | 2.2 | 1.965 | 2.165 | 1.731 | |
| BEL | 0.06 | 0.251 | 0.827 | 0.794 | 0.897 | 0.94 |
| −0.767 | −0.41 | 0.675 | 0.613 | 0.807 | 0.888 | |
| 2.75 | 2.56 | 2.239 | 1.266 | 2.065 | 1.53 | |
| DEU | 0.126 | 0.248 | 0.927 | 0.943 | 0.886 | 0.924 |
| −0.56 | −0.342 | 0.87 | 0.898 | 0.797 | 0.866 | |
| 1.885 | 1.39 | 1.83 | 2.22 | 1.7 | 1.993 | |
| DNK | 0.103 | 0.019 | 0.907 | 0.678 | 0.892 | 0.944 |
| −0.687 | −0.844 | 0.825 | 0.396 | 0.797 | 0.894 | |
| 2.247 | 2.404 | 1.224 | 2.45 | 2.085 | 1.564 | |
| ESP | 0.468 | 0.37 | 0.845 | 0.797 | 0.883 | 0.93 |
| 0.0001 | −0.184 | 0.71 | 0.62 | 0.78 | 0.869 | |
| 1.129 | 1.47 | 2.54 | 2.445 | 2.003 | 1.54 | |
| FIN | 0.336 | 0.336 | 0.92 | 0.919 | 0.893 | 0.947 |
| −0.3 | −0.299 | 0.843 | 0.841 | 0.792 | 0.895 | |
| 1.567 | 1.531 | 1.74 | 2.175 | 1.959 | 2.008 | |
| GBR | 0.045 | 0.141 | 0.613 | 0.67 | 0.907 | 0.967 |
| −0.705 | −0.534 | 0.308 | 0.41 | 0.834 | 0.942 | |
| 2.184 | 2.433 | 2.31 | 1.646 | 2.182 | 1.856 | |
| ITA | 0.234 | 0.302 | 0.88 | 0.865 | 0.94 | 0.941 |
| −0.368 | −0.247 | 0.787 | 0.76 | 0.894 | 0.894 | |
| 2.04 | 1.807 | 1.781 | 2.298 | 1.91 | 1.94 | |
| JPN | 0.633 | 0.445 | 0.946 | 0.972 | 0.908 | 0.937 |
| 0.345 | 0.0092 | 0.903 | 0.95 | 0.836 | 0.888 | |
| 2.198 | 1.835 | 2.216 | 1.56 | 2.019 | 1.756 | |
| NLD | 0.462 | 0.206 | 0.681 | 0.619 | 0.913 | 0.955 |
| 0.039 | −0.417 | 0.43 | 0.319 | 0.845 | 0.919 | |
| 1.55 | 2.06 | 2.092 | 2.445 | 2.076 | 2.096 | |
| NOR | 0.447 | 0.178 | 0.901 | 0.842 | 0.886 | 0.921 |
| −0.106 | −0.644 | 0.802 | 0.683 | 0.772 | 0.842 | |
| 1.697 | 2.12 | 1.91 | 2.31 | 1.937 | 1.853 | |
| PRT | 0.457 | 0.31 | 0.863 | 0.897 | 0.895 | 0.95 |
| 0.0298 | −0.232 | 0.756 | 0.817 | 0.812 | 0.91 | |
| 1.995 | 1.9 | 1.597 | 1.393 | 1.973 | 1.942 | |
| SWE | 0.16 | 0.265 | 0.884 | 0.914 | 0.905 | 0.944 |
| −0.58 | −0.383 | 0.782 | 0.838 | 0.821 | 0.895 | |
| 2.168 | 1.712 | 2.1 | 1.555 | 1.954 | 1.552 | |
| USA | 0.023 | −0.202 (c) | 0.863 | 0.859 | 0.926 | 0.898 |
| −0.744 | −1.146 | 0.755 | 0.747 | 0.867 | 0.818 | |
| 1.861 | 1.644 | 1.575 | 1.19 | 1.998 | 2.106 |
Appendix C

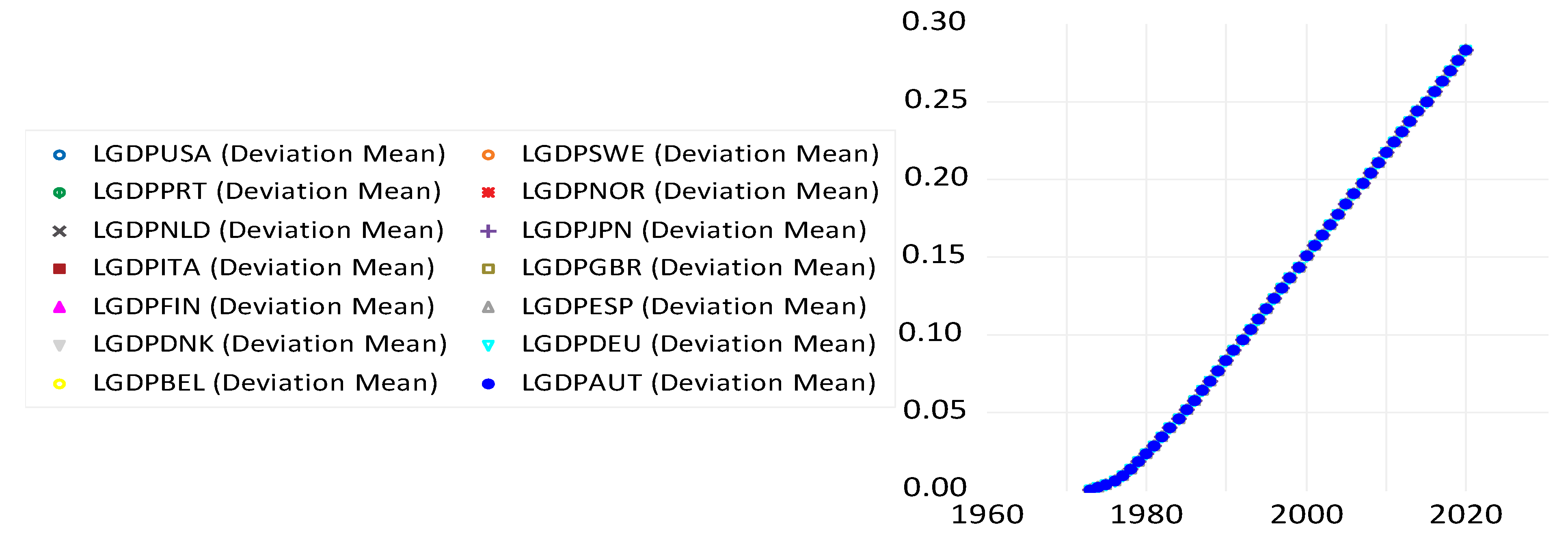



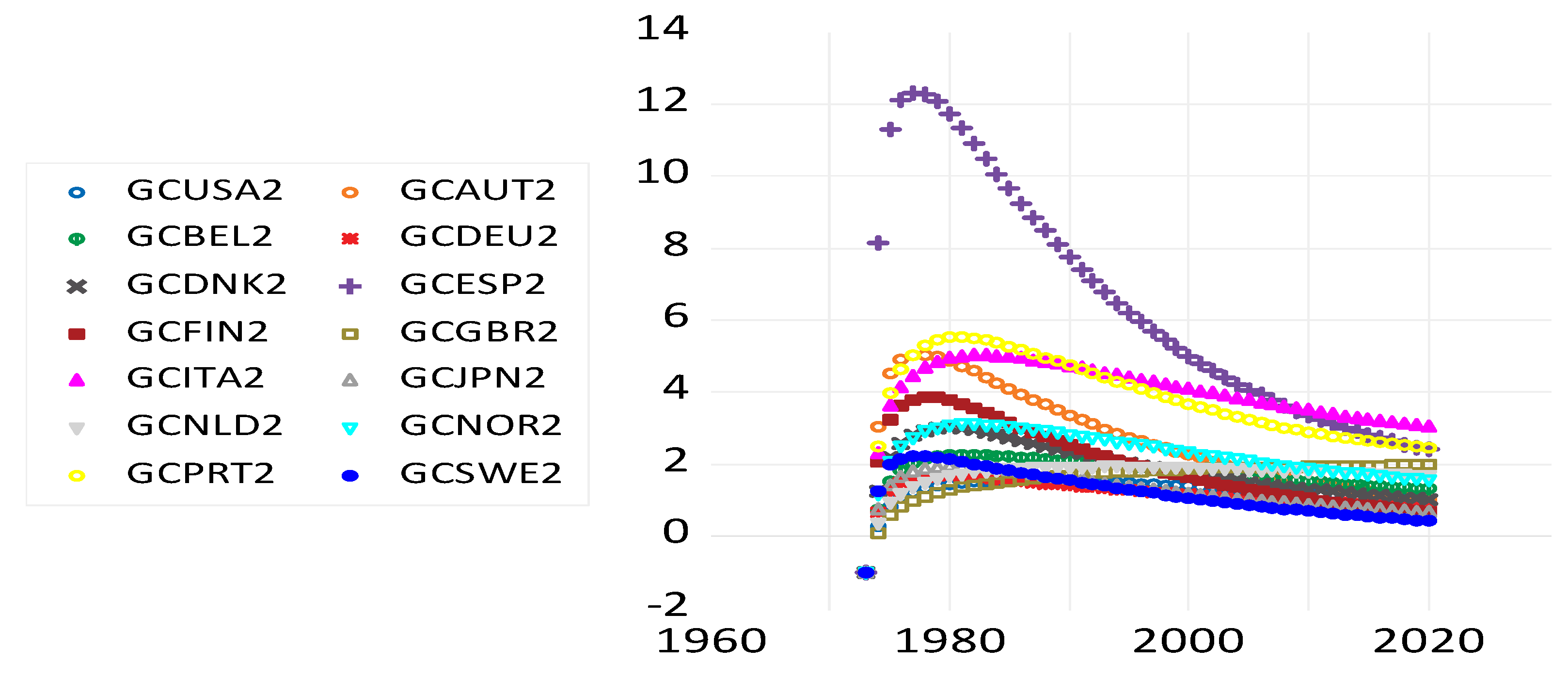
Appendix D
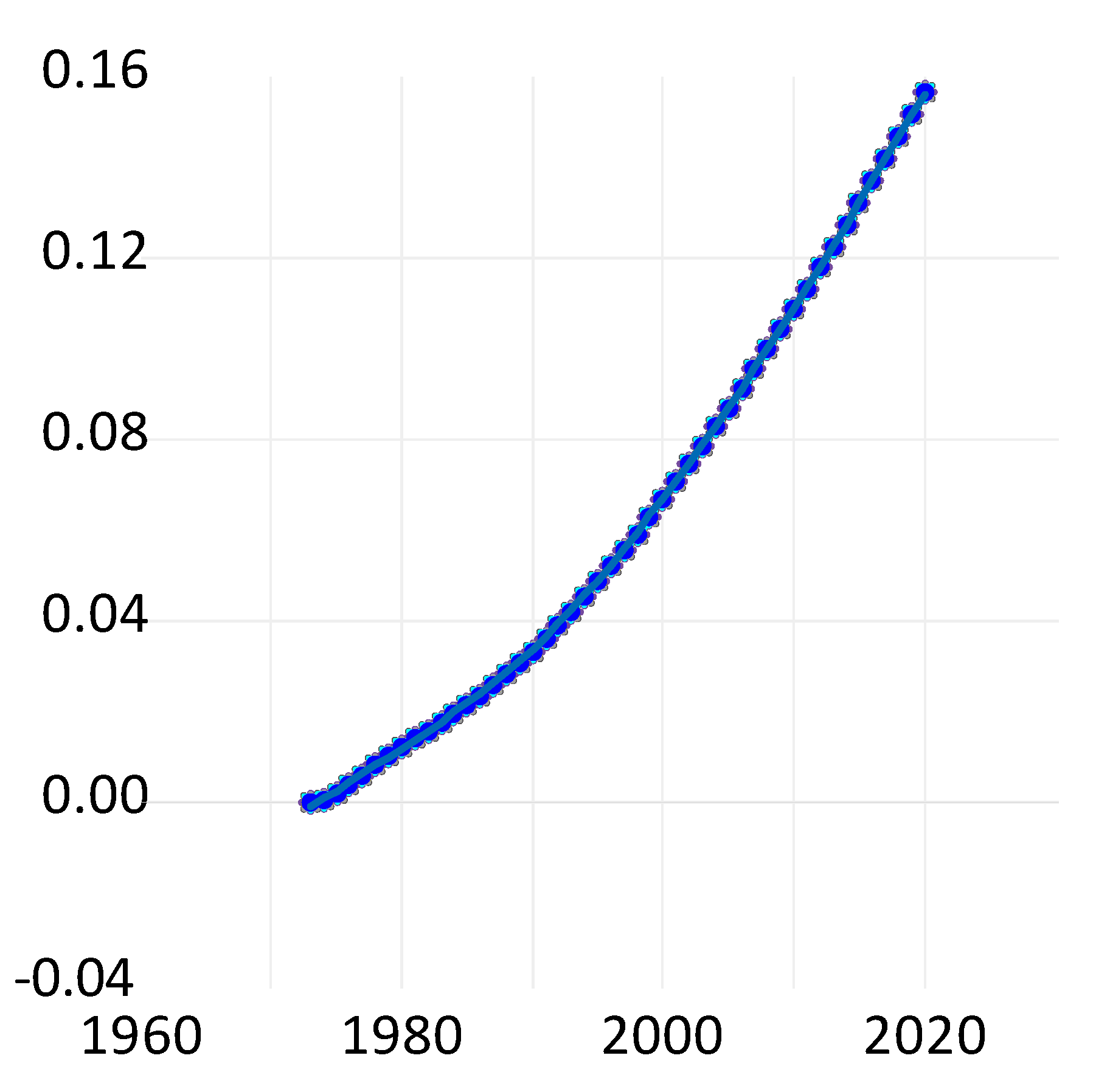
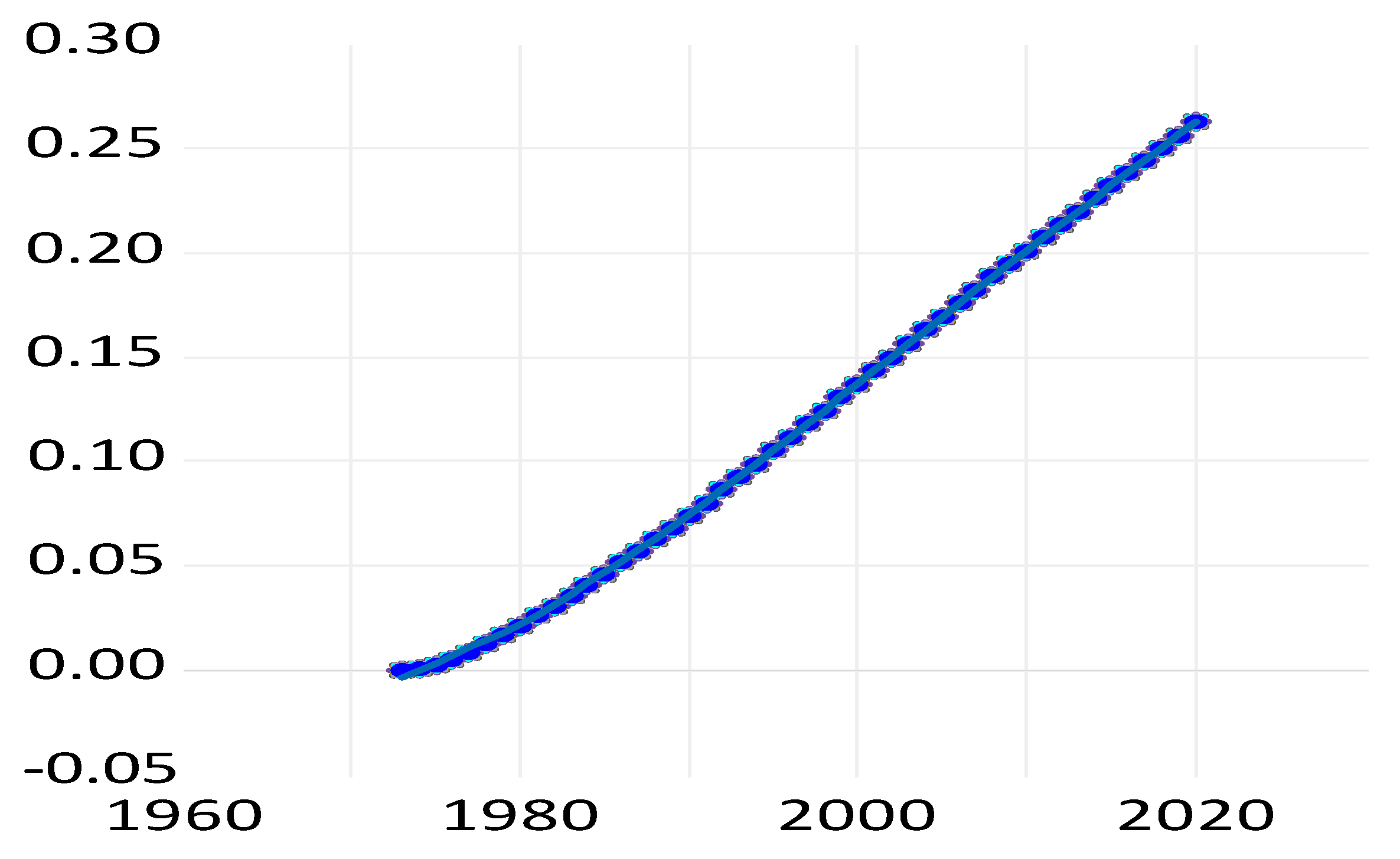
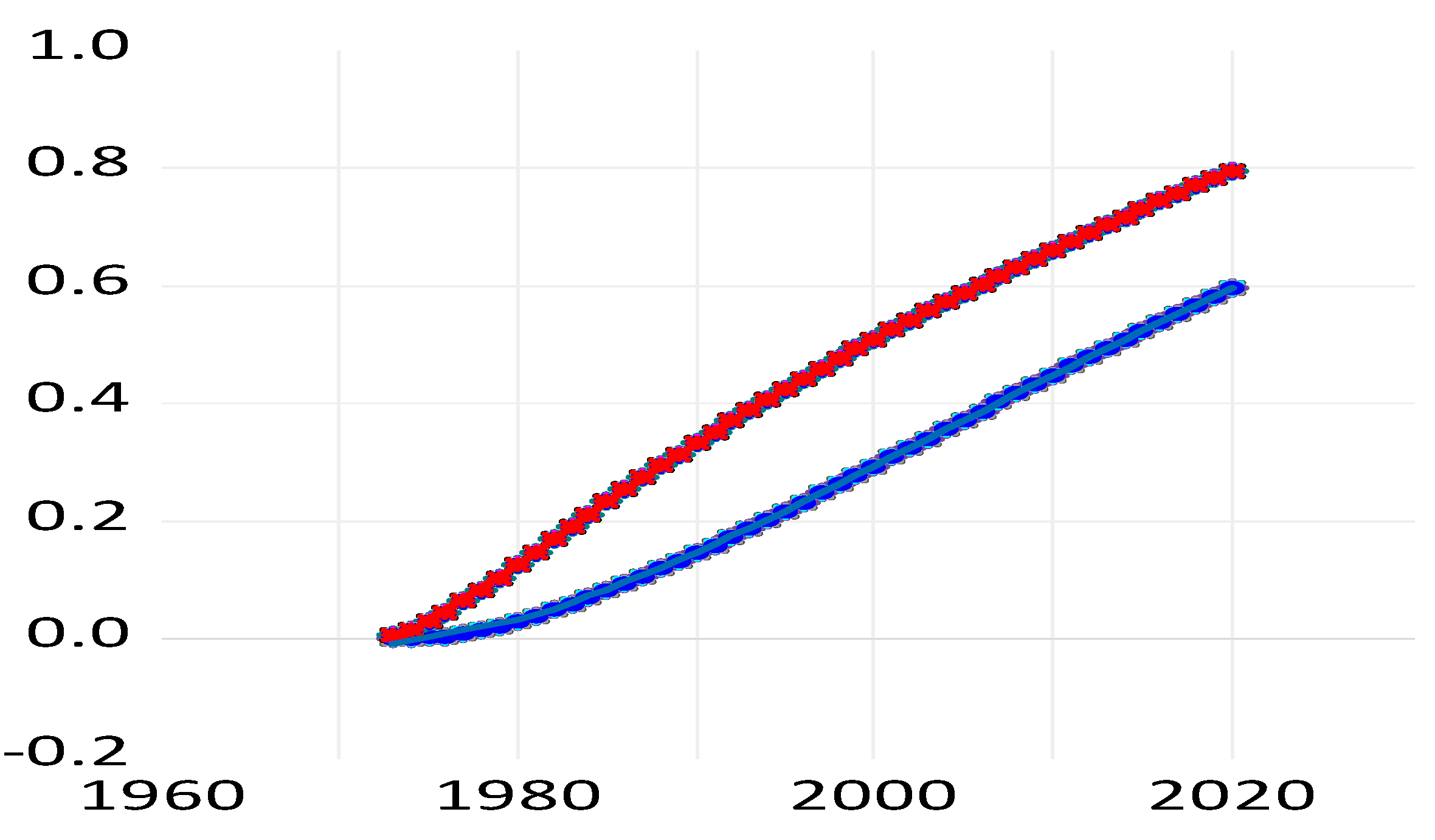
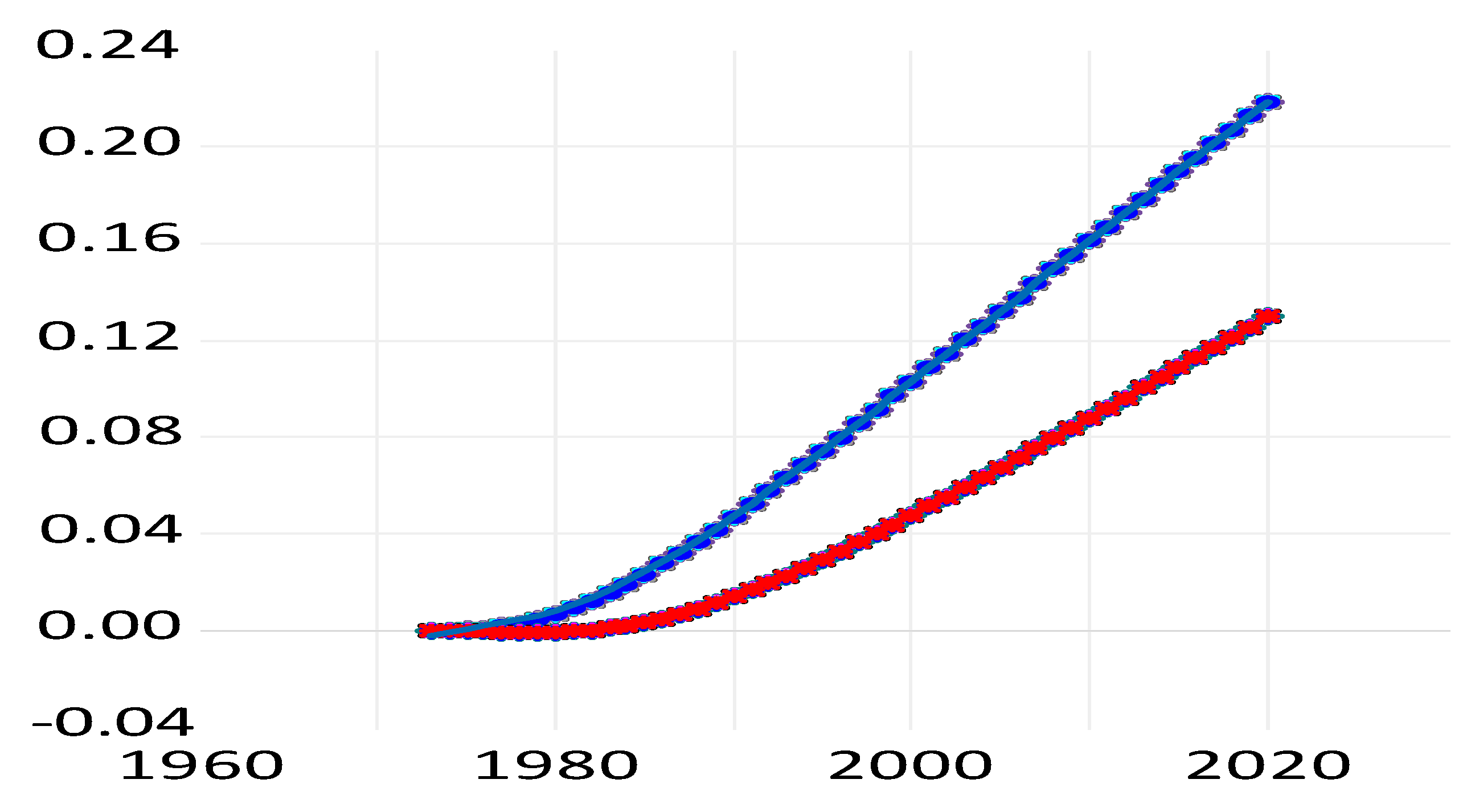
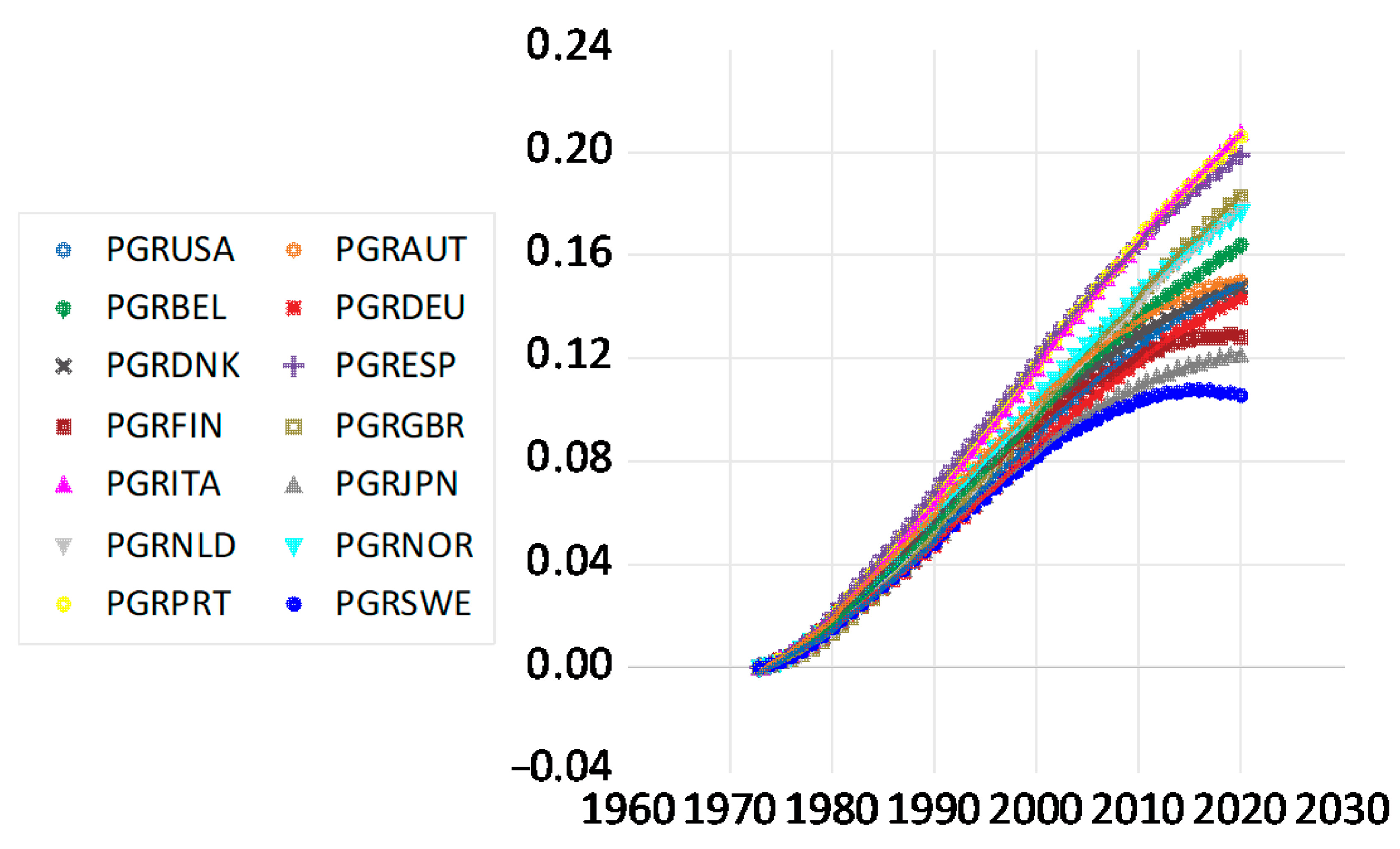

| 1 | We discuss more studies below in connection with our results but only to the extent that it is comparable, in particular with respect to distinguishing between public and private R&D for home and foreign countries. In the literature reports, we will not distinguish strictly between privately or publicly performed and financed R&D. It is conceivable that publicly performed R&D is productive whereas publicly financed R&D is less so, if the public finance means used in business are used less effectively; similar to measurement errors, this may undermine statistical significance. |
| 2 | |
| 3 | When first-order conditions do not hold with equality, a complementary slackness variable z can be added and assumed to be part of the estimated constant anxxd the residual. |
| 4 | In the case of K = six variables, five (four or three; r = 5, 4 or 3) long-term relations can determine only five (four or three) variables depending on the other variables. Therefore, all values follow from the complete system and not from partial relations. |
| 5 | Even if all regressions would find the same elasticity for public R&D, calibration using seemingly robust parameters from a variety of sources does not necessarily lead to simulation results matching the data. |
| 6 | Older panel time-series studies are occasionally criticized for not having considered the issues of unit roots and cointegration (Hsiao 2022). |
| 7 | This method is preferable to pairwise Granger causality analysis, which does not consider the impact on third variables (Lütkepohl 2005). Of course, Granger causality analysis can be useful for partial exploratory purposes. |
| 8 | Abdih and Joutz (2006) suggest making TFP dependent on knowledge stocks in the form of research outputs like patents and having a patent production function depending on R&D stocks. However, the innovation studies community emphasizes that (i) many research results are not patented, (ii) patents are a juridical step that keeps competitors at a distance, and (iii) patents describe the knowledge but are not the knowledge. We follow this latter idea, also in the interest of keeping the number of variables low. In future work with larger models, both approaches can perhaps be combined. |
| 9 | Other reasons given in the literature for having no effect from public R&D are (i) it being a substitute for private R&D (see David et al. 2000), (ii) strengthening public consumption rather than investment, (iii) a need for longer lags than usually used in growth regressions (Bassanini et al. 2001), (iv) the possibility of full employment for top researchers, resulting in mere wage effects (David and Hall 2000 for the theory and Goolsbee (1998) and Wolff and Reinthaler (2008) for some evidence), (v) the disaggregation of publicly funded R&D, which may reveal that some parts are less effective (Elnasri and Fox 2017) and (vi) the possibility that public R&D may have inverted u-shaped effects in theory (Huang et al. (2023) and the corresponding evidence in Ziesemer (2024b)). There are different studies for these aspects. Lags are well considered in the VECMs of Soete et al. (2022), which include the direct and indirect effects of public R&D and give less pessimistic results. |
| 10 | We do not go into details of the literature regarding the correct econometric handling of deterministic time trends (detrending), endogeneity, nonstationarity and perhaps other aspects. |
| 11 | The statistical significance of both foreign R&D variables in the single-country papers by Soete et al. (2020, 2022), Ziesemer (2020, 2021b, 2021c, 2022, 2024a) and this paper for the panel VECM-FM/D-OLS approach re-establishes the result of Coe and Helpman (1995) and rejects the insignificance criticism of Kao et al. (1999). Also, van Pottelsberghe de la Potterie and Lichtenberg (2001) and Erken et al. (2008, 2018) do so for the single-equation approach, and Luintel and Khan (2004) do this for the VECM approach for aggregated (private plus public) foreign R&D. The method of this paper is closer to that of Kao et al. (1999) than these other papers. |
| 12 | SMAC abbreviates the names of Solow, Minhas, Arrow and Chenery and their paper Arrow et al. (1961), dealing empirically with the CES function. |
| 13 | If first-order conditions are pairwise relations and cointegration requires having triples of variables, the two pairwise relations can be added up to form a triple. |
| 14 | This is carried out in addition to assuming the effects of a hypothetically increased regressor in the interpretation of the long-term relations of the PMG (pooled mean group) or VECM estimation. The use of VAR methods with shocks alone is not a guarantee that all results will be plausible and homogenous. Estrada and Montero (2009) find effects of public R&D from a SVAR (structural vector autoregression) model that differ from country to country. |
| 15 | Khan and Luintel (2006), Luintel et al. (2014) and van Elk et al. (2015, 2019) mitigate the problem of slope homogeneity through the use of interacting variables. |
| 16 | Austria, Belgium, Germany, Denmark, Spain, Finland, Great Britain, Italy, Japan, the Netherlands, Norway, Portugal, Sweden and the USA. |
| 17 | It is not true that this value is chosen ad hoc. Several papers indicate that their authors have experimented with other rates. The volatility of R&D capital stocks is a bit lower if depreciation rates are lower (see Figure 5.1 in Shanks and Zheng (2006)). The reason is that a higher rate of depreciation brings us closer to using flow data, which are more volatile than stock data with lower rates of depreciation. |
| 18 | I am grateful to ‘anonymous’ for providing the R&D data. |
| 19 | |
| 20 | Johansen test consisting of the trace test and the maximum eigenvalue test for a single country. |
| 21 | Three dots indicate text omitted in this citation. |
| 22 | |
| 23 | The GMM approach emphasized in the textbooks is for short panels. |
| 24 | |
| 25 | van Elk et al. (2015, 2019) see the relation as part of a production function; Huang et al. (2023) define it as a Cobb–Douglas production function; Ziesemer (2021a) models it as a combination of first-order conditions of a VES production function. |
| 26 | Their result is that a 10% increase in publicly financed R&D increases privately financed R&D, both performed by private firms, by 5 to 6% from IV (instrumental variable) estimation, but only 25% of this is under OLS; however, our result is for publicly and privately performed R&D. From a policy perspective, it is not only important to know how much funding for R&D governments want to spend, but also whether they should give it to private businesses or to public institutions performing (executing/conducting) the R&D; in more formal terms, and for the corresponding R&D capital stocks, Moretti et al. define BERD = R + S and investigate the impact of S, the publicly financed part, on R, the privately financed part. We use GERD – BERD = PPR&D (publicly performed R&D flow) and investigate the impact of the stocks of PPR&D (LPUBST) on BERD (LBERDST). The theory of Huang et al. (2023) can be interpreted as seeing a log–log effect of S/BERD on the change or growth rate of BERDST. |
| 27 | Subsidies have an inverted u-shape with a peak at 10% and negative values beyond 20%, and a negative effect for publicly performed R&D (which may have collinearity with publicly funded R&D) and negative effects for defense R&D shares all in terms of growth rate regressions, with one lag using 3SLS (three-stage least squares) for 17 OECD countries for 1984–1996. Fieldhouse and Mertens (2023) also do not find positive effects of defense R&D. In contrast, Deleidi and Mazzucato (2021) find positive growth effects of defense R&D. Studies with data ending in 1995 and earlier are surveyed by the OECD (2017), and we do not repeat them here for reasons of space. |
| 28 | |
| 29 | The rejection of cross-section independence may be an over-reaction (Pesaran and Xie 2023). If not, to remove cross-sectional dependence, we could use principal component scores (if not correlated with the regressors) as Coakley et al. (2002) do or period-specific cross-section average values of the variables in a regression as in the study of Pesaran (2007), assuming one common factor, or cross-section averages, as in Banerjee and Carrion-i-Silvestre (2017). However, then, these new variables have to be integrated into the VECM. This would be possible in the form of a weakly exogenous VAR in these factors. However, they may depend on the 84 variables of the model, and it is hard to explore how. Therefore, we do not pursue this route. |
| 30 | |
| 31 | Pegkas et al. (2020) emphasize that the effect of foreign R&D on productivity is stronger than that of domestic R&D. They disaggregate domestic R&D but not foreign R&D. |
References
- Abdih, Yasser, and Frederick Joutz. 2006. Relating the knowledge production function to total factor productivity: An endogenous growth puzzle. IMF Staff Papers 53: 242–71. [Google Scholar]
- Adema, Yvonne, Paul Verstraten, and Bastiaan Overvest. 2023. Kwantificeren Economische Baten van R&D-Beleid. Den Haag: CPB Publication. [Google Scholar]
- Ahn, Seung C., and Alex R. Horenstein. 2013. Eigenvalue ratio test for the number of factors. Econometrica 81: 1203–27. [Google Scholar]
- Antolin-Diaz, Juan, and Paolo Surico. 2022. The long-run effects of government spending. In Discussion Paper DP17433. London: Centre for Economic Policy Research. [Google Scholar]
- Arrow, Kenneth. J., Hollis. B. Chenery, Bagicha S. Minhas, and Robert M. Solow. 1961. Capital-labor substitution and economic efficiency. The Review of Economics and Statistics 43: 225–50. [Google Scholar]
- Bai, Jushan, and Serena Ng. 2004. A PANIC attack on unit roots and cointegration. Econometrica 72: 1127–78. [Google Scholar]
- Baltagi, Badi H. 2021. Econometric Analysis of Panel Data, 6th ed. Berlin: Springer. [Google Scholar]
- Banerjee, Anindya, and Josep Lluís Carrion-i-Silvestre. 2017. Testing for panel cointegration using common correlated effects estimators. Journal of Time Series Analysis 38: 610–36. [Google Scholar]
- Bassanini, Andrea, Philip Hemmings, and Stefano Scarpetta. 2001. Economic Growth: The Role of Policies and Institutions: Panel Data. Evidence from OECD Countries OECD Economics Department Working Papers No. 283. Available online: https://www.oecd-ilibrary.org/docserver/722675213381.pdf?expires=1724238970&id=id&accname=guest&checksum=D1BF24F31369E9325236A5DCBC7B77AF (accessed on 13 August 2024).
- Bengoa, Marta, Valeriano Martínez-San Román, and Patrició Pérez. 2017. Do R&D activities matter for productivity? A regional spatial approach assessing the role of human and social capital. Economic Modelling 60: 448–61. [Google Scholar]
- Branson, William H., and James M. Litvack. 1981. Macroeconomics, 2nd ed. New York: Harper&Row. [Google Scholar]
- Breitung, Jörg. 2005. A Parametric Approach to the Estimation of Cointegration Vectors in Panel Data. Econometric Reviews 24: 151–73. [Google Scholar] [CrossRef]
- Cabon-Dhersin, Marie-Laure, and Romain Gibert. 2020. R&D Cooperation, Proximity and Distribution of Public Funding Between Public and Private Research Sectors. The Manchester School 88: 773–800. [Google Scholar] [CrossRef]
- Cai, Zongwu, Jianqing Fan, and Qiwei Yao. 2000. Functional-Coefficient Regression Models for Nonlinear Time Series. Journal of the American Statistical Association 95: 941–56. [Google Scholar]
- Chen, Rong, and Ruey S. Tsay. 1993. Functional-Coefficient Autoregressive Models. Journal of the American Statistical Association 88: 298–308. [Google Scholar]
- Chudik, Alexander, M. Hashem Pesaran, and Ron P. Smith. 2023. Revisiting the Great Ratios Hypothesis. Oxford Bulletin of Economics and Statistics 85: 1023–47. [Google Scholar] [CrossRef]
- Ciaffi, Giovanna, Matteo Deleidi, and Enrico Sergio Levrero. 2023. The macroeconomic effects of public expenditure in research and development. In CIMR Research Working Paper No. 64. London: Birkbeck. [Google Scholar]
- Coakley, Jerry, Ana-Maria Fuertes, and Ron Smith. 2002. A principal components approach to cross-section dependence in panels. Paper No. B5-3. Paper presented at the 10th International Conference on Panel Data, Berlin, Germany, July 5–6. [Google Scholar]
- Coe, David T., and Elhanan Helpman. 1995. International R&D spillovers. European Economic Review 39: 859–87. [Google Scholar]
- David, Paul A., and Brownwyn H. Hall. 2000. Heart of Darkness: Modeling Public–private Funding Interactions Inside the R&D Black Box. Research Policy 29: 1165–83. [Google Scholar]
- David, Paul A., Bronwyn H. Hall, and Andrew A. Toole. 2000. Is public R&D a complement or substitute for private R&D? A review of the econometric evidence. Research Policy 29: 497–529. [Google Scholar]
- De Lipsis, Vincenzo, Matteo Deleidi, Mariana Mazzucato, and Paolo Agnolucci. 2022. Macroeconomic Effects of Public R&D. Available online: https://ssrn.com/abstract=4301178 (accessed on 13 August 2024).
- Deleidi, Matteo, and Mariana Mazzucato. 2021. Directed innovation policies and the supermultiplier: An empirical assessment of mission-oriented policies in the US economy. Research Policy 50: 104151. [Google Scholar]
- Donselaar, Piet, and Carl Koopmans. 2016. The Fruits of R&D: Meta-Analyses of the Effects of Research and Development on Productivity. VU Amsterdam Research Memorandum 2016-1. Amsterdam: Faculty of Economics and Business Administration. [Google Scholar]
- Elnasri, Amani, and Kevin J. Fox. 2017. The contribution of research and innovation to productivity. Journal of Productivity Analysis 47: 291–308. [Google Scholar]
- Enders, Walter. 2015. Applied Econometric Time Series, 4th ed. New York: Wiley. [Google Scholar]
- Erken, Hugo, Piet Donselaar, and Roy Thurik. 2008. Total factor productivity and the role of entrepreneurship. In Jena Economic Research Papers No. 2008,019. Jena: Friedrich Schiller University Jena, Max Planck Institute of Economics. [Google Scholar]
- Erken, Hugo, Piet Donselaar, and Roy Thurik. 2018. Total factor productivity and the role of entrepreneurship. Journal of Technology Transfer 43: 1493–521. [Google Scholar] [CrossRef]
- Estrada, Ángel, and José Manuel Montero. 2009. R&D Investment and Endogenous Growth: A SVAR Approach. Documentos de Trabajo N.° 0925. Madrid: BANCO DE ESPAÑA. [Google Scholar]
- Falk, Martin. 2006. What drives business Research and Development (R&D) intensity across Organisation for Economic Co-operation and Development (OECD) countries? Applied Economics 38: 533–47. [Google Scholar]
- Feenstra, Robert C., Robert Inklaar, and Marcel P. Timmer. 2015. The Next Generation of the Penn World Table. American Economic Review 105: 3150–82. [Google Scholar]
- Fieldhouse, Andrew J., and Karel Mertens. 2023. The Returns to Government R&D: Evidence from U.S. Appropriations Shocks. Dallas: Federal Reserve Bank of Dallas. [Google Scholar]
- Galor, Oded, and David N. Weil. 1999. From Malthusian Stagnation to Modern Growth. American Economic Review 89: 150–54. [Google Scholar]
- Gandolfo, Giancarlo. 1971. Economic Dynamics: Methods and Models. Amsterdan: Elsevier, vol. 16. [Google Scholar]
- Goolsbee, Austan. 1998. Does Government R&D Policy Mainly Benefit Scientists and Engineers? Working Paper No. 6532. Available online: https://www.nber.org/system/files/working_papers/w6532/w6532.pdf (accessed on 13 August 2024).
- Groen, Jan J. J., and Frank Kleibergen. 2003. Likelihood-Based Cointegration. Analysis in Panels of Vector Error-Correction Models. Journal of Business & Economic Statistics 21: 295–318. [Google Scholar]
- Guellec, Dominique, and Bruno Van Pottelsberghe de la Potterie. 2003a. R&D and Productivity Growth: Panel Data Analysis of 16 OECD Countries. OECD Economic Studies 2001/2: 103–26. [Google Scholar]
- Guellec, Dominique, and Bruno Van Pottelsberghe de la Potterie. 2003b. The impact of public R&D expenditure on business R&D. Economics of Innovation and New Technology 12: 225–43. [Google Scholar]
- Guellec, Dominique, and Bruno Van Pottelsberghe de la Potterie. 2004. From R&D to Productivity Growth: Do the Institutional Settings and the Source of Funds of R&D Matter? Oxford Bulletin of Economics and Statistics 66: 353–78. [Google Scholar]
- Hall, Brownwyn H., Jacques Mairesse, and Pierre Mohnen. 2010. Measuring the Returns to R&D. In Handbook of the Economics of Innovation 2. Edited by Bronwyn H. Hall and Nathan Rosenberg. Amsterdam: Elsevier, pp. 1033–82. [Google Scholar]
- Haskel, Jonathan, and Gavin Wallis. 2013. Public support for innovation, intangible investment and productivity growth in the UK market sector. Economics Letters 119: 195–98. [Google Scholar]
- Helpman, Elhanan. 1992. Endogenous macroeconomic growth theory. European Economic Review 36: 237–67. [Google Scholar]
- Herzer, Dierk. 2022. An empirical note on the long-run effects of public and private R&D on TFP. Journal of the Knowledge Economy 13: 1–17. [Google Scholar]
- Hsiao, Cheng. 2022. Analysis of Panel Data, 4th ed. Cambridge: Cambridge University Press. [Google Scholar]
- Huang, Chien Y., Ching Chong Lai, and Pietro F. Peretto. 2023. Public R&D, Private R&D and Growth: A Schumpeterian Approach. Available online: https://public.econ.duke.edu/~peretto/Public%20R&D%20and%20Growrh.pdf (accessed on 13 August 2024).
- Inklaar, Robert, Pieter Woltjer, and Daniel Gallardo Albarrán. 2019. The Composition of Capital and Cross-country Productivity Comparisons. International Productivity Monitor 36: 34–52. [Google Scholar]
- Jaumotte, Florence, and Nigel Pain. 2005a. From ideas to development: The determinants of R&D and patenting. In OECD Economics Department Working Paper No. 457. Paris: OECD. [Google Scholar]
- Jaumotte, Florence, and Nigel Pain. 2005b. Innovation in the business sector. In OECD Economics Department Working Paper No. 459. Paris: OECD. [Google Scholar]
- Jusélius, Katarina. 2006. The Cointegrated VAR Model: Methodology and Applications. Oxford: Oxford University Press. [Google Scholar]
- Kao, Chihwa. 1999. Spurious Regression and Residual-Based Tests for Cointegration in Panel Data. Journal of Econometrics 90: 1–44. [Google Scholar]
- Kao, Chihwa, and Min-Hsien Chiang. 2000. On the Estimation and Inference of a Cointegrated Regression in Panel Data. In Advances in Econometrics. Edited by B. Baltagi. Leeds: Emerald, vol. 15, pp. 161–78. [Google Scholar]
- Kao, Chihwa, Min-Hsien Chiang, and Bangtian Chen. 1999. International R&D spillovers: An application of estimation and inference in panel cointegration. Oxford Bulletin of Economics and Statistics 61: 691–709. [Google Scholar]
- Khan, Mosahid, and Kul B. Luintel. 2006. Sources of Knowledge and Productivity: How Robust Is the Relationship? Sti/Working Paper 2006/6. Paris: OECD. [Google Scholar]
- Kilian, Lutz, and Helmut Lütkepohl. 2017. Structural Vector Autoregressive Analysis. Cambridge: Cambridge University Press. [Google Scholar]
- Larsson, Rolf, and Johan Lyhagen. 2007. Inference in Panel Cointegration Models with Long Panels. Journal of Business & Economic Statistics 25: 473–83. [Google Scholar]
- Lau, Sau-Him P. 1997. Using Stochastic Growth Models Unit Roots and Breaking Trends. Journal of Economic Dynamics and Control 21: 1645–67. [Google Scholar]
- Loertscher, Oliver, and Pau S. Pujolas. 2024. Canadian Productivity Growth: Stuck in the Oil Sands. Canadian Journal of Economics 57: 478–501. [Google Scholar]
- Lucas, Robert E., Jr. 2015. Human capital and growth. American Economic Review 105: 85–88. [Google Scholar]
- Luintel, Kul B., and Mosahid Khan. 2004. Are international R&D spillovers costly for the United States? The Review of Economics and Statistics 86: 896–910. [Google Scholar]
- Luintel, Kul B., Mosahid Khan, and Konstantinos Theodoridis. 2014. On the robustness of R&D. Journal of Productivity Analysis 42: 137–55. [Google Scholar]
- Lütkepohl, Helmut. 2005. New Introduction to Multiple Time Series Analysis. Berlin: Springer Science & Business Media. [Google Scholar]
- Maddala, Gangadharrao S., and Shaowen Wu. 1999. A Comparative Study of Unit Root Tests with Panel Data and A New Simple Test. Oxford Bulletin of Economics and Statistics 61: 631–52. [Google Scholar]
- Moretti, Enrico, Claudia Steinwender, and John Van Reenen. 2023. The Intellectual Spoils of War? Defense R&D, Productivity, and International Spillovers. The Review of Economics and Statistics, 1–46. [Google Scholar]
- Mukerji, Vatsala. 1963. A Generalized S.M.A.C. Function with Constant Ratios of Elasticity of Substitution. The Review of Economic Studies 30: 233–36. [Google Scholar]
- OECD. 2017. The Impact of R&D Investment on Economic Performance: A Review of the econometric evidence. DSTI/STP/NESTI 2017 12. In Working Party of National Experts on Science and Technology Indicators. Paris: OECD Publishing. [Google Scholar]
- Park, Walter G. 1995. International Spillovers of R&D Investment and OECD Economic Growth. Economic Inquiry 33: 571–91. [Google Scholar]
- Park, Walter G. 1998. A theoretical model of government research and growth. Journal of Economic Behavior & Organization 34: 69–85. [Google Scholar]
- Pedroni, Peter. 1999. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxford Bulletin of Economics and Statistics 61: 653–70. [Google Scholar]
- Pedroni, Peter. 2001a. Purchasing power parity tests in cointegrated panels. Review of Economics and Statistics 83: 727–31. [Google Scholar]
- Pedroni, Peter. 2001b. Fully modified OLS for heterogeneous cointegrated panels. In Nonstationary Panels, Panel Cointegration, and Dynamic Panels. Leeds: Emerald Group Publishing Limited, vol. 15, pp. 93–130. [Google Scholar]
- Pedroni, Peter. 2019. Panel cointegration techniques and open challenges. In Panel Data Econometrics. Cambridge: Academic Press, pp. 251–87. [Google Scholar]
- Pegkas, Panagiotis, Christos Staikouras, and Constantinos Tsamadias. 2020. Does domestic and foreign R&D capital affect total factor productivity? Evidence from Eurozone countries. International Economic Journal 34: 258–78. [Google Scholar]
- Perkins, Dwight. H., Steven Radelet, David L. Lindauer, and Steven A. Block. 2013. Economics of Development, 7th ed. New York: Norton. [Google Scholar]
- Pesaran, M. Hashem. 2015. Time Series and Panel Data Econometrics. Oxford: Oxford University Press. [Google Scholar]
- Pesaran, M. Hashem, Y. Shin, and Ron P. Smith. 1999. Pooled mean group estimation of dynamic heterogeneous panels. Journal of the American statistical Association 94: 621–34. [Google Scholar]
- Pesaran, M. Hashem, and Yimeng Xie. 2023. A Bias-Corrected CD Test for Error Cross-Sectional Dependence in Panel Data Models with Latent Factors. arXiv arXiv:2109.00408. [Google Scholar]
- Pesaran, M. Hashem. 2006. Estimation and Inference in Large Heterogeneous Panels with a Multifactor Error Structure. Econometrica 74: 967–1012. [Google Scholar]
- Pesaran, M. Hashem. 2007. A Simple Panel Unit Root Test in the Presence of Cross-Section Dependence. Journal of Applied Econometrics 22: 265–312. [Google Scholar]
- Ramanathan, Ramu. 2012. Introduction to the Theory of Economic Growth. Berlin: Springer Science & Business Media, vol. 205. [Google Scholar]
- Rebucci, Alessandro. 2010. Estimating VARs with long stationary heterogeneous panels: A comparison of the fixed effect and the mean group estimators. Economic Modelling 27: 1183–98. [Google Scholar]
- Rehman, Naqeeb Ur, Eglantina Hysa, and Xuxin Mao. 2020. Does public R&D complement or crowd-out private R&D in pre and post economic crisis of 2008? Journal of Applied Economics 23: 349–71. [Google Scholar]
- Sato, Ryuzo. 1963. Fiscal Policy in a Neo-Classical Growth Model: An Analysis of Time Required for Equilibrating Adjustment. The Review of Economic Studies 30: 16–23. [Google Scholar]
- Schwert, G. William. 1989. Stock Volatility and Crash of 87. Review of Financial Studies 3: 77–102. [Google Scholar]
- Shanks, Sid, and Simon Zheng. 2006. Econometric Modelling of R&D and Australia’s Productivity. Staff Working Paper. Canberra: Productivity Commission. [Google Scholar]
- Smith, Ron P., and Ana-Maria Fuertes. 2016. Panel Time-Series. London: V cemmap. [Google Scholar]
- Soete, Luc, Bart Verspagen, and Thomas H. W. Ziesemer. 2020. The productivity effect of public R&D in the Netherlands. Economics of Innovation and New Technology 29: 31–47. [Google Scholar] [CrossRef]
- Soete, Luc, Bart Verspagen, and Thomas H. W. Ziesemer. 2022. The economic impact of public R&D: An international perspective. Industrial and Corporate Change 31: 1–18. [Google Scholar] [CrossRef]
- Solow, Robert M. 1956. A contribution to the theory of economic growth. The Quarterly Journal of Economics 70: 65–94. [Google Scholar]
- Sveikauskas, Leo. 2007. R&D and Productivity Growth: A Review of the Literature; Working Paper 408. Washington, DC: U.S. Bureau of Labor Statistics.
- Szirmai, Adam. 2011. Angus Maddison and development economics. In UNU-MERIT Working Papers No. 035. Maastricht: UNU-MERIT, Maastricht Economic and Social Research and Training Centre on Innovation and Technology. [Google Scholar]
- van Ark, Bart, Klaas de Vries, and Dirk Pilat. 2024. Are pro-productivity policies fit for purpose? The Manchester School 92: 191–208. [Google Scholar]
- van Elk, Roel, Bas ter Weel, Bart Verspagen, Karen van der Wiel, and Bram Wouterse. 2015. A Macroeconomic Analysis of the Returns to Public R&D Investments. CPB Discussion Paper 313. Maastricht: United Nations University—Maastricht Economic and Social Research Institute on Innovation and Technology (MERIT). [Google Scholar]
- van Elk, Roel, Bas ter Weel, Karen van der Wiel, and Bram Wouterse. 2019. Estimating the returns to public R&D investments: Evidence from production function models. De Economist 167: 45–87. [Google Scholar]
- van Pottelsberghe de la Potterie, Bruno, and Frank Lichtenberg. 2001. Does foreign direct investment transfer technology across borders? Review of Economics and Statistics 83: 490–97. [Google Scholar]
- Voutsinas, Ioannis, and Constantinos Tsamadias. 2014. Does research and development capital affect total factor productivity? Evidence from Greece. Economics of Innovation and New Technology 23: 631–51. [Google Scholar]
- Wagner, Martin, and Jaroslava Hlouskova. 2009. The performance of panel cointegration methods: Results from a large scale simulation study. Econometric Reviews 29: 182–223. [Google Scholar]
- Wolff, Guntram B., and Volker Reinthaler. 2008. The Effectiveness of Subsidies Revisited: Accounting for Wage and Employment Effects in Business R&D. Research Policy 37: 1403–12. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey M. 2013. Introductory Econometrics: A Modern Approach, 5th ed. Mason: Cencage Learning South Western. [Google Scholar]
- Ziesemer, Thomas H. W. 2020. Japan’s productivity and GDP growth: The Role of private, public, and foreign R&D 1967–2017. Economies 8: 77. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2021a. Semi-endogenous growth models with domestic and foreign private and public R&D linked to VECMs. Economics of Innovation and New Technology 30: 621–42. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2021b. Mission-oriented R&D and growth. Journal of Applied Economics 24: 460–77. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2021c. The effects of R&D subsidies and publicly performed R&D on business R&D: A survey. Hacienda Publica Espanola/Review of Public Economics 236: 171–205. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2022. Foreign R&D spillovers to the USA and strategic reactions. Applied Economics 54: 4274–91. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2023a. Labour-augmenting Technical Change Data for alternative Elasticities of Substitution: Growth, Slowdown, and Distribution Dynamics. Economics of Innovation and New Technology 32: 449–75. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2023b. Internal rates of return for public R&D from VECM estimates for 17 OECD countries. In UNU-MERIT Working Paper 2023-026. Maastricht: UNU-MERIT. Available online: https://econpapers.repec.org/paper/unmunumer/2023026.htm (accessed on 12 August 2024).
- Ziesemer, Thomas H. W. 2024a. Mission-oriented R&D and growth of Japan 1988–2016: A comparison with private and public R&D. Economics of Innovation and New Technology 33: 218–47. [Google Scholar] [CrossRef]
- Ziesemer, Thomas H. W. 2024b. Evidence on an endogenous growth model with public R&D. Economics of Innovation and New Technology, 1–37. [Google Scholar] [CrossRef]

| Variable | Mean | Median | Stdev | Min | Max | Growth Rate (a) | P (No csd) (b) | Data Points, obs (c) |
|---|---|---|---|---|---|---|---|---|
| LGDP | 13.12 | 12.71 | 1.137 | 10.7 | 16.6 | 0.0166 + 0.35g(−1) | 0.0000 | 770; 742 |
| LTH07 | 1.888 | 1.906 | 0.336 | 0.66 | 2.80 | 0.0124 + 0.144g(−1) | 0.0000 | 770; 742 |
| LBERDST | 10.1 | 10.0 | 1.86 | 5.76 | 14.4 | 0.0055 + 0.8g(−1) | 0.0000 | 749; 721 |
| LPUBST | 9.780 | 9.469 | 1.526 | 6.62 | 13.5 | 0.0042 + 0.872g(−1) | 0.0000 | 744; 716 |
| LFPUBST | 12.7 | 12.79 | 0.702 | 10.2 | 13.7 | 0.0039 + 0.849g(−1) | 0.0000 | 770; 742 |
| LFBERDST | 13.28 | 13.38 | 0.785 | 10.7 | 14.4 | 0.00315 + 0.898g(−1) | 0.0000 | 770; 742 |
| Variable | t-Value | p-Value | Balanced Observations | Total Observations | Number of Countries with p (Unit Root) < 0.1 |
|---|---|---|---|---|---|
| LGDP | −1.97 | ≥0.10 | 54 | 756 | 1 |
| LTH07 | −2.056 | ≥0.10 | 54 | 756 | 1 |
| LBERDST | −2.268 | ≥0.10 | 51 | 714 | 4 |
| LPUBST | −2.77 | <0.10 | 48 | 672 | 5 |
| LFPUBST | −1.4 | ≥0.10 | 54 | 756 | 0 |
| LFBERDST | −2.073 | ≥0.10 | 54 | 756 | 2 |
| dLGDP | −2.81 | <0.01 | 53 | 742 | 6 |
| dLTH07 | −3.47 | <0.01 | 53 | 742 | 9 |
| dLBERDST | −2.489 | <0.01 | 50 | 700 | 6 |
| dLPUBST | −2.85 | <0.01 | 47 | 658 | 6 |
| dLFPUBST | −2.627 | <0.01 | 53 | 742 | 5 |
| dLFBERDST | −2.39 | <0.05 | 53 | 742 | 6 |
| Fisher–Johansen Test. No. of CEs | LGDP-LTH07 | LTH07-LBERD | LBERD-LPUB | LPUB-LFPUB | LFPUB-LFBERD |
|---|---|---|---|---|---|
| No ce (b) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0651 |
| At most 1 (b) | 0.279 | 0.293 | 0.460 | 0.323 | 1 |
| Residual-based tests | |||||
| Kao test (c) | 0.0016 | 0.0710 | 0.0012 | 0.0387 | 0.0000 |
| Pedroni Group ADF (c) | 0.0815 | 0.006 | 0.004 | 0.0094 | 0.494 |
| Bai and Ng PANIC) (d) | 0.389 | 0.182 | 0.202 | 0.00015 | 0.00184 |
| Dependent Variable | LGDP | LTH07 | LBERDST | LPUBST |
|---|---|---|---|---|
| Regressors | LTH07, LBERDST | LBERDST, LPUBST | LPUBST, LFBERDST | LFPUBST, LFBERDST |
| None (b) | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| At most 1 (b) | 0.0001 | 0.0000 | 0.0000 | 0.0359 |
| At most 2 (b) | 0.7230 | 0.5337 | 0.0067 | 0.9980 |
| Kao test (c) | 0.0018 | 0.1160 | 0.0012 | 0.0389 |
| Pedroni Group ADF test (c) | 0.0110 | 0.4236 | 0.0000 | 0.0000 |
| s.e. of regress. | 0.95 | 4.938 | 6.48 | 7.67 |
| Bai and Ng PANIC (d) | 0.00002 | 0.00000 | 0.00000 | 0.0123 |
| Dependent Variable | LGDP | LTH07 | LBERDST | LPUBST |
|---|---|---|---|---|
| Regressors | LTH07, LBERDST | LBERDST, LPUBST | LPUBST, LFBERDST | LFBERDST, LFPUBST |
| Model 1 | Fully modified OLS (FMOLS) (b) | |||
| Slope (a) | 0.895 | 0.2914 | 0.4036 | −0.109 |
| Slope (a) | - | 0.2912 | 0.401214 | 3.528 |
| Trend (e) | 0.0127 | −0.013 | 0.017849 | −0.06 |
| Constant (e) | 11.0745 | −3.529 | 0.334 | −31.97 |
| Adj. R-squared | 0.997 | 0.899 | 0.986 | 0.99 |
| Observations (g) | 770 | 744 | 744 | 744 |
| No csd p-val. (f) | 0.0390 | 0.0608 | 0.1380 | 0.9504 |
| Model 2 | Dynamic OLS (DOLS) (c) | |||
| Slope (a) | 0.783 | 0.31 | 0.546 | 0.737 |
| Slope (a) | - | 0.174 (0.0014) | 0.73 | 1.475 |
| Trend (d) | 0.014 | −0.009 | - | −0.029 |
| Constant (e) | 11.245 | −2.67 | −4.93 | −17.985 |
| Adj. R-squared | 0.997 | 0.928 | 0.99 | 0.989 |
| Observations (g) | 770 | 744 | 744 | 744 |
| No csd p-val. (f) | 0.3416 | 0.3367 | 0.0004 | 0.0008 |
| Model 3 | DOLS | FMOLS | ||
| Slope (a) | 0.783 | 0.31 | 0.4036 | −0.109 |
| Slope (a) | - | 0.174 (0.0014) | 0.401214 | 3.528 |
| Trend (d) | 0.014 | −0.009 | 0.017849 | −0.06 |
| Constant (e) | 11.245 | −2.67 | 0.334 | −31.97 |
| Adj. R-squared | 0.997 | 0.928 | 0.986 | 0.99 |
| Observations (g) | 770 | 744 | 744 | 744 |
| No csd p-val. (f) | 0.3416 | 0.3367 | 0.1380 | 0.9504 |
| Cointegrating Equation → Dependent Variable ↓ | GDP, LTH07 | LTH07, LBERDST, LPUBST | LBERDST, LPUBST, LFBERDST | LPUBST, LFPUBST, LFBERDST |
|---|---|---|---|---|
| D(LOG(GDP)) | −0.079 | −0.049 | −0.0268 | −0.00116 (b) |
| D(LOG(TH07)) | −0.051 | −0.057 | −0.0229 | -0.0099 |
| D(LOG(BERDST)) | −0.0035 | −0.0195 | −0.017 | −0.0018 |
| D(LOG(PUBST)) | 0.0077 | 0.00095 (c) | 0.0017 | −0.009 |
| D(LOG(FBERDST)) | −0.0033 | 0.00039 | −0.001 | 0.002 |
| D(LOG(FPUBST)) | 0.0052 | 0.003 | 0.0011 | 0.00078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziesemer, T.H.W. Public R&D and Growth: A dynamic Panel Vector-Error-Correction Model Analysis for 14 OECD Countries. Economies 2024, 12, 216. https://doi.org/10.3390/economies12080216
Ziesemer THW. Public R&D and Growth: A dynamic Panel Vector-Error-Correction Model Analysis for 14 OECD Countries. Economies. 2024; 12(8):216. https://doi.org/10.3390/economies12080216
Chicago/Turabian StyleZiesemer, Thomas H. W. 2024. "Public R&D and Growth: A dynamic Panel Vector-Error-Correction Model Analysis for 14 OECD Countries" Economies 12, no. 8: 216. https://doi.org/10.3390/economies12080216
APA StyleZiesemer, T. H. W. (2024). Public R&D and Growth: A dynamic Panel Vector-Error-Correction Model Analysis for 14 OECD Countries. Economies, 12(8), 216. https://doi.org/10.3390/economies12080216







