Inequality in the Distribution of Wealth and Income as a Natural Consequence of the Equal Opportunity of All Members in the Economic System Represented by a Scale-Free Network
Abstract
1. Introduction
2. Methodology
2.1. Methodology Process
- (a)
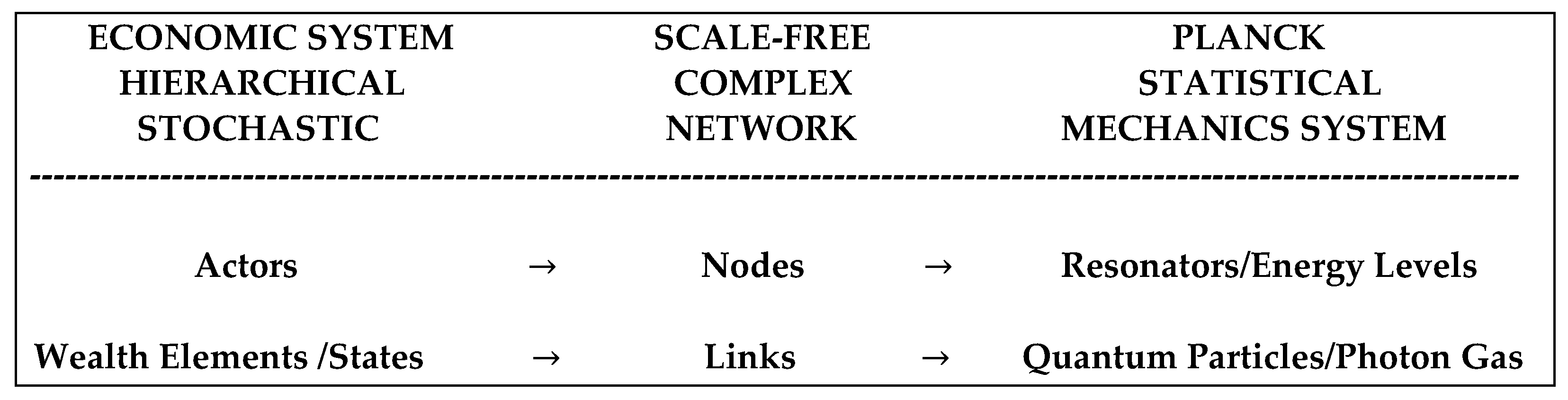
- The economic system under consideration consists of N actors. The number of actors N is assumed to be fixed, although this condition will be relaxed later in the analysis. The N actors are assumed to be independent of one another within the economic system, i.e., each actor has an equal probability as any other to attain any degree of wealth. However, no actor is identical to another from the point of view of accumulating wealth (The MIT Business Review 2018; Barabási 2014). Consequently, we assign to each actor (node) a so-called fitness factor η that describes the ability of that actor to interact (be linked) with other actors in the economic system (Barabási 2014). Moreover, each interaction (link) is identical to any other. That is to say, the number of interactions (links) of an actor to all other actors determines the amount of wealth of that actor. Lastly, each of the N actors in the economic system must have some finite (non-zero) wealth to be able to interact with any other actor in the system and be part of it.
- (b)
- The total wealth of the economic system is U. It is finite and constant over the period of examination of the state of the system. It is comprised of the sum of the wealth (number of links) of each individual actor in the system denoted by Ui with i varying from 1 to N: U = Σ Ni Ui, i = 1, 2, … N. Ui is considered to be a stochastic or random variable in our model.
- (c)
- The state of the system is in a dynamic equilibrium. Equilibrium means that the economic system has attained the most likely, i.e., the one with the highest probability, configuration in terms of the distribution of wealth levels (number of links) among its N actors (nodes) under the prevailing constraints of a fixed number of actors and fixed amount of total wealth. Dynamic implies that the economic system is free to attain a different equilibrium as the total wealth and/or the number of actors change over time.
- (d)
- The wealth is considered to have a minimum value of “h” which can be the unit or “quantum” of currency, say, a dollar in the case of the United States, such that the wealth of each actor is expressed as follows: Ui = ui·h, where ui will be an integer number varying from 1 to a very large number. Wealth is thus not infinitely divisible, but it has a minimum value of h. Consequently, the minimum amount of wealth of any actor in the economic system is at least h1. Moreover, this value h represents the minimum possible amount of wealth exchange (existence of one link) between any of the actors2.
- (e)
- Each of the N actors (nodes) can be in (connected to) any of several possible wealth elements (number of links) G, under the constraint of fixed total wealth U, whereby G could be as large as the ratio of U/h since h is the minimum wealth amount (link size). In other words, G is the number of wealth elements (links), which must be divided over the N actors. It is clear then that G can be less than, equal to, or larger than N.
- (f)
- The number of sequences of the N actors (nodes) with a particular number of wealth elements (number of links) G is designated by an index i, whereby the total wealth U is viewed as being divided up in a succession of small ranges Ui + ΔUi with ΔUi equal to or greater than h. We thus describe the range of values of G by stating the number of possible wealth elements (links) Gi for each Ni sequence of actors and a fixed wealth incremental amount (link size h).
- (g)
- Any of the G wealth elements (number of links) for each of the N actors is accessible to all of them, i.e., there are no exclusions of any actors from any wealth elements. Thus, Gi represents the number of possible wealth elements (number of links) out of the total wealth levels G associated with the actor (node) Ni, because the number of available actors N, implies that a value of Gj may be 0, i.e., no one of the N actors is found in that wealth element, while another value of the wealth element Gk may be found in more than one actor. In fact, any one of the N actors may contain all the G wealth elements at the exclusion of all other actors as distinct possibility.
2.2. Methodology Findings
3. Discussion of the Results
4. Theoretical Implications
- (I)
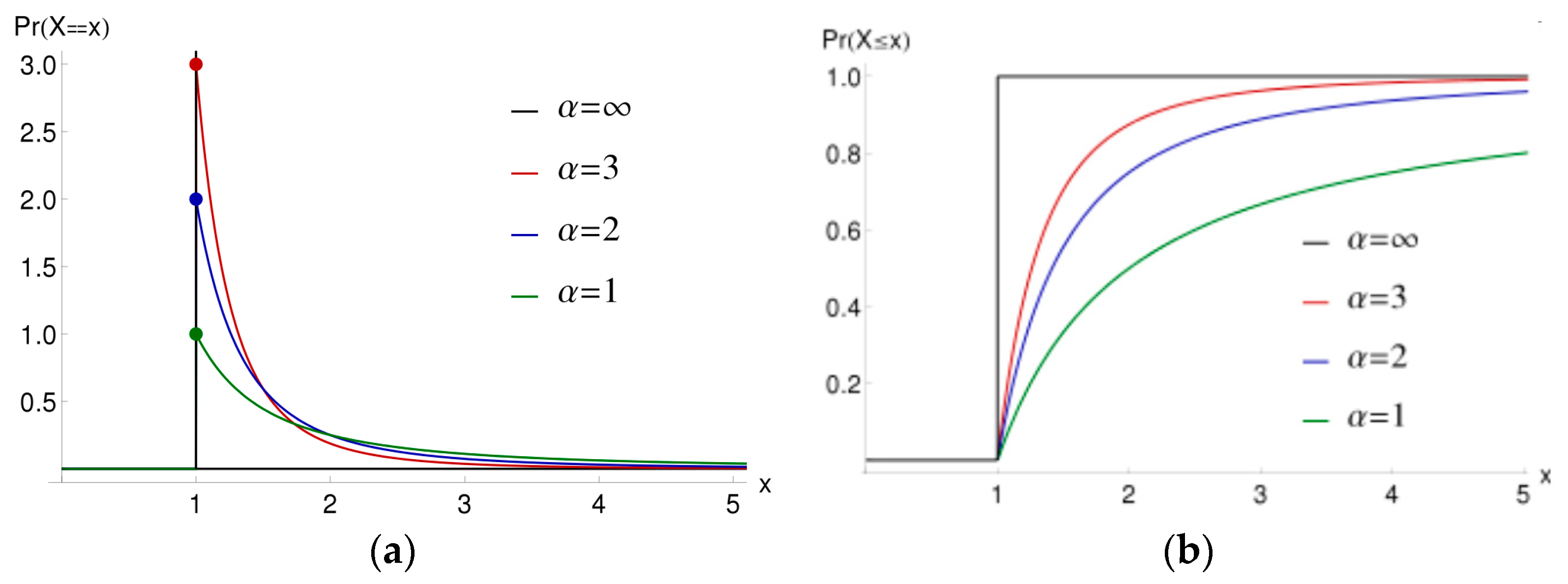
- The minimum value of the calibrated stochastic variable (x/xm) being equal to one (x/xm = 1) is indicative of the fact that in the economic system, no actors can exist with no wealth or income (see Figure 5).
- (II)
- There is a parameter designated by the symbol xm to calibrate the stochastic variable x such that (x/xm) has no physical units. We conclude that xm = h and describes the absolute minimum amount of wealth an actor possesses. Thus, xm = h is identical to the so-called quantum of wealth (income, etc.). In other words, the “quantum” nature of any economic system is an integral feature and represents a finite quantity, i.e., a quantity that is not zero.
- (III)
- The so-called Pareto index α is identified to be identical to the parameter δ in the Planck distribution, the former describing a generic scale-free system and the latter indicating the dimensionality of the economic space, which is essentially a measure of the complexity (number of eigenstates in a quantum system) of the economic system. Since power laws describe self-organizing systems, one concludes that what we call here the dimension of the economic system, in analogy to a physical system, is tantamount to the degree of the self-organization of the economic system and more specifically of the degree of the hierarchical structure of the economic system as a scale-free complex network.
- (IV)
- The power law describes an economic system that has a variable number of actors in it, whereby actors enter and exit the system at will. Moreover, one concludes based on the Planck distribution that a higher average wealth (income, etc.) per actor described by the parameter (βh) is obtained in an economic system with varying number of actors vs. one with a fixed number. In other words, an economic system has by natural design a variable number of actors so that the average wealth per actor is maximized.
- (V)
- While the empirical Pareto law allows for a variable index α > 1 and cannot determine if the index has an optimal or desired value, the derived Planck distribution indicates that for an economic system, the Pareto index has an optimal value which is equal to 2 (α = δ = 2). Optimal here is equated to the value that the parameter δ can attain in the analytical model such that the most efficient distribution of wealth and of income occurs characterized by the maximum entropy, i.e., stability, of the economic system. As already indicated, this realization can guide policymakers to devise policies that approach the optimal distribution of wealth and of income while ensuring equal opportunity to all.
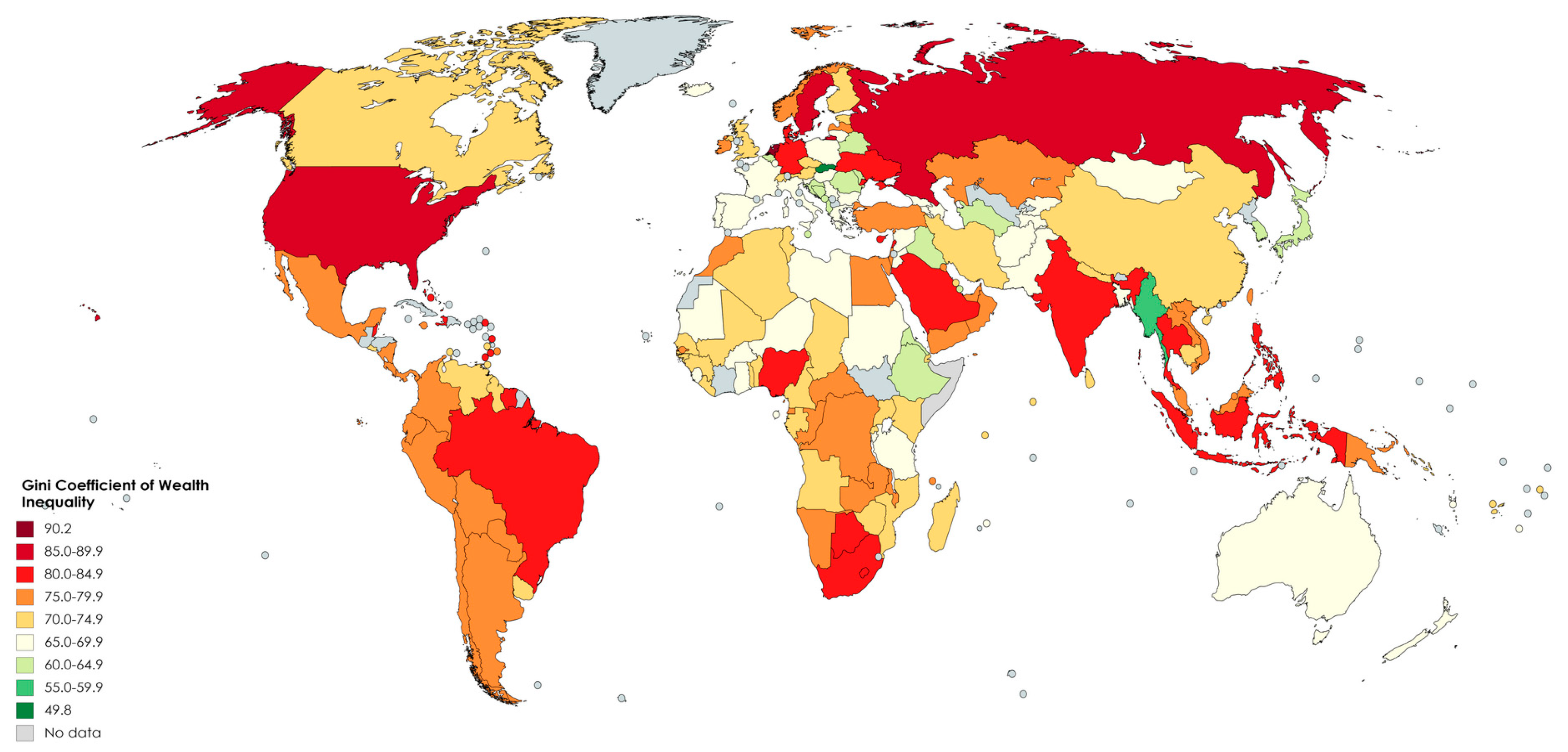
5. Status of Inequality in Wealth and in Income Globally
6. Policy Implications and Future Research Recommendations
7. Concluding Remarks
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 2Term No | γ = 2, (βh) = 0.609 | γ = 0, (βh) = 0.664 | ||
|---|---|---|---|---|
| N | {E1(βh) S1(γ, (nβh)} | {E2(βh) S2 (γ, (nβh)} | {E1(βh) S1 (γ, (nβh)} | {E2(βh) S2 (γ, (nβh)} |
| 1 | 0.02262 | 0.01375 | 0.406573 | 0.251123 |
| 2 | 0.00046 | 0.00032 | 0.163122 | 0.111953 |
| 3 | 0.00001 | 0.00000 | 0.048900 | 0.037750 |
| 4 | 0.00000 | 0.00000 | 0.025239 | 0.023395 |
| 5 | 0.00000 | 0.00000 | 0.009968 | 0.007490 |
| 6 | 0.00000 | 0.00000 | 0.003780 | 0.003200 |
| 7 | 0.00000 | 0.00000 | 0.001366 | 0.001471 |
| 8 | 0.00000 | 0.00000 | 0.000088 | 0.000800 |
| 9 | 0.00000 | 0.00000 | 0.000000 | 0.000000 |
| Sum 1–9 | 0.02309 | 0.01407 | 0.658415 | 0.437182 |
| Ratios | 0.01407/0.2309 = 0.609 | 0.437182/0.658415 = 0.664 | ||
Appendix B

| 1 | Thus, every actor N in the economic system is considered to have a non-zero, i.e., finite amount of wealth, because the state of an actor with “zero” wealth would be tantamount to that actor not participating in the economic system. Likewise, there are no actors with negative wealth because borrowing from physics such actors would be bound, i.e., inaccessible, or unable to participate in the economic system. |
| 2 | Thus, h is equivalent to the existence of one link between any two nodes in the network system. Consequently, if an actor (node) has, say, m links to other actors (nodes), then the wealth of that actor (node) will be described analytically as (m·h). See also (a) above. |
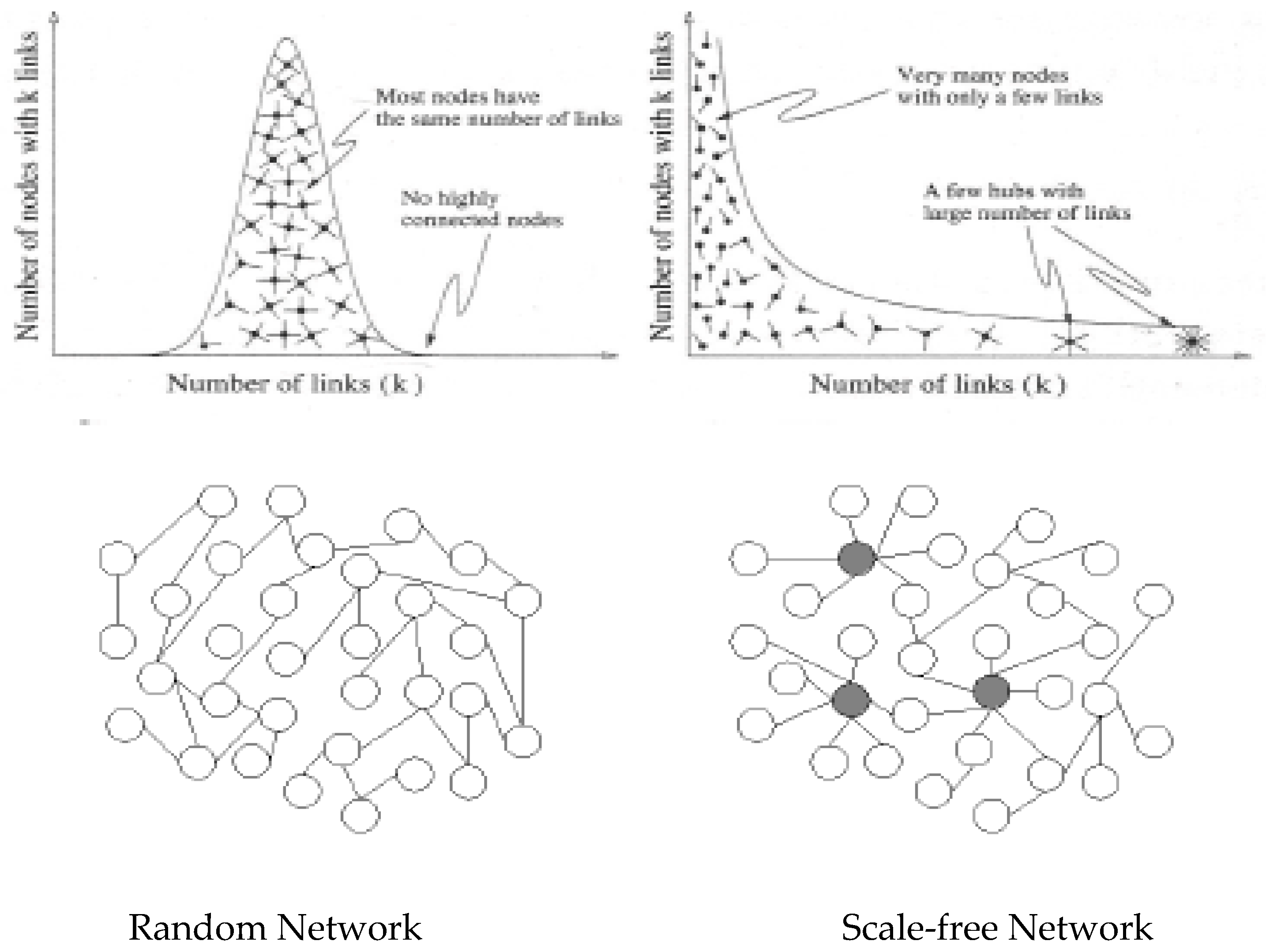
| 3 | Most quantities in nature can be described by random networks that display the familiar bell-curve distribution, which has a peak defining a scale and exponentially decaying tails. A scale-free network is described by a power law distribution, which does not have a peak, and hence it lacks scale, and comprises a continuously decreasing curve, albeit at a much lower rate than an exponential. A distinguishing feature of a power law distribution is that it describes many small events that co-exist with a few large ones. For example, the height of humans is described by a random or Gaussian (bell curve) distribution while the GDP of nations follows a power law distribution. |
| 4 | This would correspond to what is described in Statistical Quantum Thermodynamics as the Bose–Einstein statistics for particles with finite mass and integral spin. The original derivation of the Bose–Einstein statistics for photons (zero mass and integral spin) is known as the Planck statistics or black body radiation law. |
| 5 | The physical system is in a dynamic thermal equilibrium at temperature T, the term dynamic signifying that if and as T changes with time the system attains a new state of equilibrium consistent with the corresponding change in the total energy of the system. The cavity at temperature T is also designated as the thermal bath of the system. |
| 6 | From quantum mechanics, each photon can have an energy En = h (1/2 + n νN), ni = 0, 1, 2… with h being the quantum of action (Planck’s constant) and vN the photon fundamental frequency associated with the radiation modes N. The existence of Planck’s constant h signifies that energy is delivered in discrete packets (quanta). The existence of energy levels or states in a physical system has been established experimentally and the theory attempts to explain these observations. |
| 7 | In the example of Table 1, the actor Ni = 4 has zero wealth elements–links and consequently does not contribute to the economic system in that configuration. However, there will be statistically several other configurations, where this actor will have a non-zero wealth elements or links. |
| 8 | The calculation of the number of permutations is essentially equivalent to the calculation of the possible ways of allocating G identical balls into N urns, where each urn is allowed to contain 0, 1, 2,… and up to G balls. This number is N·(N + 1)·(N + 2)…(N + G − 1)/1·2·3…G = (N + G − 1)!/(N−1)! G! as indicated by Equation (1). |
| 9 | Even if we had selected the exponent in Equation (12) to be a parameter without the negative sign, we would have concluded then that this parameter should be a negative number to be consistent with the observation that the number of actors decreases monotonically as the associated wealth increases. |
| 10 | In a physical system such as, for example, photons in a black body cavity in equilibrium, the parameter β is found to be inversely proportional to the equilibrium temperature T of the system. The equilibrium temperature of the physical system is in turn proportional to the average energy per particle of the physical system. Total wealth in the economic system would be the counterpart of total energy in the physical system. However, we should keep in mind the equivalence between an economic system and a physical system, whereby the actors correspond to occupied energy states and the wealth of any actor is represented by the number of links associated with that actor, whereby links correspond to particles, i.e., photons, in the physical system. |
| 11 | Dimensionality here refers to the multiplicity of the states vs. wealth and has nothing to do with the dimensions of the physical space, although in the physical system of photons and other particles the dimension of the physical space affects the value of the corresponding δ parameter, because a higher space dimension, say three versus two, allows for more possible states. Dimensionality in an economic system is indicative of its hierachical structure and refelcts the free-scal nature of it where a small numnber of noded have a lot of links and most nodes have few links. |
| 12 | The function Eδ(nβh) for δ = 0 is well defined and is equal to a simple exponential function. |
| 13 | The maximum value of the U/N ratio is obtained for δ − 1 = 1 or δ = 2. |
| 14 | These approximations include the closed form upper bound simplification of Φ(x) per Equation (38) vis-à-vis an infinite-term series expression with additional lower (more negative) terms in powers of the variable x and the linearized interpolations in the numerical calculations of the functions E1(nβh) and E2(nβh) or the inclusion of only a small number of terms in the infinite series representing these functions. If we were to include a very large number of terms (theoretically infinite in the sum (nβh)), then its numerical value should increase from the value of 0.43718 of its first nine terms to 0.53048. Obviously, the convergence of this sum is very slow as the data in Table A1 suggest. |
| 15 | The number of states where only one actor has all the wealth and everybody else has no wealth is much higher than one and is equal to the number N of members of the system. That is to say, the likelihood of one actor controlling all the wealth is N times higher than the likelihood of all actors having equal wealth so long as each actor has equal access to the available wealth (income, etc.). And of course, the number of possible states is the highest when all actors have equal probability/oppotunity of having access to the available wealth. This results in the most equitable or optimal distribution of wealth among all the actors. |
| 16 | An economic system where in the limit one actor controls all the wealth, although having N times higher probability to occur that a system where all the actors have equal wealth, is still unstable and can only be static to remain in that state. Unstable means far from equilibrium, i.e., maximum entropy. In physics such a state can occur under certain conditions and is dscribed as a Bose-Einstein condensate. |
| 17 | The total wealth U is known/determined within plus or minus of the finite (non-zero) minimum amount of wealth or quantum of wealth h, i.e., it is not exactly U. The same is true for the income. |
| 18 | Pareto determined empirically, i.e., by examining relevant data from a variety of sources going back to the Middle Ages, that the number of people Nx with wealth higher than x could be modeled as a power law: Nx = A x−a, where A is a proportionality constant. If the total population is No and the minimum wealth is xo, we then have: Nx/No = (x/xo)−a. We can normalize this expression by putting xo = 1 and call the ratio x/xo the relative wealth S. Then the ratio X = Nx/No describes the proportion of the population that has a (relative) wealth greater than x and represents essentially the Pareto distribution survival function. The parameter “α” has a numerical value equal to or greater than one and is called the Pareto index. Since the respective areas under the curve F(x) = (x)−a for x varying (a) from one to infinity and (b) from x to infinity are equal to 1/(α − 1) and to (x)1−a/(1/(α − 1)), the ratio of the latter to the former, designated by S, is equal to (x)1−a. Since x = X−1/α we have S = X1−1/α, which represents the proportion of wealth S for the proportion in the population X. Therefore, we deduce that the value of the Pareto index α is given by the equation: α = ln(X)/(ln (X) − ln(S)). Thus, for the 80-20 rule, i.e., 20% of the population (X) control 80% of the wealth (S), the corresponding value of α is calculated to be 1.16 from the preceding equation. |
| 19 | We use the symbol F(x) for the CDF instead of the symbol Φ(x) in the remainder of this section because of the customary representation of such functional expressions. |
| 20 | The exponential distribution allows for zero wealth (x = 0) and would describe the number of people with wealth higher than x by the equation: Nx/No = exp(−λ x) where No is the total population and “λ“ is the rate of the distribution. It underestimates the wealth of fewer wealthier actors (large x) compared to the Pareto distribution. This can be readily seen if we compare the wealth ratio of populations N1 and N2 at their respectively different wealth levels, say, x1 and x2. We have for the exponential distribution: ln(N1/N2) = − λ (xi − x2). For the Pareto distribution we have ln(N1/N2) = − α ln(xi/x2). |
| 21 | Most probability distributions have well defined means, variances, and higher-order moments. The exponential distribution, for example, with rate λ has a mean of 1/λ and a variance of 1/λ2. For such distributions, outcomes far from the mean are very rare. The Pareto distribution, on the other hand, with an index α has a mean of α xm/(α − 1) for α > 1 and a variance of α (xm)2/(α − 1)2 (α − 2) for α > 2 and has infinite values for the mean and the variance for values of the index lower than those indicated. Distributions such as the Pareto one, on the other hand, have more common outcomes far from the mean and are described as having a “fat tail”. Thus, the Pareto distribution is well suited to describe empirically outcomes far from the mean such as the observed occurrence of very wealthy or high-income actors in the economy. This is essentially the gist of a power law. |
| 22 | The percent of wealth (income) S controlled by the top X percent of the population is given by the Pareto equation S = X(1−1/α) such that for α = 2 and X = 0.20 we obtain S = 0.447. In other words, in an economic system where all the actors/particpiants have equal opportunity, 20% of the them ought to control 44.7% of wealth (income) as the optimal distribution of the available income or wealth. The observed distribition of wealth in particular of 80% or even higher for 20% of the actors/population suggests the lack of equal opportunity or access to the economic system. For S = 0.80 and X = 0.20, the value of α or δ would be 1.16, i.e., well below the optimal vaue of α = δ = 2. |
| 23 | In our analytical model this difference can be accounted for by employing two different values in the parameter γ, one for wealth and one for income, such that two respective values for the parameter (βh) result. However, the justification for this differentiation at the present moment is an empirical observation based on the difference between the disribution of wealth and of income. Alternatively, the fitness η of the actors can vary between wealth and income such that the “scale-free phase” of the complex network can be modified into a “fit-get-rich phase” whereby certain nodes (actors) accumulate all the wealth, i.e., the fittest prevail. However, fitness can be viewed as an externally imposed condition to obtain certain outcome. In that instance then the actors no longer have equal opportunity, i.e., they are differentiated. This differentiation then would lead to excessive inequality, which is observed globally, particularly as it regards wealth. See also (Bianconi and Barabási 2001). |
| 24 | The Gini coefficient on income, sometimes referred to as the pre-tax Gini coefficient, is calculated on income before taxes and transfers, and it measures inequality in income without considering the effect of the taxes and social spending already in place in a country. The Gini coefficient on disposable income, sometimes referred to as the after-tax Gini coefficient, is calculated on income after taxes and transfers. |
| 25 | Absolute equality (all actors have equal wealth or income) as well as absolute inequality (one actor has all the wealth or income) are impossible states to attain and maintain (static economic system), although the latter has a higher probability to occur than the former. |
References
- Acemoglu, Daron. 2015. Lectures in Inequality, Lecture 8, Pareto Income and Wealth Distributions. Available online: https://economics.mit.edu/sites/default/files/inline-files/Lecture%208%20-%20Pareto%20Income%20and%20Wealth%20Distributuions.pdf (accessed on 20 August 2024).
- Andriani, Pierpaolo, and Bill McKelvey. 2009. From Gaussian to Paretian Thinking: Causes and Implications of Power Laws in Organizations. Available online: https://leeds-faculty.colorado.edu/dahe7472/Adriani%2025614715.pdf (accessed on 10 July 2022).
- Arrow-Debreu, Model. 2023. Available online: https://en.wikipedia.org/wiki/Arrow–Debreu_model (accessed on 8 January 2024).
- Barabási, Albert-László. 2014. Linked—How Everything Is Connected to Everything Else and What It Means for Business, Science, and Everyday Life. New York: Basic Books. [Google Scholar]
- Bianconi, Ginestra, and Albert-László Barabási. 2001. Bose-Einstein Condensation in Complex Networks. Physical Review Letters 86: 5632–35. [Google Scholar] [CrossRef] [PubMed]
- Bocquet, S. 2024. Generalized Exponential Integral. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52694-generalised-exponential-integral (accessed on 26 February 2024).
- Coogan, M. D., ed. 2007. The New Oxford Annotated Bible with the Apocrypha, 3rd ed. Oxford and New York: Oxford University Press. [Google Scholar]
- Cover, Thomas M., and Joy A. Thomas. 1991. Elements of Information Theory. New York: John Wiley & Sons, Inc. [Google Scholar]
- Deaton, Angus. 1997. Analysis of Household Surveys. Baltimore: Johns Hopkins University Press. [Google Scholar]
- Deaton, Angus. 2013. The Great Escape—Health, Wealth, and the Origins of Inequality. Princeton: Princeton University Press. [Google Scholar]
- Exponential Distribution. 2022. Available online: https://en.wikipedia.org/wiki/Exponential_distribution (accessed on 19 December 2022).
- Feynman, Richard. 1998. Statistical Mechanics—A Set of Lectures. Boulder: Westview Press—A Member of the Perseus Group, p. 6. [Google Scholar]
- Franklin, Benjamin. 1757. The Way to Wealth. Philadelphia: Sound Wisdom, Originally published in Philadelphia, PA and reprinted since then. [Google Scholar]
- Geanakoplos, John. 2004. The Arrow-Debreu Model of General Equilibrium. Cowles Foundation Paper No. 1090. New Haven: The Cowles Foundation for Research in Economics at Yale University. [Google Scholar]
- General Equilibrium Theory. 2023. Available online: https://en.wikipedia.org/wiki/General_equilibrium_theory (accessed on 8 January 2024).
- Gini Coefficient. 2024. The Wikipedia. Available online: https://en.wikipedia.org/wiki/Gini_coefficient (accessed on 14 August 2024).
- Gini Index. 2019. Metadata Glossary, The World Bank Group. Available online: https://databank.worldbank.org/metadataglossary/world-development-indicators/series/SI.POV.GINI (accessed on 14 August 2024).
- Hechler-Fayd’herbe, Natalie, ed. 2019. Global Wealth Databook. Zurich: Credit Suisse AG, pp. 117–20. [Google Scholar]
- Kafri, Oded, and Hava Kafri. 2013. Entropy—God’s Dice Game. Edited by Emanuel Lotem. Library of Congress Control Number (LCCN): 201390681. Tel Aviv: Kafri Nihul Ve’Hashkaot Ltd. ISBN 13:978-1482687699. [Google Scholar]
- Kaufmann, Stephen, and Ingo Stützle. 2017. Thomas Piketty’s Capital in the Twenty-First Century—An Introduction. Verso, London and New York: Bertz + Fischer GbR. [Google Scholar]
- Kelley, Augustus M. 1971. Manual of Political Economy. New York: Augustus M Kelley Publishers, translation of the French edition from 1927. [Google Scholar]
- Khinchin, Aleksandr I., and George Gamow. 1949. Mathematical Foundations of Statistical Mechanics. New York: Dover Publications, Inc. Mansfield Center: Martino Press. [Google Scholar]
- Kirman, Alan. 1997. The economy as an evolving network. Journal Evolutionary Economics 7: 339–53. [Google Scholar] [CrossRef]
- Kittel, Charles. 2004. Elementary Statistical Physics. Mineola: Dover Publications, Inc. [Google Scholar]
- Lorenz Curve. 2024. Available online: https://en.wikipedia.org/wiki/Lorenz_curve#:~:text=The%20Lorenz%20curve%20for%20a,perfect%20inequality%20being%20an%20example (accessed on 20 August 2024).
- Mantegna, Rosario N., and H. Eugene Stanley. 2000. An Introduction to Econophysics—Correlations and Complexity in Finance. Cambridge: Cambridge University Press. [Google Scholar]
- Milanovic, Branko. 2009. Global Inequality and the Global Inequality Extraction Ratio—The Story of the Past Two Centuries. Policy Research Working Paper 5044. Washington, DC: The World Bank, Development Research Group, Poverty, and Inequality Team. [Google Scholar]
- Newman, Mark E. J. 2006. Pareto Laws, Pareto Distributions and Zipf’s Law. Available online: https://arxiv.org/PS_cache/cond-mat/pdf/0412/0412004v3.pdf (accessed on 20 August 2024).
- NTIS. 2022. Digital Library of Mathematical Functions, National Institute of Science and Technology, U.S. Department of Commerce. Available online: https://dlmf.nist.gov/ (accessed on 2 May 2022).
- Organization for Economic Co-Operation and Development (OECD). 2012. Income Distribution—Inequality: Income Distribution—Inequality—Country Tables. Available online: http://stats.oecd.org/Index.aspx? (accessed on 7 January 2020).
- Ortiz, Isabel, and Matthew Cummins. 2011. Global Inequality: Beyond the Bottom Billion. New York: UNICEF Social and Economic Policy Working Paper. [Google Scholar]
- Oyama, Susan. 2000. The Ontogeny of Information, 2nd ed. Durham: Duke University Press. [Google Scholar]
- Pareto, Vilfredo. 1925. Écrits sur la Courbe de la Répartition de la Richesse. Edited by Œuvres Complètes T. III and Librairie Droz. Available online: https://shs.cairn.info/ecrits-sur-la-courbe-de-la-repartition-de-la-riche--9782600040211?lang=fr (accessed on 20 August 2024).
- Pareto Distribution. 2022. Available online: https://en.wikipedia.org/wiki/Pareto_distribution (accessed on 19 December 2022).
- Pareto Principle. 2024. Available online: https://en.wikipedia.org/wiki/Pareto_principle (accessed on 20 August 2024).
- Piketty, Thomas. 2014. Capital in the Twenty-First Century. Cambridge, MA: Harvard University Press, (translated from the original French publication in 2013 under the same title). [Google Scholar]
- Planck, Max. 1900. On the Theory of the Energy Distribution Law of the Natural Spectrum. Verhandlugen der Deutschen Physikalischen Gesellschaft 2: 237, English translation from the Old Quantum Theory. Edited by D. ter Haar. Oxford: Pergamon Press, 1967. p. 82. [Google Scholar]
- Prigogine, Ilya. 1980. From Being to Becoming: Time and Complexity in the Physical Sciences. San Francisco: W.H. Freeman and Company. [Google Scholar]
- Prigogine, Ilya. 2017. Non-Equilibrium Statistical Mechanics. Mineola: Dover Publications, Inc. [Google Scholar]
- Prigogine, Ilya, and I. Stengers. 1984. Order out of Chaos: Man’s New Dialogue with Nature. New York: Bantam Books. [Google Scholar]
- Sargent, Rachel L. 1925. The Size of the Slave Population at Athens during the Fifth and Fourth Centuries before Christ. Champaign: University of Illinois. [Google Scholar]
- Schrödinger, Erwin. 1944. What Is Life? Cambridge: Cambridge University Press. [Google Scholar]
- Schrödinger, Erwin. 1989. Statistical Thermodynamics. New York: Dover Publications, Inc. [Google Scholar]
- Sen, Amartya. 1997. On Economic Inequality, 2nd ed. New York: Oxford University Press. [Google Scholar]
- Shannon, Claude E., and Warren Weaver. 1949. The Mathematical Theory of Communication. Urbana: University of Illinois Press. [Google Scholar]
- Simon, Herbert A. 1996. The Sciences of the Artificial. Cambridge, MA: MIT Press. [Google Scholar]
- The MIT Business Review. 2018. If You’re so Smart, Why Aren’t You Rich? Turns out It’s Chance. The MIT Business Review, March 1. [Google Scholar]
- The World Bank Group. 2016. Taking on Inequality—Poverty and Shared Prosperity 1988–2013. Washington, DC: The World Bank Group. [Google Scholar]
- Tolman, Richard Chace. 1979. The Principles of Statistical Mechanics. New York: Dover Publications Inc., pp. 372–78, 382–85. [Google Scholar]
- Treanor, Jill. 2015. Half of the World’s Wealth Is Now in Hands of 1% of Population—Report. The Guardian. October 13. Available online: https://www.theguardian.com/money/2015/oct/13/half-world-wealth-in-hands-population-inequality-report (accessed on 15 August 2024).
- United Nations Development Program (UNDP). 2021. The Real Wealth of Nations: Pathways to Human Development, 2010. New York: United Nations Development Program, pp. 72–74. [Google Scholar]
- Von Bertalanffy, Ludwig. 1969. General System Theory: Foundations, Development, Applications, rev. ed. New York: George Braziller. [Google Scholar]
- World Bank Group. 2022. Gini Index, World Bank Open Data—All Countries and Economies, Data Ranging mostly from 2015 to 2022, Washington DC. Available online: https://data.worldbank.org/indicator/SI.POV.GINI?most_recent_value_desc=false (accessed on 15 August 2024).
- Zwillinger, Daniel. 2012. CRC Standard Mathematical Tables and Formulae. Boca Raton: CRC Press—Taylor & Francis Group. [Google Scholar]




| Actor Ni | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Wealth Element Gi | 7 | 28 | 11 | 0 | 9 | 2 | 20 | 4 | 4 | 5 |
| Βh | E1 (βh) | E2 (βh) | E2 (βh)/E1 (βh) |
|---|---|---|---|
| 0.2 | 1.22265 | 0.57420 | 0.46964 |
| 0.4 | 0.70238 | 0.38932 | 0.55436 |
| 0.6 | 0.45438 | 0.27618 | 0.60782 |
| 0.8 | 0.31060 | 0.20084 | 0.64665 |
| 1.0 | 0.21938 | 0.14850 | 0.67691 |
| 2.0 | 0.04890 | 0.03775 | 0.77198 |
| 3.0 | 0.01305 | 0.01064 | 0.81545 |
| 4.0 | 0.00378 | 0.00320 | 0.84656 |
| 5.0 | 0.00015 | 0.00060 | 4.00000 |
| Empirical Pareto Law | Scale-Free Network System |
|---|---|
| Xo = 1 minimum value of variable x | Xo = 1 normalized value of the variable x to the quantum of wealth (income) h that an actor must have to be part of the system |
| α > 1 Pareto index | δ ≥ 1 signifies the degree of allocation of links (wealth) to a node (actor) in the economic system governed by a stochastic process; at δ = 1 one node has all the links, and at δ = ∞ every node has only one link. δ = 2 optimal value of the parameter. |
| α Xo/(α − 1) expected value | 1/β denotes the average allocation of wealth (income) per actor in the economic system with (βh) < 1 optimally; 1/β is analogous to the temperature in a physical system and thus is a measure of entropy. |
| γ ≥ 0 parameter varying from zero to infinite associated with the number of actors in the economic system γ = 0 number of actors large and variable (implicit assumption in Pareto’s Law) |
| Year | GF | Year | GF | Year | GF |
|---|---|---|---|---|---|
| 1820 | 0.43 | 1950 | 0.64 | 1998 | 0.74 |
| 1850 | 0.53 | 1960 | 0.64 | 2002 | 0.71 |
| 1870 | 0.56 | 1980 | 0.66 | 2003 | 0.72 |
| 1913 | 0.61 | 1988 | 0.80 | 2008 | 0.70 |
| 1929 | 0.62 | 1993 | 0.76 | 2013 | 0.65 |
| Country | Gini Coefficient | Top Quintile Percent | |
|---|---|---|---|
| Wealth | Income | Income | |
| United States | 0.801 | 0.464 | 50.1 |
| Japan | 0.547 | 0.319 | 35.7 |
| Germany | 0.671 | 0.311 | 38.5 |
| China | 0.550 | 0.449 | 47.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ingersoll, J.G. Inequality in the Distribution of Wealth and Income as a Natural Consequence of the Equal Opportunity of All Members in the Economic System Represented by a Scale-Free Network. Economies 2024, 12, 232. https://doi.org/10.3390/economies12090232
Ingersoll JG. Inequality in the Distribution of Wealth and Income as a Natural Consequence of the Equal Opportunity of All Members in the Economic System Represented by a Scale-Free Network. Economies. 2024; 12(9):232. https://doi.org/10.3390/economies12090232
Chicago/Turabian StyleIngersoll, John G. 2024. "Inequality in the Distribution of Wealth and Income as a Natural Consequence of the Equal Opportunity of All Members in the Economic System Represented by a Scale-Free Network" Economies 12, no. 9: 232. https://doi.org/10.3390/economies12090232
APA StyleIngersoll, J. G. (2024). Inequality in the Distribution of Wealth and Income as a Natural Consequence of the Equal Opportunity of All Members in the Economic System Represented by a Scale-Free Network. Economies, 12(9), 232. https://doi.org/10.3390/economies12090232






