Predicting Convergence of Per Capita Income in Spain: A Markov and Cluster Approach
Abstract
1. Introduction
- Bode and Nunnenkamp (2011) analyze the impact of foreign direct investment on per capita income and growth, in general, in the United States, since the mid-1970s, demonstrating that the investment in employment has favored the increase in income, although the investment destined for capital has not had the same impact on the states with the greatest poverty, where it has been most intensive.
Provincial Income Disparities in Spain: A Literature Overview
2. Methodology
2.1. Markov Chains
2.1.1. Long-Term Behavior
2.1.2. States Classification
- We will say that a state is accessible from another state when at some instant of time. Furthermore, when it is probable to go from one state to another in both directions, we will say that both states communicate. If all the states of a Markov chain communicate, we say that the Markov chain is irreducible.
- However, if there is a state that cannot be reached from any other in the Markov chain, we will say that it is ephemeral.
- On the other hand, if there is a state from which we cannot reach any other one, we say that it is absorbing. Mathematically, the state will be absorbing if .
2.1.3. Estimating the Transition Probability Matrix
2.2. Data and Treatment
2.3. Cluster Analysis
- Agglomerative: they start from simple groups which become more sophisticated as more iterations are taken. It is, therefore, an ascending approach between individuals.
- Divisive: we start from the sample as a group and, at each step, smaller groups are built until the desired number of clusters is achieved. It is, therefore, a descending approach.
3. Results and Discussion
3.1. Evolution of per Capita Income in Presence of COVID-19
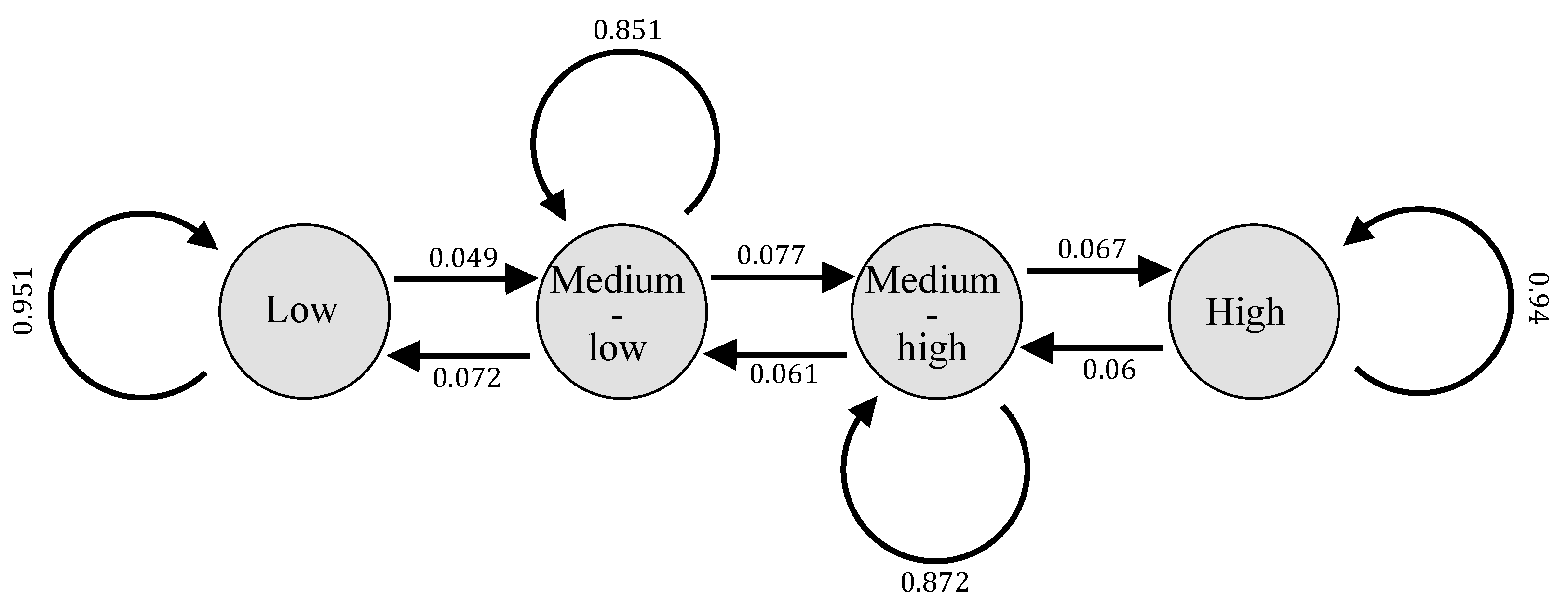
- First quartile: 0.7875988. Hence, a province will be said to be in the “low income” state if its GDP per capita divided by the annual average is less than 0.7875988.
- Second quartile: 0.8672922. In case the per capita income relative to the Spanish average is greater than 0.7875988 and less than 0.8672922, the province is said to be in the “medium-low income” state.
- Third quartile: 1.0802799. In case the per capita income relative to the Spanish average is greater than 0.8672922 and less than 1.0802799, the province is said to be in the “medium-high income” state. Finally, if the per capita income relative to the Spanish average is greater than 1.0802799, the province will be said to have high income.
- The Markov chain is aperiodic.
- Its stationary distribution is .
- Low income: years.
- Medium-low income: years.
- Medium-high income: years.
- High income: years.
3.2. Evolution of per Capita Income Without COVID-19
- Low income: years.
- Medium-low income: years.
- Medium-high income: years.
- High income: years.
- .
- .
- .
- .
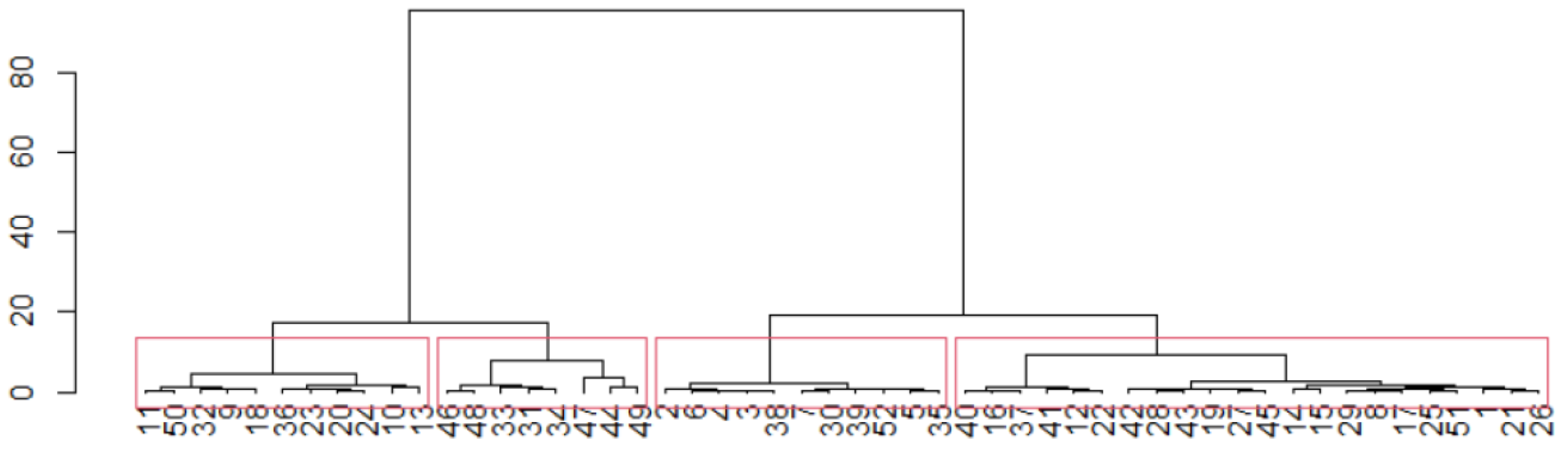
3.3. Convergence Clubs
- Group 1 (high income): Navarra, Vizcaya, Lérida, Barcelona, Tarragona, Álava, Madrid and Guipúzcoa.
- Group 2 (medium-high income): Zaragoza, La Rioja, Gerona, Huesca, Burgos, Castellón, Soria, Palencia, Valladolid, Teruel and Baleares Islands.
- Group 3 (medium-low income): La Coruña, Cantabria, Valencia, Lugo, Asturias, Segovia, Orense, Cuenca, Pontevedra, León, Ciudad Real, Murcia, Las Palmas, Santa Cruz de Tenerife, Guadalajara, Sevilla, Ávila, Zamora, Ceuta, Almería, Salamanca and Albacete.
- Group 4 (low income): Cádiz, Jaén, Granada, Córdoba, Badajoz, Málaga, Toledo, Cáceres, Melilla, Huelva and Alicante.
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GDP | Gross domestic product |
Appendix A. Preliminaries on Markov Chains
- for each .
- for each .
Appendix B. Procedures in R
Appendix B.1. Markov Chains
- steadyStates(mc)
- period(mc)
- meanRecurrenceTime(mc)
- is.irreducible(mc)
- plot(mc)
Appendix B.2. Cluster Analysis
- Standarize the variables, that is, subtract the mean from the value of each one and divide the result by the standard deviation of the values of the variable. If the data contain the information to be processed, we must implementdf=as.data.frame(scale(data))
- Calculate the proximity matrix by using the Euclidean distance:d_eu <-dist(df, method =’euclidean’ )
- Find the agglomerative hierarchical cluster with Ward’s method:cluster <- hclust(d_eu, method = ’ward.D’)
- Draw the dendrogram:plot(as.dendrogram(cluster))
- Draw rectangles that group a certain number, k, of the individuals in the sample:rect.hclust(cluster, k = 4)
References
- Anderson, T. W., & Goodman, L. A. (1957). Statistical inference about Markov chains. The Annals of Mathematical Statistics, 28(1), 89–110. [Google Scholar] [CrossRef]
- Arreola, D., & Montiel, L. V. (2024). Approximating income inequality dynamics given incomplete information: An upturned Markov chain model. Computational Statistics, 39(2), 629–651. [Google Scholar] [CrossRef]
- Ayuda, M. I., Collantes, F., & Pinilla, V. (2010). Long-run regional population disparities in Europe during modern economic growth: A case study of Spain. The Annals of Regional Science, 44, 273–295. [Google Scholar] [CrossRef]
- Bode, E., & Nunnenkamp, P. (2011). Does foreign direct investment promote regional development in developed countries? A Markov chain approach for US states. Review of World Economics, 147, 351–383. [Google Scholar] [CrossRef][Green Version]
- Chen, Y., Mamon, R., Spagnolo, F., & Spagnolo, N. (2022). Renewable energy and economic growth: A Markov-switching approach. Energy, 244, 123089. [Google Scholar] [CrossRef]
- Deaton, A. (2021). COVID-19 and global income inequality. LSE Public Policy Review, 1(4), 1. [Google Scholar] [CrossRef]
- Everitt, B., Landau, S., Leese, M., & Stahl, D. (2011). Cluster Analysis (5th ed.). John Wiley & Sons. [Google Scholar]
- Fingleton, B. (1997). Specification and testing of Markov chain models: An application to convergence in the European Union. Oxford Bulletin of Economics and Statistics, 59(3), 385–403. [Google Scholar] [CrossRef]
- Formby, J. P., Smith, W. J., & Zheng, B. (2004). Mobility measurement, transition matrices and statistical inference. Journal of Econometrics, 120(1), 181–205. [Google Scholar] [CrossRef]
- Gardeazábal, J. (1996). Provincial income distribution dynamics: Spain 1967–1991. Investigaciones Económicas, 20(2), 263–269. [Google Scholar]
- Gostkowski, M., Rokicki, T., Ochnio, L., Koszela, G., Wojtczuk, K., Ratajczak, M., Szczepaniuk, H., Bórawski, P., & Bełdycka-Bórawska, A. (2021). Clustering analysis of energy consumption in the countries of the visegrad group. Energies, 14(18), 5612. [Google Scholar] [CrossRef]
- Haller, A., Gherasim, O., & Bălan, M. (2020). Medium-term forecast of European economic sustainable growth using Markov chains. Zb. rad. Ekon. fak. Rij., 38(2), 585–618. [Google Scholar]
- He, L., Tao, J. G., Meng, P., Chen, D., Yan, M., & Vasa, L. (2021). Analysis of socio-economic spatial structure of urban agglomeration in China based on spatial gradient and clustering. Oeconomia Copernicana, 12(3), 789–819. [Google Scholar] [CrossRef]
- Karahasan, B. C. (2020). Can neighbor regions shape club convergence? Spatial Markov chain analysis for Turkey. Letters in Spatial and Resource Sciences, 13(2), 117–131. [Google Scholar] [CrossRef]
- Kassambara, A. (2017). Practical guide to cluster analysis in R: Unsupervised machine learning. Sthda. [Google Scholar]
- Kerkouch, A., Bensbahou, A., Seyagh, I., & Agouram, J. (2024). Dynamic analysis of income disparities in Africa: Spatial markov chains approach. Scientific African, 24, e02236. [Google Scholar] [CrossRef]
- Le Gallo, J., & Chasco, C. (2008). Spatial analysis of urban growth in Spain, 1900–2001. Empirical Economics, 34, 59–80. [Google Scholar] [CrossRef]
- Lipták, K. (2011). The application of Markov chain model to the description of hungarian market processes. Zarządzanie Publiczne, 16(4), 133–149. [Google Scholar]
- National Statistics Institute. (2023). Regional Accounting of Spain. Results. GDP and GDP per Capita. 2000–2022 Series. Available online: https://www.ine.es/dyngs/INEbase/es/operacion.htm?c=Estadistica_C&cid=1254736167628&menu=resultados&idp=1254735576581 (accessed on 2 October 2023).
- Papanikolaou, N. (2020). Markov-switching model of family income quintile shares. Atlantic Economic Journal, 48(2), 207–222. [Google Scholar] [CrossRef]
- Quah, D. (1993). Empirical cross-section dynamics in economic growth. European Economic Review, 37, 426–434. [Google Scholar] [CrossRef]
- Rey, S. (2023). Intersectional urban dynamics: A joint Markov chains approach. Letters in Spatial and Resource Sciences, 16(1), 36. [Google Scholar] [CrossRef]
- Shorrocks, A. F. (1978). The measurement of mobility. Econometrica: Journal of the Econometric Society, 46(5), 1013–1024. [Google Scholar] [CrossRef]
- Sommers, P. S., & Conlisk, J. (1979). Eigenvalue immobility measures for Markov chains. Journal of Mathematical Sociology, 6, 253–276. [Google Scholar] [CrossRef]
- Takács, L. (1960). Stochastic processes problems and solutions. Chapman and Hall. [Google Scholar]
- Tirado, D. A., Díez-Minguela, A., & Martinez-Galarraga, J. (2016). Regional inequality and economic development in Spain, 1860–2010. Journal of Historical Geography, 54, 87–98. [Google Scholar] [CrossRef]
- Wenxuan, Y. (2023). Human capital dynamics across provinces in china: A spatial markov chain approach. Forum of International Development Studies, 53(8), 1–17. [Google Scholar]
- Yang, Y., & Hu, A. (2008). Investigating regional disparities of China’s human development with cluster analysis: A historical perspective. Social Indicators Research, 86, 417–432. [Google Scholar] [CrossRef]
- Zarikas, V., Poulopoulos, S. G., Gareiou, Z., & Zervas, E. (2020). Clustering analysis of countries using the COVID-19 cases dataset. Data in Brief, 31, 105787. [Google Scholar] [CrossRef]
| Type of State | Conditions |
|---|---|
| accesible from | |
| ephemeral | for each i |
| absorbing | |
| Recurrent | Probability of coming back to it |
| Positive recurrent | Finite mean recurrence time |
| Transitory | Probability of coming back to it |
| Aperiodic | Period |
| Province/Auton. City | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Almería | 0.802 | 0.754 | 0.767 | 0.760 | 0.783 | 0.801 | 0.838 | 0.857 | 0.839 | 0.841 | 0.862 |
| Cádiz | 0.735 | 0.736 | 0.729 | 0.717 | 0.699 | 0.691 | 0.691 | 0.695 | 0.693 | 0.700 | 0.679 |
| Córdoba | 0.717 | 0.715 | 0.696 | 0.711 | 0.706 | 0.717 | 0.709 | 0.711 | 0.703 | 0.681 | 0.707 |
| Granada | 0.708 | 0.713 | 0.719 | 0.719 | 0.732 | 0.737 | 0.715 | 0.707 | 0.705 | 0.713 | 0.725 |
| Huelva | 0.747 | 0.779 | 0.781 | 0.732 | 0.719 | 0.729 | 0.735 | 0.763 | 0.781 | 0.757 | 0.767 |
| Jaén | 0.706 | 0.713 | 0.661 | 0.715 | 0.675 | 0.731 | 0.699 | 0.691 | 0.709 | 0.670 | 0.718 |
| Málaga | 0.758 | 0.748 | 0.731 | 0.724 | 0.730 | 0.725 | 0.715 | 0.720 | 0.726 | 0.729 | 0.710 |
| Sevilla | 0.814 | 0.815 | 0.818 | 0.799 | 0.803 | 0.790 | 0.780 | 0.782 | 0.783 | 0.785 | 0.795 |
| Huesca | 1.124 | 1.132 | 1.118 | 1.164 | 1.139 | 1.105 | 1.168 | 1.136 | 1.117 | 1.119 | 1.216 |
| Teruel | 1.045 | 1.045 | 1.062 | 1.085 | 1.084 | 1.023 | 0.994 | 0.955 | 0.977 | 0.965 | 0.994 |
| Zaragoza | 1.093 | 1.087 | 1.076 | 1.085 | 1.086 | 1.071 | 1.076 | 1.091 | 1.096 | 1.096 | 1.127 |
| Asturias | 0.917 | 0.914 | 0.905 | 0.892 | 0.883 | 0.882 | 0.872 | 0.878 | 0.880 | 0.879 | 0.887 |
| Baleares | 1.059 | 1.059 | 1.067 | 1.065 | 1.077 | 1.077 | 1.087 | 1.085 | 1.081 | 1.071 | 0.913 |
| Las Palmas | 0.838 | 0.836 | 0.824 | 0.833 | 0.820 | 0.801 | 0.811 | 0.810 | 0.810 | 0.800 | 0.716 |
| Sta. Cruz de Tenerife | 0.890 | 0.886 | 0.878 | 0.860 | 0.851 | 0.843 | 0.824 | 0.827 | 0.816 | 0.807 | 0.742 |
| Cantabria | 0.945 | 0.937 | 0.934 | 0.921 | 0.927 | 0.910 | 0.913 | 0.912 | 0.918 | 0.922 | 0.934 |
| Ávila | 0.788 | 0.801 | 0.818 | 0.808 | 0.802 | 0.788 | 0.775 | 0.776 | 0.784 | 0.791 | 0.828 |
| Burgos | 1.111 | 1.132 | 1.156 | 1.129 | 1.112 | 1.100 | 1.112 | 1.128 | 1.145 | 1.128 | 1.144 |
| León | 0.870 | 0.867 | 0.874 | 0.856 | 0.848 | 0.838 | 0.818 | 0.818 | 0.823 | 0.829 | 0.867 |
| Palencia | 1.022 | 1.043 | 1.024 | 1.028 | 1.010 | 1.027 | 1.062 | 1.004 | 1.054 | 1.041 | 1.069 |
| Salamanca | 0.804 | 0.810 | 0.810 | 0.798 | 0.796 | 0.797 | 0.810 | 0.808 | 0.811 | 0.822 | 0.855 |
| Segovia | 0.939 | 0.930 | 0.921 | 0.917 | 0.926 | 0.931 | 0.907 | 0.850 | 0.858 | 0.860 | 0.887 |
| Soria | 1.004 | 1.015 | 0.993 | 1.016 | 1.022 | 1.018 | 0.999 | 0.986 | 1.082 | 1.066 | 1.074 |
| Valladolid | 1.026 | 1.020 | 1.018 | 1.020 | 1.025 | 1.022 | 1.045 | 1.057 | 1.074 | 1.064 | 1.092 |
| Zamora | 0.798 | 0.823 | 0.851 | 0.832 | 0.819 | 0.819 | 0.810 | 0.743 | 0.756 | 0.770 | 0.807 |
| Albacete | 0.801 | 0.793 | 0.798 | 0.801 | 0.783 | 0.798 | 0.793 | 0.806 | 0.815 | 0.823 | 0.851 |
| Ciudad Real | 0.835 | 0.837 | 0.841 | 0.826 | 0.798 | 0.830 | 0.834 | 0.836 | 0.839 | 0.824 | 0.857 |
| Cuenca | 0.839 | 0.859 | 0.870 | 0.875 | 0.852 | 0.868 | 0.866 | 0.867 | 0.882 | 0.856 | 0.891 |
| Guadalajara | 0.832 | 0.836 | 0.830 | 0.814 | 0.770 | 0.742 | 0.757 | 0.776 | 0.789 | 0.794 | 0.816 |
| Toledo | 0.760 | 0.743 | 0.730 | 0.731 | 0.718 | 0.716 | 0.721 | 0.716 | 0.724 | 0.717 | 0.746 |
| Barcelona | 1.172 | 1.167 | 1.172 | 1.181 | 1.193 | 1.193 | 1.201 | 1.208 | 1.205 | 1.208 | 1.201 |
| Gerona | 1.156 | 1.143 | 1.151 | 1.144 | 1.149 | 1.143 | 1.154 | 1.093 | 1.080 | 1.084 | 1.083 |
| Lérida | 1.191 | 1.190 | 1.219 | 1.247 | 1.241 | 1.240 | 1.171 | 1.091 | 1.091 | 1.105 | 1.119 |
| Tarragona | 1.168 | 1.156 | 1.153 | 1.157 | 1.170 | 1.190 | 1.206 | 1.211 | 1.175 | 1.154 | 1.113 |
| Alicante | 0.769 | 0.749 | 0.737 | 0.738 | 0.749 | 0.747 | 0.758 | 0.762 | 0.756 | 0.754 | 0.762 |
| Castellón | 0.970 | 0.998 | 0.972 | 0.989 | 0.992 | 1.021 | 1.037 | 1.090 | 1.067 | 1.062 | 1.048 |
| Valencia | 0.940 | 0.939 | 0.930 | 0.935 | 0.944 | 0.934 | 0.920 | 0.909 | 0.922 | 0.921 | 0.929 |
| Badajoz | 0.716 | 0.709 | 0.694 | 0.702 | 0.690 | 0.702 | 0.704 | 0.715 | 0.711 | 0.704 | 0.738 |
| Cáceres | 0.715 | 0.701 | 0.716 | 0.723 | 0.720 | 0.721 | 0.730 | 0.752 | 0.765 | 0.771 | 0.786 |
| La Coruña | 0.949 | 0.938 | 0.931 | 0.940 | 0.924 | 0.935 | 0.941 | 0.930 | 0.940 | 0.935 | 0.952 |
| Lugo | 0.865 | 0.880 | 0.899 | 0.918 | 0.936 | 0.950 | 0.924 | 0.892 | 0.910 | 0.893 | 0.889 |
| Orense | 0.803 | 0.824 | 0.842 | 0.839 | 0.829 | 0.825 | 0.838 | 0.839 | 0.852 | 0.875 | 0.890 |
| Pontevedra | 0.856 | 0.842 | 0.840 | 0.852 | 0.856 | 0.854 | 0.850 | 0.871 | 0.859 | 0.869 | 0.904 |
| Madrid | 1.340 | 1.360 | 1.377 | 1.372 | 1.372 | 1.373 | 1.373 | 1.370 | 1.364 | 1.369 | 1.370 |
| Murcia | 0.832 | 0.819 | 0.823 | 0.831 | 0.822 | 0.838 | 0.833 | 0.830 | 0.816 | 0.818 | 0.834 |
| Navarra | 1.229 | 1.234 | 1.226 | 1.236 | 1.239 | 1.228 | 1.224 | 1.220 | 1.205 | 1.210 | 1.221 |
| Álava | 1.474 | 1.496 | 1.507 | 1.532 | 1.550 | 1.515 | 1.546 | 1.524 | 1.515 | 1.475 | 1.506 |
| Vizcaya | 1.235 | 1.227 | 1.239 | 1.231 | 1.245 | 1.246 | 1.237 | 1.212 | 1.217 | 1.221 | 1.220 |
| Guipúzcoa | 1.289 | 1.299 | 1.311 | 1.298 | 1.286 | 1.271 | 1.264 | 1.297 | 1.289 | 1.297 | 1.288 |
| La Rioja | 1.082 | 1.082 | 1.082 | 1.087 | 1.102 | 1.096 | 1.068 | 1.063 | 1.068 | 1.061 | 1.087 |
| Ceuta | 0.850 | 0.835 | 0.822 | 0.839 | 0.821 | 0.814 | 0.805 | 0.782 | 0.786 | 0.795 | 0.839 |
| Melilla | 0.794 | 0.777 | 0.752 | 0.759 | 0.751 | 0.743 | 0.741 | 0.717 | 0.724 | 0.728 | 0.765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gálvez-Rodríguez, J.F.; Manzano-Hidalgo, M.; García-Luengo, A.V. Predicting Convergence of Per Capita Income in Spain: A Markov and Cluster Approach. Economies 2025, 13, 17. https://doi.org/10.3390/economies13010017
Gálvez-Rodríguez JF, Manzano-Hidalgo M, García-Luengo AV. Predicting Convergence of Per Capita Income in Spain: A Markov and Cluster Approach. Economies. 2025; 13(1):17. https://doi.org/10.3390/economies13010017
Chicago/Turabian StyleGálvez-Rodríguez, José F., Miguel Manzano-Hidalgo, and Amelia V. García-Luengo. 2025. "Predicting Convergence of Per Capita Income in Spain: A Markov and Cluster Approach" Economies 13, no. 1: 17. https://doi.org/10.3390/economies13010017
APA StyleGálvez-Rodríguez, J. F., Manzano-Hidalgo, M., & García-Luengo, A. V. (2025). Predicting Convergence of Per Capita Income in Spain: A Markov and Cluster Approach. Economies, 13(1), 17. https://doi.org/10.3390/economies13010017







