Macroeconomic Determinants of the Interest Rate Term Structure: A Svensson Model Analysis
Abstract
:1. Introduction
2. Modeling the Term Structure of Interest Rates
2.1. Theoretical Framework and Model Implementation: The Brazilian Interest Rate Market
2.2. The Interest Rate Market in Brazil
3. Proposed Model
3.1. Fitting the Yield Curve
3.2. Data Sample
Regression Against State Variables
- DIPCA-Focus: Inflation expectations collected through the Central Bank of Brazil’s Focus Market Report Survey, based on the Extended National Consumer Price Index (IPCA), published by IBGE.
- DGDP-Focus: GDP growth expectations obtained from the Central Bank’s Focus Bulletin, representing market consensus for economic activity.
- IPC-Fipe: The Consumer Price Index calculated by FIPE (Economic Research Institute Foundation) for the São Paulo metropolitan region, measuring current inflation, weekly data.
- Selic: The Brazilian basic interest rate set by the Central Bank’s Monetary Policy Committee (COPOM).
- DExchangeRate: The nominal exchange rate between the Brazilian Real (BRL) and US Dollar (USD).
- Economic Activity: Estimates from the central bank’s Focus Bulletin.
- CDS: The 5-year Credit Default Swap spread for Brazil, serving as a measure of sovereign risk and country risk perception. Weekly data derived from the 5-year Brazil CDS, a daily quoted indicator.
- VIX: The CBOE Volatility Index, measuring global systemic risk through S&P 500 options implied volatility
- T-Bill 10A: The 10-year US Treasury yield, representing the external interest rate and global risk-free rate
- CRB Index: The Commodity Research Bureau index tracking commodity prices, particularly relevant given Brazil’s significant agricultural and mineral exports
3.3. The Choice of Factors
3.4. The Data Usage Interval and State Variable Statistics
- π1: Expected inflation rate for the current calendar year, obtained from the Central Bank’s Focus Market Report Survey
- π2: Expected inflation rate for the next calendar year, obtained from the Focus Market Report Survey
- t: is the first-year end date
- t0: is the current date
- y1: Expected GDP growth rate for the current calendar year from the Focus Market Report Survey
- y2: Expected GDP growth rate for the next calendar year from the Focus Market Report Survey
- t: is the first-year end date
- t0: is the current date
4. Results
4.1. Regression Results
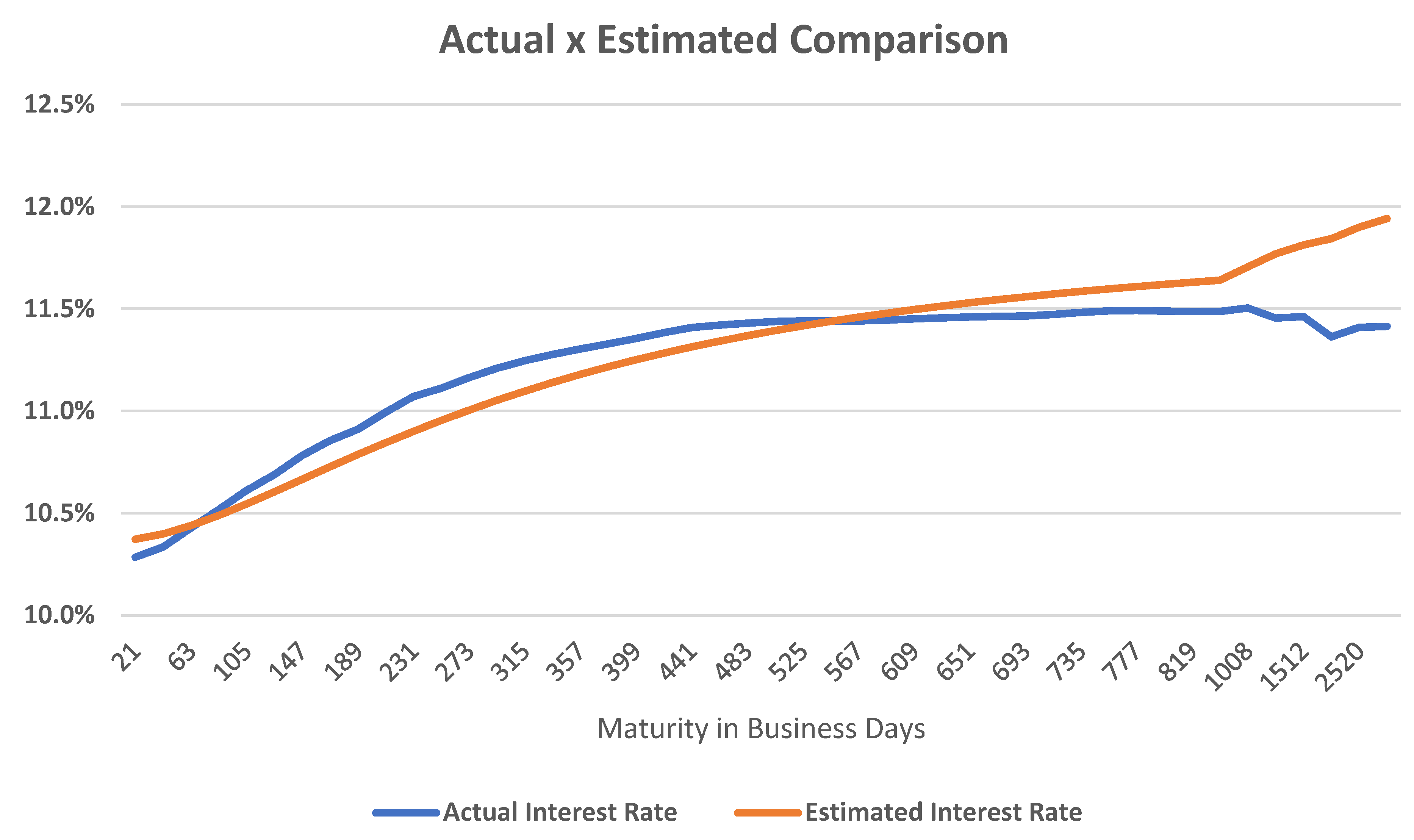
4.2. The Model in Operation
- Statistical model limitations: Forecasting models inherently have margins of error.
- Data lag: Information used for forecasting was collected up to Thursday, while interbank deposit futures contracts traded on Friday or subsequent business days. This may result in incomplete information for Friday’s predictions.
- Time-varying λ terms: The λ terms are influenced by macroeconomic variables, making them dynamic.
- Residual autocorrelation: The models exhibited residual autocorrelation, suggesting potential deficiencies in statistical specifications and the need for additional explanatory variables.
4.3. Usage in Algorithms
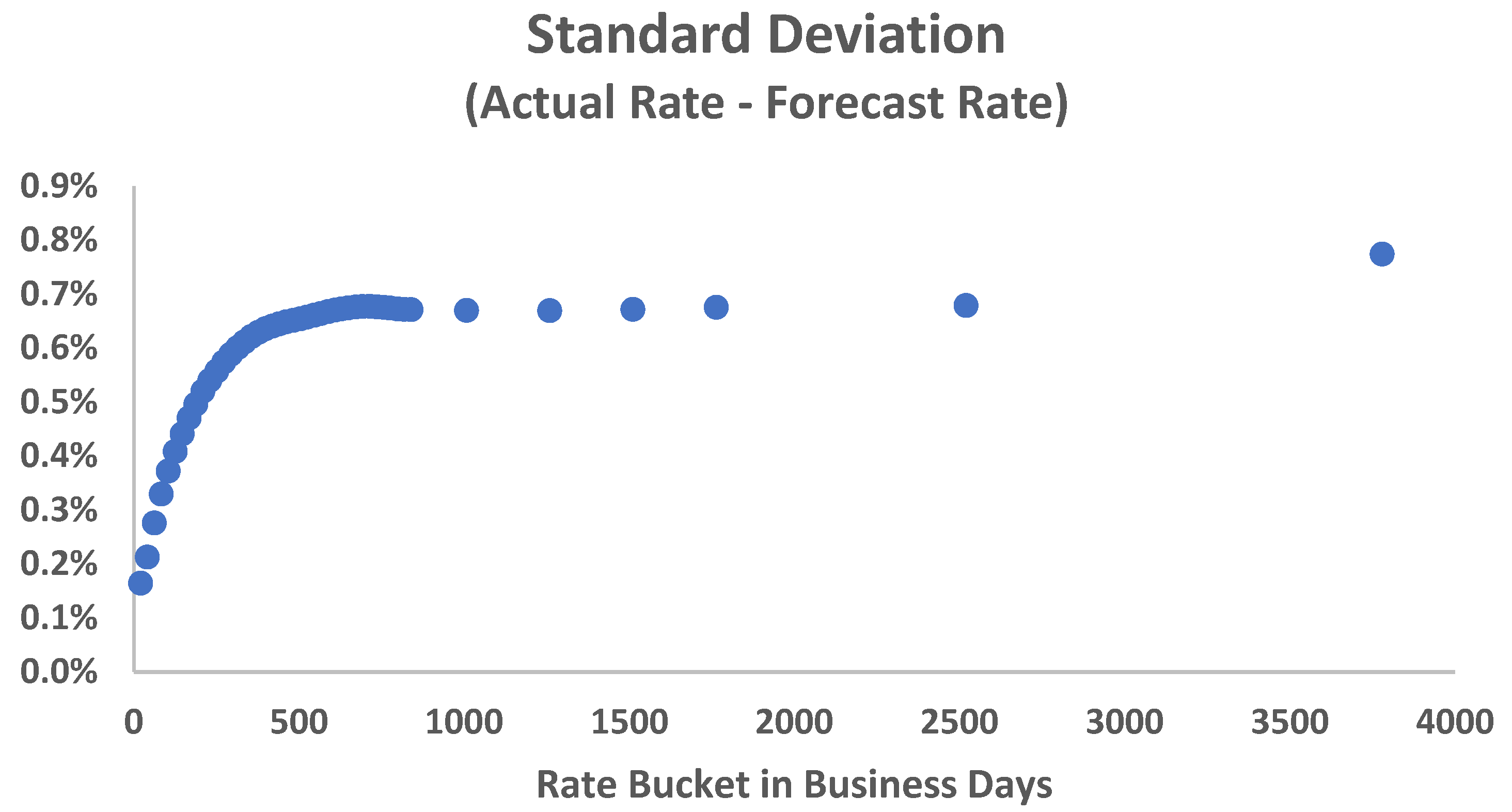
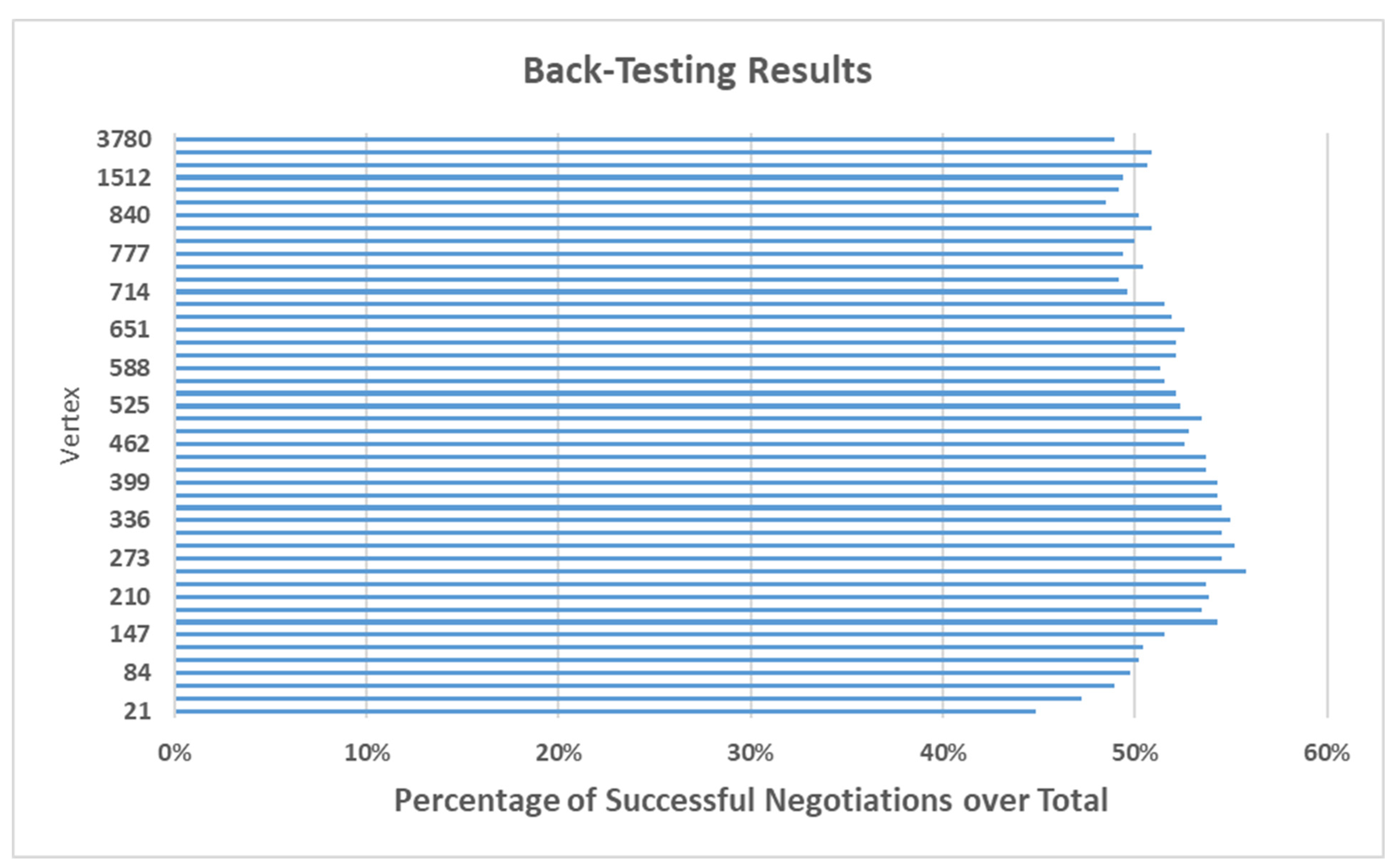
4.4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | This public database can be accessed at Brazilian Central Bank’s time series database (www.bcb.gov.br), the Brazilian Treasury’s yield curve data (www.tesourodireto.com.br), and B3’s market data portal (www.b3.com.br). Accessed during 18 November 2015 to 18 December 2015. |
| 2 | This public database can be accessed at Central Bank’s Focus Market Report (www.bcb.gov.br/en/focus), B3 BOVESPA’s derivatives trading data, and Bank for International Settlements (www.bis.org) for global market structure analysis. Accessed on 25 February 2025. |
| 3 | More information about COPOM (Monetary Policy Committee in Brazil) can be see at https://www.bcb.gov.br/en/monetarypolicy/committee. |
| 4 | The methodology employs explanatory variables observed at time t–1 to predict values at time t. This approach helps mitigate potential endogeneity issues in the model. The use of lagged variables necessarily reduces the effective sample size by one observation. Moreover, this methodology requires using Thursday’s market close data to predict Friday’s values. This temporal alignment structure results in the loss of one additional observation. This approach ensures that all relevant information is properly incorporated into the model. |
References
- Akram, T., & Uddin, S. A. H. (2021). An empirical analysis of long-term Brazilian interest rates. PLoS ONE, 16(9), e0257313. [Google Scholar] [CrossRef] [PubMed]
- Amihud, Y., & Mendelson, H. (1991). Liquidity, maturity, and the yields on US Treasury securities. The Journal of Finance, 46(4), 1411–1425. [Google Scholar] [CrossRef]
- Ariefianto, D., Amanda, C., & Ananto Husodo, Z. (2024). Term structure of interest rate and macro economy: An empirical study on selected emerging countries sovereign bond. Journal of Capital Markets Studies, 8(2), 195–211. [Google Scholar] [CrossRef]
- Bauer, M. D., & Rudebusch, G. D. (2020). Interest rates under falling stars. American Economic Review, 110(5), 1316–1354. [Google Scholar] [CrossRef]
- Caldeira, J. F. (2011). Estimação da estrutura a termo da curva de juros no Brasil através de modelos paramétricos e não paramétricos. Análise Econômica, 29(55). [Google Scholar] [CrossRef]
- Caldeira, J. F., Cordeiro, W. C., Ruiz, E., & Santos, A. A. (2025). Forecasting the yield curve: The role of additional and time-varying decay parameters, conditional heteroscedasticity, and macro-economic factors. Journal of Time Series Analysis, 46(2), 258–285. [Google Scholar] [CrossRef]
- Caldeira, J. F., Moura, G. V., & Santos, A. A. (2015). Measuring risk in fixed income portfolios using yield curve models. Computational Economics, 46(1), 65–82. [Google Scholar] [CrossRef]
- Chen, X., Wang, J., Wu, C., & Wu, D. (2024). Extreme illiquidity and cross-sectional corporate bond returns. Journal of Financial Markets, 68, 100895. [Google Scholar] [CrossRef]
- Coroneo, L., Giannone, D., & Modugno, M. (2016). Unspanned macroeconomic factors in the yield curve. Journal of Business & Economic Statistics, 34(3), 472–485. [Google Scholar]
- Cox, J. C., Ingersoll, J. E., & Ross, S. A. (1985). A theory of the term structure of interest rates. Econometrica, 53(2), 385–407. [Google Scholar] [CrossRef]
- Diebold, F. X., & Li, C. (2006). Forecasting the term structure of government bond yields. Journal of Econometrics, 130, 337–364. [Google Scholar] [CrossRef]
- Elton, E. J., & Green, T. C. (1998). Tax and liquidity effects in pricing government bonds. The Journal of Finance, 53(5), 1533–1562. [Google Scholar] [CrossRef]
- Gomes da Silva, C., Nunes, C. V. A., & Holland, M. (2011). Sinalização de política monetária e movimento na estrutura a termo de taxas de juros no Brasil (pp. 71–90). Escola de Economia de São Paulo, Fundação Getulio Vargas. [Google Scholar]
- Hull, J., & White, A. (1990). Valuing derivative securities using the explicit finite difference method. Journal of Financial and Quantitative Analysis, 25(1), 87–100. [Google Scholar] [CrossRef]
- Huse, C. (2011). Term structure modelling with observable state variables. Journal of Banking & Finance, 35(12), 3240–3252. [Google Scholar]
- Kumar, S., & Virmani, V. (2022). Term structure estimation with liquidity-adjusted Affine Nelson Siegel model: A nonlinear state space approach applied to the Indian bond market. Applied Economics, 54(6), 648–669. [Google Scholar] [CrossRef]
- Ludvigson, S. C., & Ng, S. (2009). Macro factors in bond risk premia. The Review of Financial Studies, 22(12), 5027–5067. [Google Scholar] [CrossRef]
- McCulloch, J. H. (1971). Measuring the term structure of interest rates. The Journal of Business, 44(1), 19–31. [Google Scholar] [CrossRef]
- McCulloch, J. H. (1975). The tax-adjusted yield curve. The Journal of Finance, 30(3), 811–830. [Google Scholar]
- Moench, E. (2008). Forecasting the yield curve in a data-rich environment: A no-arbitrage factor-augmented VAR approach. Journal of Econometrics, 146(1), 26–43. [Google Scholar] [CrossRef]
- Nelson, C. R., & Siegel, A. F. (1987). Parsimonious modelling of yield curves. Journal of Business, 60, 473–489. [Google Scholar] [CrossRef]
- Svensson, L. E. O. (1994). Estimating and interpreting forward interest rates: Sweden 1992–1994 [NBER Working Paper Series 4871]. National Bureau of Economic Research. [Google Scholar]
- Tavanielli, R., & Laurini, M. (2023). Yield curve models with regime changes: An analysis for the Brazilian interest rate market. Mathematics, 11(11), 2549. [Google Scholar] [CrossRef]
- Tsai, S. C. (2012). Liquidity and yield curve estimation. Emerging Markets Finance and Trade, 48(5), 4–24. [Google Scholar] [CrossRef]
- Ullah, W., Matsuda, Y., & Tsukuda, Y. (2015). Generalized Nelson–Siegel term structure model: Do the second slope and curvature factors improve the in-sample fit and out-of-sample forecasts? Journal of Applied Statistics, 42(4), 876–904. [Google Scholar] [CrossRef]
- Vasicek, O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics, 5(2), 177–188. [Google Scholar] [CrossRef]


| Data | Source | Website (Accessed on 25 February 2025) | Period |
|---|---|---|---|
| Interest Rate Market | Brazilian Mercantile & Futures Exchange (B3), now part of B3 | www.b3.com.br/en_us/market-data-and-indices/ | Daily data from January 2006 to December 2014 |
| Market Expectations | |||
| Expected Inflation (IPCA) | Brazilian Central Bank’s Focus Market Report | www.bcb.gov.br/en/publications/focusmarketreadout | Weekly |
| GDP growth expectations | Brazilian Central Bank’s Focus Market Report | www.bcb.gov.br/en/publications/focusmarketreadout | Weekly |
| Domestic Economic Indicators | |||
| Current Inflation | IPC-FIPE (Consumer Price Index) | www.fipe.org.br (São Paulo metropolitan area) | weekly |
| Basic Interest Rate (Selic) | Brazilian Central Bank (BCB) | www.bcb.gov.br | Daily updates |
| Exchange Rate | Brazilian Central Bank (BCB) | www.bcb.gov.br | Daily BRL/USD rate |
| Risk Measures | |||
| Country Risk | 5-year Brazil Credit Default Swap (CDS) quotes | Bloomberg | Daily quotes |
| Global Risk | CBOE Volatility Index (VIX)—Chicago Board Options Exchange | www.cboe.com | Daily |
| International Market | |||
| External Interest Rate | 10-year U.S. Treasury Bills—U.S. Treasury Department | www.treasury.gov | Daily |
| Commodity Index | CoreCommodity CRB Index | Thomson Reuters | Daily |
| Nelson and Siegel | Svensson | Total |
|---|---|---|
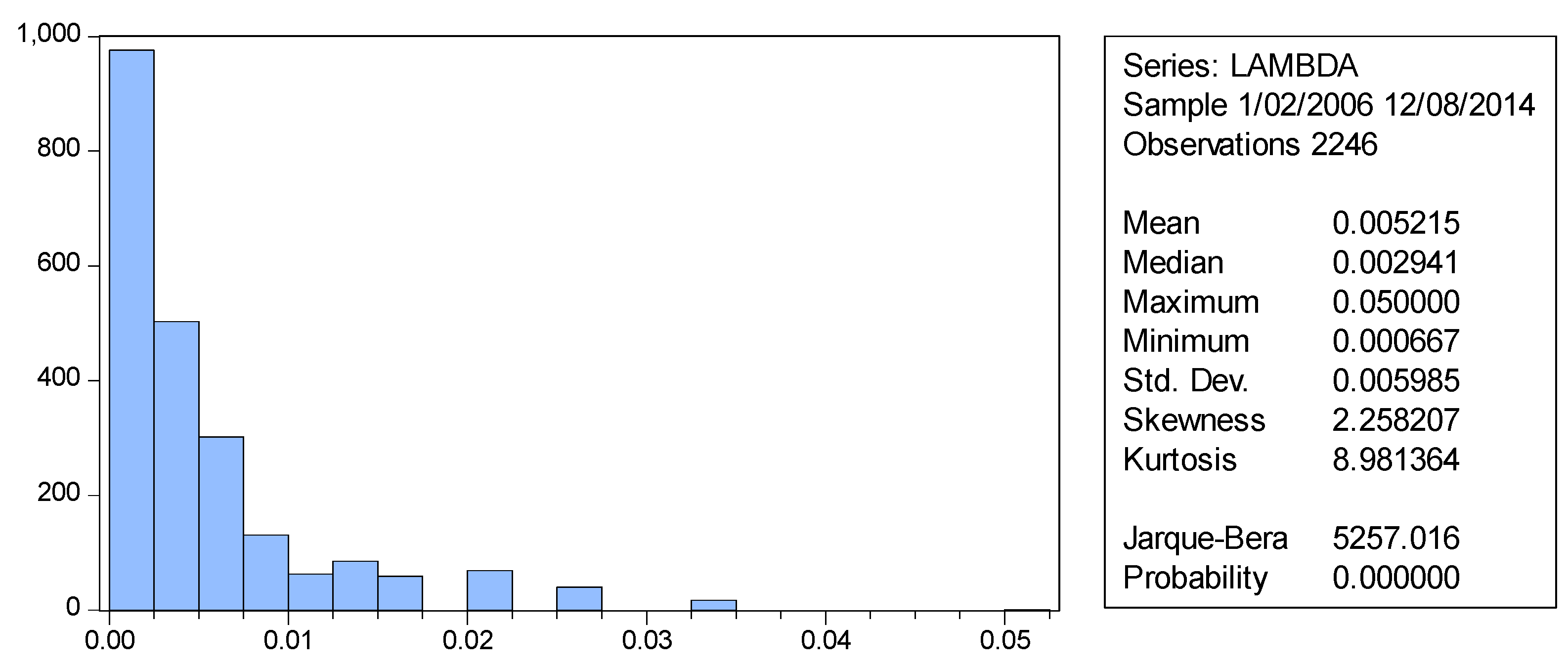
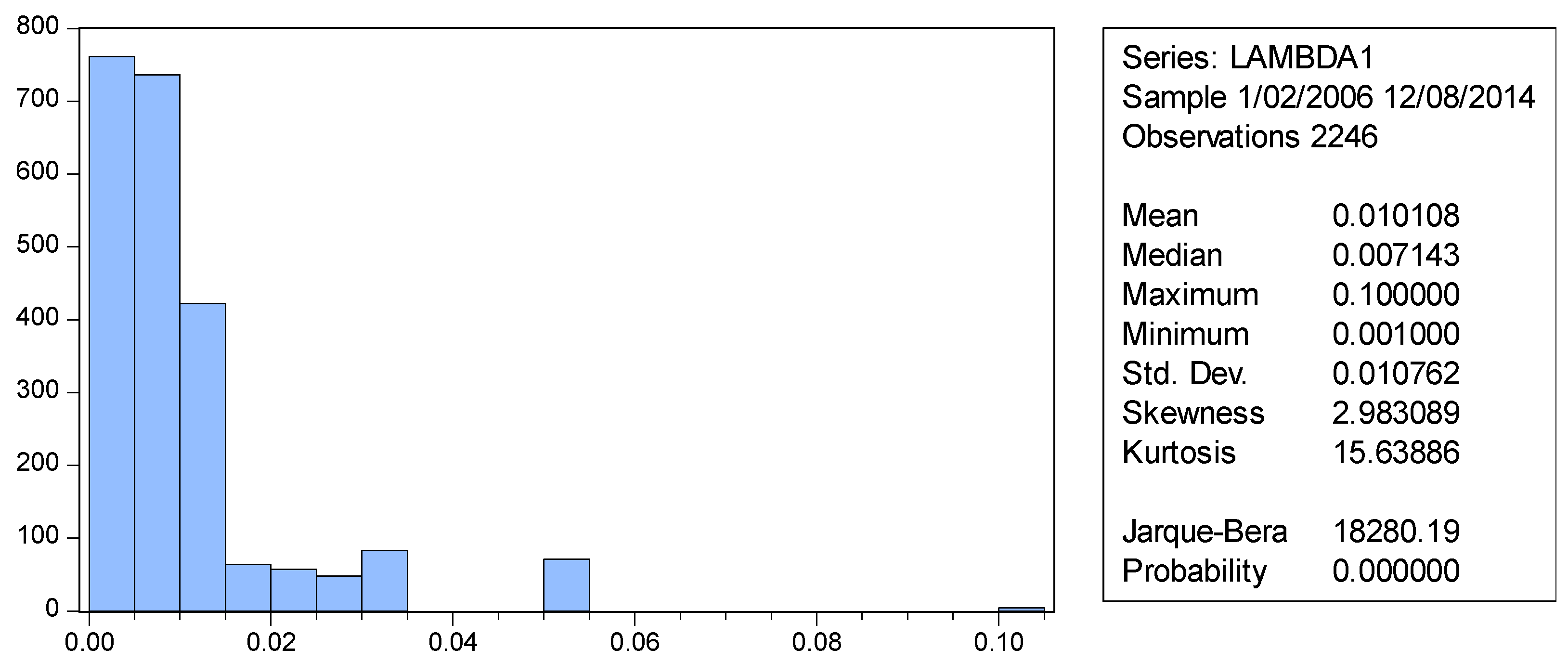
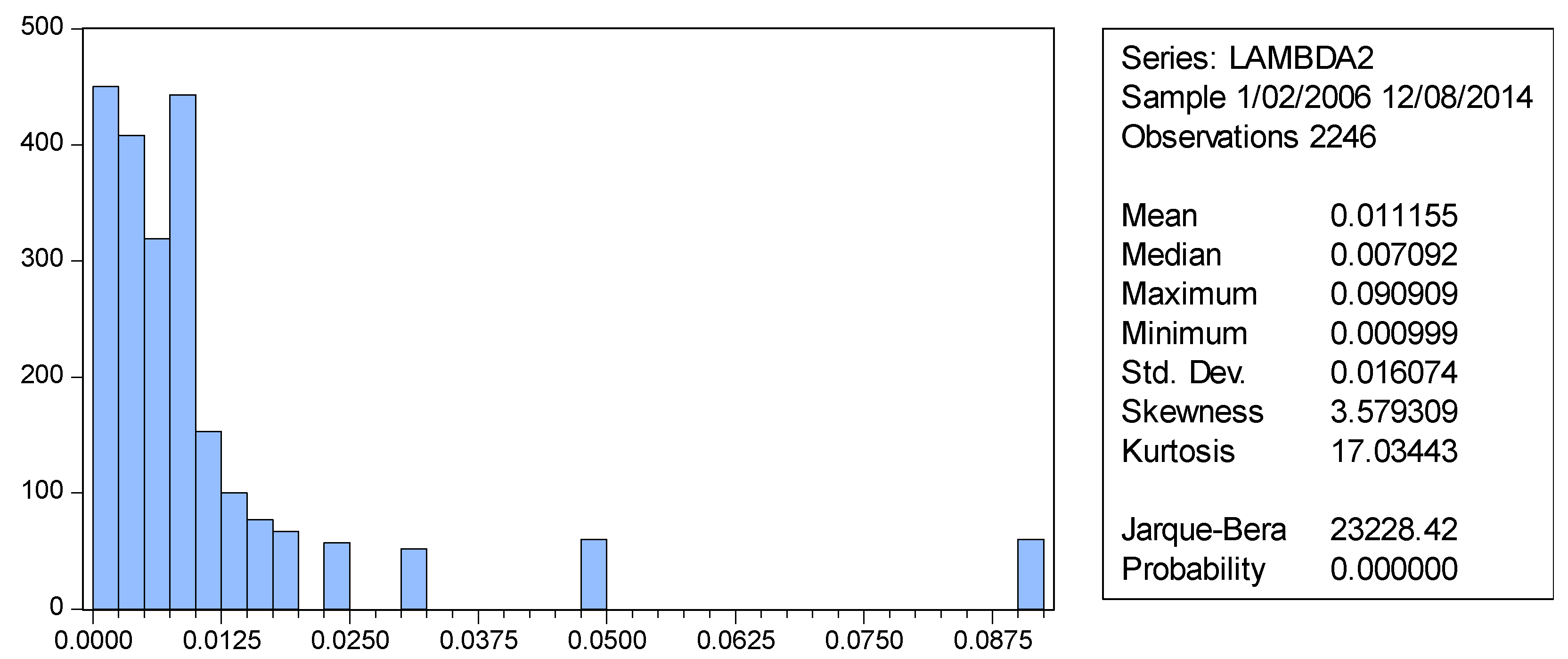
| 2240 | 6 | 2246 |
| 99.70% | 0.27% | 100.00% |
| Variable | Frequency of Disclosure | Disclosure Day | Model Used |
|---|---|---|---|
| Expected inflation | Weekly | First working day of the week | Week t − 1 |
| Expected GDP | Weekly | First working day of the week | Week t − 1 |
| SELIC * | Daily | Daily | Thursday (Week t − 1) |
| VIX | Daily | Daily | Average (Week t − 1) |
| T-Bill 10 years | Daily | Daily | Average (Week t − 1) |
| Exchange Rate | Daily | Daily | Average (Week t − 1) |
| CRB | Daily | Daily | Average (Week t − 1) |
| Current inflation (IPC-FIPE) | Weekly | First working day of the week | considered those disclosed until Thursday (week t − 1) |
| Model betas | Daily | Friday (week t) |
| Variable | β0 | p-Value | β1 | p-Value | β2 | p-Value | β3 | p-Value |
|---|---|---|---|---|---|---|---|---|
| CDS | 0.000072 | 0.06% | −0.000086 | 0.10% | −0.001820 | 0.00% | 0.001715 | 0.00% |
| DExchangeRate | 0.024447 | 4.25% | −0.026274 | 2.87% | - | - | - | - |
| DIPCA_Focus | 4.542732 | 0.10% | −3.912488 | 0.17% | 48.664810 | 4.20% | −52.565130 | 2.48% |
| DGDP_Focus | 1.848100 | 0.48% | −1.656633 | 0.75% | - | - | - | - |
| Selic | - | - | 1.025172 | 0.00% | 4.646737 | 0.00% | −4.451462 | 0.00% |
| DSelic | 0.388681 | 0.83% | −0.613091 | 0.00% | 6.417051 | 1.75% | −6.007175 | 1.70% |
| D2006 | 0.124258 | 0.00% | −0.124677 | 0.00% | −0.342133 | 0.00% | 0.317861 | 0.00% |
| D2007 | 0.102864 | 0.00% | −0.104742 | 0.00% | −0.370643 | 0.00% | 0.351778 | 0.00% |
| D2008 | 0.118093 | 0.00% | −0.116924 | 0.00% | - | - | - | - |
| D2009 | 0.108087 | 0.00% | −0.107591 | 0.00% | −0.246528 | 0.00% | 0.190165 | 0.01% |
| D2010 | 0.107514 | 0.00% | −0.107230 | 0.00% | −0.109095 | 1.26% | 0.093301 | 2.57% |
| D2011 | 0.104149 | 0.00% | −0.103726 | 0.00% | −0.249733 | 0.00% | 0.233888 | 0.00% |
| D2012 | 0.090797 | 0.00% | −0.094186 | 0.00% | −0.481133 | 0.00% | 0.434970 | 0.00% |
| D2013 | 0.095692 | 0.00% | −0.097851 | 0.00% | −0.293949 | 0.00% | 0.269358 | 0.00% |
| D2014 | 0.105784 | 0.00% | −0.105694 | 0.00% | −0.182541 | 0.01% | 0.164010 | 0.01% |
| Regression | R2 | Adjusted R2 | DW |
|---|---|---|---|
| β0 | 0.694071 | 0.685252 | 0.278329 |
| β1 | 0.826036 | 0.820624 | 0.293314 |
| β2 | 0.727979 | 0.721373 | 0.395231 |
| β3 | 0.710924 | 0.703905 | 0.407741 |
| Vertex | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 168 | 210 | 252 | 273 | 294 | 315 | 336 | 357 | 378 | 399 | |
| p-Value | 6.33% | 9.47% | 1.22% | 5.12% | 2.59% | 5.12% | 3.27% | 5.12% | 6.33% | 6.33% |
| Macro Variable | β0 | β1 | β2 | β3 |
|---|---|---|---|---|
| CDS | 0.00007 | −0.00009 | −0.00182 | 0.00172 |
| Selic | 0.00000 | 1.02517 | 4.64674 | −4.45146 |
| Dselic | 0.38868 | −0.61309 | 6.41705 | −6.00718 |
| DExchangeRate | 0.02445 | −0.02627 | 0.00000 | 0.00000 |
| DIPCA_Focus | 4.54273 | −3.91249 | 48.66481 | −52.56513 |
| DGDP_Focus | 1.84810 | −1.65663 | 0.00000 | 0.00000 |
| D2014 | 0.10578 | −0.10569 | −0.18254 | 0.16401 |
| Macro Variable | CDS | Selic | Dselic | DExchangeRate | DIPCA_Focus | DGDP_Focus | D2014 |
|---|---|---|---|---|---|---|---|
| Value | 173.05 | 10.35% | 0 | 0.0608 | 0.010% | 0.010% | 1 |
| Beta Parameters | ze |
|---|---|
| β0 | 12.03% |
| β1 | −1.66% |
| β2 | −1.19% |
| β3 | −0.50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benetti, C.; Varanda Neto, J.M.; Mori, R. Macroeconomic Determinants of the Interest Rate Term Structure: A Svensson Model Analysis. Economies 2025, 13, 108. https://doi.org/10.3390/economies13040108
Benetti C, Varanda Neto JM, Mori R. Macroeconomic Determinants of the Interest Rate Term Structure: A Svensson Model Analysis. Economies. 2025; 13(4):108. https://doi.org/10.3390/economies13040108
Chicago/Turabian StyleBenetti, Cristiane, José Monteiro Varanda Neto, and Rogério Mori. 2025. "Macroeconomic Determinants of the Interest Rate Term Structure: A Svensson Model Analysis" Economies 13, no. 4: 108. https://doi.org/10.3390/economies13040108
APA StyleBenetti, C., Varanda Neto, J. M., & Mori, R. (2025). Macroeconomic Determinants of the Interest Rate Term Structure: A Svensson Model Analysis. Economies, 13(4), 108. https://doi.org/10.3390/economies13040108






