Detection of Lead-Lag Relationships Using Both Time Domain and Time-Frequency Domain; An Application to Wealth-To-Income Ratio
Abstract
:1. Introduction
2. Literature Review
2.1. Time Domain Analysis
2.2. Wavelet Analysis
3. Data
4. Methodology
4.1. Time Domain Analysis
- Investigation of the stationarity of and to determine the order of integration of the variables.
- Specification of the lag order to include in the cointegration analysis.
- Investigation of the cointegrating relationship between and .
- Estimation of the coefficients of the VEC model in order to determine the lead-lag relationship between and .
- If , there is no cointegration among the non-stationary variables and a VAR in their first differences is consistent.
- If , all the variables in are and a VAR in their levels is consistent.
- If then can be expressed as where and are matrices of rank .
- the parameters of the cointegrating matrix ,
- the parameters of the adjustment matrix and
- the parameters of the short-run coefficient matrix .
- If the coefficients are non-zero or the error correction coefficient has a significant value, there is some information in that will be assimilated in later values of ; meaning that leads . More specifically:
- ○
- The existence of non-zero and significant coefficients in (8), i.e., the lagged coefficients of in the regression of indicate that there is a short-run causality between and : causes .
- ○
- The existence of a significant error correction coefficient indicates that there is a long-run causality between and : causes .
- If the coefficients are non-zero or the error correction coefficient has a significant value, there is some information in that will be assimilated in later values of ; meaning that leads . More specifically:
- ○
- The existence of non-zero and significant coefficients in (9), i.e., the lagged coefficients of in the regression of , indicates a short-term causality; causes .
- ○
- The existence of a significant error correction coefficient indicates that there is a long-run causality; causes .
- If all coefficients , , , have significant values, there is a two-directional relationship between the variables and .
4.2. Wavelet Analysis
5. Empirical Results
5.1. Time Domain Analysis
5.2. Wavelet Analysis
5.3. Comparison of the Two Methodologies
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Afonso, António, Michael G. Arghyrou, George Bagdatoglou, and Alexandros Kontonikas. 2015. On the time-varying relationship between EMU sovereign spreads and their determinants. Economic Modelling 44: 363–71. [Google Scholar] [CrossRef]
- Aguiar-Conraria, Luís, and Maria Joana Soares. 2014. The continuous wavelet transform: Moving beyond uni and bivariate analysis. Journal of Economic Surveys 28: 344–75. [Google Scholar] [CrossRef]
- Ajayi, Richard A., and Mbodja Mougouė. 1996. On the dynamic relation between stock prices and exchange rates. Journal of Financial Research 19: 193–207. [Google Scholar] [CrossRef]
- Akaike, Hirotogu. 1973. Information theory as an extension of the maximum likelihood principle. In Second International Symposium on Information Theory. Budapest: Akademiai Kiado, pp. 267–81. [Google Scholar]
- Alzahrani, Mohammed, Mansur Masih, and Omar Al-Titi. 2014. Linear and non-linear Granger causality between oil spot and futures prices: A wavelet based test. Journal of International Money and Finance 48: 175–201. [Google Scholar]
- Baum, Christopher F. 2013. VAR. SVAR and VECM Models. EC 823: Applied Econometrics, Boston College, Spring 2013. Available online: http://fmwww.bc.edu/EC-C/S2013/823/EC823.S2013.nn10.slides.pdf (accessed on 14 March 2019).
- Bernoth, Kerstin, and Burcu Erdogan. 2012. Sovereign bond yield spreads: A time-varying coefficient approach. Journal of International Money and Finance 31: 639–56. [Google Scholar] [CrossRef]
- Campbell, John Y., Andrew W. Lo, and Archie Craig MacKinlay. 1997. The Econometrics of Financial Markets. Princeton: Princeton University Press. [Google Scholar]
- Chang, Chun-Ping, and Chien-Chiang Lee. 2015. Do oil spot and futures prices move together? Energy Economics 50: 379–90. [Google Scholar] [CrossRef]
- Chen, Wen-Yi. 2016. Health progress and economic growth in the USA: The continuous wavelet analysis. Empirical Economics 50: 831–55. [Google Scholar] [CrossRef]
- Chung, Pin J., and Donald J. Liu. 1994. Common stochastic trends in Pacific Rim stock markets. Quarterly Review of Economics and Finance 34: 241–59. [Google Scholar] [CrossRef]
- Cong, Rong-Gang, Yi-Ming Wei, Jian-Lin Jiao, and Ying Fan. 2008. Relationships between oil price shocks and stock market: An empirical analysis from China. Energy Policy 36: 3544–53. [Google Scholar] [CrossRef]
- Corhay, Albert, A. Tourani Rad, and Jean Pierre Urbain. 1993. Common stochastic trends in European stock markets. Economics Letters 42: 385–90. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Engle, Robert F., and Clive W. J. Granger. 1987. Co-Integration and error correction: Representation, estimation, and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Frederic S. Mishkin. 1998. Predicting U.S. recessions: Financial variables as leading indicators. Review of Economics and Statistics 80: 45–61. [Google Scholar] [CrossRef]
- Fuller, Wayne A. 1996. Introduction to Statistical Time Series, 2nd ed. New York: Wiley. [Google Scholar]
- Funashima, Yoshito. 2017. Time-varying leads and lags across frequencies using a continuous wavelet transform approach. Economic Modelling 60: 24–28. [Google Scholar] [CrossRef]
- Gençay, Ramazan, Faruk Selçuk, and Brandon J. Whitcher. 2002. An Introduction to Wavelets and Other Filtering Methods in Finance and Economics. San Diego: Academic Press. [Google Scholar]
- Gonzalo, Jesus. 1994. Five alternative methods of estimating long-run equilibrium relationships. Journal of Econometrics 60: 203–33. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 1988. Some recent development in a concept of causality. Journal of Econometrics 39: 199–211. [Google Scholar] [CrossRef]
- Granger, Clive Wiliam John, and Oskar Morgenstern. 1970. The Predictability of Stock Market Prices. Lexington: Health Lexinghton Book. [Google Scholar]
- Grinsted, Aslak. 2014. Wavelet Toolbox by Grinsted. Available online: http://www.glaciology.net/wavelet-coherence (accessed on 14 March 2019).
- Grinsted, A., J. C. Moore, and S. Jevrejeva. 2004. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Processes in Geophysics 11: 561–66. [Google Scholar] [CrossRef]
- Grossmann, Volker, and Thomas Michael Steger. 2016. Das House-Kapital: A theory of wealth-to-income ratios. In Annual Conference of Demographic Change 145936. Augsburg: German Economic Association. [Google Scholar]
- Gwilym, Owain Ap, and Mike Buckle. 2001. The lead-lag relationship between the FTSE100 stock index and its derivative contracts. Applied Financial Economics 11: 385–93. [Google Scholar] [CrossRef]
- Hacker, Scott R., and Abdulnasser Hatemi-J. 2008. Optimal lag-length choice in stable and unstable VAR models under situations of homoscedasticity and ARCH. Journal of Applied Statistics 35: 601–15. [Google Scholar] [CrossRef]
- Hannan, Edward J., and Barry G. Quinn. 1979. The Determination of the order of an autoregression. Journal of the Royal Statistical Society, Series B 41: 190–95. [Google Scholar] [CrossRef]
- Hoover, Kevin D. 2008. Causality in economics and econometrics. In The New Palgrave Dictionary of Economics, 2nd ed. Edited by Steven N. Durlauf and Lawrence E. Blume. New York: Palgrave Macmillan. [Google Scholar]
- Huang, Shupei, Haizhong An, Xiangyun Gao, and Xuan Huang. 2016. Time–frequency featured co-movement between the stock and prices of crude oil and gold. Physica A: Statistical Mechanics and Its Applications 444: 985–95. [Google Scholar] [CrossRef]
- Hubrich, Kirstin, Helmut Lütkepohl, and Pentti Saikkonen. 2001. A review of systems cointegration tests. Econometric Reviews 20: 247–318. [Google Scholar] [CrossRef]
- Jackline, Stella, and Malabika Deo. 2011. Lead-lag relationship between the futures and spot prices. Journal of Economics and International Finance 3: 424–27. [Google Scholar]
- Johansen, Søren. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press. [Google Scholar]
- Johansen, Søren, Rocco Mosconi, and Bent Nielsen. 2000. Cointegration analysis in the presence of structural breaks in the deterministic trend. Econometrics Journal 3: 216–49. [Google Scholar] [CrossRef]
- Kim, Sangbae, and Francis In. 2005. The relationship between stock returns and inflation: New evidence from wavelet analysis. Journal of Empirical Finance 12: 435–44. [Google Scholar] [CrossRef]
- Ko, Jun-Hyung, and Chang-Min Lee. 2015. International economic policy uncertainty and stock prices: Wavelet approach. Economics Letters 134: 118–22. [Google Scholar] [CrossRef]
- Koutmos, Gregory. 1996. Modelling the dynamic interdependence of major European stock markets. Journal of Business Finance & Accounting 23: 975–88. [Google Scholar]
- Ljung, Lennart. 1999. System Identification: Theory for the User, 2nd ed. Prentice-Hal PTR Information and System Sciences Series; Upper Saddle River: Prentice Hall. [Google Scholar]
- Maddala, Gangadharrao S., and In-Moo Kim. 1998. Unit Roots, Cointegration, and Structural Change. Cambridge: Cambridge University Press. [Google Scholar]
- Marczak, Martyna, and Thomas Beissinger. 2016. Bidirectional relationship between investor sentiment and excess returns: New evidence from the wavelet perspective. Applied Economics Letters 23: 1305–11. [Google Scholar] [CrossRef]
- Moore, Geoffrey H. 1975. Economic indicators and econometric models. Business Economics 10: 45–48. [Google Scholar]
- Nielsen, Bent. 2006. Order determination in general vector autoregressions. IMS Lecture Notes-Monograph Series, Time Series and Related Topics 52: 93–112. [Google Scholar]
- Nijman, Theo, and Frank de Jong. 1997. High frequency analysis of lead-lad relationships between financial markets. Journal of Empirical Finance 4: 259–77. [Google Scholar]
- Olayeni, Olaolu Richard. 2016. Causality in continuous wavelet transform without spectral matrix factorization: Theory and application. Computational Economics 47: 321–40. [Google Scholar] [CrossRef]
- Piketty, Thomas. 2014. Capital in the 21st Century. Cambridge: Harvard University Press. [Google Scholar]
- Piketty, Thomas, and Gabriel Zucman. 2014. Capital is back: Wealth-income ratios in rich countries 1700–2010. Quarterly Journal of Economics 129: 1255–310. [Google Scholar] [CrossRef]
- Piketty, Thomas, and Gabriel Zucman. 2015. Wealth and inheritance in the long run. Handbook of Income Distribution 2: 1303–68. [Google Scholar]
- Polanco-Martínez, Josué, and Luis Abadie. 2016. Analyzing crude oil spot price dynamics versus long term future prices: A wavelet analysis approach. Energies 9: 1089. [Google Scholar] [CrossRef]
- Polanco-Martínez, Josué Moises, Javier Fernández-Macho, Marc Neumann, and Sérgio Henrique Faria. 2018a. A pre-crisis vs. crisis analysis of peripheral EU stock markets by means of wavelet transform and a nonlinear causality test. Physica A: Statistical Mechanics and its Applications 490: 1211–27. [Google Scholar]
- Polanco-Martínez, Josué M., Luis M. Abadie, and Javier Fernández-Macho. 2018b. A multiresolution and multivariate analysis of the dynamic relationships between crude oil and petroleum-product prices. Applied Energy 228: 1550–60. [Google Scholar]
- Ramsey, James B. 1999. The contribution of wavelets to the analysis of economic and financial data. Philosophical Transactions of the Royal Society of London Series A 357: 2593–606. [Google Scholar] [CrossRef]
- Ramsey, James B. 2002. Wavelets in economics and finance: Past and future. Studies in Nonlinear Dynamics & Econometrics 6: 1–29. [Google Scholar]
- Ramsey, James B., and Camille Lampart. 1998. The decomposition of economic relationships by time scale using wavelets: Expenditure and income. Studies in Nonlinear Dynamics and Econometrics 3: 23–42. [Google Scholar] [CrossRef]
- Rault, Christophe, and Mohamed El Hedi Arouri. 2009. Oil Prices and Stock Markets: What Drives What in the Gulf Corporation Council Countries? Working Paper No. 960. Ann Arbor, MI, USA: William Davidson Institute. [Google Scholar]
- Reboredo, Juan C., and Miguel A. Rivera-Castro. 2013. A wavelet decomposition approach to crude oil price and exchange rate dependence. Economic Modelling 32: 42–57. [Google Scholar] [CrossRef]
- Reboredo, Juan C., Miguel A. Rivera-Castro, and Andrea Ugolini. 2017. Wavelet-based test of co-movement and causality between oil and renewable energy stock prices. Energy Economics 61: 241–52. [Google Scholar] [CrossRef]
- Rognlie, Matthew. 2015. Deciphering the fall and rise in the net capital share. Brookings Papers on Economic Activity 2015: 1–69. [Google Scholar] [CrossRef]
- Silvapulle, Param, and Imad A. Moosa. 1999. The relationship between spot and futures prices: Evidence from the crude oil, market. Journal Futures Markets 19: 175–93. [Google Scholar] [CrossRef]
- Stoll, Hans R., and Robert E. Whaley. 1990. Stock market structure and volatility. Review of Financial Studies 3: 37–71. [Google Scholar] [CrossRef]
- Strang, Gilbert, and Truong Nguyen. 1997. Wavelets and Filter Banks. Wellesley: Wellesley-Cambridge Press. [Google Scholar]
- Tiwari, Aviral Kumar, Mihai Mutascu, and Alin Marius Andries. 2013. Decomposing time-frequency relationship between producer price and consumer price indices in Romania through wavelet analysis. Economic Modelling 31: 151–59. [Google Scholar] [CrossRef]
- Toda, Hiro Y., and Peter C. B. Phillips. 1994. Vector autoregressions and causality: A theoretical overview and simulation study. Econometric Reviews 13: 259–85. [Google Scholar] [CrossRef]
- Tonn, Victor Lux, and Joseph McCarthy. 2010. Wavelet domain correlation between the futures prices of natural gas and oil. The Quarterly Review of Economics and Finance 50: 408–14. [Google Scholar] [CrossRef]
- Torrence, Christopher, and Gilbert P. Compo. 1998. A practical guide to wavelet analysis. Bulletin of American Meteorological Society 79: 61–78. [Google Scholar] [CrossRef]
- Visvikis, Ilias, Panayotis Alexakis, and Manolis G. Kavussanos. 2002. An investigation of the lead-lag relationship in returns and volatility between cash and stack index futures: The case of Greece. Paper presented at European Financial Management Association Annual Meeting, London, UK, June 26–29. [Google Scholar]
- WID Database. 2017. The World Wealth and Income Database. Available online: http://www.wid.world/#Database (accessed on 14 March 2019).
- World Inequality Report. 2018. Available online: https://wir2018.wid.world/part-3.html (accessed on 14 March 2019).
- Zavadska, Miroslava, Lucía Morales, and Joseph Coughlan. 2018. The lead-lag relationship between oil futures and spot prices—A literature review. International Journal of Financial Studies 6: 89. [Google Scholar] [CrossRef]
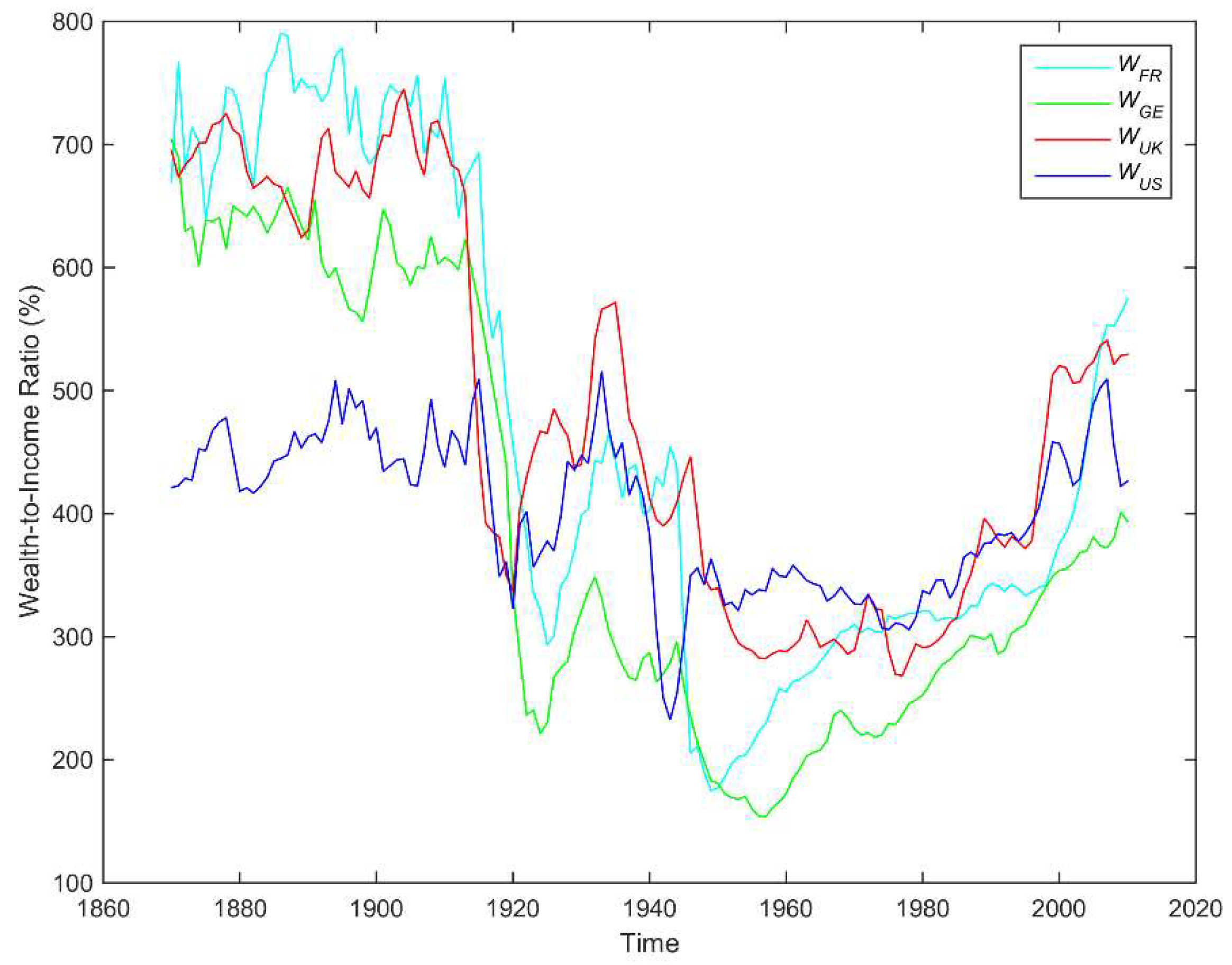


| Variable | Mean | Standard Deviation | Min | Max | Observations |
|---|---|---|---|---|---|
| 467.67 | 192.53 | 174.96 | 790.29 | 141 | |
| 384.04 | 171.05 | 153.82 | 703.72 | 141 | |
| 480.60 | 156.07 | 268.39 | 744.85 | 141 | |
| 399.96 | 62.78 | 232.56 | 515.80 | 141 |
| Unit Root Tests | |||
|---|---|---|---|
| Variable | Lag | t-Statistic | p-Value |
| 0 | −1.162 | 0.6899 | |
| 1 | −1.561 | 0.5032 | |
| 2 | −1.258 | 0.6481 | |
| 0 | −11.193 *** | 0.00 | |
| 1 | −7.377 *** | 0.00 | |
| 2 | −5.759 *** | 0.00 | |
| 0 | −1.910 | 0.3274 | |
| 1 | −1.74 | 0.4131 | |
| 2 | −1.393 | 0.5856 | |
| 0 | −8.422 *** | 0.00 | |
| 1 | −5.617 *** | 0.00 | |
| 2 | −5.101 *** | 0.00 | |
| 0 | −1.381 | 0.5915 | |
| 1 | −1.816 | 0.3728 | |
| 2 | −1.685 | 0.4387 | |
| 0 | −6.378 *** | 0.00 | |
| 1 | −6.988 *** | 0.00 | |
| 2 | −5.765 *** | 0.00 | |
| 0 | −2.236 | 0.1933 | |
| 1 | −2.673 * | 0.0789 | |
| 2 | −2.502 | 0.1151 | |
| 0 | −9.991 *** | 0.00 | |
| 1 | −8.195 *** | 0.00 | |
| 2 | −6.826 *** | 0.00 | |
| Selection of Lag Order | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Lag | FPE | AIC | HQIC | FPE | AIC | HQIC | FPE | AIC | HQIC |
| 0 | 6.7 × 107 | 23.694 | 23.7113 | 1.6 × 108 | 24.5876 | 24.6049 | 7.2 × 107 | 23.7673 | 23.7846 |
| 1 | 281,199 | 18.2226 | 18.2745 | 491,706 | 18.7814 | 18.8333 | 460,394 | 18.7156 | 18.7675 |
| 2 | 246,603 | 18.0912 | 18.1778 * | 320,585 | 18.3536 | 18.440 * | 426,324 * | 18.6386 * | 18.7253 * |
| 3 | 24,952 * | 18.0803 * | 18.2016 | 314,823 | 18.3353 | 18.4566 | 447,804 | 18.6877 | 18.8089 |
| 4 | 253,046 | 18.1176 | 18.2716 | 303,003 * | 18.2969 * | 18.4528 | 466,883 | 18.7292 | 18.8851 |
| Lag | FPE | AIC | HQIC | FPE | AIC | HQIC | FPE | AIC | HQIC |
| 0 | 1.3 × 108 | 24.3869 | 24.4042 | 5.7 × 107 | 23.5357 | 23.553 | 3.6 × 107 | 23.0649 | 23.0822 |
| 1 | 206,577 | 17.9142 | 17.9661 | 202,704 | 17.8952 | 17.9472 | 296,622 | 18.276 | 18.3279 |
| 2 | 127,167 | 17.4289 | 17.5156 | 178,230 | 17.7665 | 17.853 * | 200,433 | 17.8839 | 17.9705 * |
| 3 | 120,902 * | 17.3783 * | 17.4996 * | 175,691 * | 17.7521 * | 17.8733 | 201,810 | 17.8907 | 18.0119 |
| 4 | 126,803 | 17.4258 | 17.5817 | 183,276 | 17.7941 | 17.95 | 199,470 * | 17.8788 * | 18.0347 |
| Trace Statistic of Johansen Test | ||||||
|---|---|---|---|---|---|---|
| Maximum Rank | ||||||
| 0 | 16.4989 | 24.0862 | 25.371 | 19.8358 | 17.2377 | 21.0002 |
| 1 | 1.8499 * | 2.6225 * | 3.76 * | 2.1310 * | 1.997 * | 2.6198 * |
| Coefficients of VEC Model forand | |||
| Dependent: , Independent: | Dependent: , Independent: | ||
| −0.1220 *** (0.0321) | 0.01851 (0.0235) | ||
| 0.2176 *** (0.0819) | −0.1057 * (0.0571) | ||
| 0.0365 (0.0795) | 0.1426 ***(0.0553) | ||
| 0.1373 * (0.0766) | 0.0598 (0.0534) | ||
| −0.1125 (0.1254) | 0.7065 *** (0.0875) | ||
| 0.3099 * (0.1467) | −0.2314 **(0.1023) | ||
| −0.3419 *** (0.1275) | 0.0327 (0.0890) | ||
| Coefficients of cointegrating equation | |||
| 1 | |||
| −0.9848 *** (0.0365) | |||
| Coefficients of VEC model forand | |||
| Dependent: , Independent: | Dependent: , Independent: | ||
| −0.1352 *** (0.0502) | 0. 0498 (0.0315) | ||
| 0.1127 (0.0900) | −0.0074 (0.0565) | ||
| 0.0306 (0.0827) | 0.0543 (0.0519) | ||
| 0.2510 * (0.1374) | 0.2485 *** (0.0859) | ||
| 0.1367 (0.1406) | 0.2254 ***(0.0883) | ||
| Coefficients of cointegrating equation | |||
| 1 | |||
| −1.2154 *** (0.0311) | |||
| Coefficients of VEC model forand | |||
| Dependent: , Independent: | Dependent: , Independent: | ||
| −0.0460 *** (0.0171) | 0.0095 (0.0132) | ||
| 0.0880 (0.0806) | 0.0887 (0.0621) | ||
| −0.0452 (0.1104) | 0.1756 ** (0.0866) | ||
| Coefficients of cointegrating equation | |||
| 1 | |||
| −1.1670 *** (0.1342) | |||
| Coefficients of VEC model forand | |||
| Dependent: , Independent: | Dependent: Independent: | ||
| −0.0628 *** (0.0199) | 0.01458 (0.0227) | ||
| 0.2129 *** (0.0790) | −0.0630 (0.0901) | ||
| 0.2612 *** (0.0792) | 0.1168 (0.0903) | ||
| 0.0549 (0.0736) | 0.6908 *** (0.0839) | ||
| −0.0831 (0.0766) | 0.2274 ***(0.0873) | ||
| Coefficients of cointegrating equation | |||
| 1 | |||
| −0.8119 *** (0.0441) | |||
| Coefficients of VEC model forand | |||
| Dependent: , Independent: | Dependent: , Independent: | ||
| −0.0188 * (0.0119) | 0.0127 (0.0146) | ||
| 0.2256 *** (0.0804) | 0.0351 (0.1060) | ||
| 0.2425 *** (0.0806) | 0.1081 (0.1063) | ||
| −0.326 (0.0652) | 0.1703 ** (0.0860) | ||
| 0.468 (0.065) | −0.0784(0.0868) | ||
| Coefficients of cointegrating equation | |||
| 1 | |||
| −0.9265 *** (0.1780) | |||
| Coefficients of VEC model forand | |||
| Dependent: , Independent: | Dependent: , Independent: | ||
| −0.0294 * (0.0160) | 0.0233 (0.0188) | ||
| 0.7220 *** (0.0861) | 0.0351 ** (0.1060) | ||
| −0.2701 *** (0.1026) | −0.12579 (0.1203) | ||
| 0.0831 (0.0876) | 0.2234 **(0.1027) | ||
| −0.0920 (0.0739) | 0.1205 (0.0866) | ||
| 0.0778 (0.0747) | −0.8500 (0.0876) | ||
| −0.1644 *(0.0753) | −0.8544 (0.0883) | ||
| Coefficients of cointegrating equation | |||
| 1 | |||
| −1.1875 *** (0.1080) | |||
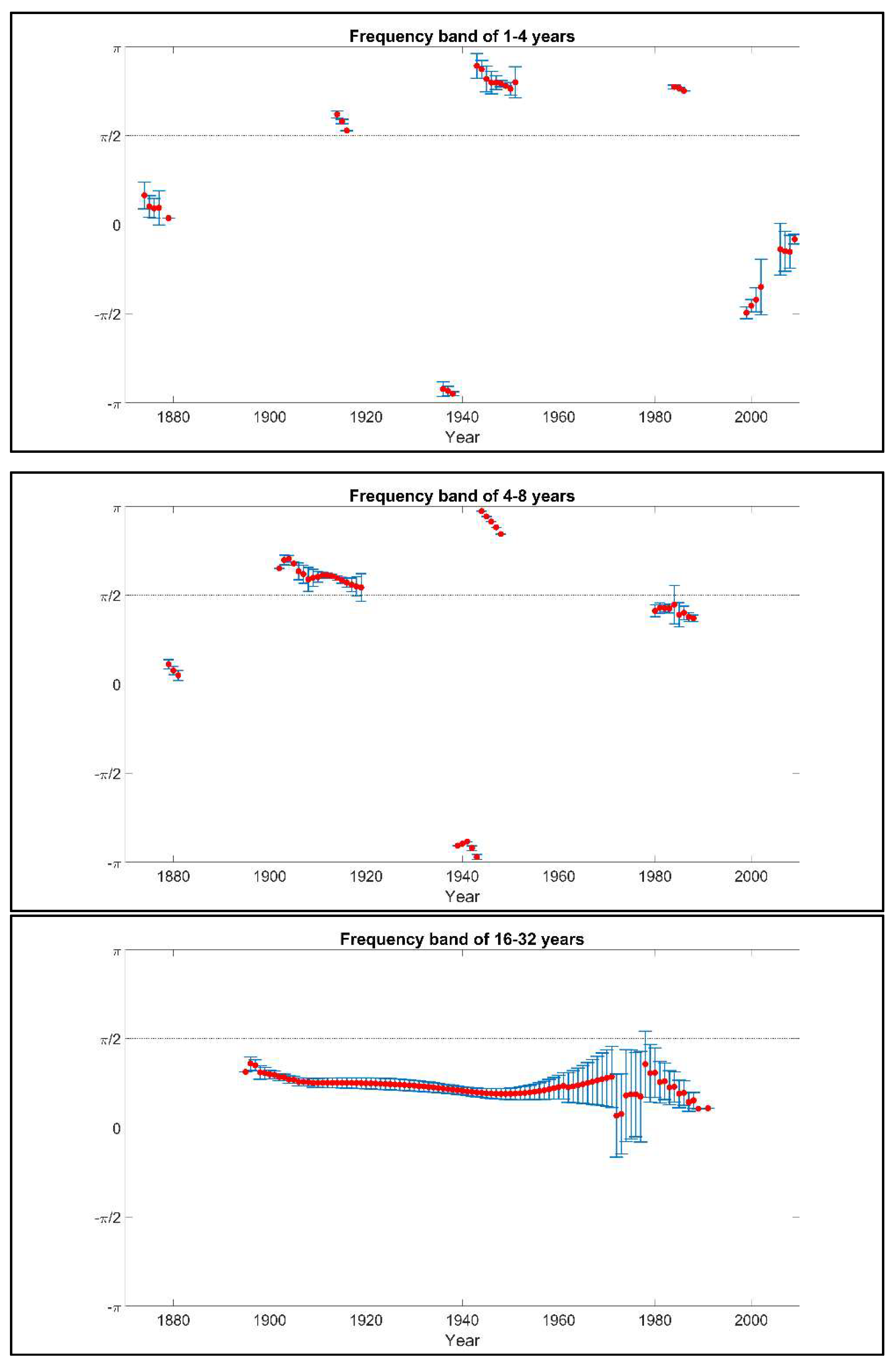
| Timescale | Years | Leading |
| 1–4 years | 1904–1910 | (positive) |
| 2007–2010 | (negative) | |
| 4–8 years | 1970–1977 | (positive) |
| 8–16 years | 1902–1905 | (positive) |
| 1906–1937 | (positive) | |
| 1938–1941 | (positive) | |
| 16–32 years | 1889–1968 | (positive) |
| Timescale | Years | Leading |
| 1–4 years | 1874–1879 | (positive) |
| 1914–1916 | (negative) | |
| 1936–1938 | (negative) | |
| 1943–1951 | (negative) | |
| 1984–1986 | (negative) | |
| 1999–2002 | (positive) | |
| 2006–2009 | (positive) | |
| 4–8 years | 1879–1881 | (positive) |
| 1902–1920 | (negative) | |
| 1939–1943 | (negative) | |
| 1945–1948 | (negative) | |
| 1980–1988 | (positive) | |
| 16–32 years | 1895–1991 | (positive) |
| Timescale | Years | Leading |
| 1–4 years | 1959–1962 | (positive) |
| 1982–1990 | (negative) | |
| 4–8 years | 1991–2004 | (positive) |
| 8–16 years | 1947–1951 | (negative) |
| 1991–1997 | (positive) | |
| 16–32 years | 1909–1993 | (positive) |
| Timescale | Years | Leading |
| 1–4 years | 1907–1909 | (positive) |
| 1922–1924 | (negative) | |
| 1966–1975 | (positive) | |
| 4–8 years | 1875–1877 | (positive) |
| 16–32 years | 1895–1969 | (positive) |
| Timescale | Years | Leading |
| 1–4 years | 1981–1896 | (positive) |
| 1956–1961 | (positive) | |
| 1966–1968 | (positive) | |
| 4–8 years | 1938–1955 | (positive) |
| 8–16 years | 1942–1952 | (positive) |
| 16–32 years | 1901–1966 | (positive) |
| Timescale | Years | Leading |
| 1–4 years | 1930–1935 | (positive) |
| 1983–1987 | (positive) | |
| 4–8 years | 2000–2010 | (positive) |
| 8–16 years | 1887–1905 | (positive) |
| 16–32 years | 1889–1989 | (positive) |
| Relationship | Evidence from the Time Domain | Evidence from the Time-Frequency Domain |
|---|---|---|
| Long-run: leadership, speed of adjustment −0.1352 Short-run: causality from to | Long-run: leadership Short-run: changes in leadership depending on the time period Medium-run: leadership in 1970–1977 | |
| Long-run: leadership, speed of adjustment −0.122 Short-run: bidirectional causality | Long-run: leadership Short-run, Medium-run: changes in leadership depending on the time period | |
| Long-run: leadership, speed of adjustment −0.046 | Long-run: leadership Short-run: changes in leadership depending on the time period Medium-run: leadership in 1991–2004 | |
| Long-run: leadership, speed of adjustment −0.0628 | Long-run: leadership Short-run: changes in leadership depending on the time period Medium-run: leadership in 1875–1877 | |
| Long-run: leadership, speed of adjustment −0.0188 | Long-run: leadership Short-run: changes in leadership depending on the time period Medium-run: leadership in 1938–1955 | |
| Long-run: leadership, speed of adjustment −0.0294 Short-run: bidirectional causality | Long-run: leadership Short-run: leadership in 1930–1935 and in 1983–1987 Medium-run: leadership in 2000–2010 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skoura, A. Detection of Lead-Lag Relationships Using Both Time Domain and Time-Frequency Domain; An Application to Wealth-To-Income Ratio. Economies 2019, 7, 28. https://doi.org/10.3390/economies7020028
Skoura A. Detection of Lead-Lag Relationships Using Both Time Domain and Time-Frequency Domain; An Application to Wealth-To-Income Ratio. Economies. 2019; 7(2):28. https://doi.org/10.3390/economies7020028
Chicago/Turabian StyleSkoura, Angeliki. 2019. "Detection of Lead-Lag Relationships Using Both Time Domain and Time-Frequency Domain; An Application to Wealth-To-Income Ratio" Economies 7, no. 2: 28. https://doi.org/10.3390/economies7020028
APA StyleSkoura, A. (2019). Detection of Lead-Lag Relationships Using Both Time Domain and Time-Frequency Domain; An Application to Wealth-To-Income Ratio. Economies, 7(2), 28. https://doi.org/10.3390/economies7020028





