Revenue Sharing and Collusive Behavior in the Major League Baseball Posting System

Abstract

This paper uses auction theory to explain the unique design of the 1998–2013 posting system agreed to between Major League Baseball and the Japanese Nippon Professional Baseball League that allowed for the transfer of baseball players from Japan to the United States. It has some similarities and many differences from the transfer system used to obtain players in European football. The unique features of the posting system were a compromise between Major League Baseball clubs and Nippon Professional Baseball clubs with the understanding that the former was a collusive group of club owners. Revenue sharing is a method to enforce a system of side payments to collusive bidders. It is then profit-maximizing to have the bidder with the highest net surplus from the player win the auction. Changes to the revenue sharing system used in Major League Baseball reduced the ability of club owners to bid for Japanese players, hence changes to the bidding rules of the posting system coincided at the same time.

1. Introduction

The transfer system in European football is well known and very lucrative for professional clubs. Large amounts of money changes hands and world quality players move among clubs such as Real Madrid and Manchester City. Little known to Europe and most of North America is the transfer system used in Major League Baseball (MLB) called the posting system. The posting system is currently used only for Japanese players wishing to move to North America (curiously, the system does not operate in reverse). The system lacks the suspense and glamour of the European system, but it is growing and could reach out to other countries in the near future. Indeed, the world took notice in November of 2006 when the Boston Red Sox paid a record $51 million for the exclusive rights to negotiate with pitcher Daisuke Matsuzaka of the Seibu Lions club. The rules and characteristics of the European transfer market are quite straightforward to readers of this journal, but the posting system might seem a mystery. This paper uses auction theory to explore why changes were made to the posting system since its inception in 1998 and solidifies the relationship between the posting system and MLB’s revenue sharing system.

2. Background

The posting system developed as a result of complaints by Japanese professional baseball clubs following the case of Hideo Nomo. Nomo, a pitcher, wished to leave his Japanese club, the Kintetsu Buffaloes, and play for the Los Angeles Dodgers, but could not secure a release from his contract. Nomo could release himself from his Japanese contract by retiring, and he did so. In 1995, he promptly signed a new contract with the Dodgers. Many Japanese baseball fans left their interest in Japanese baseball behind to follow the performances of Nomo in North America. The fear was then that the best Japanese players would follow Nomo, resulting in losses in attendance and television ratings in Japan. The first formalized posting system was agreed upon by MLB and Japanese baseball (the Puro Yakyu or Professional League (NPL)) in 1998 as a way to both discourage Japanese players from moving to MLB and to provide compensation to the Japanese clubs that lost posted players. Japanese players without contracts in Japan who wish to move to North America are not subject to the posting system. The system first came into use in the winter of 1999 with the purchase of Ichiro Suzuki by the Seattle Mariners from the Japanese club the Orix Blue Wave.

A Japanese player who wishes to leave his Japanese club and move to MLB must notify his club. The club can then agree to place the player on a posting list with any other players on any other Japanese clubs who also wish to move. Nothing prevents a MLB club from discussing the possibility of posting a player with the player’s agent or the Japanese club before the posting period closes (November to March). The posting list is then provided to the Commissioner of MLB who notifies all MLB clubs of the posted players. In the 1998–2013 system, interested MLB clubs submitted a sealed bid for a specific player to the Commissioner’s Office within four days of being notified of the posted players. The Commissioner opened the bids and notified the Japanese club of the amount of the highest bid, but did not reveal the identity of the winning bidder. The Japanese club had four days to accept or reject the bid and the bid was not subject to negotiation. If rejected, the Japanese club retained the posted player’s rights. The player could be posted again if there was enough time left during the posting period. If the bid was accepted, the Japanese player must have agreed to a playing contract with the winning bidder within 30 days. Only at that time did the Japanese club receive the funds from the winning bidder. If the player could not agree to a playing contract, his rights reverted back to his Japanese club and no payment was made.

The posting system has not been heavily used in any of its incarnations since only the top Japanese baseball players have any chance of being signed by MLB clubs. Since its inception in November of 1999, only 23 players have used the system and only 12 have signed contracts with MLB clubs1. For the most part, the winning bids are quite low ($300,000 to $1 million) compared to European standards, perhaps indicating only a passing interest by MLB clubs. Four notable exceptions are the winning bids of $13 million, $11 million, $51 million, and $51.7 million paid in the years 2000, 2003, 2006, and 2012 for the players Ichiro Suzuki, Kazuhisa Ishii, Daisuke Matsuzaka, and Yu Darvish. In these four cases and most others, the players’ Japanese clubs were in financial difficulty, requiring the sale of the player to generate needed revenue2. MLB clubs were free to bid to their maximum value for the player since the transfer fee did not count towards the team payroll (which is taxed above a threshold level) in the 1998–2012 posting system.

Revenue sharing is also used in North America with the objective of making the distribution of revenues in MLB more equitable. The revenue sharing system has evolved over the last two decades in MLB with any alterations agreed to by the players in their collective bargaining agreement. For most of the years of the first posting system, the revenue sharing system required each club to contribute 31% of its local revenue to a central fund that was divided equally among the 30 MLB clubs. The system is designed to redistribute revenue from large market to small market teams to promote the financial stability of the league. Any club paying a large amount for a Japanese player or any other player only receives a fraction of the player’s contribution towards team revenue since a portion of it must be contributed to the other MLB clubs.

The rules incorporated in the posting system are in stark contrast to the rules used in the European transfer system. Like the posting system, players can be sold across clubs and the player receives none of the transfer fee. The player must then agree to a new contract with the bidding club before the transfer fee is paid. If unsuccessful, the transfer is voided and the player’s rights remain with the original club. Like the posting system, transfers can only be made during specific periods of the year, the months of January and August. Those are the only similarities. The top executive of each country’s football league does not get involved in the sale of a player, except to approve the sale in a perfunctory way after all the agreements have been settled. Clubs wishing to sell players can negotiate transfers with any club they choose, although rather oddly, the player’s agent is usually involved in negotiating the transfer fee of which the agent may receive a percentage. Players may request to be placed on a transfer list if they wish to leave their club, but clubs may also transfer players without their initial consent. The bidding for players is not restricted to only one bidder and bidding wars are frequent. Transactions are only loosely regulated, if at all, and scandals are frequent3.

Major league baseball and Japanese baseball chose to design a very different transfer system from that used in most of the rest of the world. In the next section, we use auction theory to explore the design of the posting system.

3. An Auction Theory Approach

A private value auction occurs when each bidder has a private valuation of the player’s worth that is unique so that there is no common market value attached to the player. In this case, the true value of the player to each bidder is just equal to the bidder’s private valuation and the winning bidder is the one with the highest private valuation. Vickrey (1961) showed that the winning bid would be the same regardless of the type of auction (i.e., ascending bid, descending bid, first price sealed bid, and second price sealed bid) so that the auctioneer and the seller are indifferent between the type of auction. Club owners may very well assign different valuations to the same free agent player since the player’s revenue generating potential may differ across clubs. The auction is said to be efficient when the bidder with the highest private valuation wins the auction. We will show that this type of auction fits the European transfer system very well, but not the posting system in MLB.

Two factors distinguished the 1998–2012 posting system: the participation of the Commissioner of MLB as an intermediary in the auction and the identity of the winning bidder was not revealed to the Japanese club unless the bid was accepted. The objective of the Japanese club is to receive a bid as high as possible above its reserve price, while the objective of the Commissioner, acting as an agent for MLB clubs, is to insure the winning bid is as close to the reserve price as possible. The model developed here follows Jehiel and Moldovanu (1996) and Caillaud and Jehiel (1998) and shows that the critical factor that makes the posting system work is revenue sharing, a formalized system of side payments among the colluding clubs. Side payments are necessary to compensate the losing bidders in the posting system for the anticipated reduction in their winning percentages when the winning bidder takes possession of the player.

In MLB, the current revenue sharing arrangement requires each club to contribute approximately 48% of its annual local revenue to a central fund managed by the Commissioner’s Office (31% for most of the years of the first posting system). At periodic intervals during the season, each club receives an equal share of the central fund. Local revenue includes gate revenue, local radio, local television broadcasting revenue, and some concession revenue (food, parking, etc.), but excludes revenue from luxury suites and some other revenues. Hence, the revenue sharing system is a formal and enforceable arrangement for making side payments. The marginal revenue product of any newly acquired player is partly shared with all other clubs in the league so that the negative externality imposed on other clubs is partly eliminated.

In this paper, collusion takes the form of a sort of pre-auction among MLB clubs that determines which club makes the winning bid, what the winning bid is, and the amount of side payment that is required to each losing member of the bidding cartel. The side payment is necessary to compensate the losing bidders for the loss in revenue they may experience by allowing the winning bidder to improve his or her club (assuming that revenue is a function of winning percentage). The revenue sharing system used in MLB is a formal, but imperfect mechanism to facilitate the necessary side payments. The identity of the winning bidder is concealed from the Japanese club since this information contains a valuable rent—a more accurate estimate of the non-local revenue of the winning bidder that might be extracted by the NPL club. This knowledge could be used in a subsequent repetition of the bidding game under certain conditions.

4. Setup of the Model

There exist n clubs from a total of N clubs in a league (n ≤ N), indexed by 1, …, n, bidding to purchase a single player from a single seller (the Japanese club). Each buyer places a private valuation, v_i, on the player ideally equal to the player’s discounted lifetime marginal revenue product for the club4. We abstract from any strategic value contained in v_i that arises from preventing other clubs from signing the player. For a given player for sale, the distribution of valuations is assumed to be uniform with unknown upper and lower limits. We denote the highest private valuation as $v_i^{max}$. The position of a specific club’s valuation within the distribution is not known. We assume that the ordering of private valuations is independent of the type of auction (collusive or non-collusive) and that the attributes of the player to be sold that determines each v_i can be obtained at zero cost. The seller places a minimum reserve price of R_min on the player so that any bid below this price will not be successful. This reserve price is ideally determined by the surplus value from the player by remaining in Japan. Bidders do not know the value of R_min, instead they must form its expectation denoted as $R_{min}^e$, using an information set that is identical for all bidders. We assume that expectations are formed rationally, so that the relationship between R_min and its expectation is given by $R_{min}^e=R_{min}+u$, where $u~N\left(0,{\sigma }_u^2\right)$.

Losing bidders suffer an externality that we assume is different for each losing bidder. The magnitude of the externality is assumed to increase the greater is the value of v_i for the winning bidder. This is appropriate due to presence of diminishing marginal revenue product with each club’s winning percentage. This is a standard feature of models of professional sports clubs, beginning with Rottenberg (1956). The nature of sporting contests is that for one club to be more successful, others must be less successful. Clubs that lose contests move down their concave revenue schedules at increasing rates and the externality becomes larger.

For now, we assume an auction without side payments. Without a side payment (revenue sharing), all losing bidders will prefer that the player not be sold. The winning bidder will obtain a net profit of $v_i^{max}-b_i^{NC}-s_i$, where $b_i^{NC}$ is the amount of the winning bid $\left(b_i^{NC}\ge R_{min}\right)$ in the non-collusive auction and $s_i$ is the salary paid to the player. Any losing bidder incurs a loss equal to the monetary value of the negative externality imposed on it (it might win fewer games). A higher anticipated salary will lower the winning bid for a given valuation.

4.1. The European Transfer System

We use the European transfer system as the base case. The European transfer system can best be described, using the terminology of Vickrey (1961), as an ascending bid auction where the winning bid is just slightly higher than the second highest bidder (indexed i − 1) and less than the winning bidder’s valuation $\left(v_{i-1}-s_{i-1}<b_i^{NC}<v_i^{max}-s_i\right)$. Unlike the baseball posting system, European football clubs are free to negotiate with each other for player transfer fees within the two transfer “windows” (January and August) each year. If negotiations break down within the transfer window, perhaps because b_i < R_min, teams are free to re-enter the transfer market and negotiate a transfer fee with any other interested bidder. The results of an ascending bid auction without collusion are well known. In a private value auction, Milgrom and Weber (1982) showed that an ascending bid auction will generate the greatest winning bid among all open bid auctions. The auction is efficient in the sense that the bidder with the highest private valuation will win the auction. This keeps the player’s surplus in the hands of the team owners who will ideally be willing to bid an amount up to the anticipated surplus from the player.

4.2. The Collusive Bidding Model

We now develop an auction model with collusive side payments. The bidding model is a three-stage game. In stage 1, each buyer formulates his or her private valuation of the player under the collusive arrangement, $v{c}_i$, based on assumedly costless information about the player to be sold. In stage 2, the bidders play a collusion sub-game during in which they implicitly choose a winning bid from among a set of bids that interested clubs will offer to submit to the auction (one of which is known to the bidders as the winning bid) and they decide the distribution of side payments associated with the winning bid. In stage 3, the Commissioner selects the highest bid as the winning bid and informs the seller of the amount without revealing the identity of the winner. At this point, the seller may accept or reject the winning bid. We do not explicitly model a fourth stage, the salary bargaining process between the Japanese player and the winning bidder if the bid is accepted. Instead we assume that the Japanese player will receive a salary of s_i dollars, which is higher than the salary he is currently earning.

We focus on stage 2 of the bidding model as this largely determines the outcome for stage 3. Without defection by any of the bidding clubs, the collusive sub-game in stage 2 results in efficiency (Graham and Marshall 1987) if the side payments to all clubs, including the winning bidder, sum to zero (the winning bidder cannot borrow to make the necessary side payments). In our model, side payments are automatically collected and paid through a revenue sharing system in which each club is allowed to keep a share equal to α of its local revenues (0 ≤ α ≤ 1), the rest being contributed into a league pool that is distributed evenly among every team in MLB at the end of the playing season. The revenue for the winning bidder club i after revenue sharing is denoted $R_i^{RS}$.

$$R_i^{RS}=\alpha R_i+\frac{1-\alpha }{N}\left(R_i+{{\displaystyle \sum }}_{j\ne i}^N{R}_j\right)=\left(\frac{\alpha \left(N-1\right)+1}{N}\right)R_i+\left(\frac{1-\alpha }{N}\right){{\displaystyle \sum }}_{j\ne i}^N{R}_j$$

(1)

In this way, each of the other N − 1 clubs receives a positive side payment if the winning bidder experiences a significant increase in local revenue after acquiring the player. The same can be said for the expected marginal revenue product of the NPL player: any gain in revenue for the winning bidder must be shared with the rest of the league. We have that $v{c}_i^{max}=f\left(R_i^{RS}\right)$ is the expected marginal revenue product. Ring efficiency requires that the net profit for the winning bidder is the maximal winning profit among all bidders after all side payments have been paid, thus the ring efficiency condition is

$$v{c}_i^{max}-b_i^C-s_i\ge 0$$

(2)

where $b_i^C$ is the collusive winning bid. The first term on the left-hand side of (2) constitutes the total net revenue the winning bidder will keep from acquiring the player under the revenue sharing agreement. The winner must also pay the amount of the winning bid and the player salary. It is in the best interest of the losing bidders to select the bidder with the highest valuation to “win” the auction and to “arrange” a winning collusive bid, $b_i^C$, as close to R_min from above as possible in order to guarantee the ring efficiency condition is met and the maximum side payments can be made. If this does not occur, an ascending bid auction takes place during the pre-auction in stage 2 so that bidding club with a private valuation equal to $v{c}_i^{max}$ prevails.

Condition (2) essentially determines which bidder is chosen to win the auction. Note that there are two circumstances under which the seller (the NPL club) will refuse the winning bid in stage 3 of the game. First, the private valuation of the winning bidder, $v{c}_i^{max}$, might not be high enough so that even the highest bid falls short of the seller’s true reservation price. Second, the winning bidder could underestimate the seller’s true reservation price (u < 0) by enough to violate condition (2) and walk away from the auction. In this way, condition (2) represents the winning bidder’s expectation of the ring efficiency condition.

Under the MLB revenue sharing agreement, an additional condition is that the winning bidder is expected to be at least as well as off by colluding as by not colluding. This makes the ring efficiency condition feasible with revenue sharing.

$$v{c}_i^{max}-b_i^C-s_i>v_i^{max}-b_i^{NC}-s_i$$

(3)

Condition (3) places a constraint on the maximum valuation of the player among all bidders with revenue sharing.

$$v{c}_i^{max}-v_i^{max}>b_i^C-b_i^{NC}$$

(4)

Condition (4) states that the post-revenue sharing maximum valuation must exceed the difference in maximum bids under strategic (or implicit) collusive bidding with revenue sharing.

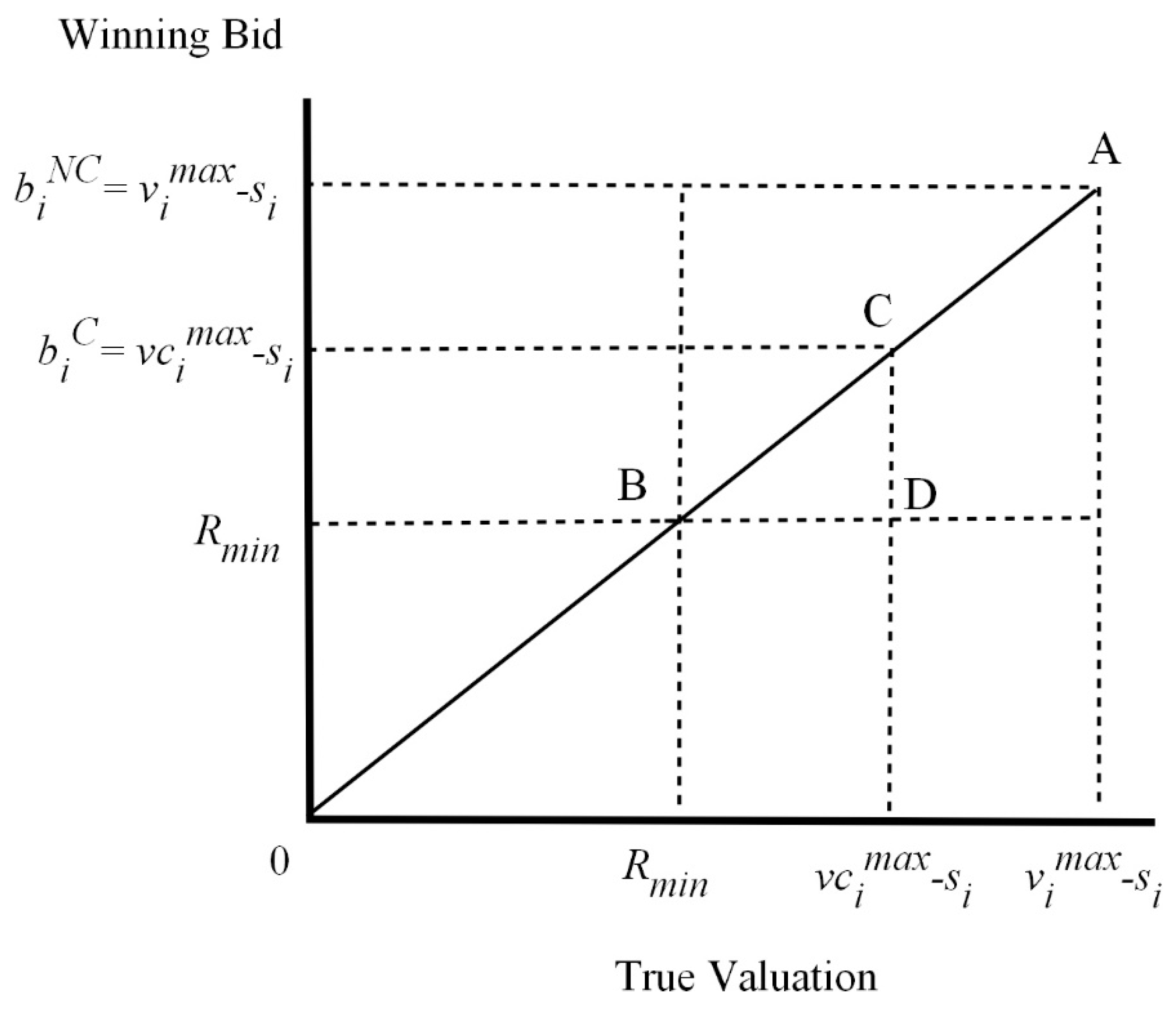
Conditions (2)–(4) are enough to describe the set of possible equilibria in the collusive bargaining game. Figure 1 plots the actual winning bid on the vertical axis and the actual valuation of the player to the winning bidder on the horizontal axis. Any equilibrium falling on the 45-degree line denotes a winning bid that is confirmed by the actual valuation (u = 0). In a sealed bid auction with no collusion and revenue sharing, the winning bidder will just pay his or her private valuation to the seller net of the player’s salary, $b_i^{NC}=v_i^{max}-s_i\ge R_{min}$. The non-collusive equilibrium is denoted by point A in Figure 1 and provides a limit on the magnitude of the surplus for a specific player and highest bidder.

Recall that the NPL club knows the minimum bid it will accept for the posted player, R_min. Any bid below this valuation is not accepted as bounded by the horizontal dashed line at R_min on the vertical axis. Each bidder must form an expectation of R_min that is subject to the random error u. If $R_{min}^e<R_{min}$, the MLB club is not interested in bidding for the posted player, represented by the vertical dashed line on the horizontal axis. The set of equilibria is then limited to the rectangle bounded by $b_i^C\ge R_{min}$ on the vertical axis and $R_{min}^e\ge R_{min}$ on the horizontal axis. Point B is a winning bid that is just equal to the minimum bid the NPL club will accept. The MLB club is indifferent to acquiring this player as there is no surplus earned. Perhaps most posted players fall around point B since they are marginal players with relatively low salaries.

Consider point C in Figure 1 that represents an NPL player of considerable talent. Point C is an equilibrium bid that falls on the 45-degree line so that the winning bid is just equal to the player’s true valuation to the winner and there is no surplus to the winning bidder. Condition (2) is an equality, while conditions (3) and (4) are satisfied since the winning bidder has evaluated them before making the bid. Any bid above the 45-degree line results in a negative surplus for the MLB club. These bids are be offered. The only equilibrium bids occur below the 45-degree line in the triangle region greater than or equal to R_min. A bid such as at point D generates the maximum surplus to the winning bidder equal to the vertical distance between points C and D. Any point in between C and D generates a positive surplus to the winning bidder.

Revenue sharing reduces the amount of the winning bid since positive side payments must be made to all of the other clubs. Formally, the change in the amount of the collusive winning bid is the change in the marginal revenue product of the posted player with the change in the revenue sharing coefficient α.

$$\frac{\partial v{c}_i^{max}}{\partial \alpha }=\frac{df}{d{R}_i^{RS}}\frac{\partial R_i^{RS}}{\partial \alpha }=f^{\prime }\left[\left(\frac{N-1}{N}\right)R_i-\left(\frac{1}{N}\right){{\displaystyle \sum }}_{j\ne i}^N{R}_j\right]=f^{\prime }\left[\left(\frac{N-1}{N}\right)R_i-{\overline{R}}_s\right]$$

(5)

In (5), ${\overline{R}}_s$ is the average of the local revenues for the other teams in the league. An increase in the revenue sharing contribution rate is a reduction in α, so that the net change in revenue for team i is positive if team is equal to or below the average revenue for all of the other teams. If N is large, this equates to the being below the average local revenue for all teams in the league (Easton and Rockerbie 2005). Greater revenue sharing moves the boundary of the equilibrium region of bids to the left, reducing the likelihood of a successful transaction. The distribution of highest bids by each club in the league is compressed, but there cannot be a situation where the overall highest bidding club is changed5. This could be offset somewhat by a reduction in s_i, the salary offered to the posted player.

5. Analysis of the Auction Model

5.1. Revenue Sharing and Market Failure

There is a potential for extensive revenue sharing to result in market failure of the posting system if the maximum colluding bid falls below the minimum reserve of the NPL club. In this case, the triangle bid region in Figure 1 vanishes. The required side payments to the non-bidding clubs becomes large enough to make the highest bid non-profitable.

MLB implemented changes to its revenue sharing system in every year from 1998 to 2001 as it moved away from the historical gate-sharing system6. A simple pooled system was adopted for the 2002 season where each club contributed 31% of its local revenue to a central pool that was then divided evenly among all MLB clubs. Changes to the revenue sharing system for the 2012 season resulted in much more extensive revenue sharing. Each club contributed 34% of its local revenue to a primary revenue sharing pool. In addition, each club contributed to a supplemental pool that totaled 14% of league local revenue with the contribution share determined by each club’s share of total league local revenue. Hence large market clubs paid much more into the supplemental pool than small market clubs as a percentage. The revenue sharing system was simplified for the 2017 season with each club contributing 48% of local revenue into a central pool to be divided equally.

It is no coincidence that the rules regarding the posting system were changed in the same years as the changes to the MLB revenue sharing system. The highest bid could be any amount in the 1998–2012 system, but the maximum bid was limited to $20 million in 2013 and the identity of the winning bidder was not kept secret from the NPL club. Further changes to the posting system in 2017 required that the bidding process was eliminated. In its place, a posted player could negotiate with any MLB club during the short posting period. If the player reached an agreement with an MLB club, the NPL club was compensated based on the value of the new MLB player contract. For contracts with a total value of $25 million or less, the posting fee is 20% of the value of the contract. For contracts with a total value of between $25 million and $50 million, the posting fee is 20% of the first $25 million and 17.5% of the overage. The posting fee is the same for contracts with a total value of over $50 million, with the additional posting fee of 15% of the total value of the contract. This succession of revisions to the posting system rules reduced the magnitudes of the necessary bids to acquire talented NPL players, much to the detriment of NPL teams. MLB clubs could be tougher on salary negotiations with the posted player in order to pay a smaller posting fee. Clearly the changes in the rules to the posting system over time have benefited MLB clubs and not the NPL clubs and their posted players.

A further change to the rules effectively restricted the salaries that posted players could demand, increasing the potential surplus to the successful MLB club. MLB clubs have a cap of approximately $5 million each season that can be spent on acquiring foreign-born players. MLB clubs can use this cap money to complete player trades to top up their spending cap to approximately $10 million. MLB clubs may use this money to make posting payments to NPL clubs, but cannot use additional monies to pay posting fees. NPL players with at least six seasons of NPL service and over 25 years of age are exempt from these restrictions. An MLB club with $5 million to spend on foreign-born players could only offer a contract to an NPL player with a total value of $25 million, using the $5 million to pay the posting fee.

It could be the case that the adoption of more extensive revenue sharing arrangements motivated the changes in the posting system to avoid the market failure of the posting system that could have resulted. Since the success of the posting system relies on the demand for posted players, that arises from the revenues held by the highest bidders, it also relies heavily on the rules of the MLB revenue sharing arrangement.

5.2. Foreclosure of Collusive Bidding

There is a potential for the collusive agreement in stage 2 of the 1998–2012 posting system game to fail if one of the losing bidders overstates his or her private valuation of the player for sale ($v_i$). This situation is known as foreclosure. Foreclosure means that one bidder prevents the bidder with the highest private valuation from obtaining the rights to negotiate with the Japanese player, even though the winning bidder has no intention of signing the player to a contract. This strategy could be used by one of two or more clubs that are strong rivals, for instance, the Boston Red Sox and the New York Yankees. The Red Sox owner simply submits a sealed bid that is inflated beyond the “arranged” collusive bid submitted by the owner of the Yankees7. Since the Red Sox owner has no intention of signing the Japanese player to a contract, but merely wishes to prevent the Yankees from obtaining the player’s negotiation rights, the size of the winning bid has no relevance. The Japanese player cannot re-enter the posting system until the next off-season, so the foreclosure is effective and costless.

Foreclosure can only occur in the bidding model if the externality is not identical for all clubs. Using the Red Sox–Yankees example, if the Yankees acquire the rights to the player up for auction, the best compensation the Red Sox will receive is a 1/30 share of the increased revenue the Yankees gain from the new player. This might not be enough to compensate for the reduction in the Red Sox revenue since the two are close divisional rivals. Conditions (2) and (3) for ring efficiency are violated and the Red Sox owner may then resort to foreclosure.

If strong rivalries are prevalent in MLB, foreclosing might prevent the posting system from operating at all. MLB clubs that anticipate foreclosing behavior by a rival club simply will not bother participating in stage 2 of the game and market failure will result. The only players who will make the jump from Japan to MLB will be marginal players that have little impact on the relative strengths of MLB clubs. Rational Japanese clubs that anticipate receiving the much-needed transfer revenues would surely anticipate foreclosing behavior and insist that some mechanism be built into the posting system to prevent foreclosure. Allowing MLB clubs to bid directly with the Japanese club will not prevent foreclosure of competitive bidding.

One solution is that the MLB clubs be required to pay a “deductible” for the right to enter the bidding process. Only the winning bidder would lose the deductible if it failed to agree to a contract with the Japanese player. The deductible would need to be high enough to discourage foreclosure and to give the posting system credibility to the Japanese club. Unfortunately, the use of a deductible may prevent some lower revenue MLB clubs from bidding since there is always some positive probability that an honest winning bidder will not be able to reach a contract agreement with the Japanese player. Currently, a deductible is not a feature of the posting system, perhaps for this reason. Alternatively, the posting system could be changed to allow a Japanese player to re-enter the system during the designated posting period if contract negotiations fail. Foreclosure could still occur if the winning bidder drags on contract negotiations to the end of the posting period.

The role of the Commissioner’s office in the 1998–2012 bidding process may have been to prevent foreclosure, particularly if the Commissioner was aware of the process in stage 2 of the game. If he knows who the “winning” bidder is and why, he might be able to detect a foreclosing bid. If it is normally the case that only one bid is submitted, then the appearance of a second unexpected bid is simply rejected. In this way, the Commissioner can act as a filter between the honest winning bidder and the Japanese club. There is then no reason the Japanese professional league would not have agreed to involve the Commissioner’s Office in the process. Alternatively, the Commissioner could impose a penalty on a club that forecloses on another. This could be modeled using a repeated game, however it would require that the Commissioner be able to discern the difference between honest negotiations with the player that fail, and foreclosure.

Foreclosure is not possible with the changes to the posting system adopted in 2017. The posted NPL player is allowed to negotiate with any MLB club willing to pay the posting fee. The Red Sox could not agree on a contract with a posted player to prevent the Yankees from signing the player and then back out of the contract. The commitment to the player contract and the resulting posting fee cannot be reversed. This is the most effective way to prevent foreclosure and provides a valuable guarantee to the posted player and the NPL club that was not available prior to 2017. Perhaps MLB clubs used this guarantee as a bargaining chip in the posting system negotiations with the NPL.

5.3. Maintaining Anonymity of the Winning Bidder

The superiority of collusive bidding over non-collusive bidding is not unique to the posting system. The distinct feature of the 1998–2012 posting system was maintaining the anonymity of the winning bidder. Anonymous bidding makes no difference to the bidders or the seller in a non-collusive sealed bid auction since the highest valuation bidder wins the auction. In the posting system, the Commissioner of MLB insured that the winning bidder remained anonymous when he presented the winning value of $b_i^C$ to the seller. The Japanese club is assumed to know that the winning bid will be the bidder with a private valuation of $v{c}_i^{max}$ since it understands the structure of the game.

We must be more specific about how the seller sets its reserve price in order to provide a motivation for the concealment of the winning bidder’s identity. We have already assumed that the seller formulates a minimum reserve price of R_min and that they would prefer to receive a bid greater than this, although they may not be able to. We now assume that there exists a desired reserve price, $\tilde{R}>R_{min}$, that is determined by the seller’s expectation of the winning bidders net profit, $v^e$, from obtaining the player after side payments are made and the player’s salary is paid. There exists a minimal value ${\underset{\_}{v}}^e$ where $\tilde{R}=R_{min}$, which might be the case of the sale of a marginal player where the highest bidder is a small market team. For better players, $v^e>{\underset{\_}{v}}^e$, and thus $\tilde{R}>R_{min}$.

Through the ring efficiency conditions in (2) and (3), the NPL club knows that the highest valuation bidder will be “allowed” to win the auction in stage 2. If the identity of the winning bidder is made known to the NPL club, it can revise its value of $v^e$ in stage 3. It can then refuse the winning bid in the hopes of receiving a higher bid in the near future, that is, $v^e>{\underset{\_}{v}}^e$ and $\tilde{R}\ge R_{min}$. The three situations that can occur at the beginning of stage 3 are summarized below.

• If $b_i^C$ < R_min and $v^e=0$ then reject the bid outright and retain the player’s rights.
• If $b_i^C$ ≥ R_min and $v^e=0$ then accept the bid.
• If $b_i^C$ ≥ R_min and $v^e>0$ then renegotiate the bid.

We now allow for the possibility of a sub-game in stage 3 in which subsequent negotiations can take place. This could occur if the NPL club convinces the winning bidder that its bid is below its minimum reservation price. The winning bidder might believe this since it cannot predict the reservation price with complete accuracy.

The threat of a repeated game might be enough to increase the winning bid in stage 2 of the game. Bidding clubs can anticipate the seller revising its expectation $v^e$ and bid some or all of their $\tilde{v}$ in stage 2 if the player is valued high enough. In this case, bidders form an expectation of the sellers $v^e$, which the bidders use to update the winning bid. The final equilibrium bid would be determined by a Nash equilibrium game. Concealing the identity of the winning bidder negates the need for bidding clubs to form an expectation of how much ${\tilde{v}}_i$ might be necessary to eventually win the player. This keeps the winning bid to the amount imposed by the ring efficiency conditions in (2) and (3). The winning bidder is always the same club in our setup, but maintaining secrecy of the winner keeps the winning bid lower than would be the case without secrecy. If the Japanese club knows that the New York Yankees club is the winning bidder, they may be able to update and form a higher $v^e$ due to the potentially high non-shared revenues that the Yankees possess. Knowing this in stage 2 of the game, the Yankees owner might choose to increase the initial winning bid, but still maintain the ring efficiency conditions in (2) and (3).

The changes to the posting system in 2017 have eliminated the opportunities for side games. The choice of which MLB club the NPL club receives a posting fee from is determined by the posted player and the posting fee is a fixed percentage of the player’s new contract.

6. Discussion

This paper began by describing the posting system used by MLB and the NPL in the 1998–2012 seasons and then posed the question why the posting system was designed the way it was. Why did the posting system not replicate the features of the European transfer system? Probably because European football clubs often bid against other clubs that are not in the same league, eliminating any negative externalities. In addition, European football leagues do not use revenue sharing, hence there is no automatic mechanism to make the necessary side payments to maintain a collusive bidding system. We argue that because the posting system has both of the features mentioned above it was an unorthodox auction design that maintained collusive profits for MLB owners. Changes to the rules of the posting system since 2012 have significantly reduced the amounts of the winning bids, much to the detriment of the NPL clubs, but have allowed the posted players to capture a greater portion of their revenue surplus to their MLB clubs in the form of higher salaries.

Three curious features of the initial posting system were identified: the use of a collusive first-price sealed bid auction, the use of the Commissioner’s Office as an auctioneer, and the inability of the Japanese club to learn the identity of the winning bidder until after the winning bid is accepted. Collusion is a reality in the collective bargaining agreements of North American professional leagues, particularly in the setting of league and team salary caps, eligibility for free agency, and other clauses that limit the ability of players to earn what they are worth. In our setup, club owners accept a revenue sharing arrangement as an involuntary system to compensate clubs for any externality imposed when one club acquires a star player (although this arrangement is not perfect). In exchange for this, “losing” bidders agree to allow the “winning” bidder to win the posting system auction with a bid that is lower than the winner’s private valuation of the player. MLB clubs will pay lower posting fees to NPL clubs that are posting players than they otherwise would. A ring efficiency condition ensures that the winning bidder will not bid too high and lose all of the expected revenue surplus. Of course, an MLB club that signs a free agent player from another MLB club also shares the revenue generated by the player with all other MLB clubs in the revenue sharing system, however the winning bidder need not make a payment to the team losing the player, much to the advantage of the free agent player when negotiating a contract.

Revenue sharing became more extensive over the 1998–2017 period. Each new arrangement required MLB clubs to contribute more of their local revenues to the central pool, resulting in larger revenue transfers from large market to small market clubs. Our model suggests that more extensive revenue sharing lowers the maximum bid for any posted NPL player and could result in market failure. This was avoided by renegotiating the rules of the posting system immediately following changes to the revenue sharing system.

In the initial posting system, the Commissioner acted as a collusion mediator to prevent the foreclosure of competing bids, particularly if two or more rival clubs considered placing bids. This was to the benefit of the NPL club in that market failure was avoided. Foreclosure can occur in the European transfer system as well, although the failure to reach a contract agreement is not definitive evidence of foreclosure. In either system, foreclosure could be avoided by requiring the winning bidder to post a bond in the event that it does not sign the Japanese player to a contract. Of course, there is some positive probability that a contract agreement will not be made without foreclosure, but this event should be discounted into the winning bid by rational bidders. The 2017 changes to the posting system effectively eliminated the possibility of foreclosure.

Maintaining the secrecy of the winning bidder prevented collusion between MLB clubs and NPL clubs in a sub-game. Such acts of collusion are to the detriment of other bidding clubs and possibly to the NPL player. We show that maintaining the secrecy of the winning bidder also prevented MLB clubs from bidding too high, while having no effect on which club won the auction. The secrecy condition was removed from the posting system in 2012 as limits to the size of the posting fee reduced the potential benefits to the NPL club from pursuing a sub-game. The rules of the 2017 posting system eliminated these potential benefits altogether.

The NBA uses an extensive revenue sharing system comparable to MLB so it is useful to ask if the posting system used by MLB could be an effective method for the NBA to acquire talented foreign players. NBA clubs employ a large number of foreign players, 108 players from 38 countries in the 2019–2020 season8. Several factors limit the ability of NBA teams to use the MLB posting system as a model. First, it is common practice for NBA teams to use draft picks to secure the rights to foreign players that are expected to develop to NBA-quality, even players currently under contract with foreign teams. This is thought necessary to insure that talented foreign players do not become the property of rival clubs. NBA draft rights extend for the playing life of the foreign player and give the holder of the rights the exclusive right to negotiate a contract with the player. MLB teams typically do not use draft picks to secure the rights to foreign players, particularly NPL players, hence an NPL player may negotiate with any MLB club. Second, the 2017 NBA collective bargaining agreement places limits on the amount of funds that may be used to purchase the rights to a foreign player that is under contract to a foreign club. That limit is just $750,000 for the 2019–2020 NBA season, increasing to $825,000 for the 2023–2024 season. Currently there is no provision to tie the payment to a foreign club to the value of the negotiated contract with an NBA team, as is the case in the MLB–NPL posting system.

The NHL is similar to the NBA in how foreign players are acquired. In 2019, the NHL featured 183 foreign players from 18 countries9. NHL teams also typically use draft picks to select young, promising foreign players, however NHL teams have only a 4-year window to sign the player to an NHL contract, after which time the rights are forfeited. The NHL has a transfer agreement with the International Ice Hockey Federation (IIHF) that governs the compensation that must be paid to clubs that lose players to NHL teams as well as the signing period (with the exception of Russia). The transfer amount is determined in a rather complicated way by the total number of players being transferred to the NHL annually and their country of origin. The agreement is renewed periodically and the two sides negotiate hard to maintain the most money for each side. Perhaps the NHL could benefit from an MLB-style posting system in which the transfer amount is tied to the value of the player and players are free to negotiate with any NHL club, however the IIHF is concerned that highly talented players could be “poached” from their European clubs and then toil in the NHL’s minor leagues.