The Dynamic Spillover Effects of Macroeconomic and Financial Uncertainty on Commodity Markets Uncertainties
Abstract
1. Introduction
2. Literature Review
3. Data and Preliminary Analysis
4. Econometric Methodology
4.1. Measuring Commodity Price Uncertainty
- Extracting the common factors among 8 commodity price returns. The statistic principal component analysis is used to estimate the common factors.
- Estimating the following factor augmented vector autoregression (FAVAR) model:where , is the commodity price returns of market , and is a vector of the estimated common factors , and a The set of predictors include the squares of the estimated common factors and common factors in to account for possible nonlinearity.
- Computing the ahead prediction error of , and each factor in and . These ahead prediction errors are assumed to have time-varying volatilities. The time-varying squared forecast error is computed using a stochastic volatility model. Jurado et al. (2015) use the STOCHVOL package in R to estimate the volatilities in AR(1) model with stochastic volatility. Then, the ahead commodity price uncertainty of market denoted by is computed as the conditional volatility of the purely unforecastable component of the future value of the series.
4.2. Measuring Commodity Price Uncertainty
5. Empirical Results
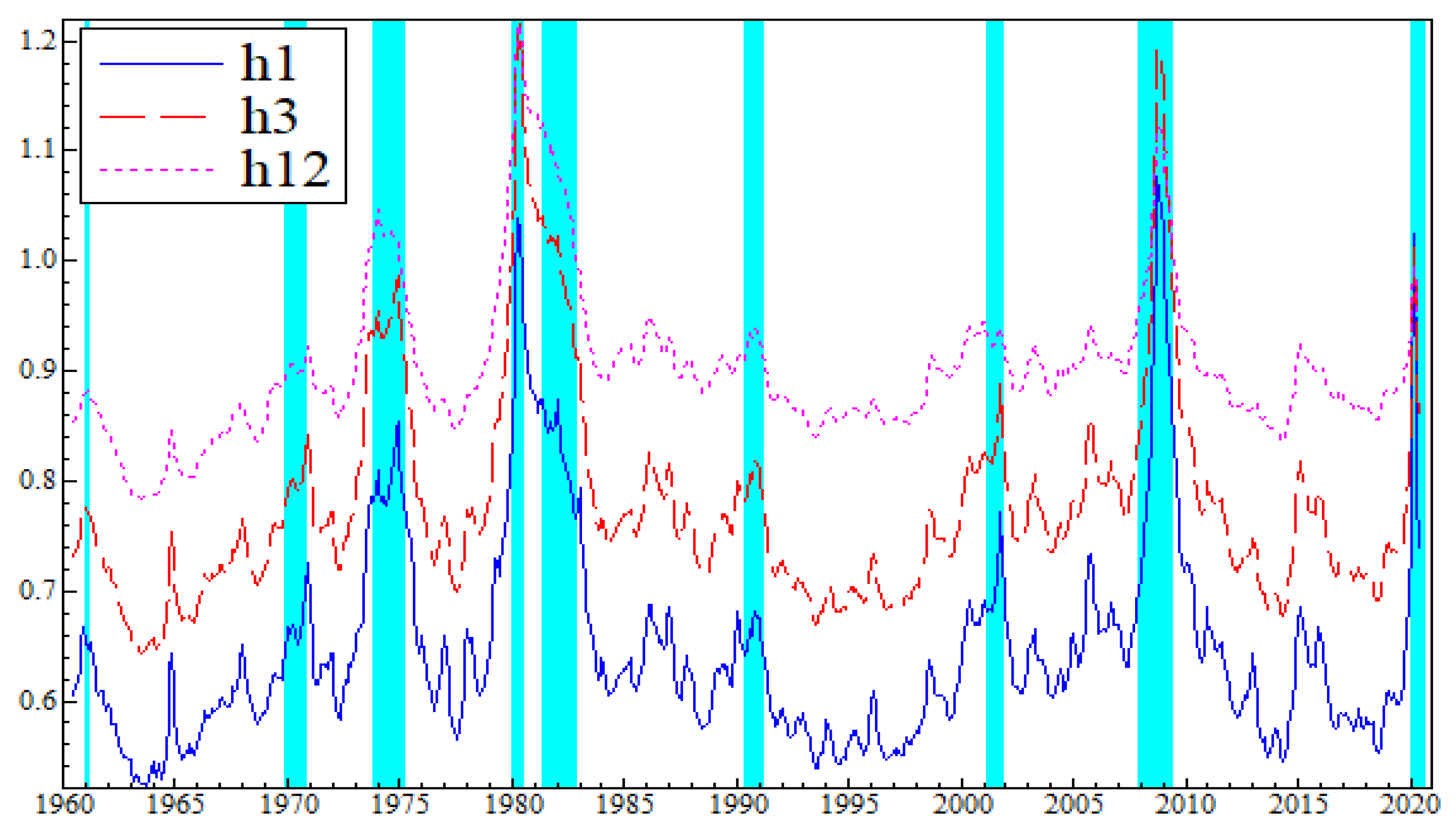
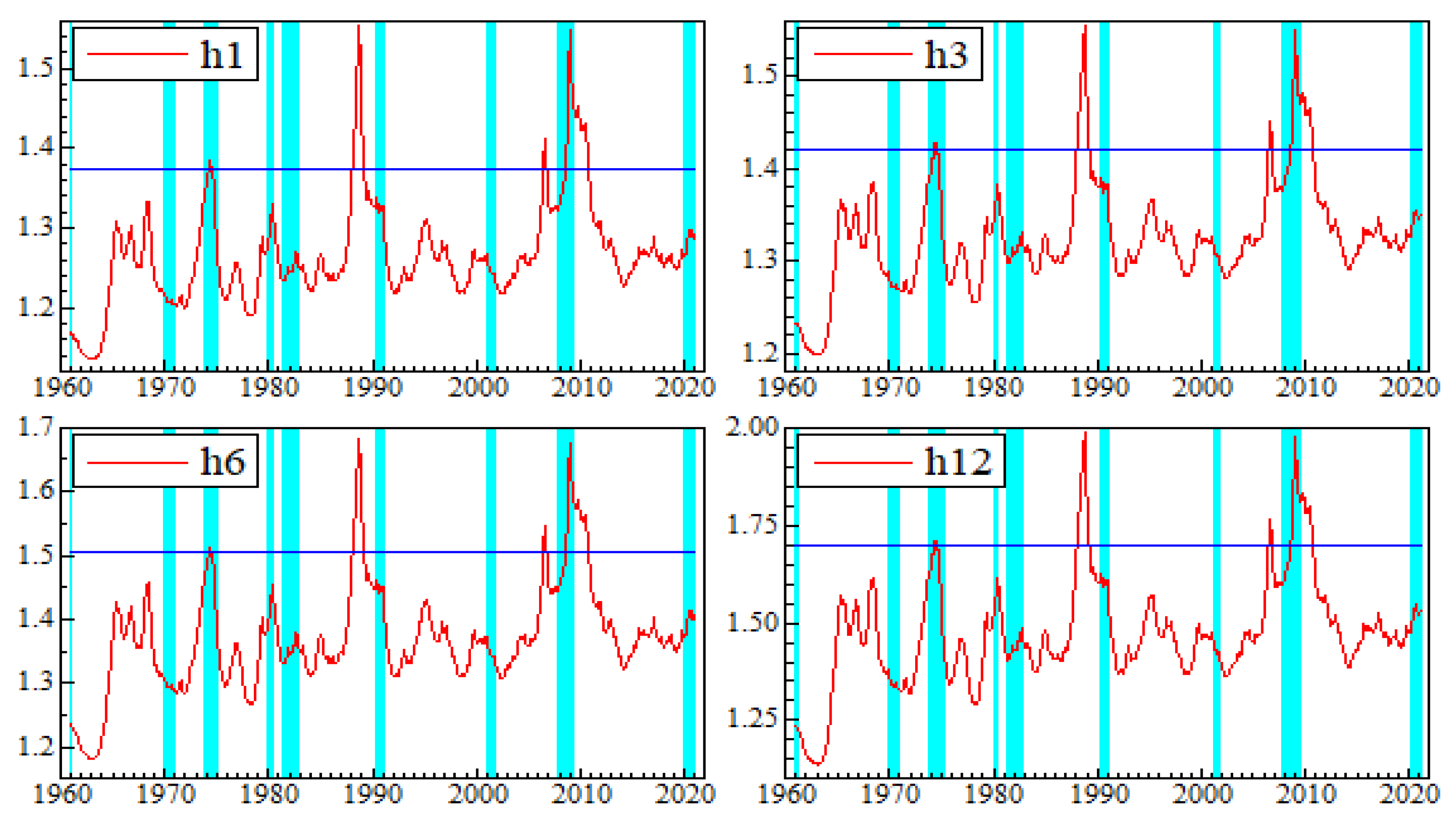
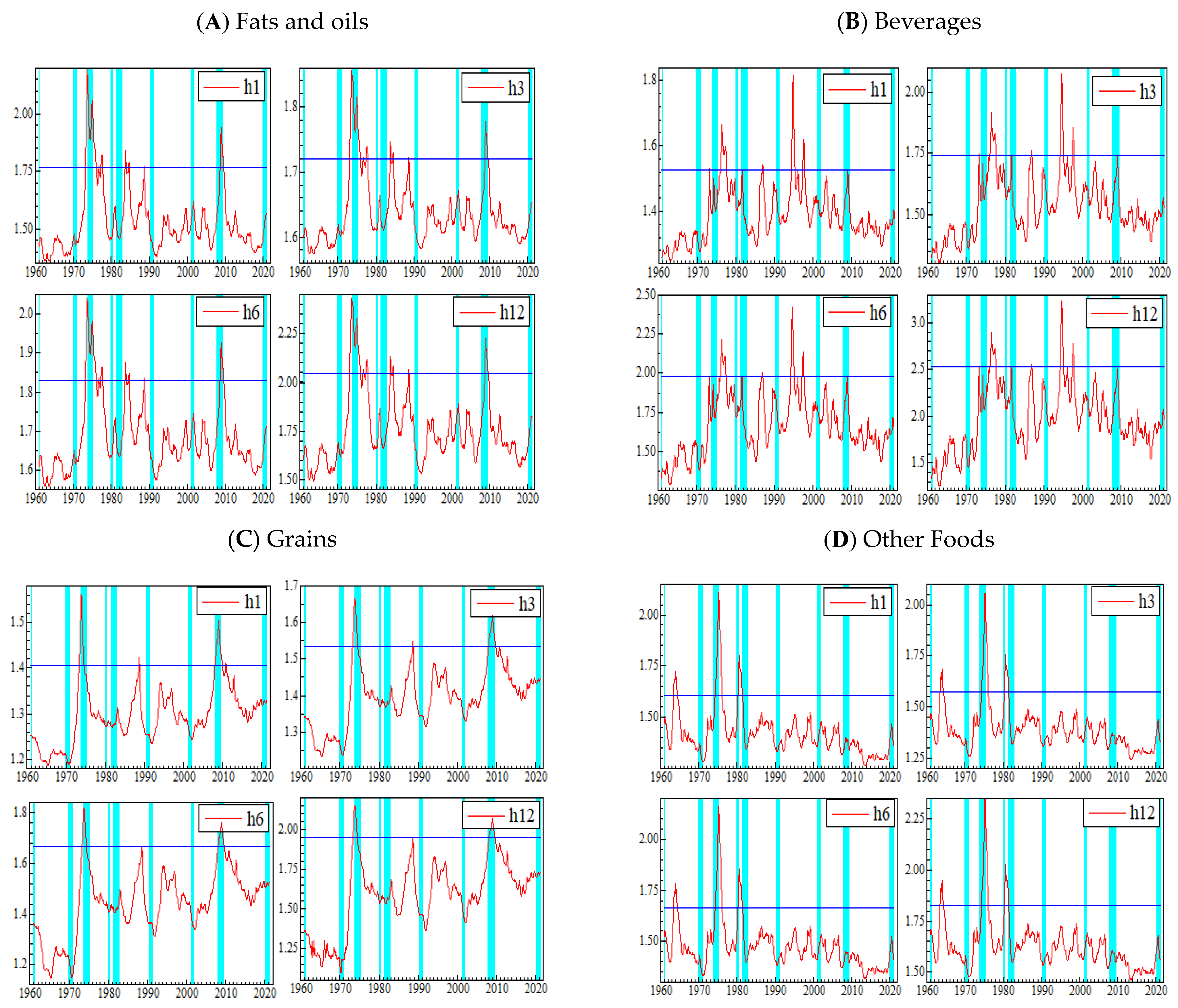
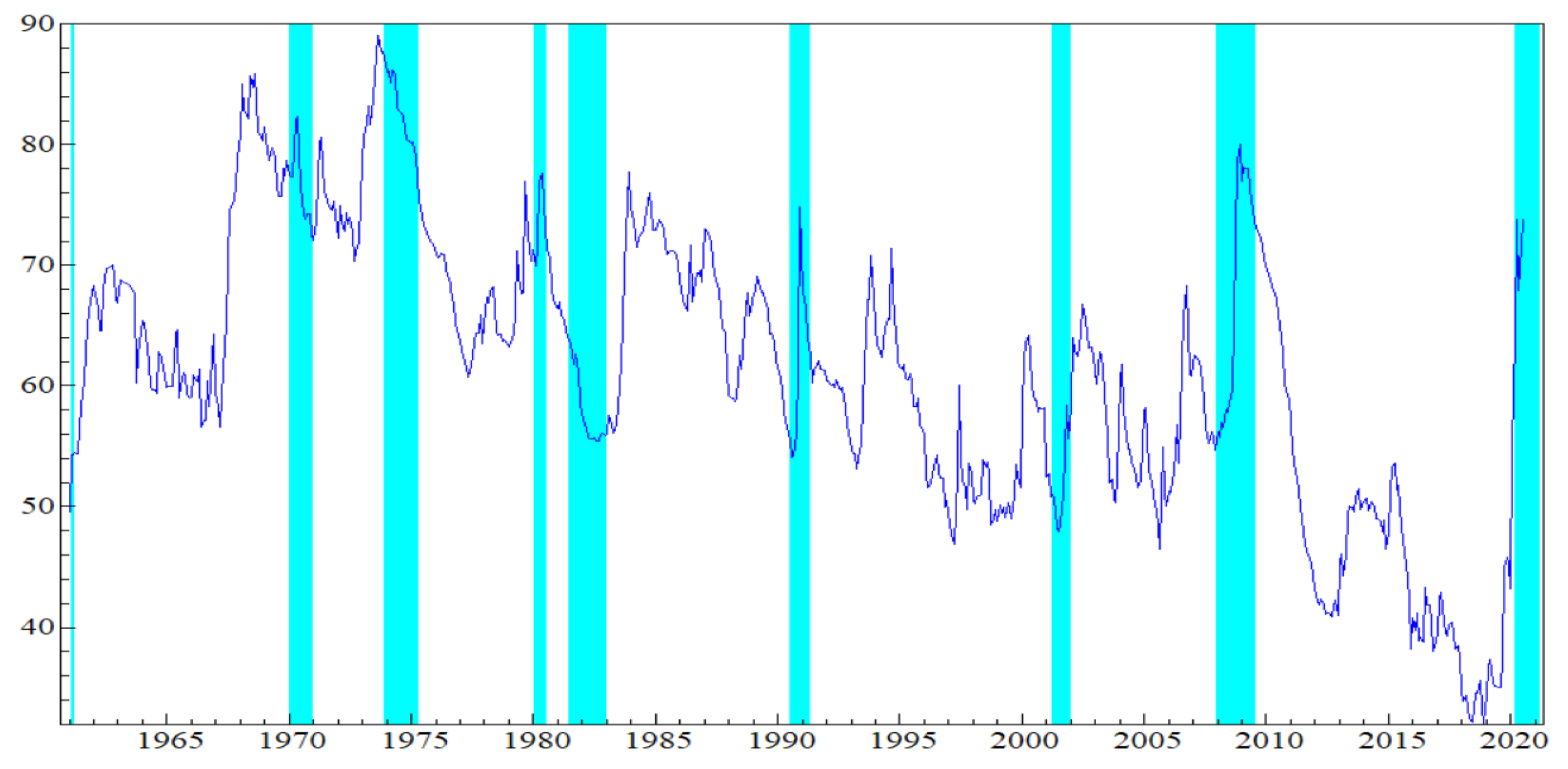
5.1. Estimates of Commodity Price Returns Uncertainty
5.2. Connectedness between Macroeconomic Uncertainty and Commodity Market Uncertainty
5.2.1. Total Connectedness among Commodities and Macroeconomic Uncertainty Indexes
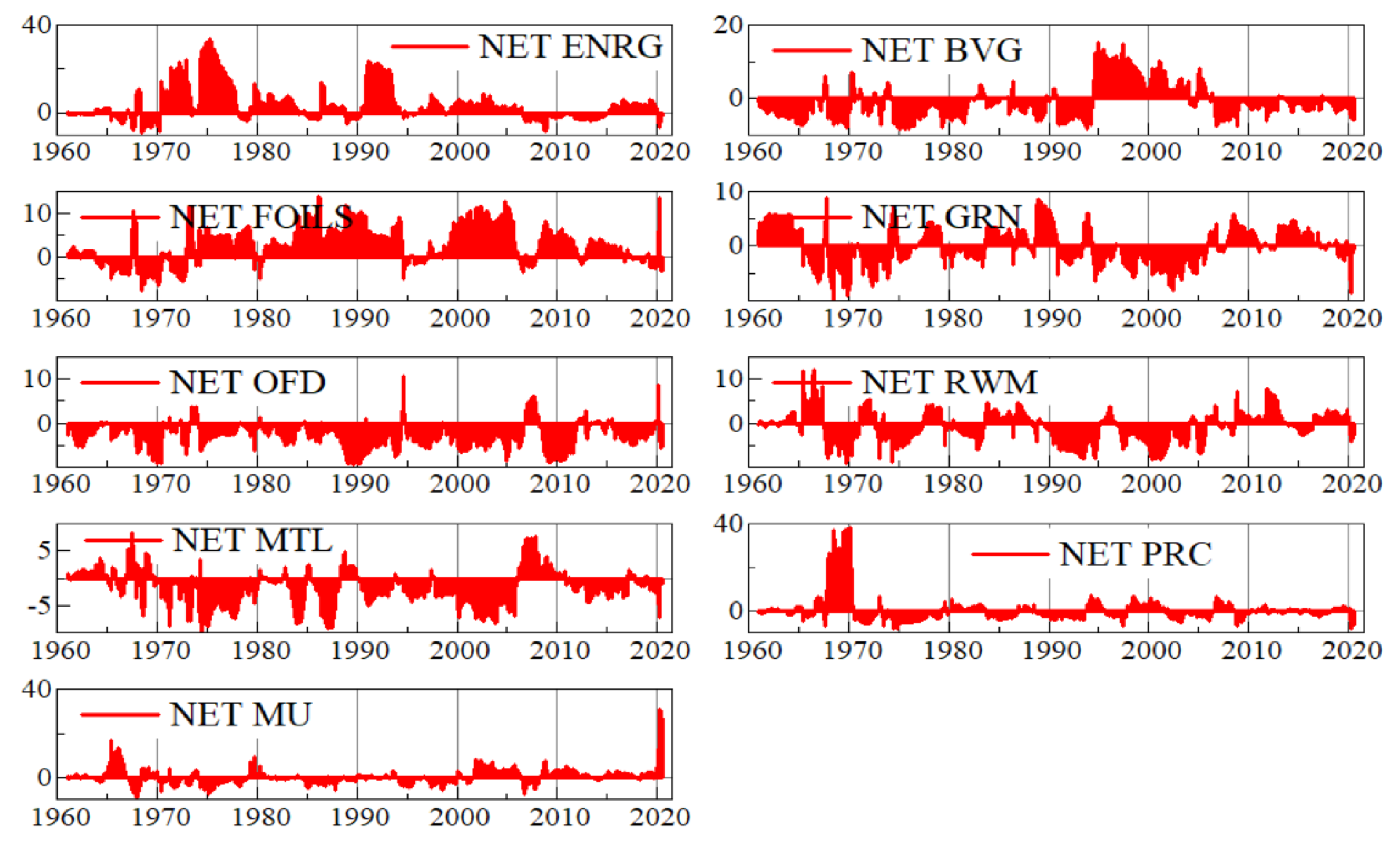
5.2.2. Net Pairwise Connectedness and Net Total Directional Connectedness Uncertainty
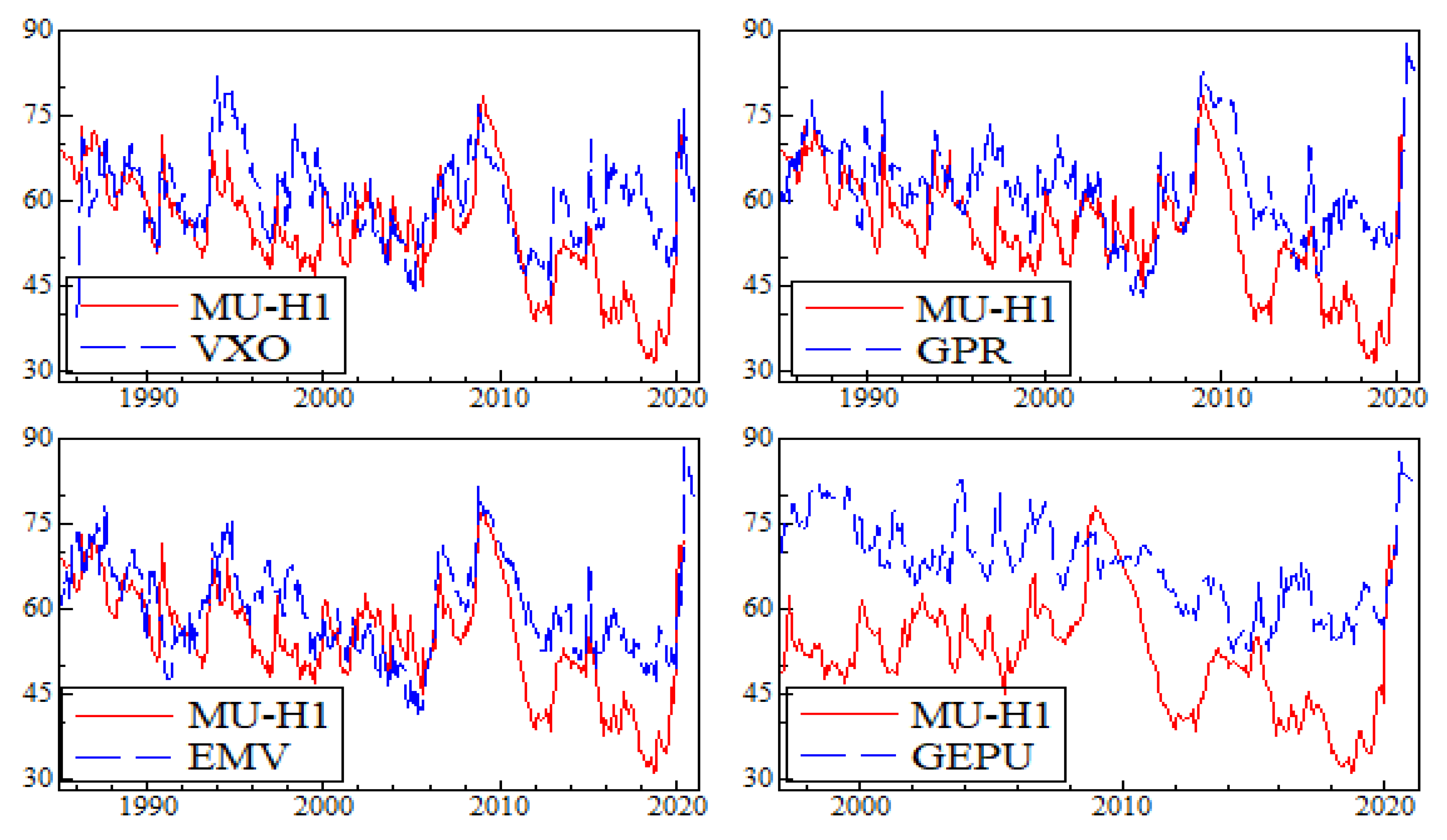
5.2.3. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources and Description
| Market | Description | Transformation | Source |
|---|---|---|---|
| Energy Market | Fuel (Energy) Index, 2010 = 100, includes Crude oil (petroleum), Natural Gas, Coal Price and Propane Indices. | ∆ln | WDI |
| Precious Metals Market | Precious Metals Price Index, 2010 = 100, includes Gold, Silver, Palladium and Platinum Price Indices | ∆ln | WDI |
| Beverage | Beverage Price Index, 2010 = 100, includes Coffee and Tea. | ∆ln | WDI |
| Fats Oils | Oils and Meals Price Index, 2010 = 100, includes Coconut oil, Copra, Fishmeal, Groundnuts, Groundnut oil, Palm oil, Palm kernel oil, Soybean meal, Soybean oil and Soybeans. | ∆ln | WDI |
| Grains | Grains Price Index, 2010 = 100, includes Barley, Maize, Rice, Sorghum and Wheat. | ∆ln | WDI |
| Other Food | Other Food Price index, 2010 = 100, includes Bananas, Meats (boeuf, chicken and sheep), Oranges, Shrimp and Sugars. | ∆ln | WDI |
| Raw Materials | Raw Materials Price index, 2010 = 100, includes Timber and other raw materials (Cotton, Rubber and Tobacco). | ∆ln | WDI |
| Metals and Minerals Market | Base Metals Price Index, 2010 = 100, includes Aluminium, Copper, Iron, Lead, Nickel, Steels, Tin and Zinc. | ∆ln | WDI |
| Macroeconomic Uncertainty (MU1) | The one-month macroeconomic uncertainty indicator proposed by Jurado et al. (2015) | https://www.sydneyludvigson.com/data-and-appendixes, (accessed on 20 December 2020) |
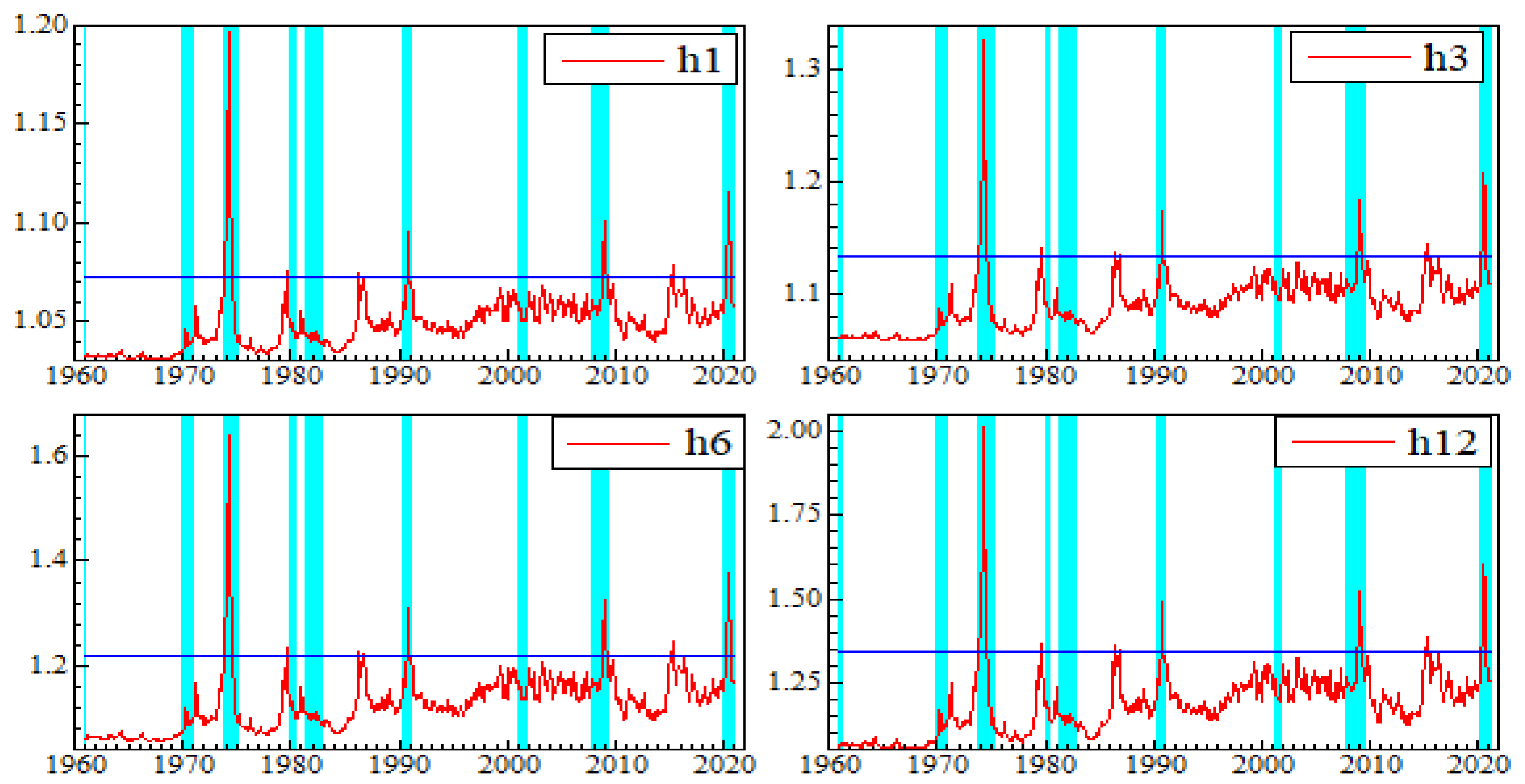
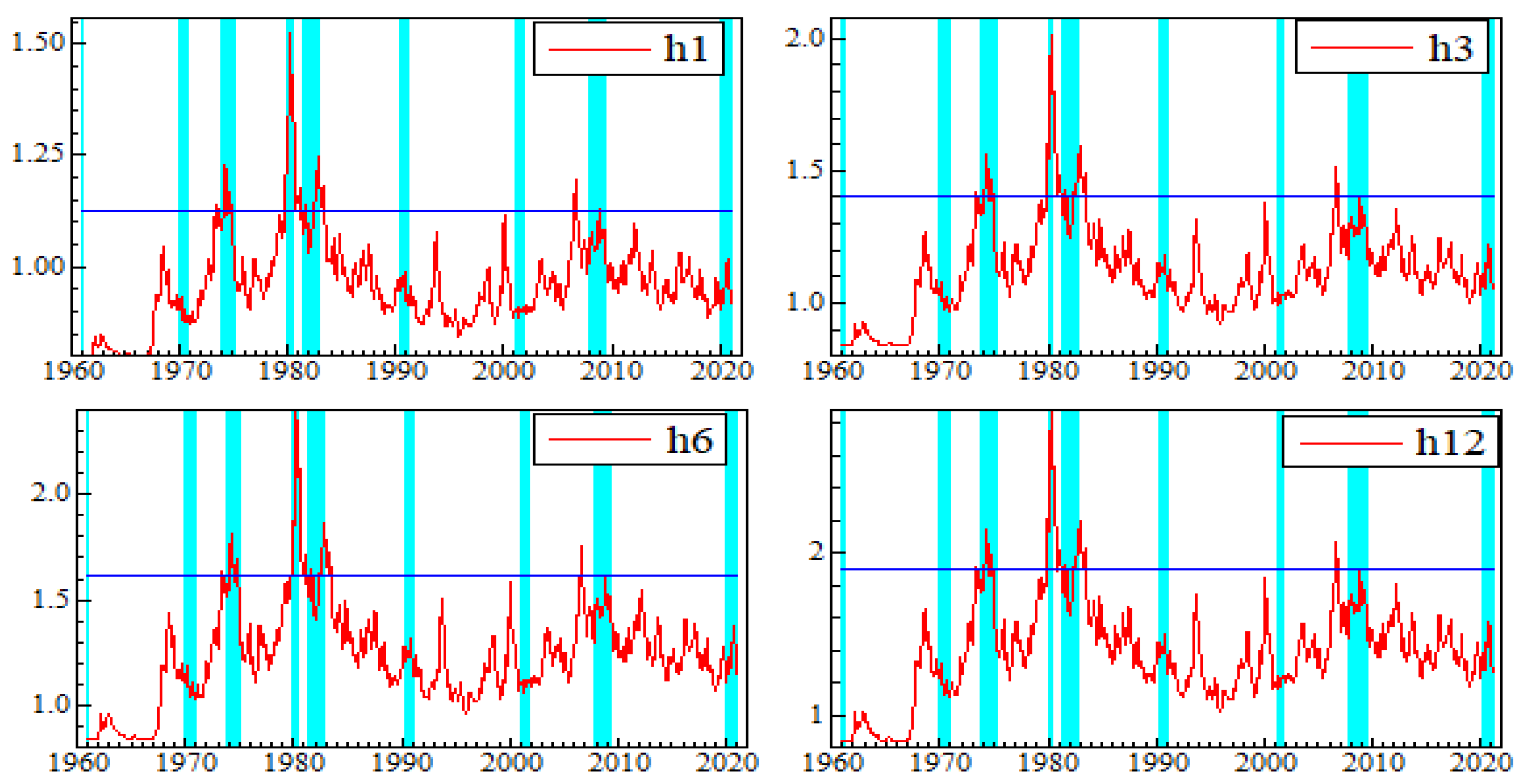
Appendix B. Graphs of Net Pairwise Connectedness Uncertainties

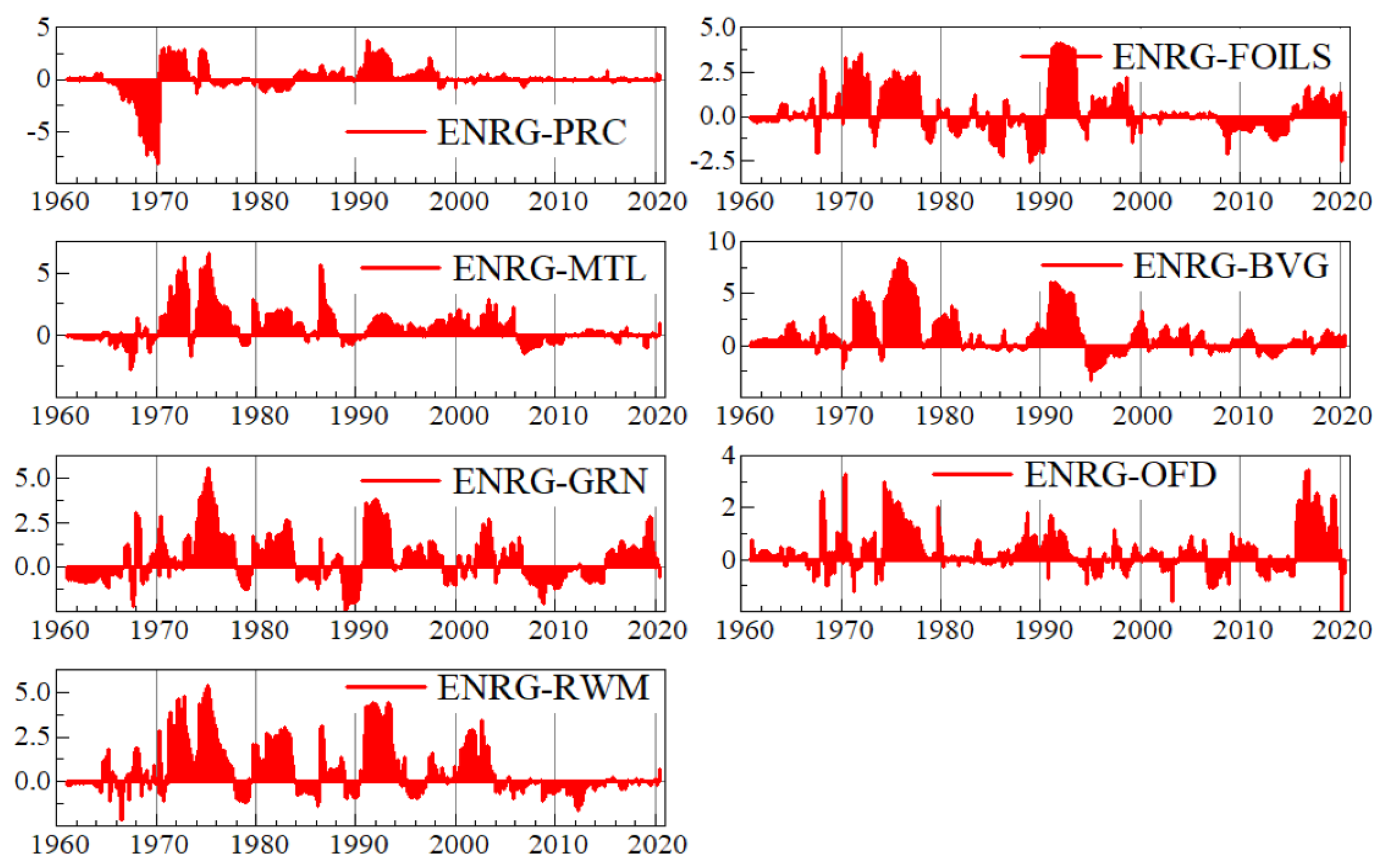
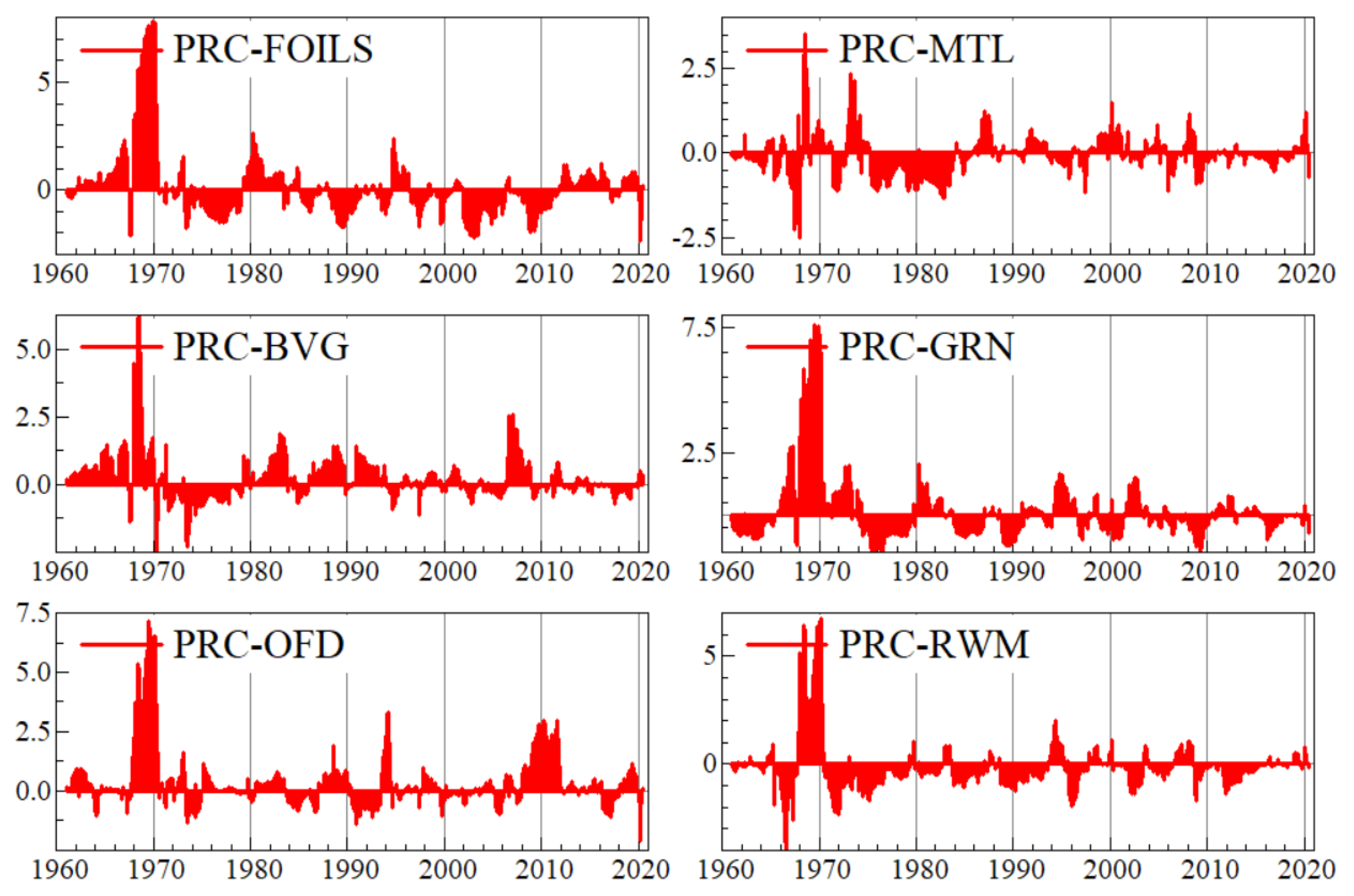
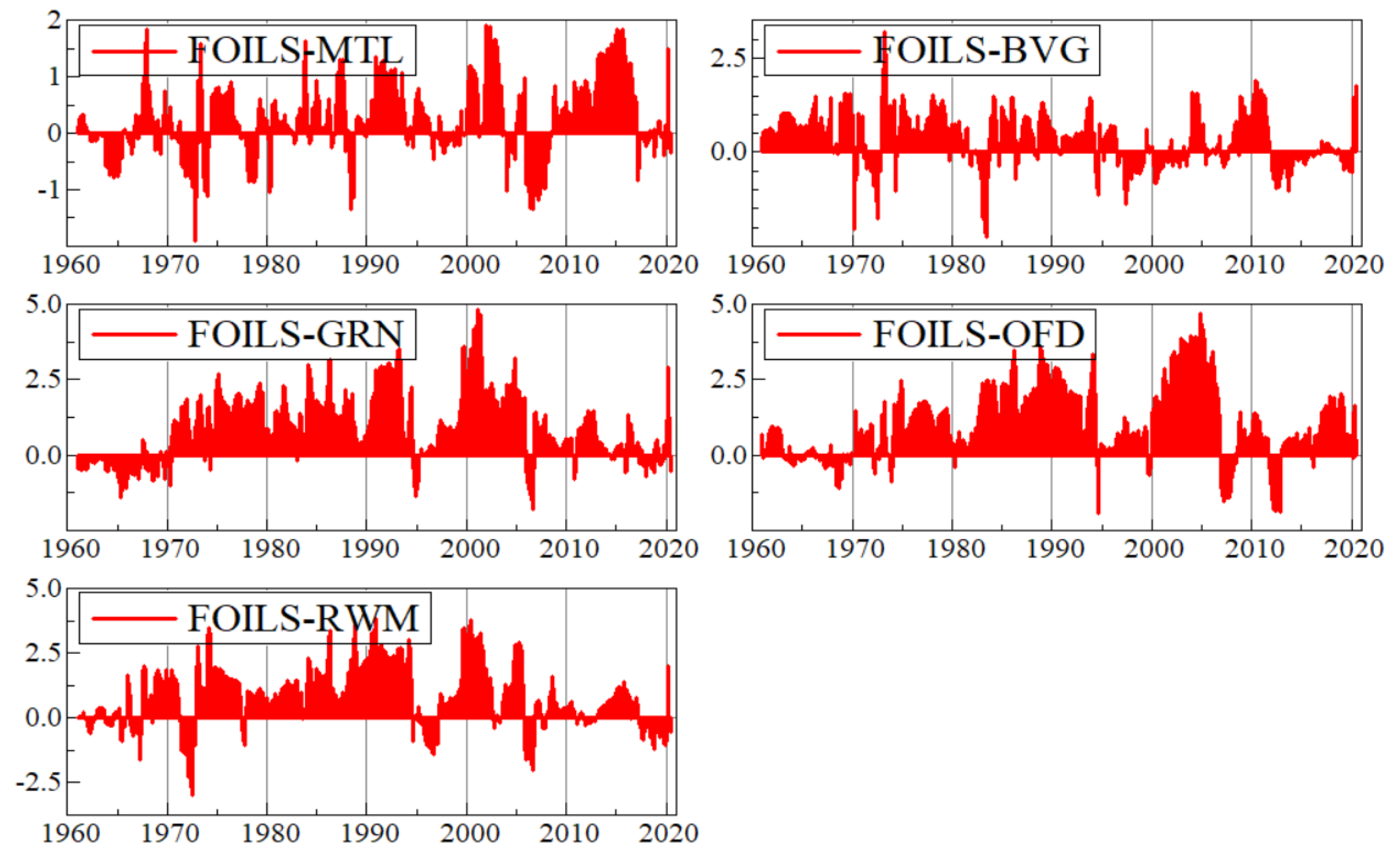
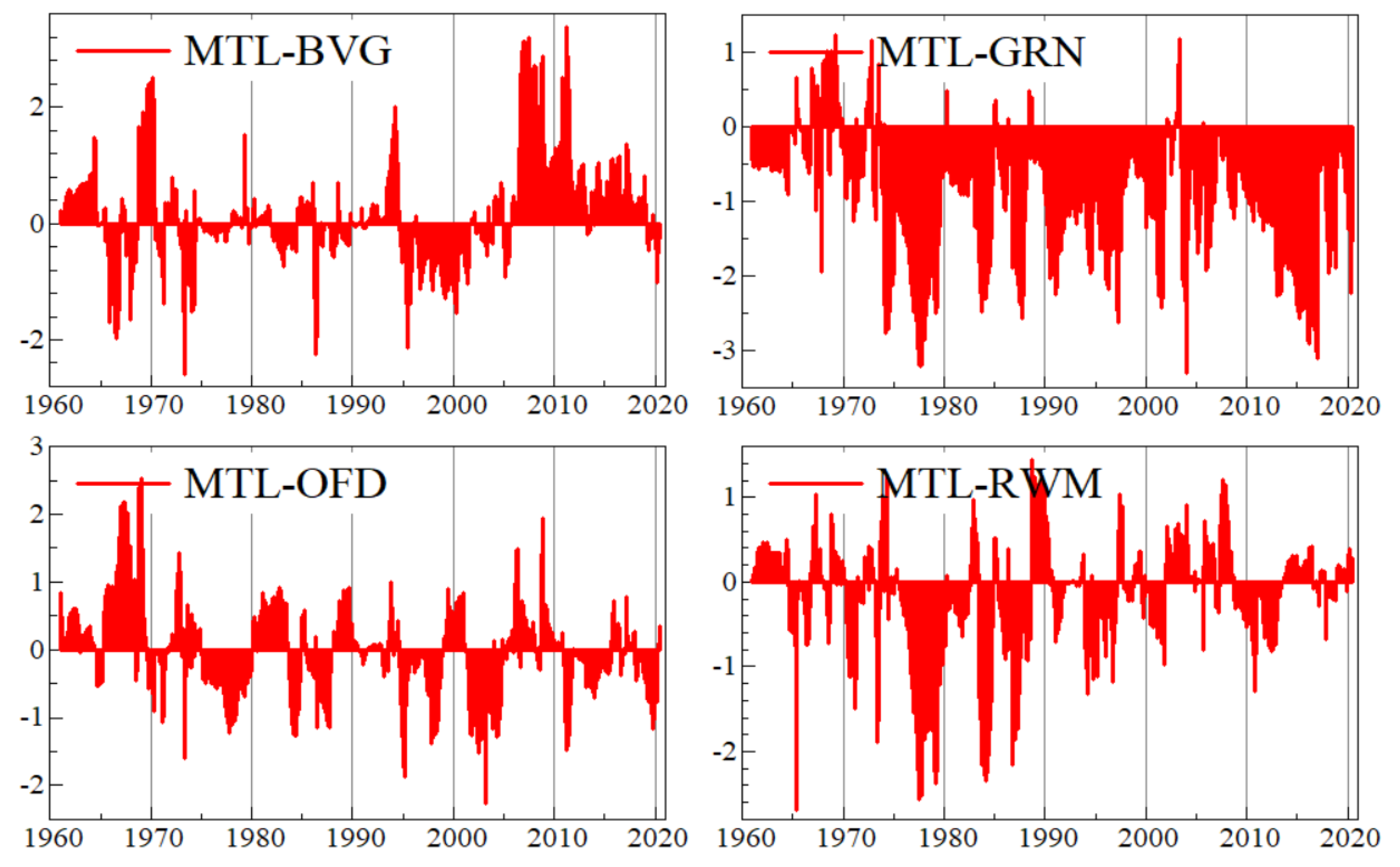

Appendix C. Graphs of Robustness Analysis

References
- Ahumada, Hildegart, and Magdalena Cornejo. 2016. Forecasting food prices: The cases of corn, soybeans and wheat. International Journal of Forecasting 32: 838–48. [Google Scholar] [CrossRef]
- Algieri, Bernardina, and Arturo Leccadito. 2017. Assessing contagion risk from energy and non-energy commodity markets. Energy Economics 62: 312–22. [Google Scholar] [CrossRef]
- Alquist, Ron, and Lutz Kilian. 2010. What do we learn from the price of crude oil futures? Journal of Applied Econometrics 25: 539–73. [Google Scholar] [CrossRef]
- Antonakakis, Nikolaos, Ioannis Chatziantoniou, and David Gabauer. 2020. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. Journal of Risk and Financial Management 13: 84. [Google Scholar] [CrossRef]
- Antonakakis, Nikolaos, Ioannis Chatziantoniou, and George Filis. 2014. Dynamic spillovers of oil price shocks and economic policy uncertainty. Energy Economics 44: 433–47. [Google Scholar] [CrossRef]
- Arouri, Mohamed El Hedi, Amine Lahiani, and Duc Khuong Nguyen. 2011a. Return and volatility transmission between world oil prices and stock markets of the GCC countries. Economic Modelling 28: 1815–25. [Google Scholar] [CrossRef]
- Arouri, Mohamed El Hedi, Jamel Jouini, and Duc Khuong Nguyen. 2011b. Volatility spillovers between oil prices and stock sector returns: Implications for portfolio management. Journal of International Money and Finance 30: 1387–405. [Google Scholar] [CrossRef]
- Badshah, Ihsan, Riza Demirer, and Muhammad Tahir Suleman. 2019. The effect of economic policy uncertainty on stock-commodity correlations and its implications on optimal hedging. Energy Economics 84: 104553. [Google Scholar] [CrossRef]
- Bahloul, Walid, Mehmet Balicilar, Juncal Cunado, and Gupta Rangan. 2018. The role of economic and financial uncertainties in predicting commodity futures returns and volatility: Evidence from a nonparametric causality-in-quantiles test. Journal of Multinational Financial Management 45: 52–71. [Google Scholar] [CrossRef]
- Bai, Jushan, and Serena Ng. 2002. Determining the number of factors in approximate factor models. Econometrica 70: 191–221. [Google Scholar] [CrossRef]
- Bakas, Dimitrios, and Athanasios Triantafyllou. 2018. The impact of uncertainty shocks on the volatility of commodity prices. Journal of International Money and Finance 87: 96–111. [Google Scholar] [CrossRef]
- Bakas, Dimitrios, and Athanasios Triantafyllou. 2019. Volatility forecasting in commodity markets using macro uncertainty. Energy Economics 81: 79–94. [Google Scholar] [CrossRef]
- Bakas, Dimitrios, and Athanasios Triantafyllou. 2020. Commodity price volatility and the economic uncertainty of pandemics. Economics Letters 193: 109283. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring economic policy uncertainty. The Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Balli, Faruk, Muhammad Abubakr Naeem, and Syed Jawad Hussain Shahzad. 2019. Spillover network of commodity uncertainties. Energy Economics 81: 914–27. [Google Scholar] [CrossRef]
- Barbaglia, Luca, Christophe Croux, and Ines Wilms. 2020. Volatility spillovers in commodity markets: A large t-vector autoregressive approach. Energy Economics 85: 104555. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2012. Real-time forecasts of the real price of oil. Journal of Business and Economic Statistics 30: 326–36. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2015. Forecasting the real price of oil in a changing world: A forecast combination approach. Journal of Business and Economic Statistics 33: 338–51. [Google Scholar] [CrossRef]
- Baumeister, Christine, Lutz Kilian, and Xiaoqing Zhou. 2018. Are product spreads useful for forecasting oil prices? an empirical evaluation of the Verleger hypothesis. Macroeconomic Dynamics 22: 562–80. [Google Scholar] [CrossRef]
- Bekiros, Stelios, Rangan Gupta, and Alessia Paccagnini. 2015. Oil price forecast ability and economic uncertainty. Economic Letters 132: 125–28. [Google Scholar] [CrossRef]
- Bessembinder, Hendrik, and Kalok Chan. 2016. Time-varying risk premia and forecastable returns in futures markets. Journal of Financial Economic 32: 169–93. [Google Scholar] [CrossRef]
- Caldara, Dario, and Matteo Iacoviello. 2018. Measuring Geopolitical Risk. FRB International Finance Discussion Paper 1222. Available online: https://ssrn.com/abstract=3117773 (accessed on 20 December 2020).
- Chen, Yu-Chin, Kenneth S. Rogoff, and Barbara Rossi. 2010. Can Exchange Rates Forecast Commodity Prices? The Quarterly Journal of Economics 125: 1145–94. [Google Scholar] [CrossRef]
- Coppola, Andrea. 2008. Forecasting oil price movements: Exploiting the information in the futures market. Journal of Futures Markets 28: 34–56. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2014. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
- Diebold, Francis X., Laura Liu, and Kamil Yilmaz. 2017. Commodity Connectedness. No. w23685. National Bureau of Economic Research. Available online: https://www.nber.org/papers/w23685 (accessed on 20 December 2020).
- Du, Xiaodong, L. Yu Cindy, and Dermot J. Hayes. 2011. Speculation and volatility spillover in the crude oil and agricultural commodity markets: A Bayesian analysis. Energy Economics 33: 497–503. [Google Scholar] [CrossRef]
- Elliott, Graham, Thomas J. Rothenberg, and James H. Stock. 1996. Efficient Tests for an Autoregressive Unit Root. Econometrica 64: 813–36. [Google Scholar] [CrossRef]
- Gankhuyag, Uyanga, and Fabrice Gregoire. 2018. Managing Mining for Sustainable Development: A Sourcebook. New York: United Nations Development Programme. [Google Scholar]
- Groen, Jan J. J., and Paolo A. Pesenti. 2011. Commodity prices, commodity currencies, and global economic developments. In Commodity Prices and Markets, East Asia Seminar on Economics. Edited by Takatoshi Ito and Andrew K. Rose. Chicago: University of Chicago Press, vol. 20, pp. 15–42. [Google Scholar]
- Hergt, Brian. 2013. Gold Prices during and after the Great Recession; Washington, DC: Bureau of Labor Statistics.
- Hong, Harrison, and Motohiro Yogo. 2012. What does futures market interest tell us about the macroeconomy and asset prices? Journal of Financial Economic 105: 473–90. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics letters 6: 255–59. [Google Scholar] [CrossRef]
- Ji, Qiang, Elie Bouri, David Roubaud, and Syed J. H. Shahzad. 2018. Risk spillover between energy and agricultural commodity markets: A dependence-switching CoVaR-copula model. Energy Economics 75: 14–27. [Google Scholar] [CrossRef]
- Joëts, Marc, Valérie Mignon, and Tovonony Razafindrabe. 2017. Does the volatility of commodity prices reflect macroeconomic uncertainty? Energy Economics 68: 313–26. [Google Scholar] [CrossRef]
- Jurado, Kyle, Sydney C. Ludvigson, and Serena Ng. 2015. Measuring uncertainty. American Economic Review 105: 1177–216. [Google Scholar] [CrossRef]
- Kang, Sang Hoon, Ron McIver, and Seong-Min Yoon. 2017. Dynamic spillover effects among crude oil, precious metal, and agricultural commodity futures markets. Energy Economics 62: 19–32. [Google Scholar] [CrossRef]
- Kang, Wensheng, and Ronald A. Ratti. 2013. Oil shocks, policy uncertainty and stock market return. Journal of International Financial Markets, Institutions and Money 26: 305–18. [Google Scholar] [CrossRef]
- Koop, Gary, M. Hashem Pesaran, and Simon M. Potter. 1996. Impulse response analysis in nonlinear multivariate models. Journal of econometrics 74: 119–47. [Google Scholar] [CrossRef]
- Korobilis, Dimitris, and Kamil Yilmaz. 2018. Measuring Dynamic Connectedness with Large Bayesian VAR Models. Available online: https://ssrn.com/abstract=3099725 (accessed on 12 December 2020).
- Krugman, Paul. 2008. The oil nonbubble. New York Times, May 12. [Google Scholar]
- Kuhns, Annemarie, and Abigail Okrent. 2019. Factors Impacting Grocery Store Deflation: A Closer Look at Prices in 2016 and 2017; EB-28. Washington, DC: U.S. Department of Agriculture, Economic Research Service.
- Ljung, Greta M., and George E. P. Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Mensi, Walid, Makram Beljid, Adel Boubaker, and Managi Shunsuke. 2013. Correlations and volatility spillovers across commodity and stock markets: Linking energies, food, and gold. Economic Modelling 32: 15–22. [Google Scholar] [CrossRef]
- Naeem, Muhammad Abubakr, Saqib Farid, Safwan Mohd Nor, and Syed Jawad Hussain Shahzad. 2021. Spillover and Drivers of Uncertainty among Oil and Commodity Markets. Mathematics 9: 441. [Google Scholar] [CrossRef]
- Pesaran, H. Hashem, and Yongcheol Shin. 1998. Generalized impulse response analysis in linear multivariate models. Economics Letters 58: 17–29. [Google Scholar] [CrossRef]
- Poncela, Pilar, Eva Senra, and Lya Paola Sierra. 2014. Common dynamics of nonenergy commodity prices and their relation to uncertainty. Applied Economics 46: 3724–35. [Google Scholar] [CrossRef]
- Shiferaw, Yegnanew A. 2019. Time-varying correlation between agricultural commodity and energy price dynamics with Bayesian multivariate DCC-GARCH models. Physica A: Statistical Mechanics and Its Applications 526: 120807. [Google Scholar] [CrossRef]
- Silvennoinen, Annastiina, and Susan Thorp. 2013. Financialization, crisis and commodity correlation dynamics. Journal of International Financial Markets, Institutions and Money 24: 42–65. [Google Scholar] [CrossRef]
- Stuermer, Martin. 2018. 150 years of boom and bust: What drives mineral commodity prices? Macroeconomic Dynamics 22: 702–17. [Google Scholar] [CrossRef]
- Taghizadeh-Hesary, Farhad, Ehsan Rasoulinezhad, and Naoyuki Yoshino. 2018. Volatility Linkages between Energy and Food Prices: Case of Selected Asian Countries. Asian Development Bank Institute. Available online: http://hdl.handle.net/11540/8113 (accessed on 20 December 2020).
- Van Robays, Ine. 2016. Macroeconomic uncertainty and oil price volatility. Oxford Bulletin of Economics and Statistics 78: 671–93. [Google Scholar] [CrossRef]
- Wang, Yudong, Bing Zhang, Xundi Diao, and Chongfeng Wu. 2015. Commodity price changes and the predictability of economic policy uncertainty. Economic Letters 27: 39–42. [Google Scholar] [CrossRef]
- Wang, Yudong, Li Liu, and Chongfeng Wu. 2017. Forecasting the real prices of crude oil using forecast combinations over time-varying parameter models. Energy Economics 66: 337–48. [Google Scholar] [CrossRef]
- Watugala, Sumudu W. 2019. Economic uncertainty, trading activity, and commodity futures volatility. Journal of Futures Markets 39: 921–45. [Google Scholar] [CrossRef]
- Wiggins, Steve, Sharada Keats, and Julia Compton. 2010. What Caused the Food Price Spike of 2007/08? Lessons for World Cereals Markets. Food Prices Project Report. London: Overseas Development Institute. Available online: www.odi.org.uk (accessed on 20 December 2020).
- Yang, Lu. 2019. Connectedness of economic policy uncertainty and oil price shocks in a time domain perspective. Energy Economics 80: 219–33. [Google Scholar] [CrossRef]
- Ye, Michael, John Zyren, and Joanne Shore. 2006. Forecasting short-run crude oil price using high- and low inventory variables. Energy Policy 34: 2736–43. [Google Scholar] [CrossRef]
- Yin, Libo, and Liyan Han. 2014. Macroeconomic uncertainty: Does it matter for commodity prices? Applied Economics Letters 21: 711–16. [Google Scholar] [CrossRef]
- Zhu, Huiming, Huang Rui, Wang Ningli, and Liya Hau. 2020. Does economic policy uncertainty matter for commodity market in China? Evidence from quantile regression. Applied Economics 52: 2292–308. [Google Scholar] [CrossRef]
- Zivot, Eric, and Donald W. K. Andrews. 1992. Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. Journal of Business & Economic Statistics 10: 251–70. [Google Scholar]

| ENRG | BVG | FOILS | GRN | OFD | RWM | MTL | PRC | ||
| Mean | 0.005 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.003 | 0.005 | |
| Variance | 0.006 | 0.002 | 0.002 | 0.002 | 0.002 | 0.001 | 0.002 | 0.002 | |
| Skewness | 3.177 *** | 0.920 *** | 0.236 *** | 0.610 *** | 0.384 *** | 0.464 *** | −0.669 *** | 1.283 *** | |
| Kurtosis | 50.725 *** | 4.839 *** | 5.701 *** | 4.228 *** | 3.481 *** | 3.604 *** | 4.998 *** | 14.115 *** | |
| JB | 79,925.904 *** | 819.528 *** | 1000.643 *** | 592.273 *** | 388.639 *** | 423.559 *** | 818.878 *** | 6294.725 *** | |
| ERS | −7.629 *** | −5.793 *** | −4.038 *** | −5.733 *** | −7.755 *** | −7.175 *** | −7.379 *** | −5.711 *** | |
| Q(20) | 44.339 *** | 87.345 *** | 121.306 *** | 131.686 *** | 40.137 *** | 162.328 *** | 96.979 *** | 85.884 *** | |
| Q2(20) | 0.051 | 36.616 *** | 166.420 *** | 109.891 *** | 60.371 *** | 47.470 *** | 37.348 *** | 13.221 | |
| LM(20) | 8.258 | 44.900 *** | 90.204 *** | 24.629 *** | 64.579 *** | 38.758 *** | 23.000 *** | 89.312 *** | |
| Z-A Unit Root Test | |||||||||
| ENRG | BVG | FOILS | GRN | OFD | RWM | MTL | PRC | MU | |
| T-Statistics | −21.339 *** | −15.158 *** | −17.242 *** | −18.469 *** | −22.402 *** | −18.132 *** | −19.547 *** | −19.574 *** | −5.8119 *** |
| Break date | 11/1979 | 3/1977 | 10/1974 | 2/1974 | 11/1974 | 2/2011 | 6/1988 | 1/1980 | 1/1983 |
| Unconditional Correlations | |||||||||
| ENRG | BVG | FOILS | GRN | OFD | RWM | MTL | PRC | ||
| ENRG | 1 | 0.168 | 0.155 | 0.069 | 0.144 | 0.226 | 0.255 | 0.192 | |
| BVG | 0.168 | 1 | 0.217 | 0.111 | 0.129 | 0.158 | 0.201 | 0.158 | |
| FOILS | 0.155 | 0.217 | 1 | 0.459 | 0.192 | 0.218 | 0.239 | 0.228 | |
| GRN | 0.069 | 0.111 | 0.459 | 1 | 0.194 | 0.192 | 0.171 | 0.109 | |
| OOFD | 0.144 | 0.129 | 0.192 | 0.194 | 1 | 0.085 | 0.188 | 0.207 | |
| RWM | 0.226 | 0.158 | 0.218 | 0.192 | 0.085 | 1 | 0.253 | 0.223 | |
| MTL | 0.255 | 0.201 | 0.239 | 0.171 | 0.188 | 0.253 | 1 | 0.294 | |
| PRC | 0.192 | 0.158 | 0.228 | 0.109 | 0.207 | 0.223 | 0.294 | 1 | |
| MU | ENRG | PRC | FOILS | MTL | BVG | GRN | OFD | RWM | |
| Mean | 0.646 | 1.049 | 1.201 | 1.529 | 1.267 | 1.388 | 1.298 | 1.420 | 1.802 |
| Variance | 0.009 | 0.014 | 0.125 | 0.143 | 0.065 | 0.083 | 0.065 | 0.114 | 0.254 |
| Skewness | 1.82 *** | 3.13 *** | 1.81 *** | 2.19 *** | 1.47 *** | 1.41 *** | 1.51 *** | 4.25 *** | 2.59 *** |
| Kurtosis | 3.87 *** | 25.07 *** | 6.97 *** | 5.54 *** | 3.73 *** | 3.51 *** | 3.63 *** | 24.36 *** | 7.95 *** |
| JB | 839.52 *** | 19,898.55 *** | 1838.95 *** | 1487.25 *** | 671.11 *** | 600.06 *** | 666.28 *** | 19,763.66 *** | 2682.87 *** |
| ERS | −3.64 *** | −2.22 ** | −1.83 * | −2.99 *** | −2.00 *** | −2.00 *** | −2.81 *** | −4.66 *** | −3.68 *** |
| Q(20) | 4353.09 *** | 2593.04 *** | 4196.53 *** | 4986.86 *** | 4646.22 *** | 4083.47 ** | 5412.72 *** | 3732.51 *** | 4644.32 *** |
| Q2(20) | 3344.93 *** | 1867.25 *** | 4192.82 *** | 3678.16 *** | 3882.19 *** | 2787.20 *** | 3458.23 *** | 1322.36 *** | 2474.62 *** |
| Unconditional Correlations | |||||||||
| MU | ENRG | PRC | FOILS | MTL | BVG | GRN | OFD | RWM | |
| MU | 1 | 0.337 | 0.681 | 0.404 | 0.381 | 0.15 | 0.399 | 0.289 | 0.318 |
| ENRG | 0.337 | 1 | 0.293 | 0.25 | 0.401 | 0.236 | 0.51 | −0.053 | 0.377 |
| PRC | 0.681 | 0.293 | 1 | 0.352 | 0.327 | 0.178 | 0.392 | 0.198 | 0.28 |
| FOILS | 0.404 | 0.25 | 0.352 | 1 | 0.363 | 0.34 | 0.677 | 0.443 | 0.36 |
| MTL | 0.381 | 0.401 | 0.327 | 0.363 | 1 | 0.129 | 0.633 | −0.039 | 0.583 |
| BVG | 0.15 | 0.236 | 0.178 | 0.34 | 0.129 | 1 | 0.312 | 0.187 | 0.064 |
| GRN | 0.399 | 0.51 | 0.392 | 0.677 | 0.633 | 0.312 | 1 | 0.104 | 0.682 |
| OFD | 0.289 | −0.053 | 0.198 | 0.443 | −0.039 | 0.187 | 0.104 | 1 | −0.029 |
| RWM | 0.318 | 0.377 | 0.28 | 0.36 | 0.583 | 0.064 | 0.682 | −0.029 | 1 |
| MU | ENRG | PRC | FOILS | MTL | BVG | GRN | OFD | RWM | FROM | |
| MU | 48.068 | 7.706 | 9.549 | 6.088 | 7.329 | 4.884 | 5.933 | 4.369 | 6.073 | 51.932 |
| ENRG | 5.26 | 51.614 | 7.215 | 6.279 | 4.901 | 6.011 | 7.235 | 4.284 | 7.2 | 48.386 |
| PRC | 9.564 | 7.335 | 45.71 | 7.963 | 6.136 | 4.478 | 6.45 | 4.606 | 7.757 | 54.29 |
| FOILS | 6.565 | 8.942 | 8.721 | 42.518 | 5.117 | 5.211 | 10.988 | 5.451 | 6.487 | 57.482 |
| MTL | 7.34 | 10.752 | 5.451 | 7.334 | 34.613 | 5.318 | 14.834 | 6.208 | 8.15 | 65.387 |
| BVG | 6.304 | 15.614 | 6.569 | 8.349 | 6.928 | 35.223 | 7.275 | 5.13 | 8.608 | 64.777 |
| GRN | 6.549 | 11.395 | 7.57 | 19.183 | 5.701 | 9.318 | 26.496 | 5.458 | 8.331 | 73.504 |
| OFD | 6.579 | 7.492 | 7.812 | 14.924 | 5.87 | 10.172 | 7.723 | 31.571 | 7.856 | 68.429 |
| RWM | 5.156 | 13.317 | 6.385 | 13.721 | 6.261 | 7.445 | 11.656 | 4.999 | 31.06 | 68.94 |
| Contribution TO others | 53.318 | 82.553 | 59.271 | 83.841 | 48.244 | 52.839 | 72.095 | 40.504 | 60.462 | 553.127 |
| Contribution including own | 101.387 | 134.167 | 104.982 | 126.359 | 82.857 | 88.062 | 98.59 | 72.075 | 91.521 | |
| Net spillovers | 1.387 | 34.167 | 4.982 | 26.359 | −17.143 | −11.938 | −1.41 | −27.925 | −8.479 | TCI = 61.46% |
| Net Pairwises | ||||||||||
| MU | 0 | −2.446 | 0.015 | 0.477 | 0.011 | 1.42 | 0.616 | 2.21 | −0.917 | 1.386 |
| ENRG | 2.446 | 0 | 0.12 | 2.663 | 5.851 | 9.603 | 4.16 | 3.208 | 6.117 | 34.168 |
| PRC | −0.015 | −0.12 | 0 | 0.758 | −0.685 | 2.091 | 1.12 | 3.206 | −1.372 | 4.983 |
| FOILS | −0.477 | −2.663 | −0.758 | 0 | 2.217 | 3.138 | 8.195 | 9.473 | 7.234 | 26.359 |
| MTL | −0.011 | −5.851 | 0.685 | −2.217 | 0 | 1.61 | −9.133 | −0.338 | −1.889 | −17.144 |
| BVG | −1.42 | −9.603 | −2.091 | −3.138 | −1.61 | 0 | 2.043 | 5.042 | −1.163 | −11.940 |
| GRN | −0.616 | −4.16 | −1.12 | −8.195 | 9.133 | −2.043 | 0 | 2.265 | 3.325 | −1.411 |
| OFD | −2.21 | −3.208 | −3.206 | −9.473 | 0.338 | −5.042 | −2.265 | 0 | −2.857 | −27.923 |
| RWM | 0.917 | −6.117 | 1.372 | −7.234 | 1.889 | 1.163 | −3.325 | 2.857 | 0 | −8.478 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Haddad, H.; Mezghani, I.; Gouider, A. The Dynamic Spillover Effects of Macroeconomic and Financial Uncertainty on Commodity Markets Uncertainties. Economies 2021, 9, 91. https://doi.org/10.3390/economies9020091
Ben Haddad H, Mezghani I, Gouider A. The Dynamic Spillover Effects of Macroeconomic and Financial Uncertainty on Commodity Markets Uncertainties. Economies. 2021; 9(2):91. https://doi.org/10.3390/economies9020091
Chicago/Turabian StyleBen Haddad, Hedi, Imed Mezghani, and Abdessalem Gouider. 2021. "The Dynamic Spillover Effects of Macroeconomic and Financial Uncertainty on Commodity Markets Uncertainties" Economies 9, no. 2: 91. https://doi.org/10.3390/economies9020091
APA StyleBen Haddad, H., Mezghani, I., & Gouider, A. (2021). The Dynamic Spillover Effects of Macroeconomic and Financial Uncertainty on Commodity Markets Uncertainties. Economies, 9(2), 91. https://doi.org/10.3390/economies9020091






