Formulating the Concept of an Investment Strategy Adaptable to Changes in the Market Situation
Abstract
1. Introduction
2. Literature Review
3. Methodology
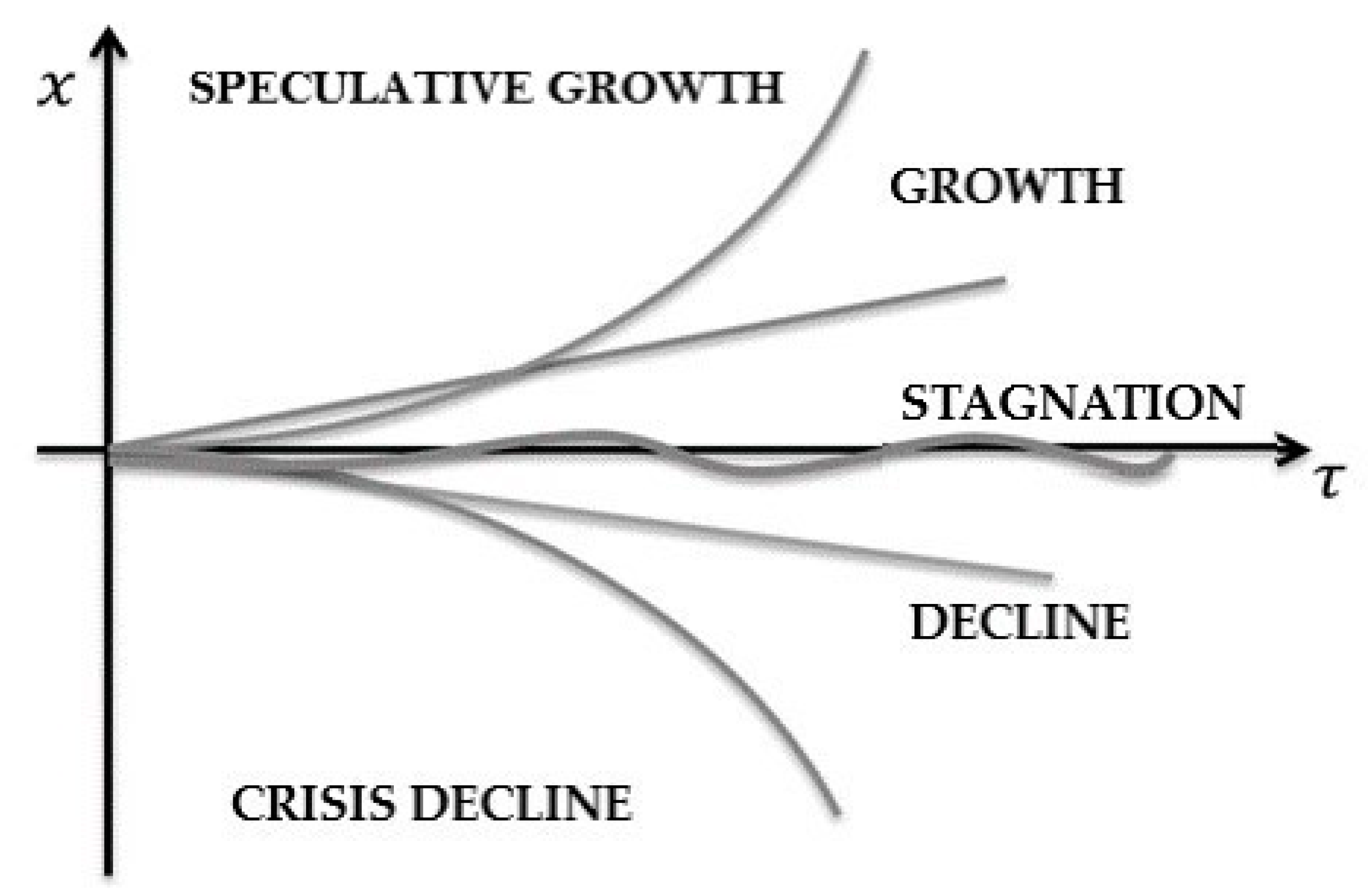
- Stagnation—a stable state;
- Growth—a situation where demand exceeds supply;
- Decline—a situation where supply exceeds demand.
3.1. The Concept of an Innovative Investment Strategy Adaptable to Changes in the Market Situation
- Combined market—part of the market information is distributed instantly, is publicly available, and directly reflected in the price of the asset; the other part is reflected with a delay or indirectly (Gataullin et al. 2020; Gorodetskaya et al. 2021; Yerznkyan et al. 2019).
- Combined return—changes in the price of an asset can be considered as an aggregated stochastic process; the speculative preferences of investors (Sunchalin et al. 2019; Ivanyuk and Tsvirkun 2013).
- Segmented market—any non-empty set of assets can simultaneously be considered as a market, a portfolio, or an asset itself if the set contains a single element.
- Limited market—in market development, time constraints are determined by the forecast horizon.
- Forecasted market—in market development, most trends are predictable.
- Rational investor—the investor’s interest is to achieve the maximum possible increase in the portfolio value during the forecast period with the minimum predicted risk.
- Finite investment period—the duration of the investment period is determined by the forecast horizon.
- balance between disregarding instantaneous market changes and taking into account fundamental market factors;
- adaptability of the strategy;
- predictively justified approach to the optimal portfolio creation.
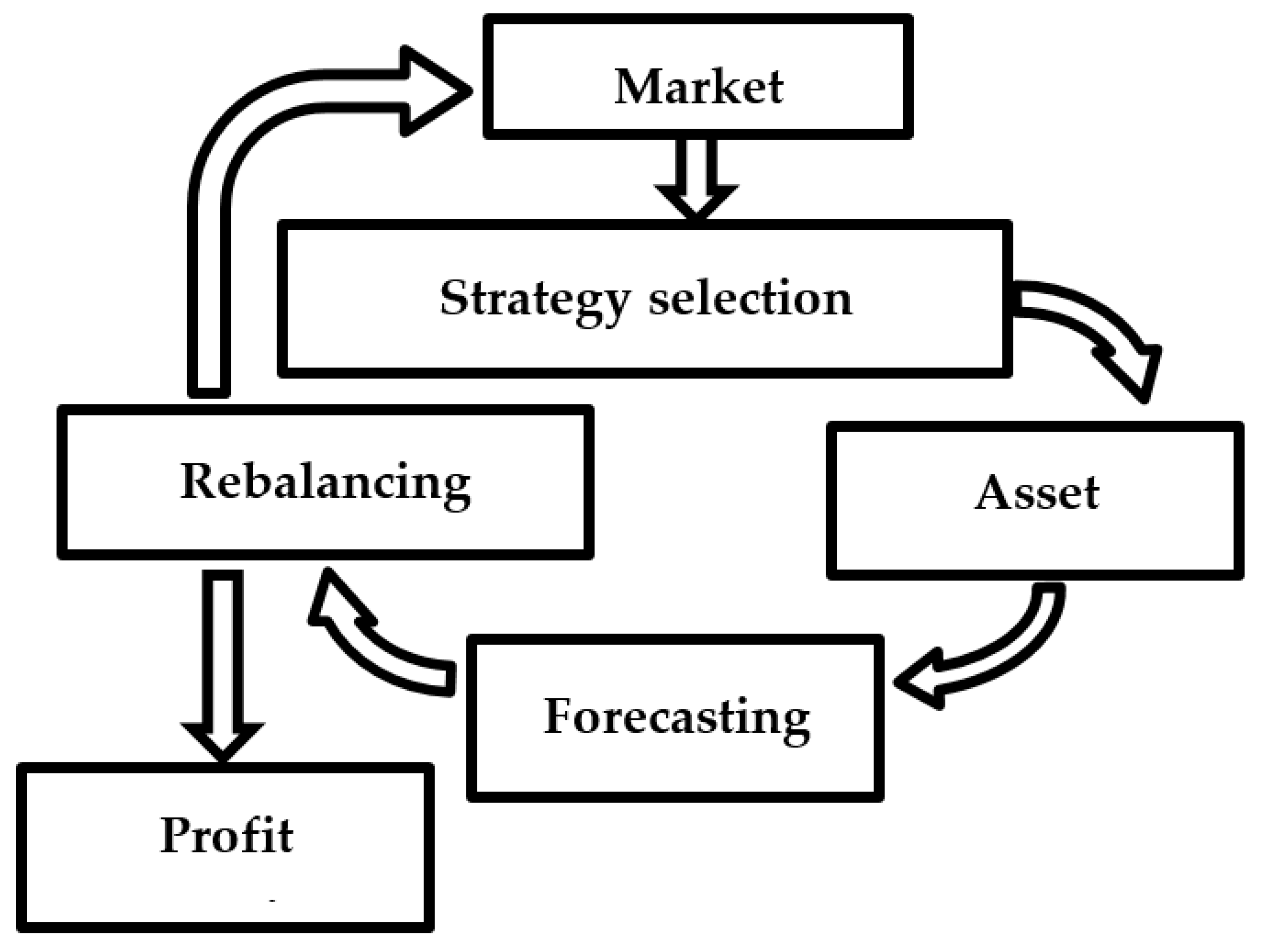
- Data acquisition;
- Market analysis;
- Portfolio strategy adjustment;
- Asset selection;
- Forecasting;
- Portfolio rebalancing.
3.2. Algorithm for Developing an Innovative Investment Strategy That Is Adaptable to Changes in the Market Situation and Has the Properties of an Open System
4. Methodology for the Development of an Adaptive Investment Strategy
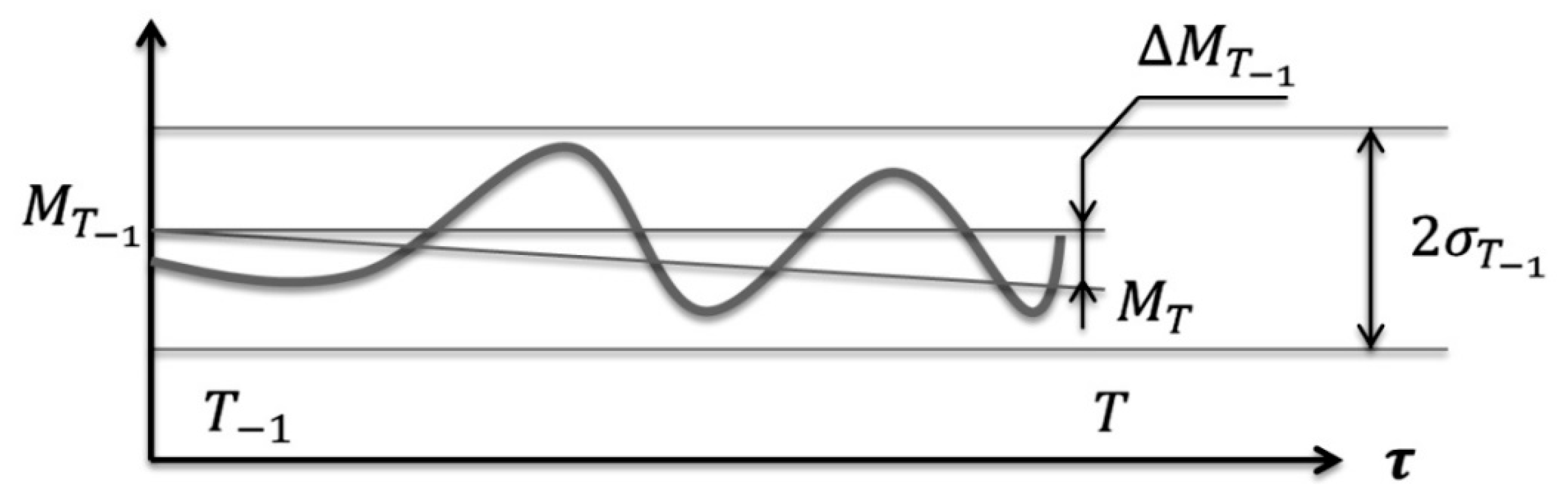
4.1. Model of Dynamic Stagnation of the Asset Value
4.2. The Model of Growth and Decline of the Asset Value
4.3. Asset Crisis Model
4.4. Asset Investment Strategy Model
- Profit-taking threshold;
- Aggregate portfolio risk;
- Type of portfolio diversification;
- Degree of portfolio diversification;
- Degree of portfolio dynamicity (rebalancing frequency).
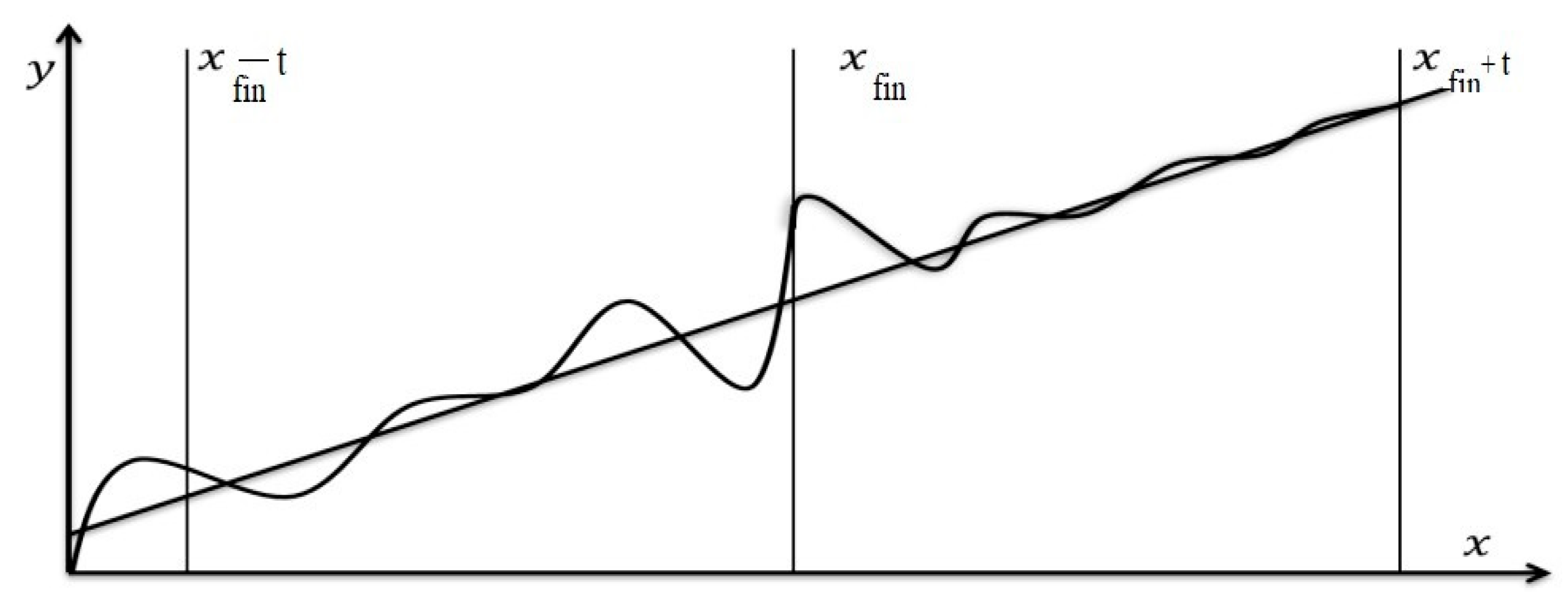
4.5. The Aggregate Forecast Model for an Asset in the Market
- Growth or decline tendencies (linear component);
- Tendencies to growth boundedness (logarithmic component);
- Seasonality and periodicity tendencies (harmonic component);
- Tendencies to the influence of prior conditions (autoregression);
- Tendencies to the influence of external factors (complex regression).
4.6. The Aggregate Risk Model for an Asset in the Market
5. Results
6. Conclusions
Supplementary Materials
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdollahi, Hooman. 2020. A novel hybrid model for forecasting crude oil price based on time series decomposition. Applied Energy 267: 115035. [Google Scholar] [CrossRef]
- Benita, Francisco, Francisco López-Ramos, and Stefano Nasini. 2019. A bi-level programming approach for global investment strategies with financial intermediation. European Journal of Operational Research 274: 375–90. [Google Scholar] [CrossRef]
- Bi, Junna, and Cai Jun. 2019. Optimal investment–reinsurance strategies with state dependent risk aversion and VaR constraints in correlated markets. Insurance: Mathematics and Economics 85: 1–14. [Google Scholar] [CrossRef]
- Borovička, Adam. 2020. New complex fuzzy multiple objective programming procedure for a portfolio making under uncertainty. Applied Soft Computing 96: 106607. [Google Scholar] [CrossRef]
- Cesarone, Francesco, Fabiomassimo Mango, Carlo Domenico Mottura, Jacopo Maria Ricci, and Fabio Tardella. 2020. On the stability of portfolio selection models. Journal of Imperial Finance 59: 210–34. [Google Scholar]
- Chang, Jinhua, Lin Sun, Bo Zhang, and Jin Pengb. 2020. Multi-period portfolio selection with mental accounts and realistic constraints based on uncertainty theory. Journal of Computational and Applied Mathematics 377: 112892. [Google Scholar] [CrossRef]
- Chen, Shun, and Lei Ge. 2021. A learning-based strategy for portfolio selection. International Review of Economics & Finance 71: 936–42. [Google Scholar]
- Chu, Gang, Wei Zhang, Guofeng Sun, and Xiaotao Zhang. 2019. A new online portfolio selection algorithm based on Kalman Filter and anti-correlation. Physica A: Statistical Mechanics and its Applications 536: 120949. [Google Scholar] [CrossRef]
- Dai Pra, Paolo, and Marco Tolotti. 2009. Heterogeneous credit portfolios and the dynamics of the aggregate losses. Stochastic Processes and their Applications 119: 2913–44. [Google Scholar] [CrossRef][Green Version]
- De Leeuw, Tim, Victor Gilsing, and Geert Duysters. 2019. Greater adaptivity or greater control? Adaptation of IOR portfolios in response to technological change. Research Policy 48: 1586–600. [Google Scholar]
- Eom, Cheoljun, and Jong Won Park. 2019. A new method for better portfolio investment: A case of the Korean stock market. Pacific-Basin Finance Journal 49: 213–31. [Google Scholar] [CrossRef]
- Gataullin, Timur M., Sergey T. Gataullin, and Ksenia V. Ivanova. 2020. Modeling an Electronic Auction. In Institute of Scientific Communications Conference. Cham: Springer, pp. 1108–17. [Google Scholar]
- Golosnoy, Vasyl, Bastian Gribisch, and Miriam Isabel Seiferta. 2019. Exponential smoothing of realized portfolio weights. Journal of Empirical Finance 53: 222–37. [Google Scholar] [CrossRef]
- Gong, Xiaomin, Changrui Yu, Liangyu Min, and Zhipeng Ge. 2021. Regret theory-based fuzzy multi-objective portfolio selection model involving DEA cross-efficiency and higher moments. Applied Soft Computing 100: 106958. [Google Scholar] [CrossRef]
- Gorodetskaya, Olga Y., Gulnara I. Alekseeva, Kira A. Artamonova, Natalia A. Sadovnikova, Svetlana G. Babich, Elvira N. Iamalova, and Anatoliy M. Tarasov. 2021. Investment Attractiveness of the Russian Energy Sector MNCs: Assessment and Challenges. International Journal of Energy Economics and Policy 11: 199. [Google Scholar] [CrossRef]
- Guan, Hao, and An Zhiyong. 2019. A local adaptive learning system for online portfolio selec-tion. Knowledge-Based Systems 186: 104958. [Google Scholar] [CrossRef]
- Hadhri, Sinda, and Zied Ftiti. 2019. Asset allocation and investment opportunities in emerging stock mar-kets: Evidence from return asymmetry-based analysis. Journal of International Money and Finance 93: 187–200. [Google Scholar] [CrossRef]
- Ivanyuk, Vera, and Anatoly Tsvirkun. 2013. Intelligent system for financial time series prediction and identification of periods of speculative growth on the financial market. IFAC Proceedings 46: 1128–33. [Google Scholar] [CrossRef]
- Jeon, Junkee, and Yong Hyun Shin. 2019. Finite horizon portfolio selection with a negative wealth constraint. Journal of Computational and Applied Mathematics 356: 329–38. [Google Scholar] [CrossRef]
- Khedmati, Majid, and Pejman Azin. 2020. An online portfolio selection algorithm using clustering approaches and considering transaction costs. Expert Systems with Applications 159: 113546. [Google Scholar] [CrossRef]
- Li, Bo, Yufei Sun, Grace Aw, and Kok Lay Teo. 2019. Uncertain portfolio optimization problem under a minimax risk measure. Applied Mathematical Modelling 76: 274–81. [Google Scholar] [CrossRef]
- Lu, Ya-Nan, Sai-Ping Li, Li-Xin Zhong, Xiong-Fei Jiang, and Fei Ren. 2018. A clustering-based portfolio strategy incorporating momentum effect and market trend prediction. Chaos, Solitons & Fractals 117: 1–15. [Google Scholar]
- Lu, Richard, Vu Tran Hoang, and Wing-Keung Wong. 2020. Do lump-sum investing strategies really outperform dollar-cost averaging strategies? Studies in Economics and Finance. [Google Scholar] [CrossRef]
- Ma, Guiyuan, Chi Chung Siu, and Song-Ping Zhu. 2019. Dynamic portfolio choice with return predictability and trans-action costs. European Journal of Operational Research 278: 976–88. [Google Scholar] [CrossRef]
- Ma, Yilin, Ruizhu Han, and Weizhong Wang. 2021. Portfolio optimization with return prediction using deep learning and machine learning. Expert Systems with Applications 165: 113973. [Google Scholar] [CrossRef]
- Mansour, Nabil, Mohamed Sadok Cherif, and Walid Abdelfattah. 2019. Multi-objective impre-cise programming for financial portfolio selection with fuzzy returns. Expert Systems with Applications 138: 112810. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Mishra, Sasmita, and Sudarsan Padhy. 2019. An efficient portfolio construction model using stock price predicted by support vector regression. The North American Journal of Economics and Finance 50. [Google Scholar] [CrossRef]
- Mo, Guoli, Chunzhi Tan, Weiguo Zhang, and Fang Liu. 2019. International portfolio of stock indices with spatiotemporal correlations: Can investors still benefit from portfolio, when and where? The North American Journal of Economics and Finance 47: 168–83. [Google Scholar] [CrossRef]
- Paiva, Felipe Dias, Rodrigo Tomás Nogueira Cardoso, Gustavo Peixoto Hanaoka, and Wendel Moreira Duarte. 2019. Decision-making for financial trading: A fusion approach of machine learning and portfolio selection. Expert Systems with Applications 115: 635–55. [Google Scholar] [CrossRef]
- Park, Hyungjun, Min Kyu Sim, and Dong Gu Choi. 2020. An intelligent financial portfolio trading strategy using deep Q-learning. Expert Systems with Applications 158: 113573. [Google Scholar] [CrossRef]
- Puerto, Justo, Moisés Rodríguez-Madrena, and Andrea Scozzari. 2020. Clustering and portfolio selection problems: A unified framework. Computers & Operations Research 117: 104891. [Google Scholar]
- Roll, Richard. 1977. A critique of the asset pricing theory’s tests Part I: On past and potential testability of the theory. Journal of Financial Economics 4: 129–76. [Google Scholar] [CrossRef]
- Sunchalin, Andrew M., Rasul A. Kochkarov, Kirill G. Levchenko, Azert. A. Kochkarov, and Vera A. Ivanyuk. 2019. Methods of risk management in portfolio theory. Revista Espacios 40: 25. [Google Scholar]
- Wang, Minggang, Longfeng Zhao, Ruijin Du, Chao Wang, Lin Chen, Lixin Tian, and H. Eugene Stanley. 2018. A novel hybrid method of forecasting crude oil prices using complex network science and artificial intelligence algorithms. Applied Energy 220: 480–95. [Google Scholar] [CrossRef]
- Wei, Jiuchang, Bing Bu, and Liang Liang. 2012. Estimating the diffusion models of crisis information in micro blog. Journal of Informetrics 6: 600–10. [Google Scholar] [CrossRef]
- Wu, Yu Xi, Qing Biao Wu, and Jia-Qi Zhu. 2019. Improved EEMD-based crude oil price forecasting using LSTM networks. Physica A: Statistical Mechanics and Its Applications 516: 114–24. [Google Scholar] [CrossRef]
- Yerznkyan, Bagrat, Svetlana Bychkova, Timur Gataullin, and Sergey Gataullin. 2019. The sufficiency principle as the ideas quintessence of the club of Rome. Montenegrin Journal of Economics 15: 21–29. [Google Scholar] [CrossRef]
- Yerznkyan, Begrat, Timur M. Gataullin, and Sergey T. Gataullin. 2021. Solow Models with Linear Labor Function for Industry and Enterprise. Montenegrin Journal of Economics 17: 111–20. [Google Scholar] [CrossRef]
- Yu, Xingying, Yang Shen, Xiang Li, and Kun Fan. 2020. Portfolio selection with parameter uncertainty under α maxmin mean–variance criterion. Operations Research Letters 48: 720–24. [Google Scholar] [CrossRef]
- Zhou, Wei, and Zeshui Xu. 2018. Portfolio selection and risk investment under the hesitant fuzzy environment. Knowledge-Based Systems 144: 21–31. [Google Scholar] [CrossRef]
- Zhu, Jiaming, Jinpei Liu, Peng Wu, Huayou Chen, and Ligang Zhou. 2019. A novel decomposition-ensemble approach to crude oil price forecasting with evolution clustering and combined model. International Journal of Machine Learning and Cybernetics 10: 3349–62. [Google Scholar] [CrossRef]
- Zhu, Shushang, Wei Zhu, Xi Pei, and Xueting Cui. 2020. Hedging crash risk in optimal portfolio selection. Journal of Banking & Finance 119: 105905. [Google Scholar]





| Market State | |
|---|---|
| Speculative growth | |
| Growth | |
| Dynamic stagnation | 0.5 |
| Decline | |
| Crisis decline |
| Market State | Profit-Taking | Portfolio Risk | Type of Diversification | Degree of Diversification | Portfolio Dynamicity |
|---|---|---|---|---|---|
| Speculative growth | Growing portfolio | Very high | Naive | Very low | Very low |
| Growth | Weakly bounded portfolio | High | Grouped | Low | Low |
| Stagnation | Bounded portfolio | Moderate | Jurisdictional | Moderate | Moderate |
| Decline | Highly bounded portfolio | Low | Covariant | High | High |
| Crisis decline | Fixed portfolio | Very low | Beta Neutral | Very high | Very high |
| Risk | Type of Diversification | |
|---|---|---|
| 0 | Minimum | Beta-neutral |
| 1 | Low | Covariant |
| 2 | Moderate | Jurisdictional |
| 3 | High | Industry-based |
| 4,5 | Maximum | Naive |
| Market State | Weight of the Market State | Profit-Taking | Portfolio Risk | Type of Diversification | Degree of Diversification | Portfolio Dynamicity |
|---|---|---|---|---|---|---|
| Speculative growth | 1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Growth | 0.75 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 |
| Stagnation | 0.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Decline | 0.25 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Crisis decline | 0 | 0 | 0 | 0 | 0 | 0 |
| Portfolio | Markowitz’s Portfolio |
|---|---|
| Strategy | Buy and Hold |
| Rebalancing | By bankruptcy |
| Diversification limit | 90.0% |
| Risk limit | 15% |
| Minimum asset share | 0.1% |
| Transaction costs | 0.2% |
| Optimization | By rate of return |
| Investment term | 10 years |
| Start of Investment | 2004 |
| Portfolio | PMPT |
|---|---|
| Strategy | Periodic Rebalancing |
| Rebalancing | On quarterly basis |
| Diversification limit | 90.0% |
| Risk limit | 20% |
| Minimum asset share | 0.1% |
| Transaction costs | 0.2% |
| Optimization | By the VaR criterion |
| Investment term | 10 years |
| Start of Investment | 2004 |
| Portfolio | Dynamic |
|---|---|
| Strategy | Dynamic |
| Rebalancing | By changes in W (market state) |
| Diversification limit | 90.0% |
| Risk limit | 20% |
| Minimum asset share | 0.1% |
| Transaction costs | 0.2% |
| Optimization | By W criterion (market state) |
| Investment term | 10 years |
| Start of Investment | 2004 |
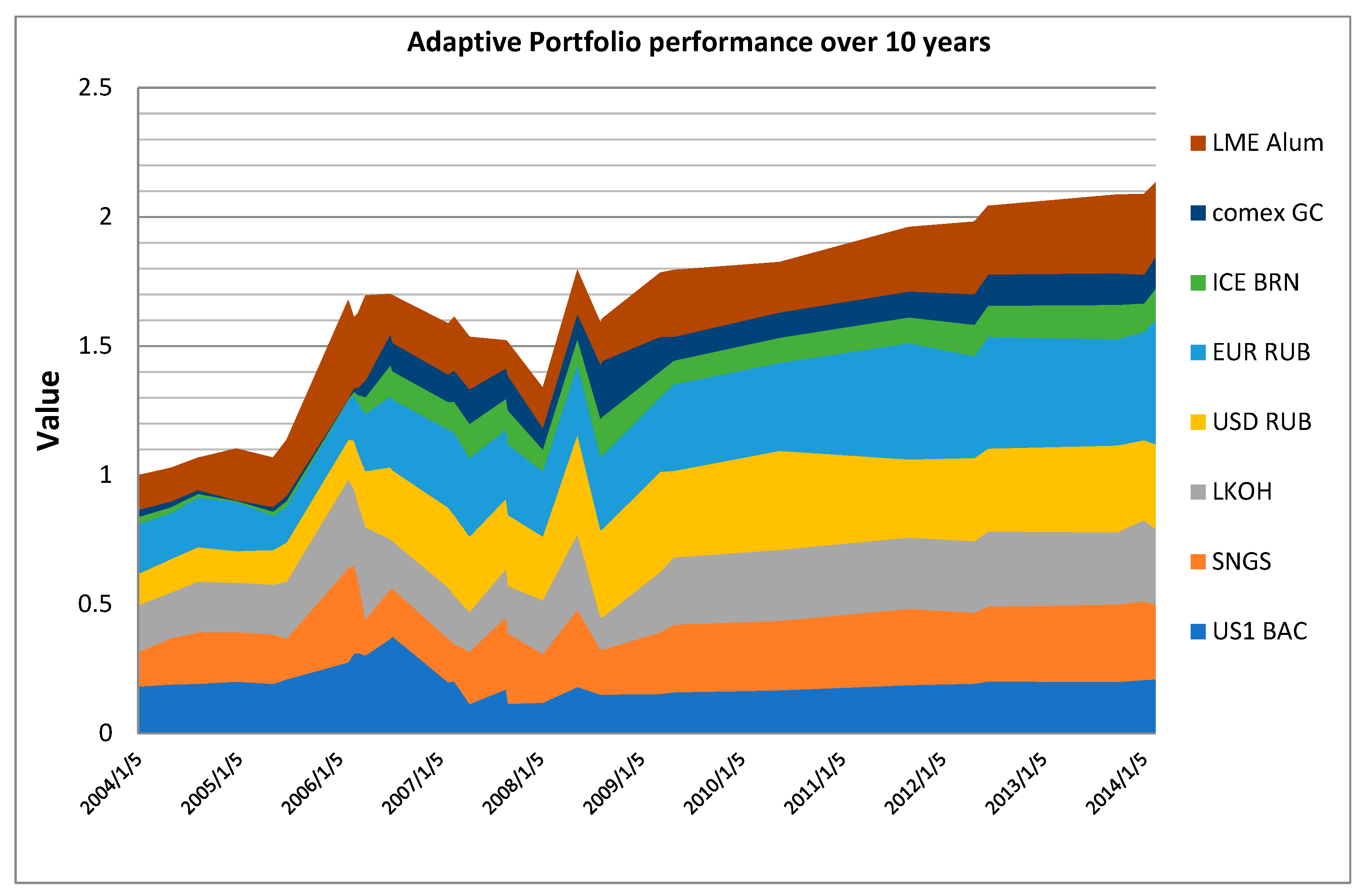
| Portfolio Type | Average Annual Return | Number of Rebalancing Events |
|---|---|---|
| H. Markowitz’s portfolio | 5.47% | 0 |
| R. Roll’s portfolio | 5.59% | 45 |
| Dynamic portfolio | 11.3% | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanyuk, V. Formulating the Concept of an Investment Strategy Adaptable to Changes in the Market Situation. Economies 2021, 9, 95. https://doi.org/10.3390/economies9030095
Ivanyuk V. Formulating the Concept of an Investment Strategy Adaptable to Changes in the Market Situation. Economies. 2021; 9(3):95. https://doi.org/10.3390/economies9030095
Chicago/Turabian StyleIvanyuk, Vera. 2021. "Formulating the Concept of an Investment Strategy Adaptable to Changes in the Market Situation" Economies 9, no. 3: 95. https://doi.org/10.3390/economies9030095
APA StyleIvanyuk, V. (2021). Formulating the Concept of an Investment Strategy Adaptable to Changes in the Market Situation. Economies, 9(3), 95. https://doi.org/10.3390/economies9030095






