Monitoring the Own Spatial Thinking in Second Grade of Primary Education in a Spanish School: Preliminary Study Analyzing Gender Differences

Abstract

Previous studies on metacognitive performance have explored children’s abilities during primary school (7–11 years) in abstract and mathematical reasoning tasks. However, there have been no studies evaluating the metamemory processes with spatial tasks in primary school children, and even more generally, only a few studies have explored spatial metacognition in adults. Taking as a preliminary study a Spanish school, the present work explores the validity of the confidence judgment model when thinking about one’s own performance in a spatial test, for boys and girls in Second Year of Primary Education (mean age of 7 years). A total of 18 boys and 15 girls applied a 4-point scale to evaluate, item by item, the confidence of their responses in the Spatial aptitude test “E” of the EFAI-1 (Factorial Assessment of Intellectual Abilities to mentally process visual stimuli). Accessibility and Accuracy Indexes were calculated for each item of the spatial task. The effect of gender was analyzed too. The tasks were administered in small groups; at the end examiners interviewed each participant, performing the confidence judgment task, item by item, of the EFAI-1 previously answered. The results (analyses carried out by SPSS) showed a high mean confidence (3 mean points out of a maximum of 4), without finding any significant differences either in the spatial performance or in the mean confidence rating between boys and girls. A significant relationship between confidence judgments and spatial task performance accuracy was found. The relationship between confidence judgments and spatial performance cannot be confirmed. The procedure adapted for testing spatial judgments about the own responses has been useful for showing the well calibrated perception about performance at this stage. The implications of the results of this exploratory study and the potential of the application of the procedure to promote thought about one’s own spatial performance and the development of strategies that modulate the effective approach of this type of spatial tasks are discussed within an educational approach.

1. Introduction

1.1. Metacognition, Spatial Reasoning and Education

Every day, we must make decisions that require an exercise of metacognitive activity, a reflection about our own mental processes that can be produced in a more or less conscious way. Metacognitive judgments have implications in the regulation of our behavior when interacting with our environment and with other people. When students decide whether they have studied enough for an exam, or whether they should study more, their decision is based on their confidence in making an accurate judgment about their knowledge. These processes applied to spatial reasoning (e.g., whether we will be able to reach a certain place without the help of a map, whether we know how to interpret a graph or we should look for more information, whether we understand data organized in a table) have been scarcely studied during childhood. The present study evaluates whether 7 year-old children are capable of analyzing the confidence they have in their answers in a spatial task, i.e., the Spatial aptitude test “E” of the EFAI-1 (Factorial Assessment of Intellectual Abilities, [1]). This test assesses an approach to the general visual processing factor, “Gv”, and represents the ability to mentally process visual stimuli (rotate, bend, develop, etc.).

If participants answer a question or solve a problem and reflect on how well or how badly they have answered it, they will be performing an exercise that in psychology is termed as metacognition. A typical example to assess the involvement of metacognition is to ask the degree of confidence (as using a 10-point Likert scale) of the correctness of one’s own answer. This assessment is known as a “confidence judgment” and it occurs regarding the answers issued, and whether they are correct or not. The present study focuses on the confidence of judgments about their own spatial task performance, asking how confident children were about their responses in the EFAI-1 test.

Along their learning path in the educational system, children are asked to learn many different topics, and not all are equally difficult. Students must divide their study times between different subjects, and for an efficient organization, it is necessary to dedicate more time to study some contents than others. To do this, as O′Leary and Sloutsky [2] noted, it is necessary to recognize that some topics are less familiar than others, and to appreciate that these topics will need more effort and study time in accordance with their perceived difficulty. This ability to evaluate one′s knowledge and performance is known as “metacognitive monitoring”; whereas the ability to adjust behaviors according to our objectives is known as “metacognitive control” and has to do with the formation of task-solving strategies [3].

In summary, metacognition studies offer a general framework to understand and optimize how we learn, remember, execute a task, and use monitoring and control actions to avoid strategies that are not useful [3]. Based on this framework, we considered the following issues in the present study: (a) whether these reflections are produced and are accurate at early ages, such as those in primary education, and (b) whether the results obtained in previous studies in the literature that have evaluated the implications of one’s own knowledge in the math and reasoning fields could be applied to the field of spatial cognition, as performance in a spatial task.

1.2. Metacognitive Processes in Primary School

Concerning metacognitive processes in primary school, there are studies that indicate that the supervision of one′s own knowledge improves with age. Children increase the monitoring of their errors with age [4,5]. Some studies have linked the increase in the conscious reflection of one′s own knowledge with a better allocation of the cognitive resources available to face the demands of a task [6]. Chevalier and Blaye [7] demonstrated that 6–10 year-olds children could effectively monitor their cognitive resources and prepare proactively for different types of stimuli that could appear in a task that changed in an unpredictable way (they had to pair stimuli according to either color or shape).

We did not find studies which had evaluated metamemory processes with spatial tasks in primary school children. There are studies with some mathematical and probabilistic reasoning tasks. Then, we reviewed the studies that we found on metamemory at ages similar to our research, although they are not spatial tasks, to learn how mnemonic processes develop at this stage of development, and what we might expect in our study.

Within the field of mathematics, one interesting topic to examine is the ability of children aged 7–10 years to perform metamemory processes of supervision and control in a number line estimation task [8]. Number line estimation is essential for school mathematics. Children who are sensitive to the difficulty of the content spend more time thinking about their estimates or adopt strategies that result in more accurate or precise performance. In addition, the awareness of the difficulty of an item can enhance asking for help and thus prevent incorrect estimates. These experiments showed that the behavior in the task was affected more by children’s confidence in the answers than by the precision of such answers. These results have educational implications, demonstrating that primary school children are sensitive to the difficulty of the more or less demanding items, and teachers can take advantage of it to recommend that they become aware of the difficulty and thus spend more or less time thinking about whether their answers to a problem are correct or not, or ask questions when in doubt. Looking for feedback when more support is needed can be learned from this awareness of the difficulty one has with a given content [8].

O′Leary and Sloutsky [2] conducted a series of experiments to compare the processes of supervision and control in children of 5–7 years of age and in adults, with a numerical discrimination task. They tested different hypotheses about how both processes acted, whether they were independent, whether supervision guided control or whether control guided supervision. Their conclusion was that both processes were relatively independent from early childhood and that they did not seem to be matched with development and experience.

De Neys and Feremans [9] conducted a study on the development of the ability to detect heuristic bias versus probabilistic reasoning by comparing third- and sixth-year children. The third-grade children already knew the principle of probability; nevertheless, when they were presented with problems that increased the heuristic bias, the supervisory processes to detect the inconsistency of the probabilities did not take place, hence the application of the heuristic bias was not detected. This supervision did occur more automatically in adults, and sixth-grade children were able to detect that they were applying a bias in their responses. That is, they detected it, but they were not able to inhibit it for the response that required the application of the probability calculation.

The authors acknowledged that this inhibition of bias is difficult even in adults [10,11,12,13]; thus, it is not surprising that it is also difficult for children of 11 years of age. The important conclusion for De Neys and Feremans [9] is that both third- and sixth-grade children failed in the application of probabilistic reasoning, instead relying on biases. However, while third-grade children were not even aware of them, the sixth-graders did know that they were being victimized by the bias. These results lead to the question of what the supervisory processes at an early age would be like in other types of tasks, specifically spatial cognition tasks, where studies that evaluate the importance of metacognitive reasoning are scarce.

A strong relationship between mathematics and spatial skills has been demonstrated in preschool, and several grades of primary education (e.g., Cheng and Mix [14]; Mix et al. [15], Gunderson et al. [16]). Some studies supported the effect that the practice of spatial tasks has on math performance. For example, Olkum, Altun, and Smith [17] found a positive effect on the learning of geometry in fourth and fifth-grade students, after practicing with Tangram puzzles, involving rotation and combination processes.

1.3. The Gender Issue in Spatial Tasks

The largest average sex differences in cognitive performance derive from spatial tasks, where males frequently obtain a better average performance than females [18]. Some studies have focused on the effect that spatial interventions have in relation to the gender gap observed in the enrollment on math and sciences courses. Sorby [19] showed that the optimal age for girls to participate in spatial training is around middle school, and that a high school intervention may be too late for girls who have poor self-efficacy beliefs about spatial task performance, math and science. This result oriented the selection of the course in our study, centered in the second grade of primary education, because this let us to assess the processes related to spatial monitoring during this critical stage. This objective complies with the recommendation made by Frick [20] who suggested that a better understanding of the early developments of spatial ability enables later success in mathematics, being instrumental for developing well directed interventions.

Through the analysis of literature on confidence judgments, few studies are available, also including the analysis of gender, given that it is a relevant factor to consider in spatial task performance (e.g., Uttal et al. [21]). Estes and Felker [10] investigated whether confidence in response-mediated execution in one of the tasks where the greatest gap between young men and women has been found; in particular, they used the Mental Rotation Test (MRT, [22]), in which participants are asked to identify two alternative options rotated—among four—from a target figure. A consistent male advantage has been found in this task [23,24,25]; women tend to respond less accurately and more slowly than the average male (i.e., [18,26]). Estes and Felker [10] analyzed whether the confidence in each of the alternatives of each item mediated the accuracy of the answers to the test. The participants had to make judgements of the confidence of their choice. The authors hypothesized that confidence would function as a mediator of the differences between and within gender, given that previous literature has shown that men are more confident than women in their execution of mental rotation tasks [27] and that confidence is a mediator in other cognitive tasks (i.e., [28]). In addition, in the experiment 4, Estes and Felker [10] manipulated the confidence of the participants as an independent variable. Participants scored higher on the MRT after being randomly informed that they were above average on a line judgment task than after being informed that they were below average on the line judgment task. The results showed that, in fact, confidence predicted the differences between genders, within each gender and for each individual (when confidence was manipulated as an independent variable and intrasubject differences were measured in situations that promoted greater or lesser confidence). In a recent study, Rahe, Ruthsatz, Jansen, and Quaiser-Pohl [29] deepened the analysis of the role of confidence (in terms of rating of the estimated performance, guessing behavior, and perceived difficulty—latter inverse sense) and the perception of time pressure in relation to the type of rotation tasks asked before and after practice. The rotation task can be a psychometric version (similar to that used by [18,28], psychometric measures of mental rotation use a target figure and four response alternatives; the label “psychometric” is applied to such a test with four response alternatives in contrast to “chronometric” tasks reflected in the approach proposed by Shepard and Metzler [30] in which a pair of stimuli is presented, and same-different judgments are made while the decision time is measured) and a chronometric version (i.e., to detect whether a couple of 3D figures were the same—even rotated—or different). The results confirmed (as [10]) that males had higher confidence than females in both rotation tasks and showed that females had a perception of time limits pressure especially after solving the psychometric version task. However, the degree of confidence has a different role in relation to type of rotation task and their order of execution: the degree of confidence and perception of time pressure is more related to the psychometric version rather than the chronometric version. When the psychometric version was performed after the chronometric version, the role of confidence in predicting the rotation performance was maintained as relevant, but the role of gender was not significant. These results showed that confidence in rotation skill increases with practice; making practice a chronometric version first, and later when the psychometric version is performed, the sex differences in performance disappeared and only the role of confidence remained relevant.

Overall these studies showed that the degree of confidence in approaching a spatial (rotation) task has an effect on its performance with difference in males and females [10,29] even the type of task and order can contribute to reducing the sex differences [29]. The self-confidence in spatial task can be considered an expression of beliefs related to one’s own ability to manage and increase mental rotation ability, which is associated with a high mental rotation performance [31,32].

1.4. Applying the Accesibility Model to Spatial Metacognition at Primary School

To date, no studies have examined the metacognitive ability in children that evaluate their own performance in spatial tasks. Therefore, the present study was developed to evaluate the monitoring processes with a confidence judgment task after performing a test that assessed spatial ability in children in the Second Year of Primary Education. Additionally, we explored gender differences in confidence judgments in a spatial task performance.

To do this, the approach carried out previously by Ruiz and Contreras [33] with a task of 300 questions of general knowledge will be replicated. These authors obtained accessibility and Accuracy Indexes, to analyze whether both properties were dissociable, following Koriat’s [34] argument in his accessibility hypothesis to explain the metamemory judgments. According to this hypothesis, individuals estimate their knowledge after answering a question based on the amount and intensity of information that elicits such a question. The more information and the faster it is recovered, the greater the feeling of knowing the correct answer. Koriat [34] suggested that the number of people who answer a question, either correctly or incorrectly, is considered the Accessibility Index (subsequently referred to as ACC) which provokes the question. It would be this accessibility and not the percentage of correct answers or accuracy (from now OBA, acronym of Output Bound Accuracy) that is most related to the confidence judgments. Ruiz and Contreras [33] applied 300 questions of Spanish general culture, and their results were adjusted to the predictions of Koriat′s accessibility model [34,35,36]. The standardized general knowledge questions showed the dissociation between the ability to generate some information (accessibility) and the ability to generate the correct information (accuracy of output). Moreover, on the other hand, Ruiz and Contreras’ [33] results indicated that the feeling of confidence was more related to accessibility rather than precision. Koriat’s model was replicated in which the judgments were more optimistic (the confidence judgment increased) as the amount of information that the question generated increased (ACC increases). To verify the Accessibility model, performance would be more related with Accessibility than with Accuracy.

The hypotheses of the present study are the following:

• It was hypothesized that boys and girls of the Second Year of Primary Education will be able to evaluate their own performance in a spatial ability test, as directly examined in other cognitive tasks for this age group (as mathematical performance, [9]).
• We will explore the metamemory processes in boys and girls in primary school, given previous evidence with adults showing that the degree of confidence affects spatial performance as a function of gender [10,21].
• It is expected to replicate the results of previous studies [33,34,35,36] in this early childhood sample and with the applied spatial task, hypothesizing a dissociation of accessibility and Accuracy Indexes. The confidence indexes of each item of the applied spatial test were obtained to analyze their relationship with the probability of receiving a correct answer (OBA) and with the probability that they receive any response (ACC). It is expected to replicate Ruiz and Contreras’ [33] results, and following Koriat’s [35] model, a greater relationship of the Confidence judgments with accessibility than with precision was hypothesized.

2. Materials and Methods

2.1. Participants

The study involved 33 students in the Second Year of Primary Education (M = 7.31 years and S.D = 0.62), from the Spanish public school Leopoldo Alas in Madrid. There were 18 boys and 15 girls.

The Research Ethics Committee of the National University of Distance Education (UNED) approved the study. All participants signed a written informed consent form, in accordance with the Helsinki declaration.

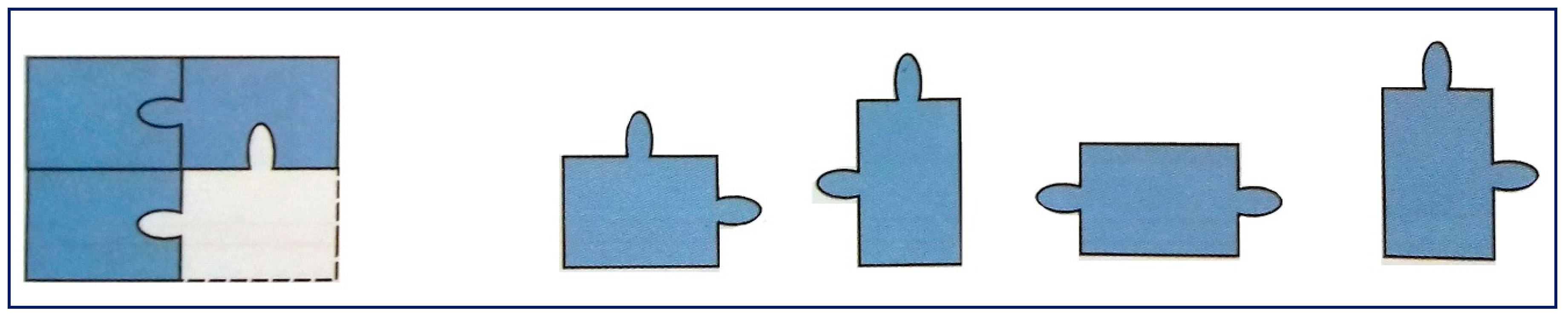
2.2. Materials

Spatial aptitude test “E” of the EFAI-1 (Factorial Assessment of Intellectual Abilities [1]).

This test reflects an approach to the visual processing factor, “Gv”, and represents the ability to mentally process visual stimuli (rotate, bend, develop, etc.). The authors found reliability coefficients of 0.86 for Level 1 of this task [1]. Level 1 of the test is appropriate for students aged between 7 and 10 years and consists of 30 evaluation exercises plus two practice examples, with four answers for each item. The task is to fit only one of the four pieces on the right into the white hole of the puzzle on the left, which is usually composed of one, two or more pieces (Figure 1). The duration of the test is six minutes. Each correct answer is assigned a point, so the maximum score of the test is 30 direct scoring points. The application of the test was carried out as described in the manual. The alpha consistency (Cronbach) obtained in the task was 0.95.

Raven’s Progressive Matrices (Standard Progressives Matrices: SPM [37]).

This task evaluates intelligence or the g factor based on non-verbal reasoning. The reliability of the test indicates a rate of two halves of up to 0.90, while the test–retest varies between 0.83 and 0.90 [37]. The version that has been used in the present study is the SPM, which can be applied from 6 years of age to adulthood. The applied scale consists of 60 problems divided into 5 series (ABCDE) with 12 elements each, the test can be applied with no time limit, although with an estimated duration of 40–90 min. For each correct answer, a point is assigned, so the maximum test score is 60 points. The application of the test was performed following the manual’s instructions.

Confidence Judgments Task (CJ: Adapted from [9]).

In order to obtain information on participants’ confidence in their performance, once the EFAI1-E task of the follow-up phase was completed, an adapted questionnaire of confidence judgments [9] was applied individually. The scale used by De Neys and Fereman [9] was adapted. These authors used a 4-point scale. In a similar way, in our study each participant was interviewed about how they thought that their responses to the answered items of the EFAI1-E task had fared. To do this, a confidence gradient of four points was created, where 1 would be the minimum confidence (not all sure) and 4 the maximum (very sure). To help participants understand the scale, they were given examples on how to apply the scale with some general knowledge questions serving as a calibration (e.g.,: “What is the name of the city where you live?”), once they had answered, they were asked about that particular answer: “Do you think your answer was right or wrong?” If the answer was right, they were asked “do you think it was a little right or very right?”. Then, participants were asked about other issues not so obvious for their age and their cultural context (e.g., “What is the capital of Italy?”, or “What colors does the flag of Portugal have?”), proceeding in the same way as with the first question. Once the participants understood the procedure, they were asked: (in an initial dichotomous format: “correct or wrong“) “how do you think you responded to item #...?” (the question was made for each EFAI-1 answer). Once the initial response was noted, participants were asked a second question (again in dichotomous format): “ok, so you answered this exercise right, but was it a little right or very right?”, if the answer was “very right”, the score would be a 4, if it was just “a little right”, the score would be a 3. Moreover, if the initial response had been “wrong”, they were asked: “but was it a little wrong or very wrong?”, with the score being a 2 in the case of answering “a little wrong” and 1 for “very wrong”. The EFAI1-E task consists of 30 items, but the time in this task was limited and participants stopped answering after six minutes. The mean responses in the total sample were 12.33 items (see Results Section), and the experimenters only asked the metamemory judgment for the items solved. The interview lasted approximately ten minutes per child, being shorter or longer depending the time that each boy and girl took for making the judgment item by item. After conducting the EFAI1-E, the five interviewers asked five children at the same time (one child per experimenter, separated appropriately to avoid overhearing). Every group of five children went out of the class for the interview during the following hour after solving the EFAI1-E.This procedure, with two phases, ensured that the children used the different categories of the scale as correctly as possible, to try and prevent a response tendency and verified that they calibrated as accurately as possible at this age at which it is not easy to apply metamemory concepts.

Afterwards, the confidence judgments obtained for each item of the spatial test were analyzed. Following Ruiz and Contreras [33], the two orthogonal indices proposed by Koriat and Goldsmith [38] were calculated:

-

Accessibility Index (ACC): which reflects the amount of information that comes to the participant’s mind once the question is raised. In order to calculate this index, the percentage of participants who have given a response is taken into account, regardless of its accuracy;

-

Precision Index (OBA): which reflects the probability that the information that comes to the participant′s mind is correct. It is calculated from the percentage of correct answers among the total answers given.

2.3. Procedure

The Ravens and EFAI1-E tests were administered in small groups, and there were five experimenters. The initial instructions were given while projecting the trial items on a digital board. The Raven test did not have a time limit, and the participants turned in the test when they had finished answering all the items. After all participants had finished the Raven test, they performed the EFAI1-E test under the limited time conditions recommended by the manual (after 6 min of application of the test, the participants must stop performing the task even if they have not finished the items), with the instruction to solve as many test items as possible. At the end of the task, the examiners went on to interview each participant individually, performing the confidence judgment task for all the items previously answered. The total application time for each participant for all tasks was around one hour (Raven) and 30 min (EFAI1-E plus the subsequent interview for confidence judgments).

3. Results

Statistical analyses were performed in SPSS, version 24.0 (IBM Corp. Released 2016) with a significance level of 0.05.

3.1. Individual and Gender Analyses

First, the relationships between the confidence judgment ratings in the spatial test and performance in both tests (EFAI1-E and Raven Progressive Matrix) were analyzed for the groups of girls and boys and the total sample.

The correlation between the EFAI1-E task and the confidence judgments task was significant: 0.42 (p < 0.05). The correlation between the EFAI1-E and the Raven test was also significant: 0.37 (p < 0.05).

Table 1. Descriptive statistics (mean and standard deviation, in parentheses), ANOVAs by gender and effect size for tasks and confidence judgments (CJs) in the spatial test.

	Total (n = 33)	Boys (n = 18)	Girls (n = 15)	F	p	Cohen’s d
EFAI-E	12.33 (5.02)	12.61 (6.25)	12 (3.16)	0.12	0.73	0.12
Raven	25.97 (9.42)	25.94 (10.16)	26 (8.79)	0.00	0.98	0.00
CJ	3.33 (0.58)	3.3 (0.69)	3.36 (0.57)	0.06	0.80	0.09

shows the descriptive statistics and the ANOVAs for the analysis of gender. No differences were found between the boys and girls in the intelligence or spatial tests, nor in the confidence judgments. The Raven test was applied as a control test to prove that the samples of boys and girls were equal in non-verbal reasoning, as it has been found that intelligence can be a mediating variable to reduce differences between genders in spatial attitude task performance [36]. In the present study, we repeated the prior analyses but adding Ravens scores as a covariate; these results were not affected by the addition of the covariate.

3.2. Items Analyses

Afterwards, the confidence judgments obtained for each item of the spatial test were analyzed.

In this procedure, the object of interest was not the differences between participants but between the items. That is, the participants’ answers were used to analyze the different indexes of accuracy and accessibility for each item.

Table 2. Descriptive statistics of the Precision Indexes and confidence judgments.

	Mean	S.D.	MEDIAN
ACC (%)	68.8	30.23	80.5
OBA (%)	57.5	21.91	55.5
CJ	3.47	0.27	3.47

shows the descriptive statistics of the items of the EFAI1-E test, observing a higher mean for the Accessibility Index than for the Precision Index.

In order to verify the existence of associations between the ACC and OBA indexes, and replicating Ruiz and Contreras′ [33] procedure, four groups were formed according to the medians of these indices, which are listed in

Table 3. Number of EFAI1-E items grouped according to their ACC and OBA indexes.

	HIGH OBA ≥55.5%	LOW OBA ≤55.5%
HIGH ACC ≥80.5%	MC = 3.53 (N = 9)	MC = 3.49 (N = 6)
LOW ACC ≤80.5%	MC = 3.58 (N = 6)	MC = 3.33 (N = 9)

Note: MC: mean confidence, N: number of items in the category.

. The group of items that obtained a greater degree of confidence included items with high accessibility and high precision. The group with the lowest degree of confidence was the one that collected the items with low accessibility and low precision. As predicted by Koriat and Goldsmith’s [38] model, and repeated by Ruiz and Contreras [33], a slight tendency was observed in which the confidence estimate seems to depend more on the ACC index than on the OBA index, since the group of high ACC/low OBA obtained a mean of 3.49 in the confidence judgments. However, when accessibility was low, the value of confidence dropped to 3.33, although this group had high precision. In any case, the mean confidence values (MC) were high (maximum 4) for all groups of items. There were no great differences in the values by groups of items.

Table 4. Spearman’s Rho correlations between the ACC, OBA and CJ indexes.

	OBA	CJ
ACC	0.22	0.06
OBA	-	0.42 *

* significant for p = 0.05 (bilateral).

shows the nonparametric correlations between the confidence estimation judgments (CJ) and the ACC and OBA indexes, where we can observe that the only significant correlation was between accuracy and confidence judgments. This result does not support the accessibility model for this age and this task, as confidence is more related to the precision with which the task is performed.

4. Discussion

The present study analyzed the confidence judgments issued by the boys and girls in Second Year of Primary Education, on their answers issued when solving a spatial ability test. Although metacognition judgments underlie many activities related to daily decision making related to the academic performance and study strategies applied by students (i.e., [2]), no previous literature related to the ability to make this type of judgments applied to the self-evaluation of spatial performance in primary school children has been found to date. The only evidence of the role of metacognition judgments (in term of confidence) in spatial tasks comes from young adults, with higher confidence in males compared to females [10,28]. We did not know, however, whether the confidence can affect the performance in primary school children too. Koriat’s model offers a useful approach to analyze the metacognition in approaching spatial tasks [36], based on the accessibility hypothesis, that allow us to distinguish the amount of information that comes to the participant’s mind once the question is raised (Accessibility Index) and the probability that the information that comes to the participant′s mind is correct (Accuracy Index). This model offers a frame of reference to analyze the contribution of metacognition as monitoring processes, in term of accessibility and accuracy, in approaching spatial task performance in primary school children.

Concerning the first goal, we examined the confidence judgment model with a spatial task among 7 year-old boys and girls. The scale used by De Neys and Feremans [9] used a 4-point scale, and following a similar procedure, in the present study, a 4-point scale was also applied, with participants having to decide in two phases: first, they would decide whether they had performed each spatial item or exercise correctly or not, and once they had decided that, they had to evaluate either how correct or how incorrect they thought they had performed every item.

The participants showed a good understanding of the metacognitive evaluation exercise that was being asked of them, although the results showed a high mean confidence judgment with very little variance for either the total sample or between genders. The mean confidence was 3.3 of a maximum confidence of 4. Therefore, in relation to the first hypothesis, children of this age seem to understand the task they are asked, are able to reflect on their ability to solve the items of the spatial tests, as has been observed in other studies with tasks of mathematical content [2,3,7].

However, it seems that, at the early age evaluated in the present study, there was a tendency towards overconfidence, granting maximum confidence values into most of the items answered. This effect was also observed by Kruger and Dunning [39], showing that people tend to hold overly favorable views of their abilities in many social and intellectual domains. Koriat, Lichtenstein, and Fischhoff [40] analyzed the psychological components underlying the effect of overconfidence in metamemory. They found that asking the participants to argue reasons in favor and against the response issued improved the calibration, that is, it reduced the effect of overconfidence. The present results, similar to Koriat et al.’s [40] findings, point to an interesting educational potential. Families and teachers should teach children from early childhood to reflect on their chosen and their correct answers, as well as on the rejected alternatives. Similarly, Estes, and Felker’s [10] procedure, applied to assess the confidence in the responses of MRT, analyzed whether the confidence mediated differences between genders, where they had to make confidence judgments not only of the chosen alternatives, but also of those discarded because they were not correct. They found that a confidence judgment was a mediator of this effect of gender and individual differences in the execution of the MRT task.

Concerning the second goal, we explored differences between boys and girls. However, no significant differences were found between the groups, either in spatial performance or in the confidence judgments of the answers. Boys and girls performed equally in the spatial task and in the confidence judgment task, with almost identical levels. This result converges with previous studies where no differences have been found between gender groups in spatial tasks at early ages [41,42,43] and where intelligence seems to have a mediating role in reducing these differences between genders that sometimes occur in spatial tasks [44]. We reviewed the literature related to the differences between sexes in spatial ability at ages close to the one analyzed in this study and found evidence in both directions (with and without significant differences between sexes), even using classic tasks of mental rotation (MR) where the effect of performance in favor of boys is usually more pronounced. Among the studies that find these differences, Geiser, Lehmann, Corth, and Eid [45] assessed 1624 participants aged between 9 and 23 years. For the age range of 9–12 years, the authors found that the scores of the boys were significantly better than those of the girls, using the MR task of Peters, Chisholm, and Laeng [46]. In addition, they observed that the size of the sex differences effect on MR seems to be variable with age, finding effect sizes greater at 9 years (d = 1.08), which decrease progressively up to 12 years (d = 0.61). Titze, Jansen, and Heil [47] found that children aged from 8 to 11 years had better performance than girls in a MR task (MRT of Peters et al. [46] adapted with animals). However, unlike the study by Geiser et al. [45], it seems that these sex differences are more evident towards 10 and 11 years old, and are practically insignificant towards 8 and 9 years old. In contrast, other studies have not found sex differences. In a study conducted by Brosnan [48] in 9 year-old boys and girls it was found that both sexes had a similar performance in the MR task. Chien [49] evaluated boys and girls from first to fifth grade (6–13 years of age) and did not find sex differences in a Vz/RM (SVAT/MR) task either before or after a spatial intervention with tasks for the acquisition of MR in a two-dimensional format. Similarly, Shavalier [50] using the MRT task of Vandenberg and Kuse [21] and another of Vz (Paper Folding Test), neither appreciated sex differences before or after the 2-D and 3-D designs in boys and girls from 4th to 6th grade (9–12 years old).

Therefore, after reviewing the literature, our study was added to those that did not find differences between boys and girls in a spatial task. In our study, we did not find any sex differences in the self-evaluation of the answers given to the task.

Concerning the third goal, we proposed the dissociation of the ACC and OBA indexes, following the model proposed by Koriat and Goldsmith [38] and replicated in Ruiz and Contreras [33]. However, the result of the correlation of both indexes with the confidence judgments confirmed that they do not seem to have the same relationship, which is coherent with certain independence. An almost null correlation was observed between the confidence judgments and the ACC index, whereas the correlation between the confidence judgments with precision was significant. This result does not corroborate the hypothesis and, therefore, is contrary to supporting the accessibility model in this task and at this age.

In the present study, confidence had a stronger relationship with the accuracy of the answers than with Accessibility Index. This may be explained because, unlike with general knowledge tasks such as that used by Ruiz and Contreras [33] where open questions were asked, the Accessibility Index makes sense because some questions can generate more memory contents than others. However, in the present study’s task, judgments had to be carried out on items with response alternatives; participants must not generate spatial contents from their memory. It does not seem so relevant in this task to have to access mnemonic content and evaluate the confidence in different amounts of accessible content. We analyzed, following previous models in the literature, four groups of items according with their high/low level of accessibility and accuracy, but the confidence values observed were high for all groups of items. The significant relationship between confidence judgments and accuracy has shown that the more success a participant had, the less likely they were to guess, and the more accurate their answers were regarding the effective performance they had carried out in the spatial task. Thus, it seems that there was a lower tendency towards overconfidence with better results and vice versa.

We believe that in a task like the one used in this study, where the participant must choose between several response alternatives, the accessibility model was not fulfilled because the amount of information that the participant must recover is not as important as in an open question task. In a task of open questions, the participant must develop a response and that amount of information to recover (Accessibility) seems more important than in a task like the EFAI1-E test with available alternatives.

5. Conclusions

The present study arose from the review of the literature and the finding of an absence of previous studies on metacognition judgments regarding the performance in spatial tasks during early childhood. Therefore, an exploratory study was carried out to analyze whether at ages in which other studies have evaluated metacognition in tasks of abstract or mathematical reasoning (7–8 years), children could address the task of reflection of their responses to each item of a previously completed spatial test. The results suggest that it is possible to make this reflection of spatial metacognition at this age and that the confidence judgments issued were significantly related to the accuracy of the answers. However, the mean confidence found was globally high, regardless of the gender of the participants, replicating the well known “Dunning–Kruger” overestimation effect [39]. As an exploratory analysis, it seems that the procedure may prove very useful in future research. The study has a very important limitation, which is the small number of participants evaluated, preventing us from being able to generalize the present results until their replication. In future studies, broader samples should be analyzed. In addition, as previous studies have been carried out with other reasoning tasks that have compared different age groups [2], future studies should analyze whether the effect of overconfidence is modulated in later developmental stages.

This preliminary study has explored the potential for reflection on spatial task performance from an early age, and the procedure adapted for testing spatial judgments about the own responses has been useful for showing a calibrated perception about performance. It seems that children at this stage know, with acceptable accuracy, if they are doing well or not in spatial problems. This result is interesting if teachers could use this knowledge about the children’s own performance in math problems where they should apply spatial thinking, such as in figure interpretation.

It is important to note that the sample in the present study is small and this may lead to effects and generalizability being limited. For future research, we need to apply new studies with a broader sample in primary schools that could replicate and consolidate our proposal. In the long run, our procedure promises interesting research possibilities. For example, in the future, it would be interesting to contrast the effect of making the confident judgment after all items (the procedure applied in the present study) or after each item (i.e., the procedure applied in [10]).

Regarding gender differences, we did not find significant differences in spatial metacognition at the primary stage, in line with recent studies. For example, Terlecki et al. [51] concluded that the gap between gender, favoring males, may be decreasing with the equalitarian use of new technologies, and recently, other studies have supported this finding [43]. There are studies that have demonstrated the potential of beliefs about one′s own intelligence, one′s ability for academic achievement and the power to modify academic results if you strive, which leads to an intrinsic motivation that results in the belief of the malleability of intelligence at the service of improving academic performance [52]. In this sense, the present study is hopeful about the potential that training would have in the ability to modulate one′s memory performance, teaching how to predict whether something is well known or not, whether or not an item has been correctly answered in a test, in this case, a spatial task, but that could be applied to mathematic performance too. We hope to advance research in this field in future studies, at the service of the impulse of spatial intelligence and its relationship with math performance, barely addressed in early childhood.