Smartphone Handwritten Circuits Solver Using Augmented Reality and Capsule Deep Networks for Engineering Education

Abstract

Resolving circuit diagrams is a regular part of learning for school and university students from engineering backgrounds. Simulating circuits is usually done manually by creating circuit diagrams on circuit tools, which is a time-consuming and tedious process. We propose an innovative method of simulating circuits from hand-drawn diagrams using smartphones through an image recognition system. This method allows students to use their smartphones to capture images instead of creating circuit diagrams before simulation. Our contribution lies in building a circuit recognition system using a deep learning capsule networks algorithm. The developed system receives an image captured by a smartphone that undergoes preprocessing, region proposal, classification, and node detection to get a Netlist and exports it to a circuit simulator program for simulation. We aim to improve engineering education using smartphones by (1) achieving higher accuracy using less training data with capsule networks and (2) developing a comprehensive system that captures hand-drawn circuit diagrams and produces circuit simulation results. We use 400 samples per class and report an accuracy of 96% for stratified 5-fold cross-validation. Through testing, we identify the optimum distance for taking circuit images to be 10 to 20 cm. Our proposed model can identify components of different scales and rotations.

1. Introduction

Circuit simulations are a standard part of engineering education as well as professional environments. Simulations are required to find the results of the circuit sketch, either drawn or printed. Different desktop software are available such as Multisim, Simulink, PSPICE, CircuitLAB, etc., often with mobile-suited versions. However, the convenience of a tool using smartphones that can capture circuit images and instantly simulate the circuit is immense for education and professional fields, as shown in Figure 1.

Educators continue to devise novel strategies to enhance students’ engagement and motivation for learning especially in STEM disciplines [1,2]. One way is using smartphones. The development of smartphones has altered how individuals interact, work, and study, particularly in higher education settings [3]. Smartphones were deemed key technologies to boost and foster innovation within teaching by 49% of Consortium for School Networking advisers [4]. Smartphones are becoming more popular in teaching due to their flexibility. Using cellphones to help students learn in higher education, although novel [5,6], is a method to boost students’ motivation [7]. When the use of smartphones is accompanied by artificial intelligence and machine learning, better higher education strategies ensue. These breakthroughs have a big impact on teaching and learning [8].

The use of smartphones can be productive or distracting depending on the learner’s perception [9,10]. Regardless of all the challenges it could pose to educators [10], we emphasize the importance of smartphones in our proposed system as educational technology in learning environments [7,10,11]. According to instructors, using digital resources in their teaching methods was substantial and strengthened the education system [12]. Not only can mobile learning improve students’ learning, but it can also assist in the training of educators [7].

Mobile applications are being developed to assist in education and students’ learning processes such as in [13]. Thus, we propose developing a mobile app that recognizes the hand-drawn circuits and simulates them in real-time. The students would draw a circuit and instantly see the simulation results to understand circuits better. One of the limitations with existing tools is that they consume time and effort as most of the tools have to be installed on workstations. Students would need to go to the lab and simulate the circuit or access a laptop with excellent simulating software that is mostly paid. As such, there is a need to address such limitations, which is possible through the use of smartphones. The portable nature of smartphones and their ease of use allows for the perfect platform for learning. We consider that in our proposed mobile application system. Developing such an app would require machine learning techniques to recognize and detect the circuit elements. Other computer vision techniques are needed to identify the nodes and connections and create a computer-readable description that can then be fed into a circuit simulation tool to produce the output, as shown in Figure 1.

Several studies have been conducted on circuit recognition due to its essential applications. Printed electric circuit images often have fewer variations than hand-drawn circuit images and can achieve better results than printed images. Hand-drawn symbol recognition has always been an exciting field of study as they are more susceptible to variances. Various computer vision techniques in machine learning have been used in hand-drawn circuit recognition in the past two decades [14,15,16,17]. Each reported study has used different machine learning and computer vision techniques to accurately identify the connections and nodes to create a Netlist, a computer-readable format for electric circuits.

Machine learning has been evolving in the past few years, especially with the improvements made in deep learning techniques. One of the essential machine learning applications is in computer vision using neural networks, especially Convolutional Neural Networks (CNNs). Some standard machine learning techniques include CNNs for classification and Recursive (R)-CNNs used for object detection applications. Object detection refers to the classification and localization of several object classes in an image. Currently used machine learning techniques often require many training data sets to achieve high classification accuracy. However, with different forms of electric circuit images available with every possible rotation, tilt, and variation to circuit elements, the training set should include all possibilities and thus increases the overall training data set size.

In this study, we propose using a novel technique in deep learning called capsules networks [18] to design an efficient mobile application for the rapid analysis of a drawn electric circuit. The authors of [18] proposed a slightly varied technique invariant to the object viewing angle, which mimics how humans actually recognize objects. The capsule network tries to preserve the spatial information between the object parts, identifying an item with its features within an object compared to an object with its parts scattered around yet still in the image. For example, a face with eyes, nose, and mouth in its place, and a face image with locations switched for eye, nose, and mouth will yield a high probability of detecting a face in CNNs as all the features exist in the object. However, CNNs often require huge training data sets to classify objects accurately as they are unaware of the spatial relationship between the objects. Images with different lighting, skewness, position, tilt, rotation, etc. need to be trained individually before the network can recognize objects with variations. Implementing capsule-network or caps-net to detect hand-drawn circuit images will significantly reduce the training data requirement.

The rest of the paper is organized as follows. Section 2 presents a comprehensive review of recent techniques for circuit image recognition. Section 3 details the proposed work in terms of materials and methods, while Section 4 presents and discusses the results for our proposed work. Finally, we sum up our findings in Section 5.

2. Literature Review

Object detection has improved in the past few decades with the evolution of machine learning techniques for computer vision. The localization and classification both combined are referred to as object detection, which is the core of our proposed work. The pioneering study in [14] utilized some of the available computer vision techniques to identify the nodes and separate the circuit components. The corner points are detected and identified as nodes, connection points are established, and a moment invariant algorithm is used for the object classification [14]. The authors of [14] used a pixel-based algorithm, and thus scaling to large-scale circuits with more components will be impractical. One of the most widely used machine learning approaches for object detection with a fast and robust technique is the viola-jones-based framework introduced in [19]. They train a detector using positive and negative images sets to create a classifier that has feature-based detection rather than pixel-based. This face detector can be implemented with less processing power. The training data set consisted of images with faces and without a face. The set also included vertically mirrored images of the face set. Multiple of these classifiers are positioned in cascaded architecture, with each having a different number for feature sets.

A similar approach as in [14] using multiple image analysis techniques is discussed in [15]. This study considers hand-drawn circuits with recognition limited to nine electrical components as inputs. After preprocessing the input images with binarization, noise cancellation, and thinning, segmentation is used to separate the connection wires’ nodes and components. The nodes are then identified using pixel tracking. The components are classified using features extracted from moment invariant, geometric features, and vector features. As the work in [14], this research also has limitations in scaling to new components and complicated circuit diagrams as they are pixel-based approaches. They achieve an accuracy of 86% for component classification.

Another famous image classification technique uses Support Vector Machine (SVM), where both positive and negative datasets are used to train the classifier. The studies of [16,17] described the use of SVM-based classification for hand-drawn digital logic circuits. As with other studies, the images are pre-processed before segmentation and classification. They use region-based segmentation techniques to segment as components and connections. Feature extraction is performed by the Fourier descriptor, a boundary-based technique as it is invariant to scale, rotation, and translation. The features are then used by SVM, which is a supervised learning algorithm that is trained to classify the circuit elements. The training was conducted on 60 training images. The drawback of the system lies in the average accuracy of 83% recognition rate. Several works highlighting the algorithms mentioned above are still common today due to the possibility of the rapid detection rate [20].

Neural networks started gaining momentum by this time, and an approach to hand-drawn optical circuit recognition was reported in [21] using Artificial Neural Networks (ANN). The system used feature extraction based on shape, followed by ANN with a backpropagation method for classification. The system only identifies the symbols, units, numbers, and alphabets in this study. However, it is possible to scale the system also to classify circuit elements.

Another category of neural networks with the state of art results is CNNs and their improved RCNN, Fast-RCNN, and faster-RCNN. CNNs are multilayer deep learning techniques used initially in the image processing field [22]. At the time, CNN achieved the best results compared to other algorithms as they reduce computations significantly for images [22]. CNN uses convolution to identify features that will be done in multiple layers. The actual location of the feature is not relevant once the feature is detected [22]. CNNs are the backbone of some of the most commonly used artificial intelligence systems globally, including face detection systems, object identifications, natural language processing [23], etc. They are being used in many different applications, such as enhancing Natural language processing by using pre-trained word vectors to train CNN for sentence classification [23]. The authors in [23] also experimented with static word vector and nonstatic word vector fine-tuned using backpropagation. Due to feature extraction using pre-trained vectors, they have better results, as explained in [24]. The study conducted in [25] found better results with CNNs than SVMs in detecting an object with invariance to lighting and pose. CNNs are similar to general neural networks in that they have neurons that are given weights [26]. The study [27] published in 2012 was able to achieve the state of art accuracy, which was made possible because of the ability to run computations on Graphical Processing Units (GPU) for computations rather than CPUs. Moreover, CNNs had great depth with eight layers, including convolutional layers and fully connected layers.

We intend to implement capsule networks in hand-drawn circuit recognition with a reduced training dataset with our proposed system. The reported work [18] described the caps-net implementation only for datasets of MNIST and Cifar10. It has achieved good results in an affine test set of MNIST and equivalent results with the MNIST data set. However, the reported results achieved 10.6% error on average with its implementation on Cifar-10, probably due to background clutter. In this study, we attempt to improve the caps-net algorithm to enhance its performance on datasets other than MNIST.

3. Materials and Methods

3.1. System Overview

We propose a smartphone system that can identify, simulate, and display the results of a hand-drawn circuit image. It will capture a circuit image, process the image to create a digital description of the circuit, and build the simulation circuit. Figure 2 shows the overall architecture of the proposed system.

The user can capture a picture that is then uploaded to the system, which processes the image and outputs the circuit creating an engaging tool for students to learn from. There are three parts to the program: region proposals, component detection, and node analysis. Figure 3 shows the image processing pipeline, which includes character detection and component detection.

Once an image of the circuit is captured, it is preprocessed to remove white spaces so that the image looks zoomed into the maximum. The character recognition is performed by identifying characters and classifying them using capsule networks. Next, the image features are extracted by identifying the component location using the Mean Shift Algorithm and place bounding boxes over components. The components are then extracted and classified using trained capsule networks. Finally, after extracting the components and removing small regions, nodes are identified to create a Netlist. The netlist is a way of representing a circuit structure in text format. We use a circuit simulation tool that takes netlist as an input and provides the results. The results are then overlaid on the circuit image, which is returned to the user. With this implementation, we attempt to achieve state-of-the-art results with reduced training data set size. Furthermore, with CNNs, due to a lack of spatial relationship analysis, we need to train the network on both vertical and horizontal data sets of the components [19]. However, with capsule networks, we can train components of different orientations as a single class.

3.1.1. Data Collection

We gathered hand-drawn circuit diagrams with different stroke sizes and rotations on plain paper for training and testing. A mobile phone camera captured the images. All the training images will be normalized; thus, it can be captured using different devices. All the images will be labeled using an image labeler. We will focus on classifying resistor, inductor, capacitor, DC voltage source, and Current source as circuit components. We received over 800 circuit images, with each circuit image having at least 7–9 components. Once the images are labeled and ready for training, we split the data into a training set, validation set, and testing set. The sets are prepared randomly so that we do not overfit the data.

3.1.2. Preprocessing

Preprocessing images before training helps in getting better training results as we reduce the clutter in the image. First, the image is thresholded and then converted into grayscale. The normalization of all the images is done to a size of 780 × 1080 to get unified training images. First, to run the region proposal algorithm, small regions are detected, mainly text or characters, and are removed from the image before applying the region proposal algorithm to reduce the error rate of detecting circuit components.

3.1.3. Region Proposal Algorithm

To locate circuit components in the image, feature detection algorithms are employed as their background has less noise and hence less susceptible to false-positive object location. The following steps describe our used Region Proposal Algorithm:

• Preprocess the image before performing a feature analysis. We convert the image to binary, filter text and symbols from the image, and dilate it.
• Perform edge and corner detection using SURF, Eigen, and FAST methods to identify capacitor, inductor, and resistor. Circuit images consist of background with less noise enabling feature detection to identify components as a concentrated set of points.
• Dilate the detected feature points to create locations for the components and filter to remove relatively small regions. Bounding boxes are placed over the remaining detected regions.
• Detect circles using Hough transform to identify Voltage and Current sources. All circles with a radii range of 20 to 500 px are accepted. Next, we identify and remove overlapping circles. Given two circles with Center $(x_1,y_1)$, radii $(r_1)$, Center $(x_2,y_2)$, and radii $(r_2)$. The distance between the two circles is calculated by $Distance={(x_1-x_2)}^2+{(y_1-y_2)}^2$ & $Radius=r_1+r_2$. If Distance > Radius, then circles overlap and vice versa. We merge both circles into one to confirm the circular component is fully localized instead of partially.
• Any bounding box overlapping a circle is removed.
• Bounding boxes are created over circles and added to the existing list of bounding boxes, creating our final list of localized components.

3.1.4. Object Classification

The components located through our region proposal algorithm is passed through our capsule network classifier. It is a new deep learning approach introduced in [18]. CNNs traditionally have a single neuron capable of giving a scalar output of probability for an object. However, in capsule networks, they propose to combine a group of neurons into capsules that will detect a particular feature for an object encoded with various other information for the object parameters such as size, thickness, skewness, rotation, etc. The traditional neural network has a scalar probability value with one neuron. It does not contain any information regarding the features of the object. However, the output of a capsule network is a vector, and the length of the vector determines the probability of the image being a particular object. The 2D vector also contains information about the rotation of the object. This resolves the issue faced in CNN with objects in different poses and rotations. In a CNN, flipped or rotated images are not detected unless the network has been trained with these variances.

The capsule networks also differ in terms of how they route the information from low-level to high-level features. They only send information to high-level entities that can process the information rather than sending it to all the classifiers in the final layer. The capsule network does this intelligently by agreeing with the low-level features that the capsule sends the information to. This is termed as routing by agreement [18]. For example, suppose the low-level capsule identifies a nose, mouth, and eyes. In that case, we multiply it with a transformation matrix, which then identifies if eyes, nose, and mouth are part of the face, and their location aligns with that of a trained face. Only then a face capsule is activated. Thereby, capsule network overcomes the issue of CNNs in identifying the spatial relationship between object parts shown in Figure 4.

Compared to traditional neural networks, capsule networks deal with vectors’ inputs and outputs to carry information on various object parameters. We have multiple capsule layers within one architecture that are capable of detecting from low to high features. For example, when detecting a circuit component such as a diode, the higher level capsule detects the diode while the lower layer detects different lines making up the diode. We have a transformation weight matrix $W_{ij}$ for the object built with backpropagation to encode the diode’s position details and parts.

Routing in the capsnet is done via dynamic routing, while in CNN, it is done via max-pooling [18]. Using this methodology, a capsule in the previous layer can identify which capsules to provide the information. This happens between the primary caps layer and the circuit caps layer. Reconstruction loss is calculated by reconstructing the image after the circuit caps layer and is added to the total loss to add lost information back into the input parameters. The results in [18] show a clear improvement in classification using reconstruction as a regularization method, which is used to avoid overfitting.

3.1.5. Identify Display Locations for Results

This process is to identify coordinates on the input image to place circuit simulation results. We determine which of their sides has the least pixel concentration for each component to hold the simulation results. The algorithm is designed so that the location chosen does not overlap with the location chosen by another component.

3.1.6. Node Detection

Once circuit components are detected using the capsule-network, we need to perform circuit node detection to identify the nodes, locations, and circuit component connection. The nodes are identified using the following procedure:

1

We increase the bounding box of detected components by 2% around all four sides and get a list of all the region’s pixels.

2

We remove the initially detected component, and we are left with the wires in the circuit. Each wire is counted as a node, and we retrieve all pixel locations in each wire after filtering any relatively small objects.

3

We loop over all components to identify the nodes it belongs to by comparing the pixel information.

4

Each component can only have two connecting points, and thus only two nodes.

5

We will be requesting user input to get the component values.

3.1.7. Circuit Simulation Results

We now have a list with all components, nodes, location, and prediction probability with all processes. We use this information to create a netlist, a digital format of a circuit diagram used by circuit simulation engines that takes circuit description as input and outputs the resulting values of power, current, voltage, resistance, etc. for all circuit elements.

3.2. Convolutional Neural Networks

CNN layers are a convolutional layer, a Rectified Linear Unit (ReLU) layer, a Pooling layer, and a fully connected layer. The convolutional layer calculates a gradient for the input image by multiplying the input image with a filter. ReLUs are nonlinear activation functions applied to the convolutional layer output without changing its volume [18]. Given that f is the output of the neuron and x is the input, the neuron can be modeled as the nonlinearity function $f(x)=max(0,x)$ [27]. The pooling layer is used for downsampling a convolutional layer to capture higher-level features in the next layer. Given $(M_x,M_y)$ the dimensions of the convolution layer, then with a kernel size of $K_x$ and Stride S, we can find the dimension of the subsampled layer as the following with the depth remaining the same:

$$f(M_x)=\frac{M_x-K_x}{S}+1$$

(1)

The final layer in a CNN is the fully connected layer, which, as the name suggests, is fully connected to the previous layer of CNN. This layer classifies while the earlier layers of convolution, ReLU, and pooling are feature learning parts. The fully connected layer outputs a K-dimensional vector where K refers to the number of classes for object classification.

3.3. Challenges with CNN

Although CNNs are the go-to deep learning methodology in computer vision for the past few years, it has some limitations. In this section, we will highlight some of the drawbacks faced by convolutional neural networks. One of the main issues with CNN is that they pose invariant to objects. For example, if trained to recognize a face, it will fail to classify an upside-down face. The CNN is invariant to rotation and tilt in images unless the training data includes all the possible transformations for an object. For example, in Figure 5, we train a resistor image using CNN. Given a resistor image similar to the training set as input, CNN will correctly classify it as a resistor as it recognizes the learned features. However, if a rotation is applied to the resistor, then CNN will classify it as non-resistor, as shown in Figure 5. In a circuit image, resistors could come in different rotations, vertical, horizontal, diagonal, etc. However, we need to gather an extensive training data set containing all the possible options to identify a resistor correctly. This is a fundamental concept tackled in [18]. They build an equivariant network that can identify an object with any transformation. This would help considerably reduce the training data set.

Another drawback for the CNNs is its lack of spatial relationship data for its object parts. A CNN will correctly classify an image as a current source as long as all its features are in the same image regardless of the image parts’ location within the current source, as shown in Figure 4. Therefore, it is easy to trick a CNN network and create false positives. Once the low-level features are classified in the CNNs, the next activation layer is fired based on the probability of having certain low-level features; however, the relative position of the parts w.r.t to the object itself is lost with CNNs. A Resistor neuron should only be activated if the parts identified result in the same pose matrix for the resistor. Figure 6 refers to how the CNN works in classifying a diode image. CNN’s initial layer will find the probable lines (horizontal, vertical, diagonal) that make up the diode’s image and match it to both diode and transistor properties. This form of routing to all possible networks is computationally expensive and can cause errors. This could be resolved by using a selective routing mechanism.

The main disadvantage of CNN is that it loses the spatial relationship between features in the image. A CNN uses convolution to extract features from the input source, and for each of the features, a weight is added, which is then summed to identify the high-level feature. Each layer extracts a particular set of features, hence is combined into multiple layers. A max-pooling function is used in each layer to reduce input size by extracting the maximum features. At this point, it starts losing the spatial information for the different parts of objects. This means CNNs do not perform well when the spatial positions of object parts are changed within the image. They do not perceive the components and their location that make the image but just the basic features. In the next section, we introduce capsule networks built to overcome the shortcoming of CNNs or any other traditional neural networks.

3.4. Capsule Network

3.4.1. Capsule Network’s Architecture

We perform classification on the region proposals using a capsule-network algorithm. Figure 7 shows a 3-layer capsule network architecture. It consists of an initial convolution network followed by two layers of capsule network:

• Convolution takes a $28\times 28$ image, which is convolved with a $9\times 9$ kernel and stride of 1. We convolve with 256 different feature maps. This layer will extract all the basic features from the input image, such as edges. This layer’s output, a $20\times 20\times 256$ image, is taken as input to the Primary capsule layer. ReLU nonlinear activation function was used where $f(x)=x>0=>xorx<0=>0$. Output image size changes from $28\times 28$ to $20\times 20$ based on the size calculation of:

  $$(s_{img}-s_{Kernel})+\frac{1}{s_{stride}}$$

  (2)
• Layer 2 consists of a primary capsule network that implements convolution with a $9\times 9$ kernel and stride 2. We also rearrange the output to resemble a capsule network; the convolution results in a $6\times 6$ image. The 256 feature maps output is divided into 32 capsules sets with a dimension of 8. Therefore, each capsule has a dimension of 8. The output image size changes from $20\times 20$ to $20\times 20$ based on the size calculation given in Equation (2). The primary capsule has three functions, first is to detect higher-level features than edges and curves. Second, it reshapes the output of 32 blocks of eight dimensions into a flatted matrix of size $(6\times 6\times 32)=1152$ capsules of 8 dimensions. Third, it predicts each capsule’s output, which is used to route the capsules to a higher capsule. The primary capsule $u_i$ is multiplied by the weight matrix $W_{ij}$ to receive a prediction for the diode’s spatial location, as shown in Equation (3). If ${\widehat{\upsilon }}_{j\mid i}$, the prediction vector turns out to be similar to the weight multiplication for other low-level features, then the probability of diode detected is higher. This is how dynamic routing is implemented in capsule networks.

  $${\widehat{\upsilon }}_{j\mid i}=W_{ij}{u}_i$$

  (3)
• The third layer represents the circuit-caps layer, which takes the inputs specified by the dynamic routing algorithm and provides a classification along with instantiating parameters measuring 16 dimensions per class.

3.4.2. Dynamic Routing Algorithm

Other than convolutional layers, CNN often uses pooling layers to reduce the representation’s size, speed up computation, and improve feature detection. However, capsule networks use a dynamic routing algorithm to send information to the next layer specified in Figure 8.

An initial value of routing weight $b_{ij}$ is initialized to 0 for all layer l capsules under each layer l + 1 capsule. $C_{ij}$ is a probability value as it is a softmax function of $b_{ij}$ known as coupling coefficients. Therefore, the sum of all $C_i$ vectors is 1. The coupling coefficient is built using the iterative dynamic routing process. The coupling coefficients decide which capsule j in layer K + 1 needs to be chosen as a parent by capsule i in layer K. If ${\widehat{\upsilon }}_{j\mid i}$ has a high value, then the coupling coefficient for that parent is increased. This method of routing is more efficient compared to max-pooling on CNN. In step 5, a weighted sum is calculated $S_{ij}$ by summing all feature vector ${\widehat{\upsilon }}_{j\mid i}$ with a coupling coefficient $c_{ij}$, as shown in Equation (4).

$$s_j=\sum _i{c}_{ij}{\widehat{\upsilon }}_{j\mid i}$$

(4)

Usually, in CNN we have a ReLU as an activation function. However, the capsule networks use a squashing function as in Equation (5). A squashing function is applied to weighted sum $s_j$ to reduce its length to less than 1, but it still keeps its direction intact. This is assigned as the output prediction $v_j$. Routing weights are updated with the following equation: $b_{ij}+=u_{j|i}.v_j$. The value of $b_{ij}$ will be high if the prediction value is strong

$$v_j=\frac{\Vert s_j{\Vert }^2}{1+\Vert s_j{\Vert }^2}\frac{s_j}{\Vert s_j\Vert }$$

(5)

$u_{j|i}.v_j$ in step 7 refers to the agreement between the output prediction of the primary capsule and circuit capsule layer. We use an adapted version of the Capsnet code provided by the authors of [28].

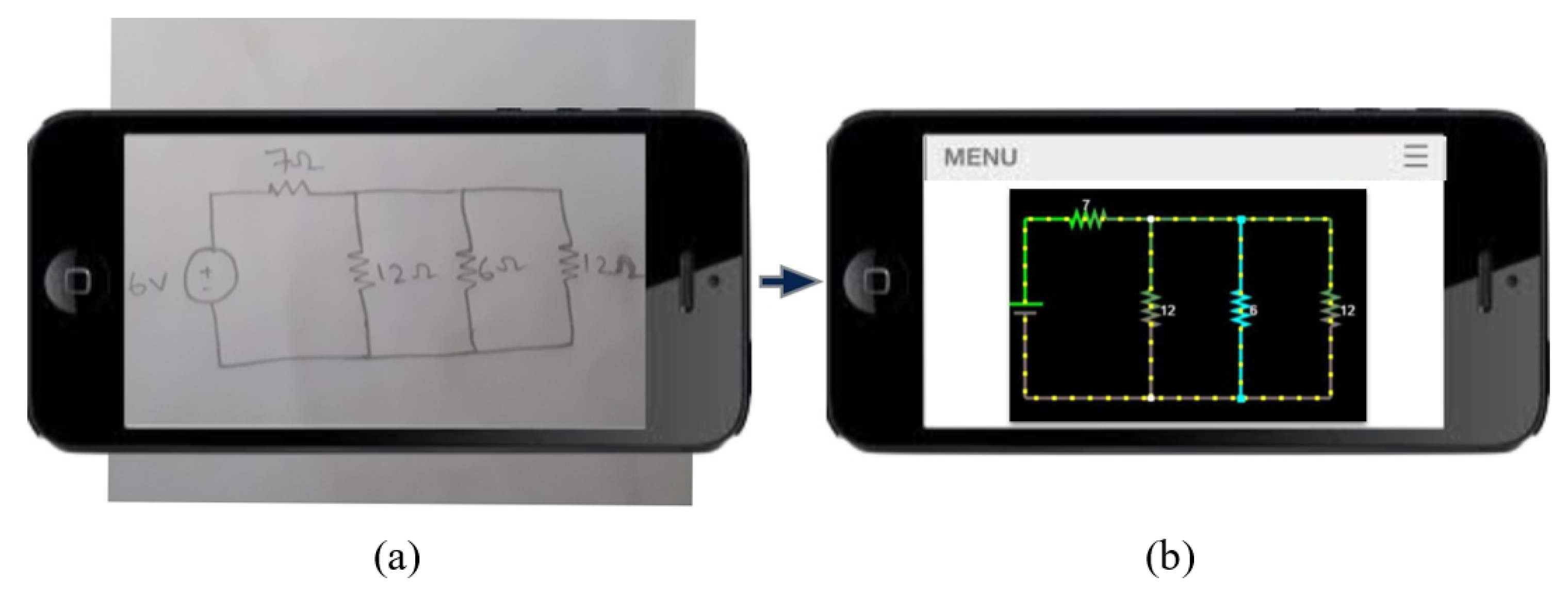
4. Results & Discussions

4.1. Circuit Recognition System

Figure 9 shows the full cycle of object detection and circuit simulation for a hand-drawn circuit. The system takes an image as input, locates the components, classifies the detected components, identifies nodes, builds the netlist, runs the simulation, and finally overlays the input image results.

Once the input image is received, we perform the following pre-processing steps before performing feature detection: remove white spaces, reduce the image size to $720\times 1080$, identify relatively small regions and remove them from the image resulting in Figure 10.

We then proceed to use a region proposal algorithm composed of two sections. First, we detect components: resistors, capacitors, and inductors, and second, we detect circular components voltage and current source. We perform feature detection for the former, which locates edges and corner points, providing approximate locations of the circuit components, as shown in Figure 11a. We filter unwanted regions by dilating points removing relatively small regions. The final detected regions are plotted in Figure 11c.

To detect voltage and current sources, we use the Hough transform to identify circles. Our region proposal algorithm hence allows creating a bounding box around the components. Once the component locations are identified, we perform the following.

• Object classification using capsule network, as illustrated in Figure 12. An additional class called ‘Node’ was added to identify wrongly localized components, e.g., wires or corners that do not fall under the circuit component category.
• Identify coordinates to display the final circuit simulation result shown in Figure 13a.
• Node detection is shown in Figure 13c.
• The netlist is automatically built based on the previous detection results and user input for the component values, as shown in Figure 13d. The netlist is then passed to the circuit simulator tool to obtain results.
• Results are overlaid on the input circuit image shown in Figure 13e.

Figure 14 shows the analysis of more complex circuits in various stages. All images pass through the initial stages of feature extraction for object detection. Circles of Current and Voltage sources are detected separately using Circular Hough Transform [29]. Once circles are identified, we overlay a rectangle bounding box to extract the circle component and identify any overlap between feature detection and circle detection. The components are then passed for classification, after which the node extraction is performed to create a netlist. The netlist is built using the node numbers rather than coordinate points, allowing a better netlist creation approach.

4.2. Validation Results

We test our model with different scales and rotations, and the results are shown in Figure 15. Our model can provide a good recognition rate for images taken between 10 cm to 25 cm. However, the optimum distance to take images is between 10 cm to 20 cm from our testing. Our model is also able to identify components of different rotations.

To validate our capsule networks classifier, we performed stratified 5-fold cross-validation. We kept 5% of the data for testing, and the remaining were used for the cross-validation split. Figure 16 shows the results of our cross-validation. All training was performed using a batch size of 50, a learning rate of 0.0001, and 30 epochs. The model converges faster due to less training samples.

We use 400 samples per class, and we receive an accuracy of 96%. Figure 17 shows the training accuracy and training loss per step during the capsule network training.

To compare the results, we use a baseline CNN model and only receive 80% accuracy for the same set of parameters. We compare the accuracy rates across different sample sizes, as shown in Figure 18. We train both capsule networks and CNN with 100 to 1400 samples, with the former performing better. This validates that capsule networks provide better accuracy with a low number of training samples than untrained CNN. Although several papers have tested capsule networks on different image sets, the accuracy tends to be lower as the image complexity increases. Circuit component images are similar to MNIST dataset as the images have less background noise.

To analyze our multi-class classification system accuracy, we calculate the confusion matrix shown in Figure 19. It was computed with 100 images per class.

Table 1. Confusion matrix scores.

	Precision	Recall	F1-Score	Support
Capacitor	1.00	1.00	1.00	100
Current	0.92	0.91	0.91	100
Resistor	0.99	1.00	1.00	100
Voltage	0.92	0.89	0.90	100
Inductor	0.97	1.00	0.99	100
Micro Avg.	0.96	0.96	0.96	500
Macro Avg.	0.96	0.96	0.96	500
Weighted Avg.	0.96	0.96	0.96	500

shows the scores per class and the overall accuracy of = 0.96 and loss of = 0.05497217.

We use mean average precision to measure the accuracy of our object localization and classification algorithm. Figure 20 shows the average precision (AP) for each class capacitor, current, inductor, voltage, and resistor for 0.3 Intersection over the union threshold. The system is trained with 400 samples per class that are real-time augmented to provide good accuracy. To compare the results to an existing algorithm, we run the Capsule networks and RCNN with a pretrained VGG16 architecture comprising 38 layers on 400 samples without augmentation.

Table 2. Average precision values for 0.3 and 0.5 threshold values.

Class	Capsule Network (with Data Augmentation)		Capsule Network (without Data Augmentation)		RCNN (without Data Augmentation)
	0.3 IOU	0.5 IOU	0.3 IOU	0.5 IOU	0.3 IOU	0.5 IOU
Capacitor	94.74%	82.40%	86.09%	78.63%	99.93%	57.41%
Current	92.02%	92.02%	73.06%	73.06%	54.07%	16.58%
Inductor	88.97%	52.53%	83.03%	58.84%	81.20%	23.83%
Resistor	97.38%	82.64%	94.61%	80.95%	86.55%	48.90%
Voltage	95.08%	93.47%	71.38%	69.20%	77.31%	51.11%
mAP	93.64%	80.61%	81.63%	72.14%	79.81%	39.56%

shows the summary of AP value per class for both 0.3 and 0.5 thresholds.

With capsule network results for 0.5 IOU, we see that inductor has the least precision. Our object detection model sometimes detects circles inside inductors. As per our object detection algorithm, we prioritize circles. This reduces the area captured to identify inductors. However, the capsule network can perform classification with limited data. The inductor value change is evident as it increases by 30% when we reduce the IoU value. The current and voltage values have less change as the object is localized similarly to the ground truth bounding box, given its circular shape. For a resistor, object localization is slightly shifted than the ground truth bounding box resulting in a 4% difference between both thresholds. Average precision is checked on unseen data.

To compare the results of Capsnet with RCNN, we plot the precision-recall curve for RCNN trained and tested on the same dataset without augmentation. Figure 21 shows the results of the comparison. The graphs of RCNN shows lower precision and recall value for all components compared to our model. This shows the effect of low training samples on the RCNN based object detection model. The RCNN model, which classifies five different classes with a training sample of 200 circuit images, containing 400 samples per class, produces results similar to Capsnet in terms of classification. Our object localization algorithm is far better than the object localization algorithm of RCNN; however, in terms of classification, it is producing results similar to the Capsule network.

Overall, the results verify that our object detection algorithm with capsule networks performs slightly better in circuit component detection than RCNN. We can provide satisfactory results based on the theory that capsnet can achieve high accuracy with a low sample size due to its algorithm. However, we need to note that we compare a 3-level architecture to a 38-layer pretrained architecture that deduces that capsule networks have great potential to perform better than the current state of the art programs. This would require considerable research into optimizing the algorithm. We have successfully implemented circuit data to capsule networks in this work, where we achieved high accuracy using less training data compared to all current research based on MNIST and CIFAR10.

5. Conclusions

Although several tools are available to sketch and simulate the circuits, the first draft of any circuit diagram is hand-drawn on paper. The availability of a smartphone educational technology helps students and professionals convert the sketch into a digital format directly using a mobile app instead of redrawing the circuit on simulating tools, especially given the large-scale drawings in professional environments. Once a tool can successfully create a computer-readable description of the diagram, it can be used for instant identification of unknown parameters in the circuit that can be useful for the students for learning purposes. However, difficulty in scaling to complex circuits, classification accuracy, and the need for a large training data set has been a setback in making progress with hand-drawn circuit recognition. In this work, we proposed the implementation of a smartphone hand-drawn circuits solver using augmented reality and capsule deep networks for engineering education. We used capsule networks as they have been theorized to require less training data while still achieving high accuracy. This is because they can overcome some of the common issues with CNNs, such as lack of equivariance and more training data. However, our test results show that Capsnet outperforms RCNN in object detection although it provides similar classification results. Capsnet is still a novel technology and requires a lot more research before reaching its full potential. In the future, we aim to improve the object localization algorithm to capture circuits of all scales as size variations such as too large or too small components can cause issues in locating the object.