Making Good of a Pandemic: A Long-Distance Remedial Summer Course in Calculus

Abstract

What do you do when a change in enrollment policies leaves you with more than 600 students in a first-term university calculus class, three-quarters of those students had a failing mark in mathematics in the pre-enrollment test, you planned a series of remedial activities for the second term, and the COVID-19 pandemic shuts the university down with a two-day notice? The pandemic hit instruction with might, forcing schools and universities that were timidly experimenting with digital tools to reinvent themselves in days. The pandemic also offered incentives for creative solutions that, in normal times, would have been considered fit for submission to the committee for recursive committee submissions at best. This paper narrates a teaching experience of how we proposed and managed an at-distance remedial course in August that not only catered to more than twice the number of students expected by our best forecasts, but was a very good success once its effectiveness was compared to the outcomes predicted by the pre-enrollment test scores. We expose the design of the course and link its measured effectiveness with both its design and student engagement; in particular, we show that a different approach to the examination of cognitive load and to fostering student–teacher and student–student communication thanks to digital mediation could be effective in countermanding the math-induced drop-out phenomenon in STEM.

1. Introduction

1.1. The Context

Istituzioni di matematiche for Natural Sciences students at the University of Milan is a standard first-term 8 ETCS credit introductory course in calculus. Since the three-year bachelor program removed limits on admissions in the 2018/2019 academic year, enrollment has been skyrocketing, and the level of incoming students, as measured by the non-selective national standardized test, TOLC-C ([1]), has been dropping. In 2019, 621 students enrolled, of whom 72.3% had a failing mark in mathematics (defined as a score less than 10 out of 20); some of them even had a negative score ([2]).

Academic regulations stipulate that students can take every exam at least seven times per year at their discretion. As a result, only a minority of students usually pass an exam at each time, with 30–45% being a common percentage. Rizzo ([2]) showed a good correlation between the mathematics marks in the TOLC-C and the number of times that a student had to take an exam before passing it (if ever).

The lockdown for the COVID-19 pandemic came into effect in Milan on the 24 February, 2020, which meant that only one examination—rather than two—was available to students during the winter recess. The pandemic and the forced and rapid move to distance learning made it impossible to implement the actions that had been devised to help the weaker students to cope with their low mathematical skills during the second term (we were planning to have weekly gatherings of small groups, each focusing on a granular topic with the goal of fostering student engagement by using a “mathematics laboratory” approach (see, for example, [3]) combined with a peer-evaluation-based formative assessment cycle).

A busy examination schedule in June, July, and September made it nigh impossible to envision a remedial course, even supposing that it would have been possible to hold it face to face; the lack of time urged against creating an MOOC (even supposing that an MOOC would be effective, a hypothesis that is not necessarily supported by the literature [4]).

1.2. A Course in August

The course coordinator for the degree asked for a solution, any solution—the only requirement was that it had some chance to be effective. Pandemic measures made it possible to be creative.

The only free slot was in August. “Are you out of your mind? No one would accept spending August studying math” was the reaction of one of the course’s teaching assistants to the first proposal.

Indeed, common lore states that August is a dead month in Italy, and particularly so in Milan; data partially confirm the statement: General crime rate is halved in August [5], while bike theft is only slightly reduced with respect to July [6]; on the other hand, car access to the central part of the city is reduced to a quarter [7]. In any case, the regulations of the University of Milan state [8] that: “No examination can be held in the month of August”.

A perfunctory analysis of the summer courses of the University of Milan showed that summer meant any time from May to September, except for August.

An enrollment between 20 and 40 students was expected, and resources were allocated to that extent. The real numbers were above one hundred!

1.3. Terms

As pointed out by the anonymous reviewers, the terms used to describe the teaching settings at a tertiary level are dependent on the country and institution, so we provide here a description of our English translations of the relevant Italian terms.

Teaching hours are divided into lectures (in Italian: lezioni) and recitations (esercitazioni); the former are usually taught by a professor and present theory with some relevant examples, while the latter are usually taught by a teaching assistant (PhD students, junior staff, high-school teachers) and present mainly exercises.

Tutors are a kind of teaching assistant (usually master-/PhD-level students or high-school teachers) who grade homework, answer questions on an online forum, and monitor students during tests.

Lecture captures are recordings of the live lectures (or recitations); they consist of an audio recording together—at least in math—with a video recording of the mathematics being written on the relevant medium (be it a chalkboard, a whiteboard, paper, or a tablet).

2. Literature Review

2.1. Dropping out of STEM

Math is scary. For life science students, math is even scarier ([9,10]).

“Considerable progress has been recently made in increasing enrollment in Science, Technology, Engineering, and Mathematics (STEM) study programs. High drop-out rates in STEM programs, however, tend to undermine the beneficial effects of all current attempts to increase student enrollment in these programs” ([11]). The Italian national program for increasing enrollment in the sciences (Progetto Lauree Scientifiche, later Piano Lauree Scientifiche) recently established the reduction of dropouts as one of its six goals; especially in the life sciences, this phenomenon is linked to poor results in mathematics (cfr. [12]), with good correlation between entrance exam scores and chances of passing the first-term calculus class ([2]). On one hand, “withdrawing from enrollment and failing to graduate actually represents a final and critical step in a larger continuum of beliefs, attitudes, and behaviors that, together, reflect students’ academic disengagement”; on the other, “[c]ollege dropouts also consume institutional and financial resources that might otherwise support students who would persist and graduate” ([13]).

2.2. Mathematics Support for College-Level Calculus

Mathematics support can be defined as “a facility offered to students (not necessarily of mathematics) which is in addition to their regular programs of teaching through lectures, tutorials, seminars, problems classes, personal tutorials, etc.” ([14]). A promising development of mathematics support is the support center, which, as reported in [15] and later in [16], is now quite common in the Anglosphere; it is a structure which exists physically on campus where the on-going needs of college students can be met.

Dedicated facilities—whether physical, digital, or just makeshift—that are separate from the classroom are important since “students often avoid participating in mathematical discussions because publicly sharing their thinking is a socially risky endeavor. Social risk means threats to one’s status in a community. Young people often come to school uncertain of their standing with their peers and teachers. At the same time, they are often highly preoccupied with their status. [...] Although social risk is felt in many classrooms, mathematics classrooms are particularly burdened with social risk. Mathematics, as a school subject, is culturally anointed as the ultimate measure of smartness. The logic goes: If you are good at math, you are truly smart. If you are not good at math, you are not truly smart. Many of us, as mathematics educators, have encountered competent adults who confess their insecurity over not being ‘good at math.’ Because of the linking of mathematics and ‘true’ smartness, when students share their thinking in the public space of the classroom, they often perceive risks to their academic status that go beyond the immediate content, extending instead to their overall intelligence” ([17]).

Blended and distance learning offer an alternative model of mathematics support for college-level students (cfr. [18] for a panoramic review of the state of the art and [19,20,21,22] for the Italian context). The COVID-19 pandemic made at-distance teaching the only viable possibility, but one should take notice of its effects on teachers’ praxeologies ([23]) and evaluate the advantages in assessments—such as the greater flexibility in test-taking and faster scoring—towards the importance “that mathematics education should be for all students, including those who have special needs, who live in poverty” ([24]).

2.3. Attitude towards Mathematics

Negative attitudes are often used as an explanation of students’ failure in mathematics (cfr. [25]); similarly, another explanation is the rupture of the Schunk–Zimmerman self-regulation cycle of engagement, reflection, and anticipation ([26]).

What is possibly even more worrisome is that [27] showed that “after taking Calculus, [students] showed a reduction in positive attitudes about mathematics”. According to [28] “[b]etween the start and the end of the students’ college calculus class, their confidence and enjoyment of mathematics dropped sharply, with confidence falling by half a standard deviation and enjoyment of mathematics by a third”; even among students that do well in such a class, many lose any interest in taking further mathematics classes, and some even leave the STEM track. The report showed that only ambitious teaching (i.e., active learning approaches) combined with good teaching is effective in avoiding this tendency.

2.4. Formative Assessment

Formative assessment is a didactical tool consisting of five main strategies ([29,30]):

FA1

Clarifying and sharing learning intentions and criteria for success;

FA2

Engineering effective classroom discussions and other learning tasks that elicit evidence of student understanding;

FA3

Providing feedback that moves learners forward;

FA4

Activating students as instructional resources for one another;

FA5

Activating students as the owners of their own learning.

The formative use of tests is usually considered as the main activity to be used in order to implement these strategies in a standard classroom setting; the literature shows that “digital technologies can be a powerful tool for teachers in order to monitor students’ progress, provide immediate feedback to students, enhance self-monitoring of the students, and highlight the deeper roots of an error” ([31]). On the other hand, “[t]he strong rupture that the emergency brought into teaching–learning practices is that digital technologies have suddenly become the only means to carry out educational activities in mathematics” (ibidem, emphasis added).

It follows from the very definition of formative assessment that the evidence gathered from the assessments must affect the instruction: “Assessments are formative [...] if and only if something is contingent on their outcome, and the information is actually used to alter what would have happened in the absence of the information” ([32]).

2.5. Inclusiveness

Italy, indeed, has the lowest percentage of resilient students (i.e., students from a disadvantaged background who are top performers in the Ocse-Pisa assessments) among the G7 countries and shows a striking inverse correlation between the socioeconomic status of students and competence levels in mathematics ([33]).

The literature on learning outcomes in Italian universities is scarce and very much in progress (cfr. [34]), but comparison with the international literature affords few doubts that the pandemic made participation even more unequal: “Pupils with low prior attainment and other disadvantaged pupils are participating less and, when they do, they have been less engaged. Three reasons for disadvantaged pupils’ low levels of participation and engagement were identified: limited access to technology; low levels of parental support and involvement with schoolwork, as well as specific ‘new’ personal or family-related challenges faced by vulnerable pupils during the lockdown ([35]).”

Of the many possible theoretical definitions of inclusion (cfr. [36]), we will make particular use of the discourse of teaching interventions for mathematical engagement and the discourse of teaching for maximizing opportunities in mathematics for all.

It should be pointed out that it has been shown in [37] that (automatic) formative assessment is particularly effective in improving the results of students from disadvantaged backgrounds, with little to no effect on students with a high socioeconomic level.

3. Theoretical Framework

The theoretical framework that we use to analyze the teaching experience is that of formative assessment in a digital learning environment as presented by Cusi, Morselli, and Sabena ([38]) as an extension of Wiliam’s and Thompson’s formative assessment model ([29]) by adding three functionalities to the key strategies of formative assessment (FA1–FA5):

F1

Sending and receiving messages and files, displaying documents;

F2

Processing and analyzing data collected during the lessons;

F3

Providing an interactive environment for the interactions of students

We adapt this model, which is based on three agents (teacher, students, peers), to a four-agent model by adding tutors that mediate between students and the teacher.

4. Didactical Design

The subject matter lent itself to a natural five-topic subdivision: linear algebra, functions, limits, differential calculus, and integral calculus. Each topic was assigned one week. Each week was structured in the same way: a two-hour recitation on Monday, followed by a homework assignment; homework was due on Wednesday at 11 a.m. and was marked on the same day; a one-hour recitation on Thursday was designed in reaction to problems and misconceptions appearing in the homework; a test was given on Friday. The high risk of cheating brought us to decide that homework would not count towards the final grade and that it would be completely voluntarily; removing the weight on the homework was also expected to be instrumental in fostering a collaborative environment based on formative assessment from Monday to Thursday, with only the partial test on Friday reserved as a summative assessment.

Because 20–40 students were expected to participate, the plan was to have tutors give individual feedback for each homework submission and to create a report for the teaching assistant. Moreover, a discussion forum was created for the students’ eyes only.

The course design was inspired by [39]; due to time constraints, only recitations were offered. On one hand, this choice significantly simplified the course design; on the other hand, it meant that very weak students were not catered to. The very low number of downloads of the class notes (i.e., the pdf files produced by the instructors while teaching the first term) during the course schedule (the most downloaded topic was linear algebra, with 16 different users and 23 downloads; note this was also the first in the chronological order and the least known for students leaving Italian high schools) offered some evidence that most participants had already started studying the subject matter (or, alternatively, that most decided it was ineffective to do so; Maria expressed “no theory, just exercises” and Gaia expressed “just the necessary theory” as positive points). Some students suggested “to possibly integrate theory”, or to add “one hour of theory [per week?]”; however, out of the 26 requests for more teaching time, only three students asked specifically for some theory lectures.

5. The Course

The data used in the following section came from the university’s e-learning platform, from the course records, and from a questionnaire that was given one week after the end of the summer course. The questionnaire was required in order to validate the summer course, but most students that did not pass the course took it anyway.

5.1. The Distance Learning Setting

Three people were hired for the summer course: a teaching assistant and two tutors. The three of them were high-school teachers who had been hired with the same roles for the standard course in the previous years. The teaching assistant had always received very good feedback in the student surveys at the end of the term (no student feedback was gathered on the tutors).

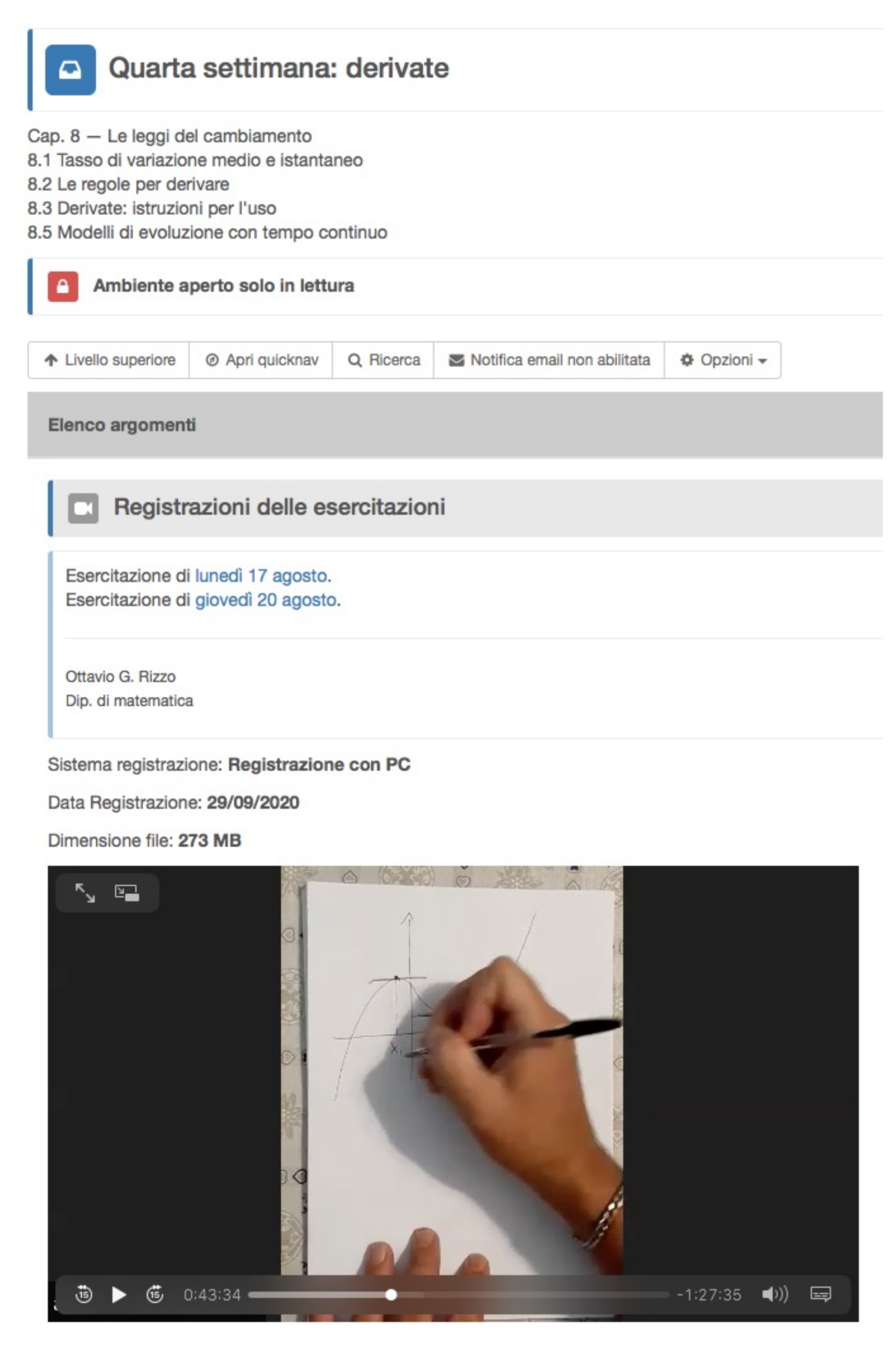
In addition to the course textbook, the students had on hand the (first-term) class notes, the texts of all exercises presented during (first-term) recitations, and 4½ years’ worth of exam texts (that is, 34 different exams) with commented solutions. All of the material was uploaded to the university’s e-learning platform, a simple in-house CMS; see Figure 1 for a partial view of week 4.

Classes were held using Zoom, with the lecture capture of each lesson uploaded on the university’s e-learning platform as soon as technically possible, together with the texts of all exercises and instructors’ notes.

Homework was submitted on the e-learning platform, usually as scans of texts written on paper.

A self-help forum was opened on the e-learning platform (for students, from students) in order to encourage active engagement (and to deal with the most trivial questions, such as “on what page is exercise 3?”). Given the size of the class, we decided not to offer a public discussion channel (e.g., a WhatsApp or Telegram group), since our experience showed a high risk of any information being drown in noise without active moderation (and no resources were budgeted for such active moderation). Students were asked to pose questions at the end of lessons, to send them by e-mail, or to use the interactive features of the homework uploading system. Answers to organizational inquiries were gathered in an FAQ, while other interactions were fed into the formative assessment loop (see Section 5.3).

5.2. Attendance

In

Table 1. Students per week.

	Week 1	Week 2	Week 3	Week 4	Week 5	Total
Freshmen	79	87	82	81	63	90
Non-freshmen	22	26	25	25	22	26
Total	101	113	107	106	85	116

, we see the number of students that attended the weekly tests; two different populations were considered: Non-freshmen were generally very weak students (if sophomores, they were not yet allowed to take any second-year exams; if seniors, they might just have chosen to delay calculus until the very end, and the rules had changed in the meantime), and we did not necessarily have entrance exam scores for them. The low attendance in week 1 was explained partly by news about the remedial course not having reached everyone and partly by some of the students being in field trips and unable to attend. The low attendance in week 5 was most likely explained by students that had either given up or were already sure of having passed the course; three students explicitly mentioned connection issues that forced them to skip that test (were they traveling back home?). The numbers in the “Total" column count all different students that ever took a test.

5.3. The Formative Assessment Feedback Loop

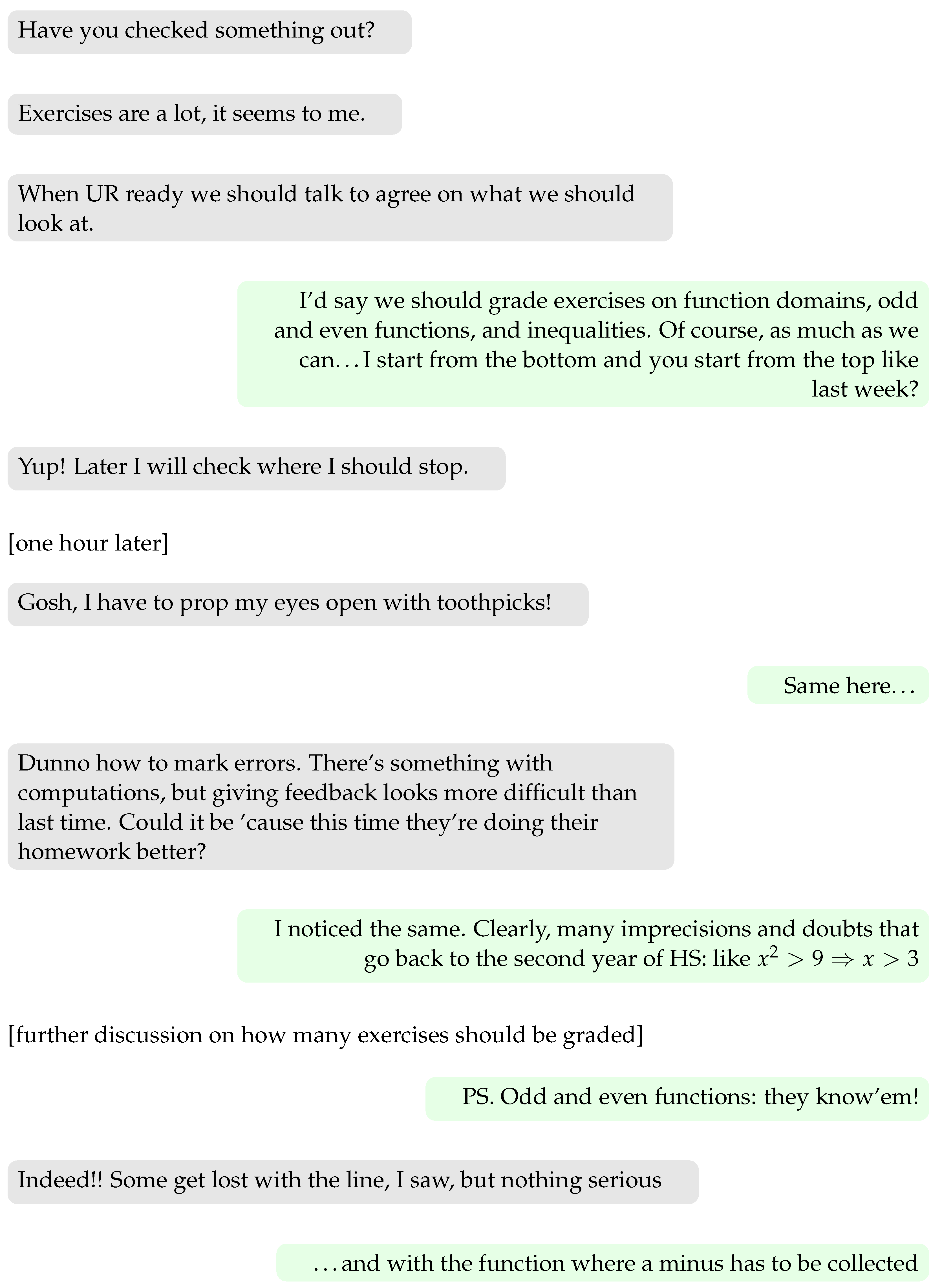
The sheer number of participants made it impossible to give thorough feedback on the weekly homework; tutors were instructed to give individual feedback only on the basis of need and to give the teaching assistant an overview of the issues. The two tutors exchanged between one and two dozen WhatsApp messages and had a 10–15 min Zoom call each Wednesday.

A short transcript (translated into English) of the tutors’ exchange in week 2 is as follows:

[…]

The tutors were apparently discussing the exercises from Figure 2, Figure 3 and Figure 4.

On Thursday morning, the tutors and the teaching assistant had a 15–20 min Zoom call. The tests on Fridays were automatically marked, with granular results that were immediately available for discussion with the author, the teaching assistant, and the tutors.

As could be expected, the choice of sacrificing student feedback was not welcomed by some students: “I would have liked to get the corrections to my homework, at least when I made serious mistakes”. “I think that if homework is not corrected, it is useless”.

Nevertheless, ten students explicitly mentioned having weekly assignments as a positive aspect, and 15 students appreciated the Thursday feedback-based recitation. This supports the hypothesis that granular individual feedback is not strictly necessary as long as some feedback is given and self-correction is made possible; in other words, in reference to the assumed theoretical framework, granular individual feedback does not appear to be an indispensable part of key strategies 3 and 5.

5.4. The Weekly Tests

The sheer number of students and the need for speedy evaluation forced us to use closed-ended questions. This was indeed problematic, but at least we had no issues with the (lack of) formative value of closed-ended questions.

Similar considerations forced a partial introduction of closed-ended questions in at-distance examinations; the exam was split into three shorter parts. The first part consisted of only closed-ended questions, and admittance to the second (semi-open-ended) part was allowed with a strictly positive score in the first part (wrong answers granted a negative score in such a way that the expected result of choosing random answers was equal to nil). Despite the very lax requirements, only 65% of students who took such an exam passed the first part; 27% of the students had a passing score (at least 4 out of 8) for the closed-ended questions, which was consistent with the rate of passing scores in the equivalent open-ended part in pre-pandemic tests (and was better with tests taken later on in the academic year, after most of the good students had passed the exam).

As opposed to the standard exams of the class, during the weekly tests, students were not allowed to use any material apart from a formula sheet that was provided to them; this allowed the introduction of simple questions on definitions or theorems, which replaced the open-ended questions of standard exams. This means that it was not possible to directly compare the difficulty of the weekly tests to that of the standard exams; nevertheless, the closed-ended exercises were similar enough that we felt that there was not any particular unfairness.

The tests were administered with the exam.net platform using a secured enclave that did not allow students to exit the examination window. Students were monitored by their phone camera, which was placed at their side, and each tutor was responsible for at most 20 students. As evidence that these measures were adequate in order to avoid cheating, we report that in June 2021, when the first in-person examination became possible, no students elected to take an at-distance exam. Students had one hour to take the exam, which was consistent with the timing of standard exams.

One version of the exam of week 2 is presented in Figure 5. Slight variants of the tests were used to impede cheating. Notice that the third question was actually somewhat open ended. The syllabus of week 2 consisted of functions, increasing and decreasing functions, maxima and minima, linear, quadratic, and power functions, exponentials, and logarithms.

The first question was graded as correct (+2 points), incorrect (−1 point), or no answer (0 points). Each correct item of the second question gave ½ point (0 points if incorrect). Partial credit was awarded for answers to the third question that were almost right. As was done during standard exams, the question were similar to some of the exercises shown during the recitations. A total of 113 students took the test, and 71 passed it (total score $\ge 4$); itemised results (average, standard deviation, percentiles) are provided in

Table 2. Results of the test in week 2.

	Exercise 1	Exercise 2	Exercise 3	Total
$\mu$	0.613	1.842	1.680	4.062
$\sigma$	1.089	0.344	0.571	1.53
10%	−1	1.5	1	2.5
25%	0	2	1.5	3
50%	0	2	2	4
75%	2	2	2	5.5
90%	2	2	2	6

.

5.5. Working at a Distance

The students could attend the recitations live on Zoom, but some of them chose only to follow them asynchronously, confirming the post-pandemic literature (cfr. [40]) that stated that the added liberty in choosing when to follow classes could outweigh the advantage of being able to interact with the teacher; 17 students mentioned the availability of lecture captures—which, at the University of Milan, were still a novelty in March 2020—as a plus, and one student stated that recordings made it possible for him to reconcile his summer job with the course. It should be mentioned that five students were working during the summer, and two gave up a summer job in order to spend enough time on the course. Some students explicitly claimed that lecture captures enabled them to watch lectures at a later and more convenient time, as well as to watch them again as needed.

The numbers of times that the material was accessed on the university’s e-learning platform during the five-week course are presented in

Table 3. Access numbers per week: individual users/downloads.

	Recitation Transcript	Homework	Test Solutions
Week 1	126/261	106/224	96/158
Week 2	116/200	122/229	62/85
Week 3	103/157	106/161	88/141
Week 4	109/202	106/186	45/58
Week 5	75/116	85/121	—

, and they confirm the previous points; unfortunately, the data on the lecture capture streams were not available. The test solutions for week 5 were not available during the time period under investigation.

Using Stanford’s Bandwidth Immediacy Matrix (Figure 6), the course could be classified as High Bandwidth/High Immediacy, and this, as will be discussed later, was a significant issue.

One remarkable fact emerging from the followup questionnaire is that at-distance teaching was seen by some as a way to improve classroom dynamics and partially solved the issued reported in [17]. Federico wrote: “This [course], I have to admit, is one of those rare occurrences where at-distance teaching was better than face-to-face teaching, since it was possible to see each exercise clearly, to hear clearly, and it was so much easier to ask questions—things that, when I attended recitations in my first year, were much more difficult to have”. In total, seven students praised the ability to interact with the teacher, although it is possible that some were comparing not with a pre-pandemic classroom, but with asynchronous classes in the spring term, as Ezio’s comment suggests: “Classes were live, so we could ask for clarification on the spot”.

Only one student mentioned the students’ forum. Indeed, only five threads were opened on mathematical topics (as opposed to organizational ones or those related to the interface), and each received an average of $0.6$ answers. This is consistent with the author’s experience with most single-purpose education- and non-education-related forums.

5.6. Helpfulness

Twenty-three students mentioned the helpfulness of the teaching staff as one of the positive aspects of the course. For some, this was connected to being “available during the summer break” or to being “willing to go overtime with lectures”, but for many, this helpfulness related to “going over basic topics that my colleagues who graduated from the more math-oriented high schools did not need, but were very useful to me” or to “the creation of a setting where no one would have been judged for the kind of question or clarification asked”. We can infer from these assertions and from the 16 mentions of clarity in the recitations that, most likely, good teaching as defined by [28] was attained; assuming that the summer course actually attained ambitious teaching, this was consistent with the results on affection towards mathematics mentioned at the end of Section 7.1.

5.7. Affect

Students were asked to describe mathematics with three adjectives. A total of 199 useful answers were gathered, and those that occurred the most were (translated by the author, gathering together different adjectives that could be translated with the same English word): difficult (27 occurrences), complicated (20), demanding (14), interesting (10), useful (9), anxiety-provoking, logical (7), boring (6), incomprehensible (5), precise, fascinating, and frustrating (3). In total, 77 descriptions bore a positive connotation, 50 referred to the cognitive load, 40 were a refusal of mathematics, and 32 referred to engagement.

While 46% of respondents claimed that their view of mathematics did not change, 39% answered that it improved slightly or very much after the course; this is important because teaching mathematics at the middle-school level (G6–G9) is a common job perspective for these students.

6. Forecasting Success

We followed Rizzo’s definition of success as passing the exam, with no reference to the grade [2]. Because Italian universities allow students to take an exam as many times as possible, we introduced two different metrics: passing the remedial course as a result of the weekly partial tests or having attended the course and passing the exam in September, the latest date that would unlock the second-year exams in February. In

Table 4. Freshman vs. non-freshman success.

	Total	Passed in August		Passed in September		Total Success
Freshmen	90	46	51%	18	21%	64	71%
Non-freshmen	26	18	69%	3	12%	21	81%
Total	116	64	55%	21	18%	85	73%

, we break down the numbers of students who succeeded, separating freshmen from other students.

Because we have little data about non-freshmen and we can assume they are, per se, weaker students, their better results could possibly be explained by a higher engagement.

6.1. Success and Attendance

In the following, for the reasons outlined above, we consider only the 90 freshman students that took part in the course. In

Table 5. Freshman success as a function of weeks attended.

Weeks Attended	Total	Passed in August		Passed in September		Total Success
1	5	0	0%	0	0%	0	0%
2	1	0	0%	0	0%	0	0%
3	4	0	0%	0	0%	0	0%
4	24	9	38%	5	21%	14	58%
5	56	37	66%	13	23%	50	89%

, we see that only students that missed at most one class were able to succeed; if this is perfectly reasonable for the first metric (it would have been technically possible to pass with only three tests, but it would have required very good grades), it shows a correlation between taking the course seriously and grasping any benefits in view of the September exam. We also saw that the success rate was significant for students who attended the whole course (of the six missing students, four could not pass the exam in February and two disappeared, most likely because they transferred to another program).

If we break down the group of students who skipped a week according to which week was skipped, we get the results in

Table 6. What happened to those that skipped exactly one week.

Skipped Week #	Total	Passed in August		Passed in September		Total Success
1	6	5	83%	0	0%	5	83%
3	2	0	0%	0	0%	0	0%
5	16	9	56%	2	13%	11	69%

. Since the weeks were independent and the grades were adjusted for missed weeks, we can conclude that those that skipped the first week because they were not aware of the course or were stilled involved in field activities fared as well as those who attended every week, while it is reasonable to assume that those who skipped the last week did so because their pass/fail status would not be affected, but only their grades (thus giving support to the assumption that we should use passing as a metric of success and not grades). Notice that the third week was the Ferragosto week, the central holiday of the holiday month; although there were not enough data to properly infer any conclusions, it could make sense to suppose a correlation between lack of success and setting of priorities.

We thus conclude that having attended weeks 2 to 5 was correlated positively with success in August ($p=0.0027$) and in September ($p<0.001$), and that having skipped more than one week implied a lack of success ($p<0.001$), even in September.

6.2. Success and Entrance Examination Results

Are the results from Table 4 and Table 6 any good? Reference [2] offered a way to relate the TOLC-C entrance exam score to the likelihood of passing an exam; we summarize the findings in

Table 7. Likelihood of passing the exam according to the TOLC-C score.

TOLC Result	${\mathbf{p}}_1$	${\mathbf{p}}_2$
≤0	0%	0%
1–3	7%	14%
4–6	14%	33%
7–9	36%	55%
10–12	58%	73%
13–15	59%	76%
16–18	87%	93%
19–20	100%	100%

, where $p_1$ is the likelihood of passing the exam at the first attempt, and $p_2$ is the likelihood of passing after any number of attempts within the same year.

Using the TOLC-C entrance exam score for the 90 freshmen, we can compare the expected outcome with the actual outcome; in

Table 8. Expected outcome vs. actual outcome of the course.

	Passed in August		Passed in September		Total Success
Expected outcome	16	18%	11	13%	28	31%
Actual outcome	46	51%	18	21%	64	71%

, we compare the number of students that one could expect to pass the exam given the population with the number of students that actually passed the exam to conclude that the course was indeed a success ($p<0.001$).

7. Conclusions and Outlook

The remedial course was an outright success; according to the estimates of the previous section, it allowed 36 students to pass an exam that they would not have passed during the year, forcing them either to drop out of the program or significantly delay it. Because 307 students were then (2020–2021) enrolled in the second year, 21% of the sophomores passed mathematics thanks to the summer course; of those, 12% would not have passed any exams.

Our data show that an at-distance remedial course during a time usually used for vacation could be implemented and, given the human resources, it might be a good idea to do so in a similar setting (i.e., a very high percentage of students with poor pre-academic knowledge of math).

What surprised us most was the number of participants; indeed, out of 114 answers to the final survey, 52 answered that they had already planned to spend the whole month studying math; four would be traveling, four working, four studying something else, and three resting (47 did not provide any answers).

The main issue was the sad condition of broadband access for many students (and for the teaching assistant); 47% spent the five weeks at home and 40% mostly or completely spent them at a vacationing spot; only 46% had a optic fiber/ADSL/wi-fi connections all the time, while 47% claimed to never have had any connection issues. Lecture captures and transcriptions of the teaching assistant’s notebook allowed some students to shift into a High-Bandwidth/Low-Immediacy course (see Figure 6). This did not solve the issue with the weekly tests, when connection difficulties were a significant source of stress for the students.

7.1. Why Was the Course a Success?

The availability of lecture captures, despite being explicitly mentioned only by 12 students, undoubtedly played a role (cfr. [42]); a key advantage was “being able to follow classes when you want it and where you want it, and then having a direct feedback with instructors during class”.

Many students mentioned the subdivision into five different subtopics—each with its own partial exam—as a key factor: “Every examination should be structured in the same way; I’d pass them all at the first strike. I don’t think I would have ever passed the normal math exam, since there are too many things that have to be remembered and dealt with all at the same time”. Some students welcomed the subdivision as “less university-like and more high-school-like, easing one’s organization”; this may alarm some colleagues, since a topos of Italian academia is the fear of turning tertiary education into a high school, following the Anglo-Saxon model ([43]).

Some underlined the importance of at-distance teaching in such a course: “I have to admit this is one of those rare instances when at-distance teaching was better than face-to-face teaching: I could clearly see each exercise, sound was good, and it was so much easier to ask questions”. “An environment was created where one was not judged for the type of question”. “I loved being able to study with my friends via Skype [sic!]”. Although these comments should inspire a different approach to face-to-face instruction, the rupture of immediacy in at-distance settings is difficult to duplicate in a classroom, especially given the importance of “fare la bella figura” (which could be roughly translated as “making a good impression” or “keeping up with appearances”, and could be argued as being the real Italian Weltanschauung) in Italian culture.

Many students expressed appreciation for the weekly homework and the corresponding markings; this came as a surprise to the author, since the few times that funding was made available for such tutoring, the results were less than stellar given a lack of interest on the part of the students (cheating being commonly considered in Italy a “student right”, it is usually considered unadvisable to count homework towards the final grade, as is usually done in other countries).

The psychological effect on students should not be understated: “[one thing I loved] was the vague similarity between [at-distance] recitations and face-to-face ones, which we miss, apart from the 2-h daily commute”; “I want to thank the instructors for dispelling the urban myth that professors see students just as student identification numbers”.

All of this points to two main explanations for the results observed: We were able to engage students (using attendance as a proxy for engagement), and the week-by-week approach together with a fast formative assessment feedback loop reduced the affective issues of students.

7.2. Is This the Right Approach?

One of the anonymous reviewers pointed out the risk of fragmentation in the view of mathematics that could be advanced by the approach we used.

I will not deny this risk, but I am not sure that a student sporting such a view—undoubtedly the result of thirteen years of frightful exposition to mathematics—could effectively be brought to overcome it in one term while struggling with understanding why $x\ge 3$ is not equivalent to $x^2\ge 9$.

This is much more of an affective rather than a cognitive issue. Computing the area of a plane region bounded by the graph of a function requires solving an inequality, while even the simplest differential equation will require a working knowledge of derivatives (indeed, these were two of the three items in the week 5 test).

Even more so when we, as mathematics instructors, ponder on the fact that most students dropping out of STEM degrees (or electively not enrolling in STEM degrees) do so because of fear of mathematics; for most life scientists, mathematics is just ancillary to statistics, which is just one of the tools that they will use in their academic careers.

Once enough data have been collected about the second-term statistics, it will be interesting to compare the outcomes of the students that passed this summer course against those of the other students.

7.3. What Should Be Changed?

A thorough revision of teachers’ praxeologies relating to a transmissive approach to teaching should be conducted in order to encourage situations where students would be more active ([23]). A better tutor–student ratio should allow for individual granular feedback on weekly homework, although, as mentioned, this fact is possibly not very important. Peer interaction should be fostered, both on the students’ forum and on informal channels; peer-to-peer review of assignments could be instrumental towards the goal of actually implementing key strategy 4.

Although it would not be feasible to add “theory” lessons (i.e., lectures) to the course schedule, the availability of short prerecorded videos from the fall 2020 term should allow students to address gaps in their preparation; the proposed exercises should be linked to specific videos.

Students should be better warned of what will be expected of them, especially in terms of the time involved (FA1).

7.4. What Cannot Be Changed?

The quality of an internet connection is completely out of our control; all teaching assistants and tutors were on vacation during the course and often had to rely on unreliable 4G connections. Some students had to drop out of the course for similar reasons.

The time schedule: Some students appreciated the structure given to their summer studies, and some students complained that superposition with their vacations was the main bad point. External constraints (July exams and field trips for the students; school opening on September 1st for many of the staff involved) made for very little play in the schedule.

The precalculus competence of many students was too low; most students spent the last two years of high school doing nothing more than calculus in their math classes, but issues stemmed from gaps at a much lower level. We wholeheartedly agree with the conclusion of [28]: “An alternative to calculus in high school that focuses on strengthening students’ understanding of algebra, geometry, trigonometry, and functional relations while building problem-solving skills would be very welcome”.

7.5. What Is Next?

Financial support for a 2021 summer course has been granted by the University of Milan; because enrollment has been halved, we expect to have fewer students and a much better tutor–student ratio. Some of the feedback gathered by the summer course will be integrated into the fall 2021 class; the number of mid-term exams should be increased from two to at least three, some kind of at distance communication (instant chat?) should be envisioned even if classes will return to being completely face to face, and, in general, the class should be redesigned around a formative assessment scheme.