Investigative Activities for Statistics Learning with 1st Grade Portuguese Students
Abstract
1. Introduction
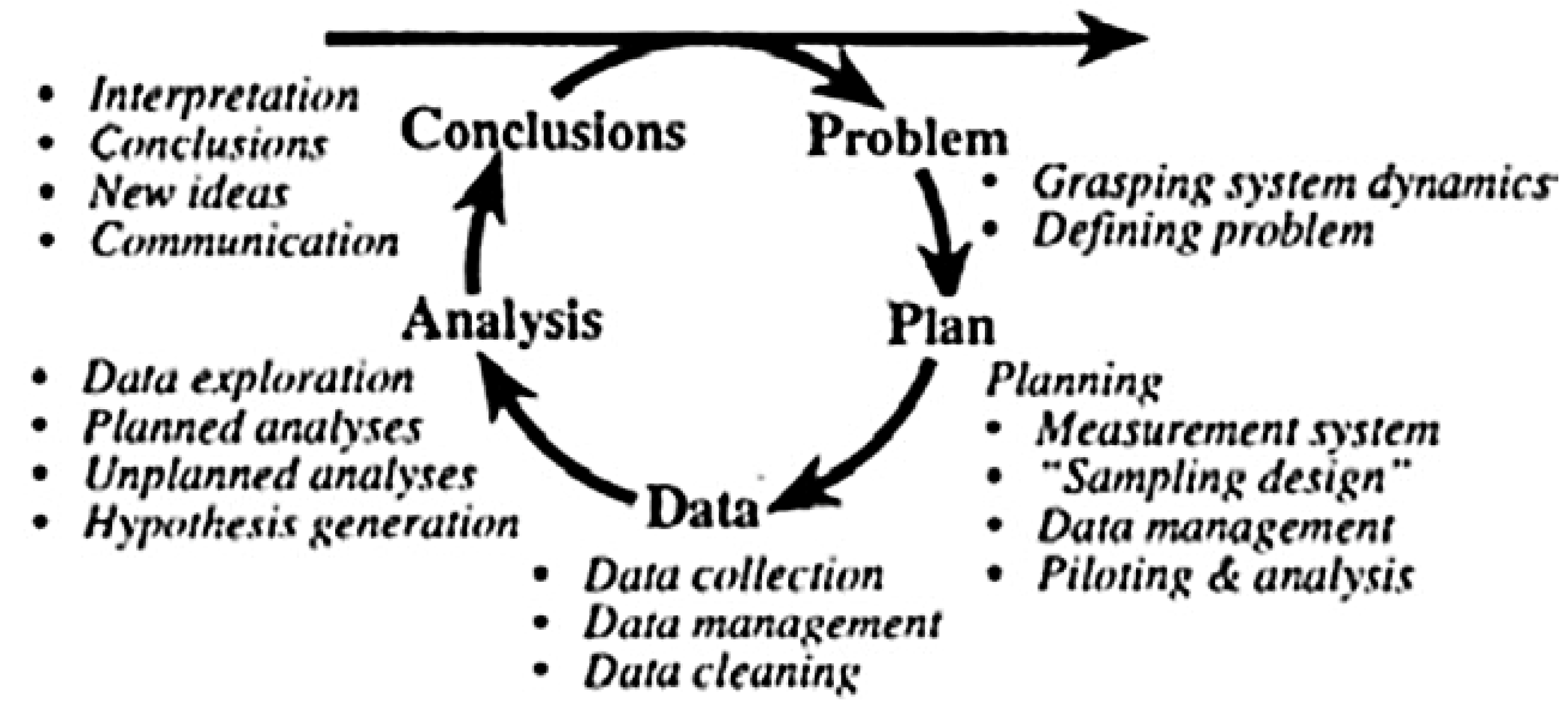
2. Investigative Activities in Learning Statistics
3. Method
3.1. Participants
3.2. Procedures
3.3. Method of Analysis
4. Results and Discussion
4.1. Execution of the Statistical Investigative Activity
4.1.1. Stage 1: Problem
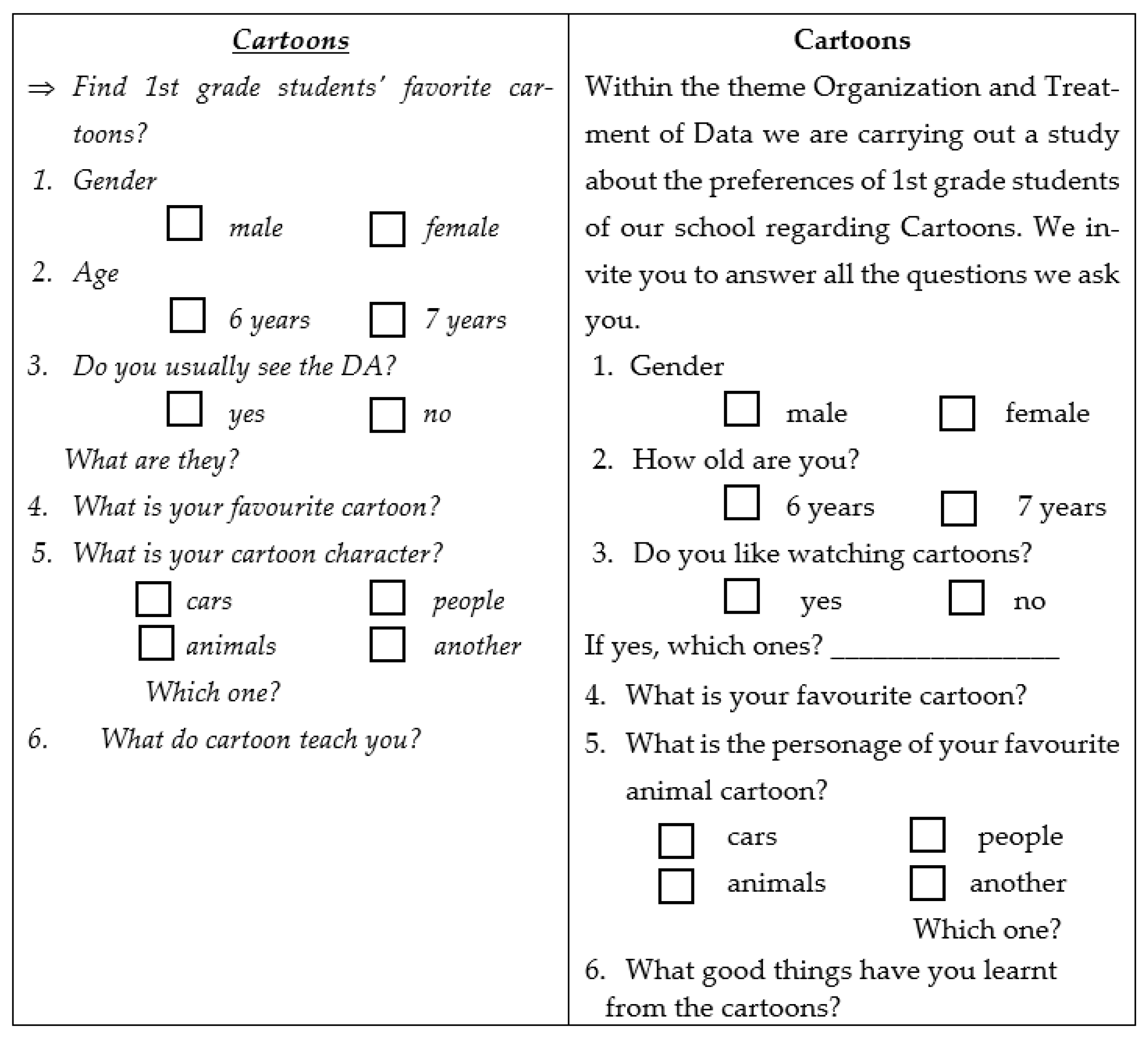
4.1.2. Stage 2: Plan
4.1.3. Stage 3: Collecting and Organizing Data
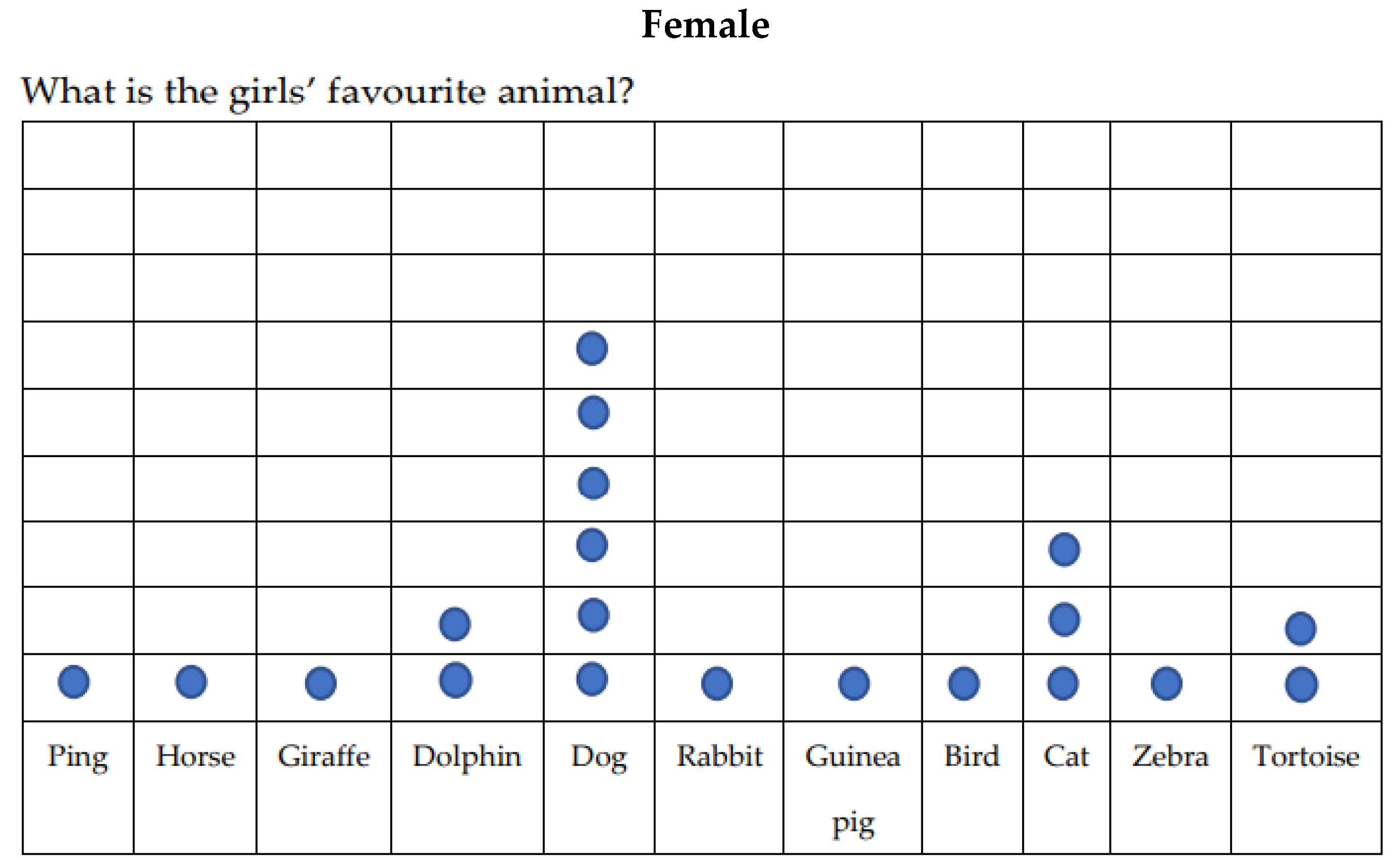
4.1.4. Stage 4: Data Analysis
4.1.5. Stage 5: Conclusion
4.2. Presentation of the Investigative Activity
4.3. Evaluation of the Learning Experience
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A


Appendix B

Appendix C

Appendix D

References
- Ministério da Educação e Ciência [MEC]. Aprendizagens Essenciais de Matemática para o Ensino Básico; Ministério de Educação e Ciência: Lisboa, Portugal, 2018. [Google Scholar]
- Abrantes, P.; Serrazina, L.; Oliveira, I. A Matemática na Educação Básica; Ministério da Educação, Direcção-Geral de Inovação e Desenvolvimento Curricular: Lisboa, Portugal, 1999; ISBN 9727421237. [Google Scholar]
- Batanero, C. Didáctica de la Estadística; Departamento de Didáctica de la Matemática, Universidad de Granada: Granada, Spain, 2001; ISBN 84-699-4295-6. [Google Scholar]
- Batanero, C.; Los Retos de la Cultura Estadística. Jornadas Interamericanas de Enseñanza de la Estadística. Buenos Aires: Conferência Inaugural. 2002. Available online: https://www.ugr.es/~batanero/pages/ARTICULOS/CULTURA.pdf (accessed on 10 July 2022).
- Ponte, J.P.; Noll, J. Building capacity in statistics teacher education. In The International Handbook of Research in Statistics Education; Springer International Handbooks of Education: Cham, Switzerland, 2017; pp. 433–455. ISBN 978-3-319-66193-3. [Google Scholar] [CrossRef]
- Martins, G.D.O.; Gomes, C.A.S.; Brocardo, J.; Pedroso, J.V.; Camilo, J.L.A.; Silva, L.M.U.; da Encarnacao, M.M.G.A.; Horta, M.J.d.V.C.; Calcada, M.T.C.S.; Nery, R.F.V.; et al. Perfil do Aluno à Saída da Escolaridade Obrigatória; Ministério de Educação e Ciência: Lisboa, Portugal, 2016; Available online: https://dge.mec.pt/sites/default/files/Curriculo/Projeto_Autonomia_e_Flexibilidade/perfil_dos_alunos.pdf (accessed on 5 July 2022).
- Ponte, J.P.; Serrazina, L. Didática da Matemática para o 1.º Ciclo do Ensino Básico; Universidade Aberta: Lisboa, Portugal, 2000. [Google Scholar]
- Ponte, J.P. Investigações Matemáticas e Investigações na Prática Profissional, 1st ed.; Editora Livraria da Física: Lisboa, Portugal, 2018; ISBN 9788578614881. [Google Scholar]
- Ponte, J.P. Gestão Curricular em Matemática; Associação dos Professores de Matemática: Lisboa, Portugal, 2005; pp. 11–34. ISBN 972-8768-16-8. [Google Scholar]
- Ponte, J.P.; Brocardo, J.; Oliveira, H. Investigações Matemáticas na Sala de Aula, 1st ed.; Autêntica: Belo Horizonte, Brasil, 2003. [Google Scholar]
- Santos, R.F.M. O Conhecimento de Estatística e da sua Didática de Futuros Professores. Ph.D. Thesis, Universidade de Lisboa, Lisboa, Portugal, 2015. [Google Scholar]
- Almeida, M.R. Imagens Sobre o Ensino e a Aprendizagem da Estatística; Instituto de Inovação Educacional: Lisboa, Portugal, 2002. [Google Scholar]
- Dias, E.; Viseu, F.; Cunha, M.C.; Martins, P.M. A natureza das tarefas e o envolvimento dos alunos nas atividades da aula de matemática. In Proceedings of the Atas do XII Congresso Internacional Galego-Português de Psicopedagogia, Braga, Portugal, 11–13 September 2013. [Google Scholar]
- Vara Pires, M. Investigações matemáticas: Aprender matemática com compreensão. Saber Educ. 2015, 20, 42–51. [Google Scholar] [CrossRef][Green Version]
- MacGillivray, H.; Pereira-Mendoza, L. Teaching statistical thinking through investigative projects. In Teaching Statistics in School Mathematics—Challenges for Teaching and Teacher Education: A Joint ICMI/IASE Study: The 18th ICMI Study; Burrill, G., Reading, C., Batanero, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 109–120. [Google Scholar]
- NCTM. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics, Inc.: Reston, VA, USA, 2002; ISBN 0-87353-480-8. [Google Scholar]
- Gal, I. Understanding statistical literacy: About knowledge of contexts and models. In Proceedings of the Actas del Tercer Congreso Internacional Virtual de Educación Estadística (CIVEEST), Granada, Spain, 21–24 February 2019. [Google Scholar]
- Gould, R. Data literacy is statistical literacy. Stat. Educ. Res. J. 2017, 16, 22–25. [Google Scholar] [CrossRef]
- Fernandes, J.A.; Portela, J. Elementos de estatística descritiva—A folha de cálculo no estudo de estatística. In Elementos da Matemática para Professores do Ensino Básico; Palhares, P., Ed.; Lidel: Lisboa, Portugal, 2004; pp. 53–112. [Google Scholar]
- Sousa, O. Investigações estatísticas no 6.º ano. In Reflectir e Investigar Sobre a Prática Profissional; GTI, Ed.; Associação dos Professores de Matemática: Lisboa, Portugal, 2002; pp. 75–97. [Google Scholar]
- Martins, M.E.; Ponte, J.P. Organização e Tratamento de Dados; Ministério da Educação, Direcção-Geral de Inovação e Desenvolvimento Curricular: Lisboa, Portugal, 2010. [Google Scholar]
- Martins, M.E.G.; Loura, L.C.C.; Mendes, M.F. Análise de Dados: Texto de apoio Para Professores do 1.º ciclo; Ministério da Educação, Direcção-Geral de Inovação e Desenvolvimento Curricular: Lisboa, Portugal, 2007. [Google Scholar]
- Fernandes, J.A.; Carvalho, C.F.; Correia, P.F. Contributos para a Caracterização do Ensino da Estatística nas Escolas. Bolema 2011, 24, 585–606. Available online: https://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/5109 (accessed on 3 June 2022).
- Batanero, C.; Godino, J.D. Prespectivas de la esducación estadística como área de investigación. In Líneas de Investigacional en Didática de las Matemáticas; Luengo, R., Ed.; Universidad de Extremadura: Extremadura, Spain, 2005; pp. 203–226. [Google Scholar]
- Ponte, J.P.; Fonseca, H. Orientações curriculares para o ensino da estatística: Análise comparativa de três países. Quadrante 2001, 10, 93–115. [Google Scholar]
- Alsina, A.; Annexa, E. Estadistica en contexto: Desarrollando un enfoque escolar comun para promover la alfabetizacion. TANGRAM 2021, 4, 71–98. [Google Scholar] [CrossRef]
- Branco, J.A. Mudanças no Ensino da Estatística. Bol. Soc. Port. Estatística, 2006; 19–23. [Google Scholar]
- Batanero, C.; Godino, J.D.; Roa, R. Training teachers to teach probability. J. Stat. Educ. 2004, 12, 1–19. [Google Scholar] [CrossRef]
- Chick, H.L.; Pierce, R.U. Teaching Statistics at the primary school level: Beliefs, affordances, and pedagogical content knowledge. In Proceedings of the ICMI Study 18, Monterrey, Mexico, 30 June–4 July 2008. [Google Scholar]
- Gal, I. Adults’ statistical literacy: Meanings, components, responsabilities. Int. Stat. Rev. 2002, 70, 1–25. [Google Scholar] [CrossRef]
- Garfield, J.; Franklin, C. Assessment of learning, for learning, and as learning in Statistics Education. In Teaching Statistics in School Mathematics—Challenges for Teaching and Teacher Education: A Joint ICMI/IASE Study; Batanero, C., Burril, G., Reading, C., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 133–145. [Google Scholar]
- Rumsey, D.J. Statistical Literacy as a Goal for Introductory Statistics Courses. J. Stat. Educ. 2002, 10, 1–12. [Google Scholar] [CrossRef]
- Curcio, F. Developing Graph Comprehension: Elementary and Middle School Activities; NCTM: Reston, VA, USA, 1994. [Google Scholar]
- Santos, L.; Brocardo, J.; Pires, M.; Rosendo, A.I. Investigações matemáticas na aprendizagem do 2.º ciclo do ensino básico ao ensino superior. In Actividades de Investigação na Aprendizagem da Matemática e na Formação de Professores; Ponte, J.P., Costa, C., Rosendo, A.I., Maia, E., Figueiredo, N., Dionísio, A.F., Eds.; Secção de Educação Matemática da Sociedade Portuguesa de Ciências da Educação: Lisboa, Portugal, 2002; pp. 83–106. [Google Scholar]
- Brocardo, J. As Investigações na Aula de Matemática: Um Projecto Curricular no 8.º ano. Ph.D. Thesis; Universidade de Lisboa: Lisboa, Portugal, 2001. [Google Scholar]
- Fertuzinhos, M.L.R. As Tarefas de Natureza Investigativa na Aprendizagem de Conteúdos do Tema Funções do 10.º ano; Master´s Thesis, Universidade do Minho: Braga, Portugal, 2014. [Google Scholar]
- Ernest, P. Investigações, resolução de problemas e pedagogia. In Investigar para Aprender Matemática: Textos Selecionados; Abrantes, P., Leal, L., Ponte, J.P., Eds.; APM: Lisboa, Portugal, 1996; pp. 25–47. [Google Scholar]
- Serrazina, L.; Vale, I.; Fonseca, H.; Pimentel, T. Investigações matemáticas e profissionais na formação de professores. In Actividades de Investigação na Aprendizagem da Matemática e na Formação de Professores; Ponte, J.P., Costa, C., Rosendo, A.I., Maia, E., Figueiredo, N., Dionísio, A.F., Eds.; Secção de Educação Matemática da Sociedade Portuguesa de Ciências da Educação: Lisboa, Portugal, 2002; pp. 41–58. [Google Scholar]
- Batanero, C.; Arteaga, P.; Gea, M.M. El Currículo de estadística: Reflexiones desde uma prespectiva internacional. UNO 2012, 59, 9–17. [Google Scholar]
- PfannKuch, M.; Horring, J. Developing statistical thinking in a secondary school: A collaborative curriculum development. In Curricular Development in Statistics Education International Associations for Statistical Educacion; Burril, G., Camden, M., Eds.; International Statistical Institute: Lund, Sweden, 2004; pp. 204–218. [Google Scholar]
- Wild, C.J.; Pfannkuch, M. Statistical thinking in empirical enquiry. Int. Stat. Rev. 1999, 67, 223–265. [Google Scholar] [CrossRef]
- Shaughnessy, J.M. Research on statistics learning and reasoning. In The Second Handbook of Research on Mathematics; Lester, F.K., Ed.; NCTM: Reston, VA, USA, 2007; pp. 957–1010. [Google Scholar]
- Burgess, T.A. Teacher Knowledge of and for Statistical Investigations. In Teaching Statistics in School Mathematics- Challenges for Teaching and Teacher Education: A Joint ICMI/IASE Study; Batanero, C., Burril, G., Reading, C., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 259–270. [Google Scholar]
- Veia, L.; Brocardo, J.; Ponte, J.P. Uma tarefa de investigação em organização e tratamento de dados no 1. º ciclo: Realização da tarefa e reflexão da professora. In Proceedings of the Atas do XXV Seminário de Investigação em Educação Matemática, Braga, Portugal, 9–10 April 2014; Martinho, M.H., Ferreira, R.A., Boavida, A.M., Menezes, L., Eds.; 2014; pp. 229–242. [Google Scholar]
- McMillan, J.; Schumacher, S. Research in Education Evidence-Based Inquiry, 7th ed; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Cunha, C.; Galindro, P. O Cuquedo; Livros Horizonte: Lisboa, Portugal, 2011. [Google Scholar]
- Sfard, A. Thinking as Communicating: Human Development, the Growth of Discourses, and Mathematizing; Universtity Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Vieira, I.S. Organização e Tratamento de Dados Estudo de Caso no 5.º ano de Escolaridade. Master’s Thesis, Instituto Politécnico de Leiria, Leiria, Portugal, 2012. [Google Scholar]
- Ponte, J.P. Investigations and explorations in the mathematics classroom. ZDM 2007, 39, 419–430. [Google Scholar] [CrossRef]
- Andrade, N.M.G. Aprendizagem da Estatística no 2.º ano de Escolaridade Através de Atividades Investigativas. Master’s Thesis, Universidade do Minho, Braga, Portugal, 2012. [Google Scholar]
- Fernandes, J.A.; Carvalho, C.F.; Ribeiro, S.A.L. Caracterização e implementação de tarefas de Estatística: Um exemplo no 7.º ano de escolaridade. Zetetiké 2007, 15, 27–61. [Google Scholar]
- Martins, C.; Pires, M.V.; Barros, P.M. Conhecimento estatístico: Um estudo com futuros professores. In Proceedings of the Actas do XIX Encontro de Investigação em Educação Matemática, Números e Estatística—Refletindo no Presente, Perspetivando o Futuro, Vila Real, Portugal, 6–9 July 2009; Secção de Educação Matemática da Sociedade Portuguesa de Ciências da Educação: Lisboa, Portugal, 2009; pp. 1–12. [Google Scholar]
- Carvalho, C. Interação Entre Pares: Contributos Para a Promoção do Desenvolvimento Lógico e do Desempenho Estatístico, no 7.º ano de Escolaridade. Ph.D. Thesis, Universidade de Lisboa, Lisboa, Portugal, 2001. [Google Scholar]
- Balachowski, M.M. Trends in the statistics classroom since NCTM standards. In Proceedings of the Fifth International Conference on Teaching of Statistics, Singapore, 21–26 June 1998; Volume 1, pp. 75–76. [Google Scholar]






| Types of Answer | % of Students | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pre-Test | Post-Test | |||||||||||
| 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | |
| Correct | 15 | 100 | 30 | 75 | 10 | 5 | 95 | 100 | 100 | 100 | 100 | 95 |
| Incorrect | 85 | 0 | 70 | 25 | 70 | 60 | 5 | 0 | 0 | 0 | 0 | 5 |
| No answer | 0 | 0 | 0 | 0 | 20 | 35 | 0 | 0 | 0 | 0 | 0 | 0 |
| Types of Answer | % of Students | |||||||
|---|---|---|---|---|---|---|---|---|
| Pre-Test | Post-Test | |||||||
| 2.1 | 2.2 | 2.3 | 2.4 | 2.1 | 2.2 | 2.3 | 2.4 | |
| Correct | 85 | 10 | 10 | 0 | 100 | 100 | 100 | 100 |
| Incorrect | 15 | 90 | 85 | 15 | 0 | 0 | 0 | 0 |
| No answer | 0 | 0 | 5 | 85 | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, A.C.; Viseu, F.; Aires, A.P.; Neto, T.B. Investigative Activities for Statistics Learning with 1st Grade Portuguese Students. Educ. Sci. 2022, 12, 665. https://doi.org/10.3390/educsci12100665
Silva AC, Viseu F, Aires AP, Neto TB. Investigative Activities for Statistics Learning with 1st Grade Portuguese Students. Education Sciences. 2022; 12(10):665. https://doi.org/10.3390/educsci12100665
Chicago/Turabian StyleSilva, Ana Catarina, Floriano Viseu, Ana Paula Aires, and Teresa B. Neto. 2022. "Investigative Activities for Statistics Learning with 1st Grade Portuguese Students" Education Sciences 12, no. 10: 665. https://doi.org/10.3390/educsci12100665
APA StyleSilva, A. C., Viseu, F., Aires, A. P., & Neto, T. B. (2022). Investigative Activities for Statistics Learning with 1st Grade Portuguese Students. Education Sciences, 12(10), 665. https://doi.org/10.3390/educsci12100665







