The Concept of Observer in Science Teaching in Middle School: Pre-Instructional Knowledge as a Lever for Learning rather than an Obstacle
Abstract
:1. Introduction
2. Theoretical Background
2.1. Cognitive Difficulties in Learning Science
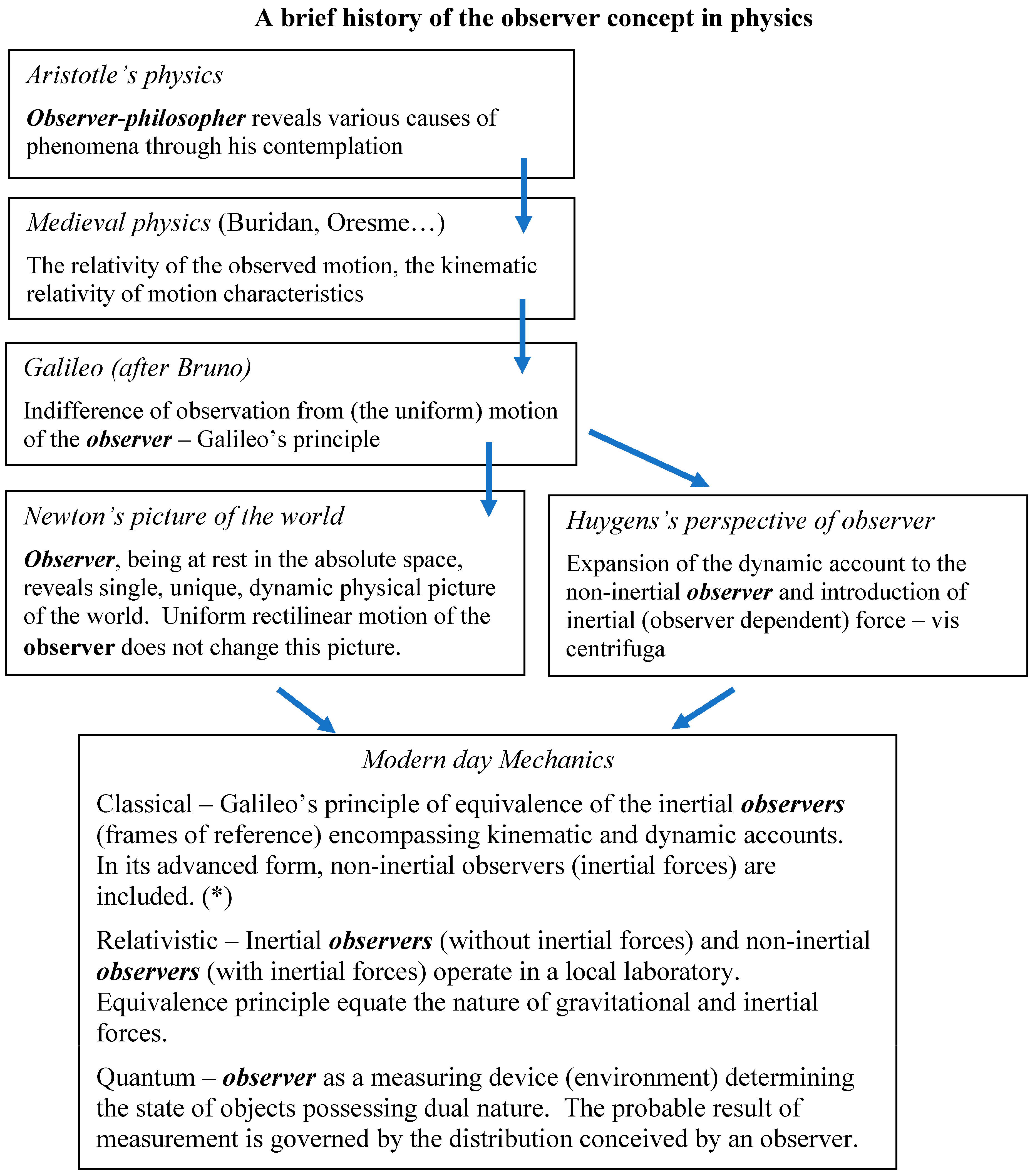
2.2. The Concept of Observer in Physics
2.3. The Observer in Physics Teaching in School
2.4. Intuitive Knowledge and the Observer Concept
2.5. Concept Definition and the Concept of Observer
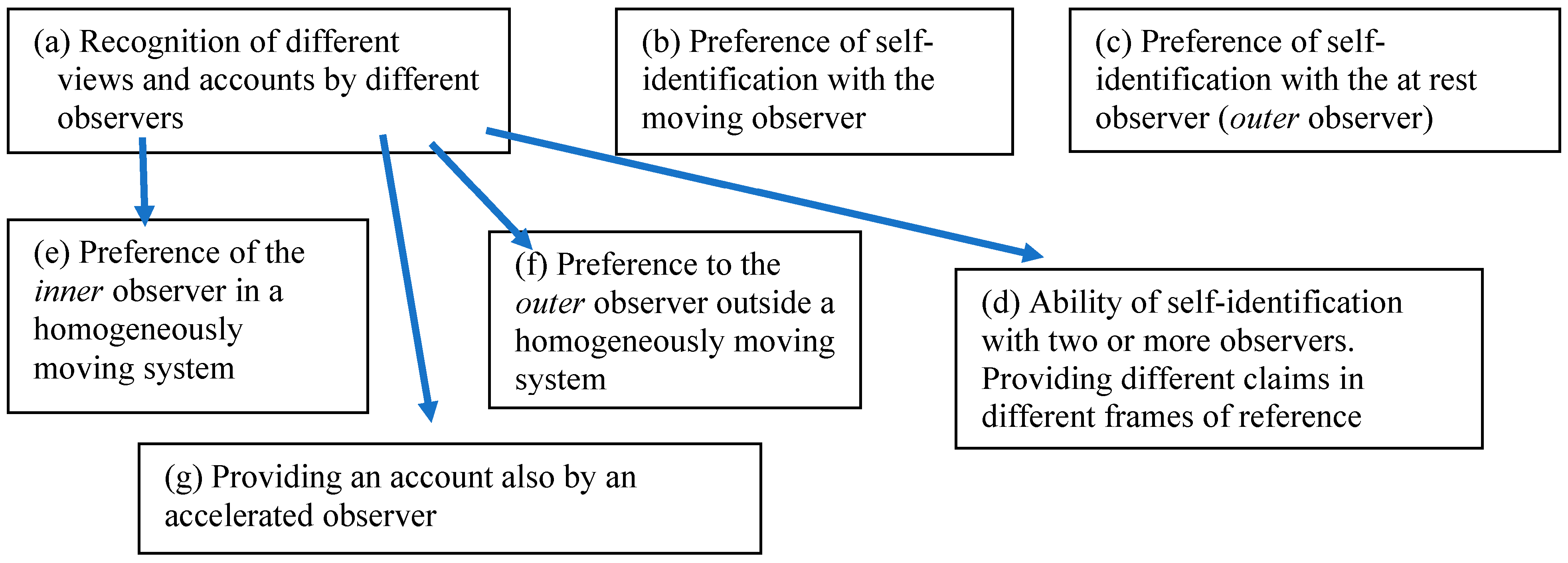
2.6. Space of Learning and the Observer
2.7. The Intention of This Study
3. The Experiment and Its Methodology
3.1. Rational and Research Questions
3.2. Participants and Setting
3.3. Learning Materials and Teaching
3.4. Data Collection and Assessment Tools
3.4.1. Pre-Test
3.4.2. Post-Test-A
3.4.3. Post-Test-B
3.4.4. Attitude Feedback
4. Main Findings and Analysis
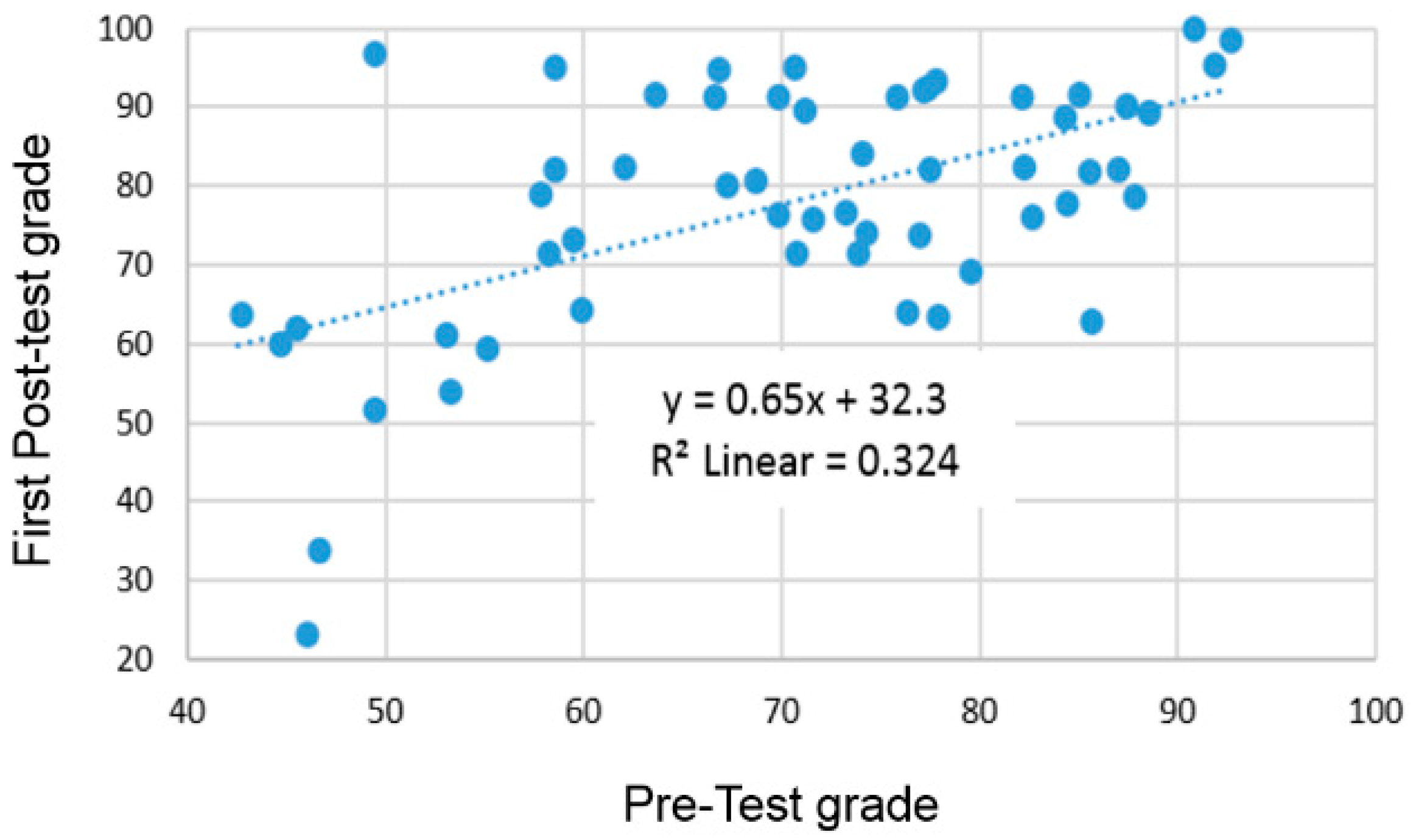
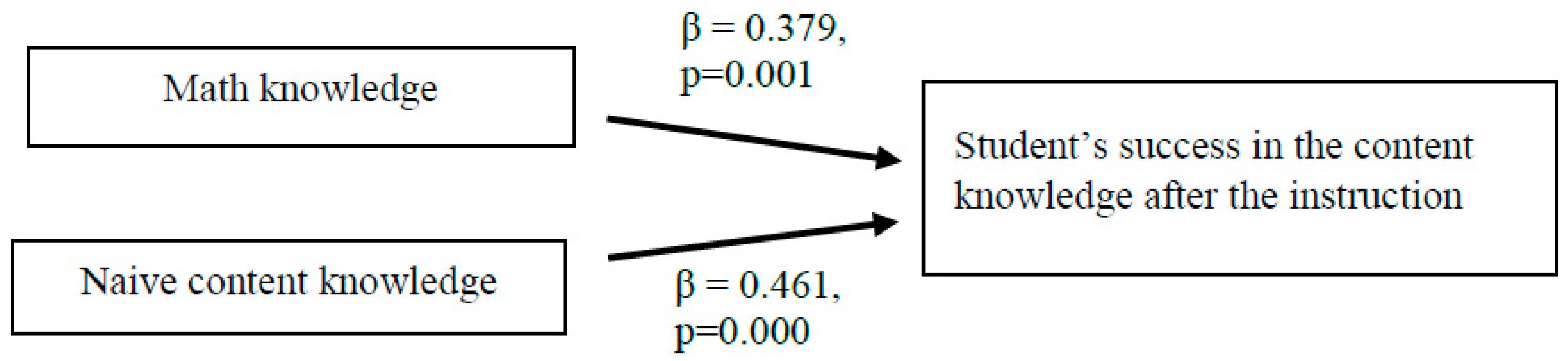
4.1. Pretest
- Question: Guy claims that the earth we live on is in the shape of a sphere.
- Ben claims that the ground is as flat as a round disk.
- Who do you think is right? How do you know?
- What is the reason for the disagreement between Guy and Ben?
- Students answered:
- -
- Guy is right, because I have seen images of the Earth from a distance and it is really a sphere (Category c).
- -
- Ben trusts what he sees, and he sees that the earth is flat. It happens that the Earth is a large star relative to humans, and we cannot appreciate its shape when we are on it (Category a).
- -
- Actually, both of them are right, the disagreement stems from the different spatial perception by the two. Ben perceives reality directly and Guy treats it in a more inclusive way. Each of them holds a view from a different place (Category d)
4.2. Post-Test-A
| Topic | The Abilities Examined | Average Scores (%) |
|---|---|---|
| Kinematics | Manipulation with the graphs of time dependence of displacement, distance and velocity in different frames of reference | 86 (25 *) |
| Calculation of displacement and distance by three inertial observers | 76 (31) | |
| Algebraic accounts of motion by three inertial observers (computation of time to the meeting) | 83 (30) | |
| Understanding of legitimate accounts by different observers (variants and invariants) | 79 (35) | |
| Choosing the most efficient frame of reference | 78 (32) | |
| Ability to relate between the graphs by different observers | 69 (24) | |
| Describing trajectory by different observers | 92 (18) | |
| Weighted average | 80 (18) | |
| Forces | Providing examples of force dependence on the observer | 64 (41) |
| Distinguishing between theoretical and operational force definitions | 86 (23) | |
| The force account by an observer on a rotating platform. Inertial force. | 81(33) | |
| The force account of the rotation motion by an inertial observer | 77 (34) | |
| The force account of linearly accelerated body by a non-inertial observer | 83 (23) | |
| The force account of linearly accelerated body by an inertial observer | 79 (18) | |
| Explanation and implementation of Galileo’s principle of relativity | 95(06) | |
| Weighted average | 76 (20) | |
| Weight and Gravitation | Weight and gravitation—the account by operational and gravitational definitions | 73 (23) |
| Explanation of Newton’s cannonball thought experiment | 79 (28) | |
| Explanation of weightlessness in a satellite by an observer at rest relating to the Sun | 63 (40) | |
| The force account for an astronaut orbiting the Earth and for a person in a free-falling elevator by the observer at rest on the ground | 74 (16) | |
| Explaining weightlessness by an astronaut in a satellite and by a person in a free-falling elevator | 85 (30) | |
| Identifying the forces acting on the astronaut orbiting the earth and acting on a person in a falling elevator by an inside observer | 81 (24) | |
| Understanding up and down directions as operationally defined relative concepts | 89 (21) | |
| Weighted average | 81 (15) |
4.3. Post-Test-B
- (i)
- The experimental group’s answers were more accurate with accounts involving frames of reference/observer, while the students in the control group never used this concept.
- (ii)
- The experimental group used richer vocabulary and precise concept definitions.
- (iii)
- Many in the experimental group introduced more than one solution to each problem, for example, two explanations addressing the falling of heavy and light bodies. One student wrote:
“both bodies have the same velocity because the earth attracts with greater force the heavier body (greater mass) and therefore the acceleration is the same as the formula F = ma implies”. Using the operational definition of weight, he wrote: “as they are free falling, the weight of both is zero.”
- (iv)
- In the questions that addressed a moving train or ship, a substantial portion (30% to 62% of the control group, depending on the problem) solved the problem with respect to the accelerated platform, in contrast to the traditional curriculum. This confirmed the previous finding that students, even those never instructed in the use of accelerated frames of reference and inertial force, in practice do employ accelerated frames and introduce inertial forces [61].
4.4. Affective Feedback
“I think this expansion of material helps [the class] to be interesting and attract people to study physics.” (S-1)
“With the observer concept, it was more interesting and more challenging, more fun to learn and listen in classes.” (S-2)
“I think learning the subject of the observer overall is important, but for me it was difficult because I did not fully understand things. But this subject made me think about life differently.” (S-3)
“I think the benefit of the method is that it makes students understand the material better and be more interested, but it’s also more to learn, so for some it’s harder.” (S-4)
“I liked the fact that it really interested me. The account is more difficult but raises greater interest. Due to the learning about observer all my thinking on questions and problems has changed.” (S-5)
“The advantages of this material are that it makes you more thoughtful, but the disadvantage is that everyday things we thought obvious, can be confusing when you look at them from different perspectives.” (S-6)
“I liked that there was no single correct answer to explain a phenomenon but several. The advantages in my opinion is the link to everyday life and the disadvantage is that it can be confusing. It totally changed my attitude to physics and made me want to learn and know it more.” (S-7)
“My attitude towards physics has changed because I have seen that physics is not just one view, the same answer can be reached in variety of ways.” (S-8)
“I loved that we learned about how to see the world in different ways and how to analyze different situations. Because of the learning this year I chose to keep learning physics in high school.” (S-9)
“I was sure that physics is a very difficult stuff, full of formulas, and when I learned about the observer, I realized that physics explains life and phenomena easily.” (S-10)
“This subject [observer] connects physics to everyday life and makes it more interesting… I’ll take physics in high school (S-11)
5. Discussion and Conclusions
5.1. The Feasibility and Effectiveness of the New Teaching
5.2. Curricular Representation of the Classical Theory
5.3. Curricular Relationship with Intuition
... one of the difficulties in achieving this goal is the fact that students come to mechanics classes with intuitive perceptions about motion and its causes, perceptions built from an early age during interaction with the environment, and therefore well rooted in consciousness. The intuitive perceptions are far from the Newtonian worldview and weigh on its internalization and formation. (our emphasis)
5.4. Impact on Misconceptions
6. Coda
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gagne, R.M. The Conditions of Learning; Holt, Rinehart and Winston: New York, NY, USA, 1970. [Google Scholar]
- Ginsburg, H.; Opper, S. Piaget’s Theory of Intellectual Development; Prentice Hall: Englewood Cliff, NJ, USA, 1969. [Google Scholar]
- Flavell, J.H.; Miller, P.H.; Miller, S.A. Cognitive Development; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Karplus, R. Science Teaching and the Development of Reasoning. J. Res. Sci. Teach. 1977, 14, 169–175. [Google Scholar] [CrossRef]
- Smith, J.P.; DiSessa, A.A.; Roschelle, J. Misconceptions reconceived: A constructivist analysis of knowledge in transition. J. Learn. Sci. 1994, 3, 115–163. [Google Scholar] [CrossRef]
- DiSessa, A. A Bird’s-Eye View of the “Pieces” vs. “Coherence” Controversy (From the “Pieces” Side of the Fence). In International Handbook of Research on Conceptual Change; Vosniadou, S., Ed.; Routledge: New York, NY, USA, 2008; pp. 35–60. [Google Scholar]
- Minstrell, J. Facets of students’ knowledge and relevant instruction. In Research in Physics Learning: Theoretical Issues and Empirical Studies; Duit, R., Goldberg, F., Niedderer, H., Eds.; IPN: Kiel, Germany, 1992; pp. 110–128. [Google Scholar]
- DiSessa, A. Toward an epistemology of physics. Cogn. Instr. 1993, 10, 105–225. [Google Scholar] [CrossRef]
- Galili, I.; Hazan, A. The influence of historically oriented course on students’ content knowledge in optics evaluated by means of facets-schemes analysis. Phys. Educ. Res. Am. J. Phys. 2000, 68, S3–S15. [Google Scholar] [CrossRef]
- Kuhn, T.S. The Structure of Scientific Revolutions; University of Chicago Press: Chicago, IL, USA, 1970. [Google Scholar]
- Posner, G.J.; Strike, K.A.; Hewson, P.W.; Gertzog, W.A. Accommodation of a Scientific Conception: Toward a Theory of Conceptual Change. Sci. Educ. 1982, 66, 211–227. [Google Scholar] [CrossRef]
- Piaget, J. Genetic Epistemology; Columbia University Press: New York, NY, USA, 1970. [Google Scholar]
- Viennot, L. Spontaneous Reasoning in Elementary Dynamics. Eur. J. Sci. Educ. 1979, 1, 205–221. [Google Scholar] [CrossRef]
- Champagne, A.B.; Klopfer, L.E.; Anderson, J.H. Factors influencing the learning of classical mechanics. Am. J. Phys. 1980, 48, 1074–1079. [Google Scholar] [CrossRef]
- McCloskey, M. (a) Naïve Theories of motion. In Mental Models; Genter, D., Stevens, A.L., Eds.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1983; pp. 299–324. [Google Scholar]
- McCloskey, M. (b) Intuitive Physics. Sci. Am. 1983, 248, 122–130. [Google Scholar] [CrossRef]
- Brown, D.E. Students’ concept of force: The importance of understanding Newton’s third law. Phys. Educ. 1989, 24, 353–358. [Google Scholar] [CrossRef]
- Driver, R.; Squires, A.; Rushworth, P.; Wood-Robinson, V. Making Sense of Secondary Science: Research into Children’s Ideas; Routledge: New York, NY, USA, 1994. [Google Scholar]
- Galili, I.; Bar, V. Motion implies force. Where to expect vestiges of the misconception? Int. J. Sci. Educ. 1992, 14, 63–81. [Google Scholar] [CrossRef]
- Shtulman, A.; Harrington, K. Tensions between science and intuition across the lifespan. Top. Cogn. Sci. 2016, 8, 118–137. [Google Scholar] [CrossRef] [PubMed]
- Singh, C.; Schunn, C.D. Connecting three pivotal concepts in K-12 science state standards and maps of conceptual growth to research in physics education. arXiv 2016, arXiv:1603.06024. [Google Scholar]
- Stein, H.; Galili, I. The Impact of Operational Definition of Weight Concept on Students’ Understanding of Physical Situations. Int. J. Res. Sci. Math. Educ. 2014, 13, 1487–1515. [Google Scholar] [CrossRef]
- Stein, H.; Galili, I.; Schur, Y. Teaching New Conceptual Framework of Weight and Gravitation in the Middle School. J. Res. Sci. Teach. 2015, 52, 1234–1268. [Google Scholar] [CrossRef]
- Galili, I.; Bar, V.; Brosh, Y. Teaching Weight-Gravity and Gravitation in Middle School—Testing a New Instructional Approach. Sci. Educ. 2017, 26, 977–1010. [Google Scholar]
- Hewson, P.W.; Hewson, M.G. The role of conceptual conflict in conceptual change and the design of science instruction. Instr. Sci. 1984, 13, 1–13. [Google Scholar] [CrossRef]
- Grayson, D. Concept substitution: A teaching strategy for helping students disentangle related physics concepts. Am. J. Phys. 2004, 72, 1126–1133. [Google Scholar] [CrossRef]
- Losee, J. A Historical Introduction to the Philosophy of Science; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Clagett, M. The Science of Mechanics in the Middle Ages; The University of Wisconsin Press: Madison, WI, USA, 1959. [Google Scholar]
- De Angelis, A.; Santo, C.E. The contribution of Giordano Bruno to the principle of relativity. J. Astron. Hist. Herit. 2015, 18, 241–248. [Google Scholar]
- Galilei, G. Dialogue Concerning the Two chief World Systems—Ptolemaic and Copernican; University of California Press: Berkeley, CA, USA, 1632/1953. [Google Scholar]
- Mach, E. The Science of Mechanics, a Critical and Historical Account of Its Development; Open Court: La Salle, IL, USA, 1883/1989. [Google Scholar]
- Huygens, C. ; Mahoney, M.S., Translator; 1659/1703; XVI. On Centrifugal Force. De vi Centrifuga, Oeuvres Complètes. pp. 255–301. Available online: https://www.princeton.edu/ (accessed on 5 January 2023).
- Galili, I. Scientific Knowledge Considered as a Culture–The Pleasure of Understanding (Ch.4); Springer: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-030-80200-4. [Google Scholar]
- Galili, I.; Goren, E. Summary Lecture as a Delay Organizer of Cultural Content Knowledge–The Case of Classical Mechanics. Sci. Educ. 2022, 1–50. [Google Scholar] [CrossRef]
- Galili, I.; Kaplan, D. Extending the use of the relativity principle: Some pedagogical advantages. Am. J. Phys. 1997, 65, 328–335. [Google Scholar] [CrossRef]
- Galili, I.; Kaplan, D. Changing approach in teaching electromagnetism in a conceptually oriented introductory physics course. Am. J. Phys. 1997, 65, 657–668. [Google Scholar] [CrossRef] [Green Version]
- Tefft, B.J.; Tefft, J.A. Galilean Relativity and the Work-Kinetic Energy Theorem. Phys. Teach. 2007, 45, 218–220. [Google Scholar] [CrossRef]
- Kaufman, R. Work & Inertial Frames. Phys. Teach. 2017, 55, 561. [Google Scholar]
- Ohanian, H.C. Physics; Norton: New York, NY, USA, 1989. [Google Scholar]
- Einstein, A.; Infeld, L. Evolution of Physics; Cambridge University Press: Cambridge, UK, 1938. [Google Scholar]
- Born, M. Einstein’s Theory of Relativity; Dover: New York, NY, USA, 1962. [Google Scholar]
- Born, M. Atomic Physics; Hafner: New York, NY, USA, 1962. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Calendon Press: Oxford, UK, 1958. [Google Scholar]
- Hobson, A. Phys. Concepts and Connect.; Person Education: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Galili, I. Towards a Refined Depiction of Nature of Science. Applications to Physics Education. Sci. Educ. 2019, 28, 503–537. [Google Scholar] [CrossRef]
- Nussbaum, J. Children’s conception of the Earth as a cosmic body. Sci. Educ. 1979, 63, 83–93. [Google Scholar] [CrossRef]
- Nussbaum, J. The Earth as a cosmic body. In Children’s Ideas in Science; Driver, R.E., Tiberghien, G.A., Eds.; Open University Press: Milton Keynes, UK, 1985; pp. 170–192. [Google Scholar]
- Askari, E. Teaching Seasons as Conceptually Rich Subject Matter of Optics to the Gifted Students of Elementary School. Master’s Thesis, The Hebrew University of Jerusalem, Jerusalem, Israel, 2015. [Google Scholar]
- Gredler, M.E. Learning and Instruction; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Piaget, J. The Child’s Conception of Physical Causality; Harcourt Brace & Co.: New York, NY, USA, 1930. [Google Scholar]
- Dugas, R. A History of Mechanics; Dover: New York, NY, USA, 1988. [Google Scholar]
- Galili, I.; Tseitlin, M. Newton’s first law: Text, translations, interpretations, and physics education. Sci. Educ. 2003, 12, 45–73. [Google Scholar]
- French, A. Newtonian Mechanics; MIT Press: Boston, MA, USA, 1971. [Google Scholar]
- Alonso, M.; Finn, E.J. Physics; Eddison-Wesley: Reading, MA, USA, 1991; pp. 112–114. [Google Scholar]
- Kleppner, D.; Kolenkow, R. An Introduction to Mechanics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Müller, R.; Wiesner, H. Teaching quantum mechanics on an introductory level. Am. J. Phys. 2002, 70, 200–2009. [Google Scholar] [CrossRef] [Green Version]
- Weissman, E.Y.; Merzel, A.; Katz, N.; Galili, I. Teaching quantum mechanics in high-school—Discipline-Culture approach. J. Phys. Conf. Ser. 2019, 1287, 012003. [Google Scholar] [CrossRef] [Green Version]
- Weissman, E.Y.; Merzel, A.; Katz, N.; Galili, I. Teaching quantum physics as a structured physics theory in high school. J. Phys. Conf. Ser. 2021, 1929, 012051. [Google Scholar] [CrossRef]
- Camp, C.W.; Clement, J.J. Preconceptions in Mechanics; Kendall/Hunt: Dubuque, Iowa, 1964. [Google Scholar]
- Mazur, E. Peer Instruction. In A User’s Manual; Prentice HallUpper: Saddle River, NJ, USA, 1997. [Google Scholar]
- Galili, I.; Kaplan, D. Students interpretation of water surface orientation and inertial forces in physics curriculum. Prax. Nat. Phys. Sch. 2002, 51, 2–11. [Google Scholar]
- Pendrill, A.-M. Comment on ‘Pendulum: The partial and global approach’. Phys. Educ. 2023, 58, 018001. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Nature of Some of Physical Concepts; Philosophical Library: New York, NY, USA, 1927/1952. [Google Scholar]
- Reichenbach, H. The Philosophy of Space and Time; Dover: New York, NY, USA, 1927/1958. [Google Scholar]
- Hesse, M. Operational Definition and Analogy in Physical Theories. Br. J. Philos. Sci. 1952, 2, 281–294. [Google Scholar] [CrossRef]
- Margenau, H. The Role of Definitions in Science. In The Nature of Physical Reality; McGraw-Hill: New York, NY, USA, 1950. [Google Scholar]
- Karplus, R. Introductory Physics: A Model Approach; Benjamin: New York, NY, USA, 1969/2003. [Google Scholar]
- Arons, A.B. A Guide to Introductory Physics Teaching; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Reif, F. Understanding Basic Mechanics; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Galili, I. Weight versus gravitational force: Historical and educational perspectives. Int. J. Sci. Educ. 2001, 23, 1073–1093. [Google Scholar] [CrossRef]
- Galili, I.; Lehavi, Y. Definitions of physical concepts: A study of physics teachers’ knowledge and views. Int. J. Sci. Educ. 2006, 28, 521–541. [Google Scholar] [CrossRef]
- Wong, C.L.; Chu, H.-E.; Yap, K.C. A Framework for Defining Scientific Concepts in Science Education. Asia-Pac. Sci. Educ. 2020, 6, 615–644. [Google Scholar] [CrossRef]
- Chang, H. Operationalism. Stanford Encyclopedia of Philosophy. 2009. Available online: https://plato.stanford.edu/entries/operationalism/ (accessed on 5 January 2023).
- Bunge, M. Causality and Modern Science; Transaction Publishers: New Brunswick, NJ, USA, 2009. [Google Scholar]
- Galili, I.; Kaplan, D. Students’ operations with the weight concept. Sci. Educ. 1996, 80, 457–487. [Google Scholar] [CrossRef]
- Marton, F.; Runesson, U.; Tsui, A.B.M. The Space of Learning. In Classroom Discourse and the Space of Learning; Marton, F., Tsui, A., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2004; pp. 3–40. [Google Scholar]
- Stein, B. Introduction of Observer Concept into Physics Teaching of Middle School. Ph.D. Thesis, The Hebrew University of Jerusalem, Jerusalem, Israel, 2019. [Google Scholar]
- Vygotsky, L. Thought and Language; The MIT Press: Cambridge, MA, USA, 1934/1986. [Google Scholar]
- Levrini, O.; Fantini, P. Encountering productive forms of complexity in learning modern physics. Sci. Educ. 2013, 22, 1895–1910. [Google Scholar] [CrossRef]
- Galili, I. Promotion of cultural content knowledge through the use of the history and philosophy of science. Sci. Educ. 2012, 21, 1283–1316. [Google Scholar] [CrossRef]
- Osgood, W.F. Mechanics; Macmillan: New York, NY, USA, 1937. [Google Scholar]
- Starling, S.G.; Woodall, A.J. Physics; Longmans: London, UK, 1950. [Google Scholar]
- Chaikin, S.E. Physical Foundations of Mechanics; Nauka: Moscow, Russia, 1971; pp. 332–398. [Google Scholar]
- Ogborn, J. Science and Commonsense. Braz. J. Res. Sci. Educ. 2011, 6. Available online: https://periodicos.ufmg.br/index.php/rbpec/article/view/4050 (accessed on 5 January 2023).
- Viennot, L. Reasoning in Physics. In The Part of Common Sense; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Vosniadou, S. International Handbook of Research on Conceptual Change; Routledge: New York, NY, USA, 2008. [Google Scholar]
- Chi, M.T.H. Three Types of Conceptual Change: Belief Revision, Mental Model Transformation, and Categorical Shift. In International Handbook of Research on Conceptual Change; Vosniadou, S., Ed.; Routledge: New York, NY, USA, 2008; pp. 61–82. [Google Scholar]
- Brown, D.E. Facilitating conceptual change using analogies and explanatory models. Int. J. Sci. Educ. 1994, 16, 201–214. [Google Scholar] [CrossRef]
- Ioannides, C.; Vosniadou, S. The changing meanings of force. Cogn. Sci. Q. 2002, 2, 5–62. [Google Scholar]
- Available online: https://meyda.education.gov.il/files/Tochniyot_Limudim/Phisica/5/MechanicaMavo.pdf (accessed on 10 September 2020).
- Galili, I.; Hazan, A. Experts views on using history and philosophy of science in the practice of physics instruction. Sci. Educ. 2001, 10, 345–367. [Google Scholar] [CrossRef]
- Galili, I. Students’ conceptual change in geometrical optics. Sci. Educ. 1996, 18, 847–868. [Google Scholar] [CrossRef]
- Reiner, M.; Slotta, J.D.; Chi, M.T.; Resnick, L.B. Naive physics reasoning: A Commitment to substance-based conceptions. Cogn. Instr. 2000, 18, 1–34. [Google Scholar] [CrossRef]










| # | Research Questions | Applied Methodology |
|---|---|---|
| 1 | Feasibility and Ability What is the evidence that middle school students are able to learn observer-dependent concepts and handle their application? | Testing the problem-solving success, ability of drawing force diagrams, graphs of velocity and displacement dependence on time by different observers, and students’ choosing convenient frames of reference. |
| 2 | Efficiency of the new teaching To what extent is the observer-dependence mastered by students? | Comparison between the test results of students from the research group (enhanced observer-dependence) and the control group (taught the regular curriculum). |
| 3 | The success of learning What are the features of students’ knowledge regarding observer dependent concepts? What is the relationship between the initial and the post instructional knowledge in this domain? | Pre-test for mapping students’ naive knowledge of the observer dependent concepts. Examining the relationship (significance and statistical correlation) between students’ naive knowledge and their achievements in the post-test. |
| 4 | The affective impact What is the impact of teaching observer-dependence on students’ engagement in lessons, and their attitude towards physics and interest in learning? | Collecting data on students’ learning experience, the evidence of affective impact of the teaching, features of students’ learning and their attitude towards physics. |
| # | Activity Subject | Activity Content |
|---|---|---|
| 1 | The relative nature of scientific concepts used in the physical account | Aristotle’s account of feature variation (cold-heat, heavy-light). Quantitative and qualitative descriptions with respect to accuracy. “Anchors” guiding in characteristic features (“heavy body” in specific experience). Relative and absolute difference. Multiplicity of perspectives and interpretations |
| 2 | Definition of important concepts and ideas | Definition of observer and frame of reference. Invariance (constancy) versus relativity. “Physical law” as an invariant. Velocity as a relative concept; Galileo’s principle of relativity. |
| 3 | Aspects of observer dependence | Theoretical and operational definitions. Inertial motion and observer dependence. The history of the geocentric and heliocentric models. Plato’s ‘Cave Parable’, observer dependence and reliance on senses. “If a tree falls in the forest and no one is there, did it make a sound?” Newton and his relation to the observer. |
| 4 | Account of Motion | Basic concepts and their computation. Choice of the axis and its freedom. Distance and displacement, velocity and acceleration. Uniform and inertial motion. Distance, displacement, and velocity as relative concepts |
| 5–6 | Problem solving and changing perspectives on the given motion | Analysis, graphing and computational solution of motion problems (distance, displacement, and velocity as a function of time) in relation to inertial observers. The invariance of physical laws and different numerical accounts. The choice of the convenient frame of reference. |
| 7–8 | Interaction and forces (the Newtonian paradigm) | Force as intensity of interaction. Newton’s third law. Inertial observer. Types of forces—normal in contact, friction (kinetic and static), gravitation at a distance. The net force. Operational definition of acceleration. The first law of motion. The second law of motion. Force diagram for inertial observers. |
| 9 | Force as a relative concept. | Force operationally defined. Observers disagree on the state of motion. Implication regarding forces identification (Huygens’ case of an observer on a rotating disc). Centrifugal force as an observer dependent construct |
| 10 | The dynamical account of motion in inertial and non-inertial frames of reference | Force account as observer related: in a free-falling elevator, in a suddenly stopping or accelerated train/car, in riding a bus on a turn. Force diagrams in these cases by different observers. Accelerated frame of reference and the “feeling of force”. Inertial force and interactive force. |
| 11–12 | Gravitation | Manifestation of gravitation (planets, the Moon, the tides, falling) and Newton’s law of gravitation. Orbiting as continuous falling. Motion inside a satellite, floatation, the presence of gravitation and lacking of gravity. Newton’s cannon. Force diagrams for the objects in a satellite by different observers. Force-meter and weighing. The operational definition of weight and its difference from gravitational force (the weightlessness in a spacecraft). Weight and gravitation as forces applied to different bodies. |
| Stage | Research Tool |
|---|---|
| A | Pre-Test |
| Post-Test-A | |
| Collected Feedback | |
| B | Pre-Test (experimental and control groups) |
| Post-Test-A (experimental teaching group) | |
| Post-Test-B (experimental and control groups) | |
| Collected Feedback (experimental teaching group) |
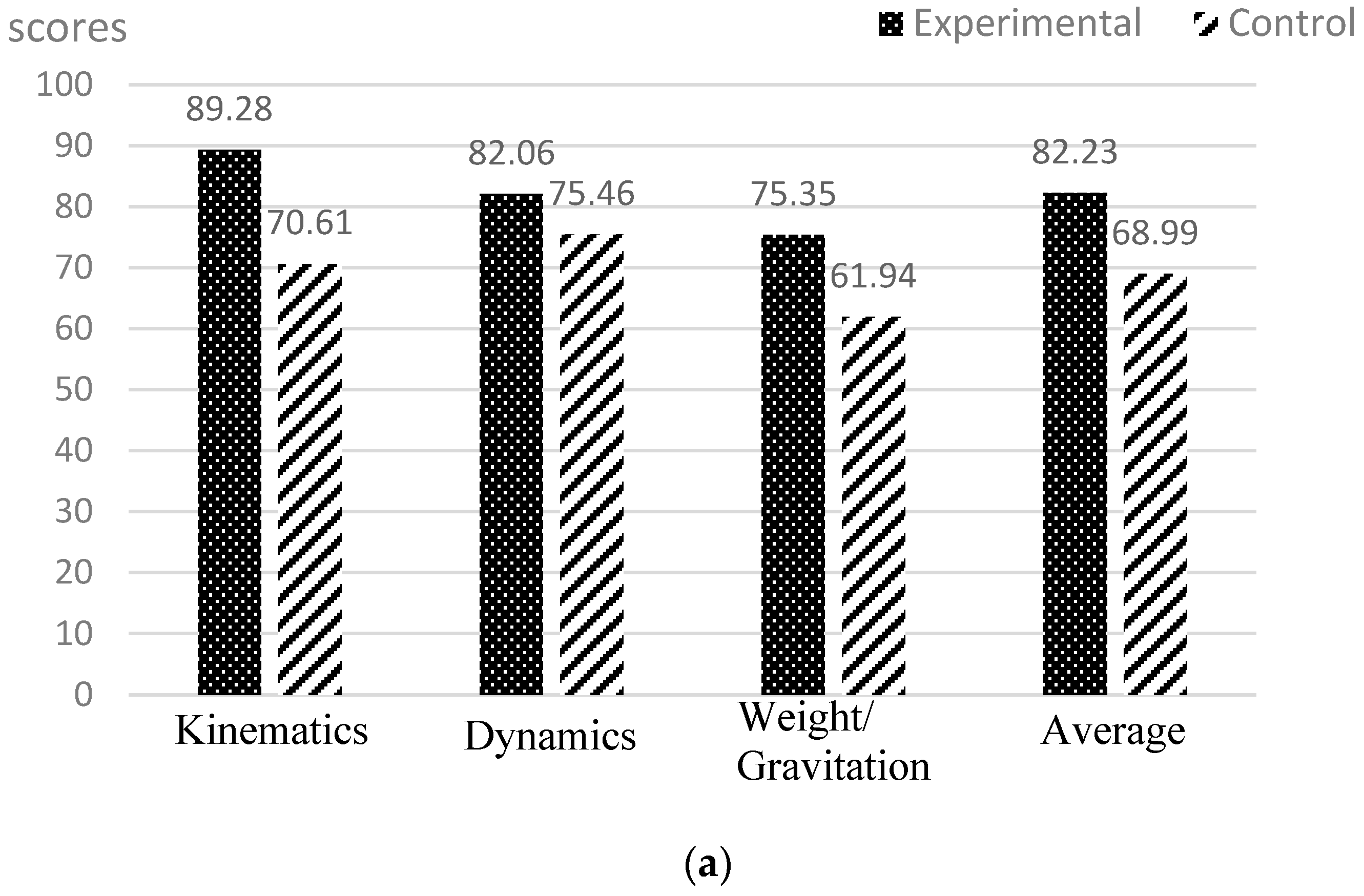
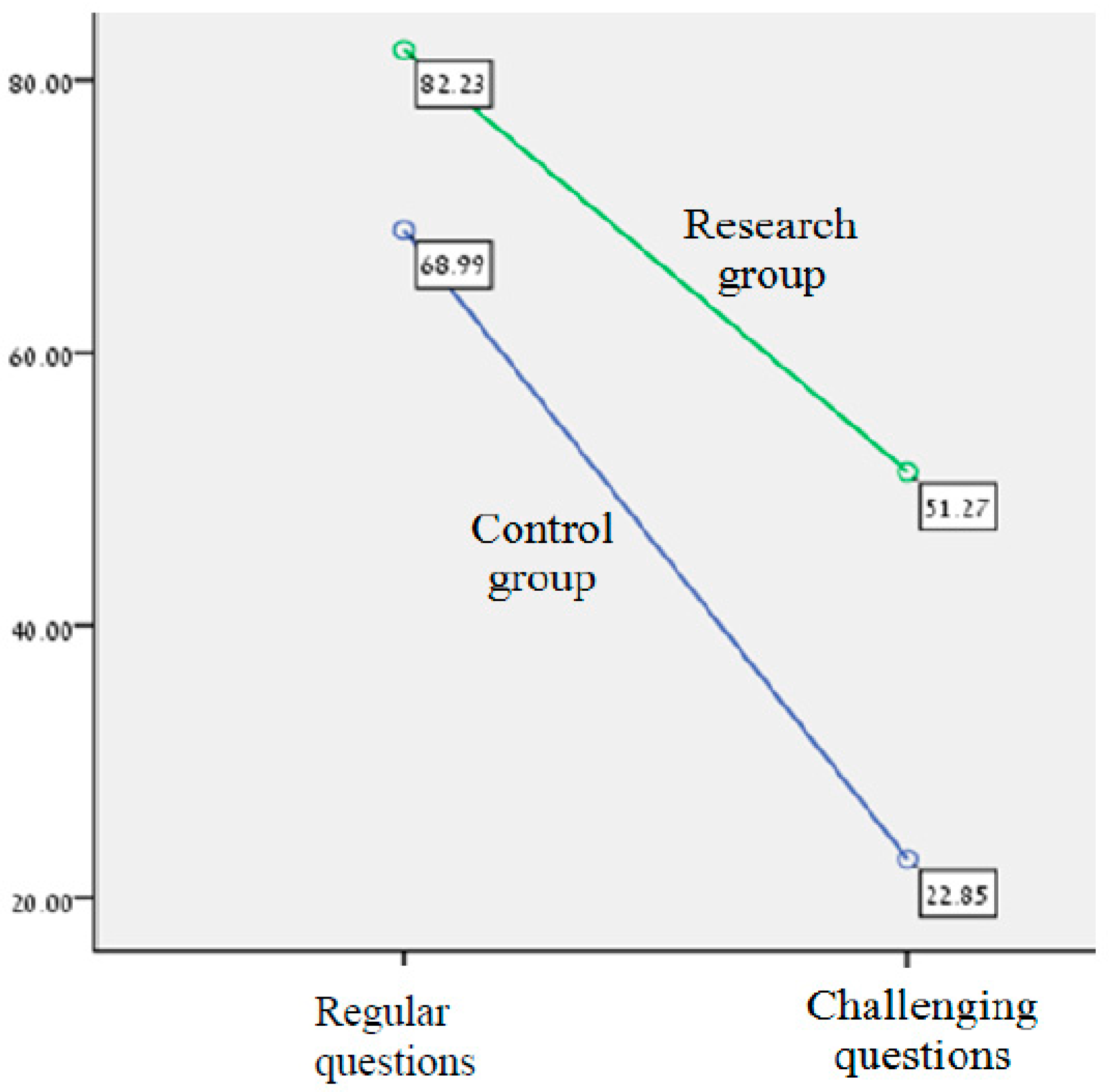
| Questions | Groups | Grades (%) Kinematics | Grades (%) Dynamics | Grades (%) Weight/Gravitation | Grades (%) Average |
|---|---|---|---|---|---|
| Regular | Experimental | 89.28 (20.05 *) | 82.06 (25.59) | 75.35 (21.81) | 82.23 (17.20) |
| Control | 70.61 (24.37) | 75.46 (24.73) | 61.94 (24.78) | 68.99 (17.35) | |
| t-test → | t(111) = 4.411 p = 0.000 | t(114) = 1.405 p = 0.082 ^ | t(108) = 3.017 p = 0.002 | t(115) = 4.129 p = 0.000 | |
| Challenging | Experimental | 57.50 (34.84) | 52.54 (39.61) | 45.28 (43.52) | 51.27 (23.37) |
| Control | 13.68 (22.23) | 36.51 (36.13) | 19.47 (31.94) | 22.85 (21.83) | |
| t-test → | t(111) = 8.060 p = 0.000 | t(114) = 2.259 p = 0.013 | t(108) = 3.581 p = 0.001 | t(115) = 6.115 p = 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stein, B.; Stein, H.; Galili, I. The Concept of Observer in Science Teaching in Middle School: Pre-Instructional Knowledge as a Lever for Learning rather than an Obstacle. Educ. Sci. 2023, 13, 95. https://doi.org/10.3390/educsci13010095
Stein B, Stein H, Galili I. The Concept of Observer in Science Teaching in Middle School: Pre-Instructional Knowledge as a Lever for Learning rather than an Obstacle. Education Sciences. 2023; 13(1):95. https://doi.org/10.3390/educsci13010095
Chicago/Turabian StyleStein, Ben, Hana Stein, and Igal Galili. 2023. "The Concept of Observer in Science Teaching in Middle School: Pre-Instructional Knowledge as a Lever for Learning rather than an Obstacle" Education Sciences 13, no. 1: 95. https://doi.org/10.3390/educsci13010095
APA StyleStein, B., Stein, H., & Galili, I. (2023). The Concept of Observer in Science Teaching in Middle School: Pre-Instructional Knowledge as a Lever for Learning rather than an Obstacle. Education Sciences, 13(1), 95. https://doi.org/10.3390/educsci13010095






