Mathematical Modeling Approach and Exploration of Geometric Properties as Part of an Outdoor Activity for Primary-School Pupils in Out-of-School Learning

Abstract

School-age children and being outdoors are intrinsically linked. Education and the outdoors offer unique opportunities to extend the learning potential of children at this age in a more engaging way. From the point of view of mathematics, this way of learning is very suitable and certainly motivating for the pupils since mathematics, especially geometry, is not very popular among pupils. Therefore, in this article, we describe how we used an out-of-school learning experience for second-level primary school pupils (sixth to ninth grade) to link mathematics to outdoor learning. Activities that we solved with pupils in the outdoor environment were solved in the teaching process using only modeling. Practical applications were illustrated through interesting topographic fieldwork, which we analyzed for their appropriate integration into the teaching process by means of a priori analysis. The inclusion of these practical problems was preceded by research on 781 pupils of primary schools who solved application problems related to the circle and the square. It was clear from the research that pupils have a significant problem with the geometric interpretation of simple geometric concepts, which can be improved with the use of mathematical modeling and the linking of similar problems that can be carried out in a non-school environment.

1. Introduction

Teachers can plan different didactic activities for pupils to perform outside of the classroom, but why not start with a more open-ended activity where pupils link their mathematical knowledge to solving problems in an atypical outdoor environment? In this way, it is possible to help pupils begin to make connections with the work that they perform in the classroom and to see how the problem is related to real-life situations.

As noted in [1], modeling still plays a much smaller role in school practice worldwide than is desirable. In fact, there is a tendency in several countries to include more mathematical modeling in the curriculum.

The aim of this article is to highlight the link between mathematical modeling, which is often used in geometric problem solving, and teaching outside the classroom, where there is a suitable space to use modeling in activities that are interesting for pupils. The activities are based on the principles of design research and are implemented in science and mathematics intervention programs.

1.1. Modeling in Mathematics Education

Mathematical modeling is a process where there is no need to follow a certain rule in achieving a goal using what is given. In the modeling process, more than one procedure can be used between what is given and the goal of achieving the desired solution to the problem [2]. Why use modeling in mathematics education? The process of creating and evaluating models can help pupils develop and reinforce connections between seemingly disparate ideas, leading to deep and lasting learning [3]. It seems that modeling as a means of teaching mathematics is developed mainly for more pedagogical purposes. Integrating modeling into mathematics education is important for improving pupils’ problem-solving skills as well as their analytical thinking [4].

During activities aimed at modeling approaches to problems, pupils develop their knowledge in the given topics by using problem situations independently and then mathematize these given situations. These activities are organized in such a way that children are encouraged to study and clarify problem situations. These result in models that are in the form of different illustrative systems such as written symbols, oral reports, diagrams on paper, or pictures [5]. Term “model” is part of modeling. According to [6], mathematical models are conceptual tools that are required by individuals to mathematically interpret the problems and situations that they come across.

According to [7], using mathematical modeling activities in the classroom offers several key benefits. Learners become more engaged as they explore specific circumstances within a problem or interpret situations that might initially seem unrelated to real life or mathematics. This approach gives learning genuine significance, making it easier for both learners and teachers to connect the material to other scenarios and challenges. Students also gain greater confidence in applying mathematical concepts across diverse fields, learning strategies that help them relate math to other, particularly physical, situations. Moreover, this method is versatile and can be integrated into any educational level, from primary- to middle-school curricula.

Many researchers in the field of mathematics education write that mathematical modeling is one of the foundations of mathematics education. Mathematical modeling is described as the conversion activity of a real problem into mathematical form [8]. According to this approach, mathematical models are an important part of all areas of mathematics, and certainly for geometry, and mathematical modeling can be part of the education of all age groups of pupils.

1.2. Outdoor Activities in Math Education

Outdoor math activities allow pupils and students to interactively explore the world beyond the classroom. These activities make learning more relevant and enjoyable [9]. By taking math lessons outside, pupils can connect abstract ideas to real-world contexts [10].

The literature lists many benefits of outdoor mathematics activities. In [11], outdoor mathematics activities are described as a practical way to implement constructivist learning through both a psychological learning philosophy and a socio-cultural perspective. As the author mentions, there are also mental, physical, and psychological benefits to spending time outdoors. He also notes that collaboration between mathematics educators and teachers of other disciplines can help both teachers and students make these connections. The author of [12] states that outdoor math activities promote collaboration, multimodality, and performance. The research in [13,14,15] confirms a positive correlation between students’ motivation and their learning achievement after the outdoor mathematics activities. In [16], six core principles of outdoor activities are summarized. This approach to education is experience-based, takes place outdoors, engages all senses, is holistic, interdisciplinary, and fosters relationships between people and natural resources.

Outdoor education is a complement to traditional classroom education. Outdoor activities should be started as early as possible. This type of activity has higher goals than memorization. Like any other activity, this one also needs to have a certain procedure. According to [17], outdoor education must be carried out in three phases:

• Preparatory phase: In this phase, it is important to think about the objectives, forms, and methods of teaching;
• Implementing phase: This is the key phase regarding the student activities that take place in the field;
• Final phase: This phase should ideally take place immediately after the implementation phase, or as soon as possible, and involves a reflection on and an evaluation of the learning that has taken place.

In [12], it is stated that every “good” task in mathematical outdoor activities should meet four essential criteria: students should gain meaningful knowledge about real-world objects, apply substantial mathematical knowledge from school, use mathematics to deepen their understanding of real-world contexts, and focus on thoroughly exploring the object of study as the core of their activities.

Outdoor activities for geometry lessons offer a creative and effective approach to teaching mathematical concepts [18]. This method makes learning more enjoyable and helps them see the relevance of geometry in their everyday lives [13].

2. Materials and Methods

In recent years, we have observed a very low level of pupils’ geometric knowledge in Slovakia. This trend is indicated by the national test during the second level of elementary school, which is intended for ninth-grade pupils. For this reason, in our research, we focus on solving two geometric problems that are solved by pupils from different schools in the Slovak Republic. In both problems, the central concept is the circle, and the problems are supplemented by patterns. In the evaluation, we focus on the success rate of the given problems and the analysis of the pupils’ solutions. Based on the findings from the solutions to Problem 1 and Problem 2, we designed activities that were carried out in the outdoor environment. The outdoor environment is inspiring for the pupils, as we have personal experience in implementing an out-of-school club with them. Section 2.2 and Section 2.3 provide a description of each participant group.

2.1. Research Objectives

The following are the stated research goals:

• To quantitatively evaluate the solution of two geometric problems;
• To qualitatively evaluate and analyze pupils’ misconceptions in solving the problems;
• To design activities for non-standardized teaching (in the form of outdoor activities) in the context of mathematical modeling.

2.2. Research Sample 1—Indoor Problems

For our research, we selected pupils in the ninth grade. Our research sample consisted of 781 pupils from 29 schools in 23 towns and cities in Slovakia. These pupils have completed their primary education and have all the academic requirements for lower-secondary education in Slovakia. Depending on the type and focus of the secondary school, the differentiation of the geometry curriculum takes place only during further studies. Depending on the type of secondary school they will attend, some pupils will not continue to develop their knowledge of geometry.

2.2.1. Research Tools—Indoor Problems

Both geometric problems are related to the geometric pattern shown in the picture and are also focused on the competencies of pupils in reading from the picture. The first problem focuses on the relative position of the centers of the circles and the distance between them (see Figure 1).

2.2.2. Problem 1

Problem assignment: A rectangle measuring 10 cm by 8 cm is shown. Find the distance between the centers of two congruent circles that overlap each other inside the rectangle.

Figure 1. Modeling the situation of Problem 1.

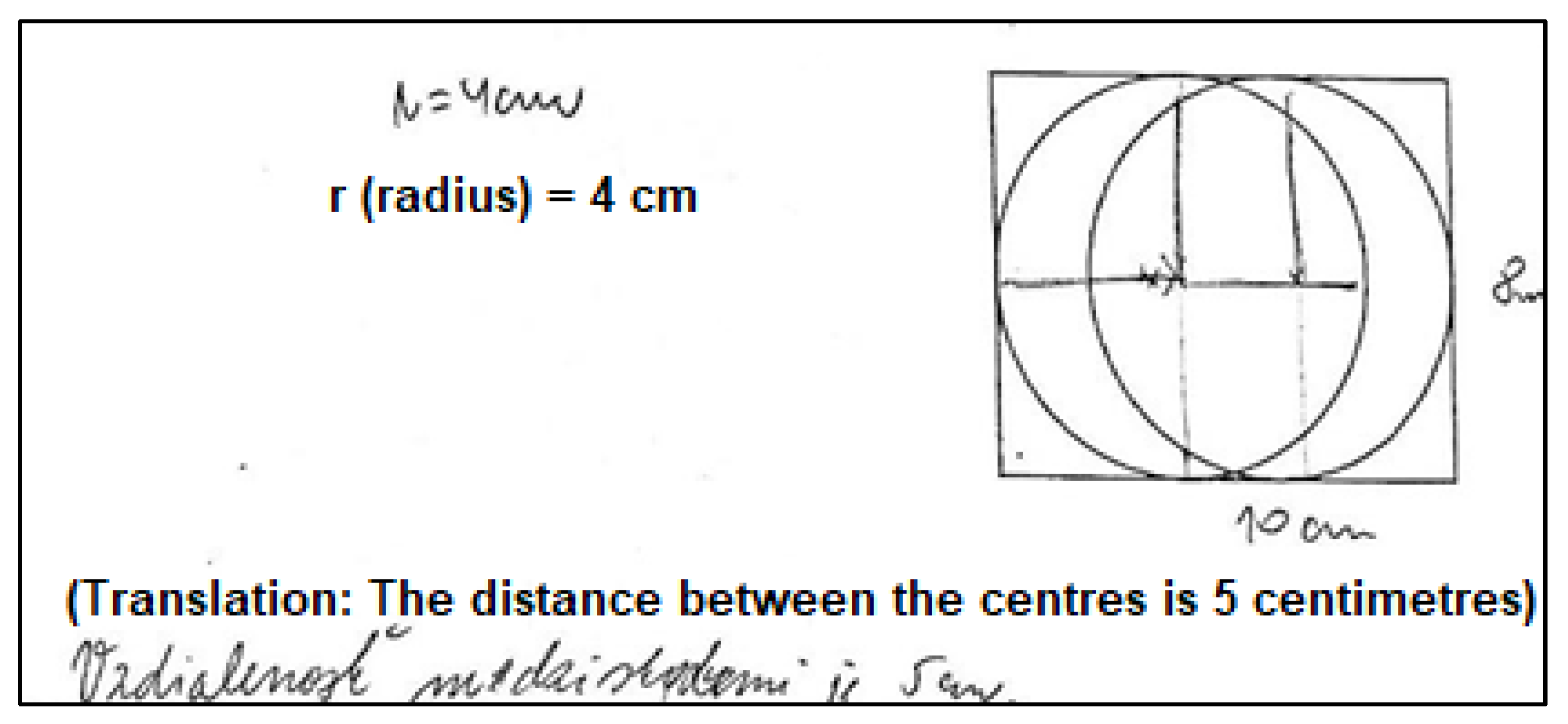
Figure 1. Modeling the situation of Problem 1.

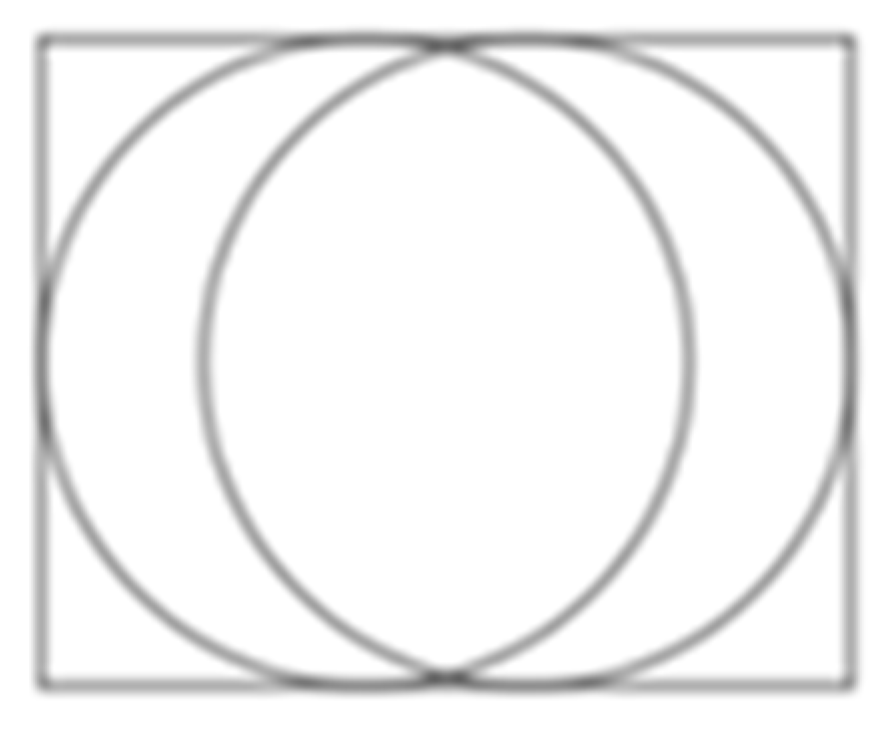
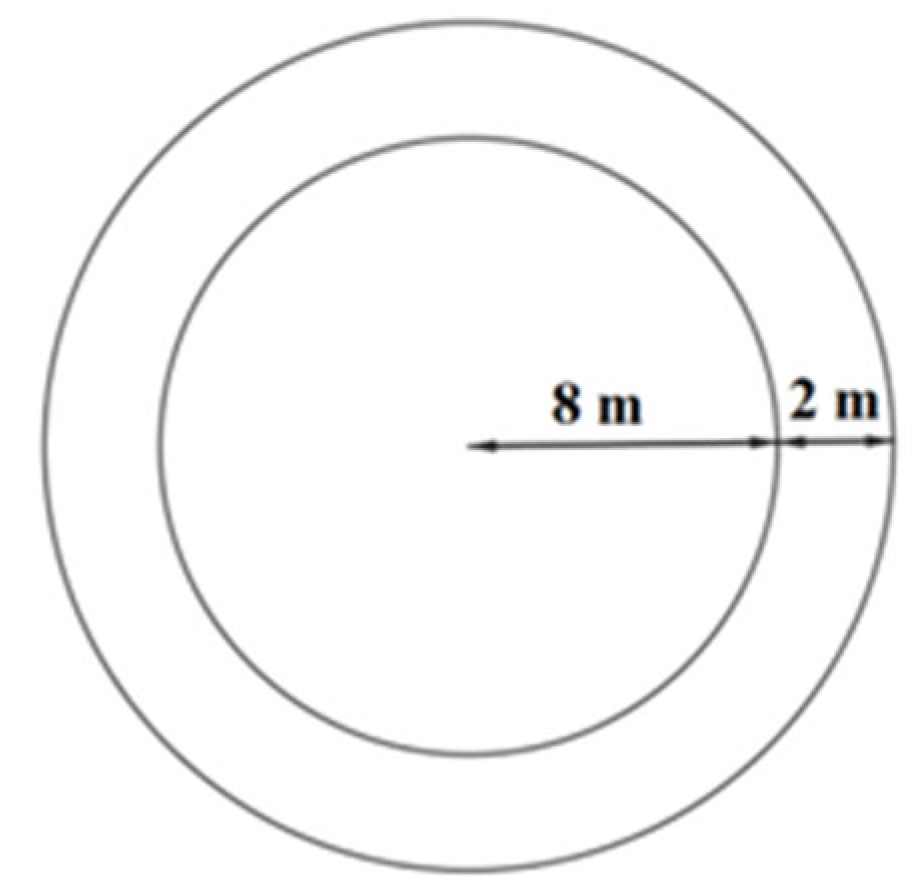
2.2.3. Problem 2

Problem assignment: In the park, there is a circular flower bed with a radius of 8 m. Around the perimeter of the bed, there is a path 2 m wide. How many kilograms of pebbles are needed to make the path? One kg of pebbles covers an area of 5 ${\mathrm{m}}^2$.

The second problem is more complex. The goal is to determine the mass of pebbles needed to fill the path around the circular flower bed. The pupils know the size of the area covered by 1 kg of pebbles (Figure 2).

2.3. Research Sample 2—Outdoor Activities

At the Faculty of Natural Sciences and Informatics at Constantine the Philosopher University in Nitra, intervention programs in science and mathematics have been developed and piloted since 2022. These programs are based on design-research principles, with the first round being implemented during the 2022/23 academic year, followed by the second in 2023/24, and the final round is planned for 2024/25.

The intervention program is open to pupils from all primary schools in Nitra. Our research sample for outdoor activities consisted of pupils in grades 6–9.

The program is delivered through weekly 60 min sessions led by a main teacher overseeing the entire program, along with one or two co-teachers, who are experts in various fields of science and mathematics. These areas include physics (introductory physics, material physics, astronomy), biology (genetics, botany), geography (pedology), computer science (hardware, computational thinking), and mathematics (functions, geometry, topology, fractions, combinatorics, and probability). Each topic is explored over two to four consecutive sessions.

Research Tools

We decided to design activities for pupils to develop the concept of basic geometric concepts through the implementation of an intervention program at our university and the realization of topology and geometry lessons:

• Activity 1: Draw a line segment 6 m long;
• Activity 2: Construct a perpendicular to the line segment from Activity 1;
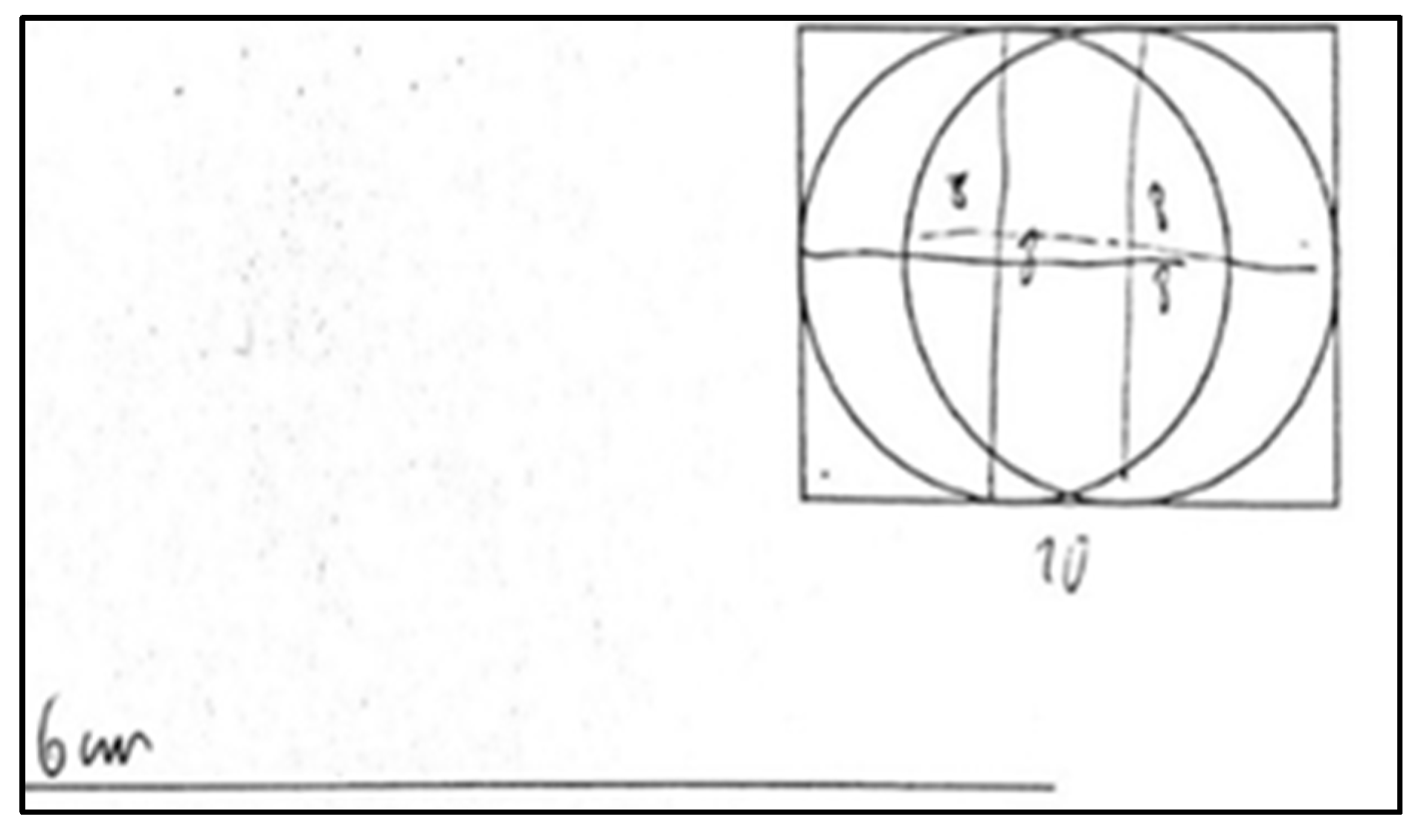
• Activity 3: Mark out a site for a swimming pool with a diameter of 7 m;
• Activity 4: Mark out a site for a gazebo with a 5 m long square base.

Before implementing the outdoor activities, we made an a priori analysis of the teachers’ preparation in terms of the pupils’ expected didactic situations. The a priori analysis includes different perspectives on the problem-solving strategies that are expected by the teacher from the pupils. The analysis requires observation of the activity solvers.

3. Data Analysis of Indoor Problems

Problem 1 and Problem 2 have different levels of difficulty. Problem 1 is at the level of the interconnection of mathematical competences, and Problem 2 is at the level of reflection on mathematical competence. The pupils who have solved the given problems have successfully completed primary-school education and have fulfilled all the academic requirements for lower-secondary-school education in Slovakia. Although each problem is different and requires different pupil knowledge, approximately the same percentage of pupils solved both tasks correctly. Figure 3 shows the success rate for both problems. The success rate for Problem 1 is 26.8% and 26.6% for Problem 2. As you can see in the graph, although Problem 1 is easier, 70.3% of the students solved it incorrectly. Only 2.9% of the students found a partially correct solution to the problem. Problem 2 was solved incorrectly by 71.4% of the pupils and partially correctly by 2% of the pupils.

Due to the low success rate of the problem, we decided to perform an analysis of the pupils’ solutions to these problems.

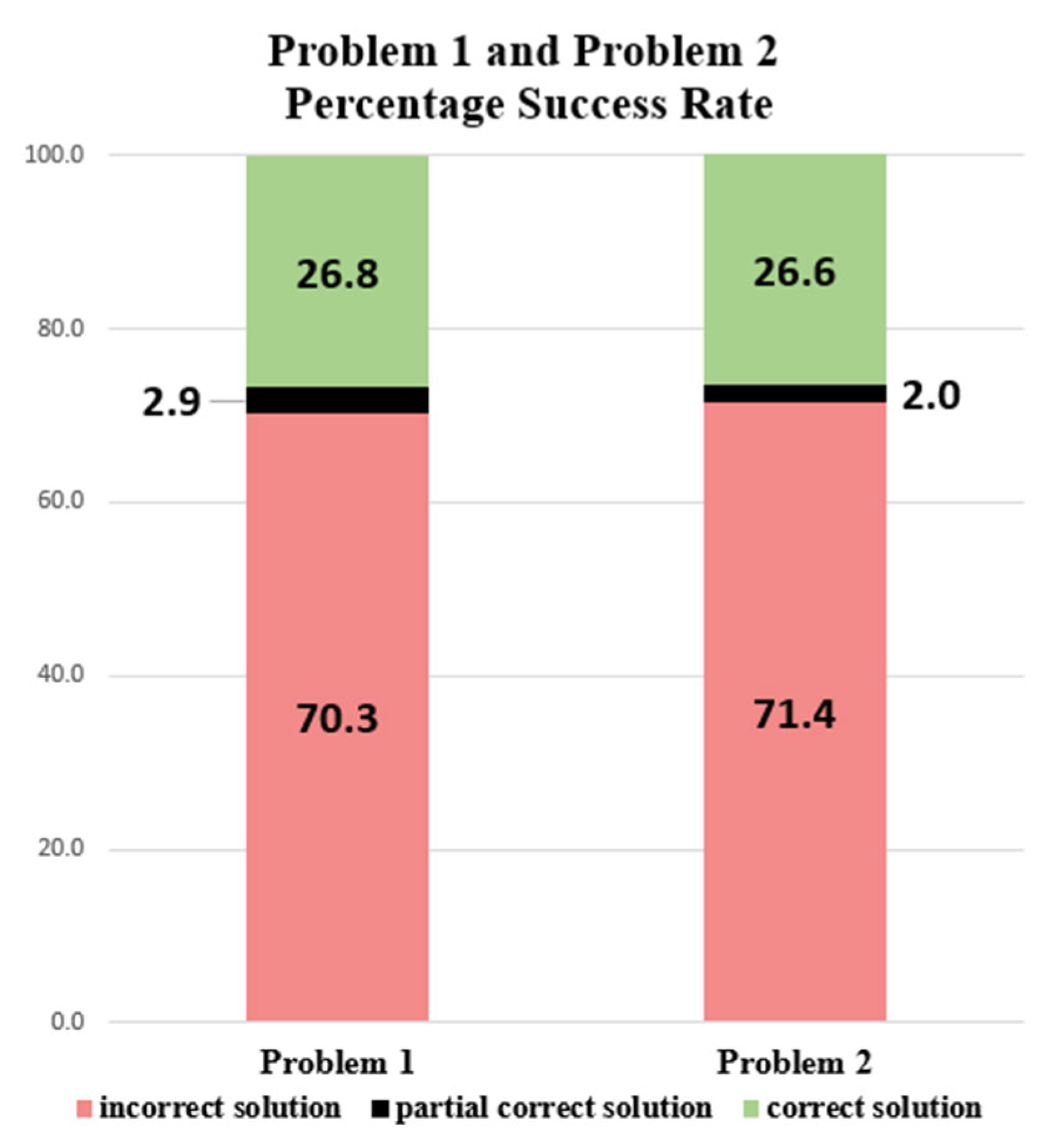
3.1. Problem 1 with Regard to Pupils’ Solutions

In the correct solution of the problem, we observed division of the figure and recording of the centers of the circles or the lengths of the individual parts of the rectangle. In Figure 4, you can see the correct detailed solution to the problem.

Some pupils recognized the position of the centers of the circles (partially correct solution), but they were not able to determine the distance between the centers of the circles. After correctly determining the positions of the centers of the circles, the pupils determined that the centers of the circles were 1 cm or 5 cm apart. Figure 5 shows an example of this solution.

Most of the incorrect solutions involved the subtraction of some value from the diameter of the circle. Others involved the difference of the sum of the opposite sides of a rectangle. Pupils also divided the diameters of the circles into parts, but incorrectly located the centers of the circles (Figure 6).

3.2. Problem 2 with Regard to Pupils’ Solutions

The correct solution to Problem 2 requires a more comprehensive approach to the solution. Figure 7 shows the correct solution to the problem.

If pupils were able to correctly determine the area of the circular ring, then they were also able to correctly determine the weight of the pebbles that were needed. When calculating the weight of the pebbles, only 2% of the pupils made an error.

Pupils knew the formula to calculate the area of a circle. The most common error was in the calculation of the area of the circular ring. They calculated the area of the circular ring as the area of a circle with a radius of 2 m, or as the area of a circle with a radius of 10 m. Some pupils calculated the area as the difference between the areas of circles with a radius of 8 m and 2 m. The pupils did not understand the geometric meaning of the circular ring. Examples of incorrect solutions are shown in Figure 8.

Based on the solutions to the two problems, pupils have a significant problem with the geometric interpretation of simple geometric concepts. For this reason, there is a need to develop their perception of the concepts and the way that they are formed.

4. A Priori Analysis of the Activity and Teacher Preparation for Working with Pupils in Out-of-School Learning

Out-of-school activities, such as math clubs, science workshops, and intervention programs play a crucial role in expanding students’ knowledge beyond the regular classroom setting [19]. These programs provide a more relaxed environment where students can explore topics in greater depth and at their own pace. By participating in hands-on activities, solving challenging problems, and collaborating with peers, students develop critical thinking and problem-solving skills. [20]. Out-of-school learning often introduces new concepts that complement the school curriculum, making subjects like mathematics more engaging and relevant. Regular participation can positively impact their academic performance in the classroom [21].

4.1. A Priori Analysis of the Activities

As part of our preparation as teachers for the teaching process, we used the theory of didactic situations (TDS); specifically, we conducted a priori analysis tasks before working with pupils on the activities. The TDS may be a tool for the researcher to understand teaching practices and the way it may contribute to developing teaching practices, helping teachers to identify questions useful for their practice and to understand teaching practices [22]. The theory is based on the principles of the French school, and according to its creator, TDS in mathematics is related to a priori analysis, which is one of the tools available to the teacher in preparing for the teaching process [23]. The theory is structured around the concepts of a didactic situation, where there are no explicit didactic intentions—pupils work as if there are no didactic intentions, and the teacher refrains from interfering—and didactic situations, which includes concepts relevant to teaching and learning in mathematics [24]. If a teacher plans to teach pupils some mathematical knowledge so that they will learn it, then situation theory suggests that you need to organize the didactic environment so that this mathematical knowledge turns out to be the best available means of working out a winning strategy. As stated in [25], mathematical knowledge cannot be comprehended other than through the activities that it allows us to realize and, therefore, the problems that it makes possible to solve. Mathematics is not simply a logically consistent conceptual system for producing rigorous proof; it is, first, an activity that is realized in a situation and against a milieu. One can agree that the TDS in mathematics and its applications in mathematics classrooms are valuable because they do not deal with a set of apparent components but discuss phenomena by analyzing knowledge in given situations. Meanings emerge in the proposed situations by analyzing and elaborating on a set of possible meanings that pupils can use [26]. Researchers and teachers have, on many occasions, commented on the fact that the TDS can represent any situation in which there is an intention to teach someone some specific mathematical knowledge.

In our opinion, the TDS is suitable for us because the notion of milieu in this theory helps us to predict what part of knowledge may be produced by pupils themselves and what part will stay in our charge as the teachers.

4.1.1. Characteristics of Activity Assignments

The teacher gives the pupils assignments in written form. The assignments are easy for them to understand and chosen with reference to the curriculum for the lower-secondary school. The tasks are related to constructing a circle and square without the use of drawing aids.

4.1.2. Thematic Unit Where the Task Can Be Classified

Pupils can distinguish, name, model, and describe basic planar and spatial shapes, identify their representation in the real world after graduating from the third class of primary school (children who are 6–9 years old). In the fourth year of primary school, pupils can mark and name the center, radius, and diameter of circle and draw a circle with a compass. From the above facts, it is possible to assign tasks to pupils from the fifth year of lower-secondary school (where the children are 10–15 years old). We recommend that the teacher implement the activities after the thematic units of “The Circle and Its Properties”, “Parallelism and Quadrilaterals”, and “Geometric Constructions”, or within the recommended unit of “Topographic Fieldwork” (thematic area: Geometry and Measurement).

4.1.3. Activity Goal

Based on the properties of a circle as a set of points in a plane and the properties of basic geometric shapes (such as segment, square, perpendicularity, parallelism), the pupil should be able to construct the given shapes in the activities using only a few tools.

4.1.4. Problem-Solving Time Range

Pupils work on an activity during one lesson in an outdoor environment.

4.1.5. Course of Work

We recommend that pupils work in pairs or, at the teacher’s discretion, pupils can solve the activity independently. Pupils should not have a problem understanding the assigned task, but they can discuss ambiguities with the teacher individually. To ensure that every student is involved, we do not recommend that students work in larger groups.

4.1.6. Tools

Pupils have the following tools to solve the activities: string, chalk, a long measuring tape, or materials available in the outdoor environment around them. In the case of classroom work, pupils use only basic drawing tools (compass, line ruler).

4.1.7. Didactic Variables for a Priori Analysis

The didactic variables of the formulation are drawing and construction. Cognitive didactic variables are perpendicularity, parallelism, regularity, radius, and diameter. If these concepts are not used in the activity statement, pupils may be confused about the type of geometric figures in the plane. Depending on the age of the pupils, the construction of parallels and perpendiculars may cause a problem, given that these properties are included in the fifth year of primary school. There may also be an error in the solution to the activity where the diameter of the circle is given (unfamiliarity between the terms radius and diameter). The teacher can also specify other values or data related to the construction of the basic shape that will change the solution to the problem. Activities set to be solved in an outdoor environment are expected to be more challenging for pupils than activities set to be solved on paper.

4.1.8. Pupils’ Initial Knowledge and Skills

Pupils must have mastered the basic rules of drawing and be able to use drawing aids. They must also be able to distinguish between plane geometric shapes and to sketch them. Pupils must be able to use known properties of geometric shapes in solving application problem tasks. Specifically, for a circle, pupils should be able to distinguish among concepts such as radius, diameter, and a set of points, and for a square, concepts such as parallelism, perpendicularity, and congruent segments.

4.1.9. Pupils’ Reactions

We expect pupils to ask questions about the tools they can use to solve the problems and about the concepts related to each shape.

4.1.10. Teachers’ Reactions

The teacher can modify the tasks according to the age and abilities of the pupils.

4.1.11. Problem-Solving Strategies

We assume that pupils will be able to perform the following in their solutions to individual problems:

• Use the correct lengths (for a segment, diameter of a circle, sides of a square);
• Use the following properties: parallel lines, perpendiculars, radius, and diameter;
• Correctly display a circle with its geometric properties (definition, a set of points in a plane, center, radius, diameter);
• Correctly display a square with its geometric properties (definition, all sides are equal, opposite sides are parallel, adjacent sides are perpendicular);
• Use only tools such as paper, pen, chalk, string, a long measuring tape, and a line ruler.

4.1.12. Incorrect Problem-Solving Strategies

We expect pupils to:

• Confuse the terms as radius and diameter, parallel lines, and perpendiculars;
• Not know how to use circles to construct the perpendicular to a segment;
• Not be able to draw a square without using a ruler and protractor;
• Not be able to use only the tools listed to construct a circle perpendicular to the segment and then a square.

4.1.13. Assessment of the Problem Task

The teacher’s assessment will be formative only and may also take place at the next meeting with the pupils.

5. Results and Reflections from a Priori Problem Solving

We present our findings in the form of evaluations of the problem-solving activities that were carried out in the outdoor leisure time environment. We identified four activities that were solved by a group of pupils as part of the intervention program. Based on our a priori analysis, we describe these individual activities.

5.1. Activity 1—Draw a Line Segment 6 m Long

The construction of the line segment did not confuse any group of pupils. They used a measuring tape to construct the segment of the line that was 6 m long. The pupils used chalk to mark the line, and they marked the line along the length of the measuring tape. The use of other measuring tools was not expected. Figure 9 shows the real situation of the pupils’ work.

5.2. Activity 2—Construct a Perpendicular to the Line Segment from Activity 1

Activity 2 was more difficult for the pupils than Activity 1. In this construction, pupils could not use the necessary tools to construct the perpendicular. The correct solution was to use the isosceles triangle, as shown in Figure 10, based on the line segment from Activity 1.

The vertex of the triangle was constructed with springs of the same length above a given point of the line segment. One pupil held the spring at one distinct end point of the line segment. The other pupil described the circle with the spring and the chalk. The process was repeated from the second end of the line segment. Using the same approach, they constructed two isosceles triangles (see Figure 11), and the pupils connected the constructed vertices of the triangles by using a measuring tape.

The solution described for Activity 2 was correct, which was made by only one group of pupils. There were no other correct solutions by the other groups of pupils. Some pupils tried to construct a perpendicular using the ends of the measuring tape. We believe this approximate solution would not have been correct.

5.3. Activity 3—Mark out a Site for a Swimming Pool with a Diameter of 7 m

In solving the problem, there were no complications with the design of the circular pool. The pupils chose the center of the circle. They automatically used string and chalk to construct it. One pupil stood at the chosen center of the circle with one end of the string, and the other pupil moved around it with a 7 m length of string. In this way, they drew the base of a circular pool on the ground with chalk (Figure 12). All groups of students solved the activity correctly.

5.4. Activity 4—Mark out a Site for a Gazebo with a 5 m Long Square Base

Based on our observations and findings, Activity 4 was the least successful. This activity was linked to the previous activity. As the pupils did not construct the perpendicular to the line segment, they also failed to construct it in this activity. Figure 13 shows an appropriate solution to Activity 4.

As can be seen in Figure 13, two perpendicular segments are constructed using an approximate construction using a small radius circle at the distinct end point of the line segment. This is an approximate solution. Nonetheless, the pupils solved the activity.

6. Discussion and Conclusions

The aim of the article was to analyze, quantitatively and qualitatively, the solutions to two geometric problems and to propose activities for non-standardized teaching related to mathematical modeling. The resolution of the two issues reveals that pupils face considerable difficulties in the geometric interpretation of basic geometric concepts. Therefore, it is essential to enhance their understanding of these concepts and of how they are constructed. As part of the intervention program at the University of Constantine the Philosopher, pupils were given activities to develop an understanding of basic geometric concepts. An a priori analysis was carried out before the implementation of the proposed activities.

The results of the solutions to two geometry problems (Problem 1 and Problem 2) show that it is important to pay attention to the teaching of geometry in grades 5–9 of primary school. According to the results of Testing 9—the external test of ninth-grade pupils in Slovakia—pupils have not reached the expected level of geometric knowledge [27]. Of course, to avoid rote learning and the acquisition of only formal knowledge, geometric knowledge must be adapted to the methods as well as to the language of mathematics and the expression of the teacher [28,29]. Based on the results of solving Problem 1 and Problem 2, we developed activities to be carried out in an outdoor environment. This environment is motivating for the pupils as we have first-hand experience in running an out-of-school club.

An a priori analysis was carried out within the framework of the TDS before implementing the given activities in the school club. Using observation and interview with pupils, which are parts of the TDS, an a posteriori analysis was carried out. The designed activities were linked to modeling the geometric properties of objects and, as mentioned in [3], pupils can develop and reinforce connections between different geometric knowledge in these activities, leading to deep and lasting learning. During the solution of the activities, it could be observed that the pupils had no problem with the geometric representation of a line and a circle. All the pupils solved the problem on their own without any help from the teacher. Problems arose when trying to draw the perpendicular and the square. Using common drawing tools on paper, the pupils could draw the geometric objects (from interviewing the pupils). They could not draw the objects without a compass and a right-angle ruler (at some point in the activity, all pupils needed help from the teacher). These activities encouraged pupils to reflect on the properties of geometric objects and to apply these to design them.

It can be concluded that the pupils enjoyed the activities based on their positive feedback (from observation and interviews with the pupils). As we mentioned, one of the benefits of outdoor activities is the positive feedback that the pupils gave in their opinions. The most common responses were that they enjoyed being outdoors, combining their knowledge of different teaching subjects and working in groups. These statements are in line with the research findings reported in [12,13,14]. From our point of view, it is important that the pupils enjoy working in groups, using non-traditional resources (string, chalk, ruler), and working outside their school. The activities encouraged discussion in groups. Pupils helped each other to solve problems and complemented each other’s knowledge. Such activities can foster a positive attitude toward geometry. Pupils see its practical applications and learn a lot of new knowledge.