Abstract
This paper aims to develop a new model of Project-Based Instructional Taxonomy (PBIT) that provides a tool of course design that facilitates Computational Thinking (CT) development as creative action in solving real-life problems. Theoretically, PBIT is built on an integrative framework bringing together with studies on CT education, creativity, Bloom’s Taxonomy, and Project-Based Instruction (PBI). This guides the course design to make alignment between diverse elements including education objectives, categories of CT, levels of learning ability, process of project facilitation, and methods of grading. A case will be discussed that focuses on a course Deep Learning and Technologies in AI bachelor program at Northeastern University (NEU) in China. It also shows how PBIT is applied in teaching practice that benefits students’ CT development. As the conclusion indicates, this paper has contributions to future research on creativity, PBI, CT, and AI education.
1. Introduction
We are living in a digital age that is powerfully shaped by computing, algorithmic, big data, and Artificial Intelligence (AI). To be successful in future professional practice, students must learn how to creatively use digital technologies to solve diverse problems [1,2]. This leads us to increasingly recognize Computational Thinking (CT) as one of fundamental skills that the next generation should master in diverse education programs, especially in AI education [3,4].
The literature has shown growing interests in understanding CT development as a creative process [5,6,7]. CT has been regarded used to design and develop new strategies to link theories and practice [3], which help to analyze, identify, and organize relatively complex and ill-defined tasks [8]. This brings studies on CT education development from a creativity perspective [9,10]. Yadav and Cooper [11] described how platforms like Alice or Scratch provide opportunities for students to extend their creative expression to solve problems and create computational artifacts. The ‘creative artifacts’ can be understood as the products of CT development [12]. Therefore, CT is more about thinking and doing than only computing [13,14,15].
This means the focus of understanding CT has been shifted from what CT is to how CT can be taught as a literacy [16] and how evidence of its acquisition might be observed in practice of teaching and learning [17,18,19]. Then, strategies have been explored in educational contexts [20], such as facilitating students in creative programming [9], setting students in problem-solving contexts, and encouraging students to work with meaningful projects [21]. Pedagogical models are also calling for students’ authentic learning experience [22]; attention has been paid to Problem-Based Learning [23,24], Project-Based Learning [25,26], and Project-Based Instruction [27]. With these efforts, the goal of computing education is moving beyond CT to a perspective of ‘computational action’; in other words, ‘computational action’ becomes a new framework of developing CT towards ‘creative action’ [13].
However, the ability to foster authentic learning experience represents a fundamental shift that will open new avenues for young people to see their worlds as ‘possibility spaces’ [28,29]. Students should have as many opportunities as possible to ask questions and build new solutions or new designs that address personally identified needs [30]. This also brings new challenges [31]: teachers need to be comfortable in complex, real world situations that do not have a predefined solution; students need to learn in depth to understand how to decompose their apps into manageable and buildable parts [32,33]. This indicates the necessity to design new instructional methods that can manage these challenges.
Following the above lines, this paper focuses on developing a new model of Project-Based Instructional Taxonomy (PBIT) that contributes to developing CT towards an educational objective of creative action. The model is rooted in an interdisciplinary theoretical framework that brings together theories of CT, creativity, Bloom’s Taxonomy, and Project-Based Instruction. A case will be discussed on a course in Deep Learning Technologies in the AI Bachelor program at Northeastern University, China. The case shows how PBIT is applied in teaching practice that improves students’ learning abilities. This further implies how to develop PBIT in creativity, CT, and AI education in the future.
2. Creativity, CT, and Education
2.1. Creativity as an Inherent Component of CT
The literature shows that since the 1990s, CT has been studied in diverse topics such as teaching methods, learning environments, and evaluation strategies [34,35,36,37]. According to Wing [38], we should call to make thinking like a computer scientist a fundamental skill for everyone. Even though Wing [38] did not state exactly what CT is, there are growing interests in defining CT as one of the terms in relation to problem solving [39]. CT involves solving problems, designing systems, and understanding human behavior. It is the thought process involved in solving problems; the solutions are represented in forms of being carried out by information-processing agents [39]; where the agent can be a computer, a machine, or a human being [40]. In this sense, CT is one of the daily life skills that everyone needs [41,42], just like reading or writing, that should be added to every learner’s analytical ability, rather than just being a programming skill [43]. Accordingly, CT is no longer just essential for learners in computer science, but also indispensable to the learners in other domains [44,45,46].
Creativity is related to CT [47]. According to the literature, creativity is the ability to generate novel ideas, raise new questions, and come up with solutions to ill-defined problems [48]; it helps to gain new knowledge in crossing disciplinary boundaries [49]; it is not only ‘know-what’ but also ‘know-how’ that are skills involved in maneuvering and operating concepts, ideas, and behaviors in the physical and social world—including the skills of social interaction and engagement [50]. As Romero, Lepage, and Lille [51] described, when students engage in programming activities, they are working in creative processes. The students solve problems or meet users’ needs; they engage in activities to design, write, test, debug, and maintain a set of information and instructions using a particular programming language. This is not a linear predefined process, but rather a prototype-oriented approach; students need to always test and improve their ideas before releasing a final solution [52]. Therefore, creativity is one of inherent components in CT education that motivates students to propose ideas, engage in action, reflect from practice, and finish satisfying products [5].
2.2. ‘Creating’ as an Education Objective
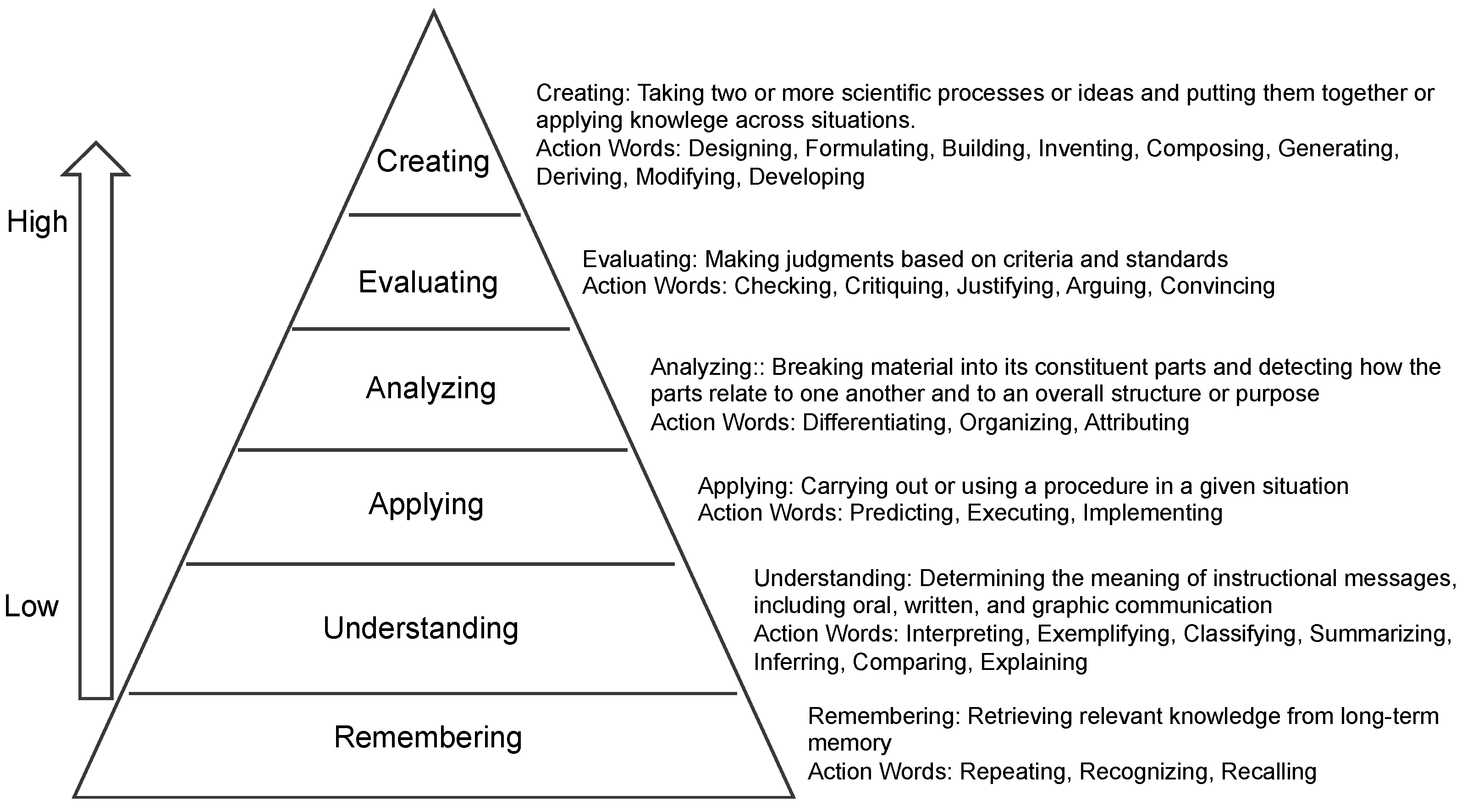
Teachers classify objectives because the type of objectives attempted dictate the selection of instructional methods, media, and evaluation used in the lessons [53]. By a review of the literature, different taxonomies have been developed for this purpose [54]. One of the most widely used ways of organizing levels of expertise is the model of Bloom’s Taxonomy of Educational Objectives [55]. It is well known that Bloom’s Taxonomy includes three hierarchical levels to classify educational learning objectives. It was developed to promote higher forms of thinking in education, such as analyzing and evaluating concepts, processes, procedures, and principles, rather than simply memorizing facts. In 2001, a newer version of Blooms’ Taxonomy was published [56] that defined a more dynamic conception of classification (Figure 1).
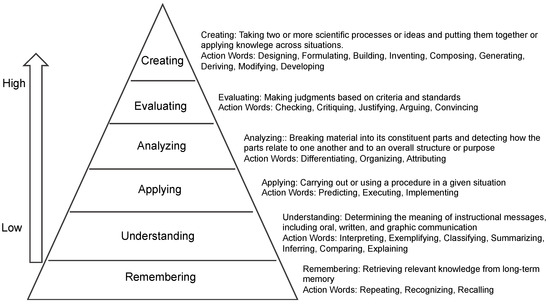
Figure 1.
The Revised Blooms’ Taxonomy.
From Figure 1, we can see ‘Creating’ is on the top of the revised taxonomy, which means the abilities to design, formulate, build, invent, compose, generate, derive, modify, or develop something new. It also involves the abilities to take two or more scientific processes or ideas and put them together or take a process and place it in new contexts. These abilities of ‘Creating’, lead to ‘creative action’, which is what CT development requires in education. In the taxonomy, ‘Creating’ involves abilities based on Remembering, Understanding, Applying, Analysing, and Evaluating. As Almerico [57] suggested, to underscore this dynamism, we use verbs and gerunds to label the categories and subcategories (rather than use the nouns in the original taxonomy). Accordingly, Figure 1 also shows some examples of ‘action words’ describing the cognitive processes by which thinkers encounter and work with knowledge.
Besides the above, a knowledge dimension is also enriched with different types of knowledge. According to Zhu and Zhou [58], it consists of (a) factual knowledge, (b) conceptual knowledge, (c) procedural knowledge, and (d) metacognitive knowledge. By using this categorization, courses can be designed with appropriate content and instruction that may lead students to learn in depth. It also provides the standardization of the teaching–learning process as the instruction provided to help students to meet the education objectives. So, a clear, unambiguous education objective improves the interaction between the instructors and the students; this further helps students to learn the detailed requirements and expectations needed to complete the course [59]. In other words, the specification of education objectives is aimed at achieving the desired teaching and learning outcomes [60].
3. A Model of Project-Based Instructional Taxonomy (PBIT)
Recently, CT development has been much-studied in contexts such as Problem-Based Learning [49] and Project-Based Learning [61]. These pedagogies allow students to participate in learning activities by investigation of problems, organization of projects, and formulation of solutions [62]. According to Railsback [63] and Martinez [64], Project-Based Instruction (PBI) should be promoted that is an authentic instructional model or strategy in which students plan, implement, and evaluate projects that have real-world applications beyond the classroom.
Historically, PBI was developed in 1960s in McMaster University in Canada [65], where the pedagogy of Problem-Based Learning originally started, which helped students to apply their basic scientific knowledge to clinical situations [49]. Since then, many medical schools in the USA, Canada, and Europe have implemented PBL and adopted PBI as part of their curricula. Until the mid-1990s, PBI was spread and widely implemented in diverse contexts beyond medical education. This further helped it gain acceptance in more and more fields and across the globe [49]. Accordingly, the authentic projects have become increasingly popular in curriculum design that show the following principles [66]:
- (a)
- Student-centered or student-directed;
- (b)
- A definite beginning, middle, and end;
- (c)
- Content meaningful to students; directly observable in their environment;
- (d)
- Real-world problems;
- (e)
- First-hand investigation;
- (f)
- Sensitivity to local culture and culturally appropriate;
- (g)
- Specific goals related to curriculum and school, district, or state standards;
- (h)
- A tangible product that can be shared with the intended sources;
- (i)
- Opportunity for reflective thinking and student self-assessment;
- (j)
- Authentic assessments (portfolios, journals, etc.).
In learning environments like PBI, students are facilitated to develop CT and creative action [49]. As Papert [34] argued, in the process of personally meaningful projects, students would be able to forge ideas and learn the necessary coding elements by addressing challenges as they naturally arise. This learning context is similar to how computational solutions work in professional practice [13]. As Zhou [67] described, all students’ learning activities center on project work; projects lead students to achieve both individual and group learning goals. Projects increase motivation, stimulate interplay between individual creativity and group creativity, and construct a creative learning community.
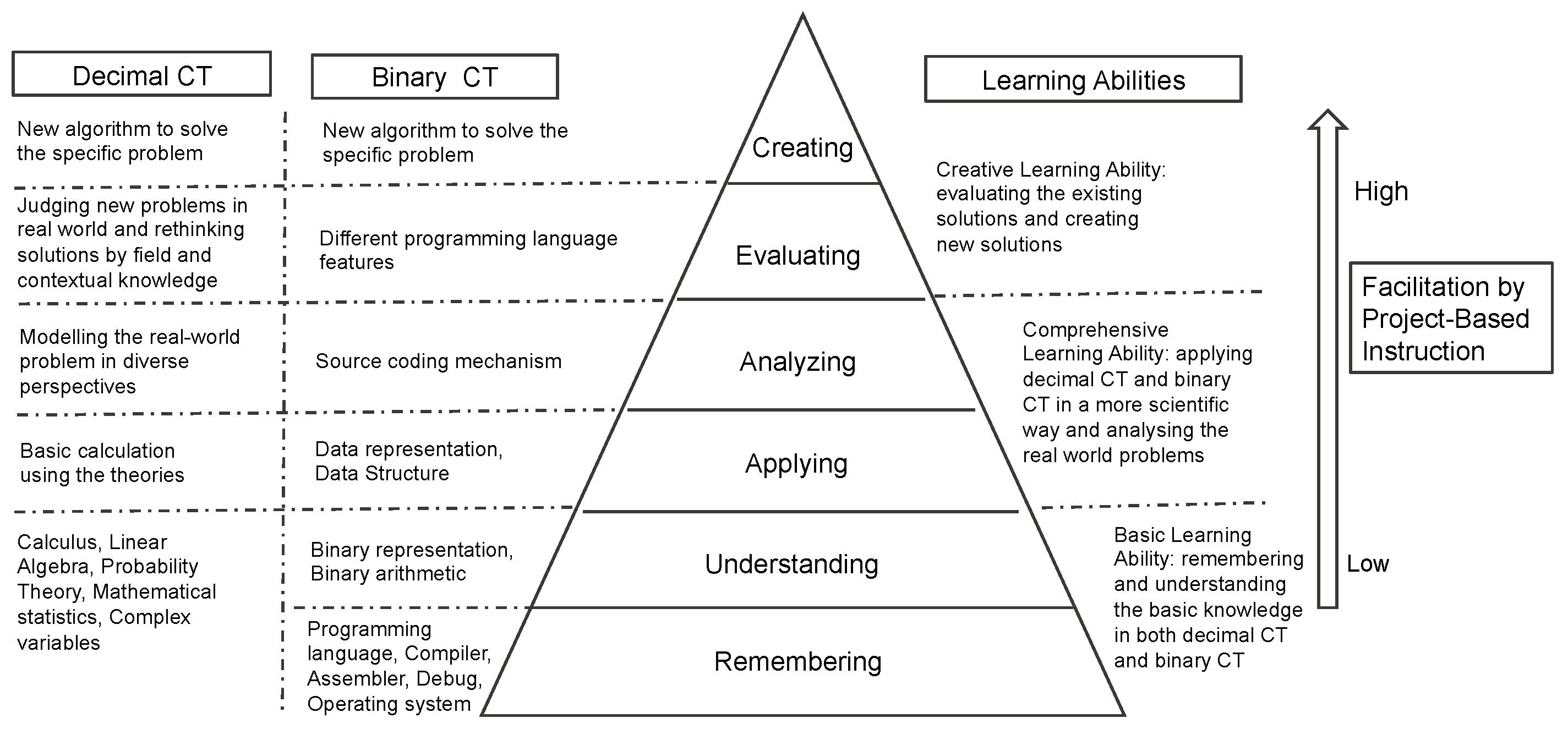
The development of learner-driven and action-focused education requires providing students with clear guidelines. We need to identify learning objectives that are statements of what students are expected to know, understand, and/or be able to demonstrate after completion of a course [53]. It is also necessary to rethink how to classify educational objectives that show what teachers expect or intend students to learn through instruction. All these ideas drive us to develop PBI further by taking creativity, CT education, and Bloom’s Taxonomy into account. Accordingly, an integrative model is designed, as Figure 2 shows.
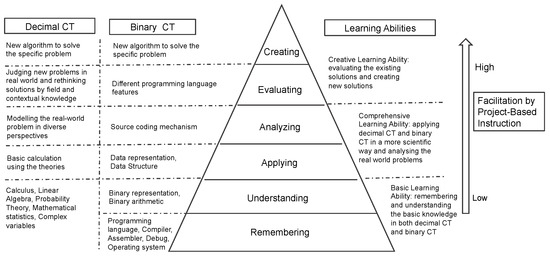
Figure 2.
The Model of Project-Based Instructional Taxonomy (PBIT).
As shown in Figure 2, we classify CT into two categories: Binary CT and Decimal CT. Binary CT is the fundamental understanding of the computer system, which is also the basis of operating system, programming language, compiler, and data structure. This also includes other algorithms such as the data compression algorithm, source coding algorithms, encryption algorithms, and the transmission algorithm. For example, the C programming language is widely used in all aspects in software engineering, which can directly manipulate the main memory working in binary. Using the C programming language, all the modern operating systems have been created, like Windows, Unix, iOS, Mac OS, Linux, and Android; the C programming language also plays an important part in understanding the source code of deep learning architecture. A student could not properly program or debug to simulate the designed algorithm if he/she did not have a deep understanding of binary architecture.
Understanding binary arithmetic is also crucial for students to master how a computer works and how to design new algorithms to solve new problems. Since binary CT relates to programming, debugging, and considering the solution in a machine way, it is the basis to develop decimal CT which aims to define a new problem and look for a mathematical solution. Teaching knowledge in binary CT is difficult. Decimal mathematics can solve higher level problems; it is relatively easier to employ exiting mathematic theories when finding solutions to a specific problem. In AI education, both categories are important, and, meanwhile, they relate to three levels of learning abilities of CT:
- (a)
- Basic Learning Ability of CT (remembering and understanding the basic knowledge in both decimal CT and binary CT), which means students should master the basic mathematical theories and basic programming skills while still lacking experience of and deep understanding of the real-world problems. They gain the basic knowledge in both decimal CT and binary CT but are not able to properly divide a big problem into several smaller problems. On this level, students can hardly provide a feasible solution to solve a problem; they tend to be very idealistic about the solution in neglecting issues such as the hardware limitations, algorithm efficient, programming language limitations, or platform problems.
- (b)
- Comprehensive Learning Ability of CT (applying decimal CT and binary CT in a scientific way and analyzing real-world problems), which means students have a deeper understanding of the knowledge of mathematics and computer science and they can apply decimal CT and binary CT in scientific ways to analyze real-life problems. They also have good understanding of the limitations of computational systems. They master the ability to connect a specific small problem to a mathematical theory and to implement a proper programming language. These abilities help them to formulate feasible solutions in solving real-life problems.
- (c)
- Creative Learning Ability of CT (evaluating the existing solutions and creating new solutions), which means students have mastered a full body of knowledge about how a computer works and how related mathematical theories help to solve different problems in various contexts. They also master methods of evaluation of existing solutions and creating new ones. When facing a problem, they have strong abilities to figure out several solutions with different technical and mathematical paths. With understanding of the domain knowledge in various industrial fields, they can select one proper technical path among several potential solutions. They have also good understanding of project budget, time plan, company size, and legacy system in the company, etc.
Additionally, it always takes time to deliver knowledge and facilitate students to gain new learning experience in depth. This indicates when PBIT is applied in teaching practice, the course design should take a reasonable time plan into account to plan lectures and hands-on learning activities. This should also be aligned with education objectives and evaluation requirements. These points lead us to discuss a case on a course Deep Learning Technologies in AI bachelor education in a Chinese university.
4. A Case: Applying PBIT in Education Practice
4.1. Method: A Case as an Example
In teaching practice, how can we use PBIT as a tool to develop teaching practice? This section shows a detailed case as an example on a new course design. We show a case as an example that indicates a way of conducting and disseminating research to impact upon practice, and to refine the ways in which practice is theorized [68].
In this paper, the example links the theoretical framework with practice in the particular setting of a bachelor AI education program in one of Chinese universities. As Freebody [68] described, in the cases, teachers are always teaching some subject matter, with some particular learners, in particular places, and under conditions that significantly shape and temper teaching and learning practices. These conditions are not taken to be ‘background’ variables, but rather lived dimensions that are indigenous to each teaching-learning event. One of the authors’ own teaching experience is the resource in the description of the case that visualizes the process of a course’s development. Based on showing students’ learning outcomes, the case is described by transferring the author’s participatory experience to research resources in this paper. So, the researcher himself also plays multiple roles, such as of being a course designer, an AI educator, and a participant in a PBI environment.
As mentioned, the main purpose of this paper is to develop a new model of Project-Based Instructional Taxonomy (PBIT) that provides a tool of course design that facilitates CT development as a creative action in solving real-life problems. Accordingly, the case reflects how we can deepen theoretical understanding through a course process with details of ‘how’ the teaching practice is developed. As Dowling and Cooney [69] suggested, in designing and developing a research project, the researchers must choose the method that is most appropriate to answer the research question while also considering the approach that will make the best of their own knowledge and experience in the phenomenon under consideration to achieve credibility. In educational contexts, people’s practices and experiences have been described as displaying uncertain, complex, messy, and fleeting properties, which together call distinct research approaches to description, understanding, and explanation [68].
4.2. Background of a Course Design
As mentioned, the case focuses on how PBIT is applied in the course Deep Learning and Technologies, which is one of elective courses in a bachelor education in the Faculty of Software Engineering, Northeastern University (NEU), China. At NEU, a reform from traditional teaching to Problem and Project-Based Learning (PBL) carried out in bachelors’ and masters’ education since 2018. PBI has been one of the new methods used to redesign courses that are involved in the reform. Meanwhile, NEU has close collaboration with local and national high-tech AI industries such as Kuangshi Technology, iFLYTEK, Huawei Technology, and Alibaba. This provides conditions and resources to design innovative pedagogies such as PBL in AI education.
Since 2019, the course Deep Learning and Technologies has been open to all students in third-year bachelor education within NEU. The course has been focused on the improvement of CT development. Usually, there are around 100 students who come from 13 different majors in the course every year. Even though students have diverse educational backgrounds and knowledge foundations, a basic level of mathematical and programming skills are required to enroll in this course. The students are required to work 56 h in this course. The new PBIT model has been employed in this course since 2021.
4.3. Course Design
The principles of the course design include (a) all principles of PBI as discussed in Section 3, and (b) inclusive education aiming to encourage every student to develop CT. By an overview of the course structure, there are three main parts:
- (a)
- Lectures on Computer and Programming (8 h);
- (b)
- Lectures on Deep Learning and Technologies (24 h);
- (c)
- Student Project Work (24 h).
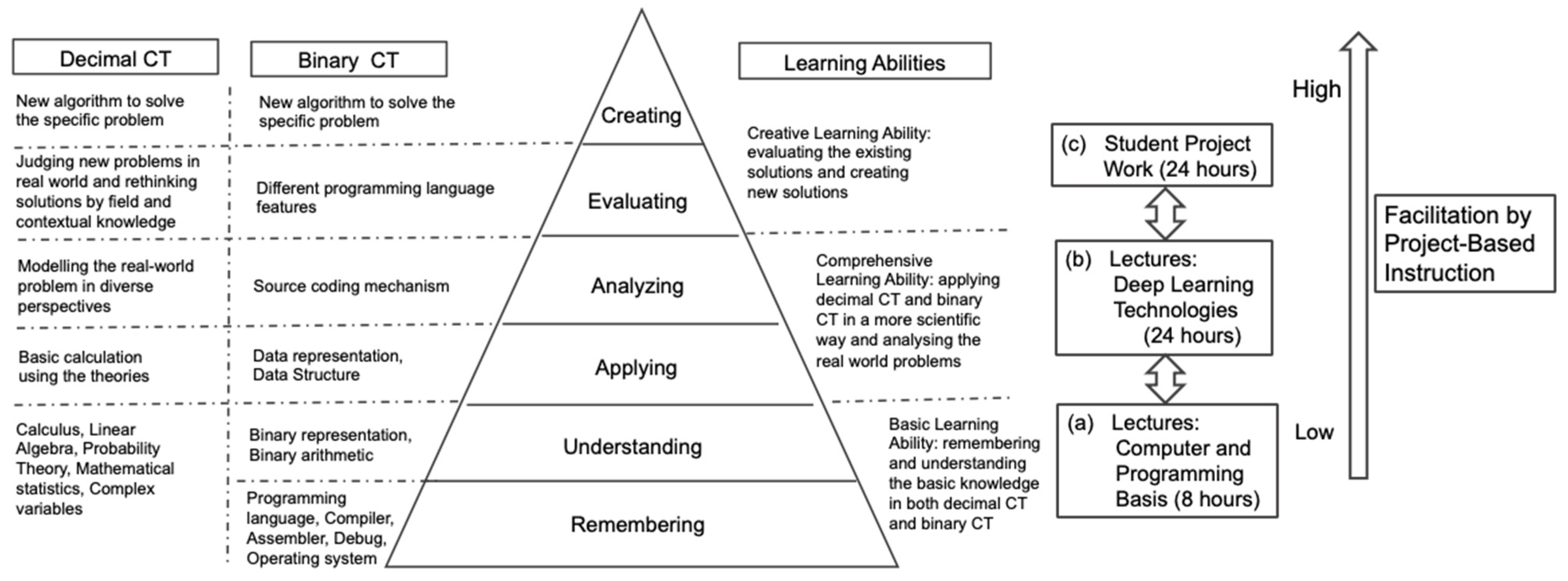
The alignment is made between the course structure and different education objectives, as shown in Figure 3.
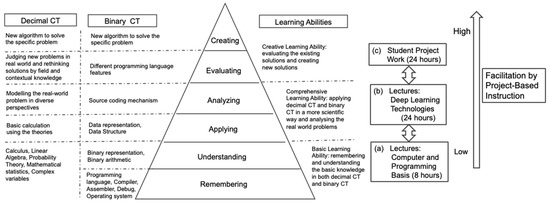
Figure 3.
Course Design in PBIT.
As shown Figure 3, there are two parts of the lectures that support students’ project work. In the first 8 teaching hours, knowledge on computers and programming is introduced, which includes basic programming knowledge, basic calculus and linear algebra, and Python platform. The first stage of teaching aims to cultivate the students to learn basic abilities in both binary and decimal CT. Students are required to remember and understand basic knowledge to be able to apply and analyze a given algorithm in the course.
The second stage involves lectures to teach knowledge of deep learning and technologies that facilitates students to gain comprehensive learning ability. Students should not only be able to remember and understand the basic concepts in Deep Learning, like neuron network, loss function, forward propagation, backward propagation, and data set, but also be able to apply and analyze models of deep learning, such as VGG, U-net, and Mobile-Net. They are also expected to evaluate different models that they develop by themselves or their peers.
In the third stage, students participate in group work and develop their projects. Each student group (4–5 members) will first identify a problem related to the course and then work on a problem-solving process until the solution is achieved. The students are expected to apply theoretical knowledge learned from the lectures in the practice of their projects. To support CT development, a project workflow is designed, as discussed in Section 4.3.
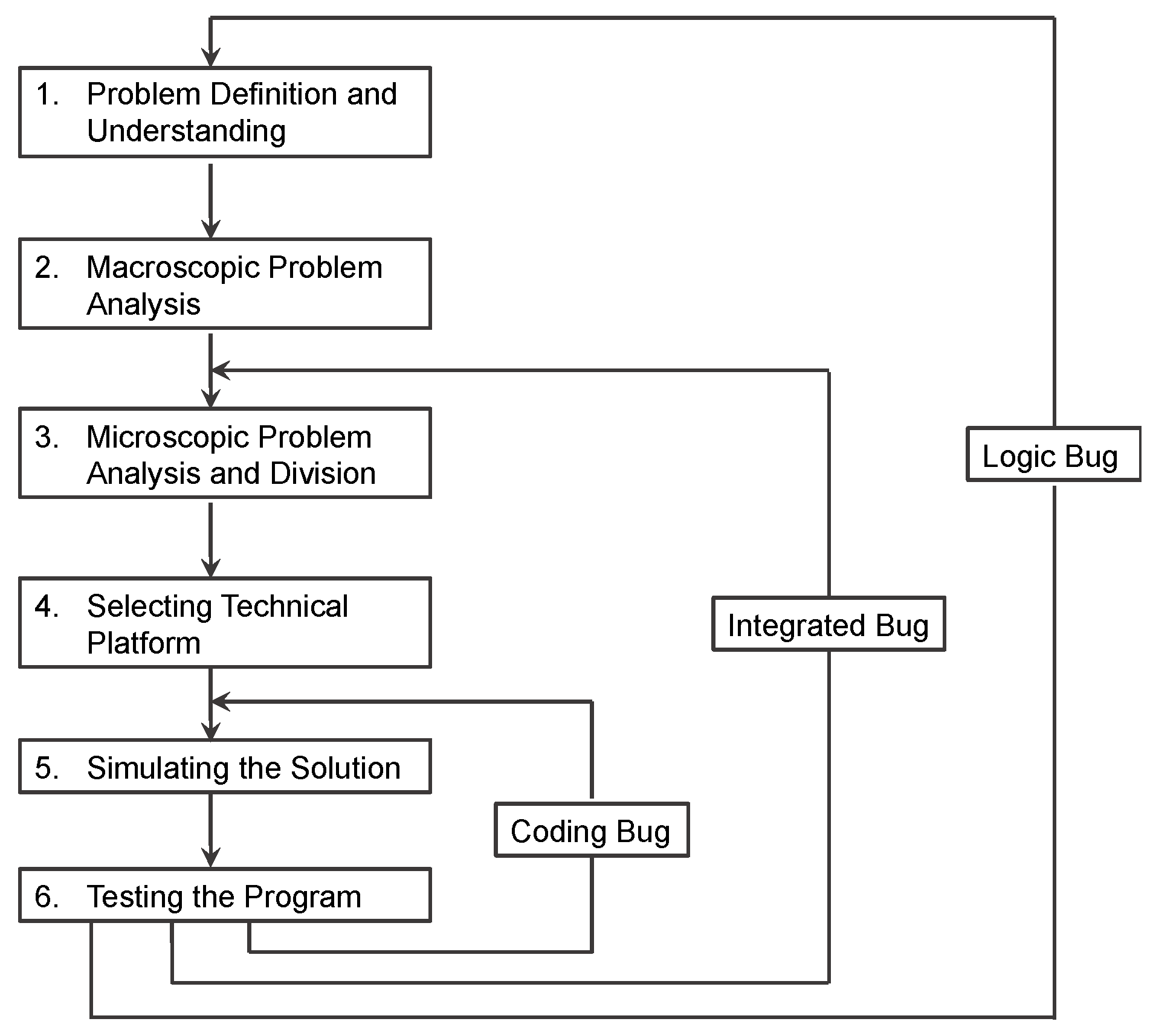
4.4. A Project Workflow
A project workflow is designed to facilitate students’ learning experience (Figure 4). Overall, there are six recursive stages: (1) Problem Definition and Understanding, (2) Macroscopic Problem Analysis, (3) Microscopic Problem Analysis and Division, (4) Selecting Technical Platform, (5) Simulating the Solution, and (6) Testing the Program. During the test stage, bugs always exist. If there is a logic bug, the students may go to stage (1) for recursive operations; while if there is a coding bug or integrated bug, students need to check again from stage (3) to (6).
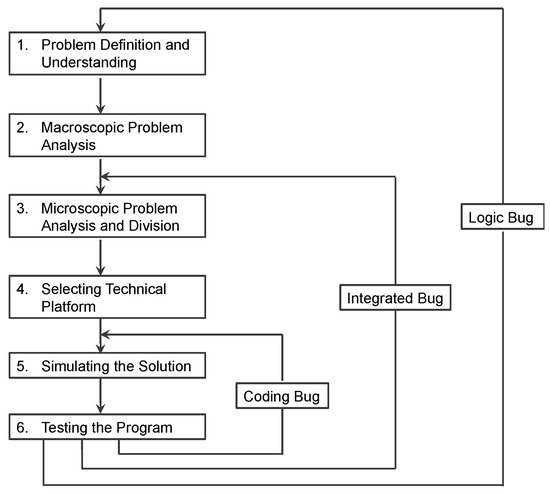
Figure 4.
Workflow in Student Project Work.
In the first stage, Problem Definition and Understanding, student groups need to identify the real-world problems based on collaboration with local software enterprises. They choose the company partners themselves or under a teacher’s recommendations. They will visit the companies and consult the engineers and collect information in relation to different problems. With the help of teachers and enterprise engineers, student groups should identify specific problems.
In the second stage, Macroscopic Problem Analysis, the group members try to seek solutions for the problems. Usually, there are several potential directions to explore solutions from both mathematical and technical perspectives. Some of the potential solutions are feasible while some are not. In this situation, computational thinking plays a significant role to determine the most feasible solution. This also requires students to apply knowledge they learn from the lectures on Deep Learning and Technologies in practice. For example, if students do not master knowledge on derivative, matrix vector, probabilities, mean, or standard deviation, they will be unable to find good solutions to move on their project work.
In the third stage, Microscopic Problem Analysis and Division, the predefined problem is divided into several smaller tasks; each task corresponds to one or two mathematical or technical problems. In the project, the algorithm part includes data collection and preprocessing, designing the deep network structure, selecting the loss function, training strategies, and hyper-parameter selection. These tasks require knowledge of sparse representation, partial derivative, matrix operation, and probability, etc. The students are encouraged to find and understand the mathematical theories behind the tasks, and further to use the theories to solve the problems.
In the fourth stage, Selecting Technical Platform, the students are expected to implement the solutions on machines based on their selection of technical platforms. In software engineering, different technical platforms aim to solve different problems. For example, in developing a server-end system, a Linux operating system with JVM is suitable; while in developing a front-end software artifact, JavaScript and other related libraries are good choices. The students should fully consider the mathematical solutions designed in the first three stages and distinct features of different technical platforms that help them to make correct selections. Teachers and enterprise engineers also provide suggestions to students.
In the fifth stage, Simulating the Solution, learning activities are more software-engineering related. Students should simulate solutions on the technical platforms. During this stage, some students may feel frustrated, as writing a program is not as easy as they expect. They maybe meet some challenges such as Installing Integrated Environment (IDE), configuration of the development, importing the libraries, or dealing with different kinds of bug. In this situation, students are encouraged to help each other, and teachers are also expected to facilitate students to manage diverse challenges.
The last stage is Testing the Program. In general, debugging is a thorny problem for most software developers. In this stage, a comprehensive understanding of binary computational thinking is required. Bugs can be classified into three categories, including coding bug, integrated but, and logic bug. Regarding the first category, the students need to firstly check the source code of the program and read the API (Application Programming Interface) that is provided by the platform supplier. They then go back to the fifth stage, fix the bugs, and test the program again and again until the program can run successfully. Regarding the second category, there may be an integrated bug, for two reasons: One reason is the integration of different modules related to software engineering. In such situations, the students are required to go back to the third stage to check the interfaces among different modules. The second is that the defined problem is not divided into microscopic tasks correctly. Regarding the third category, if there is a logic bug, it means the inconsistency exists between the problem defined and its proposed solution. The students need to go back to the beginning stage to redefine the problem or rethink the direction of solutions.
The collaboration between NEU and local enterprises provides resources for students’ projects. The above stages in the Project Workflow motivate students to achieve CT abilities deeper and deeper through working with problem-oriented projects. This also provides opportunities for students to learn other skills such as project management, communication, and collaboration.
4.5. Teaching and Facilitation
There are three teachers in the teaching group. One teacher is from an enterprise and the other two are from Software College at NEU. The teaching responsibilities include delivering lectures in the first and second stages and supervision of student projects in the last stage in the course. Usually, the teachers meet student project groups every two weeks.
When students develop their project groups, diversity of members’ backgrounds is encouraged. Including students from different majors work in a group (with four to five members) helps students to learn from each other and collect different perspectives to solve a specific problem. Each group selects one group leader who helps to negotiate with supervisors, organize group meetings, and book supervision meetings. In these meetings, teachers and students are equally to engage in discussions that facilitates the process of solving problems in projects. Student groups should also collaborate with local enterprises. The group leaders help to coordinate the groups to work together with enterprise engineers.
The identification of problems and plans of implementation of student projects should be approved by teachers that will ensure students to meet learning objectives of the course. During the implementation of projects, there is no restriction in selecting the technical platforms. Students can choose the platforms that they are familiar with, such as Keras, Tensorflow, or Pytorch. Before the end of the projects, student groups are required to submit project reports which is a part of their examination.
4.6. Methods of Grading
According to the course structure, there are three parts in examination. The final score will be given individually by the sum of the scores from different parts. The proportion of score in part a, b, and c is, respectively, 20%, 30%, and 50%. Table 1 shows detailed exam requirements and grading methods. In examinations of (a) and (b), students are required to submit individual reports. In Student Project Work, students should submit group reports and attend group oral examination; when individual score is given, peer evaluation is also considered.

Table 1.
Grading in the Course.
In group exams, students’ learning experience is checked according to different educational objectives as designed in the course. Besides project reports, students’ CT development, methods of creation action, and abilities of applying theories in practice are also evaluated in Student Project Work. This also includes reflection of individual student and peer evaluation that helps to avoid freeloaders in student groups.
5. Discussion
As the course design shows, the links between theories and practice, problem-oriented projects, and student group work are key dimensions to apply PBIT in education practice. To help students to achieve education objectives, we should be aware of these key dimensions. Overall, education systems in Chinese schools and universities are exam-oriented. Chinese students have been used to paying attention to their memory, article recitation, numeracy, reading, writing, and other basic skills that are assessed in examinations. Such background provides opportunities for reform to integrate PBIT into the current education system, change methods of teaching and learning, and improve students’ learning abilities.
As mentioned, the PBIT model has been applied in the course since autumn semester in 2021; before 2021, the course was organized by lecture-based teaching. To meet the requirements of the examination policy, an individual grade is given in the implementation of PBIT; meanwhile, peer evaluation and group reports are also considered for individual grade. Moreover, students are motivated to learn both individually and collaboratively. In comparison with the same course in the autumn semester in 2020, it shows PBIT gains very positive effects. The total average grade among students was 90.4 in 2021 and 93.92 in 2022, which were higher than 87.1 in 2020. Since 2023, the course examination has followed the overall changes in examination policies at NEU. As a new point scale should be adapted, the condition of comparing students’ average grade with previous years has been missing; however, the method of grading in this course has not been changed.
Along with the learning process in the course, every student should submit two individual reports and contribute to one group report. All the requirements and evaluation criteria of reports are made based on the model of PBIT. The work on different project reports provides students opportunities to engage to identify new research questions, communicate and collaboration with others, learn how to apply theories in practice, and seek solutions. As students come from different backgrounds, PBIT also helps students to link knowledge they learn from the course to their own subject majors. This further improves their skills in solving problems across disciplinary contexts as well as their abilities of ‘creative action’ in CT development.
The design of students’ examination was in line with the framework of three-level learning abilities: Basic Learning Ability (in part A), Comprehensive Learning Ability (in part B), and Creative Learning Ability (in part C). From the submitted reports in 2021, how students improve their learning abilities can also be seen. For example, when students finished Part A, they were required to submit reports under a topic of ‘Using Python or C Programming Language to Solve a Specific Problem’. Then the students showed their diverse interests, proposed different problems, and formulated solutions. For example, students provided solutions to solve problems like ‘Simulating AND, OR, and NAND Gates with Perceptron’ or ‘Simulating Loss Function in High-Level Programming Language’. In 2022 and 2023, it was suggested that the student reports focus on the theme of ‘Application of Deeping Learning in Industrial Contexts’. Students showed their interests in their reports such as ‘Methods of Material Surface Defect Detection Based on Deep Learning’, ‘Application of Deep Learning in Image Processing’, and ‘Solving Problems of Tourism Management by Deep Learning’. As mentioned, all student projects were proposed and developed in collaboration with local companies, which means through the projects, students gained abilities to formulate feasible solutions in solving real-life problems. This indicated that students mastered comprehensive understanding of binary CT, decimal CT, and programming skills. In Part B, the submission of reports required students to investigate ‘How Artificial Intelligence Technologies Improve Productivity and Effectivity in Certain Field’. Most of the students responded to this assignment by rethinking the application of AI technologies in the field that they majored. Accordingly, the submitted reports showed students’ work in diverse fields such as Mechanical Engineering, Materials Science, Environment Science, Health Care, and Business Service. In Part C, students should experience deeper learning and show their abilities to solve the problems by ‘Using Artificial Intelligence Technology and Deep Learning in Practice’. The students worked in groups, defined appropriate problems, provided feasible solutions, and finished the program with high-level programming language. This has been evidenced by titles of student reports such as ‘Classification of Metallographic Images of Fe-C Alloys Based on Keras Neural Network Framework’ and ‘Image Recognition of Metal Microstructure’.
All teachers in the course finished their participation of Teacher Education Program (TEP) at NEU. From TEP, teachers mastered knowledge, skills, and competencies to design and apply PBIT in the course. As PBIT is a new model, some techniques have been also employed to facilitate students to learn ‘how to learn’ step by step. For example, at the beginning of the course, teachers firstly addressed some examples of research problems, then students gradually learned how to identify problems by themselves under the support of teachers. During the course, teachers also reflected themselves as learner experts, who shared learning experience with students and who were equal with students in problem-solving processes and in collaboration with enterprises. Thus, their roles were more facilitators of the learning process than providers of problems’ solutions. This also laid basis to motivate students to work on open and real-life problems in the period of the Student Project Work.
6. Conclusions
Fostering students’ authentic learning experience is very important in CT development in AI education. Students should be encouraged to develop computational products that have an authentic impact on their lives from the moment they begin to code; all they need is to be situated in contexts that allow them to do so. AI educators should design and apply new pedagogical models that are more inclusive to motivate and empower students to learn through creative action. This paper highlights creativity as an inherent element of CT development; this means ‘creative action’ stands at the top of the agenda in AI education. The new model of PBIT proposed in this paper is accordingly developed, and provides a useful tool of course design; it makes alignment between education objectives, knowledge categories of CT, levels of learning ability, process of project facilitation, and methods of grading. As the case on the course ‘Deep Learning and Technologies’ reveals, PBIT provides students opportunities to learn CT in-depth and master skills for solving practical problems under the support of teachers. The university, NEU, also paid attention to policy support, management of changes, and development of teacher education. These measures help to overcome barriers to education reforms and shape a friendly environment to develop PBIT in AI education. Since PBIT has been developed since 2021, a strategy should be considered for its long-term development. This paper also shows its limitation in providing more evidence to support a broader scope of study related to more research questions, for example, how can PBIT stimulate students’ reflective learning experience and critical thinking in their practice of creative problem solving? Additionally, the implementation of PBIT involves diverse participant groups including teachers, students, university leaders, and enterprise engineers; it is necessary to explore how different participants perceive their collaboration in PBIT. Accordingly, future research will focus on more evidence-based education improvement and a holistic view to develop CT in AI education.
Author Contributions
Conceptualization, C.Z.; methodology, C.Z. and W.Z.; formal analysis, C.Z. and W.Z.; investigation, W.Z. resources, W.Z.; writing—original draft preparation, C.Z. and W.Z.; writing—review and editing, C.Z. and W.Z.; visualization, C.Z. and W.Z.; supervision, C.Z.; project administration, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethical review and approval were waived for this study due to a study focusing on a model of pedagogical design and its implementation.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lye, S.Y.; Koh, J.H.L. Review on teaching and learning of computational thinking through programming: What is next for K-12? Comput. Hum. Behav. 2014, 41, 51–61. [Google Scholar] [CrossRef]
- Agbo, F.J.; Oyelere, S.S.; Suhonen, J.; Laine, T.H. Co-design of mini games for learning computational thinking in an online environment. Educ. Inf. Technol. 2021, 26, 5815–5849. [Google Scholar] [CrossRef]
- Angeli, C.; Giannakos, M. Computational thinking education: Issues and challenges. Comput. Hum. Behav. 2020, 105, 106185. [Google Scholar] [CrossRef]
- Dolgopolovas, V.; Dagienė, V. Computational thinking: Enhancing STEAM and engineering education, from theory to practice. Comput. Appl. Eng. Educ. 2021, 29, 5–11. [Google Scholar] [CrossRef]
- Brennan, K.; Balch, C.; Chung, M. Creative Computing; Harvard University Press: Cambridge, UK, 2014. [Google Scholar]
- Kim, Y. The Effects of PBL-based Data Science Education classes using App Inventor on elementary student Computational Thinking and Creativity improvement. J. Korean Assoc. Inf. Educ. 2020, 24, 551–562. [Google Scholar]
- Israel-Fishelson, R.; Hershkovitz, A.; Eguíluz, A.; Garaizar, P.; Guenaga, M. The associations between computational thinking and creativity: The role of personal characteristics. J. Educ. Comput. Res. 2021, 58, 1415–1447. [Google Scholar] [CrossRef]
- Brennan, K.; Resnick, M. Imagining, creating, playing, sharing, reflecting: How online community supports young people as designers of interactive media. In Emerging Technologies for the Classroom; Springer: New York, NY, USA, 2013; pp. 253–268. [Google Scholar]
- Dagienė, V.; Futschek, G.; Stupurienė, G. Creativity in solving short tasks for learning computational thinking. Constr. Found. 2019, 14, 382–396. [Google Scholar]
- Glezou, K.V. Fostering computational thinking and creativity in early childhood education: Play-learn-construct-program-collaborate. In Research Anthology on Computational Thinking, Programming, and Robotics in the Classroom; IGI Global: Hershey PA, USA, 2022; pp. 21–45. [Google Scholar]
- Yadav, A.; Cooper, S. Fostering creativity through computing. Commun. ACM 2017, 60, 31–33. [Google Scholar] [CrossRef]
- Hershkovitz, A.; Sitman, R.; Israel-Fishelson, R.; Eguíluz, A.; Garaizar, P.; Guenaga, M. Creativity in the acquisition of computational thinking. Interact. Learn. Environ. 2019, 27, 628–644. [Google Scholar] [CrossRef]
- Tissenbau, M.; Sheldon, J. Abelson. From computational thinking to computational action. Commun. ACM 2019, 62, 34–36. [Google Scholar] [CrossRef]
- Li, Y.; Schoenfeld, A.H.; DiSessa, A.A.; Graesser, A.C.; Benson, L.C.; English, L.D.; Duschl, R.A. Computational thinking is more about thinking than computing. J. STEM Educ. Res. 2020, 3, 1–18. [Google Scholar] [CrossRef]
- Kuo, W.C.; Hsu, T.C. Learning computational thinking without a computer: How computational participation happens in a computational thinking board game. Asia-Pac. Educ. Res. 2020, 29, 67–83. [Google Scholar] [CrossRef]
- Tsai, M.J.; Liang, J.C.; Hsu, C.Y. The computational thinking scale for computer literacy education. J. Educ. Comput. Res. 2021, 59, 579–602. [Google Scholar] [CrossRef]
- Guzdial, M. A Definition of Computational Thinking from Jeannette Wing; Computing Education Blog: Atlanta, GA, USA, 2011. [Google Scholar]
- Tang, X.; Yin, Y.; Lin, Q.; Hadad, R.; Zhai, X. Assessing computational thinking: A systematic review of empirical studies. Comput. Educ. 2020, 148, 103798. [Google Scholar] [CrossRef]
- Ezeamuzie, N.O.; Leung, J.S. Computational thinking through an empirical lens: A systematic review of literature. J. Educ. Comput. Res. 2022, 60, 481–511. [Google Scholar] [CrossRef]
- Lyon, J.A.; Magana, A.J. Computational thinking in higher education: A review of the literature. Comput. Appl. Eng. Educ. 2020, 28, 1174–1189. [Google Scholar] [CrossRef]
- Barr, D.; Harrison, J.; Conery, L. Computational thinking: A digital age skill for everyone. Learn. Lead. Technol. 2011, 38, 20–23. [Google Scholar]
- Zhou, C.; Krogh, L. Developing Successful Group Processes in Interdisciplinary Projects. Interdisciplinarity and Problem-Based Learning in Higher Education: Research and Perspectives from Aalborg University; Innovation and Change in Professional Education; Jensen, A.A., Stentoft, D., Ravn, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 18, pp. 103–116. [Google Scholar]
- Zhou, C. In between Ha-Ha and Aha!: Technology Designers’ Humor as a Way of Creativity in Group Innovation Experience. Kindai Manag. Rev. 2019, 7, 9–19. [Google Scholar]
- Salam, S. A systemic review of Problem-Based Learning (PBL) and Computational Thinking (CT) in teaching and learning. Int. J. Humanit. Innov. (IJHI) 2022, 5, 46–52. [Google Scholar] [CrossRef]
- Saad, A.; Zainudin, S. A review of Project-Based Learning (PBL) and Computational Thinking (CT) in teaching and learning. Learn. Motiv. 2022, 78, 101802. [Google Scholar] [CrossRef]
- Valls Pou, A.; Canaleta, X.; Fonseca, D. Computational Thinking and Educational Robotics Integrated into Project-Based Learning. Sensors 2022, 22, 3746. [Google Scholar] [CrossRef]
- Yang, Y.; Lang, H. Project based instruction for computer aided design and mechatronics courses. In Proceedings of the 2020 15th International Conference on Computer Science & Education (ICCSE), Delft, The Netherlands, 18–22 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 406–410. [Google Scholar]
- Machado, C.T.; Carvalho, A.A. Concept mapping: Benefits and challenges in higher education. J. Contin. High. Educ. 2020, 68, 38–53. [Google Scholar] [CrossRef]
- Henriksen, D.; Richardson, C.; Shack, K. Mindfulness and creativity: Implications for thinking and learning. Think. Ski. Creat. 2020, 37, 100689. [Google Scholar] [CrossRef]
- Apiola, M.; Sutinen, E. Design science research for learning software engineering and computational thinking: Four cases. Comput. Appl. Eng. Educ. 2021, 29, 83–101. [Google Scholar] [CrossRef]
- Navy, S.L.; Kaya, F. PBL as a pedagogical approach for integrated STEM: Evidence from prospective teachers. Sch. Sci. Math. 2020, 120, 285–296. [Google Scholar] [CrossRef]
- Hardjanto, M.F.N.; Budiyanto, C.; Hafid, Y. Exploring the impact of design thinking on the development of computational thinking skill: Review of the literature. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Istanbul, Turkey, 7–10 March 2022. [Google Scholar]
- Zhou, C. A Study on Creative Climate in Project-Organized Groups (POGs) in China and Implications for Sustainable Pedagogy. Sustainability 2018, 10, 114. [Google Scholar] [CrossRef]
- Papert, S. Mindstorms: Children, computers, and Powerful Ideas; Basi Books Inc: New York, NY, USA, 1996. [Google Scholar]
- Grover, S.; Pea, R. Computational thinking in K-12: A review of the state of the field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Tikva, C.; Tambouris, E. Mapping computational thinking through programming in K-12 education: A conceptual model based on a systematic literature Review. Comput. Educ. 2021, 162, 104083. [Google Scholar] [CrossRef]
- Knie, L.; Standl, B.; Schwarzer, S. First experiences of integrating computational thinking into a blended learning in-service training program for STEM teachers. Comput. Appl. Eng. Educ. 2022, 30, 1423–1439. [Google Scholar] [CrossRef]
- Wing, J.M. Computational Thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Cuny, J.; Snyder, L.; Wing, J.M. Demystifying Computational Thinking for Non-Computer Scientists. Unpublished Manuscript in Progress. 2010. Available online: http://www.cs.cmu.edu/~CompThink/resources/TheLinkWing.pdf (accessed on 1 December 2023).
- Palts, T.; Pedaste, M. A model for developing computational thinking skills. Inform. Educ. 2020, 19, 113–128. [Google Scholar] [CrossRef]
- Wang, C.; Shen, J.; Chao, J. Integrating computational thinking in stem education: A literature review. Int. J. Sci. Math. Educ. 2021, 20, 1949–1972. [Google Scholar] [CrossRef]
- Papert, S. A critique of techno centrism in thinking about the school of the future. In Epistemology and Learning Memo #2; MIT: Cambridge, MA, USA, 1990. [Google Scholar]
- Parsazadeh, N.; Cheng, P.Y.; Wu, T.T.; Huang, Y.M. Integrating computational thinking concept into digital storytelling to improve learners’ motivation and performance. J. Educ. Comput. Res. 2021, 59, 470–495. [Google Scholar] [CrossRef]
- McGuinness, C.; O’Hare, L. Introduction to the special issue: New perspectives on developing and accessing thinking: Selected papers from the 15th international conference on thinking (ICOT2011). Think. Ski. Creat. 2012, 7, 75–77. [Google Scholar] [CrossRef]
- Sen, C.; Ay, Z.S.; Kiray, S.A. Computational thinking skills of gifted and talented students in integrated STEM activities based on the engineering design process: The case of robotics and 3D robot modelling. Think. Ski. Creat. 2021, 42, 100931. [Google Scholar] [CrossRef]
- Denning, P.J.; Tedre, M. Computational thinking: A disciplinary perspective. Inform. Educ. 2022, 20, 361–390. [Google Scholar] [CrossRef]
- Israel-Fishelson, R.; Hershkovitz, A. Studying interrelations of computational thinking and creativity: A scoping review (2011–2020). Comput. Educ. 2022, 176, 104353. [Google Scholar] [CrossRef]
- Sternberg, R.J. Handbook of Creativity; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Zhou, C. Introducing Problem-Based Learning (PBL) for Creativity and Innovation in Chinese Universities: Emerging Research and Opportunities; IGI Global: Hershey, PA, USA, 2020. [Google Scholar]
- Craft, A. Creativity in schools. In Developing Creativity in Higher Education: An Imaginative Curriculum; Jackson, N., Oliver, M., Shaw, M., Wisdom, J., Eds.; Routledge: London, UK, 2006; pp. 19–28. [Google Scholar]
- Romero, M.; Lepage, A.; Lille, B. Computational thinking development through creative programming in higher education. Int. J. Educ. Technol. High. Educ. 2017, 14, 42. [Google Scholar] [CrossRef]
- Bjögvinsson, E.; Ehn, P.; Hillgren, P.A. Design things and design thinking: Contemporary participatory design challenges. Des. Issues 2012, 28, 101–116. [Google Scholar] [CrossRef]
- Nayef, E.G.; Yaacob, N.R.N.; Ismail, H.N. Taxonomies of educational objective domain. Int. J. Acad. Res. Bus. Soc. Sci. 2013, 3, 166–175. [Google Scholar] [CrossRef]
- Clark, D. Bloom’s Taxonomy of Learning Domains. Big Dog & Little Dog’s Performance Juxtaposition, 2013. Available online: http://www.nwlink.com/~donclark/hrd/bloom.html (accessed on 1 December 2023).
- Bloom, B.; Englehart, M.; Furst, E.; Hill, W.; Krathwohl, D. Taxonomy of Educational Objectives: The Classification of Educational Goals. In Handbook I: Cognitive Domain; Longmans, Green: New York, NY, USA; Toronto, ON, USA, 1956. [Google Scholar]
- Anderson, L.W.; Krathwohl, D.R. A Taxonomy for Learning, Teaching, and Assessing: A Revision of Bloom’s Taxonomy of Educational Objectives; Addison Wesley Longman, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Almerico, G.M. Bloom’s Taxonomy Illustrative Verbs: Developing a Comprehensive List for Educator Use. Fla. Assoc. Teach. Educ. J. 2004, 1, 1–10. [Google Scholar]
- Zhu, Z.; Zhou, C. Global Perspectives on Fostering Problem-Based Learning in Chinese Universities; IGI Global: Hershey, PA, USA, 2019. [Google Scholar]
- Krathwohl, D.R. A revision of Bloom’s taxonomy: An overview. Theory Pract. 2002, 41, 212–261. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, C.; Sun, X. Big Data plus Business Administration: Applying Problem-Based Learning to Enrich the Design of Interdisciplinary Education. Int. J. Eng. Educ. 2022, 38, 786–798. [Google Scholar]
- Shin, N.; Bowers, J.; Krajcik, J.; Damelin, D. Promoting computational thinking through project-based learning. Discip. Interdiscip. Sci. Educ. Res. 2021, 3, 7. [Google Scholar] [CrossRef]
- Juškevičienė, A.; Dagienė, V. Computational thinking relationship with digital competence. Inform. Educ. 2018, 17, 265–284. [Google Scholar] [CrossRef]
- Railsback, J. Project-Based Instruction: Creating Excitement for Learning; U.S. Department of Education, Office of Educational Research and Improvement: Washington, DC, USA, 2002. [Google Scholar]
- Martinez, C. Developing 21st century teaching skills: A case study of teaching and learning through project-based curriculum. Cogent Educ. 2022, 9, 2024936. [Google Scholar] [CrossRef]
- Neufeld, V.R.; Barrows, H.S. The ‘McMaster Philosophy’: An approach to medical education. J. Med. Educ. 1974, 49, 1040–1050. [Google Scholar] [CrossRef]
- Zhou, C. Supporting Creative Learning by Information Communication Technology (ICT) in Project Teams. In Information Technology as a Facilitator of Social Processes in Project Management and Collaborative Work; Bagwell, T.C., Cropf, R.A., Foster-Gadkari, S.L., Eds.; IGI Global: Hershey, PA, USA, 2018; pp. 1–20. [Google Scholar]
- Zhou, C. A Student Project as an ‘Extra Group Member’: A Metaphor for the Development of Creativity in Problem-Based Learning (PBL). Akad. Kvarter 2014, 9, 223–235. [Google Scholar]
- Freebody, P. Qualitative Research in Education: Interaction and Practice; SAGE Publications: London, UK, 2003. [Google Scholar]
- Dowling, M.; Cooney, A. Research approaches related to phenomenology: Negotiating a complex landscape. Nurse Res. 2012, 20, 21–27. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).