Inquiry and Mathematical Modelling with Real-Archaeological Objects in Secondary Education

Abstract

Inquiry and modelling are relevant processes of mathematical activity, and both are considered as important competencies for problem solving, since their subprocesses have a family resemblance that makes them mutually complementary and enriched. In this line, we report an investigation focused on the study of the synergies and relationships established between the inquiry and modelling processes emerging in a learning situation, based on a realistic and authentic archaeological context. To this end, we considered one theoretical cycle to explain each process, and then designed a learning situation contextualised in a realistic and authentic archaeological context which promoted the development of inquiry and modelling skills for its solving. Methodologically, we conducted a case study with students in a secondary school of Badalona (Catalonia, Spain), who solved the learning situation grouped into working teams. Through a thematic analysis, we identified the steps of both processes followed by the students when solving the learning situation, and thus we delved into the synergies and relationships established between inquiry and modelling processes. Finally, we reflect on how both processes mutually enrich when dealing with a problem-situation and propose an integrative cycle for the development of inquiry and modelling skills in the classroom.

1. Introduction

Didactics of mathematics faces a double purpose as a science: on one hand, this discipline has a descriptive function, in which it studies the teaching and learning processes of a variety of mathematical contents and competencies attempting to understand how these processes take place and which elements interfere with them; on the other hand, when this discipline describes the different methodologies and processes for learning mathematics, it provides teachers with tools for improving their practice through gaining a better understanding [1].

Among these efforts made by didactics of mathematics to improve mathematical teaching, there exists current trends pointing to the importance of problem solving and inquiry (for example, [2,3]), as well as strengthening the work with modelling (see [4]). Both inquiry and modelling are considered to be relevant and enriching processes of mathematical activity, and have been widely studied and described in specialised literature (see [5,6]). Actually, both processes have also been mentioned together as interesting methodologies for mathematical problem solving [7].

However, despite the family resemblance (in terms of [8]) between some of the subprocesses concerning each of the inquiry and modelling processes, studies of both of them have been conducted separately until a recently published article [9]. This first approach to an integrative model, which could be useful for the study of learning situations where both inquiry and modelling processes emerge, started a path that this investigation aims to develop and delve into. As it is seen for the first time in the work presented in [9], both inquiry and modelling have subprocesses showing a notorious family resemblance between them and, from the perspective of Realistic Mathematics Education (see [7]), we can assert that both processes arise from situations which present realistic and authentic contexts (see a broader explanation in Section 2.3).

In fact, when inquiry and modelling processes are needed to solve a problem-situation, they present synergies. In this article, we understand ‘synergies’ as the relationships established between two processes in which each one of them enriches another one, making them deeper and stronger as if they were separated. As we shall see throughout the reported investigation, when both processes appear in the solving of a problem-situation, inquiry subprocesses allow the emergence/use of more accurate and closer-to-reality mathematical models, provide more specific data regarding the dealt problem, and facilitate the interpretation and validation of the results obtained after performing a mathematical work; while modelling provides inquiry of a rigorous method of obtaining results as well as facilitating the development of new questions from the results given. Then, we asked the following research questions: What synergies between the inquiry and mathematical modelling processes can be identified in a task of archaeological context? What could an integral cycle look like as a result of characterising these synergies between the inquiry and mathematical modelling processes?

Therefore, this article reports an investigation focused on the study of the synergies and relationships established between the inquiry and modelling processes emerging in a learning situation based on a real-archaeological context. This investigation aims to analyse how both processes mutually enrich, promoting the emergence/use of more accurate and closer-to-reality mathematical models than they would have been without the previous development of inquiry tasks. Finally, this work proposes an integrative cycle, representing the relationships established between both processes, based on the inquiry and modelling cycles that currently have major consensus in the research community of didactics of mathematics.

2. Theoretical Framework

In this section, we explain the theoretical framework adopted in our study by describing not only the modelling process, but also the inquiry learning education for a complete understanding of the investigation here reported.

2.1. Inquiry Learning Education

The approach to learning and teaching processes based on inquiry, both from research in general didactics and in didactics of mathematics, is not new. However, the interest of educational research on inquiry has increased during the last few years, working with the conviction that this methodology is highly suitable for preparing students for a dynamic knowledge-based society requiring the development of critical thinking and the ability to keep on learning autonomously and continuously, as well as being creative when solving new problems [2].

The Rocard Report [3] points to this direction and exhorts didactics of sciences to address science education towards methodologies that encourage students to investigate, produce questions, explore, and evaluate their conclusions. This report remarks on the need for a change in science teaching programs and is very critical of the so-called deductive approach teaching model, that is, the traditional teaching model in which a teacher shows concepts and their logical-deductive implications to his/her students and proposes some examples of their application. Therefore, this model is considered as one of the reasons behind the growing lack of interest of students in sciences and mathematics, and the consideration of such disciplines as closed systems with few or no practical use in real life.

Instead of the deductive approach teaching model, the Rocard Report proposes using the so-called inductive approach teaching model to revert this tendency, since this approach is based precisely on inquiry learning processes. We can thus see how the interest in an inquiry-based science education (IBSE from now on) is a current occupation for research in didactics and that there exists a consensus about considering this model as a way to ensure a significant learning adapted to prepare students for society education [7]. According to the interest in IBSE, there have been many approaches to inquiry processes from the research in didactics, where all these contributions share a common idea with particular accents in the different aspects of inquiry.

The American philosopher and educator John Dewey (1859–1952) was the first who talked of an inquiry-based education (referred to as IBE from now on). Dewey was a member of the so-called liberal education style, which aimed to discern which concepts and skills education had to be focused on to enable students to be competent for real life in society once they were adults [10]. Dewey defined inquiry as “the controlled or directed transformation of an indeterminate situation into one that is so determinate in its constituent distinctions and relations as to convert the elements of the original situation into a unified ‘Whole’” ([10], pp. 104–105). Dewey considered inquiry as a process in which what is not known and has to be learnt must be interesting and motivating, but also can be achieved by taking what students do know as a starting point; hence, previous knowledge and experience are of high relevance for Dewey, since there is the basis for the construction of new knowledge as well as pragmatism and connections with real life’s needs [7].

Artigue and Blomhøj [7] propose a very illustrative definition of IBE when they state that it is the way of work that scientists use and, in our particular case, the way of work that mathematicians use. Thus, inquiry-based mathematical education (referred to as IBME from now on) is defined by these authors as the learning model in which students are encouraged to act as scientists and mathematicians do when they solve real-world problems [7].

Another definition of IBSE that we consider important is that provided by the National Science Education Standards [11] since it is quite complete and refers to the processes arising when students learn throughout the IBSE model:

Scientific inquiry refers to the diverse ways in which scientists study the natural world and propose explanations based on the evidence derived from their work. Inquiry also refers to the activities of students in which they develop knowledge and understanding of scientific ideas, as well as an understanding of how scientists study the natural world.

Inquiry is a multifaceted activity that involves making observations; posing questions; examining books and other sources of information to see what is already known; planning investigations; reviewing what is already known in light of experimental evidence; using tools to gather, analyze, and interpret data; proposing answers, explanations, and predictions; and communicating the results. Inquiry requires identification of assumptions, use of critical and logical thinking, and consideration of alternative explanations.

([11], p. 23)

Finally, Sala-Sebastià [5] defines inquiry as a transversal competency that must be developed during students’ school education. This competency consists of the capacity to formulate questions and try to discover their answers by using mathematical or scientific knowledge. This author describes inquiry competency as one of methodological (which is focused on the learning of strategies and working methods that allow students to solve problems in school and, eventually, in adult life) and transversal (which is achieved by students throughout the work done in the different subjects of curriculum) nature [5]. Moreover, Sala-Sebastià et al. [9] developed a model to characterise the inquiry process in terms of seven subprocesses (see Figure 1).

As the authors explain in the work presented in [9], the inquiry comes from the motivation to solve a problem-situation beyond the wording of the task. This is the starting point of the inquiry cycle and when students are expected to develop some of (or all) the seven subprocesses of the cycle, progressing (and/or receding; for this reason, the arrows are bidirectional) throughout the cycle. Subprocesses 1 to 3 consider posing partial questions to make operative the problem-situation (or big question) and searching for information to delve into the issue to formulate hypotheses that could answer the questions and, consequently, the big question. In an ideal inquiry cycle, when students formulate hypotheses, it is time to plan how to act to verify them (subprocess 4). Then, following the plan, students can perform actions to collect and work with data (classifying, elaborating, and interpreting them) for their analysis and to obtain some results. As we can see in Figure 1, if students arrive at subprocess 6 of the cycle and they cannot validate their results related to the hypotheses initially formulated, they can return to formulate new hypotheses (this action is represented with the dotted arrow). In the case that students can validate their results, they can move on to communicate their results and answer the partial questions and/or the big question of the problem-situation. We stress the dynamic and cyclic nature of this model, in which students constantly validate their hypotheses and construct new ones.

2.2. Mathematical Modelling

Research within didactics of mathematics has increased its interest on IBME during the last few years, so has been exemplified with mathematical modelling. The latter has been defined as a mathematical process that describes the translation of a problem-situation from a real context into mathematics and its subsequent return to reality [12]. Throughout the construction of the theoretical framework of modelling, the inclusion of this process in the teaching and learning of mathematics has been justified based on the benefits it brings to students. More specifically, Blum [13] states that modelling aims to improve students’ understanding of the world and mathematical learning, as well as contribute to the development of other mathematical competencies and a more positive image of this subject.

The specialised literature in modelling has reported proposals of different cycles to characterise this process (see [14]) as well as of different perspectives to implement it (see [15]). Despite the differences in the structure of the modelling cycles, most of them tend to converge on similar phases and transitions to characterise this process [16]. Particularly in our study, we take as a reference the modelling cycle proposed by Blum and Leiß [17] (see Figure 2), which can be classified within the realistic perspective of modelling [18], and which explains the phases and transitions an individual goes through to solve a modelling problem.

The choice of this particular cycle is justified by the authors’ previous experience in its study (see [19]). In terms of what is described by [17], the real situation is provided by the wording of the problem, which must be understood to construct (1) a situation model. Then, this situation must be simplified and structured (2) to form a real model of it. As a product of mathematising (3) the latter model, it will be transformed into a mathematical model that, by working mathematically (4) with it, will allow obtaining mathematical results. These results must be interpreted (5) in the context of the real situation and problem to obtain real results, which must be validated (6) in real-world terms. Finally, the solver exposes (7) a plausible answer for the problem (a more illustrative example of how the cycle in Figure 2 works can be found in [17], pp. 225–227).

The modelling process should not be understood in linear terms, but rather as one with cyclical and non-linear characteristics, where both the mathematical model and extra-mathematical considerations determine the solving process of the problem–situation [20]. Therefore, since a fundamental step in the modelling process is the construction of one or various models, depending on the conditions determined by the context of the problem–situation, mathematical models can be normative (when they have a prescriptive character y are used to make decisions) or descriptive (when they capture the most relevant characteristics of the problem-situation to being able to solve it) [21]. In this cycle, the mathematical model is considered as those intervening mathematical objects that allow explaining the real-world scenario initially posed [18], that is, it is a descriptive mathematical model [22].

Throughout the entire modelling cycle, the mathematical modelling competency is presented, defined by Niss and Højgaard [23] as “being able to construct mathematical models, […] to critically analyse and evaluate existing or proposed models, whilst [considering] purposes, data, facts, features, and properties of the extra-mathematical domain being modelled” (p. 16). In the work presented in [23], it is also established that, to achieve this competency, it is necessary to previously develop the modelling sub-competencies [24] or subprocesses (as described above), which are numbered at the right of Figure 2.

2.3. Relationships between Both Processes

The relationships between the inquiry and modelling processes are slightly mentioned by Artigue and Blomhøj [7] when they briefly describe the modelling process as one of the ways how research in didactics of mathematics has attempted to make an approach to IBE. However, we can find the first synergies between these two processes in two recently published articles (see [9,25]). In these works, the authors aim to provide an integrated analysis tool to apply on both processes together. This first proposal of a joint process is based on the Sala-Sebastià’s [5] approach for the inquiry process, on the one hand, and the Blomhøj’s [20] approach for the modelling process on the other.

An important relationship between both processes is the consideration of two aspects that characterise an inquiry/modelling problem: it must be a realistic and authentic situation. In this study, we assume the consensual position of considering a problem to be realistic when it includes elements from the real world, and to be authentic when these elements, which are not created for educational purposes, are used in a task with this purpose [26]. More specifically, “a task can have some authentic aspects, while other aspects are included for educational purposes” ([26], p. 721). This position can also be complemented with the notion of authenticity in a task when it includes a fact that is feasible to have occurred in the past, to be occurring in the present, or to occur in a near future [27].

This investigation intends to study the integrative analytical model of the inquiry and modelling processes in greater detail. To this end, we have taken the Sala-Sebastià’s [5] approach for the inquiry process and Blum and Leiß’s [17] approach for the modelling process. We chose these two approaches for our investigation since, after having worked with the first integrative approach to develop learning situations with students in class, we found that the Blum and Leiß’s [17] approach could better fit the Sala-Sebastià’s [5] approach. We have also kept in mind that both approaches, taken as a starting point, are widely accepted by the research community in didactics of mathematics, and that define both processes similarly. That is, both approaches consider inquiry and modelling to be dynamic and cyclic processes, whose subprocesses do not need to be followed by moving sequentially forward, and this similar description eases the conjunction of both approaches. Moreover, these two approaches are usually set in motion by real-world questions which are close to students’ context, and both processes connect real situations with the mathematical knowledge that students already have or need to learn.

3. Methodology

In this study, we followed a qualitative research methodology from an interpretative paradigm [28], which mainly consists of an instrumental case study [29]. In this section, we describe the methodological aspects.

3.1. Learning Situation and Context

The case study conducted for this investigation used a learning situation (LS from now on) designed by the first and the third author seeking the emergence of evidence of inquiry and modelling processes. This LS was designed to be implemented with students aged 12–13 during the first year of Compulsory Secondary Education (ESO from now on, for its Spanish acronym). The implementation took place at a school in Badalona (Catalonia, Spain) in February 2023, during the 2022–2023 school year, with 93 students, who were divided into three heterogeneous class groups (1st grade A, B, and C) of 31 students each by the management team of the educational centre at the beginning of the school year due to organisational reasons.

The school in which the LS took place covers the entire educational stage, that is, from early childhood to baccalaureate education, with different substages distributed in two separate buildings: one for kindergarten and primary education and another for secondary and baccalaureate education. The students attending the first year of ESO at the school during the 2022–2023 school year mostly lived in Badalona, and 76 of them had also studied their primary education at the same school. Therefore, most of the students were familiar with the school building for kindergarten and primary education and knew that it was placed just in front of the main building of the Badalona Museum (located in front of the schoolyard, on the sidewalk in front of Via Augusta Street). Most of the students were also familiar with the museum building and its structure, as it is an institution that offers multiple educational activities and it is very common for schools in Badalona to visit it, thus, the students had already visited the museum. More specifically, they knew that, beneath the white building of the museum, one could visit a part of the ancient Roman city of Baetulo and see sections of the cardo minor and the cardo maximus, a small section of the decumanus, as well as the building of the baths and numerous insulae that once contained shops.

In other words, the students were aware that the ancient Baetulo extended beneath the Museum and partially beneath what is now the playground for kindergarten and primary school. Additionally, this playground is largely below the street level. As seen in Figure 3, the Temple (blue line) and Pare Claret (red line) streets are parallel to each other and perpendicular to the sea, having a certain slope; and the schoolyard, located between these two streets, is flat (green circle). Therefore, the schoolyard is necessarily below ground level, which becomes plain from Via Augusta Street, located at the top of the slope of Temple and Pare Claret streets and which is much higher than the schoolyard, about three or four metres. Hence, it is not difficult to deduce that the Roman remains beneath the schoolyard are not at a great depth relative to this schoolyard.

Furthermore, during the 2022–2023 school year, the wall surrounding the schoolyard of the kindergarten and primary school building on Pare Claret and Via Augusta streets needed renovation. Therefore, anyone who transited near the Badalona Museum between September and November 2022 would have seen this work: how the school’s wall was covered with a construction fence and a semi-transparent green canvas, and how the old brick wall was gradually brought down to put up a new base of concrete and a wedged blue metal fence. Up to this point, the whole situation could be considered as totally realistic and authentic.

Considering the school’s situation regarding the known remains of ancient Baetulo based on what it is known of this Roman city (its location and the depth at which the Roman remains are found), the possibility of an archaeological discovery during the renovation works of the school’s wall, especially when reinforcing its foundations, was very high. The first year of ESO students had the contextual knowledge needed to realise this plausibility. Taking into consideration these conditions, the students were told that, during the building works conducted to renew the walls surrounding the building for kindergarten and primary education on Temple and Via Augusta streets, a discovery had been made while drilling the base of the wall facing Via Augusta Street. Some ceramic pieces which did not appear to be modern, but whose age and historical value could not be determined at first sight were discovered. The students were also told that, consequently, the workers on the site left the pieces where they found them and reported the discovery to the headmaster of the school, who informed the Badalona Museum as required by law. Shortly after, two archaeologists of the museum photographed, collected, cleaned, and catalogued the pieces, taking them away for some preliminary tests. The students were finally told that, after a week, the archaeologists of the museum returned to the school and handed the pieces over to the headmaster, also providing a preliminary report of the excavation and the results of some tests conducted to the objects found. Since the pieces had been found on the schoolyard and did not seem to be of a high value, the archaeologists of the museum lent them to the school for a period of three months after an initial cataloguing, so they could be exhibited at the school with the commitment to take proper care of them.

Despite the fact that this whole discovery was not true, that is, nothing was found during the works carried out at the wall surrounding the school and the foundations of that wall were never touched, the presented situation could still be considered as realistic and authentic because it was feasible to have occurred and drew a scenario, absolutely for educational purposes, close to the students’ context to which they could be interested.

Based on this supposed discovery, and taking advantage of the fact that the first year of ESO students had just been learning about the romanisation process in Catalonia during their History classes, the headmaster suggested that they could take care of the found ceramic pieces and try to investigate their origin through what they had learned and the resources the school could offer them. Therefore, the students had to take care of the pieces (as an example, they were told that the pieces could be touched only when wearing gloves) and do their best to discover from which historical period the found ceramic pieces could be and what they had originally been. Hence, the students were grouped into 18 working teams (about five students each) for a few days with the goal of uncovering all the secrets hidden in these ceramic remains, which they assumed to be discovered at the school. The different teams worked to formulate hypotheses, which were then confirmed by those formulated by the rest of the working teams in the class, and a consensus to the conducted research was reached.

It is important to remark that, to implement the LS described, the authors collaborated with archaeologists from the Badalona Museum, who provided actual Roman ceramic pieces from the 1st century A.D. which were not currently in exhibition at the museum (see Figure 4). These pieces had sufficient observable characteristics for the students to deduce—by using their previous knowledge about Roman society and, particularly, about the ancient city of Baetulo, or through accessible documentary sources—the period in which they were made, as well as their uses (domestic, religious, social, etc.), the social class to which their owners belonged, etc. Preliminary reports were also provided to the students, simulating the actual reports prepared by the archaeologists of the museum, with details of other contextual objects that could shed light on the origin of the ceramic pieces.

Thus, the problem–situation presented to the students used a historical and archaeological context as a basic source to promote the inquiry process and was placed in a context close to the students’ everyday lives. More specifically, since the discovery was a realistic and authentic situation which was supposed to occur in a certain place (the schoolyard) where the students played some months ago, this context made the LS potentially motivating for them and was totally aligned with our educational purposes. Finally, we must stress two preconditions for the implementation of this LS: on one hand, it was the very first time the students faced this type of activity, which represented a challenge for them; on the other hand, the students did not have knowledge of neither the inquiry nor modelling processes, therefore, they did not know the heuristics (steps, cycles) to solve this type of problem–situation.

3.2. Data Collection Instruments and Techniques

The data collected during the implementation of the LS were organised in different stages, which helped us (as researchers) to better organise the data and the observation of those subprocesses that tended to appear together. We shall refer to a stage as a class session (or sessions) in which the students focused on a specific task from the LS. Thus, the LS consisted of seven stages—each stage explained in detail when presenting the results—during which the first author played a double role as researcher and support teacher.

Also, different instruments and techniques for data collection were used, according to the available resources in the school and the thematic analysis intended to be performed by we the researchers. As stated before, the first author played a double role, staying along the different stages of implementation of the LS with the students, conducting a direct observation of the sessions and preparing a dairy of sessions with notes written by himself; photographing and videorecording the work performed by the students during the sessions and transcribing their interactions (discussions, reasonings, deductions); and collecting the productions of the students, such as their work diaries (where they wrote down their activities and discoveries along the different work stages) and final reports of every working team (which consisted of a summary of the research conducted by them and their conclusions).

We must stress that all the students involved in the implementation of the LS were provided with the corresponding informed consent for their participation, which was also signed by their legal guardians (parents or adult person in charge of them).

3.3. Data Analysis

Once data were collected by the first author using the instruments mentioned in Section 3.2, we conducted a thematic analysis, following an adaptation of the methodology of six phases proposed by Braun and Clarke [31], as detailed in

Table 1. Phases of thematic analysis.

Phase	Process	Description
1	Familiarising yourself with your data.	Transcribing data (if necessary), reading, and re-reading the data, noting down initial ideas.
2	Generating initial codes.	Coding interesting features of the data in a systematic fashion across the entire data set, collating data relevant to each code.
3	Searching for themes.	Collating codes into potential themes, gathering all data relevant to each potential theme.
4	Reviewing themes.	Checking if the themes work in relation to the coded extracts (Level 1) and the entire data set (Level 2), generating a thematic ‘map’ for each theme.
5	Defining and naming themes.	Ongoing analysis to refine the specifics of each theme, and the overall story the analysis tells, generating clear definitions and names for each theme.
6	Producing the report.	The final opportunity for analysis. Selection of vivid, compelling extract examples, final analysis of selected extracts, relating back of the analysis to the research question and literature, producing scholarly report of the analysis.

Note: The phases of thematic analysis were adapted from Braun and Clarke [31] (p. 87).

.

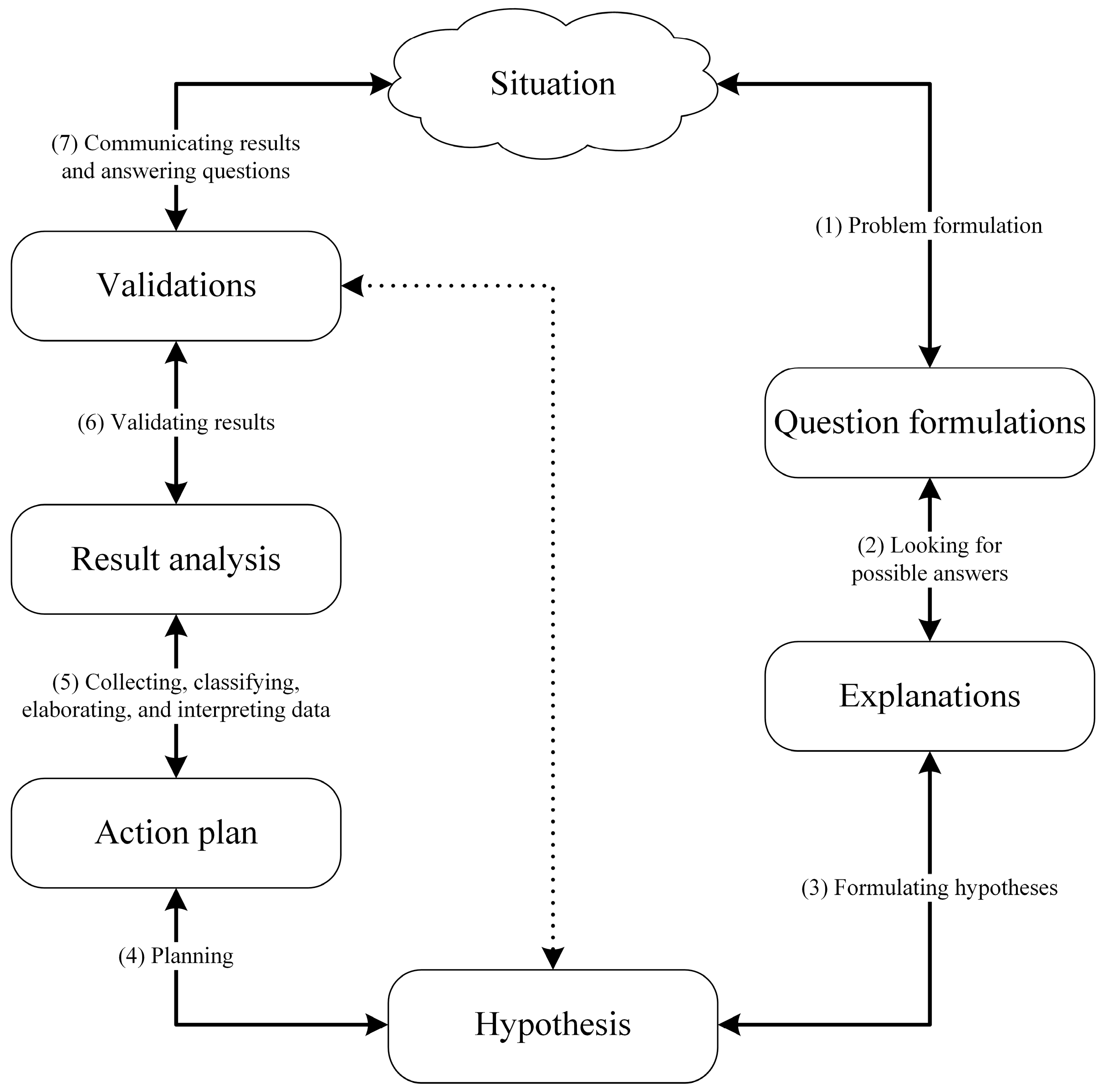
We must stress that we adapted the thematic analysis proposed by the work presented in [31] to the needs of our study, since we do not intend to discover new processes (or subprocesses) but to observe how the already known processes appeared in relation to one another. Therefore, we firstly conducted a literature review both in inquiry and modelling processes to elaborate our theoretical framework, from which we determined the a priori themes appearing in

Table 2. Codes used in this study.

Codes for Inquiry Subprocesses	Codes for Modelling Subprocesses
- Problem formulation (I1). - Looking for possible answers (I2). - Formulating hypotheses (I3). - Planning (I4). - Collecting, classifying, elaborating, and interpreting data (I5). - Validating results (I6). - Communicating results and answering questions (I7).	- Understanding/Constructing (Ma). - Simplifying/Structuring (Mb). - Mathematising (Mc). - Working mathematically (Md). - Interpreting (Me). - Validating (Mf). - Exposing (Mg).

Note: The presentation of this table does not necessarily imply a one-to-one relationship between the inquiry and modelling subprocesses.

, corresponding to the different subprocess of the inquiry and modelling processes described in Figure 1 and Figure 2, respectively. Since we also followed the methodology applied by the work presented in [9], we considered it relevant to foresee similar initial codes.

Once we implemented the LS and collected the data (as described in Section 3.2), we proceeded with the thematic analysis. To this end, we firstly transcribed the videorecorded data, read the dairy of sessions (with the notes taken by the first author), and reviewed the students’ productions (Phase 1 in Table 1). Secondly, we assigned the codes in Table 2 to the data collected from each of the 18 participating working groups in each stage of the LS (Phase 2 in Table 1). In this phase, the first author proposed a first codification for the collected data and divided them into seven stages of implementation, which led us to a triangulation in the following way: first, the remaining three authors codified individually the episodes from the stages of implementation; second, we compared our codifications, achieving an agreement percentage of 91% among the four of us; and finally, we discussed our differences of codification until we reached a consensus, due to our previous experience in this type of analysis.

Thirdly, according to the characteristics of these data, there was no need of searching for new potential themes since they corresponded to the inquiry and modelling subprocesses shown in Table 2 (Phase 3 in Table 1). Fourthly, we compared the frequency of the codes assigned to the data collected in each stage of implementation for each working team, observing how the data fitted each theme or, in terms of our investigation, the inquiry or modelling subprocesses, according to their characterisation in the specialised literature (Phase 4 in Table 1). Fifthly, based on the latter, we produced a general process (unifying the inquiry and modelling subprocesses), where there was no need of defining new themes, for the same reasons explained above (Phase 5 in Table 1). Finally, we produced the report of the thematic analysis conducted, pointing out which subprocesses appeared together in the different stages of implementation and stating possible relationships and synergies among them, as intended in our investigation (Phase 6 in Table 1).

After having conducted the thematic analysis described above on the 18 working teams of students who were involved in the LS, we selected the productions of four teams to report in this article. This selection is justified because, according to the objectives set out in this investigation, these four working teams were the most involved during the implementation of the LS and, based on the direct observations of the first author, they showed the development of inquiry and modelling subprocesses, by reasoning their steps and justifying their conclusions more clearly than the rest of working teams. Therefore, we report the analyses of: Team 3, Team 4, Team 5, and Team 8.

3.4. Example of Thematic Analysis on One Episode

We shall now exemplify how we conducted the thematic analysis on one particular episode from the implemented LS. This example corresponds to the analysis of the data collected from Team 5 during the fourth stage of implementation. As we will widely explain when presenting the results of our study, the work performed by the students during this stage consisted of the reproduction of the original sections of the ceramic piece by using geometric methods, based on the fact that the different pieces were solids of revolution.

The first author, who played a double role as researcher and support teacher, stayed along the different stages of implementation of the LS with the students, and prepared a dairy of sessions with notes written by himself (based on his direct observation), also assigned the codes shown in Table 2 (Phase 1 in Table 1). We must stress that we adapted the thematic analysis proposed by the work presented in [31] to the needs of our study, since we do not intend to discover new processes (or subprocesses) but to observe how the already known processes appeared in relation to one another. Hence, we determined the a priori themes appearing in Table 2, corresponding to the different subprocess of the inquiry and modelling processes described in Figure 1 and Figure 2, respectively.

Firstly, we transcribed the videorecorded data and observed the pictures taken during the corresponding session, and read the students’ productions where they described their work (Phase 1 in Table 1). Secondly, we took the codification agreed upon for Team 5 (Phase 2 in Table 1), which we developed starting from the following two observations:

• The students wrote down the following tasks in their dairy of work during the fourth stage of implementation: “To take measures of the superior part of the pieces; to take measures of the inferior part of the pieces; to improve the questions”.
• The first author wrote down the following notes in his diary of sessions during the same stage: “There are groups that realise that they need to take more than one section to measure the ceramic piece with the profilometer and write it down; they also refine the questions they posed during the first stage [of implementation], from more general to more particular questions regarding the shape of the pieces”.

After discussing these two observations, we assigned the code Planning [I4] to the work performed by Team 5 in the fourth stage of implementation. To obtain the needed measures of the contour of the ceramic piece, the students fabricated a profilometer with cardboard and skewers, so when they pressed this instrument against one of the ceramic pieces, the piece pushed the skewers inside the cardboard and the contour of the piece remained drawn in the skewers, as shown in Figure 5.

The procedure shown in Figure 5 allowed the students to reproduce that contour on a paper sheet to work with later. Then, we continued with the following two observations:

• The first author wrote down the following notes in his diary of sessions during the fourth stage of implementation: “The students are obtaining measures of different parts of the ceramic pieces (thickness, height, contours of the different circles that conform the sections perpendicular to the base of the piece)”.
• The students wrote down the following notes in their diary of work during the same stage: “By using a piece of cardboard and some wooden skewers, we fabricated a tool that we could use to obtain the contour of the [ceramic] pieces”.

After discussing these two observations, we assigned the code Collecting, classifying, elaborating, and interpreting data [I5] to the work performed by Team 5 in the fourth stage of implementation. During the third stage of implementation, the students had been conducting research about the pieces using, among other sources, a catalogue of Roman ceramic pieces provided by the Badalona Museum. Therefore, when they began the fourth stage, they already knew that the ceramic pieces were fabricated using a potter’s wheel, which led them to suppose that these pieces had to be solids of revolution and their sections had to be circumferences. Despite the relatively obvious fact that the contours of these pieces were not perfect circumferences since they were old, slightly eroded, and craft pottery does not produce perfect shapes, all the working teams treated these contours as part of a perfect circumference to being able to perform a geometric analysis on them. Then, we continued with the following two observations:

• The first author wrote down the following notes in his diary of sessions during the fourth stage of implementation: “All the students use the properties of circumference despite the potter’s wheel does not produce perfect circumferences. Some of them realise of this idealisation and verbalise it”.
• The students wrote the following in their final report: “We retraced the shape marked in the skewers on a paper sheet and highlighted three points on it” (this procedure is shown in Figure 6).

Up to this point of the implementation, we had not found any explicit evidence of mathematical procedures followed by the students; however, the consideration made by them regarding a supposedly perfect circumference shed light on an idealisation of the shape, which is an important aspect of the modelling process. After discussing these two observations, we assigned the code Simplifying and structuring [Mb] to the work performed by Team 5 in the fourth stage of implementation. The procedure described by the students led them to build a real model of the ceramic piece, mainly guided by the fact that they already knew that a circumference can be obtained from the three known points. Again, we found interesting data revealing the mathematisation of the real model, and the intention of conducting a mathematical work to obtain the complete shape of the circumference, that is, the students continued a portion of the modelling cycle. At this point, we assigned the code Mathematising [Mc] to the work performed by Team 5 in the fourth stage of implementation. In addition to the production shown in Figure 6, we continued with the following observation:

• The students wrote the following in their final report: “We used a geometric technique by which using only three points of a circle we can reproduce all the other points” (there were other working teams describing a similar procedure, but it will be widely shown in Section 4.4).

Therefore, we assigned the code Working mathematically [Md] to the work performed by Team 5 in the fourth stage of implementation. Once the students had obtained the complete circumference and drawn it on their paper sheets, they consider it as the original shape of the section of the ceramic piece they had. In other words, we could infer that the students were interpreting their mathematical results in the context of the real object they were working with, that is, the ceramic piece, which can be supported by Figure 6, where they wrote “Part superior” and “Part inferior” (“Superior part” and “Inferior part”, respectively, in Catalan language) besides the two obtained circumferences to refer the parts of the ceramic piece. Therefore, we assigned the code Interpreting [Me] to the work performed by Team 5 in the fourth stage of implementation.

Finally, the students checked the accuracy of their results, comparing the pieces with the drawn sections they had constructed, and observing how they fitted. This procedure was written down by the first author in his diary of sessions as follows: “All the groups compare the circumferences obtained by applying geometric methods on the contours of the [drawn] pieces and the real pieces to check how accurately the former fits the latter”. Thus, after discussing this observation and the data collected, we assigned the codes Validating [Mf] and Validating results [I6] to the work performed by Team 5 in the fourth stage of implementation. There were no more codes assigned to Team 5 in this stage.

Once we replicated this thematic analysis with the 18 working teams, we compared the different codifications assigned to them and observed which codes recurrently appeared in each stage of implementation. With this latter procedure, we could also identify which inquiry and modelling subprocesses appeared together, which led us to develop a general process (Phase 5 in Table 1). Finally, we produced a report, checking again the thematic analysis previously performed and observing how it fitted the data, and proposed the integrative cycle for inquiry and modelling subprocesses that we present in Section 5 (Phase 6 in Table 1).

4. Results and Discussion

The results derived from the thematic analysis performed on the data collected by using the methodology described in the previous section shall be presented in relation to the stage of implementation in which these results were made evident.

4.1. First Stage of Implementation

In the first stage, the situation was presented to the students with the collaboration of the headmaster of the school, and they raised questions about the found objects to determine what information could be discovered from each object, as well as to check if the discovery had occurred within the limits of the ancient Baetulo. All working teams raised questions arising from the different pieces based on the information provided by the presented situation. These first questions raised by the students helped them to understand the problem [Ma], by transforming the set-out situation into a formulated problem [I1]. For example, Team 3 posed the following questions: “Which period is the object from? Was it an important object? What is it made of? Which civilisation is it from? What is it for? Was it a daily object? Was it valuable?” (Evidence 1; E1 from now on).

Subsequently, the different working teams speculated about possible answers and hypotheses, focusing on the historical period to which the object belonged. For example, Team 5 wrote in their report: “We suspect that the found remains could be Roman, since Baetulo¸ the current city of Badalona, was an important Roman city” and “Since the pieces were buried beside the Badalona Museum, in a soil known for containing Roman remains, we thought that the ceramic pieces we had could be one of these Roman remains” (E2). The students also discarded some of the first hypotheses they formulated for various reasons; for example, some working teams suggested that the found ceramic remains could correspond to a Roman cemetery, but they soon discovered that the pieces were found inside the walls area of Baetulo and that Roman cemeteries used to be outside the city walls, so they discarded the cemetery hypothesis. Thus, the students looked for possible answers [I2] to the questions previously raised and formulated some first hypotheses [I3] from these preliminary answers, which helped them to gain a deeper understanding of the problem [Ma].

At the end of the first stage, the students deduced that they needed to know for certain whether the found ceramic pieces were of Roman origin or not and, if so, which Roman period they belonged to (since their first investigations lead them to discover that the Roman presence in Badalona had not always had the same characteristics). This information was key to narrowing down the formulated problem and gaining a better understanding of the situation [Ma]. Consequently, they planned [I4] to focus the following class session on discovering the age of the ceramic pieces. As an example, Team 5 wrote in their planning dossier that “we have formulated these hypotheses and can check them on the internet […]; we need to determine the age of the pieces to know if our hypotheses are valid” (E3). We can see a synthesis of the relationships between the inquiry and modelling subprocesses found in the results analysed during this stage in

Table 3. Relationships between inquiry and modelling subprocesses found in the first stage of implementation.

Evidence	Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
E1	I1	X
E2	I2	X
E2	I3	X
E3	I4	X
	I5
	I6
	I7

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

.

4.2. Second Stage of Implementation

The dating of the pieces was carried out during the second stage, based on the preliminary report from the Badalona Museum which stated that some organic remains were found among the ceramic pieces and indicated the concentration of the radioactive isotope carbon-14 (C-14 from now on) present in these organic remains. During this part of the second stage, the students checked the data that they had available and collected the specific data that they needed, classifying and interpreting [I5] what they could use to get the results they were seeking. To this end, the teachers involved in the LS presented the model for obtaining the C-14 concentration in the organic remains to their students, that is, they presented a normative mathematical model. Thus, the students focused specifically on finding this percentage of C-14, guided by the question: What year are the organic remains found inside the ceramic pieces?

This data selection helped the students to structure and simplify [Mb] the problem-situation and provided them the useful data they had to focus on. As an example, Team 8 wrote the following in their report: “Inside the found ceramic pieces some remains of partridge eggs were found; we can determine the approximate age of our pieces by knowing the C-14 those eggs contained” (E4). They selected this information to be relevant for their goal (to determine the age of the ceramic pieces they had) among other information present in the report they had (such as the depth at which the ceramic pieces were found or the exact location of the discovery).

Using this information, the students represented the data that they had selected by creating graphs of C-14 using GeoGebra 5.0 software; thus, they used a mathematical model to represent the relation between the C-14 concentration of the organic remains found inside the ceramic pieces and the age of the pieces. The students of Team 8 explained it in their report as follows: “We used the formula 100 × (1/2)^(x/5730) in the GeoGebra calculator” (E5, writing the formula as the students did). Regarding the latter, we remark that the students used the term «formula» to refer to a function since they had no previous notion of what functions are nor the idea of variable correspondence. We must stress that the students applied this normative mathematical model (the function relating the C-14 concentration and the age of the ceramic pieces) but did not deduce it. In other words, the students used a normative mathematical model that was provided to them to deduce unknown physical properties of the ceramic pieces (their age) throughout it, but they were not able to deduce the needed function by themselves since their previous mathematical knowledge was far from what is needed to do so.

Having this model, they used the two variables of the graph: the percentage of C-14 contained in the organic remains and the years since the death of the animal or plant corresponding to those organic remains, which had to be assumed as being close to the years of the ceramic piece age and thus approximate this age. Since the students knew the percentage of C-14 present in the organic remains, as part of the museum report that they had, they were able to determine the age of the remains as follows: by moving a point along the graph drawn in the GeoGebra calculator until the «percentage of C-14» variable fitted the corresponding value, they could know the «age» value by looking at the other variable. Thus, the students had to perform a mathematical work [Md], that is, applying mathematical methods and properties to the mathematical model they had to obtain a result. This first result was of a mathematical nature (the years passed by since the death of the living being corresponding to the organic remains found). Then, the students needed to interpret [Me] these results in the context of the situation, so they could get those they were seeking: the year of the death of that living being, which had to be assumed to be close to the year of origin of the ceramic piece.

As an example, Team 8 wrote the following in their report: “If we take the % [sic] of C-14 (78,6435%) of the found organic matter in the remains and we use GeoGebra, we can find that the remains of partridge eggs are 1986 years old. […] We have looked for the corresponding point of % of C-14 in the graph and the result is that 1986 years went by [since the death of the eggs]. If we subtract that to the current year [2023], we get that the remains date from 37 A.D.” (E6). An example of the graph can be seen in Figure 7.

We can see a synthesis of the relationships between inquiry and modelling subprocesses found in the results analysed during this stage in

Table 4. Relationships between inquiry and modelling subprocesses found in the second stage of implementation.

Evidence	Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
	I1
	I2
	I3
	I4
E4	I5		X
	I6
	I7

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

.

4.3. Third Stage of Implementation

In the third stage, the students tried to verify and validate [I6]–[Mf] the results that they had obtained after having worked mathematically on the pieces during the previous stage. They compared the data that they already had with those obtained, and checked how the results fitted their initial hypothesis. To this end, the students conducted research on the uses and types of ceramics from the Roman period in which the pieces were dated, comparing what they found with the observations made, and elaborating and contrasting hypotheses until reaching a consensus. This research included, for example, comparing the pieces that they had with a catalogue of Roman ceramic pieces from the 1st century facilitated by the Badalona Museum. Such comparison with the pieces of the catalogue helped the students to discard some possibilities due to the observable shape of the piece or the period of time they were from. That is, the students could narrow the possible shapes, since all the possible pieces were solids of revolution, and the possible range of time, in case it did not fit the dating determined during the second stage of implementation, both data according to the catalogue.

The discoveries made during the second stage placed the research in a new context, and the students regressed in both the inquiry and modelling processes. They did not formulate new questions, but knowing the age in which the ceramic pieces were made led them to focus on some questions that had raised during the first stage of implementation, and which could now be more easily answered. Thus, the students formulated a more specific problem-situation [I1] and, from this more specific problem, they tried again to look for specific answers [I2] to the questions made and formulated new hypotheses [I3]. All this work led the students to a deeper understanding of the problem [Ma] from which they could construct new real models. They ended up this stage by deciding that, after collecting some information about possible uses that the pieces might have had, it would be interesting to know which was its original shape and dimensions (recall that the pieces were all broken).

As the first author observed in his notes when conducting this research, “now the students have certainty that the ceramic pieces they are dealing with are Roman and can be dated during the first century CE; using this new knowledge, they are revisiting the questions raised during the first stage and focusing their investigation on what they can now observe considering the Roman context. They are restarting the process, reformulating the problem with new and concrete focuses, looking for concrete explanations to these more concrete questions, and elaborating concrete hypotheses related to these focuses to work with” (E7). We can see a synthesis of the relationships between inquiry and modelling subprocesses found in the results analysed during this stage in

Table 5. Relationships between inquiry and modelling subprocesses found in the third stage of implementation.

Evidence	Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
	I1
E7	I2	X
E7	I3	X
	I4	X
	I5
	I6						X
	I7

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

.

4.4. Fourth Stage of Implementation

In the fourth stage, the students investigated the shape and dimensions that the piece originally had by using geometric properties of the circle to determine the original radius of the different pieces. This stage proved to be rich in subprocesses, as the students revisited the issue of the original shape of the pieces, putting the focus of the problem formulation [I1] on a different question among those originally proposed, namely, what shape and dimensions may the original ceramic piece have had? By taking advantage of the fact that all the Roman ceramic pieces were solids of revolution, the students could get the contour of some sections of the piece perpendicularly to the axis of revolution and obtain the complete circle that formed that section; thus, obtaining enough sections of the piece, they could estimate the original shape that it had. Therefore, the students planned [I4] the number of circular sections of the piece they needed to reproduce to accurately estimate the original shape of the piece.

Once they had a new goal, the students collected the data [I5] that they needed to fulfil their objectives: the contours of a certain number of sections of the piece, parallel among them and perpendicular to the axis of revolution of the piece. To this end, they fabricated a profilometer with cardboard and skewers, so when they pressed this instrument against one of the ceramic pieces, the piece pushed the skewers inside the cardboard and the contour of the piece remained drawn in the skewers, as shown in Figure 8.

The students needed to use the contours of the ceramic piece to get the complete circular profile. To be able to work with these contours, they had to consider the circles described by the sections of the pieces as perfect circles –which were clearly not perfect–thus, simplifying [Mb] the ceramic piece and structuring it as a real model. Having these contours drawn in the profilometer, the students drew three points of the obtained contours on a paper sheet; among all the points of the contour, they could use only three points (by applying the Euclidean proposition stating that a circumference can be determined from three given points) and thus, mathematising [Mc] the real model into a geometric object (by transforming the points of the contour into three dots on a paper sheet). Once the students had these three points, they could interpret them as three given points of a circumference –that is, as a mathematical representation of the section of the ceramic piece– thus constructing a descriptive mathematical model with which they could work mathematically [Md] using a geometric method by which a circumference can be found from three known points as follows: the students had to find the mediatrices between two pairs of the points; the point where the two found mediatrices meet is the centre of the circumference containing the three points of the contour and the distance between any of the three points and the point where the mediatrices meet is the radius of this circumference. Thus, the obtained circumference was interpreted [Me] by the students as the complete section of the ceramic piece.

It is important to remark that, unlike when they dated the ceramic pieces during the second stage of implementation, the students were not provided with a normative mathematical model (as the C-14 formula) but they constructed a descriptive mathematical model to work with. To this end, these models were based on the use of geometric methods already known, allowing us to deduce that the sections of the ceramic pieces had to be circumferences, as stated before, by comparing them with the catalogue of Roman ceramic pieces provided by the Badalona Museum.

As an example, Team 8 wrote the following in their report: “We took two of the three points and, with the compass at the same size, we made two semi circumferences. We joined the two points where the circumferences met with a straight line named mediatrix. We took the point that we had not used yet and one of the points we had already used and performed the same operation, obtaining another mediatrix. The point where these two mediatrices met was the centre of the piece. From the centre, we drew the circumference by using the compass that crossed the three points”. We can also see an example of this in Figure 9 (E8).

After having performed this mathematical work and having interpreted the obtained results under the light of the context on which they were working, the students compared the pieces with the drawn sections they had constructed to validate their results [I6]–[Mf], by superposing the ceramic piece and the mathematically obtained shape considered as the original contour of that piece, observing how they fitted. We can see an example of this validation in Figure 10 (E9).

We can see a synthesis of the relationships between inquiry and modelling subprocesses found in the results analysed during this stage in

Table 6. Relationships between inquiry and modelling subprocesses found in the fourth stage of implementation.

Evidence	Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
	I1
	I2
	I3
	I4
E8	I5		X
E9	I6						X
	I7

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

.

4.5. Fifth Stage of Implementation

In the fifth stage, the students used the geometric information obtained in the previous stage to digitalise the pieces with their original and complete shapes, creating a three-dimensional reconstruction of them using the Tinkercad software. The original problem was once again reformulated by setting a new goal: to design a three-dimensional model of the original piece. To achieve this goal, the students made a brief work plan [I4], starting from mastering Tinkercad better than most did and then reproducing the pieces, considering the shapes and dimensions deduced from the previous stage.

Thus, the two-dimensional models of the pieces’ sections previously determined became now the new data from which the students had to construct their three-dimensional representations. They needed to collect these data and select [I5] what dimensions they would use to simplify [Mb] the problem. Therefore, with these data, the students constructed a geometric representation using Tinkercad, representing the original shape of the Roman ceramic piece that they had. We can observe an example of the students’ production in this stage in Figure 11 (E10).

Once the students obtained their three-dimensional models, they validated [I6]–[Mf] them by comparing the accuracy of the obtained shape concerning the ceramic piece that they had. However, they performed no mathematical work with the three-dimensional models once obtained and only verified their accuracy. We can see a synthesis of the relationships between inquiry and modelling subprocesses found in the results analysed during this stage in

Table 7. Relationships between inquiry and modelling subprocesses found in the fifth stage of implementation.

Evidence	Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
	I1
	I2
	I3
	I4
	I5		X
E10	I6						X
	I7

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

.

4.6. Sixth and Seventh Stage of Implementation

In the sixth stage, the students visited the Badalona Museum. The archaeologists of the Museum, who had collaborated in preparing the LS, also prepared a special visit for the students. This visit was focused on Roman ceramics and the period of the Roman city of Baetulo, from which the pieces originated, and included a visit of the laboratory where the found pieces were restored by the archaeologists of the Museum. In this way, the students were able to compare their discoveries and working methods with those used by professionals, as well as verifying whether their conclusions were reliable or not and validating them [I6]–[Mf]. Finally, in the seventh stage, the students exposed [Mg] their reports (E11—this evidence corresponds to the reports made by the working teams to present their results and conclusions; however, they are too long to be shown in this article) in the classroom, communicating their results [I7]. We can see a synthesis of the relationships between inquiry and modelling subprocesses found in the results analysed during this stage in

Table 8. Relationships between inquiry and modelling subprocesses found in the sixth and seventh stage of implementation.

Evidence	Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
	I1
	I2
	I3
	I4
	I5
	I6						X
E11	I7							X

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

.

4.7. Discussion on the Explicit Relationships Found in Our Investigation

After having presented the results and analyses conducted in this study, based on the implementation of the LS, we can observe that there are several subprocesses of both the inquiry and modelling cycle that appear together. As a way of synthesising these findings, in

Table 9. Synthesis of the relationships between inquiry and modelling subprocesses found throughout the seven stages of implementation.

Codes	Ma	Mb	Mc	Md	Me	Mf	Mg
I1	X
I2	XX
I3	XX
I4	XX
I5		XXX
I6						XXXX
I7							X

Note: The table shows only the subprocesses and evidence relating inquiry and modelling, but not those subprocesses appearing unrelated to any other, nor their evidence.

we present all the relationships found between both types of subprocesses throughout the seven stages of implementation performed.

Considering the relationships synthesised in Table 9 and the procedures performed by the students during the implementation of the LS, we can interpret the path followed by them throughout the inquiry and modelling cycles as described in the following paragraphs.

Firstly, the students needed to formulate the problem [I1] and, once stated, they needed to understand the problem [Ma] to be able to deal with it. To do this, and based on the formulation of the problem, the students conducted a preliminary investigation and looked for possible answers [I2] that they could use to formulate hypotheses [I3] to work with. After that, they planned [I4] the steps needed to solve the problem regarding their hypotheses. The first time that the students confronted the problem-situation, they had to pass through the first four subprocesses of the inquiry cycle (i.e., problem formulation [I1], looking for possible answers [I2], formulating hypotheses [I3], and planning [I4]). By passing through [I1], the students developed a first wording of the problem that they had to face and then they needed to get a proper understanding of the problem [Ma], that is, the first subprocess of the modelling cycle, by passing to the following three inquiry subprocesses [I2]–[I4]. Later, when the students went backwards in both cycles and revisited the previous steps, they sometimes missed some of the first four subprocesses of the inquiry cycle, but some of these subprocesses performed appeared together with the first subprocess of the modelling cycle.

Then, the students collected the data they had at their disposal, interpreting [I5] which data were useful (or not) for reaching a solution for the problem. This data selection helped them to structure and simplify [Mb] the problem initially posed, focusing on the most relevant aspects of the situation. These subprocesses of the inquiry and the modelling cycles appeared together when the students were collecting data to set a first real model of the problem (the graphs used for dating the ceramic pieces), along with a kind of first mathematisation [Mc] of the situation. These subprocesses were important for the students when they later went backwards in the cycles to construct new real models to answer new questions raised by the problem–situation, that is, the shape and dimensions of the two-dimensional sections of the ceramic piece perpendicular to the axis of revolution and its consequent three-dimensional model.

Once the students had a more specific problem to be faced, they used some data, as the percentage of the isotope C-14 present in the organic remains found within the ceramic pieces (which did not need to be mathematised due to its mathematical nature), which were key data to obtain a mathematical model based on the real model representing the situation. However, despite of not having performed an actual mathematisation of these data, when the students were working to determine the age of the ceramic pieces, the mathematical model was the functional correspondence between the percentage of C-14 contained in the organic remains and the years since the death of the living being corresponding to those organic remains, more specifically, the graph representing the degradation of the radioactive isotope C-14 in terms of time (see Figure 7). When they were working to determine the complete contour of the sections of the ceramic piece, the students collected and selected the data [I5] (by obtaining the contours of the ceramic piece sections) and simplified [Mb] them (by assuming that these contours corresponded to a perfect idealised circumference). In this way, they could structure [Mb] a real model of the problem (the contour of the piece obtained by using the profilometer) from which they could mathematise [Mc] these data (the three points of the contour on which they would later perform a mathematical work) and then use a mathematical model (the underlying circumference whose complete profile they sought to obtain). The students also obtained a third real model during the fifth stage of implementation, that is, the geometric three-dimensional representation of the ceramic pieces based on the two-dimensional representation they had obtained with the mathematical work previously performed.

Having performed this, the students worked mathematically [Md] with the different models (all but the three-dimensional representation of the ceramic piece, that were taken as a final result and needed no further mathematical work) applying, on one hand, mathematical properties (regarding variables and graphs) to the first model as follows: they needed to identify the two variables of the drawn function and, by approximating the «percentage of C-14» variable to the known percentage of C-14 value, obtain the «years» variable; and on the other hand, geometric properties to the second model as follows: they applied a well-known method to determine the profile of a circumference given three points that belong to that circumference.

Once the students obtained a mathematical result after the mathematical work with the model, they had to interpret [Me] it under the light of the problem-situation. Thus, knowing the years that had passed by since the death of the living being that originated the organic remains found within the ceramic pieces (the result that they obtained with the mathematical model), they could find the year of origin of these ceramic pieces (the interpretation of the mathematical result in terms of the problem that they wanted to solve); and, having the complete circumference drawn in a paper, they could identify it with the contour of the shape of the ceramic piece section, with the corresponding circular dimensions.

After having obtained these first results, the students validated [I6]–[Mf] them by contrasting them with the data they knew about the Roman ceramic pieces. These two subprocesses appeared together in the following moments:

• when the students were verifying the dating that they had obtained using the data they knew about the ceramic pieces (where they were founded, the closeness of the Roman remains of Baetulo), and the new data that they could get (the types of first-century Roman ceramics according to the catalogue provided by the Badalona Museum);
• when the students were verifying the geometrically obtained circumferences with the shape of the ceramic pieces, perpendicular to their axis of revolution by superimposing the ceramic piece to the circumference drawn on a paper sheet;
• when the students were validating the three-dimensional representations of the ceramic pieces that they had constructed using Tinkercad software by comparing the representation with the piece;
• and finally, when the students visited the Badalona Museum, they were validating their research and conclusions by confronting them to the discoveries and methods that had been made by professional archaeologists of the museum throughout years, which represents an external validation by experts.

Finally, the students presented their reports in the classroom to expose [Mg] and communicate their results [I7]. These two subprocesses of the modelling and the inquiry cycles, respectively, appeared together, a fact which was not particularly surprising given that the definition of both subprocesses in [5,17], respectively, share family resemblance.

5. Conclusions

5.1. On the Theoretical Relationships between Both Cycles

Based on the results synthesised in the previous subsection, we can draw some conclusions. The evidence of the following inquiry subprocesses: problem formulation [I1], looking for possible answers [I2] formulating hypotheses [I3], and planning [I4] appeared together with the evidence of the modelling subprocess of understanding/constructing [Ma] the problem. Even if not all the four inquiry subprocesses mentioned above emerge in the path of the students along the cycle —since they can, for example, skip one of the steps of the inquiry cycle—these subprocesses do appear to come together with the modelling subprocess [Ma], that is, students first formulate the problem [I1] and then they need to understand this problem [Ma]. To do so, they tried to look for possible answers [I2] and formulated hypotheses [I3] from this first research. This fact enabled a first understanding of the problem from which start working and, from this point, the students planned the action [I4] needed to deal with the situation. We can thus, understand the inquiry subprocesses [I2] and [I3] as inner steps of the modelling subprocess [Ma], since the inquiry cycle develops the latter in a more specific way.

The inquiry subprocess of collecting, classifying, elaborating, and interpreting data [I5] appears together with the modelling subprocess of simplifying/structuring [Mb]. Nevertheless, unlike the comparison previously made, in this case both subprocesses are not of the same nature, since they have important differences. Particularly, while the inquiry subprocess [I5] is focused on the data treatment and selection to discern which is useful (or not) for the solving process of the problem, the modelling subprocess [Ma] is focused on the elaboration of the initial representation of the problem-situation, that is, the real model, which assumes certain idealisations and extra-mathematical considerations. However, both subprocesses sequentially appear when the data are of a mathematizable nature; otherwise, when the data are not, only the inquiry subprocess [I5] appears.

The following modelling subprocesses: mathematising [Mc], working mathematically [Md], and interpreting [Me] appear when there are mathematical or mathematizable data involved (this result coincides with what is reported in the work presented in [9]). These three modelling subprocesses show no explicit relation with any inquiry subprocess; however, if the research performed did not contain mathematizable data, the inquiry cycle could be carried out without passing through these subprocesses of the modelling cycle.

Finally, we consider two pairs of subprocesses (one from each cycle) to have a family resemblance. On one hand, the inquiry subprocess of validating results [I6] and the modelling subprocess of validating [Mf], since both express the need of making sure that the obtained results fit the problem-situation initially posed and can then be taken as a plausible solution. On the other hand, the inquiry subprocess of communicating results and answering questions [I7] and the modelling subprocess of exposing [Mg], since both express the need of making others know about the problem-situation faced, how it was dealt with, and which solutions have been found. Regarding the latter, both subprocesses are open to generating new problem-situations from the answers given when communicating and the new questions these answers might raise.

When a problem–situation like that proposed in the designed and implemented LS is dealt with, nor the inquiry neither the modelling cycle alone are sufficient to find a plausible solution. More specifically, both cycles need to be combined, enriching both processes. For example, the representations made (real models) and the mathematical models used by the students who actually performed the previous subprocesses from the inquiry cycle are more accurate and closer to reality than those models made/used by those students who did not perform those subprocesses.

Likewise, in both the inquiry and the modelling cycles, the steps followed by the students to find a plausible solution to the problem-situation of the LS do not need to be unidirectional; conversely, the students can skip subprocesses or go backwards in the steps, revisiting subprocesses of the inquiry or the modelling cycles that they had previously performed. These findings fit the results reported by XXX [5] (for inquiry) and Blomhøj [20] (for modelling) regarding the cyclical and non-lineal nature of both processes.

5.2. Proposal of an Integrative Cycle

Considering the results and conclusions exposed, we propose the integrative cycle shown in Figure 12 for inquiry and modelling processes, which represents the steps followed by the students who worked in a problem–situation designed with the goal of developing both inquiry and modelling skills.

In general terms, this integrative cycle takes the subprocesses from the two theoretical approaches considered in our study [5,17] and offers a common path for the design and implementation of learning situations aiming to develop both inquiry and modelling skills. This cycle starts by presenting a problem-situation which must be realistic and authentic (see Section 2.3) and then problematised (subprocess (1) in Figure 12). Once the problem is stated and the questions related to the problem that are to be answered have been formulated, students need to understand the problem; this subprocess appears divided in two more specific subprocesses in the integrative cycle: departing from the questions that have been formulated during the previous step, students try to look for possible answers (subprocess (2) in Figure 12) that provide them with preliminary explanations about the problem (these explanations are not supposed to solve the problem, but they are a first approach to the solving procedure and help students to develop a better understanding of the problem); and, among these possible explanations, students formulate their hypotheses (subprocess (3) in Figure 12) that they shall validate or reject during the following steps. With their formulated hypotheses to work with, students plan the actions (subprocess (4) in Figure 12) they must perform in order to get the solution. Then, students collect and classify data considered relevant for the purpose pursued, elaborating, and interpreting these data (subprocess (5) in Figure 12) in terms of the problem goal. An analysis of results can now be conducted.

It is at this point where modelling skills might come into play if the data collected are of a mathematizable nature. Under this condition, to enrich the analysis of results, a real model can be structured by simplifying (subprocess (5a) in Figure 12) the problem–situation, for example, by idealising it. After that, a mathematical model can be used/obtained after mathematising (subprocess (5b) in Figure 12) the real model and the data resulting of the work conducted in the previous inquiry subprocesses. By working mathematically (subprocess (5c) in Figure 12) with the model, mathematical results will emerge, which will be considered abstractly and are, hence, suitable for a mathematical analysis that will polish the analysis obtained merely by working with data. Finally, these results need to be interpreted (subprocess (5d) in Figure 12) in terms of the conditions imposed by the context of the problem-situation, obtaining a new result after the mathematical analysis conducted, more accurate, rigorous, and reliable than the first result obtained by only performing the subprocess (5). However, if there are no such mathematisable data related to the problem-situation, the work conducted with the available data shall provide a result analysis referring to the data, with no possible abstraction to be made, and the inquiry cycle shall go on.

In any case, once these mathematical results have been obtained after the conducted analyses, students must validate (subprocess (6) in Figure 12) them to make sure that these really are the answers they have been seeking for the problem initially stated; this is a common subprocess in both the inquiry and the modelling processes. Finally, students communicate their results and answer the questions (subprocess (7) in Figure 12) that their presentation might raise.

We observed that students could directly validate their hypotheses if the data they have allow them to do so and, eventually, they could skip the intermediate subprocesses if the validation shows a hypothesis to be true and fulfilling the demand of the problem-situation. Also, we observed that students can go through the different subprocesses onwards and backwards, revisiting the steps that they have already made or skipping some subprocesses. Finally, we observed that the proposed integrative cycle is suitable for the understanding of learning situations that require inquiry, modelling, or both skills despite having been designed especially for this last case. Nevertheless, the subprocesses that might be developed by students depend on the nature of the data available and the context of the problem-situation, and both inquiry and modelling processes could match the proposed cycle, considering that some subprocesses would be ignored if only one of the processes took place.

It must be considered that the study presented in this article is a first approach to the relationships and synergies between the inquiry and the mathematical modelling cycles, and so its conclusions must be deepened in further investigations. Although many investigations have been conducted on studying the development of IBME and many others focused on the development of modelling, there are still few studies like the one we report in this article, aiming to consider the implications for mathematical teaching and learning from a LS based on realistic and authentic contexts, where both inquiry and modelling are promoted. Actually, it is of our interest to conduct this further research on the topic in order to reinforce the integrative cycle presented in Figure 12, as well as develop each subprocess contained as part of a general inquiry and mathematical modelling competency. The goal of this research is not whatsoever limited to a theoretical approach, but it aims to provide mathematics teachers with an innovative tool with which they can promote inquiry and modelling processes, and with which they can assess their students’ performances when conducting these processes, thus promoting collaboration for the improvement of mathematical education practice.