A Quasi-Experimental Study of the Achievement Impacts of a Replicable Summer Reading Program
Abstract
1. Introduction
1.1. Kids Read Now
1.2. The Current Study
- What is the non-experimental impact of KRN on participating students’ literacy outcomes relative to their non-participating peers?
- To what extent does active engagement in the KRN program, as measured by the number of books participating students received, predict students’ literacy outcomes?
- Are impacts observed in response to questions 1 and 2 moderated by the district context and the students’ grade level?
2. Method
2.1. Sample
2.2. KRN Implementation in Troy City and Battle Creek
2.3. Transparency, Openness, and Research Ethics
2.4. Measures
2.4.1. Dependent Variable
2.4.2. Independent Variables
2.5. Analytical Strategy
2.5.1. Propensity Score Matching Methods
2.5.2. KRN Quasi-Experimental Impact Estimates
3. Results
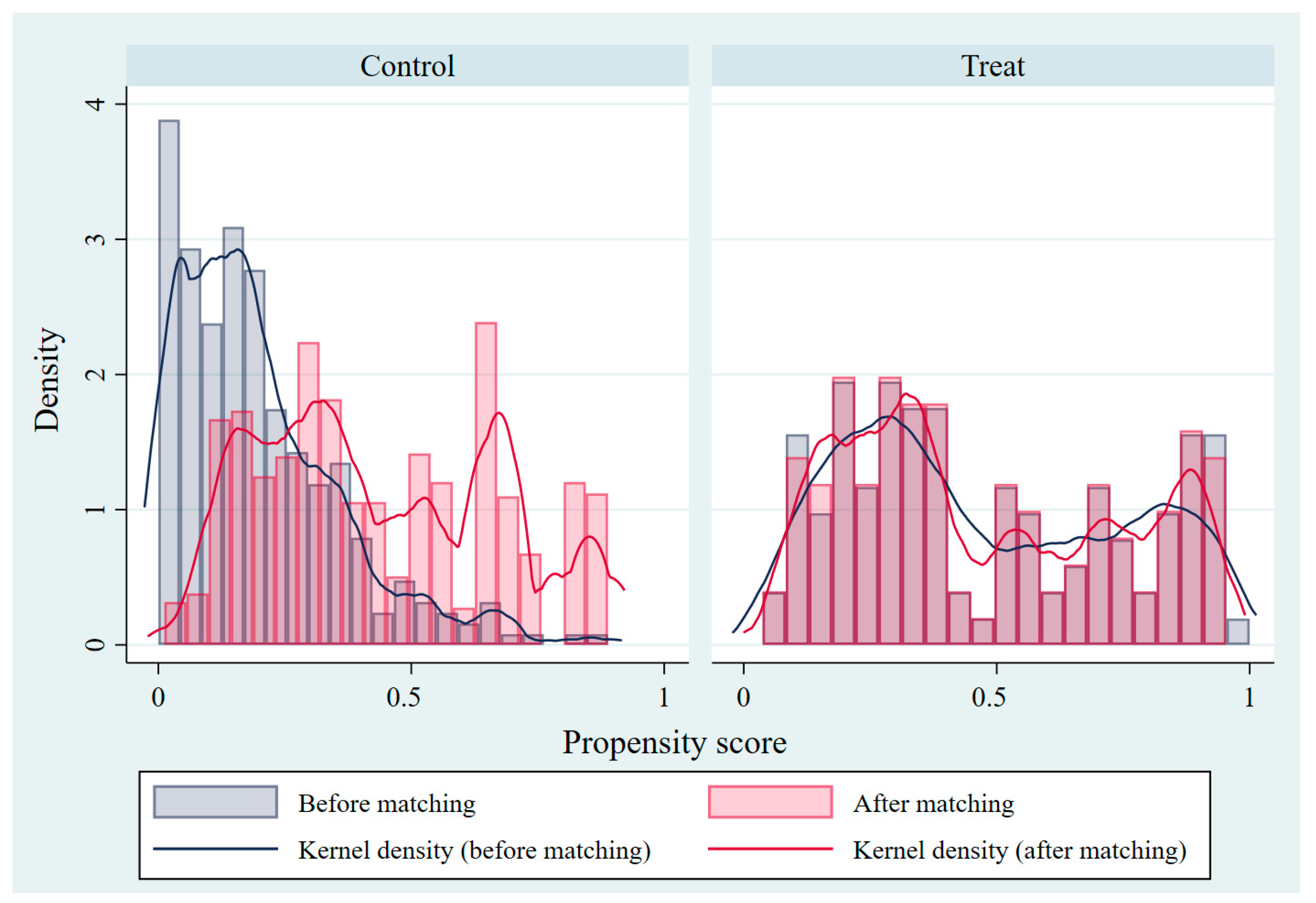
3.1. Descriptive Statistics and Balance Checks
3.2. Quasi-Experimental Estimates of Treatment Effects
3.3. Supplemental Analyses
3.3.1. Impact Estimate Differences by Grade Level
3.3.2. Impact Estimate Differences by District
4. Discussion
4.1. Connections to Prior Evidence
4.2. Substantive and Theoretical Connections
The Coleman Report (Coleman et al., 1966) identified the available reading materials in the home as one of the six key objective family background factors linked to student performance—a conclusion reaffirmed in later analyses (Borman & Dowling, 2010) and in subsequent research across economics, sociology, and education (e.g., Duncan & Magnuson, 2005; Evans et al., 2010; Fryer & Levitt, 2004; Hanushek & Woessmann, 2011; Linver et al., 2002; Manu et al., 2019).“If a person wished to forecast, from a single objective measure, the probable educational opportunities which the children of the home have, the best measure would be the number of books in the home.”
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- aimswebPlus. (n.d.). aimswebPlus overview. Available online: https://www.pearsonassessments.com/content/dam/school/global/clinical/us/assets/aimswebPlus-overview.pdf (accessed on 1 March 2020).
- Allington, R. L., McGill-Franzen, A., Camilli, G., Williams, L., Graff, J., Zeig, J., & Nowak, R. (2010). Addressing summer reading setback among economically disadvantaged elementary students. Reading Psychology, 31(5), 411–427. [Google Scholar] [CrossRef]
- Allington, R. L., & McGill-Franzen, A. M. (2021). Reading volume and reading achievement: A review of recent research. Reading Research Quarterly, 56(S1), S231–S238. [Google Scholar] [CrossRef]
- Angrist, J. D., & Imbens, G. W. (1995). Two-stage least squares estimation of average causal effects in models with variable treatment intensity. Journal of the American Statistical Association, 90(430), 431–442. [Google Scholar] [CrossRef]
- Atteberry, A., & McEachin, A. (2021). School’s out: The role of summers in understanding achievement disparities. American Educational Research Journal, 58(2), 239–282. [Google Scholar] [CrossRef]
- Bloom, H. S., Hill, C. J., Black, A. B., & Lipsey, M. W. (2008). Performance trajectories and performance gaps as achievement effect-size benchmarks for educational interventions. Journal of Research on Educational Effectiveness, 1, 289–328. [Google Scholar] [CrossRef]
- Borman, G. D., & Dowling, M. (2010). Schools and inequality: A multilevel analysis of Coleman’s equality of educational opportunity data. Teachers College Record, 112(5), 1201–1246. [Google Scholar] [CrossRef]
- Borman, G. D., Schmidt, A., & Hosp, M. (2016). A national review of summer school policies and the evidence supporting them. In The summer slide: What we know and can do about summer learning loss (pp. 90–107). Teachers College Press. [Google Scholar]
- Borman, G. D., Yang, H., & Xie, X. (2020). A quasi-experimental study of the impacts of the Kids Read Now summer reading program. Journal of Education for Students Placed at Risk, 26, 316–336. [Google Scholar] [CrossRef]
- Bourdieu, P. (1986). The forms of capital. In J. Richardson (Ed.), Handbook of theory and research for the sociology of education (pp. 241–258). Greenwood. Available online: https://home.iitk.ac.in/~amman/soc748/bourdieu_forms_of_capital.pdf (accessed on 1 October 2025).
- Briggs, D. C., & Wellberg, S. (2022). Evidence of “summer learning loss” on the i-Ready Diagnostic Assessment. The Center for Assessment, Design, Research and Evaluation (CADRE), University of Colorado Boulder. Available online: https://www.colorado.edu/cadre/2022/09/27/evidence-summer-learning-loss-i-ready-diagnostic-assessment (accessed on 1 October 2025).
- Caliendo, M., & Kopeinig, S. (2008). Some practical guidance for the implementation of propensity score matching. Journal of Economic Surveys, 22(1), 31–72. [Google Scholar] [CrossRef]
- Camerer, C. F., Dreber, A., Holzmeister, F., Ho, T.-H., Huber, J., Johannesson, M., Kirchler, M., Nave, G., Nosek, B. A., Pfeiffer, T., Altmejd, A., Buttrick, N., Chan, T., Chen, Y., Forsell, E., Gampa, A., Heikensten, E., Hummer, L., Imai, T., … Wu, H. (2018). Evaluating the replicability of social science experiments in Nature and Science between 2010 and 2015. Nature Human Behaviour, 2, 637–644. [Google Scholar] [CrossRef]
- Coleman, J. S., Campbell, E. Q., Hobson, C. J., McPartland, J., Mood, A. M., Weinfeld, F. D., & York, R. L. (1966). Equality of educational opportunity (Report No. OE-38001). U.S. Department of Health, Education, and Welfare, Office of Education. Available online: https://eric.ed.gov/?id=ED012275 (accessed on 1 October 2025).
- Cook, T. D., & Steiner, P. M. (2010). Case matching and the reduction of selection bias in quasi-experiments: The relative importance of pretest measures of outcome, of unreliable measurement, and of mode of data analysis. Psychological Methods, 15(1), 56–68. [Google Scholar] [CrossRef]
- Cooper, H., Charlton, K., Valentine, J. C., Muhlenbruck, L., & Borman, G. D. (2000). Making the most of summer school: A meta-analytic and narrative review. Monographs of the Society for Research in Child Development, 65(1), i–127. [Google Scholar]
- Cooper, H., Nye, B., Charlton, K., Lindsay, J., & Greathouse, S. (1996). The effects of summer vacation on achievement test scores: A narrative and meta-analytic review. Review of Educational Research, 66(3), 227–268. [Google Scholar] [CrossRef]
- Dahl-Leonard, K., Hall, C., Cho, E., Capin, P., Roberts, G. J., Kehoe, K. F., Haring, C., Peacott, D., & Demchak, A. (2025). Examining the effects of family-implemented literacy interventions for school-aged children: A meta-analysis. Educational Psychology Review, 37(1), 10. [Google Scholar] [CrossRef]
- Dickinson, D. K., Golinkoff, R. M., & Hirsh-Pasek, K. (2010). Speaking out for language: Why language is central to reading development. Educational Researcher, 39(4), 305–310. [Google Scholar] [CrossRef]
- Downey, D. B. (2024). How does schooling affect inequality in cognitive skills? The view from seasonal comparison research. Review of Educational Research, 94(6), 927–957. [Google Scholar] [CrossRef]
- Dujardin, E., Ecalle, J., Gomes, C., & Magnan, A. (2022). Summer reading program: A systematic literature review. Social Education Research, 4(1), 108–121. [Google Scholar] [CrossRef]
- Duncan, G. J., & Magnuson, K. (2005). Can family socioeconomic resources account for racial and ethnic test score gaps? The Future of Children, 15(1), 35–54. [Google Scholar] [CrossRef] [PubMed]
- Evans, M. D. R., Kelley, J., & Sikora, J. (2014). Scholarly culture and academic performance in 42 nations. Social Forces, 92(4), 1573–1605. [Google Scholar] [CrossRef]
- Evans, M. D. R., Kelley, J., Sikora, J., & Treiman, D. J. (2010). Family scholarly culture and educational success: Books and schooling in 27 nations. Research in Social Stratification and Mobility, 28(2), 171–197. [Google Scholar] [CrossRef]
- Fryer, R. G., & Levitt, S. D. (2004). Understanding the Black–white test score gap in the first two years of school. Review of Economics and Statistics, 86(2), 447–464. [Google Scholar] [CrossRef]
- Funk, M. J., Westreich, D., Wiesen, C., Stürmer, T., Brookhart, M. A., & Davidian, M. (2011). Doubly robust estimation of causal effects. American Journal of Epidemiology, 173(7), 761–767. [Google Scholar] [CrossRef]
- Glazerman, S., Levy, D. M., & Myers, D. (2002). Nonexperimental replications of social experiments: A systematic review. Mathematica Policy Research, Inc. Available online: https://www.researchgate.net/publication/254430866_Nonexperimental_Replications_of_Social_Experiments_A_Systematic_Review_Interim_ReportDiscussion_Paper (accessed on 1 October 2025).
- Hanushek, E. A., & Woessmann, L. (2011). The economics of international differences in educational achievement. In E. A. Hanushek, S. Machin, & L. Woessmann (Eds.), Handbook of the economics of education (Vol. 3, pp. 89–200). Elsevier. Available online: https://econpapers.repec.org/bookchap/eeeeduhes/3.htm (accessed on 1 October 2025).
- Hedges, L. V., & Schauer, J. M. (2019). More than one replication study is needed for unambiguous tests of replica-tion. Journal of Educational and Behavioral Statistics, 44(5), 543–570. [Google Scholar] [CrossRef]
- Hill, C. J., Bloom, H. S., Black, A. R., & Lipsey, M. W. (2008). Empirical benchmarks for interpreting effect sizes in research. Child Development Perspectives, 2(3), 172–177. [Google Scholar] [CrossRef]
- Holley, C. E. (1916). The relationship between persistence in school and home conditions. University of Chicago Press. Available online: https://archive.org/details/relationshipbetw0005holl (accessed on 1 October 2025).
- Ichimura, H., & Taber, C. (2001). Propensity-score matching with instrumental variables. American Economic Review, 91(2), 119–124. [Google Scholar] [CrossRef]
- Kang, J. D., & Schafer, J. L. (2007). Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science, 22(4), 523–539. [Google Scholar] [CrossRef]
- Kazak, A. E. (2018). Editorial: Journal article reporting standards. American Psychologist, 73(1), 1–2. [Google Scholar] [CrossRef] [PubMed]
- Kim, J. S., Guryan, J., White, T. G., Quinn, D. M., Capotosto, L., & Kingston, H. C. (2016). Delayed effects of a low-cost and large-scale summer reading intervention on elementary school children’s reading comprehension. Journal of Research on Educational Effectiveness, 9(Suppl. 1), 1–22. [Google Scholar] [CrossRef]
- Kim, J. S., & Quinn, D. M. (2013). The effects of summer reading on low-income children’s literacy achievement from kindergarten to grade 8: A meta-analysis of classroom and home interventions. Review of Educational Research, 83(3), 386–431. [Google Scholar] [CrossRef]
- Lanza, S. T., Moore, J. E., & Butera, N. M. (2013). Drawing causal inferences using propensity scores: A practical guide for community psychologists. American Journal of Community Psychology, 52(3–4), 380–392. [Google Scholar] [CrossRef]
- Lee, W. S. (2013). Propensity score matching and variations on the balancing test. Empirical Economics, 44(1), 47. [Google Scholar] [CrossRef]
- Linden, A. (2017). Improving causal inference with a doubly robust estimator that combines propensity score stratification and weighting. Journal of Evaluation in Clinical Practice, 23(4), 697–702. [Google Scholar] [CrossRef] [PubMed]
- Linver, M. R., Brooks-Gunn, J., & Kohen, D. E. (2002). Family processes as pathways from income to young children’s development. Developmental Psychology, 38(5), 719–734. [Google Scholar] [CrossRef]
- Makel, M. C., & Plucker, J. A. (2014). Facts are more important than novelty: Replication in the education sciences. Educational Researcher, 43(6), 304–316. [Google Scholar] [CrossRef]
- Makel, M. C., & Plucker, J. A. (2015). An introduction to replication research in gifted education: Shiny and new is not the same as useful. Gifted Child Quarterly, 59(3), 157–164. [Google Scholar] [CrossRef]
- Makel, M. C., Plucker, J. A., Freeman, J., Lombardi, A., Simonsen, B., & Coyne, M. (2016). Replication of special education research: Necessary but far too rare. Remedial and Special Education, 37(4), 205–212. [Google Scholar] [CrossRef]
- Makel, M. C., Plucker, J. A., & Hegarty, C. B. (2012). Replications in psychology research: How often do they really occur? Perspectives on Psychological Science, 7(6), 537–542. [Google Scholar] [CrossRef]
- Manu, A., Ewerling, F., Barros, A. J. D., & Victora, C. G. (2019). Association between availability of children’s book and the literacy-numeracy skills of children aged 36 to 59 months: Secondary analysis of the UNICEF multiple-indicator cluster surveys covering 35 countries. Journal of Global Health, 9(1), 010403. [Google Scholar] [CrossRef]
- May, H., Perez-Johnson, I., Haimson, J., Sattar, S., & Gleason, P. (2009). Using state tests in education experiments: A discussion of the issues (NCEE 2009-013). National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Available online: https://files.eric.ed.gov/fulltext/ED511776.pdf (accessed on 10 October 2025).
- McCombs, J. S., Augustine, C. H., Schwartz, H. L., Bodilly, S. J., McInnis, B. I., Lichter, D. S., & Cross, A. B. (2011). Making summer count: How summer programs can boost children’s learning. RAND Corporation. [Google Scholar]
- Mol, S. E., & Bus, A. G. (2011). To read or not to read: A meta-analysis of print exposure from infancy to early adulthood. Psychological Bulletin, 137(2), 267–296. [Google Scholar] [CrossRef]
- Mol, S. E., Bus, A. G., De Jong, M. T., & Smeets, D. J. (2008). Added value of dialogic parent–child book readings: A meta-analysis. Early Education and Development, 19(1), 7–26. [Google Scholar] [CrossRef]
- Neuman, S. B., & Moland, N. (2019). Book deserts: The consequences of income segregation on children’s access to print. Urban Education, 54(1), 126–147. [Google Scholar] [CrossRef]
- NWEA. (n.d.). The MAP suite. Available online: https://www.nwea.org/the-map-suite/ (accessed on 10 October 2025).
- Pirracchio, R., Carone, M., Rigon, M. R., Caruana, E., Mebazaa, A., & Chevret, S. (2016). Propensity score estimators for the average treatment effect and the average treatment effect on the treated may yield very different estimates. Statistical Methods in Medical Research, 25(5), 1938–1954. [Google Scholar] [CrossRef]
- Plucker, J. A., & Makel, M. C. (2021). Replication is important for educational psychology: Recent developments and key issues. Educational Psychologist, 56(2), 90–100. [Google Scholar] [CrossRef]
- Pridemore, W. A., Makel, M. C., & Plucker, J. A. (2018). Replication in criminology and the social sciences. Annual Review of Criminology, 1(1), 19–38. [Google Scholar] [CrossRef]
- Pustejovsky, J. E., & Tipton, E. (2018). Small-sample methods for cluster-robust variance estimation and hypothesis testing in fixed effects models. Journal of Business & Economic Statistics, 36(4), 672–683. [Google Scholar] [CrossRef]
- Reese, E., Leyva, D., Sparks, A., & Grolnick, W. (2010). Maternal elaborative reminiscing increases low-income children’s narrative skills relative to dialogic reading. Early Education and Development, 21(3), 318–342. [Google Scholar] [CrossRef]
- Richardson, J. T. E. (2011). Eta squared and partial eta squared as measures of effect size in educational research. Educational Research Review, 6(2), 135–147. [Google Scholar] [CrossRef]
- Robins, J., Sued, M., Lei-Gomez, Q., & Rotnitzky, A. (2007). Comment: Performance of double-robust estimators when “inverse probability” weights are highly variable. Statistical Science, 22(4), 544–559. [Google Scholar] [CrossRef]
- Rubin, D. B. (2001). Using propensity scores to help design observational studies: Application to the tobacco litigation. Health Services and Outcomes Research Methodology, 2(3–4), 169–188. [Google Scholar] [CrossRef]
- Sikora, J., Evans, M. D. R., & Kelley, J. (2019). Scholarly culture: How books in adolescence enhance adult literacy, numeracy and technology skills in 31 societies. Social Science Research, 77, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Slavin, R., & Smith, D. (2009). The relationship between sample sizes and effect sizes in systematic reviews in education. Educational Evaluation and Policy Analysis, 31(4), 500–506. [Google Scholar] [CrossRef]
- Snow, C. E. (2010). Academic language and the challenge of reading for learning about science. Science, 328(5977), 450–452. [Google Scholar] [CrossRef]
- StataCorp. (2019). Stata statistical software: Release 16. StataCorp LLC. [Google Scholar]
- Stuart, E. A. (2010). Matching methods for causal inference: A review and a look forward. Statistical Science: A Review Journal of the Institute of Mathematical Statistics, 25(1), 1–21. [Google Scholar] [CrossRef]
- Tan, Z. (2010). Bounded, efficient and doubly robust estimation with inverse weighting. Biometrika, 97(3), 661–682. [Google Scholar] [CrossRef]
- Tyson, C. (2014, August 13). Failure to replicate. Inside Higher Education. Available online: https://www.insidehighered.com/news/2014/08/14/almost-no-education-research-replicated-new-article-shows (accessed on 1 October 2025).
- Wasik, B. A., & Hindman, A. H. (2020). Increasing preschoolers’ vocabulary development through a streamlined teacher professional development intervention. Early Childhood Research Quarterly, 50, 101–113. [Google Scholar] [CrossRef]
- What Works Clearinghouse. (2022). What works clearinghouse procedures and standards handbook, version 5.0. U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance (NCEE). Available online: https://ies.ed.gov/ncee/wwc/Handbooks (accessed on 10 October 2025).
- White, T. G., Kim, J. S., & Foster, L. (2013). Replicating the effects of a teacher-scaffolded voluntary summer reading program: The role of poverty. Reading Research Quarterly, 49(1), 5–30. [Google Scholar] [CrossRef]
- Whitehurst, G. J., Fischel, J. E., Lonigan, C. J., Valdez-Menchaca, M. C., DeBaryshe, B. D., & Caulfield, M. B. (1988). Verbal interaction in families of normal and expressive-language-delayed children. Developmental Psychology, 24(5), 690. [Google Scholar] [CrossRef]
- Whitehurst, G. J., & Lonigan, C. J. (1998). Child development and emergent literacy. Child Development, 69(3), 848–872. [Google Scholar] [CrossRef]
- Workman, J., von Hippel, P. T., & Merry, J. (2023). Findings on summer learning loss often fail to replicate, even in recent data. Sociological Science, 10, 251–285. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z., Kim, H. J., Lonjon, G., & Zhu, Y. (2019). Balance diagnostics after propensity score matching. Annals of Translational Medicine, 7(1), 16. [Google Scholar] [CrossRef]
| Grade | 1 | 2 | 3 | 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Non-KRN | KRN | Non-KRN | KRN | Non-KRN | KRN | Non-KRN | KRN | |
| Battle Creek District | ||||||||
| Dudley Elementary | 35 | 6 | 33 | 8 | ||||
| Valley View Elem. | 71 | 14 | 67 | 21 | 66 | 24 | ||
| Verona Elementary | 71 | 11 | ||||||
| Troy City District | ||||||||
| Hook Elementary | 22 | 21 | 28 | 27 | ||||
| Kyle Elementary | 23 | 11 | 24 | 18 | ||||
| Total | 129 | 31 | 79 | 47 | 95 | 48 | 137 | 35 |
| Variables | Before Matching | After Matching | ||||
|---|---|---|---|---|---|---|
| Non-KRN Student | KRN Student | Non-KRN Student | KRN Student | |||
| Mean (SD) | Mean (SD) | Mean Difference | Mean (SD) | Mean (SD) | Mean Difference | |
| 2018 Fall | 0.00 | 0.09 | −0.09 | 0.30 | 0.20 | 0.11 |
| (1.03) | (1.02) | (1.04) | (1.11) | |||
| 2018 Winter | 0.02 | 0.12 | −0.10 | 0.38 | 0.22 | 0.16 |
| (1.00) | (0.97) | (0.91) | (1.00) | |||
| 2019 Spring | −0.03 | 0.11 | −0.14 | 0.34 | 0.21 | 0.13 |
| (1.02) | (0.97) | (0.91) | (1.01) | |||
| Female | 0.41 | 0.50 | −0.09 * | 0.44 | 0.44 | 0.01 |
| Economic disadvantage | 0.79 | 0.50 | 0.29 *** | 0.60 | 0.58 | 0.02 |
| Black | 0.45 | 0.11 | 0.34 *** | 0.18 | 0.15 | 0.03 |
| Asian | 0.07 | 0.02 | 0.04 | 0.02 | 0.02 | 0.00 |
| White | 0.39 | 0.70 | −0.30 *** | 0.68 | 0.70 | −0.02 |
| Hispanic | 0.05 | 0.04 | 0.01 | 0.07 | 0.05 | 0.02 |
| Multiracial | 0.05 | 0.14 | −0.09 *** | 0.06 | 0.08 | −0.03 |
| Minority | 0.55 | 0.25 | 0.31 *** | 0.25 | 0.24 | 0.01 |
| Female × Economic disadvantage | 0.35 | 0.28 | 0.07 | 0.28 | 0.27 | 0.01 |
| Female × Black | 0.17 | 0.06 | 0.11 *** | 0.08 | 0.07 | 0.01 |
| Female × Asian | 0.03 | 0.02 | 0.00 | 0.02 | 0.02 | 0.00 |
| Female × White | 0.16 | 0.35 | −0.19 *** | 0.31 | 0.31 | 0.00 |
| Female × Hispanic | 0.03 | 0.02 | 0.01 | 0.03 | 0.04 | 0.00 |
| Female × Multiracial | 0.02 | 0.04 | −0.02 | 0.00 | 0.00 | 0.00 |
| Economic disadvantage × Black | 0.36 | 0.09 | 0.26 ** | 0.16 | 0.13 | 0.03 |
| Economic disadvantage × Asian | 0.06 | 0.01 | 0.05 ** | 0.02 | 0.02 | 0.00 |
| Economic disadvantage × White | 0.30 | 0.26 | 0.04 | 0.30 | 0.31 | −0.01 |
| Economic disadvantage × Hispanic | 0.04 | 0.04 | 0.00 | 0.07 | 0.05 | 0.02 |
| Economic disadvantage × Multiracial | 0.04 | 0.10 | −0.06 *** | 0.05 | 0.07 | −0.03 |
| n | 440 | 161 | 133 | 133 | ||
| Before Matching | After Matching | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean Difference | Standardized Mean Difference | Eta-Squared Effect Size | Variance Ratio | Mean Difference | Standardized Mean Difference | Eta-Squared Effect Size | Variance Ratio | |
| 2018 Fall | 0.09 | 0.092 | 0.002 | 0.983 | −0.11 | −0.102 | 0.002 | 1.143 |
| 2018 Winter | 0.10 | 0.102 | 0.002 | 0.925 | −0.16 | −0.174 | 0.007 | 1.215 |
| 2019 Spring | 0.14 | 0.137 | 0.004 | 0.913 | −0.13 | −0.148 | 0.005 | 1.239 |
| Female | 0.09 * | 0.186 | 0.007 | 1.036 | −0.01 | −0.012 | 0.000 | 1.000 |
| Economic disadvantage | −0.29 *** | −0.715 | 0.081 | 1.530 | −0.02 | −0.034 | 0.000 | 1.015 |
| Black | −0.34 *** | −0.683 | 0.099 | 0.384 | −0.03 | −0.079 | 0.002 | 0.860 |
| Asian | −0.04 | −0.165 | 0.006 | 0.395 | 0.00 | 0.000 | 0.000 | 1.003 |
| White | 0.30 *** | 0.619 | 0.072 | 0.891 | 0.02 | 0.042 | 0.000 | 0.968 |
| Hispanic | −0.01 | −0.049 | 0.001 | 0.793 | −0.02 | −0.059 | 0.001 | 0.798 |
| Multiracial | 0.09 *** | 0.417 | 0.023 | 2.606 | 0.03 | 0.112 | 0.003 | 1.423 |
| Minority | −0.26 *** | −0.524 | 0.054 | 0.814 | −0.02 | −0.043 | 0.000 | 0.964 |
| Female × Economic disadvantage | −0.070 | −0.148 | 0.004 | 0.889 | −0.01 | −0.02 | 0.000 | 0.983 |
| Female × Black | −0.12 *** | −0.304 | 0.021 | 0.375 | −0.01 | −0.043 | 0.001 | 0.871 |
| Female × Asian | −0.00 | −0.015 | 0.000 | 0.917 | 0.00 | 0.000 | 0.000 | 1.003 |
| Female × White | 0.20 *** | 0.532 | 0.045 | 1.716 | 0.00 | 0.007 | 0.000 | 1.008 |
| Female × Hispanic | −0.010 | −0.04 | 0.000 | 0.79 | 0.00 | 0.017 | 0.000 | 1.09 |
| Female × Multiracial | 0.020 | 0.139 | 0.003 | 1.88 | . | . | . | . |
| Economic disadvantage × Black | −0.26 *** | −0.55 | 0.067 | 0.37 | −0.03 | −0.090 | 0.002 | 0.826 |
| Economic disadvantage × Asian | −0.05 ** | −0.198 | 0.010 | 0.222 | 0.00 | 0.000 | 0.000 | 1.003 |
| Economic disadvantage × White | −0.04 | −0.081 | 0.001 | 0.926 | 0.01 | 0.013 | 0.000 | 1.014 |
| Economic disadvantage × Hispanic | −0.00 | −0.018 | 0.000 | 0.918 | −0.02 | −0.059 | 0.001 | 0.798 |
| Economic disadvantage × Multiracial | 0.06 ** | 0.315 | 0.014 | 2.419 | 0.03 | 0.121 | 0.003 | 1.511 |
| Intent-to-Treat | Treatment-on-the-Treated | |||||
|---|---|---|---|---|---|---|
| Coefficient | (Clustered SE) | Effect Size (d) | Coefficient | (Clustered SE) | Effect Size (d) | |
| Treatment | 0.149 * | (0.072) | 0.145 | |||
| Number of books | 0.023 * | (0.011) | 0.023 | |||
| 2018 Fall | 0.200 ** | (0.067) | 0.197 ** | (0.064) | ||
| 2018 Winter | 0.367 ** | (0.086) | 0.366 ** | (0.082) | ||
| 2019 Spring | 0.338 ** | (0.079) | 0.339 ** | (0.075) | ||
| Black | 0.048 | (0.202) | 0.058 | (0.177) | ||
| Asian | 0.312 | (0.426) | 0.348 | (0.407) | ||
| White (Ref.) | ||||||
| Hispanic | 1.035 ** | (0.374) | 1.043 ** | (0.356) | ||
| Multiracial | −0.127 | (0.123) | −0.078 | (0.109) | ||
| Female | 0.095 | (0.138) | 0.094 | (0.131) | ||
| Female × Black | −0.300 | (0.324) | −0.280 | (0.304) | ||
| Female × White (Ref.) | ||||||
| Female × Hispanic | −1.102 ** | (0.405) | −1.084 ** | (0.384) | ||
| Economic disadvantage | −0.148 | (0.109) | −0.138 | (0.104) | ||
| Econ disadv. × Black | 0.163 | (0.295) | 0.154 | (0.267) | ||
| Econ disadv. × White (Ref.) | ||||||
| Econ disadv. × Multiracial | −0.068 | (0.291) | −0.123 | (0.279) | ||
| Female × Econ disadv. | 0.264 | (0.200) | 0.252 | (0.191) | ||
| Constant | −0.222 | (0.948) | −0.239 | (0.892) | ||
| n | 266 | 266 | ||||
| Panel A: Intent-to-Treat (ITT) Estimates | |||||
| Grade | Coefficient | SE | Effect Size (d) | p-Value | N |
| 1 | 0.309 | 0.155 | 0.302 | 0.049 | 63 |
| 2 | 0.178 | 0.151 | 0.174 | 0.241 | 32 |
| 3 | 0.108 | 0.141 | 0.106 | 0.446 | 84 |
| 4 | 0.071 | 0.082 | 0.069 | 0.387 | 87 |
| Panel B: Treatment-on-the-Treated (TOT) Estimates | |||||
| Grade | Coefficient | SE | Effect Size (d) | p-Value | N |
| 1 | 0.049 | 0.024 | 0.048 | 0.037 | 63 |
| 2 | 0.032 | 0.027 | 0.031 | 0.227 | 32 |
| 3 | 0.015 | 0.018 | 0.015 | 0.423 | 84 |
| 4 | 0.013 | 0.015 | 0.013 | 0.361 | 87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borman, G.D.; Yang, H. A Quasi-Experimental Study of the Achievement Impacts of a Replicable Summer Reading Program. Educ. Sci. 2025, 15, 1422. https://doi.org/10.3390/educsci15111422
Borman GD, Yang H. A Quasi-Experimental Study of the Achievement Impacts of a Replicable Summer Reading Program. Education Sciences. 2025; 15(11):1422. https://doi.org/10.3390/educsci15111422
Chicago/Turabian StyleBorman, Geoffrey D., and Hyunwoo Yang. 2025. "A Quasi-Experimental Study of the Achievement Impacts of a Replicable Summer Reading Program" Education Sciences 15, no. 11: 1422. https://doi.org/10.3390/educsci15111422
APA StyleBorman, G. D., & Yang, H. (2025). A Quasi-Experimental Study of the Achievement Impacts of a Replicable Summer Reading Program. Education Sciences, 15(11), 1422. https://doi.org/10.3390/educsci15111422






