Dynamic Assessment to Assess Mathematical Problem Solving of Students with Disabilities
Abstract
1. Introduction
1.1. Enhanced Anchored Instruction
1.2. EAI Assessment
1.3. Dynamic Assessment
1.4. Study Purpose and Research Questions
2. Materials and Methods
2.1. Research Design
2.2. Setting and Context
2.3. Participants
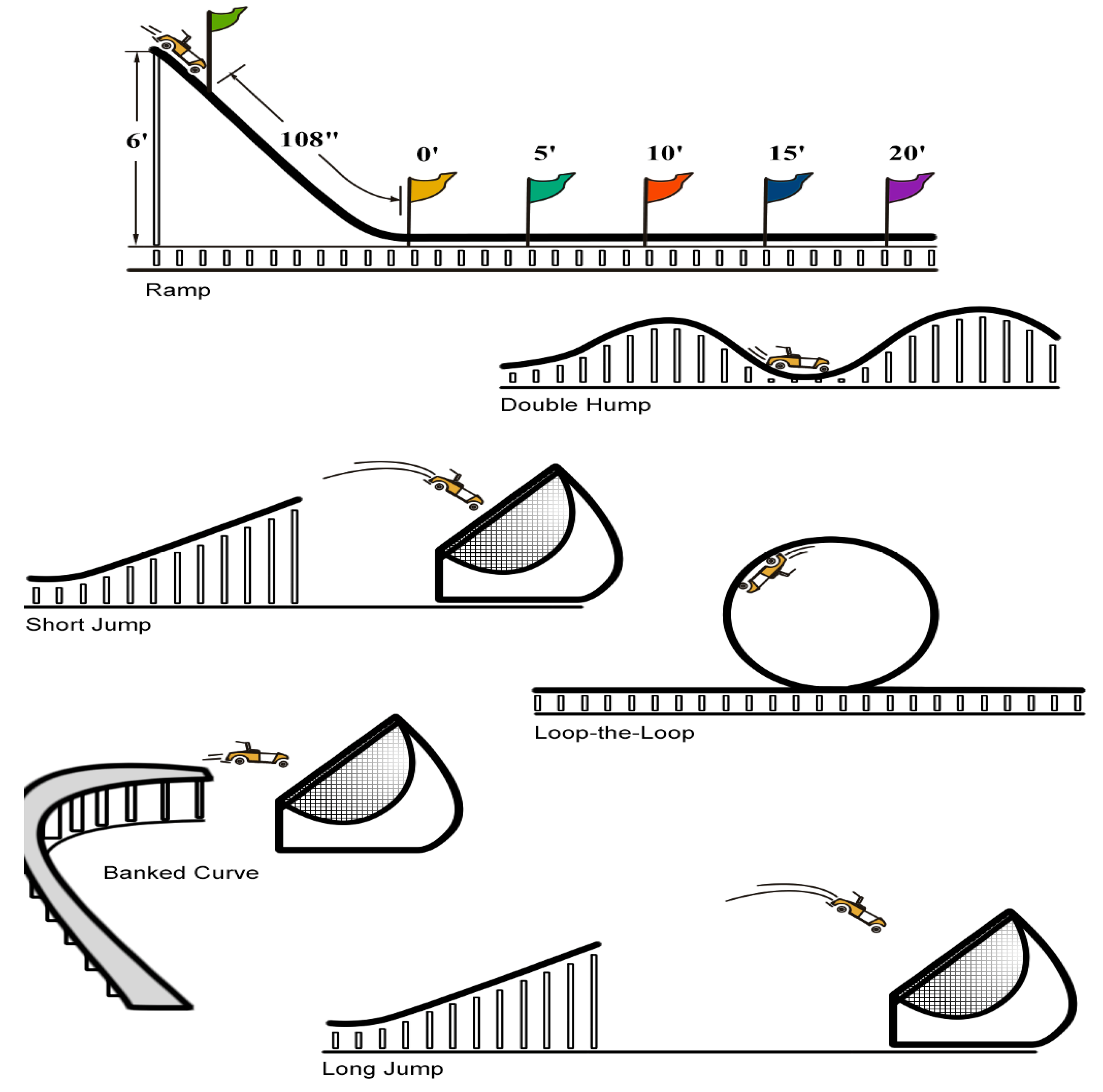
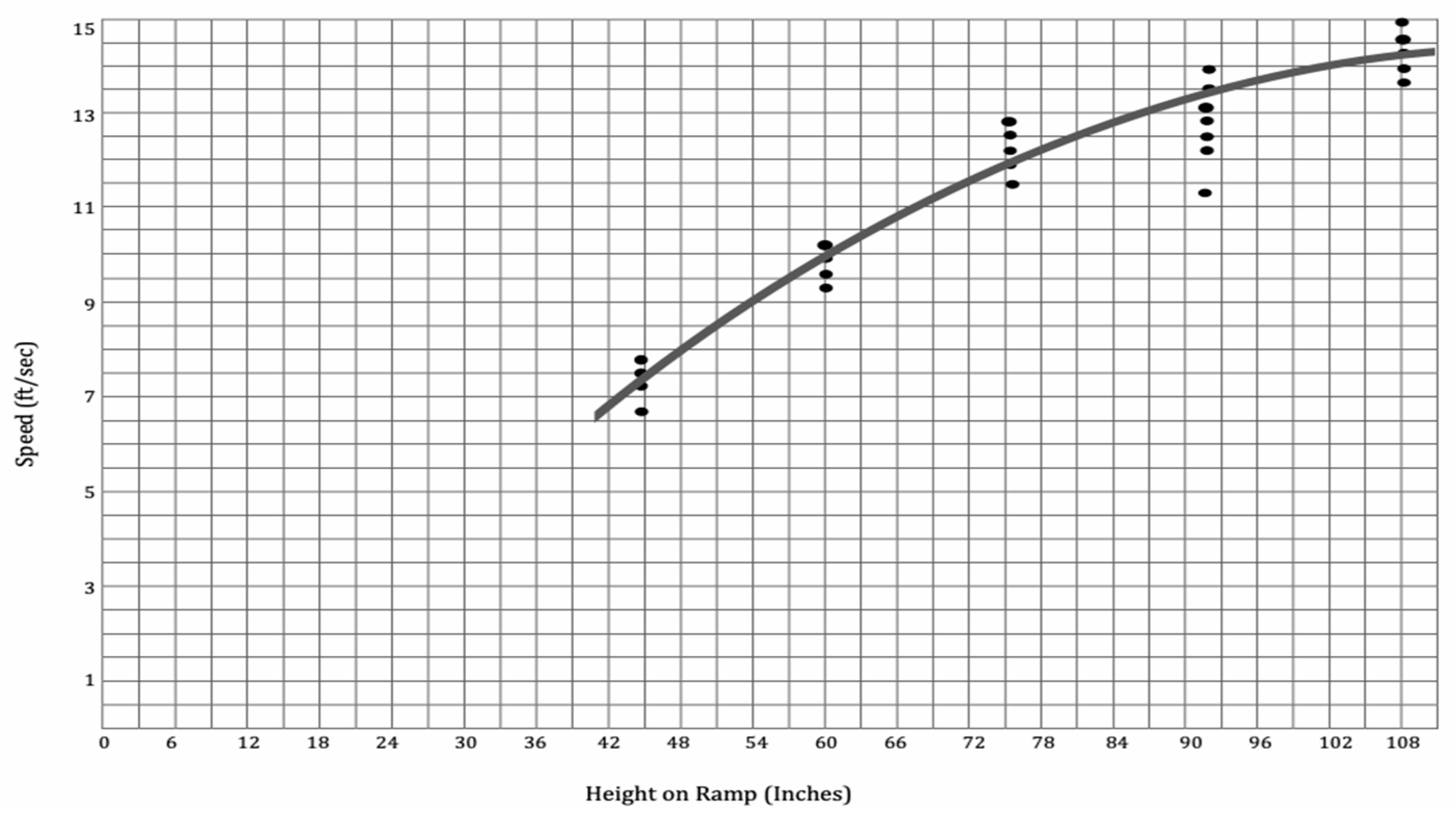
2.4. EAI Problem-Solving Units
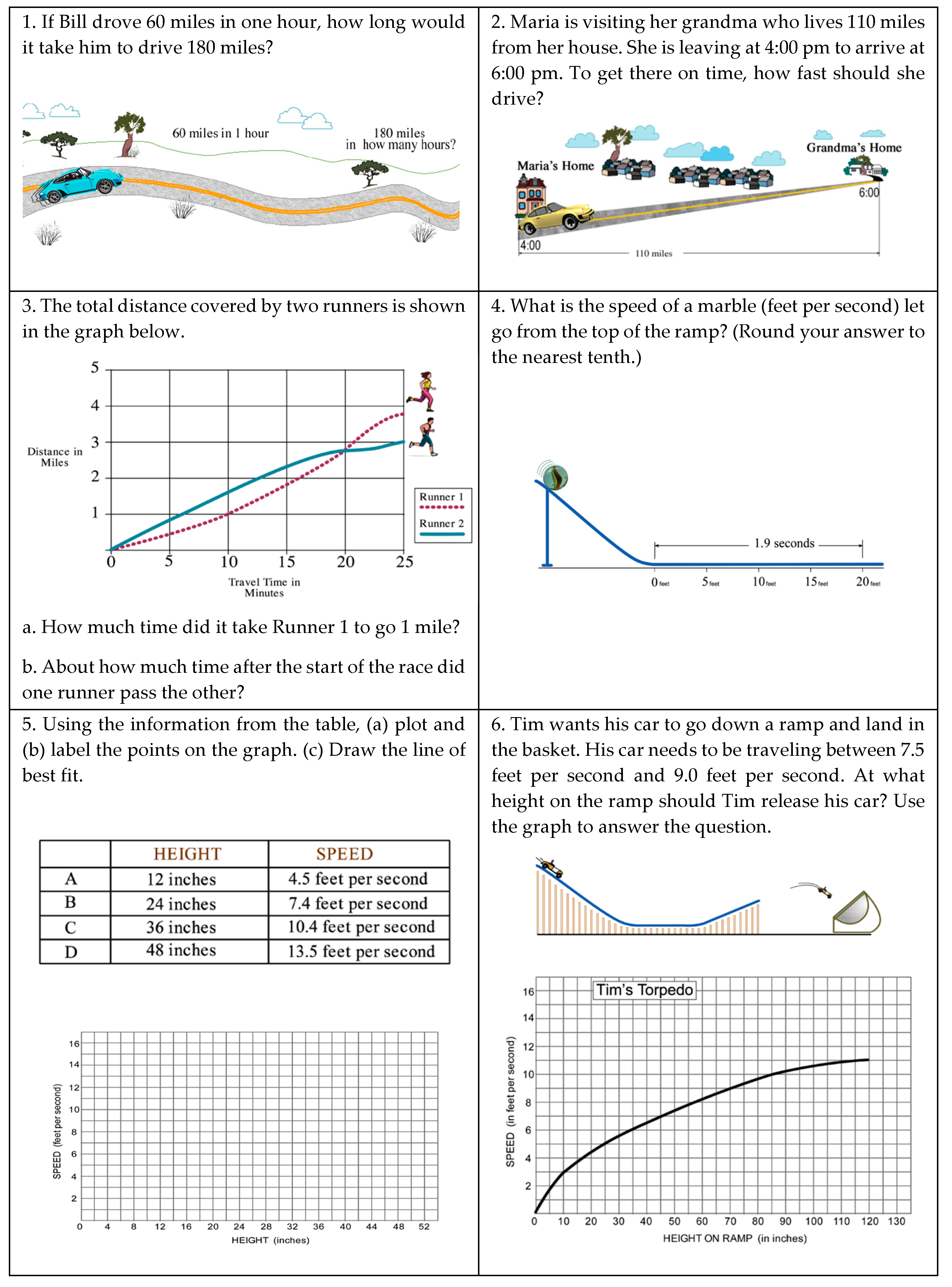
2.5. Mathematical Problem-Solving Written Test
2.5.1. Written Test Administrations
2.5.2. Written Test Scoring
2.6. Problem-Solving Dynamic Assessment
2.6.1. Dynamic Assessment Administrations
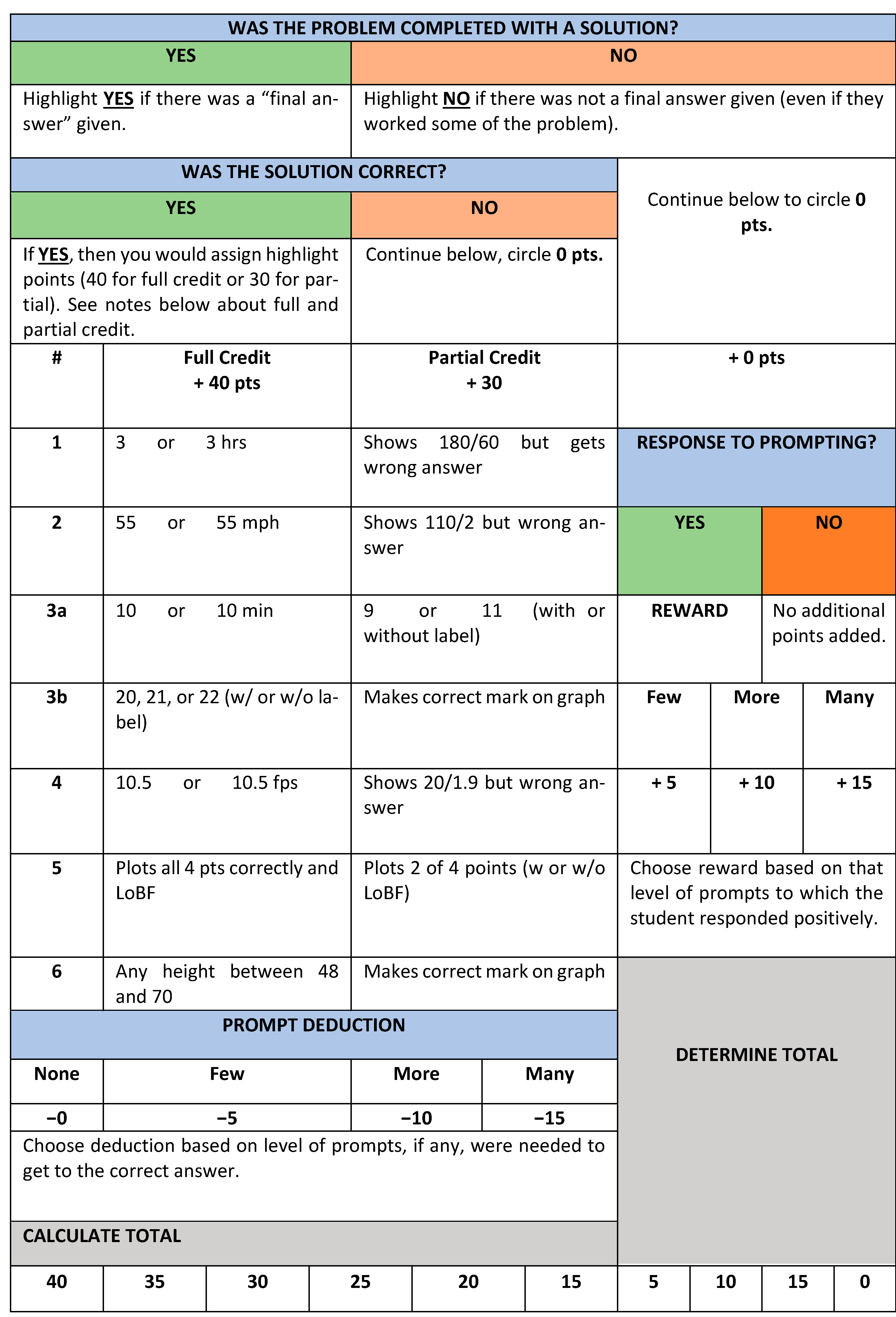
2.6.2. Dynamic Assessment Scoring
2.7. Data Analysis
2.7.1. Quantitative Analysis
2.7.2. Qualitative Analysis
3. Results
3.1. Adequacy of DA (RQ 1)
3.2. MPS Process of Students with Disabilities (RQ 2)
3.2.1. Stage 1: Understanding the Mathematical Problem’s Context
3.2.2. Stage 2: Thinking Through the Mathematical Problem While Forming a Plan
3.2.3. Stage 3: Carrying out the Plan
3.2.4. Stage 4: Looking Back
3.3. Interactions Between the Examiner and Examinees (RQ 3)
4. Discussion
4.1. Adequacy of DA
4.2. MPS Process
4.3. Instruction and Feedback of DA
4.4. Limitations and Suggestions for Future Research
4.5. Implications for Practice
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPS | Mathematical problem solving |
| DA | Dynamic assessment |
| SWDs | Students with disabilities |
| EAI | Enhanced Anchored Instruction |
| RQ | Research question |
| IEP | Individualized Education Program |
| KK | Kim’s Komet |
| GP | Grand Pentathlon |
| CCSSI-M | Common Core State Standards for Mathematics |
| WT | Written test |
| GRA | Graduate research assistant |
Appendix A
References
- Aceves, T. C., & Kennedy, M. J. (Eds.). (2024). High-leverage practices for students with disabilities (2nd ed.). Council for Exceptional Children and CEEDAR Center. [Google Scholar]
- American Educational Research Association, American Psychological Association & National Council on Measurement in Education. (2014). Standards for educational and psychological testing. American Educational Research Association. [Google Scholar]
- Arias Valencia, M. M. (2022). Principles, scope, and limitations of the methodological triangulation. Investigación y Educación En Enfermería, 40(2), e03. Available online: https://pubmed.ncbi.nlm.nih.gov/36264691 (accessed on 1 January 2025).
- Baddeley, A. (2000). The episodic buffer: A new component of working memory? Trends in Cognitive Sciences, 4(11), 417–423. [Google Scholar] [CrossRef]
- Baddeley, A. (2012). Working memory: Theories, models, and controversies. Annual Review of Psychology, 63, 1–29. [Google Scholar] [CrossRef]
- Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. [Google Scholar] [CrossRef]
- Bengtsson, M. (2016). How to plan and perform a qualitative study using content analysis. NursingPlus Open, 2, 8–14. [Google Scholar] [CrossRef]
- Bottge, B. A., Cohen, A. S., & Choi, H.-J. (2018). Comparisons of mathematics intervention effects in resource and inclusive classrooms. Exceptional Children, 84(2), 197–212. [Google Scholar] [CrossRef]
- Bottge, B. A., Ma, X., Gassaway, L., Toland, M. D., Butler, M., & Cho, S. J. (2014). Effects of blended instructional models on math performance. Exceptional Children, 80, 423–437. [Google Scholar] [CrossRef]
- Bottge, B. A., Ma, X., Gassaway, L. J., Jones, M., & Gravil, M. (2021). Effects of formative assessment strategies on the fractions computation skills of students with disabilities. Remedial and Special Education, 42(5), 279–289. [Google Scholar] [CrossRef]
- Bottge, B. A., Rueda, E., LaRoque, P. T., Serlin, R. C., & Kwon, J. (2007). Integrating reform–oriented math instruction in special education settings. Learning Disabilities Research & Practice, 22(2), 96–109. [Google Scholar] [CrossRef]
- Bottge, B. A., Toland, M., Gassaway, L., Butler, M., Choo, S., Griffin, A., & Ma, X. (2015). Impact of enhanced anchored instruction in inclusive math classrooms. Exceptional Children, 81(2), 158–175. [Google Scholar] [CrossRef]
- Brookhart, S., & Lazarus, S. (2017). Formative assessment for students with disabilities. Council of Chief State School Officers. Available online: https://famemichigan.org/wp-content/uploads/2018/04/Formative-Assessment-for-Students-with-Disabilities.pdf (accessed on 1 January 2025).
- Cai, J., Koichu, B., Rott, B., & Jiang, C. (2024). Advances in research on mathematical problem posing: Focus on task variables. The Journal of Mathematical Behavior, 76, 101186. [Google Scholar] [CrossRef]
- Campione, J. C., & Brown, A. L. (1987). Linking dynamic assessment with school achievement. In C. S. Lidz (Ed.), Dynamic assessment: An interactional approach to evaluating learning potential (pp. 82–115). The Guilford Press. [Google Scholar]
- Choo, S. (2024). Enhanced anchored instruction: A radical way of teaching problem solving to students with learning disabilities (pp. 5–7). LD Forum. [Google Scholar] [CrossRef]
- Cognition and Technology Group at Vanderbilt. (1990). Anchored instruction and its relationship to situated cognition. Educational Researcher, 19(6), 2–10. [Google Scholar] [CrossRef]
- Cognition and Technology Group at Vanderbilt. (1997). The Jasper project: Lessons in curriculum, instruction, assessment, and professional development. Lawrence Erlbaum Associates. [Google Scholar]
- Council for Exceptional Children. (2014). Council for exceptional children: Standards for evidence-based practices in special education. Exceptional Children, 80(4), 504–511. [Google Scholar] [CrossRef]
- Creswell, J. W., & Clark, V. L. P. (2017). Designing and conducting mixed methods research (3rd ed.). SAGE Publications, Inc. [Google Scholar]
- Creswell, J. W., Plano Clark, V. L., Gutmann, M. L., & Hanson, W. E. (2003). Advanced mixed methods research designs. In A. Tashakkori, & C. Teddlie (Eds.), Handbook of mixed methods in social and behavioral research (pp. 209–240). Sage. [Google Scholar]
- Crooks, T. J., Kane, M. T., & Cohen, A. S. (1996). Threats to the valid use of assessments. Assessment in Education: Principles, Policy & Practice, 3(3), 265–286. [Google Scholar] [CrossRef]
- Dixon, C., Oxley, E., Nash, H., & Gellert, A. S. (2023). Does dynamic assessment offer an alternative approach to identifying reading disorder? A systematic review. Journal of Learning Disabilities, 56(6), 423–439. [Google Scholar] [CrossRef] [PubMed]
- Elliott, J. (2003). Dynamic assessment in educational settings: Realising potential. Educational Review, 55(1), 15–32. [Google Scholar] [CrossRef]
- Fetters, M. D., Curry, L. A., & Creswell, J. W. (2013). Achieving integration in mixed methods designs-principles and practices. Health Services Research, 48((6 Pt 2)), 2134–2156. [Google Scholar] [CrossRef]
- Fuchs, D., Fuchs, L. S., Compton, D. L., Bouton, B., Caffrey, E., & Hill, L. (2007). Dynamic assessment as responsiveness to intervention: A scripted protocol to identify young at-risk readers. TEACHING Exceptional Children, 39(5), 58–63. [Google Scholar] [CrossRef]
- Fuchs, L. S., Compton, D. L., Fuchs, D., Hollenbeck, K. N., Craddock, C. F., & Hamlett, C. L. (2008). Dynamic assessment of algebraic learning in predicting third graders’ development of mathematical problem solving. Journal of Educational Psychology, 100(4), 829–850. [Google Scholar] [CrossRef]
- Fuchs, L. S., Compton, D. L., Fuchs, D., Hollenbeck, K. N., Hamlett, C. L., & Seethaler, P. M. (2011). Two-stage screening for math problem-solving difficulty using dynamic assessment of algebraic learning. Journal of Learning Disabilities, 44(4), 372–380. [Google Scholar] [CrossRef]
- Gu, P. Y. (2021). An argument-based framework for validating formative assessment in the classroom. Frontiers in Education, 6, 605999. [Google Scholar] [CrossRef]
- Ho, K. F., & Hedberg, J. G. (2005). Teachers’ pedagogies and their impact on students’ mathematical problem solving. The Journal of Mathematical Behavior, 24(3), 238–252. [Google Scholar] [CrossRef]
- Ivankova, N. V., Creswell, J. W., & Stick, S. L. (2006). Using mixed-methods sequential explanatory design: From theory to practice. Field Methods, 18(1), 3–20. [Google Scholar] [CrossRef]
- Jitendra, A., DiPipi, C. M., & Perron-Jones, N. (2002). An exploratory study of schema-based word-problem—Solving instruction for middle school students with learning disabilities: An emphasis on conceptual and procedural understanding. The Journal of Special Education, 36(1), 23–38. [Google Scholar] [CrossRef]
- Jitendra, A. K., & Kame’enui, E. J. (1993). An exploratory study of dynamic assessment involving two instructional strategies on experts and novices’ performance in solving part-whole mathematical word problems. Diagnostique, 18(4), 305–324. [Google Scholar] [CrossRef]
- Kennedy, M. J., Aronin, S., O’Neal, M., Newton, J. R., & Thomas, C. N. (2014). Creating multimedia-based vignettes with embedded evidence-based practices: A tool for supporting struggling learners. Journal of Special Education Technology, 29(4), 15–30. [Google Scholar] [CrossRef]
- Kenward, M. G., & Roger, J. H. (1997). Small sample inference for fixed effects from restricted maximum likelihood. Biometrics, 53(3), 983–997. [Google Scholar] [CrossRef]
- Kong, J. E., & Orosco, M. J. (2016). Word-problem-solving strategy for minority students at risk for math difficulties. Learning Disability Quarterly, 39(3), 171–181. [Google Scholar] [CrossRef]
- Kong, J. E., Yan, C., Serceki, A., & Swanson, H. L. (2021). Word-problem-solving interventions for elementary students with learning disabilities: A selective meta-analysis of the literature. Learning Disability Quarterly, 44(4), 248–260. [Google Scholar] [CrossRef]
- Krawec, J., Huang, J., Montague, M., Kressler, B., & Melia de Alba, A. (2012). The effects of cognitive strategy instruction on knowledge of math problem-solving processes of middle school students with learning disabilities. Learning Disability Quarterly, 36(2), 80–92. [Google Scholar] [CrossRef]
- Le, H., Ferreira, J. M., & Kuusisto, E. (2023). Dynamic assessment in inclusive elementary education: A systematic literature review of the usability, methods, and challenges in the past decade. European Journal of Special Education Research, 9(3), 94–125. [Google Scholar] [CrossRef]
- Leko, M. M., Cook, B. G., & Cook, L. (2021). Qualitative methods in special education research. Learning Disabilities Research & Practice, 36(4), 278–286. [Google Scholar] [CrossRef]
- Lidz, C., & Elliott, J. G. (Eds.). (2000). Dynamic assessment: Prevailing models and applications (pp. 713–740). Elsevier. [Google Scholar]
- Lidz, C. S. (2014). Leaning toward a consensus about dynamic assessment: Can we? Do we want to? Journal of Cognitive Education and Psychology, 13(3), 292–307. [Google Scholar] [CrossRef]
- Love, H. R., Cook, B. G., & Cook, L. (2022). Mixed–methods approaches in special education research. Learning Disabilities Research & Practice, 37(4), 314–323. [Google Scholar] [CrossRef]
- Lovett, B. J. (2021). Educational accommodations for students with disabilities: Two equity-related concerns. Frontiers in Education, 6, 795266. [Google Scholar] [CrossRef]
- Marriott, J., Davies, N., & Gibson, L. (2009). Teaching, learning and assessing statistical problem solving. Journal of Statistics Education, 17(1), 17. Available online: https://jse.amstat.org/v17n1/marriott.html (accessed on 1 January 2025). [CrossRef]
- McNeish, D., & Kelley, K. (2019). Fixed effects models versus mixed effects models for clustered data: Reviewing the approaches, disentangling the differences, and making recommendations. Psychological Methods, 24(1), 20–35. [Google Scholar] [CrossRef]
- Montague, M., Enders, C., & Dietz, S. (2011). Effects of cognitive strategy instruction on math problem solving of middle school students with learning disabilities. Learning Disability Quarterly, 34(4), 262–272. [Google Scholar] [CrossRef]
- Myers, J. A., Hughes, E. M., Witzel, B. S., Anderson, R. D., & Owens, J. (2023). A meta-analysis of mathematical interventions for increasing the word problem solving performance of upper elementary and secondary students with mathematics difficulties. Journal of Research on Educational Effectiveness, 16(1), 1–35. [Google Scholar] [CrossRef]
- Nakagawa, S., Johnson, P. C. D., & Schielzeth, H. (2017). The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Journal of the Royal Society, Interface, 14(134), 1–11. [Google Scholar] [CrossRef]
- National Association of School Psychologists. (2010). Model for comprehensive and integrated school psychological services. Available online: http://www.nasponline.org/standards/practice-model (accessed on 1 January 2025).
- National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. NCTM. [Google Scholar]
- National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Authors. [Google Scholar]
- Nur, A. S., Kartono, K., Zaenuri, Z., & Rochmad, R. (2022). Solving mathematical word problems using dynamic assessment for scaffolding construction. International Journal of Evaluation and Research in Education (IJERE), 11(2), 649–657. [Google Scholar] [CrossRef]
- Orosco, M. J. (2014). Word problem strategy for Latino English language learners at risk for math disabilities. Learning Disability Quarterly, 37(1), 45–53. [Google Scholar] [CrossRef]
- Orosco, M. J., Swanson, H. L., O’Connor, R., & Lussier, C. (2011). The effects of dynamic strategic math on English language learners’ word problem solving. The Journal of Special Education, 47(2), 96–107. [Google Scholar] [CrossRef]
- Pearce, J., & Chiavaroli, N. (2020). Prompting candidates in oral assessment contexts: A taxonomy and guiding principles. Journal of Medical Education and Curricular Development, 7, 2382120520948881. [Google Scholar] [CrossRef]
- Peel, K. L. (2020). A beginner’s guide to applied educational research using thematic analysis. Practical Assessment Research and Evaluation, 25(1), 2. [Google Scholar] [CrossRef]
- Pólya, G. (1945). How to solve it. Princeton University Press. [Google Scholar]
- Rosas-Rivera, Y., & Solovieva, Y. (2023). A dynamic evaluation of the process of solving mathematical problems, according to N.F. Talyzina’s method. Psychology in Russia: State of the Art, 16(3), 88–103. [Google Scholar] [CrossRef]
- Schumacher, R., Taylor, M., & Dougherty, B. (2019). Professional learning community: Improving mathematical problem solving for students in grades 4 through 8 facilitator’s guide (REL 2019-002). U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, Regional Educational Laboratory Southeast. Available online: http://ies.ed.gov/rel-southeast/2025/01/tool-5 (accessed on 1 January 2025).
- Seethaler, P. M., Fuchs, L. S., Fuchs, D., & Compton, D. L. (2012). Predicting first graders’ development of calculation versus word-problem performance: The role of dynamic assessment. Journal of Educational Psychology, 104(1), 224–234. [Google Scholar] [CrossRef]
- Spector, J. E. (1992). Predicting progress in beginning reading: Dynamic assessment of phonemic awareness. Journal of Educational Psychology, 84(3), 353–363. [Google Scholar] [CrossRef]
- Spencer, M., Quinn, J. M., & Wagner, R. K. (2014). Specific reading comprehension disability: Major problem, myth, or misnomer? Learning Disabilities Research & Practice: A Publication of the Division for Learning Disabilities, Council for Exceptional Children, 29(1), 3–9. [Google Scholar] [CrossRef]
- Stevens, E. A., Leroux, A. J., & Powell, S. R. (2024). Predicting the word-problem performance of students with mathematics difficulty using word-problem vocabulary knowledge. Learning Disabilities Research & Practice, 39(4), 202–211. [Google Scholar] [CrossRef]
- Stringer, P. (2018). Dynamic assessment in educational settings: Is potential ever realised? Educational Review, 70(1), 18–30. [Google Scholar] [CrossRef]
- Talbott, E., De Los Reyes, A., Kearns, D. M., Mancilla-Martinez, J., & Wang, M. (2023). Evidence-based assessment in special education research: Advancing the use of evidence in assessment tools and empirical processes. Exceptional Children, 89(4), 467–487. [Google Scholar] [CrossRef]
- Ukobizaba, F., Nizeyimana, G., & Mukuka, A. (2021). Assessment strategies for enhancing students’ mathematical problem-solving skills: A review of literature. Eurasia Journal of Mathematics, Science and Technology Education, 17(3), 1–10. [Google Scholar] [CrossRef]
- VERBI Software. (2021). MAXQDA 2022 [Computer software]. VERBI Software. Available online: https://www.maxqda.com (accessed on 1 January 2025).
- Verdugo, M. A., Aguayo, V., Arias, V. B., & García-Domínguez, L. (2020). A systematic review of the assessment of support needs in people with intellectual and developmental disabilities. International Journal of Environmental Research and Public Health, 17(24), 9494. [Google Scholar] [CrossRef]
- Vygotsky, L. S., Cole, M., John-Steiner, V., Scribner, S., & Souberman, E. (1978). Mind in society: Development of higher psychological processes. Harvard University Press. [Google Scholar] [CrossRef]
- Woodward, J., Beckmann, S., Driscoll, M., Franke, M., Herzig, P., Jitendra, A., Koedinger, K. R., & Ogbuehi, P. (2012). Improving mathematical problem solving in grades 4 through 8: A practice guide (NCEE 2012-4055). National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. [Google Scholar]
- Yin, R. K. (2014). Case study research: Design and methods (5th ed.). Sage. [Google Scholar]
| Activities in Order | Days | Days per Activity |
|---|---|---|
| Pretest: written test | 1 | 3 days pretest |
| Pretest: dynamic assessment | 2 | |
| Kim’s Komet instructional days in classroom | 13 | 22 days classroom instruction |
| Other instructional days in classroom | 8 | |
| Holidays in classroom | 1 | |
| Days out of school for COVID-19 non-traditional instruction planning | 10 | 15 days break with no school |
| Days off for spring break | 5 | |
| Kim’s Komet + Grand Pentathlon instructional days via Zoom | 12 | 16 days online Zoom instruction |
| Other instructional days in classroom | 4 | |
| Posttest: written test | 1 | 4 days of posttest |
| Posttest: dynamic assessment | 3 | |
| 60 days | 12 weeks total |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choo, S.; Mergen, R.; An, J.; Li, H.; Liu, X.; Odima, M.; Gassaway, L.J. Dynamic Assessment to Assess Mathematical Problem Solving of Students with Disabilities. Educ. Sci. 2025, 15, 419. https://doi.org/10.3390/educsci15040419
Choo S, Mergen R, An J, Li H, Liu X, Odima M, Gassaway LJ. Dynamic Assessment to Assess Mathematical Problem Solving of Students with Disabilities. Education Sciences. 2025; 15(4):419. https://doi.org/10.3390/educsci15040419
Chicago/Turabian StyleChoo, Sam, Reagan Mergen, Jechun An, Haoran Li, Xuejing Liu, Martin Odima, and Linda J. Gassaway. 2025. "Dynamic Assessment to Assess Mathematical Problem Solving of Students with Disabilities" Education Sciences 15, no. 4: 419. https://doi.org/10.3390/educsci15040419
APA StyleChoo, S., Mergen, R., An, J., Li, H., Liu, X., Odima, M., & Gassaway, L. J. (2025). Dynamic Assessment to Assess Mathematical Problem Solving of Students with Disabilities. Education Sciences, 15(4), 419. https://doi.org/10.3390/educsci15040419







