Validation of a Scale on University Teaching Quality in the Area of Mathematics
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodological Design
2.2. Sample
2.3. Data Collection Instrument
- Teaching effectiveness: This is a key aspect for the success of the teaching-learning process, as it focuses on the teacher’s ability to transmit knowledge effectively and adapted to the needs of students. This is achieved through continuous professional development and research-based learning (Santelices Etchegaray & Valenzuela Rojas, 2015; Maulana et al., 2023).
- Instructional planning: It is essential to ensure a quality teaching-learning process, where contents, methods and resources must be coherently organized to achieve educational objectives (Gutiérrez et al., 2020; Hernandez et al., 2024).
- Teaching performance: It involves not only the transmission of knowledge, but also the creation of an environment that fosters student participation. Good teaching performance includes pedagogical skills that help students develop complex competencies and attitudes that prepare them for their professional life (Hortigüela Alcalá et al., 2017).
- Tutorials: they play a key role in academic accompaniment, allowing personalized support to students, which improves learning and strengthens the educational bond (Aguilera García, 2019).
- Bibliography: The adequate use of bibliography and support resources is fundamental to strengthen university teaching. The bibliography acts as a complementary tool that enriches the learning process and allows students to deepen the topics covered in class (Seivane & Brenlla, 2021).
2.4. Data Collection and Analysis Procedure
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Questionnaire
| Date: |
| Student Opinion Survey on Faculty Teaching Performance |
| Professor: |
| Course: |
| Degree Program: |
| Principio del formulario |
| Gender: |
 Male Male |
 Female Female |
| Age: |
| Highest year of enrollment: |
 1st 1st  2nd 2nd  3rd 3rd  4th 4th |
| Lowest year of enrollment: |
 1st 1st  2nd 2nd  3rd 3rd  4th 4th |
| My interest in this subject is: |
 None None  Somewhat Somewhat  Quite a bit Quite a bit  A lot A lot |
| The level of difficulty of this subject is: |
 Low Low  Medium Medium  High High  Very Very  high high |
| I attend classes: |
 Less than 25% of the time Less than 25% of the time  26% to 50% of the time 26% to 50% of the time  51% to 75% of the time 51% to 75% of the time  More than 75% of the time More than 75% of the time |
| I have attended the professor’s office hours: |
 Never Never  Once Once  2 or 3 times 2 or 3 times  More than 3 times More than 3 times |
| Below is a series of questions related to the teaching performance of this professor in this course. Your collaboration is essential and consists of indicating your level of agreement with each statement on a scale, where 1 indicates the lowest level of agreement and 5 indicates the highest. If you lack sufficient information or consider the question not applicable, select the option “NA”. |
| A1. The resources used for teaching are appropriate |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| A2. Motivates students to take an interest in the course |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| A3. Treats students with respect |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| A4. Teaching helps me achieve the course objectives |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| A5. The assessment criteria and methods are appropriate |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| A6. Overall, I am satisfied with the teaching performance of this professor |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| B7. Provides guidance on the course syllabus and objectives |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| B8. Teaching aligns with the planned syllabus |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| B9. Teaching is well-organized |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| B10. Shows concern for students’ understanding of the material |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| C11. Explains clearly |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| C12. Provides examples to apply course content |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| C13. Resolves students’ questions and concerns |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| C14. Encourages a productive and participative learning environment |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| D15. Provides adequate support during office hours |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| D16. Adheres to scheduled office hours |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| E17. Recommended bibliography and other learning materials are useful for following the course |
 1 1  2 2  3 3  4 4  5 5  NA NA |
| E18. Recommended bibliography and other learning materials are accessible to students |
 1 1  2 2  3 3  4 4  5 5  NA NA |
References
- Aguilera García, J. L. (2019). La tutoría universitaria como práctica docente: Fundamentos y métodos para el desarrollo de planes de acción tutorial en la universidad. Pro-Posições, 30, e20170038. [Google Scholar] [CrossRef]
- Alsina, Á. (2023). Formación de profesores de matemáticas para la sostenibilidad: Una agenda de investigación emergente. Avances de Investigación en Educación Matemática, 23, 1–5. [Google Scholar] [CrossRef]
- Aroca Reyes, C., & Llorente Cejudo, C. (2023). Design, construction and validation of a rubric to measure motivation in Early Childhood Education with the use of Augmented Reality. Innoeduca. International Journal of Technology and Educational Innovation, 9(1), 143–156. [Google Scholar] [CrossRef]
- Carretero-Dios, H., & Pérez, C. (2005). Normas para el desarrollo y revisión de estudios instrumentales. International Journal of Clinical and Health Psychology, 5(3), 521–551. Available online: https://www.redalyc.org/pdf/337/33705307.pdf (accessed on 31 December 2024).
- Castilla, F. (2011). Calidad docente en el ámbito universitario: Un estudio comparativo de las universidades andaluzas. Revista de Educación en Contabilidad, Finanzas y Administración de Empresas, 2, 157–172. [Google Scholar] [CrossRef]
- Castro-Morera, M., Navarro-Asencio, E., & Blanco-Blanco, Á. (2020). La calidad de la docencia percibida por el alumnado y el profesorado universitarios: Análisis de la dimensionalidad de un cuestionario de evaluación docente. Educación XX1, 23(2), 41–65. [Google Scholar] [CrossRef]
- De-Juanas Oliva, Á., & Beltrán-Llera, J. A. (2014). Valoraciones de los estudiantes de ciencias de la educación sobre la calidad de la docencia universitaria. Educación XXI, 17(1), 57–82. [Google Scholar] [CrossRef]
- Durán-Aponte, E., & Durán-García, M. (2015). Adaptación y validez de un instrumento para la evaluación de docencia universitaria: Escala de Desempeño Docente Institucional (EDDI). Perspectiva Educacional, Formación de Profesores, 54(1), 75–89. Available online: https://www.redalyc.org/comocitar.oa?id=333333042006 (accessed on 31 December 2024).
- Fernández-Borrero, M. A., & González-Losada, S. (2012). El perfil del buen docente universitario. Una aproximación en función del sexo del alumnado. Revista de Docencia Universitaria, 10(2), 237–249. [Google Scholar] [CrossRef]
- Galván-Salinas, J. O., & Farías-Martínez, G. M. (2018). Características personales y práctica docente de profesores universitarios y su relación con la evaluación del desempeño. Revista Iberoamericana de Evaluación Educativa, 11(2), 9–33. [Google Scholar] [CrossRef]
- Galvis, S. (2015). La interacción docente-estudiante en el aula: Una visión humanizada de la educación. Revista De Investigaciones UCM, 15(26), 70–78. [Google Scholar] [CrossRef]
- García-Valcárcel Muñoz-Repiso, A., Basilotta Gómez-Pablos, V., Cabezas González, M., Casillas Martín, S., González Rodero, L., Hernández Martín, A., & Mena Marcos, J. (2015). La formación del profesorado universitario en tecnologías de la información y la comunicación en la Universidad de Salamanca. RELATEC: Revista Latinoamericana de Tecnología Educativa, 14(1), 75–88. [Google Scholar] [CrossRef]
- Gargallo-López, B., Pérez-Pérez, C., Verde-Peleato, I., & García-Félix, E. (2017). Estilos de aprendizaje en estudiantes universitarios y enseñanza centrada en el aprendizaje. Revista Electrónica de Investigación y Evaluación Educativa, 23(2), 9078. [Google Scholar] [CrossRef][Green Version]
- Gálvez Gamboa, F. A., Arriaga Poblete, C. A., & Adasme Jara, B. A. (2024). Diseño y validación de un cuestionario para evaluar la satisfacción en universitarios. Revista Fuentes, 26(1), 23–35. [Google Scholar] [CrossRef]
- Gisbert, M., & Lázaro, J. (2015). Professional development in teacher digital competence and improving school quality from the teachers’ perspective: A case study. New Approaches in Educational Research, 4(2), 124–131. [Google Scholar] [CrossRef]
- Graus, M. E. G. (2020). Escala estadística y software para evaluar coherencia didáctica en procesos de enseñanza-aprendizaje de Matemáticas. Didasc@lia: Didáctica y Educación, 11(1), 140–165. Available online: https://revistas.ult.edu.cu/index.php/didascalia/article/view/936 (accessed on 31 December 2024).
- Guerrero Luzuriaga, A. d. C., & García Ancira, C. (2024). Evaluación de confiabilidad y validez del cuestionario que mide el nivel de satisfacción: Hacia un modelo predictivo efectivo. Ciencia Latina Revista Científica Multidisciplinar, 8(1), 9991–10009. [Google Scholar] [CrossRef]
- Gutiérrez, A. B., Palacios-Garay, J., Fuster-Guillén, D., & Hernández, R. M. (2020). Evaluación del desempeño docente en el logro de aprendizaje del área de matemáticas. Revista de Psicología, 16(31), 48–57. Available online: https://erevistas.uca.edu.ar/index.php/RPSI/article/view/3071 (accessed on 31 December 2024).
- Hair, J., Black, W., Babin, B., & Anderson, R. (2010). Multivariate data analysis. Prentice-Hall, Cengage Learning EMEA. Available online: https://www.drnishikantjha.com/papersCollection/Multivariate%20Data%20Analysis.pdf (accessed on 31 December 2024).
- Hernandez, O., Villamonte, A., Rodriguez, L., Rodriguez, M., & Rojas, N. (2024). La planificación curricular como herramienta clave para el aprendizaje efectivo. Revista Semilla Científica, 1(6), 489–494. [Google Scholar] [CrossRef]
- Hernández-Sampieri, R., Fernández-Collado, C., & Baptista-Lucio, P. (2014). Metodología de la investigación (6th ed.). McGraw-Hill Education. Available online: https://www.esup.edu.pe/wp-content/uploads/2020/12/2.%20Hernandez,%20Fernandez%20y%20Baptista-Metodolog%C3%ADa%20Investigacion%20Cientifica%206ta%20ed.pdf (accessed on 31 December 2024).
- Hortigüela Alcalá, D., Ausín Villaverde, V., Delgado Benito, V., & Abella García, V. (2017). Análisis de la importancia de los criterios de evaluación y el reconocimiento académico docente universitario como indicadores de la calidad educativa en España. Revista de la Educación Superior, 46(181), 75–87. [Google Scholar] [CrossRef]
- Jacques, V., & Boisier, G. (2019). La calidad en las instituciones de educación superior. Una mirada crítica desde el institucionalismo. Revista Educación, 43(1), 1–24. [Google Scholar] [CrossRef]
- Juárez Ruiz, E. L., Hernández Rebollar, L. A., & Castañeda, A. (Eds.). (2023). Tendencias en la educación matemática 2023. SOMIDEM Editorial. [Google Scholar] [CrossRef]
- Lancheros, L. C., Ramírez, E., & Alvarado, J. (2022). Satisfacción con la calidad docente en el ámbito universitario: Potenciales sesgos de análisis para su evaluación. Revista Iberoamericana de Diagnóstico y Evaluación, 65(14), 69–83. [Google Scholar] [CrossRef]
- Lévy Mangin, J. P., Varela Mallou, J., & Abad González, J. (2006). Modelización con estructuras de covarianzas en ciencias sociales: Temas esenciales, avanzados y aportaciones especiales. Netbiblo. Available online: https://dialnet.unirioja.es/servlet/libro?codigo=402086 (accessed on 31 December 2024).
- Llinares, S. (2018). La formación del docente de matemáticas. Realidades y desafíos. Cuadernos de Investigación y Formación en Educación Matemáticas, 13(17), 55–61. Available online: https://revistas.ucr.ac.cr/index.php/cifem/article/view/34363/33950 (accessed on 31 December 2024).
- Marimon-Martí, M., Romeu, T., Ojando-Pons, E. S., & Esteve-González, V. (2022). Competencia Digital Docente: Autopercepción en estudiantes de educación. PixelBit. Revista de Medios y Educación, 19l(65), 275–303. [Google Scholar] [CrossRef]
- Maulana, R., Kington, A., & Ko, J. (2023). Editorial: Effective teaching: Measurements, antecedents, correlates, characteristics, and links with outcomes. Frontiers in Education, 8, 1170854. [Google Scholar] [CrossRef]
- Montenegro, J. (2020). La calidad en la docencia universitaria. Una aproximación desde la percepción de los estudiantes. Educación XXIX, 56, 116–145. [Google Scholar] [CrossRef]
- O’Dwyer, L., & Bernauer, J. (2014). Quantitative research for the qualitative researcher. SAGE Publications, Inc. [Google Scholar] [CrossRef]
- Onwuegbuzie, A. J., Slate, J. R., Leech, N. L., & Collins, K. M. (2009). Mixed data analysis: Advanced integration techniques. International Journal of Multiple Research Approaches, 3(1), 13–33. [Google Scholar] [CrossRef]
- Palacios-Rodríguez, A., Llorente-Cejudo, C., Lucas, M., & Bem-haja, P. (2025). Macroevaluación de la competencia digital docente. Estudio DigCompEdu en España y Portugal. RIED-Revista Iberoamericana de Educación a Distancia, 28(1), 41379. [Google Scholar] [CrossRef]
- Pardo Fernández, G. (2024). El buen docente universitario. La opinión del estudiantado de la Universidad de la Rioja [Tesis doctoral, Universidad de la Rioja]. Available online: https://investigacion.unirioja.es/documentos/664259571d009a2fb172e275 (accessed on 31 December 2024).
- Rodríguez Duarte, A. G., & Alay Giler, A. D. (2023). Continuous training of Mathematics teachers: An analysis from its relationship with pedagogical practice. Minerva, 2023, 9–18. [Google Scholar] [CrossRef]
- Rodríguez-García, A. M., Raso Sánchez, F., & Ruiz-Palmero, J. (2019). Digital competence, higher education and teacher training: A meta-analysis study on the Web of Science. Pixel-Bit. Revista de Medios y Educación, 3(54), 65–81. Available online: https://recyt.fecyt.es/index.php/pixel/article/view/62197/42099 (accessed on 31 December 2024). [CrossRef]
- Rodríguez-Sabiote, C., Valerio-Peña, A. T., & Batista-Almonte, R. (2023). Validación de una escala del Modelo Ampliado de Aceptación de la Tecnología en el contexto dominicano: [Validation of a scale of the Extended Technology Acceptance Model in the dominican context]. Pixel-Bit. Revista De Medios Y Educación, 68, 217–244. [Google Scholar] [CrossRef]
- Ruiz, M. A., Pardo, A., & San Martín, R. (2010). Modelos de ecuaciones estructurales. Papeles de Psicólogo, 31(1), 34–45. Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=3150815 (accessed on 21 December 2024).
- Santelices Etchegaray, M. V., & Valenzuela Rojas, F. (2015). Importancia de las características del profesor y de la escuela en la calidad docente: Una aproximación desde la Teoría de Respuesta al Ítem. Estudios Pedagógicos (Valdivia), 41(2), 233–254. [Google Scholar] [CrossRef]
- Sánchez-Luján, B. I. (2017). Aprender y enseñar Matemáticas: Desafío de la educación. IE Revista de Investigación Educativa de la REDIECH, 8, 15. [Google Scholar] [CrossRef]
- Seivane, M. S., & Brenlla, M. E. (2021). Evaluación de la calidad docente universitaria desde la perspectiva de los estudiantes. Revista Iberoamericana de Evaluación Educativa, 14(1), 35–46. [Google Scholar] [CrossRef]
- Zabaleta, F. (2007). The use and misuse of student evaluation of teaching. Teaching in Higher Education, 12, 55–76. [Google Scholar] [CrossRef]
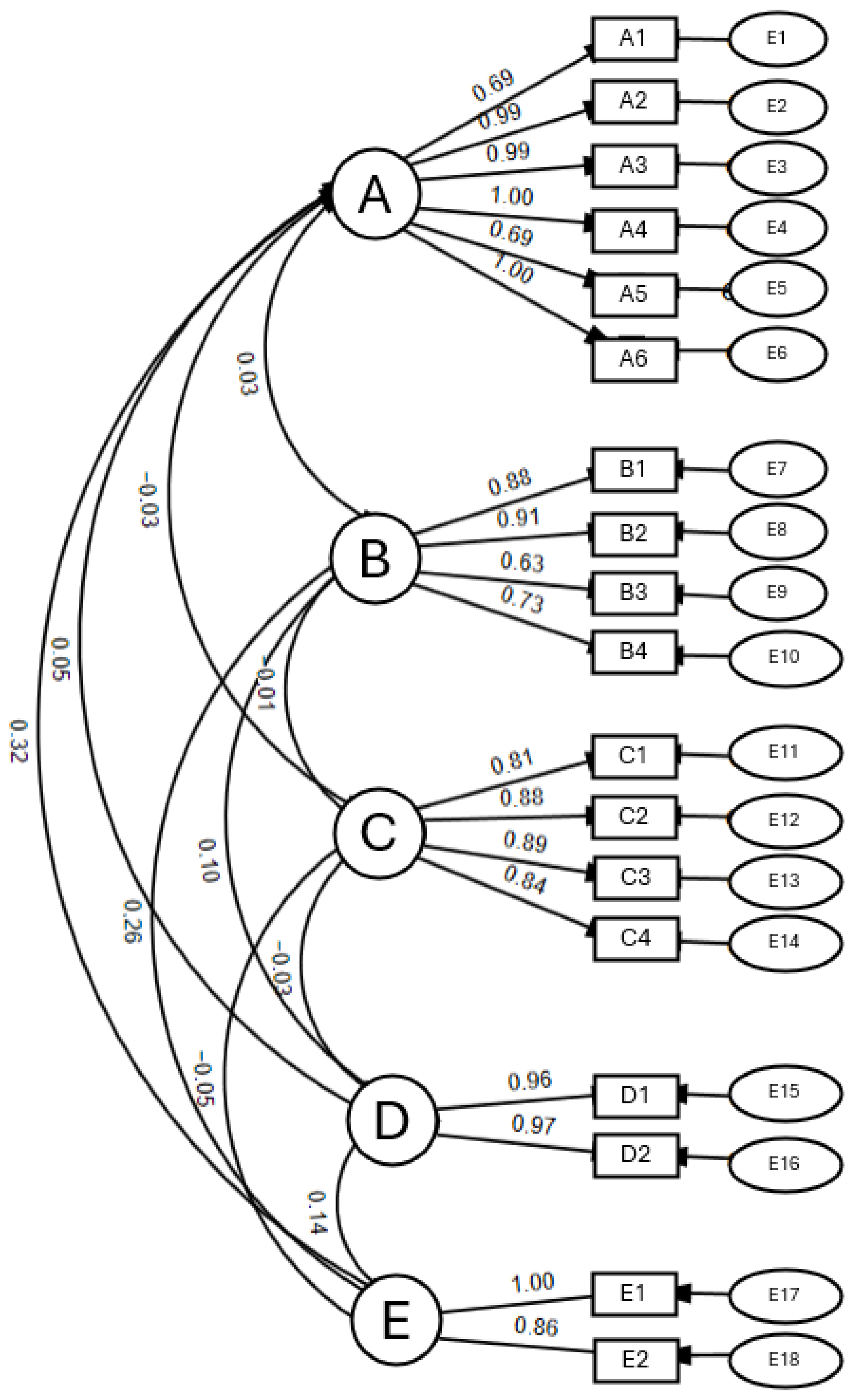
| Dimension | Item | Descriptor |
|---|---|---|
| Teaching effectiveness | A1 | Use of adequate means in teaching. |
| A2 | Motivation of students in the interest of the subject. | |
| A3 | Respectful treatment of students. | |
| A4 | Achievement of the objectives of the subject helped by the teaching given. | |
| A5 | Adequacy of the evaluation criteria and systems carried out by the teacher. | |
| A6 | Satisfaction with the teaching performance in general. | |
| Teaching planning | B7 | Orientations for the teaching project. |
| B8 | Adjustment of the teaching to the planning of the teaching project. | |
| B9 | Well-organized teaching. | |
| B10 | Interest in the degree of understanding of their explanations. | |
| Teaching performance | C11 | Clear explanations. |
| C12 | Use of examples that put into practice the contents of the subject. | |
| C13 | Resolution of doubts raised. | |
| C14 | Encouragement of participation and work environment. | |
| Tutorials | D15 | Adequate attention during tutorial hours. |
| D16 | Fulfillment of the established schedule for tutoring. | |
| Bibliography | E17 | Use of bibliography and other recommended teaching material are useful for the follow-up of the subject. |
| E18 | The bibliography and other recommended teaching material are available to the students. |
| Dimension | CR | Adjustment | AVE | Adjustment | MSV | Adjustment |
|---|---|---|---|---|---|---|
| A | 0.963 | CR > 0.7 | 0.815 | MSV < AVE | 0.631 | MSV < AVE |
| B | 0.901 | 0.698 | 0.395 | |||
| C | 0.940 | 0.797 | 0.593 | |||
| D | 0.977 | 0.955 | 0.910 | |||
| E | 0.920 | 0.852 | 0.705 |
| Item | Dim_A | Dim_B | Dim_C | Dim_D | Dim_E |
|---|---|---|---|---|---|
| A1 | 0.880 | ||||
| A2 | 0.891 | ||||
| A3 | 0.917 | ||||
| A4 | 0.895 | ||||
| A5 | 0.690 | ||||
| A6 | 0.895 | ||||
| B7 | 0.729 | ||||
| B8 | 0.716 | ||||
| B9 | 0.777 | ||||
| B10 | 0.734 | ||||
| C11 | 0.722 | ||||
| C12 | 0.732 | ||||
| C13 | 0.753 | ||||
| C14 | 0.773 | ||||
| D15 | 0.930 | ||||
| D16 | 0.929 | ||||
| E17 | 0.734 | ||||
| E18 | 0.774 |
| Item | Dim_A | Dim_B | Dim_C | Dim_D | Dim_E |
|---|---|---|---|---|---|
| A1 | 0.673 | ||||
| A2 | 0.983 | ||||
| A3 | 0.981 | ||||
| A4 | 0.983 | ||||
| A5 | 0.763 | ||||
| A6 | 0.982 | ||||
| B7 | 0.887 | ||||
| B8 | 0.896 | ||||
| B9 | 0.677 | ||||
| B10 | 0.861 | ||||
| C11 | 0.874 | ||||
| C12 | 0.896 | ||||
| C13 | 0.918 | ||||
| C14 | 0.882 | ||||
| D15 | 0.977 | ||||
| D16 | 0.977 | ||||
| E17 | 0.914 | ||||
| E18 | 0.933 |
| Index | Result | Adjustment |
|---|---|---|
| GFI | 0.999 | GFI > 0.7 |
| PGFI | 0.730 | PGFI > 0.7 |
| NFI | 0.997 | NFI > 0.7 |
| PNFI | 0.815 | PNFI > 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Jaraba, M.d.V.; Llorente-Cejudo, C.; Palacios-Rodríguez, A. Validation of a Scale on University Teaching Quality in the Area of Mathematics. Educ. Sci. 2025, 15, 424. https://doi.org/10.3390/educsci15040424
Jiménez-Jaraba MdV, Llorente-Cejudo C, Palacios-Rodríguez A. Validation of a Scale on University Teaching Quality in the Area of Mathematics. Education Sciences. 2025; 15(4):424. https://doi.org/10.3390/educsci15040424
Chicago/Turabian StyleJiménez-Jaraba, María del Valle, Carmen Llorente-Cejudo, and Antonio Palacios-Rodríguez. 2025. "Validation of a Scale on University Teaching Quality in the Area of Mathematics" Education Sciences 15, no. 4: 424. https://doi.org/10.3390/educsci15040424
APA StyleJiménez-Jaraba, M. d. V., Llorente-Cejudo, C., & Palacios-Rodríguez, A. (2025). Validation of a Scale on University Teaching Quality in the Area of Mathematics. Education Sciences, 15(4), 424. https://doi.org/10.3390/educsci15040424







