Next Article in Journal
Exploring the Relationship Between Critical Thinking and Creativity in University Students: Gender Differences and the Assessment of Skills
Previous Article in Journal
Participative Multilingual Identity Construction in Higher Education: Challenging Monolingual Ideologies and Practices
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 15
Issue 4
10.3390/educsci15040462
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Enhancing Mathematical Education Through Mobile Learning: A Problem-Based Approach

by
Javier Martínez-Gómez
1,2,* and
Juan Francisco Nicolalde
1,2,3
1
Área de Ingeniería Mecánica, Departamento de Teoría de la señal y Comunicación, Escuela Politécnica, Universidad de Alcalá, 28805 Alcalá de Henares, Spain
2
Facultad de Arquitectura e ingenierías, Universidad Internacional SEK, Quito 170302, Ecuador
3
Facultad de Ciencias Técnicas, Universidad Internacional del Ecuador (UIDE), Quito 170411, Ecuador
*
Author to whom correspondence should be addressed.
Educ. Sci. 2025, 15(4), 462; https://doi.org/10.3390/educsci15040462
Submission received: 17 February 2025 / Revised: 24 March 2025 / Accepted: 29 March 2025 / Published: 8 April 2025
(This article belongs to the Special Issue Research Needs in Mathematical Giftedness and Creativity)
Browse Figures
Versions Notes

Abstract

:
The use of mobile phones in teaching processes, in the context of technological convergence, involves considering educational intention, pedagogical tactics, and the capacity of digital media for learning. The utilization of mobile phones in the classroom gives the students instant access to a wide range of educational resources, including educational applications, specialized websites, and multimedia material. Learning to use mobile devices responsibly and productively is essential in today’s digital age, as it prepares them for future technological interactions. The present study examines the intermediary function of a mobile education application, conceived under the problem-based learning approach, in the field of mathematics. This research was carried out with a descriptive approach. A pretest, a post-test, and a survey were created and administered for the collection of numerical data, along with an observation grid for qualitative information. The results highlight the contribution of mobile devices and problem-based learning in the development of skills for collaborative work, decision-making, and problem-solving through systems of linear equations using four techniques. The conclusions highlight the potential of mobile devices in the educational field since they are a resource that provides access to information without time or location limitations. However, it is necessary to focus on the design of pedagogical strategies to carry out a pedagogical and planned use of this resource.

1. Introduction

The rapid advancement of technology has impacted all areas of life. Society has been transformed in response to the demands of digital convergence and technological development. The evolution of information technology has increased public expectations for educational changes. Furthermore, with the rapid advancement of technology, people have come to expect that education will keep pace with these changes and provide students with the skills and knowledge needed to thrive in a digital world. Education is not separate from this reality. The massification of the Internet, easy access to technological devices, and online resources, among other aspects, have transformed training processes. Therefore, it is necessary to analyze the relationship between information and communication technologies (ICTs) and education to determine their contributions, benefits, and challenges. In particular, it is important to identify the changes that technology has brought in the relationship between teachers, students, and knowledge (Peter, 2022; Bustamante-Mora et al., 2023).
Even though technology is prevalent in educational contexts, a problem that has been identified from a pedagogical perspective corresponds to the scarce incorporation of didactic strategies that make use of technological resources in teaching and learning processes. In the case of the area of mathematics, traditional education is predominantly taught via the expository method (Amjad et al., 2023). Students are now expected to have access to computers, tablets, and other digital devices and to use these tools to support their learning across various subjects, including mathematics, science, language arts, and social studies. In a world immersed in information and communication technologies, with a student population that easily accesses digital content, interactive communication is on the rise (Wardoyo et al., 2021). It is necessary to reconfigure educational strategies and practices of interaction among humans, languages, and machines to enhance these conditions and strengthen training processes (Isnawan et al., 2023).
Currently, educational institutions have technological resources such as computers, video projectors, digital whiteboards, tablets, educational applications, and internet access, among others. Additionally, students have smartphones for use in school activities. The massification of the internet and the possibility of wireless connections through mobile devices have enabled access to educational materials and information from anywhere and without time limits (Strzelecki, 2024). This situation has given rise to mobile learning (m-learning), a new educational modality that shows the transformation of training processes thanks to technology.
In this way, the following research presents a native mobile educational application designed for devices with the Android operating system, which can be widely used in classrooms. The EQUALINEALES app includes a conceptual section on linear equations, as well as an explanatory space where various problems related to the student’s context are presented. These resources are thought to help students consolidate concepts and conduct group work to assess their performance in assimilating these concepts. Through short videos, the solution is indicated step by step using the substitution, equalization, reduction, and Gauss Jordan methods. This approach will improve students’ understanding of the most difficult methods to learn. In addition, the app includes an area of challenges and exercises so that students can self-evaluate their progress as they work through the thematic content.

Literature Review

Elkhair and Abdul Mutalib (2019) indicate that m-learning integrates the characteristics of e-learning in terms of platforms, resources, activities, and the roles of the teacher and the student, along with the access and interaction possibilities of mobile devices. On the other hand, Qashou (2021) conceives m-learning as a process in which one learns through interactions with different subjects in various contexts using technological tools. M-learning is a learning modality that offers students a more active role in education, moves away from the scheme of traditional methodologies, and enhances the technological infrastructure of the Internet and mobile devices in favor of autonomous learning. Voshaar et al. (2023) presents the technical functioning of mobile devices and their advantages in information management.
Mobile devices in educational activities are used every day, playing a mediating role in training processes. Sitar-Taut and Mican (2021) showed that m-learning has high predictive power and confirmed 15 out of 16 hypotheses. The most powerful relationship is between performance expectancy and motivation (Al-Adwan et al., 2021). Information quality affected learning value the most, since motivation influenced behavioral use. Zakaria et al. (2023) showed that, overall, there are 30 relevant Master of Problem-Based Learning (MPBL) teaching activities that can be carried out by teachers. The findings also show that teachers sharing the learning objectives that pupils need to achieve using learning applications that are available on mobile devices (98%) ranked first, while the teachers that classify the information obtained from each group according to priority through learning applications available on mobile devices (75%) ranked last. These technological resources can be used to consult educational materials online or installed on the device. In addition, they allow the generation of communication strategies for collaborative work. In this sense, these are considered tools that favor the development of skills oriented to learning in various areas of knowledge (Yaniawati et al., 2023), highlighting the motivating factor that mobile devices generate in students, leading to improved attention to educational content (Poçan et al., 2023).
Apps are computer programs specifically designed to be used on mobile devices (Janiesch et al., 2021). This type of software is characterized by its flexibility in access, some in a centralized way and others distributed, taking advantage of the benefits of connectivity (Van de Ven et al., 2022). Mobile applications are created with a particular purpose, are interactive, and offer added value to users so that they become commonly used tools (Mystakidis et al., 2022). Apps are classified into three types:
  • Native apps are computer programs created to work on a specific operating system so that their stability is ensured for that system, and they are downloaded from the App Store (Play Store for Android or iOS).
  • Web apps are applications that can be accessed online from any mobile device. There is no requirement for a specific operating system. They are characterized by implementing databases and are coded in programming languages, such as CSS, HTML, or JavaScript, which allow the integration of various web developments.
  • Native web apps are a type of hybrid application that combines the advantages of the web development framework and native applications. It is developed in programming languages for web design so that they are multiplatform, and, additionally, they can be downloaded from the Play Store.
Gonzalez-Argote and Castillo-González (2024) point out the recognition of the advantages of problem-based learning (PBL) over conventional learning methods. Among the advantages argued by these authors, PBL stimulates the student’s motivation and interest in learning, since it offers an environment of interaction with reality, giving the possibility for the student to actively get involved, feel part of the learning process, and build their knowledge through observation and practice. It is possible to establish a link between the knowledge that the student has and the new information that they receive during their educational path. This learning experience gives meaning to the new knowledge and generates interest in continuing to investigate and delve deeper into the subjects of study (Dita et al., 2021). The PBL methodology enables a greater degree of assimilation and appropriation of knowledge since it is based on experimentation (Marchy et al., 2022). The student learns through practice, making mistakes, and getting things right. Mistakes are identified in the transition from theory to practice. Likewise, the student defines hypotheses, applies ideas, builds arguments, and reconstructs knowledge based on the results obtained from the experience. It stimulates reflective and creative thinking, promotes the development of skills to identify problems, and proposes innovative solutions appropriate to the need at hand. PBL encourages the integration of knowledge. In this sense, when faced with a problem situation, the subject must apply knowledge from various areas of knowledge to establish and apply the solution. This interdisciplinary approach allows for dynamic and contextualized learning (Smith et al., 2022).
Skills for cooperation and group work are promoted. In this methodology, interaction between students is fundamental, and the presentation and justified support of ideas, peer evaluation, the definition of common objectives, group decision-making, and respect for the ideas of others are encouraged (Islamiati et al., 2024; Ssemugenyi, 2023).
In summary, PBL is a methodological proposal that places the student as the central axis of the educational process, who assumes an active role in the construction of their knowledge, while the teacher guides the learning process. It is an active learning methodology that promotes skills to identify problems; collect, assess, and analyze information about the problems or needs detected; propose contextualized and theoretically argued solutions; put the proposed solutions into practice; and reach conclusions based on the findings in the experimentation (Salam, 2022).
On the other hand, PBL relies on two theoretical arguments: the first goes back to the work of Elliott (2023), with his postulation on learning through experience. For Dewey, contact with the real world allows students to identify problems that activate their thinking and generate a state of curiosity, which leads to the search for information to understand the elements underlying these problems, propose possible solutions and, through experimentation or the development of the planned solution and the analysis of results, foster a learning environment. The second argument corresponds to the sociocultural theory of Vygotsky (1977), who establishes the importance of social learning, where sharing, comparing, and discussing ideas with others enhance thinking skills and the collective construction of knowledge (Krieglstein et al., 2023).

2. Materials and Methods

This research used a mixed approach that involves a process of collecting, analyzing, and interpreting quantitative and qualitative data to respond to the problem statement (Hernández-Sampieri & Mendoza, 2023). In the study, quantitative information was collected through a survey, a pretest, and a post-test, and qualitative information was collected through an observation grid, allowing for the establishment of the progress of the students in the work sessions with the educational strategy mediated by the PBL and a mobile educational application.
The concurrent triangulation design (DITRIAC), proposed by Hernández-Sampieri and Mendoza (2023), was applied to determine the relationship between the independent variable that corresponds to PBL mediated by a mobile application and the dependent variables that refers to problem-solving skills in the area of mathematics and contributions to the learning process.
The research was developed with the first-year mathematics students at the university. Students who regularly attended the class and were enrolled in the study were considered. Missing data, outliers, etc., are thus mitigated by the absence of students who do not follow the course. For the collection of information, two knowledge tests (pretest and post-test) were designed and validated to identify the degree of ability to solve algebraic problems based on systems of linear equations with four resolution methods (equalization, substitution, reduction, and Gauss Jordan), the recognition of the theoretical components related to linear equations, and the ability to relate the conceptual elements with the problems of the context. Also, an observation grid was developed and validated, which was completed in each of the class sessions.
In the research, the PBL of eight phases or steps was selected and applied (Kilroy, 2004; Wells et al., 2009; Prince et al., 2005; Choon-Eng Gwee, 2008). This method was chosen because it includes elements of the didactic structure for teaching mathematics, and an adaptation was made to make use of the mobile educational application. Below is the description of each phase of the PBL defined for the research:
Step 1—Explore the problem, create hypotheses, and identify aspects related to the problem. In this phase, a problematic situation was raised that included elements of the student’s context and required the application of linear equations. Each student searched for information about the problem, analyzed the elements of the situation presented, and proposed an idea to tentatively explain that problem.
Step 2—Try to solve the problem with what is already known. It is based on the student’s prior knowledge, so they tried to identify the steps to solve the problem according to the indicated method of the system of linear equations. This takes into account that the students have some skills in problem-solving.
Step 3—Identify what is not known and what is needed to know how to solve the problem. Groups of four students were formed. Each group made a list of everything they considered should be known to solve the problem in relation to the topic of linear equation systems. In the same way, they indicated the procedure to consider in each method to solve the proposed exercises.
Step 4—Prioritize learning needs. The students made a list of actions to perform, defined new learning objectives and the information resources necessary to carry out the activities, and distributed the tasks among the participants.
Step 5—Self-study and preparation. The information recorded in the notes was consulted during the explanation of the topic by the teacher. The interaction was carried out with the mobile application to consult the specific method and the way to carry out the procedure. Each team located, organized, and interpreted the information consulted.
Step 6—Share information with everyone. Each member of the group shared the most relevant information found in the mobile application, where the procedure for each method was presented in a clear way.
Step 7—Apply knowledge to solve the problem. Each group applied the new knowledge acquired, interacting with the mobile application, through the Challenge X activity, which presented several problems for each of the methods of the system of linear equations.
Step 8—Evaluate the new knowledge acquired. The solution given and the effectiveness of the entire process: each member of the group had the opportunity to carry out a self-assessment process, available within each method in the mobile application. In this way, it was possible to identify the degree of effectiveness in solving the problems posed and the progress in the learning process.
Among the information analysis techniques, it is worth mentioning that the Student t-test was used to establish significant differences between the means of two groups, and a descriptive analysis of frequencies was carried out to establish trends in the qualitative data collected through the observation grid. This study was carried out in five stages: theoretical foundation, the design of the didactic sequence and the mobile application, the construction of the App, the implementation of the educational strategy with the didactic sequence, and the analysis of the results. Each stage is described below. For the theoretical foundation, we reviewed and analyzed the research background and theoretical elements on PBL, m-learning, and mobile educational applications.

App Development

The app development takes place with the construction of the graphic and multimedia elements, the programming and assembly of the application, and pilot tests. In this stage, the app was validated from three aspects: usability, relevance of the content, and pedagogical component. An expert in software design and development evaluated usability through the attributes and metrics proposed by Enríquez and Casas (2013). Two mathematics teachers with more than ten years of experience in the area evaluated the thematic content and the didactic strategy implemented in the app. Additionally, two pilot tests were carried out with a group of first-grade students from another campus of the institution. This was carried out to identify and correct errors in the app and ensure its quality before implementing it with a sample of students. The following were also carried out: implementation to the design and validation of the instruments for collecting information, as well as the application of the pretest, intervention, and thematic development through the didactic sequence in four sessions. During each session, the observation grid was filled out, and the post-test was applied.
Furthermore, the analysis of the results was performed by the systematization of the information collected, application of data analysis techniques, and elaboration of the results and conclusions.
The PBL structure was developed in each class session through a teaching sequence, which was built by incorporating basic information to address the following topics: objectives, competencies, performances, the role of the student, and the role of the teacher. Likewise, the moments of the class, the stages of PBL, resources, activities, and time to develop them were indicated. An example of the teaching sequence is presented in Table 1.
For the construction of the app, the MIT App Inventor application was selected. It is a Google Labs platform that allows the creation of applications for mobile devices (tablets or smartphones) with the Android operating system. Block programming is used, and the reference code is in Java.
Within the app, the thematic content related to the system of linear equations is presented. Initially, there is a Generalities section, explaining the concept of linear and algebraic equations, and their respective graph in the Cartesian plane. In addition, there is the possibility of watching a video that explains the procedure when posing a linear or algebraic equations. Within Generalities, there is the Equation relation option, where the student can solve a series of questions related to the concepts seen in the App, and it is required to answer the questions correctly to advance to the next question.
In another section, there is the method option of four methods for solving linear equation systems of two equations with two unknowns and three equations with three unknowns explained with the procedure to solve each one of them. Supported by a video, each method is explained to the students through the resolution of a problem.
Within each method, there is the Challenge X option. In this space, the student has the possibility of solving a series of problems related to the corresponding method, applying problem-based learning.
The internal consistency of the EVS was assessed as a measure of scale reliability. Cronbach’s coefficient α is one of the most widely adopted measures of the lower bound of the reliability (Hair et al., 1995; Pombo & Marques, 2020). An α value that exceeds 0.7 can be considered acceptable (Hair et al., 1995). However, other authors consider the value 0.6 as the lower bound of reliability acceptance, particularly in the early stage of research (Van Griethuijsen et al., 2015). For both the pretest and post-test data, Cronbach’s alpha was shown to be within acceptable values.
In the Evaluation option, there are exercises of the different methods explained in the mobile application. In this section of the app, the student is forced to solve the exercises correctly to advance. At the end of the evaluation, the student is asked to enter their name to obtain the grade and feedback on the evaluation process. By completing the assessment, the student can determine how much they have learned about the topic of linear equations and the different methods used to solve a system of linear equations with two unknowns, and three unknowns, explained in the mobile application.

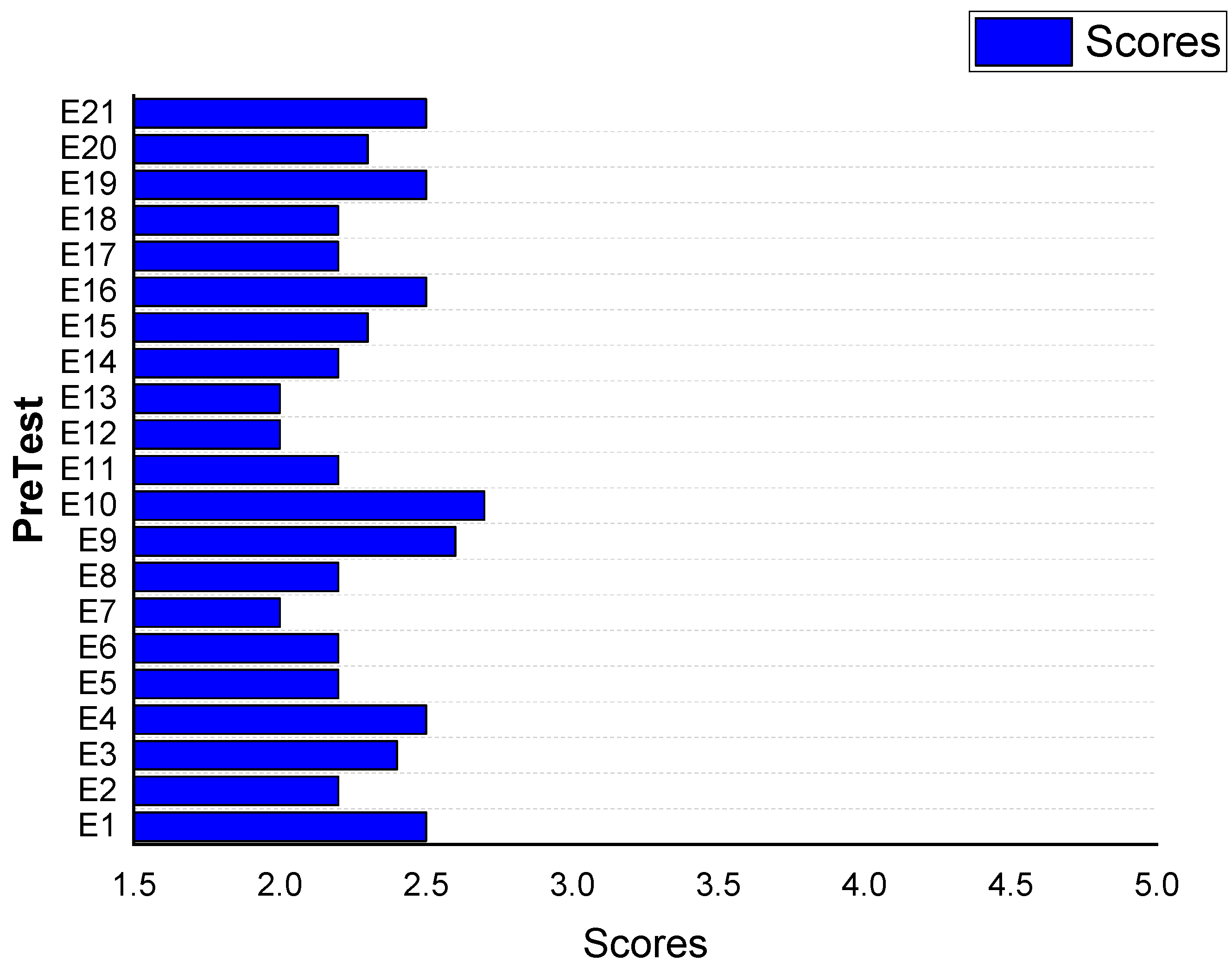
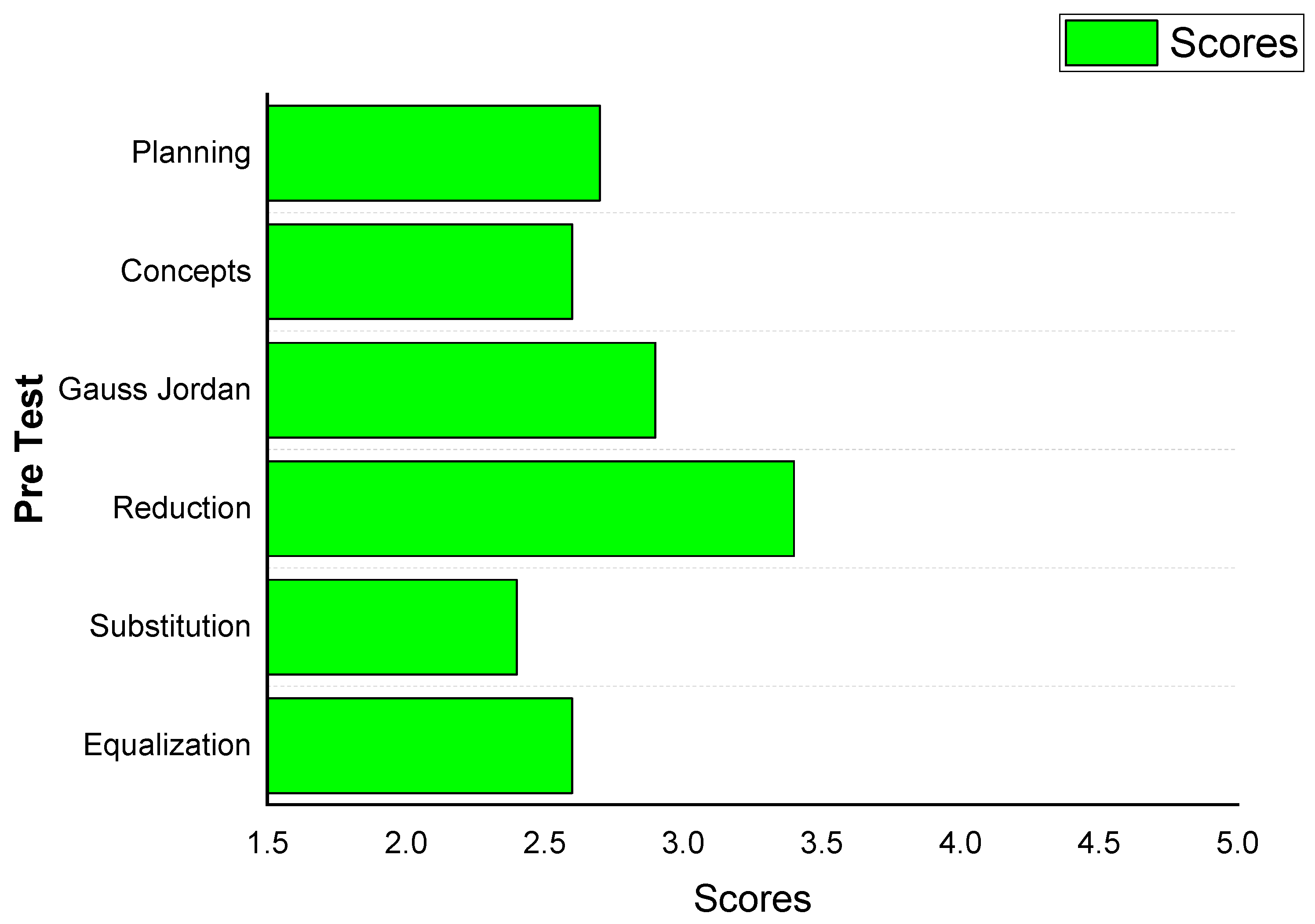
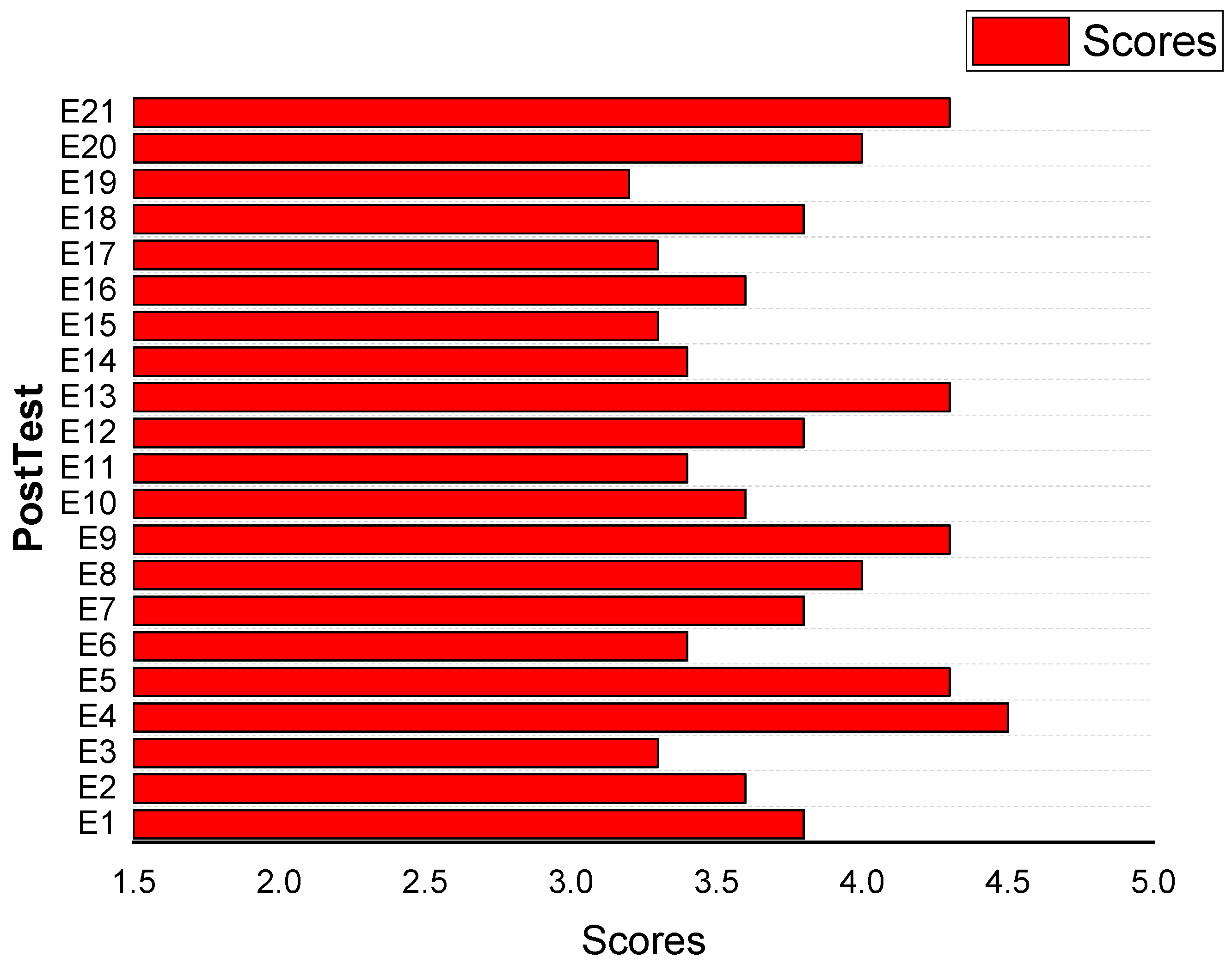
3. Results

To determine the contributions of the designed educational strategy, a pretest was initially applied to the target population, and then four class sessions were developed based on the didactic sequence described before. After implementation, the post-test was applied. During each session, an observation grid was filled out with the purpose of evaluating aspects of usability, content, and pedagogical and methodological aspects. Likewise, the grid established how the students interacted with the application and the development of skills in solving problems with linear equations.
Figure 1 shows that 100% of the students obtained low grades in the pretest, so they failed the subject related to linear equations. Using pretest scores as a baseline for a rating scale of the evaluation system of the institution under study, in which, a rating scale of 1 to 5 is stipulated, and it is established that a grade lower than 3.2 is considered a failure. In total, 100% of the students were in the range of 2.0 to 2.7, that is, at a low level. This result is consistent with the diagnosis made at the beginning of the research. The low results are related to the difficulties that students have in associating the problems of the context with mathematics topics, i.e., the low interest in this area and the teaching methodology that was being implemented.
Figure 2 shows that, in 79% of the methods, except for the reduction method with 21%, the grades were below 3.2, which means that there was a failure in the mastery of conceptual elements and skills to pose and solve problems on linear equations with the equalization, substitution, and Gauss Jordan methods.
It was evident that the students passed the exercises planned with the reduction method, since, through observation, it is easier for them to identify the two unknowns that can be eliminated, either by performing multiplication, addition, or subtraction between the two equations to cancel one of the variables, and then replacing the value obtained in one of the two equations. The other methods, different from the reduction method, required a more complex procedure, and it was possible to identify that the students were not clear about the logical sequence that must be applied to these methods. They mismatched the procedures. Additionally, they had difficulty identifying some key concepts in the topic of linear equations and interpreting the statement of a problem even when it was related to elements of their environment.
After having implemented the teaching sequence with the mobile educational application, 100% of the students obtained high grades in the post-test. They passed the topic on linear equations. The majority is in the range of 3.2 to 4.5, which corresponds to a high level. The results in the grouping by methods indicated that 100% of the students passed the four methods, with grades between 3.9 and 4.3, indicating a high level. In the post-test, it was established that the students improved their skills for problem-solving by applying the four methods studied. It should be noted that, during the sessions with the teaching sequence, the students developed each of the steps of the PBL, following the instructions of the teacher. They learned to work collaboratively, contributing ideas to solve the problems proposed. They interacted with the app constantly. When they had doubts, they turned to the explanatory videos within the app. Additionally, the development of the challenges and activities proposed in the mobile application became a motivating factor.
Figure 3 displays the results of the post-test, allowing us to determine that 100% of the students obtained better grades after having implemented the teaching sequence with the mobile educational application.
Figure 4 shows the results obtained from the post-test in different methods. It was determined that 21% of the students obtained a score higher than 3.2 in the pretest, while in the post-test, 100% of the students obtained scores higher than 3.9. The range of scores in the pretest was from 2.2 to 3.4, while the range of scores in the post-test was from 3.9 to 4.3. The students demonstrated greater mastery of the conceptual elements and established that two factors influenced this. On the one hand, they had the possibility of consulting the information in the app on repeated occasions, and, in order to make contributions in the group, they were forced to be clear about the topics and prepare the ideas proposed in the work teams with arguments.
The discussions in the groups favored the identification and relationship of the problems raised with elements known in the student’s environment. In this case, topics on crops in the region were addressed. Regarding the methods of the linear equation system, it was identified that the videos with the step-by-step explanation were the key tool for the students to assimilate the procedure and be able to apply it in solving the problems.
Furthermore, to establish whether there is a significant difference, the Student t-test was applied. An analysis of the results of the grades obtained in the pretest versus the post-test was carried out, calculating the mean and variance of the population sample, obtaining a significant difference in terms of the weight of the mean in the pretest of 2.3048 and in the post-test of 3.7619. When working with two tails, a significance level equal to 0.0000000000021 was obtained. To obtain the Gauss bell curve, the value of the mean of the student’s grades was calculated as well as the standard deviation. The Gaussian bell graph allowed us to identify that the maximum value is obtained in the fourth data point when one of the students obtained a grade equal to 4.5 in the post-test.
Based on the results of the statistical analysis carried out in the pretest and the posttest, it is confirmed that the teaching sequence based on PBL with the mobile educational application effectively contributed to the student’s learning in terms of linear equations.
Regarding the qualitative data, the analysis carried out on the observation grids allowed us to show that when working in a group, each member contributed to addressing the problem, and decision-making in a concerted and global manner was favored in the workgroups, ensuring satisfactory results in the development of the proposed problems. It was possible to identify that, through dialog and discussion among students, they learned how to think together, and this allowed a better understanding of the problem and how to solve it. In each group, it was observed that there was a leader who played the role of facilitator and energized communication to keep the group united and for everyone to contribute to the problem-solving process.
By coming into direct contact with the mobile application, the students maintained their interest in exploring the content. They focused on searching for information to understand the topic related to the system of linear equations, especially the methods to solve the problems proposed. On the other hand, it was observed that the educational application strengthened the sense of responsibility and autonomy on the part of the students by discovering a different way of obtaining knowledge and awareness of their role in the identification of their needs during the educational process and choosing a strategy that allows them to advance in their training process.
It was observed that the students developed teamwork skills, classmates listened to each other, and the opinions and points of view of everyone were considered to build knowledge collaboratively. The teaching strategy helped students review and reflect on their prior knowledge and organize the information contained in the mobile application in such a way that it allowed them to restructure that knowledge, expand it, and apply it to problem-solving.
The role of the teacher was key as a guide and facilitator of the process. Initially, advising students on the implementation of the teaching sequence and the use of the mobile application as a technological tool for mediation in the educational process. The teacher was a motivator on the possibilities and benefits of trying an innovative strategy, which led to awakening in students the desire to learn for themselves, through discovery and exploration with the mobile application.
The students considered the explanation video of each of the methods to be a good learning strategy since it clarified the procedure to be applied in each case. It offered the possibility of watching it again if it was not clear to them or they had omitted a step. Another aspect to take into account is that the students considered the evaluation carried out upon reaching the end of the content in each method. The final evaluation of the application allowed them to determine how much they had learned about the subject. In this way, reflection, self-evaluation, and logical argumentation about the learning process were encouraged.

4. Discussion

  • Finding interpretation: This study showed that the training of students through the expository method makes it difficult to adapt to the implementation of other learning strategies, such as the problem-solving methodology. The expository method is the predominant strategy in traditional teaching, where the teacher is the center of the educational process, and the student assumes a passive role (Karan & Brown, 2022), while PBL is a methodology that encourages the construction of knowledge by the student (Zakaria et al., 2025). This methodological clash is felt at the beginning of the implementation of the didactic sequence with PBL and the mobile application (Herdianto & Indriati, 2021; Srikan et al., 2021). A reasonable amount of time is required for the application of the new strategy so that the adaptation achieves the expected effects (Susilawati & Supriyatno, 2023; Nasori et al., 2022; Setyani & Susilowati, 2022). The results of the research coincide with the statements of Jahnke and Liebscher (2020). It is confirmed that the use of mobile applications for educational purposes promotes the motivation to learn and favors the development of skills for communication, teamwork, and creativity in students, especially when it involves the analysis and solution of problems related to the context. Additionally, the explanatory videos, included in a didactic way within the app, contributed to the assimilation of the procedures to apply each method of the system of linear equations. In relation to the didactic videos, Ortega González et al. (2019) indicate that they are a powerful tool to mediate learning due to their functions of informing, motivating, playing, expressing, and evaluating.
  • Theoretical implications: The research allows us to show that the pedagogical use of videos within the framework of a didactic has satisfying results. However, videos also fulfill a guiding function since they guide the interpretation of procedural structures. PBL mediated with a mobile educational application allows the development of some interpersonal skills, in the same sense as stated by Chung et al. (2019). The educational strategy contributed to the strengthening of collaborative work. Other interpersonal skills evidenced in the research include the ability to argue ideas in front of a workgroup, respect for the opinions and contributions of colleagues, and decision-making based on discussion and analysis within the team.
  • Practical implications: In this research, it is possible to confirm that mobile devices contribute to the methodological change required to respond to the current educational needs of the subjects. According to what was expressed by Prahani et al. (2022), the use of mobile educational applications facilitates the student’s autonomous learning, an essential skill for training processes in the 21st century. In this sense, with mobile devices, it is possible to access information without time or place limits (Chan et al., 2023). Therefore, students can access the content, activities, and assessment in real time, learning at their own pace and according to their needs and interests. Additionally, implementing mobile learning allows for choosing multiple work strategies, establishing the degree of depth of the thematic content, and various forms of assessment (Sophonhiranrak, 2021).
  • Limitations and future research: The research allows us to affirm that PBL mediated with an app favors the assessment processes. The teacher can assess the contributions of group work, interpersonal relationships with team members, leadership, motivation, assertive communication, and the quality of contributions, leading to a more comprehensive assessment tailored to student achievements. In this regard, a larger sample in other regions and universities would be useful to corroborate the study.

5. Conclusions

PBL is a methodology that contributes significantly to the teaching and learning process of mathematics in which students feel more involved and actively contribute to the construction of knowledge, privileging collaborative work.
Considering that teamwork is essential in the implementation of the PBL methodology. It is worth noting that students must have minimum communication skills that allow them to express their ideas, comments, contributions, and doubts, among others, giving rise to a dynamic of cooperation and collaboration in the construction of learning.
At the end of the research implementation of the mobile educational application, it was implemented, and it was possible to observe a greater interest on the part of students in solving exercises in the mathematics subject about the topic of the system of linear equations of two equations with two unknowns and three equations with three unknowns. The portability of the application on the cell phone allows students to access information easily and efficiently and carry out activities aimed at strengthening their knowledge, anywhere and at any time.
PBL allowed students to develop the ability to investigate different sources of information and, from there, organize the content, plan the best solution to the problems posed, and be able to work as a group, favoring collaborative work, sharing and corroborating sources of information, and discussing the different aspects of their analysis to solve a given problem. The strategy incorporating PBL allowed students to develop critical thinking and decision-making. PBL is a methodology based on problem-posing to guide students towards identifying the knowledge required to understand and provide an effective solution to the problem. In this way, the student investigates and builds knowledge during the process of solving the situation posed, allowing them to achieve the educational objectives.
The mobile educational application as a technological component, immersed in the didactic sequence, was fundamental to achieving the objectives since the students had the information at hand and could consult it at any time. The application was key to maintaining the students’ interests and strengthened the learning of the four methods (Gauss Jordan, substitution, reduction, and equalization) for the algebraic resolution of systems of equations by posing everyday problems.
The incorporation of technological tools in the classroom, in this case, mobile devices, is considered a necessity and, at the same time, a challenge for the teacher. Also, it is a technological element available and within the reach of students, and various studies have demonstrated its advantages in education. However, it is a challenge to the extent that it can become a distracting mechanism within the classroom. Therefore, it is necessary to prioritize the analysis of methodological strategies and appropriate applications that keep students connected to educational objectives and promote meaningful learning with these devices.

Author Contributions

Methodology, J.M.-G.; software, J.M.-G.; validation, J.M.-G. and J.F.N.; formal analysis, J.M.-G. and J.F.N.; investigation, J.M.-G.; resources, J.M.-G.; data curation, J.M.-G.; writing—original draft preparation, J.M.-G.; writing—review and editing, J.M.-G. and J.F.N.; visualization, J.M.-G. and J.F.N.; supervision, J.M.-G.; project administration, J.M.-G.; funding acquisition, J.M.-G. All authors have read and agreed to the published version of the manuscript.

Funding

This study is a component of the Parque de Energías Renovables project P121819, supported by Universidad Internacional SEK. The APC was funded by Universidad Internacional SEK.

Institutional Review Board Statement

Ethical review and approval were waived for this study due to the following points regarding the nature of the study: 1. Non-invasive educational research: The study solely focused on educational practices and student academic outcomes without any physical or psychological interventions. 2. Informed consent: All participants were informed of the study’s objectives, methods, and their voluntary participation, with consent obtained prior to data collection. 3. Anonymity and confidentiality: All data collected were anonymized, and no personal or sensitive information was recorded or reported. 4. Standard educational practices: The research methods aligned with standard educational practices and did not introduce any undue risks or burdens on participants. Given the above considerations, the study qualifies for exemption from full IRB review, as it pertains strictly to educational strategies and tools without human subject risks.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Al-Adwan, A. S., Albelbisi, N. A., Hujran, O., Al-Rahmi, W. M., & Alkhalifah, A. (2021). Developing a holistic success model for sustainable e-learning: A structural equation modeling approach. Sustainability, 13(16), 9453. [Google Scholar] [CrossRef]
  2. Amjad, A. I., Habib, M., Tabbasam, U., Alvi, G. F., Taseer, N. A., & Noreen, I. (2023). The impact of brain-based learning on students’ intrinsic motivation to learn and perform in mathematics: A neuroscientific study in school psychology. International Electronic Journal of Elementary Education, 16(1), 111–122. [Google Scholar] [CrossRef]
  3. Bustamante-Mora, A., Diéguez-Rebolledo, M., Hormazábal, Y., Valdés, Y., & Cadena, R. (2023). Learning models for higher education in engineering: Motivation, self-determination, and the role of information and communication technologies. Sustainability, 15, 12869. [Google Scholar] [CrossRef]
  4. Chan, C. L., Shroff, R. H., Tsang, W. K., Ting, F. S., & Garcia, R. C. (2023). Assessing the effects of a collaborative problem-based learning and peer assessment method on junior secondary students’ learning approaches in mathematics using interactive online whiteboards during the COVID-19 pandemic. International Journal of Mobile Learning and Organisation, 17(1–2), 6–31. [Google Scholar]
  5. Choon-Eng Gwee, M. (2008). Globalization of problem-based learning (PBL): Cross-cultural implications. The Kaohsiung Journal of Medical Sciences, 24, S14–S22. [Google Scholar]
  6. Chung, C. J., Hwang, G. J., & Lai, C. L. (2019). A review of experimental mobile learning research in 2010–2016 based on the activity theory framework. Computers & Education, 129, 1–13. [Google Scholar]
  7. Dita, P. P. S., Utomo, S., & Sekar, D. A. (2021). Implementation of problem-based learning (PBL) on interactive learning media. Journal of Technology and Humanities, 2(2), 24–30. [Google Scholar]
  8. Elkhair, Z., & Abdul Mutalib, A. (2019). Mobile learning applications: Characteristics, perspectives, and future trends. International Journal of Interactive Digital Media, 5(1), 18–21. [Google Scholar]
  9. Elliott, J. (2023). The relationship between ‘understanding’ and ‘developing’ teachers’ thinking. In Routledge Library Editions: Education Mini-Set N Teachers & Teacher Education Research 13 (pp. 189–221). Routledge. [Google Scholar]
  10. Enríquez, J. G., & Casas, S. I. (2013). Usabilidad en aplicaciones móviles. Informes Científicos Técnicos-UNPA, 5(2), 25–47. [Google Scholar] [CrossRef]
  11. Gonzalez-Argote, J., & Castillo-González, W. (2024). Problem-based learning (PBL), review of the topic in the context of health education. Seminars in Medical Writing and Education, 3, 57–57. [Google Scholar] [CrossRef]
  12. González, I. M. O., Álvarez, G. A. R., & Suárez, C. A. H. (2019). Uso del video como estrategia pedagógica para el desarrollo de la competencia escritora en estudiantes de educación básica. Revista Perspectivas, 4(2), 52–63. [Google Scholar]
  13. Hair, J. F., Jr., Anderson, R. E., Tatham, R. L., & Black, W. C. (1995). Multivariate data analysis with readings. Prentice-Hall. [Google Scholar]
  14. Herdianto, E. N., & Indriati, D. (2021). E-book based on mobile learning used problem-based learning (PBL) model to improve problem-solving ability in statistical material. Journal of Physics: Conference Series, 1808(1), 012066. [Google Scholar]
  15. Hernández-Sampieri, R., & Mendoza, C. (2023). Metodología de la investigación: Las rutas cuantitativa, cualitativa y mixta. McGraw-Hill. [Google Scholar]
  16. Islamiati, A., Fitria, Y., Sukma, E., Fitria, E., & Oktari, S. T. (2024). The influence of the problem-based learning (PBL) model and learning style on the thinking abilities. Jurnal Penelitian Pendidikan IPA, 10(4), 1934–1940. [Google Scholar]
  17. Isnawan, M. G., Sudirman, S., Sukarma, I. K., Wahyuni, F., & Alsulami, N. M. (2023). Optimizing students’ mathematical problem-solving abilities through geoboard-assisted didactic design on triangular number pattern material. Journal of Didactic Mathematics, 4(3), 200–213. [Google Scholar] [CrossRef]
  18. Jahnke, I., & Liebscher, J. (2020). Three types of integrated course designs for using mobile technologies to support creativity in higher education. Computers & Education, 146, 103782. [Google Scholar]
  19. Janiesch, C., Zschech, P., & Heinrich, K. (2021). Machine learning and deep learning. Electronic Markets, 31(3), 685–695. [Google Scholar]
  20. Karan, E., & Brown, L. (2022). Enhancing student’s problem-solving skills through project-based learning. Journal of Problem Based Learning in Higher Education, 10(1), 74–87. [Google Scholar]
  21. Kilroy, D. A. (2004). Problem based learning. Emergency Medicine Journal, 21(4), 411–413. [Google Scholar]
  22. Krieglstein, F., Schneider, S., Gröninger, J., Beege, M., Nebel, S., Wesenberg, L., Suren, M., & Rey, G. D. (2023). Exploring the effects of content-related segmentations and metacognitive prompts on learning with whiteboard animations. Computers & Education, 194, 104702. [Google Scholar]
  23. Marchy, F., Murni, A., & Muhammad, I. (2022). The effectiveness of using problem-based learning (PBL) in mathematics problem-solving ability for junior high school students. AlphaMath: Journal of Mathematics Education, 8(2), 185–198. [Google Scholar]
  24. Mystakidis, S., Christopoulos, A., & Pellas, N. (2022). A systematic mapping review of augmented reality applications to support STEM learning in higher education. Education and Information Technologies, 27(2), 1883–1927. [Google Scholar] [CrossRef]
  25. Nasori, A., Putra, I., Sari, N., & Dwijayanti, N. S. (2022). Challenges digital literacy in era of Society 5.0: Effectiveness problem-based learning with mobile learning to accelerate digital literacy. Journal on Teacher Education, 4(2), 97–106. [Google Scholar]
  26. Peter, L. (2022). Information and communication technologies and education. In I. Panagoret, & G. Gorghiu (Eds.), International conference globalization, innovation and development: Trends and prospects (G.I.D.T.P.) (pp. 344–353). Editura Lumen. [Google Scholar]
  27. Poçan, S., Altay, B., & Yaşaroğlu, C. (2023). The effects of mobile technology on learning performance and motivation in mathematics education. Education and Information Technologies, 28(1), 683–712. [Google Scholar] [CrossRef] [PubMed]
  28. Pombo, L., & Marques, M. M. (2020). The potential educational value of mobile augmented reality games: The case of EduPARK app. Education Sciences, 10, 287. [Google Scholar] [CrossRef]
  29. Prahani, B., Jatmiko, B., Hariadi, B., Sunarto, D., Sagirani, T., Amelia, T., & Lemantara, J. (2022). Blended web mobile learning (BWML) model to improve students’ higher-order thinking skills. International Journal of Emerging Technologies in Learning (iJET), 15(11), 42–55. [Google Scholar] [CrossRef]
  30. Prince, K. J., Van Eijs, P. W., Boshuizen, H. P., Van Der Vleuten, C. P., & Scherpbier, A. J. (2005). General competencies of problem-based learning (PBL) and non-PBL graduates. Medical Education, 39(4), 394–401. [Google Scholar] [CrossRef]
  31. Qashou, A. (2021). Influencing factors in M-learning adoption in higher education. Education and Information Technologies, 26(2), 1755–1785. [Google Scholar] [CrossRef]
  32. Salam, S. (2022). A systemic review of problem-based learning (PBL) and computational thinking (CT) in teaching and learning. International Journal of Humanities and Innovation (IJHI), 5(2), 46–52. [Google Scholar] [CrossRef]
  33. Setyani, N. S., & Susilowati, L. (2022). The effect of e-problem-based learning on students’ interest, motivation, and achievement. International Journal of Instruction, 15(3), 503–518. [Google Scholar]
  34. Sitar-Taut, D. A., & Mican, D. (2021). Mobile learning acceptance and use in higher education during social distancing circumstances: An expansion and customization of UTAUT2. Online Information Review, 45(5), 1000–1019. [Google Scholar] [CrossRef]
  35. Smith, K., Maynard, N., Berry, A., Stephenson, T., Spiteri, T., Corrigan, D., Mansfield, J., Ellerton, P., & Smith, T. (2022). Principles of problem-based learning (PBL) in STEM education: Using expert wisdom and research to frame educational practice. Education Sciences, 12(10), 728. [Google Scholar]
  36. Sophonhiranrak, S. (2021). Features, barriers, and influencing factors of mobile learning in higher education: A systematic review. Heliyon, 7(4), e06696. [Google Scholar] [PubMed]
  37. Srikan, P., Pimdee, P., Leekitchwatana, P., & Narabin, A. (2021). A problem-based learning (PBL) and teaching model using a cloud-based constructivist learning environment to enhance Thai undergraduate creative thinking and digital media skills. International Journal of Interactive Mobile Technologies, 15(22), 68. [Google Scholar]
  38. Ssemugenyi, F. (2023). Teaching and learning methods compared: A pedagogical evaluation of problem-based learning (PBL) and lecture methods in developing learners’ cognitive abilities. Cogent Education, 10(1), 2187943. [Google Scholar]
  39. Strzelecki, A. (2024). To use or not to use ChatGPT in higher education? A study of students’ acceptance and use of technology. Interactive Learning Environments, 32(9), 5142–5155. [Google Scholar]
  40. Susilawati, S., & Supriyatno, T. (2023). Problem-based learning model in improving critical thinking ability of elementary school students. Advances in Mobile Learning Educational Research, 3(1), 638–647. [Google Scholar]
  41. Van de Ven, G. M., Tuytelaars, T., & Tolias, A. S. (2022). Three types of incremental learning. Nature Machine Intelligence, 4(12), 1185–1197. [Google Scholar] [CrossRef]
  42. Van Griethuijsen, R. A., van Eijck, M. W., Haste, H., Den Brok, P. J., Skinner, N. C., Mansour, N., Gencer, A. S., & BouJaoude, S. (2015). Global patterns in students’ views of science and interest in science. Research in Science Education, 45, 581–603. [Google Scholar]
  43. Voshaar, J., Knipp, M., Loy, T., Zimmermann, J., & Johannsen, F. (2023). The impact of using a mobile app on learning success in accounting education. Accounting Education, 32(2), 222–247. [Google Scholar]
  44. Vygotsky, L. S. (1977). The development of higher psychological functions. Soviet Psychology, 15(3), 60–73. [Google Scholar]
  45. Wardoyo, C., Satrio, Y. D., Narmaditya, B. S., & Wibowo, A. (2021). Gamification in economics and its impact on students’ achievement: Lesson from COVID-19 in Indonesia. Cypriot Journal of Educational Sciences, 16(3), 1194–1203. [Google Scholar]
  46. Wells, S., Warelow, P., & Jackson, K. (2009). Problem based learning (PBL): A conundrum. Contemporary Nurse, 33(2), 191–201. [Google Scholar]
  47. Yaniawati, P., Fisher, D., Permadi, Y. D., & Yatim, S. A. M. (2023). Development of mobile-based digital learning materials in blended learning oriented to students’ mathematical literacy. International Journal of Information and Education Technology, 13(9), 1338–1347. [Google Scholar]
  48. Zakaria, M. I., Abdullah, A. H., Alhassora, N. S. A., Osman, S., & Ismail, N. (2025). The impact of m-learning and problem-based learning teaching method on students’ motivation and academic performance. International Journal of Instruction, 18(1), 503–518. [Google Scholar]
  49. Zakaria, M. I., Hanid, M. F. A., & Hassan, R. (2023). Combination of M-learning with problem-based learning: Teaching activities for mathematics teachers. International Journal of Interactive Mobile Technologies, 17(9), 4–19. [Google Scholar]
Education 15 00462 g001
Figure 1. Scores obtained in the pretest.
Figure 1. Scores obtained in the pretest.
Education 15 00462 g001
Education 15 00462 g002
Figure 2. Scores obtained in the pretest grouped by methods.
Figure 2. Scores obtained in the pretest grouped by methods.
Education 15 00462 g002
Education 15 00462 g003
Figure 3. Post-test scores.
Figure 3. Post-test scores.
Education 15 00462 g003
Education 15 00462 g004
Figure 4. Post-test scores by method.
Figure 4. Post-test scores by method.
Education 15 00462 g004
Table 1. Teaching sequence.
Table 1. Teaching sequence.
Beginning
Stages of PBLResources/MaterialsDescription of ActivitiesTime
Explore the issueClassroom space in which students meet in groups of 4 members reading and talking to analyze the problem.Problem: In the construction of wooden boxes, a carpenter needs to cut a 20 cm long board into two parts that have a difference of 6 cm between them.
Determine the length of the parts.		15 min
Try to solve the problem with what you know Each member of the group gives an idea of how to solve the problem with what they know. All members should participate. All members must reach a joint solution.The above situation can be solved by proposing a system of two linear equations of the first degree with two unknowns. 10 min
Identify what you do not know to solve the problem On a sheet of paper, make a list of the information that is required and should be consulted to solve the problem. Develop the information individually and share it with everyone. In this situation, what would be the unknowns? How would the equations be posed? Propose a system of two equations with two unknowns and try to solve it. Relate the thinking of other group members.10 min
Development
ABP StagesResources/MaterialsDescription of ActivitiesTime
Prioritize learning needs Each group defines learning objectives, and resources, and distributes consultation tasks among participants.Know what the Equalization method consists of and the steps necessary to solve a problem, 10 min
Self-study and preparation Use the EQUALINEALES mobile educational application.Use the EQUALINEALES mobile application to determine what the Equalization method consists of and the necessary steps to solve a system of linear equations with two unknowns. 30 min
Closing
ABP StagesResources/MaterialsDescription of ActivitiesTime
Share information among group membersUse the EQUALINEALES mobile educational app Take into account the information present in the mobile application: generalities, methods, and procedures for solving problems. 20 min
Apply knowledge to the solutionUse the EQUALINEALES mobile educational application in the X Challenge optionProvide solutions to the problems raised within the APP.10 min
Assess new knowledge Use the EQUALINEALES mobile educational application in the Evaluation optionSelf-evaluation of the exercise carried out and the group analysis, explaining the procedures put into practice by each group. 15 min
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Martínez-Gómez, J.; Nicolalde, J.F. Enhancing Mathematical Education Through Mobile Learning: A Problem-Based Approach. Educ. Sci. 2025, 15, 462. https://doi.org/10.3390/educsci15040462

AMA Style

Martínez-Gómez J, Nicolalde JF. Enhancing Mathematical Education Through Mobile Learning: A Problem-Based Approach. Education Sciences. 2025; 15(4):462. https://doi.org/10.3390/educsci15040462

Chicago/Turabian Style

Martínez-Gómez, Javier, and Juan Francisco Nicolalde. 2025. "Enhancing Mathematical Education Through Mobile Learning: A Problem-Based Approach" Education Sciences 15, no. 4: 462. https://doi.org/10.3390/educsci15040462

APA Style

Martínez-Gómez, J., & Nicolalde, J. F. (2025). Enhancing Mathematical Education Through Mobile Learning: A Problem-Based Approach. Education Sciences, 15(4), 462. https://doi.org/10.3390/educsci15040462

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop