Development and Validation of a Questionnaire on Students’ Mathematics Capital: A Tool to Explore Opportunities in the Mathematics Classroom
Abstract
:1. Introduction
1.1. Opportunities in the Mathematics Classroom: Mathematics Capital as a Framework for Equity
1.2. Mathematics Capital, Beliefs, and Subjective Relevance: A Theoretical Distinction
1.3. State of the Art, Research Gap, and Research Question
2. The Development of the Mathematics Capital Questionnaire
2.1. The Original Science Capital Questionnaire
2.2. The New Mathematics Capital Questionnaire
- Linguistic adjustments consist of simple changes in terminology, replacing references to science with mathematics. Such terminology shifts ensure that the questionnaire becomes mathematics-specific without altering the nature of the items. Examples include items 1 to 4, item 6, items 10 and 11, and items 13 and 14.
- Epistemological adjustments are made to better reflect the nature of mathematical reasoning within the items. These adjustments ensure that the focus shifts from empirical validation to logical deduction, which is a core characteristic of mathematical thinking. While the original questionnaire focuses on scientific evidence to produce argumentations (item 5) and the utility of science in daily life (item 12), the reframed version highlights mathematical reasoning, its role in constructing arguments, and its usefulness in everyday life.
- Contextual adjustments are introduced to align the questionnaire with the educational environment and extracurricular activities relevant to mathematics (items 7 and 8) and to reflect peculiarities of the local school system (items 9 and 10). Specifically, for item 7, the original item focuses on places specifically dedicated to science, while the reframed item concentrates on events exclusively related to mathematics (such as mathematics workshops and conferences). In both cases, the focus is on opportunities that one participates in only if specifically interested in the subject. Concerning item 8, the original item focuses on places that provide a more leisure-oriented experience rather than direct educational interaction with science, like zoos and aquariums. The reframed item concentrates on science outreach events. In both cases, the focus is on experiences that participants engage in for reasons that may extend beyond a specific interest in the subject. For item 9, the original item refers to a type of after-school activity (science clubs) that is not common in the local school context. The reframed item focuses on popular extracurricular activities dedicated to mathematics, like mathematics competitions. This change reflects the reality of the local educational system to which the questionnaire is directed. Similarly, in item 10, a terminology adjustment, from science to mathematics, is combined with a contextual adjustment, from GCSEs to high schools, to align with the local school context.
3. Materials and Methods: The Validation of the Mathematics Capital Questionnaire
3.1. Experimental Setting
3.2. Sample
3.3. Measures and Procedures
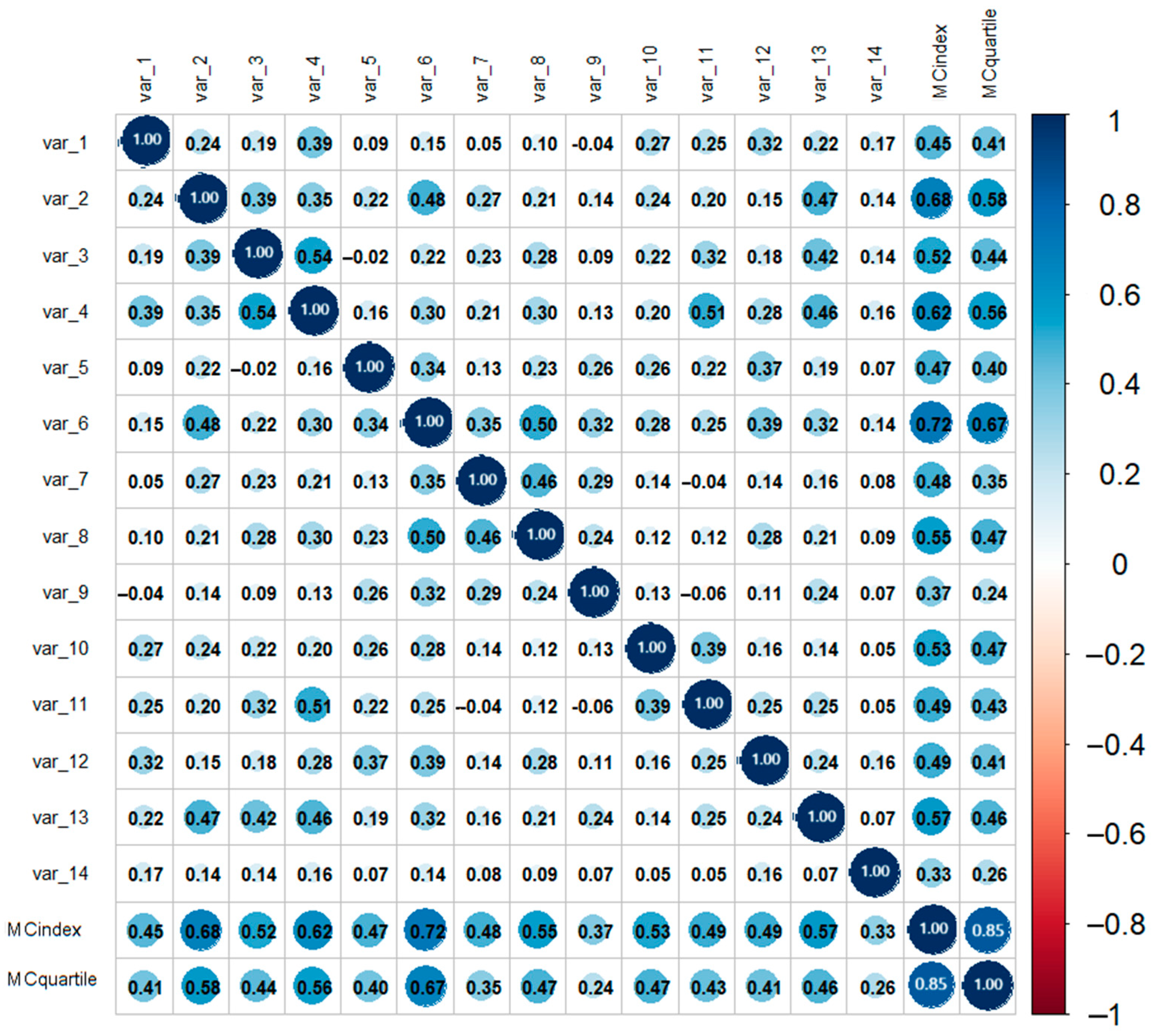
4. Results
Distribution of the Mathematics Capital Index’s Items and Variables
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| MC | Mathematics Capital |
Appendix A
| Item | Response Options and Weighting |
| -2 fortemente in disaccordo, -1 in disaccordo, 0 indifferente, 1 d’accordo, 2 fortemente d’accordo |
| -2 mai, -1 almeno una volta l’anno, 0 almeno 4 volte l’anno, 1 almeno una volta al mese, 2 almeno una volta a settimana |
| -1 fortemente in disaccordo, -0.5 in disaccordo, 0 indifferente, 0.5 d’accordo, 1 fortemente d’accordo |
| -1 fortemente in disaccordo, -0.5 in disaccordo, 0 indifferente, 0.5 d’accordo, 1 fortemente d’accordo |
| -2 fortemente in disaccordo, -1 in disaccordo, 0 indifferente, 1 d’accordo, 2 fortemente d’accordo |
| -2 mai, -1 almeno una volta l’anno, 0 almeno 4 volte l’anno, 1 almeno una volta al mese, 2 almeno una volta a settimana |
| -2 mai, -1 almeno una volta l’anno, 0 almeno 4 volte l’anno, 1 almeno una volta al mese, almeno una volta a settimana |
| -2 mai, -1 almeno una volta l’anno, 0 almeno 4 volte l’anno, 1 almeno una volta al mese, almeno una volta a settimana |
| -2 mai, -1 almeno una volta l’anno, 0 almeno 4 volte l’anno, 1 almeno una volta al mese, 2 almeno una volta a settimana |
| -2 fortemente in disaccordo, -1 in disaccordo, 0 indifferente, 1 d’accordo, 2 fortemente d’accordo |
| -2 fortemente in disaccordo, -1 in disaccordo, 0 indifferente, 1 d’accordo, 2 fortemente d’accordo |
| -1 fortemente in disaccordo, -0.5 in disaccordo, 0 indifferente, 0.5 d’accordo, 1 fortemente d’accordo |
| 0.5 genitori o tutori, 0.5 fratelli/sorelle, 0.5 altri famigliari, 0.5 amici, 0.5 scienziati, 0.5 insegnanti, 0.5 altri, 0 nessuno |
| 2 genitori o tutori, 1 fratelli/sorelle, 1 altri famigliari, 1 altri, 0 nessuno |
References
- Alesina, A., Carlana, M., La Ferrara, E., & Pinotti, P. (2024). Revealing stereotypes: Evidence from immigrants in schools. American Economic Review, 114(7), 1916–1948. [Google Scholar] [CrossRef]
- Archer, L., Dawson, E., DeWitt, J., Seakins, A., & Wong, B. (2015). “Science capital”: A conceptual, methodological, and empirical argument for extending bourdieusian notions of capital beyond the arts. Journal of Research in Science Teaching, 52(7), 922–948. [Google Scholar] [CrossRef]
- Bachelard, G. (2002). The formation of the scientific mind: A contribution to a psychoanalysis of objective knowledge (M. McAllester Jones, Trans.). Clinamen Press. Available online: https://www.topoi.net/wp-content/uploads/2012/12/The-Formation-of-the-Scientific-Mind.pdf (accessed on 17 April 2025). (Original work published 1938).
- Bakker, A., Cai, J., & Zenger, L. (2021). Future themes of mathematics education research: An international survey before and during the pandemic. Educational Studies in Mathematics, 107(1), 1–24. [Google Scholar] [CrossRef]
- Bills, T., & Hunter, R. (2015). The role of cultural capital in creating equity for Pāsifika learners in mathematics. In M. Marshman, V. Geiger, & A. Bennison (Eds.), Mathematics education in the margins (pp. 109–116). MERGA. Available online: https://files.eric.ed.gov/fulltext/ED572423.pdf (accessed on 17 April 2025).
- Bini, G. (2024). From the web to the mathematics classroom: Investigating internet phenomena as educational resources in mathematics. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of digital resources in mathematics education (pp. 1–32). Springer International Handbooks of Education. Springer. [Google Scholar] [CrossRef]
- Black, L., & Hernandez-Martinez, P. (2016). Re-thinking science capital: The role of ‘capital’ and ‘identity’ in mediating students’ engagement with mathematically demanding programmes at university. Teaching Mathematics and Its Applications: An International Journal of the IMA, 35(3), 131–143. [Google Scholar] [CrossRef]
- Boaler, J. (2002a). Experiencing school mathematics: Traditional and reform approaches to teaching and their impact on student learning. Routledge. [Google Scholar] [CrossRef]
- Boaler, J. (2002b). Learning from teaching: Exploring the relationship between reform curriculum and equity. Journal for Research in Mathematics Education, 33(4), 239–258. [Google Scholar] [CrossRef]
- Bonett, D. G., & Wright, T. A. (2015). Cronbach’s alpha reliability. Journal of Organizational Behavior, 36(1), 3–15. [Google Scholar] [CrossRef]
- Bourdieu, P. (1986). The forms of capital. In J. Richardson (Ed.), Handbook of theory and research for the sociology of education (pp. 241–258). Greenwood. [Google Scholar]
- Bourdieu, P. (2004). Science of science and reflexivity (R. Nice, Trans.). University of Chicago Press and Polity Press. [Google Scholar]
- Carroll, J. (1963). A model of school learning. Teachers College Record, 64, 723–733. [Google Scholar] [CrossRef]
- Choudry, S., Williams, J., & Black, L. (2016). Peer relations and access to capital in the mathematics classroom: A Bourdieusian social network analysis. British Journal of Sociology of Education, 38(7), 1037–1053. [Google Scholar] [CrossRef]
- Chronaki, A., & Kollosche, D. (2019). Refusing mathematics: A discourse theory approach on the politics of identity work. ZDM Mathematics Education, 51(3), 457–468. [Google Scholar] [CrossRef]
- Cobb, P. (1986). Contexts, goals, beliefs, and learning mathematics. For the Learning of Mathematics, 6(2), 2–9. Available online: https://www.jstor.org/stable/40247805 (accessed on 17 April 2025).
- Cohen, S. M., Hazari, Z., Mahadeo, J., Sonnert, G., & Sadler, P. M. (2021). Examining the effect of early STEM experiences as a form of STEM capital and identity capital on STEM identity: A gender study. Science Education, 105(6), 1126–1150. [Google Scholar] [CrossRef]
- DeWitt, J., Archer, L., & Mau, A. (2016). Dimensions of science capital: Exploring its potential for understanding students’ science participation. International Journal of Science Education, 38(16), 2431–2449. [Google Scholar] [CrossRef]
- Dobie, T. E., Carlsruh, R., & Aina, D. K., Jr. (2021). Utility in context: A sociohistorical lens for examining students’ conceptions of the usefulness of mathematics. In D. Kollosche (Ed.), Proceedings of the eleventh international mathematics education and society conference (Vol. 2, pp. 414–422). Tredition. [Google Scholar] [CrossRef]
- Dou, R., & Cian, H. (2022). Constructing STEM identity: An expanded structural model for STEM identity research. Journal of Research in Science Teaching, 59(3), 458–490. [Google Scholar] [CrossRef]
- Ernest, P. (1996). Popularization: Myths, mass media, and modernism. In A. J. Bishop, K. Clements, C. Keitel, J. Kilpatrick, & C. Laborde (Eds.), International handbook of mathematics education (Vol. 4, pp. 785–817). Kluwer International Handbooks of Education. Springer. [Google Scholar] [CrossRef]
- Gresalfi, M. S. (2009). Taking up opportunities to learn: Constructing dispositions in mathematics classrooms. The Journal of the Learning Sciences, 18(3), 327–369. [Google Scholar] [CrossRef]
- Gutiérrez, R. (2012). Context matters: How should we conceptualize equity in mathematics education? In B. Herbel-Eisenmann, J. Choppin, D. Wagner, & D. Pimm (Eds.), Equity in discourse for mathematics education: Theories, practices, and policies (pp. 17–33). Springer. [Google Scholar] [CrossRef]
- Howson, A. G., & Kahane, J.-P. (Eds.). (1990). The popularization of mathematics (Vol. 5). Cambridge University Press. [Google Scholar]
- Husen, T. E. (1967). International study of achievement in mathematics: A comparison of twelve systems. John Wiley & Sons. [Google Scholar]
- Jorgensen, R. (2018). Building the mathematical capital of marginalised learners of mathematics. ZDM Mathematics Education, 50(6), 987–998. [Google Scholar] [CrossRef]
- Jorgensen Zevenbergen, R. (2011). Young workers and their dispositions towards mathematics: Tensions of a mathematical habitus in the retail industry. Educational Studies in Mathematics, 76(1), 87–100. [Google Scholar] [CrossRef]
- Kloosterman, P. (2002). Beliefs about mathematics and mathematics learning in the secondary school. In G. C. Leder, E. Pehkonen, & G. Törner (Eds.), Beliefs: A hidden variable in mathematics education? (pp. 247–269) Springer. [Google Scholar] [CrossRef]
- Kollosche, D. (2017). A socio-critical analysis of students’ perceptions of mathematics. In H. Straehler-Pohl, N. Bohlmann, & A. Pais (Eds.), The disorder of mathematics education (pp. 173–189). Springer. [Google Scholar] [CrossRef]
- Langford, E. (2006). Quartiles in elementary statistics. Journal of Statistics Education, 14(3). [Google Scholar] [CrossRef]
- Lareau, A. (2018). Unequal childhoods: Class, race, and family life. University of California Press. [Google Scholar]
- Lockhart, P. (2009). A mathematician’s lament: How school cheats us out of our most fascinating and imaginative art form. Bellevue Literary Press. [Google Scholar]
- Moote, J., Archer, L., DeWitt, J., & MacLeod, E. (2020). Science capital or STEM capital? Exploring relationships between science capital and technology, engineering, and maths aspirations and attitudes among young people aged 17/18. Journal of Research in Science Teaching, 57(8), 1228–1249. [Google Scholar] [CrossRef]
- Noyes, A. (2016). Bringing Bourdieu to mathematics education: A response to Williams and Choudry. Research in Mathematics Education, 18(1), 22–26. [Google Scholar] [CrossRef]
- OECD. (2018). Equity in education: Breaking down barriers to social mobility. PISA, OECD Publishing. [Google Scholar] [CrossRef]
- Op’t Eynde, P., De Corte, E., & Verschaffel, L. (2002). Framing students’ mathematics-related beliefs. In G. C. Leder, E. Pehkonen, & G. Törner (Eds.), Beliefs: A hidden variable in mathematics education? (Vol. 31, pp. 13–37) Springer. [Google Scholar] [CrossRef]
- Schneider, T., & Jackson, M. (Eds.). (2014). Determined to succeed? Performance versus choice in educational attainment. European Sociological Review, 30(3), 410–412. [Google Scholar] [CrossRef]
- Schoenfeld, A. H. (1989). Explorations of students’ mathematical beliefs and behavior. Journal for Research in Mathematics Education, 20(4), 338–355. [Google Scholar] [CrossRef]
- Skeggs, B. (2004). Class, self, culture. Routledge. [Google Scholar]
- Tavakol, M., & Dennick, R. (2011). Making sense of Cronbach’s alpha. International Journal of Medical Education, 2, 53–55. [Google Scholar] [CrossRef] [PubMed]
- Terzi, L. (2008). Justice and equality in education. Bloomsbury Publishing. [Google Scholar]
- Vithal, R., Brodie, K., & Subbaye, R. (2024). Equity in mathematics education. ZDM Mathematics Education, 56(1), 153–164. [Google Scholar] [CrossRef] [PubMed]
- Williams, J., & Choudry, S. (2016). Mathematics capital in the educational field: Bourdieu and beyond. Research in Mathematics Education, 18(1), 3–21. [Google Scholar] [CrossRef]

| Item | Science Capital Dimension | Theoretical Aspect | Response Options and Weighting |
|---|---|---|---|
| Knowledge about the transferability of science | Habitus (disposition) | −2 for strongly disagree, −1 for disagree, 0 for neither, 1 for agree, and 2 for strongly agree |
| Talking about science in everyday life | Capital (social capital) | −2 for never, −1 at least once a year, 0 at least once a term, 1 at least once a month, and 2 at least once a week |
| Family science skills, knowledge and qualifications | Habitus (disposition) Capital (social capital) | −1 for strongly disagree, −0.5 for disagree, 0 for neither, 0.5 for agree, and 1 for strongly agree |
| Family science skills, knowledge and qualifications | Habitus (disposition) Capital (social capital) | −1 for strongly disagree, −0.5 for disagree, 0 for neither, 0.5 for agree, and 1 for strongly agree |
| Scientific literacy | Capital (cultural capital) | −2 for strongly disagree, −1 for disagree, 0 for neither, 1 for agree, and 2 for strongly agree |
| Science media consumption | Capital (cultural capital) | −2 for never, −1 at least once a year, 0 at least once a term, 1 at least once a month, and 2 at least once a week |
| Participation in out-of-school science learning contexts | Capital (cultural capital) | −2 for never, −1 at least once a year, 0 at least once a term, 1 at least once a month, and 2 at least once a week |
| Participation in out-of-school science learning contexts | Capital (cultural capital) | −2 for never, −1 at least once a year, 0 at least once a term, 1 at least once a month, and 2 at least once a week |
| Participation in out-of-school science learning contexts | Capital (cultural capital) | −2 for never, −1 at least once a year, 0 at least once a term, 1 at least once a month, and 2 at least once a week |
| Science-related attitudes, values and dispositions | Habitus (disposition) Capital (social capital) | −2 for strongly disagree, −1 for disagree, 0 for neither, 1 for agree, and 2 for strongly agree |
| Knowledge about the transferability of science | Habitus (disposition) Capital (social capital) | −2 for strongly disagree, −1 for disagree, 0 for neither, 1 for agree, and 2 for strongly agree |
| Science-related attitudes, values and dispositions | Habitus (disposition) | −1 for strongly disagree, −0.5 for disagree, 0 for neither, 0.5 for agree, and 1 for strongly agree |
| Talking about science in everyday life | Habitus (disposition) Capital (social capital) | 0.5 for parents or carers, 0.5 for extended family, 0.5 for friends, 0.5 for siblings, 0.5 for directly with scientists, 0.5 for teachers, 0.5 for other, and 0 for no one |
| Knowing people in science-related roles | Habitus (disposition) Capital (social capital) | 2 for parents or carers, 1 for siblings, 1 for extended family members, and 1 for other |
| Science Capital | Mathematics Capital | Adjustment | ||
|---|---|---|---|---|
| Item | Dimension | Item | Dimension | |
| Knowledge about the transferability of science |
| Knowledge about the transferability of mathematics | Linguistic |
| Talking about science in everyday life |
| Talking about mathematics in everyday life | Linguistic |
| Family science skills, knowledge and qualifications |
| Family mathematics skills, knowledge and qualifications | Linguistic |
| Family science skills, knowledge and qualifications |
| Family mathematics skills, knowledge and qualifications | Linguistic |
| Scientific literacy |
| Mathematics literacy | Epistemological |
| Science media consumption |
| Mathematics media consumption | Linguistic |
| Participation in out-of-school science learning contexts |
| Participation in out-of-school mathematics learning contexts | Contextual |
| Participation in out-of-school science learning contexts |
| Participation in out-of-school mathematics learning contexts | Contextual |
| Participation in out-of-school science learning contexts |
| Participation in out-of-school mathematics learning contexts | Contextual |
| Science-related attitudes, values and dispositions |
| Mathematics-related attitudes, values and dispositions | Linguistic Contextual |
| Knowledge about the transferability of science |
| Knowledge about the transferability of mathematics | Linguistic |
| Science-related attitudes, values and dispositions |
| Mathematics-related attitudes, values and dispositions | Epistemological |
| Talking about science in everyday life |
| Talking about mathematics in everyday life | Linguistic |
| Knowing people in science-related roles |
| Knowing people in mathematics-related roles | Linguistic |
| Variable | Categories | Frequency |
|---|---|---|
| Class | 9th grade | 24 |
| 11th grade—class 1 | 26 | |
| 11th grade—class 2 | 20 | |
| 11th grade—class 3 | 23 | |
| 13th grade | 26 | |
| Gender | Female | 49 |
| Male | 69 | |
| Prefer not to say | 1 |
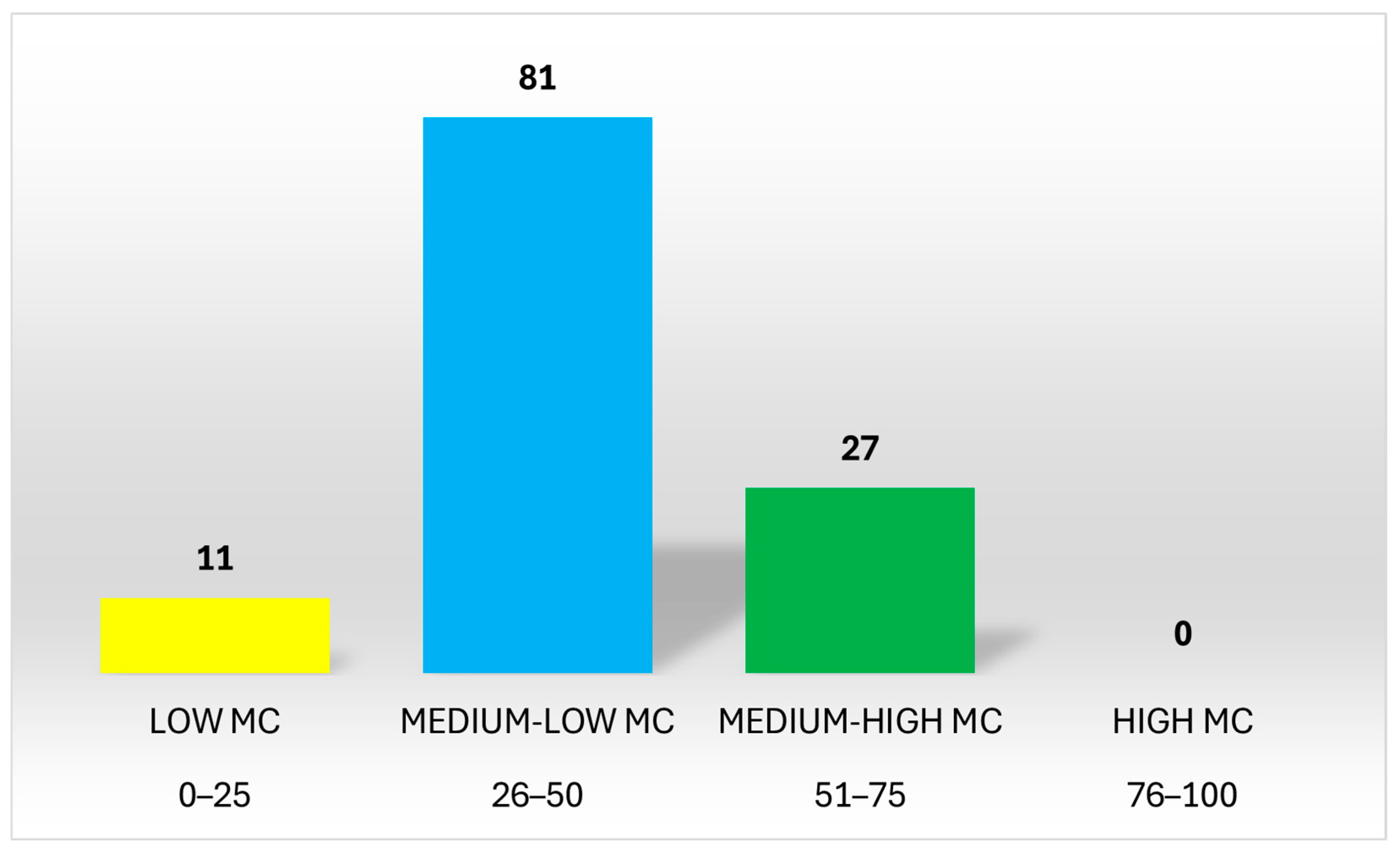
| Quartile | MC Index Range |
|---|---|
| Low | 0–25 |
| Medium-Low | 25–50 |
| Medium-High | 50–75 |
| High | 75–100 |
| Item | Variable | Mean | St. Deviation | Min. | Max. |
|---|---|---|---|---|---|
| Var_1 | 0.68 | 0.75 | −2 | +2 |
| Var_2 | 0.38 | 1.34 | −2 | +2 |
| Var_3 | 0.44 | 0.45 | −1 | +1 |
| Var_4 | 0.47 | 0.42 | −1 | +1 |
| Var_5 | 0.52 | 0.67 | −1 | +2 |
| Var_6 | −1.22 | 0.99 | −2 | +2 |
| Var_7 | −1.57 | 0.78 | −2 | +2 |
| Var_8 | −1.37 | 0.81 | −2 | +1 |
| Var_9 | −1.64 | 0.59 | −2 | +1 |
| Var_10 | −0.15 | 0.99 | −2 | +2 |
| Var_11 | 0.84 | 0.77 | −2 | +2 |
| Var_12 | 0.47 | 0.44 | −1 | +1 |
| Var_13 | 1.12 | 0.63 | 0 | +2.5 |
| Var_14 | 0.96 | 0.85 | 0 | +4 |
| Variable | Mean Low Quartile | Mean Medium-Low Quartile | Mean Medium-High Quartile | Mean High Quartile |
|---|---|---|---|---|
| Var_1 | 0.27 | 0.72 | 0.91 | / |
| Var_2 | −1.54 | 0.20 | 1.41 | / |
| Var_3 | 0 | 0.40 | 0.66 | / |
| Var_4 | −0.18 | 0.44 | 0.73 | / |
| Var_5 | −0.09 | 0.44 | 0.81 | / |
| Var_6 | −2.00 | −1.66 | −0.02 | / |
| Var_7 | −2.00 | −1.70 | −1.14 | / |
| Var_8 | −1.90 | −1.58 | −0.73 | / |
| Var_9 | −2.00 | −1.70 | −1.42 | / |
| Var_10 | −1.36 | −0.27 | 0.47 | / |
| Var_11 | −0.27 | 0.70 | 1.26 | / |
| Var_12 | 0.18 | 0.39 | 0.75 | / |
| Var_13 | 0.50 | 1.06 | 1.47 | / |
| Var_14 | 0.27 | 0.31 | 0.48 | / |
| Alpha | Confidence Interval at 95% |
|---|---|
| 0.8 | 0.743–0.840 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bini, G.; Gagliani Caputo, S.; Zanga, G. Development and Validation of a Questionnaire on Students’ Mathematics Capital: A Tool to Explore Opportunities in the Mathematics Classroom. Educ. Sci. 2025, 15, 510. https://doi.org/10.3390/educsci15040510
Bini G, Gagliani Caputo S, Zanga G. Development and Validation of a Questionnaire on Students’ Mathematics Capital: A Tool to Explore Opportunities in the Mathematics Classroom. Education Sciences. 2025; 15(4):510. https://doi.org/10.3390/educsci15040510
Chicago/Turabian StyleBini, Giulia, Sara Gagliani Caputo, and Giulietta Zanga. 2025. "Development and Validation of a Questionnaire on Students’ Mathematics Capital: A Tool to Explore Opportunities in the Mathematics Classroom" Education Sciences 15, no. 4: 510. https://doi.org/10.3390/educsci15040510
APA StyleBini, G., Gagliani Caputo, S., & Zanga, G. (2025). Development and Validation of a Questionnaire on Students’ Mathematics Capital: A Tool to Explore Opportunities in the Mathematics Classroom. Education Sciences, 15(4), 510. https://doi.org/10.3390/educsci15040510






