Multimodal Languaging as a Pedagogical Model—A Case Study of the Concept of Division in School Mathematics

Abstract

The purpose of this study is to present a multimodal languaging model for mathematics education. The model consists of mathematical symbolic language, a pictorial language, and a natural language. By applying this model, the objective was to study how 4th grade pupils (N = 21) understand the concept of division. The data was collected over six hours of teaching sessions, during which the pupils expressed their mathematical thinking mainly by writing and drawing. Their productions, as well as questionnaire after the process, were analyzed qualitatively. The results show that, in expressing the mathematical problem in verbal form, most of the students saw it as a division into parts. It was evident from the pupils’ texts and drawings that the mathematical expression of subtraction could be interpreted in three different ways. It was found that the pupils enjoyed using writing in the solution of word problems, and it is suggested that the use of different modes in expressing mathematical thinking may both strengthen the learning of mathematical concepts and support the evaluation of learning.

1. Introduction

Traditionally, there has been a strong emphasis on the use of symbolic mathematical language in representing mathematics. This has, however, been found to be a limiting factor in expressing mathematical thinking in learning processes [1,2,3]. The aim of this article is to present a multimodal languaging model, in which the ways to express mathematical thinking are expanded beyond mathematic symbolic language. A second objective is to observe how 4th grade pupils understand the concept of division based on this model.

Different ways of expressing thinking and making meaning form the underlying theoretical basis for this study. Theoretically, the multimodal languaging model is related to multiliteracy, a concept referring to various modes in the current communications environment [4]. The present model includes three types of semiotic systems of meaning-making: a symbolic mathematical language, a natural language, and a pictorial language [2,5]. It has been suggested that the use of different semiotic systems such as these supports the development of conceptual knowledge [6,7]. Furthermore, it has been recommended that, in a national assessment of learning outcomes [8], languaging should be an integral to the pedagogical method in learning mathematics.

In our earlier paper [9], we published the outline of our pedagogical model and preliminary results in Finnish from the point of view of integrating school subjects. In this paper, we will link the multimodal languaging model to a multiliteracies framework, present new data, and further discuss the concept of division based on the data.

2. The Theoretical Framework

2.1. Multiliteracy

The multimodal languaging model is connected to a multiliteracies framework. The basic principles of multiliteracy were set out in the manifesto of the New London Group (NLG) [10]. Since then, multiliteracies has become a key concept in describing the changes in the current textual world, in which the written mode can be complemented by, or even replaced by, other modes [4,11].

In research, multiliteracies is usually framed by semiotics, which emphasizes the “semiotic resource” as a potential key term in meaning-making [12]. Sociocultural approaches also seem to be inherent in multiliteracy [12]. These aspects reflect two of the "multis" inherent in multiliteracies, as stated by Kalantzis and Cope [4]. First of all, the variety of modes provides more options for meaning-making; secondly, a text may vary enormously, depending on social context such as different cultural settings, gender identity, or the subject matter [4].

Multimodal resources in school mathematics have been highlighted in several studies (e.g., O’Halloran [13]). The aspect of social diversity of multiliteracies in the context of mathematics is also acknowledged, for example, by Takeuchi [14], who studied English language learners (ELLs) in mathematics practices in an urban Canadian classroom.

The present multimodal languaging model intentionally takes advantage of different modes in making meaning. The underlying idea is that, if the pupils are obliged to use different modes in their expression, they gain a greater understanding of the topic. Thus, the students in this study wrote and drew while performing mathematical tasks. Culturally, our study is in the context of school mathematics in Finland: the study combines the international symbolic mathematical language with other ways of meaning-making. Students’ productions must therefore be interpreted from this cultural point of view.

The multiliteracies approach has only recently been incorporated into the Finnish core curriculum [15] as one of the transversal competencies. It is defined as follows [15] (p. 33): “the competence to interpret, produce and make a value judgement across a variety of different texts, which will help the pupils to understand diverse modes of cultural communication and to build their personal identity.”

We can see this idea, for example, in the objectives of instructions in mathematics for Grades 3–6 [15] (p. 398), for example: “…to encourage the pupil to present his or her conclusions and solutions to others through concrete tools, drawings, speech, and writing, also using information and communication technology.”

It is to be noted that the theoretical concept of multiliteracies is rather complex. It is described as being a pedagogical approach, but in the Finnish curriculum is applied as a set of communication abilities [12,16]. However, there is an urgent need for research into the implementation of a multiliteracies approach in all school subjects by developing concrete yet theoretically relevant educational models.

2.2. Languaging of Mathematical Thinking

Traditionally, at least in Finnish mathematics education, pupils often work silently and independently in the mathematics classroom, and the solutions to mathematical problems are usually presented by mathematical symbols alone, without any clarifying text or drawing. Owing to this tradition, it is often difficult for mathematics teachers to follow how a pupil has thought through his/her solution to a mathematical problem. Has the pupil really understood the main idea of the solution?

The use of languaging breaks this tradition and serves as a means to express thinking in several different ways. It has been shown that writing and the use of natural language in the solutions of mathematical problems may in fact boost learning in mathematics, develop mathematical understanding, change the pupil’s attitude towards mathematics for the better, and help the teacher’s evaluation [17]. The use of natural language, both in the solution process of mathematical problems, and in formulating the presentation of the solutions, helps a pupil to organize her/his mathematical thinking for herself/himself and for the peer group [2,9,18]. In fact, it seems that the use of natural language and drawings helps most students in the solution process of mathematical problems not only at primary level, but also at higher levels of the education system [19].

At the primary school level, we have recognized three useful semiotic systems or “languages” of meaning-making in mathematical presentations (Figure 1). These semiotic systems are a mathematical symbolic language, a natural language, and a pictorial language [2,12,19]. In the school context, this means students are able to express their mathematical thinking either by using mathematical symbols (e.g., numbers, symbols), a natural language (mother tongue and/or second language), or pictures or other tangible devices [12,19]. The modes in using these are writing, speaking, and drawing.

Mathematical thinking is described as an information process monitored by one’s metacognition [7]. The main purpose of using several semiotic systems in learning activities (e.g., in studying new mathematical concepts and doing exercises) is to develop the student’s own meaning-making processes. We call this process “languaging”, a concept that has been used in mathematics and in mother tongue didactics since the 1990s [21].

Languaging in mathematics refers to expressing one’s mathematical thinking by different modes either orally (by natural language) or in writing (by natural language, mathematical symbolic language, or pictorial language) [12,20]. From a multiliteracies aspect, languaging can be seen as a multimodal approach to making meanings of mathematical concepts and procedures.

In addition to the meaning-making of concepts and procedures for a learner, multimodal languaging is also a tool for a teacher to evaluate how the learner has understood mathematics. In this study, we will use pupils’ texts and drawings as a resource for semantic interpretations.

2.3. The Concept of Division in School Mathematics

In the Finnish National core curriculum for basic education, the objectives in division learning in Grades 3-6 are described as follows: “They learn division in cases of both quotition and partition. They practise division by number units. They utilise the properties of operations and the connections between them.” [15] (p. 399).

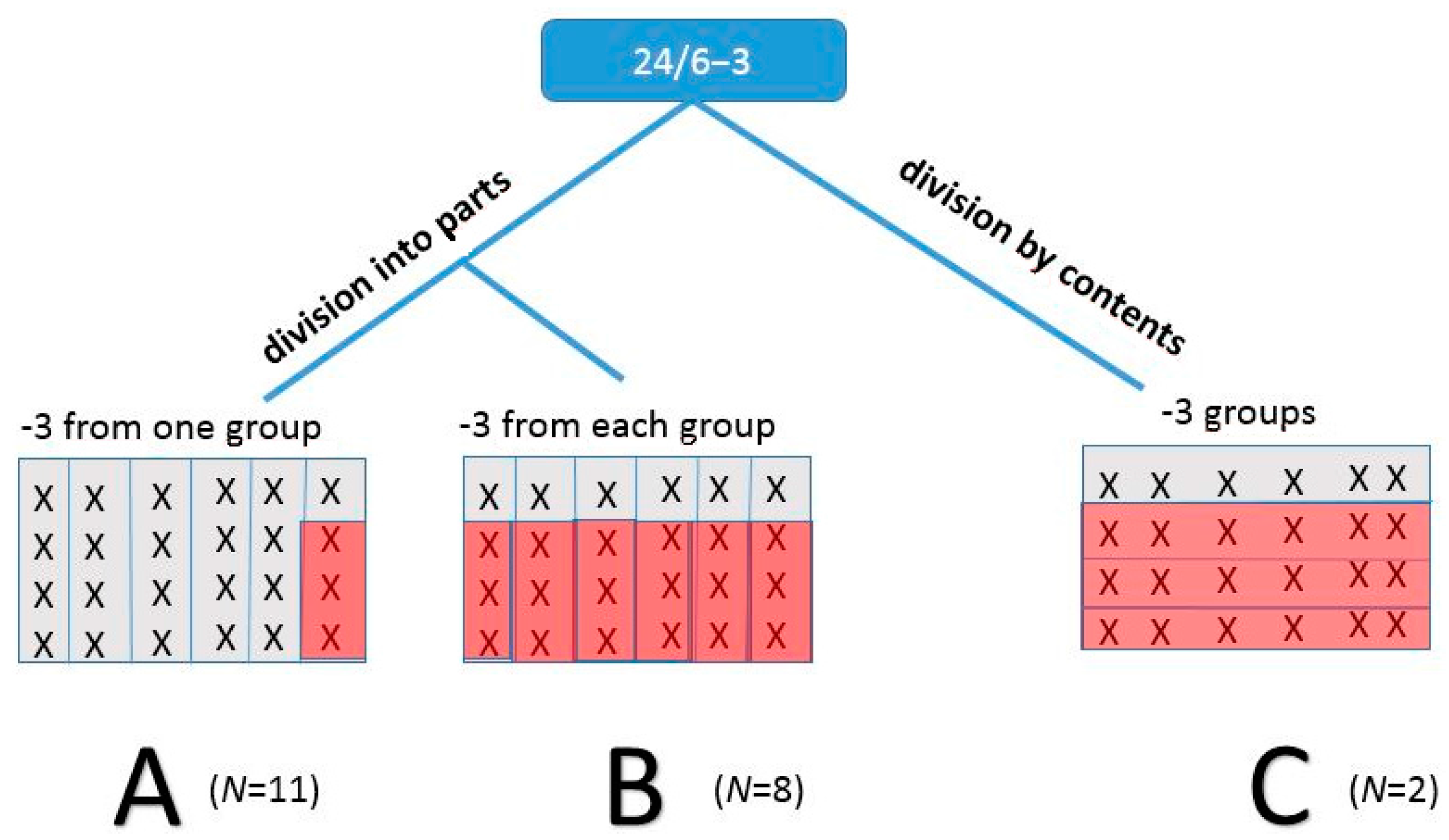
Pupils are introduced to the concept of division after they have learned multiplication. The objective is that they should understand the connection between multiplication and division in Grade 3. In several studies, the concept of division is observed to be difficult to understand for pupils and even for prospective teachers [22], especially in word problems and in recognizing both of the aforementioned types of division. Typically, if we ask pupils to give an example of division, they describe it as being division into parts: e.g., “Mother had 24 cookies and she promised to divide them equally to me and my five friends. How many cookies did I get?” We could describe this as the primitive model of division [22]. In fact, the model of division by contents (e.g., “For how many children can mother divide packages of four cookies, if she has 24 cookies?”) is understood by systemically teaching in upper grades [23].

3. The Division Research: Data Collection and Analysis

The use of different modes in mathematics was modeled and explored via a six-hour teaching process, which took place in the Training School of University of Tampere in 2012 in a 4th grade class of 21 pupils. All of the pupils were monolingual Finnish speakers. The process was planned and conducted in co-operation with the class teacher. After the teaching, we submitted a written questionnaire in order to evaluate the students’ experiences and thoughts on the process. In this article, we concentrate on the following research questions:

• How do the pupils interpret the concept of division?
• How did the pupils experience the use of writing and drawing in learning mathematics?

The key idea in the teaching process and data collection was that the students were given a mathematical expression (24/6−3), which was then the starting point for several different tasks. At first, the pupils were to invent a typical school word problem based on the given expression. This means that they had to construct verbal meanings and context for the numbers, division, and subtraction by themselves, in contrast to the usual ways of presenting mathematical problems. Then, the students were to solve their own invented mathematical word problem by using the multimodal languaging method: in this phase, they worked with a mathematical symbolic language, a natural language via writing, and a pictorial language by drawing. After this, they were to extend their own word problem into a story by planning and processing their stories as typically done in developing writing skills. The stories based on the mathematical word problem were eventually transformed into strip cartoon form in order to practice textual skills and to evaluate the student’s mathematical thinking.

A qualitative content analysis was conducted on pupils’ productions during the teaching process (word problems, written and drawn solutions, stories, and cartoons) and on the written answers to the questionnaire. Based on the productions, we were able to interpret what kind of meanings pupils constructed for the given mathematical expression. The process was successful, as nearly all of the pupils cooperated willingly during all the steps.

4. Results

4.1. How Do the Pupils Interpret the Concept of Division?

The use of multimodal languaging model in the process revealed the contexts into which abstract mathematical symbolic language was referring to in the student’s thinking. Most of the students (N = 21) equated the contexts with food, e.g., cookies (N = 9), or animals, e.g., bunnies (N = 6).

Languaging through writing revealed how the students understood the mathematical concepts of division and subtraction. In the expression 24/6−3, the key issue is what kind of meanings pupils gave to the subtraction “minus three.” Interestingly, in the division into parts the subtraction was understood in two different ways: A: “minus three” from only one group (N = 11) or B: “minus three” from each of the six groups (N = 8) (Figure 2).

Against our expectations, we found two cases where the pupils had constructed division by contents. The two pupils had problems in formulating the word problem correctly to the end, but the main idea of the division by contents was properly presented (see

Table 1. Word problem examples of divisions and subtractions (Types A, B, and C from Figure 1).

Type of Division	An Example
A	“In the tree there were 24 apples. Aku, Santeri, Miina, Liisa, Kaisa and Laura divided them. After that Kaisa gave to her mother 3 apples. How many apples did Kaisa get?” (Pupil 1)
B	“Emma divided 24 cookies to her six friends. Emma’s sister took 3 cookies from each friend. How many cookies did each friend get?” (Pupil 2)
C	“Samppa had 24 ice hockey sticks. His task was to divide them into groups of six sticks.” Three groups were left in the storage. How many groups of six sticks were taken to the training hall?” (This example is a combination of several pupils: First two sentences are from Pupil 3 and the rest of the problem from others)

, Case C). In the next two tables and in Figure 3, we show how three pupils constructed the word problem, its solution, and the whole story in the cartoons. In Table 1, we have taken three examples of the word problems in which division is needed for their solution.

In the second phase, pupils constructed solutions to their word problem firstly via natural language, and secondly via pictorial language (

Table 2. Pupils’ word problem solutions of divisions and subtractions by natural and pictorial language (Types A, B, and C from Figure 1). The solutions via pictorial language are based on pupils’ drawings.

Type of Division	The Solution by Natural and Pictorial Language
A	“Kaisa got at first 24/6 = 4 (apples). When Kaisa came home she gave three apples to the mother 4 − 3 = 1. Kaisa got one apple.” (Pupil 1).
B	“24/6 = 4, 4 – 3 = 1. The cookies were divided and everyone got four (cookies). The sister takes from everyone else three cookies. Every girl got only one cookie.” (Pupil 2).
C	“24/6 − 3 = 1. Samppa divides the ice hockey stics into six groups. He left three groups in the storage and took one group including four ice hockey sticks to the training camp.” (Two sentences from Pupil 3 and the rest of the solution from others).

). The solutions by natural language were like little stories, which also contained mathematical symbolic language. The original handmade drawings were completed as shown in Table 2 (drawn by computer). Only Pupil 3 of the three pupils had problems in logically making a solution and cartoons. Pupil 3 had made the beginning of the solution of the word problem correctly, but the rest of the solution was insufficient. We present here only the correct parts of the example of Model C.

At the end, pupils drew cartoons in which they told the whole story: the word problem and its solution (Figure 3). Pupil 1 drew the cartoon about how Kaisa divided 24 apples, Pupil 2 drew the cartoon about how Emma divided 24 cookies (Case B in Figure 1), and Pupil 3 drew the cartoon about how Samppa divided 24 ice hockey sticks (Case C in Figure 1). The last cartoon, C, is not complete, because there were some misunderstandings at the end of the solution.

All the pupils in the study succeeded in drawing logical cartoons from their word problem. All three pupils created a reliable context in their word problem (Table 1) and in their cartoons (Figure 3) for the mathematical expression. The division into parts and the subtraction have acquired real meanings in the pupil’s own cartoons from their point of views.

4.2. How Did the Pupils Experience the Use of Writing and Drawing in Mathematics Learning?

After the teaching process, we asked the pupils how they had experienced the multimodal approach in mathematics learning by a questionnaire. The results are shown in

Table 3. The most agreeable part in the project from the pupils’ points of view (N = 21).

	Girls	Boys
Drawing cartoons	1	6
Writing word problem and story	11	1
Making mind map for a story	0	2

,

Table 4. Do you think that writing (natural language) supports the solutions of word problems? (N = 21).

Answer	Girls	Boys
Yes	12	6
No	0	2
No answer	0	1

and

Table 5. Examples of pupils' opinions on the importance of using natural language in solutions of word problems.

Theme	Examples
Better understanding	“I understand better how I have solved the problem.” (5 pupils)
Easier to construct the solution	“It is easier to solve the problem when you can write.” (5 pupils)
Checking of the answer	“You can justify from the written text that you have solved it correctly” (2 pupils)
Mother tongue learning (writing)	“You learn at same time mathematics and mother tongue” (1 pupil)

. Most of the pupils liked writing the word problem and constructing a larger story about it. An interesting detail in Table 3 is that almost all of the girls liked writing the most, whereas most of the boys liked drawing cartoons. A mind map was needed in the planning of the story; that part of the study is omitted from this article. Mind map making develops analytical thinking.

The pupils were asked whether they thought that writing (the use of natural language) supported the solution making for word problems. Almost all of the pupils thought that writing supported it (Table 4). The result is interesting, because writing was not favored by the boys.

The pupils also provided their opinions as to why writing is important or not in the solving process. By content analysis, four main themes were found, which are presented in Table 5 with text examples.

5. Discussion

The pedagogical model described in this paper is an example of using multimodal ways of meaning-making in school mathematics. The intentional use of multimodal languaging model revealed the meanings pupils made for the mathematical symbolic language and concepts (here, division and subtraction) and served in interpreting their thinking. These various types of ways to express one’s thinking serve also as a way for the teacher to evaluate the students’ understanding of the concepts.

Despite the unfamiliarity of the task, every pupil in the class managed to produce a proper word problem, solutions by natural language, and a pictorial language for the problem and the cartoons. The most typical interpretation of division was division into parts (Figure 1). From the point of view of the pupils, writing was seen as useful for a better understanding of the solution, and for constructing the solution more easily (Table 4 and Table 5). A similar result has also been observed in the languaging surveys of university mathematics teaching. The girls liked writing more than the boys, and the boys liked drawing more than the girls (Table 3). Boys having problems in writing are seen on a wider scale in Finland; national Finnish assessments of learning outcomes at the end of comprehensive school have shown that boys are significantly worse than girls in writing [24]. There were no differences in the data between how pupils made solutions via natural or pictorial languages: all pupils could do both of them mainly correctly. All pupils were able to draw cartoons, presenting both the problem and its solution.

We suggest that the broadened ways of expressing mathematical thinking may help those who struggle with mathematics and for whom mathematical symbolic language as such is difficult to comprehend. The use of writing and drawing in problem solving may also strengthen the learning of mathematical concepts, as the use of different modes leads to organizing one’s mathematical thinking. In this study, all of the pupils were monolingual Finnish speakers; however, the use of multimodality may also support, for example, L2 learners for whom the pictorial language may serve as a way to understand mathematical concepts.

The use of different modes in learning mathematics could easily be extended to the use of, for example, videos. The use of various modes and even digital technology would connect the symbolic mathematical language to more familiar ways of meaning-making for young students. In a broader sense, these kinds of educational applications are closely related to a multiliteracies approach and serve as a way to understand the various ways of making meaning in todays textual environment.

A few limitations of this study are to be mentioned. First of all, the data was collected in a specific educational context (monolingual Finnish classroom); secondly, the sample size is small, as is common in case studies. Nevertheless, the data showed potential in developing the multimodal languaging model, as it served to express thinking.

The multiliteracies framework with multimodality brings new insights into school mathematics. Further research is needed into how the intentional use of different modes serves in learning specific concepts, such as multiplication, or in multilingual classrooms.