Extending Universal Design for Learning through Concurrent Enrollment: Algebra Teachers’ Perspectives

Abstract

Concurrent enrollment refers to partnerships between postsecondary institutions and schools through which secondary school students can complete a university class taught by a qualifying secondary school teacher at their secondary school. We propose that concurrent enrollment programs are an under-recognized tool for extending the impact of Universal Design for Learning (UDL). The context of our study is an equity-focused university course in algebraic mathematical modeling that is also offered through concurrent enrollment in over 30 secondary schools to over 800 secondary students annually in our state of Minnesota, U.S.A. This paper presents a qualitative analysis of secondary school teachers’ experiences implementing the inquiry pedagogy and the equity goals of the course. Several results are important for UDL. Teachers (1) describe equity in social terms of race, ethnicity, income, immigration, and language status in addition to measures of academic success; (2) perceive improvements in students’ attitudes towards mathematics, school, and university education; (3) perceive student academic growth through mathematical writing; and (4) report close relationships with students. If higher education faculty design their on-campus classes to incorporate UDL principles, concurrent enrollment offers the potential to improve inclusive pathways from secondary schools to universities.

1. Introduction

In the United States and Canada, students and their families increasingly rely on programs that allow secondary school students to complete university classes before the student graduates from secondary school [1]. These dual enrollment or concurrent enrollment programs allow the secondary student to enroll in a university course that is taught at their secondary school by a secondary school teacher who receives substantial, ongoing university training. In global perspective, this blurring of boundaries of secondary and postsecondary education does not seem to be widespread, but it is commonplace in North America. By 2011 in the United States, 82% of public secondary schools offered at least one of several types of concurrent enrollment options, and 2.04 million students participated compared to 1.16 million students in 2003 [2]. Our local program, known as College in the Schools (CIS), allows public school students to earn university credit that is free to them (In the U.S., the terms “college” and “university” are used interchangeably). The secondary school pays a nominal fee per student registration to the sponsoring postsecondary institution. The secondary school teacher does not receive additional compensation for teaching the university class. For students and families, the opportunity to reduce the cost of higher education, gain experience with advanced academic expectations, and shorten completion time for a postsecondary degree are all strong motivations to participate in concurrent enrollment programs.

Traditionally, most concurrent enrollment courses in North America have been offered to the highest performing students in secondary schools, but over the last fifteen years some programs have committed themselves to increasing the participation of students who are underrepresented in higher education [3]. In 2009, our own university launched several equity-focused concurrent enrollment courses through the Entry-Point Project [4]. Secondary teachers for the Entry-Point Project are asked to reserve at least 60% of the seats in their classroom for students who are racially or ethnically underrepresented in higher education, of low to moderate income, first in their families to attend university (“first generation” students), English Language Learners (ELLs), members of immigrant families, or in the “academic middle”, the top 50th–80th percentile of their secondary school class rank. The program criteria refer to any combination of these social identities of students and of their academic performance at the secondary schools.

Principles of Universal Design for Learning (UDL) are the core of the Entry-Point concurrent enrollment program. Its university courses must incorporate elements of UDL course design, including [4] (pp. 120–121):

• Integrating skill-building (e.g., critical thinking, problem-solving, written and verbal communication) with the acquisition of content knowledge
• Communicating clear expectations and providing constructive feedback
• Promoting interaction among and between teachers and students;
• Using teaching methods that consider diverse learning styles, abilities, ways of knowing, previous experience, and background knowledge
• Articulating a commitment to diversity and integrating multicultural perspectives into all aspects of the learning process.

Currently, six courses are offered through this program: algebra, physics, writing, family sociology, and two courses that explore teaching as a profession. Although many contemporary concurrent enrollment programs seek to improve access to higher education for underserved students, few align themselves explicitly with the principles of UDL that could strengthen this goal, perhaps because UDL principles are not widely articulated in early undergraduate classes in North America. Relatively little scholarship has explored the potential connections between the equity and access mission of many modern concurrent enrollment programs and UDL principles of course design [5,6].

In this paper, we report on secondary teachers’ experiences teaching a university algebra concurrent enrollment course that uses a UDL-focused inquiry pedagogy. This mathematical modeling pedagogy encourages multiple ways of engaging mathematical scenarios and expressing solutions. The first author teaches the algebra course on the university campus and has served as the faculty coordinator for the concurrent enrollment algebra course offerings since 2009; the second author is a doctoral student who provides support for the concurrent enrollment algebra program.

The concurrent enrollment algebra course is complex to implement. Secondary teachers in widely differing communities across our state must juggle the Entry-Point criteria that reference race, class, language, income, and family history. They must learn to teach and grade inquiry-oriented mathematical assignments that are not typical in most secondary mathematics curricula. Many of the algebra assignments are set in “realistic” contexts that allow students to engage personal knowledge, but it is not clear that they are actually realistic to students in all communities.

To better understand how secondary teachers grapple with the complexities of delivering a concurrent enrollment algebra course that has core values of inclusivity, institutional pathway-building, and challenging, inquiry pedagogy, we conducted focus groups to investigate the research questions: (a) How do teachers understand the equity mission of the course at their school? and (b) How do teachers understand the association of the inquiry pedagogy and the equity mission of the course?

We use the results to comment on the final question: (c) How can teachers’ experiences in an equity- and inquiry-oriented concurrent enrollment algebra class inform higher education faculty who wish to extend UDL through concurrent enrollment?

1.1. Concurrent Enrollment as Access Strategy

The scope of concurrent enrollment programs is determined by state-level legislation. State governments set eligibility criteria for the academic credentials that secondary students must possess and the types of post-secondary institutions that can offer concurrent enrollment classes [3]. For this reason, the categories of students who participate in concurrent enrollment and their outcomes vary substantially. Quantitative assessment of outcomes for concurrent enrollment can be challenging, as we have found in our own setting, due to limited articulation of school district, state, and national educational databases. Reviews of quantitative studies of concurrent enrollment show a variable, but generally positive outlook for using concurrent enrollment programs as a strategy to improve access and success in higher education for traditionally underrepresented groups of students [3,7,8].

At times, concurrent enrollment programs continue to support students who already enjoy broad pathways into university education [9]. For example, a study in Virginia found that White female students, who already have strong representation in universities, tended to be over-enrolled in concurrent enrollment courses relative to their portion of upper-level secondary school classes, while African-American, Latino, and Asian students were under-enrolled [10]. Analysis of enrollments in our University of Minnesota concurrent enrollment algebra class portray mixed success in program participation. We tend to over-enroll Latino, Southeast Asian, and Native American students and under-enroll White students compared to the school populations, which would be expected in a program with racial equity goals, but we also tend to under-enroll African-American students [11]. These data are limited because they do not account for the effect of small class sizes, low racial diversity in some schools, or for the possible enrollment of racially underrepresented students in higher-level mathematics classes in their secondary schools (which is a positive reason for under-enrollment in algebra).

On the other hand, in dual enrollment programs in Florida and New York, career and technical education students improved postsecondary education measures, such as second semester retention, earning credits toward a degree, and grade point average [12]. The authors found that students who have difficulty entering and persisting in postsecondary settings, especially males and low-income students, benefited from concurrent enrollment participation. A study in the University of Missouri system showed that concurrent enrollment experiences predicted retention into the second year at university, although it had no correlation with grade point average [13]. A critical review of several types of concurrent enrollment programs found that the strongest positive effects are the tendency to enroll in a postsecondary program, accumulate postsecondary credits, and complete a postsecondary degree [8].

Karp [14] suggests that concurrent enrollment student gains are due to anticipatory socialization—learning about a new role through discussion or observation—into the expectations of higher learning and to role rehearsal—temporary, direct enactment of the roles. Acosta [7] extends this idea for first generation college students, arguing that dual enrollment programs should intentionally incorporate support services around these experiences and should build on first generation students’ typical strengths of resilience, pride, and loyalty to family and community.

1.2. UDL Framework for Concurrent Enrollment

UDL research has produced a very rich set of recommendations for inclusive education, especially in the areas of course design and interactional features of classrooms. Somewhat less attention has been paid to the ways students move through educational structures in postsecondary settings, though some important work reports on learners’ experiences with advising, counseling services, residential life, tutoring centers, and in administrative organization [15].

Katz’ Three-Block Model of Universal Design for Learning is useful for analysis of inclusivity in concurrent enrollment programs because it attends to pedagogical design, the nature of teacher and student interaction, and educational systems and structures [16]. Block one of Katz’ model involves attending to social and emotional aspects of students’ classroom experiences. Students should improve their self-awareness and self-concept, and better understand the social identities and varied perspectives of their classmates. Block two, inclusive instructional practice, involves a range of inclusive practices at the level of course organization: group assignments, varied assignments with student choice, and an integrated curriculum. Block three on systems and structures attends primarily to developing administrative staff and policies that support educational inclusion. How students are supported, or not, as they navigate educational structures is a critical determinant of the inclusivity of their experience [15]. Because concurrent enrollment is a pathway across distinct educational systems, block three could easily be expanded to include it.

2. Concurrent Enrollment Context: College Algebra through Modeling

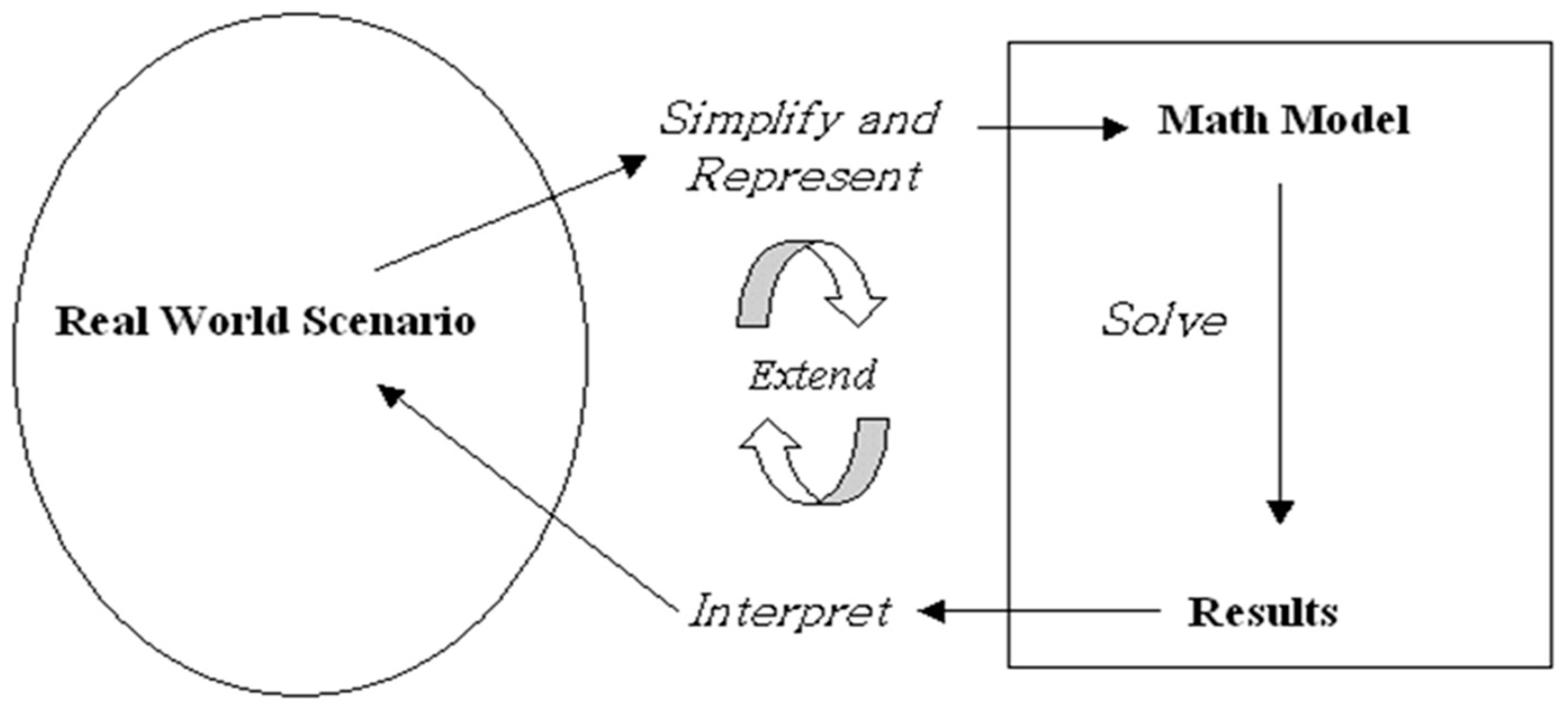
2.1. What Is Mathematical Modeling Pedagogy?

Mathematical modeling is a professional approach in applied mathematics in which an initial solution is improved systematically through multiple cycles of problem-solving [17]. In the U.K. and in Europe, mathematical modeling has been used as a teaching approach in secondary and early undergraduate mathematics classes since at least the 1980s, but has only begun to enter early undergraduate mathematics teaching in the U.S. over the last fifteen years [18]. Using the modelling perspective, students create mathematical methods for solving realistic problems instead of recreating a predetermined method that the teacher demonstrates.

The mathematical modeling course that is described in this paper covers algebraic topics including linear, quadratic, exponential, and logarithmic functions, and basic concepts in probability and counting. Courses that cover similar topics through a procedurally oriented pedagogy are among the most highly enrolled courses in the first year of undergraduate studies in the United States, in many settings, with a low rate of passing grades [19].

Our mathematical modeling assignments are based on mathematics education research perspectives on modeling [20,21] and are mostly derived from tasks developed through partnerships between teachers and mathematicians or education researchers [22,23]. Examples include how to design a public-rent-based bike-sharing program, planning to maximize profit in a historic hotel, describing the mathematics of games, or how to divide student athletes into “fair” teams based on their performance data.

Writing usually plays an important role in mathematical modeling pedagogy. In our course, students write about their mathematical solutions with reference to five stages of the modeling cycle (Figure 1). Students must define variables, state assumptions and outline other ways in which they “simplify” a realistic scenario. They must choose and reflect on the mathematical “representations” that they used in their approach, for example, whether graphs, equations, tables of values, or algorithms were most useful to them. Students “interpret” their results in terms of the original scenario and explain whether the results are reasonable. Finally, students must “extend” their original solution either by generalizing it or by posing a new, slightly more complex version of the original task and solving it mathematically.

2.2. Correspondences between Math Modeling Pedagogy and UDL

Mathematical modeling in educational settings has several correspondences with Universal Design for Learning. First, both fields have historical roots in understanding the educational experiences of students with learning disabilities. Lesh proposed mathematical modeling activities as a means to research and improve problem-solving approaches among students with learning disabilities and with “average abilities” in mathematics [24], but the approach also has been recognized as an approach that can engage many learners [21]. Students often work in groups that must define key aspects of the task. As in UDL, mathematical modeling pedagogy allows students multiple points of entry to connect knowledge to academic work and encourages varied forms of assessment. Our concurrent enrollment algebra class also emphasizes teachers’ growth in the use of questioning techniques rather than direct lecture [25,26].

All on-campus instructors and secondary school teachers are expected to incorporate accommodations from school and university special education systems. However, because the university course offering incorporates principles of UDL in multiple ways, the secondary school offerings must adopt inclusive teaching practices beyond the legal obligations of special education administration.

2.3. Concurrent Enrollment Features of the Algebra Course

At our university, the College in the Schools program organizes and provides administrative support for concurrent enrollment offerings across all disciplines. The CIS program manages partnerships between the faculty coordinator and her academic department on the one hand, and a secondary school teacher and her school administration on the other hand. The faculty coordinator (for the algebra class, this is the first author) leads professional development sessions three times per year for secondary teachers to ensure that their classes match the pedagogy and content of on-campus classes. The faculty coordinator and doctoral research assistant (the second author) also conduct site visits in the schools to ensure this equivalency. Professional development addresses topics including learning modeling pedagogy; learning question-based pedagogies; grading models and written work; and learning new modeling activities. The concurrent enrollment algebra course is currently offered in over 30 secondary schools statewide to over 800 secondary students annually.

The concurrent enrollment algebra class is offered in an academic setting that values teaching that is interdisciplinary, experimental, and civically engaged. On-campus instructors are encouraged to try new modeling activities in their classes, and so this opportunity to experiment with new assignments is open to secondary teachers as well, as long as the assignment is written in terms of the five stages of modeling (Figure 1) and supports mathematical learning of one of the required algebra topics.

3. Methods

3.1. Participants

In order to understand teachers’ experiences delivering an equity-focused concurrent enrollment course, the second author conducted six semi-structured focus group interviews with 27 secondary mathematics teachers out of the 31 teachers who offered the concurrent enrollment algebra class in their secondary schools that year. One teacher was African-American; the rest were White. Seventeen teachers were women; 10 were men. The focus groups took place during two days at the university campus when the concurrent enrollment teachers from across the state gather together for professional development training. The focus group size ranged from three to six teachers. Teachers were grouped together using our state government’s demographic categories for their school’s region, so that there were two focus groups for teachers in the Inner Metropolitan area surrounding our university campus; two focus groups for teachers in the Outer Metropolitan area; and two for teachers in rural parts of the state, the Greater Minnesota region. Because our university is sometimes perceived as prioritizing the interests of its surrounding metropolitan area, or as representing politically more liberal interests in comparison with the Outer Metropolitan and Greater Minnesota regions, we organized the focus groups in this way to allow for regional patterning of teaching experiences to emerge, if these differences were important to teachers.

3.2. Materials

In the focus groups, the moderator asked teachers to describe their implementation of the program’s equity criteria at their school; their perception of the mathematical modeling pedagogy of the class; and to tell a story that exemplifies their experience in the program. Appendix A provides the focus group questioning sequence. The research was conducted under University of Minnesota Institutional Research Board protocol number 00000560. This protocol does not allow publication of focus group transcripts or written comments.

To clarify and extend the focus group comments, and to probe for additional negative experiences with the program, teachers at a subsequent professional development meeting provided written comments on the categories of students at their school who need college readiness opportunities; whether the teacher modifies the curriculum to better serve students at their school; and whether the teacher experiences negative pressures at their school through participation in the concurrent enrollment program. Data analysis focused almost entirely on interview commentary, but we used written comments to check our understanding of teacher experiences in a few cases.

3.3. Data Analysis

The authors worked together to develop a qualitative data analysis plan for the transcribed focus group interviews. The first author led the coding with review from the second author. We needed to attend to interactional features of the group discussion and abstract perspectives for each teacher’s comments across a discussion and produce summaries at the regional level before collecting overall results. To achieve this, we used a multi-stage, mixed coding approach that combined structural coding and grounded theory methods. In the initial stages of coding, we used structural coding based on the research questions to collect and summarize each teacher’s comments on the research questions: implementation of the equity criteria, and the relation of pedagogy to the equity mission [27]. In creating these abstracted summaries, though, we used in vivo coding to capture the teachers’ forms of expression [28]. Because the two research questions were closely related to each other, this combination of structural and in vivo coding allowed the subsequent constant comparative method to better capture teachers’ perspectives on their experiences [28,29]. We noted interactional features of the interviews by noting teachers’ responses to other teachers’ statements when they expressed an elaborated agreement that was more detailed than mere affirmations, such as “yes” or “Ummhmm”. The constant comparative method allowed codes to be recategorized into prominent themes at the level of focus group, and then again for the two focus groups for a region [28,29]. A final round of comparison of themes allowed us to create summaries for the full teacher cohort. While the teacher was the focus of analysis, we were interested to retain information on any regional patterning of teacher experiences that might emerge.

3.4. Limitations

The semi-structured focus group method and qualitative data analysis method identifies perspectives that are commonly held among teachers. However, these methods cannot establish a firm ranking of themes. Teachers might really agree with some of the themes, but they did not consider it the most important or interesting idea to express, or they did not express the idea because another teacher had already contributed it. For example, we believe that if asked directly, nearly all teachers would agree that earning free university credit is a benefit of the program. Another important limitation is that the results represent teachers’ beliefs about their program participation and student reactions, but do not provide an objective measure. Teachers widely report that they observe positive changes in students’ self-confidence and enjoyment of mathematics, but we do not know if students would also report this, and we do not know if students improve their ability to enter higher education institutions and to be successful there as a result of the program. Finally, teachers might have hesitated to discuss negative program experiences due to the dual role of Staats as program coordinator and lead researcher. We dealt with this possibility by reporting single negative comments in Section 4.3.

4. Results

4.1. Common Perspectives on Pedagogy and Program Structure in the CIS Algebra Course

Overall, four themes relating to the mathematical modeling pedagogy (

Table 1. Teachers’ perspectives on concurrent enrollment algebra pedagogy.

Pedagogy Themes and Examples
1. Modeling changes students’ attitudes.
18 teachers, 67%.
Broad agreement in five out of six focus groups. Students’ adjustment to inquiry mathematics is difficult but valuable. Students’ adjustment to university expectations is difficult but valuable. Students can improve self-confidence in mathematics or in school performance. Students can improve enjoyment of mathematics. Students can improve attitude towards success in university studies.
2. Student growth through writing.
17 teachers, 63%.
Broad agreement in five out of six focus groups. Uses peer review or multiple drafts. Scaffolded assignments for English Language Learner (ELL) students. Writing allows students to express mathematical thinking. Writing enhances creativity in mathematical thinking.
3. Rewrites or selects models for greater local relevance.
14 teachers, 52%.
Agreement in Greater Minnesota and Inner Metro. Teachers articulated regionally specific issues. Several Greater Minnesota and Inner Metro teachers rewrote models to improve local cultural relevance. Teacher enjoys experimenting with new models.
4. Close relationships with and understanding of students.
10 teachers, 37%.
Agreement in Inner Metro. Students can have a closer learning relationship with a secondary teacher as compared to university professors. Modeling pedagogy allows teachers to have greater insight into student learning needs compared to other secondary classes.

) and six themes relating to the structure of the concurrent enrollment program (

Table 2. Teachers’ perspectives on concurrent enrollment algebra program structure.

Program Structure Themes and Examples
1. Socioeconomic or demographic categories describe students.
23 teachers, 85%.
Broad agreement in all six focus groups. Inner and Outer Metro teachers tended to use multiple categories. Greater Minnesota teachers tended to use low income and first-generation categories.
2. Teacher negotiates tensions in University and school administrative expectations.
17 teachers, 63%.
Agreement in Greater Minnesota and Outer Metro. Advocating for class despite low class sizes. Enrolling students different from program criteria in order to reach an adequate class size.
Balances different grading procedures for university and school grades. Educating school administration about student selection criteria. Educating school administration about student course sequences.
3. “Academic middle” describes students in the class.
12 teachers, 44%.
Agreement in Greater Minnesota and Outer Metro. Teachers articulated regionally specific issues. Only two teachers from the Inner Metro relied on the “academic middle.”
4. Free university credit motivates students or their parents.
13 teachers, 48%.
Agreement in Greater Minnesota. Teachers articulated regionally specific issues. Greater Minnesota students have limited options to earn university credit.
5. Class serves more females than males.
10 teachers, 37%.
Agreement in Greater Minnesota. Teachers articulated regionally-specific issues. Nearly unanimous in Greater Minnesota.

) captured teachers’ most commonly expressed experiences teaching the university algebra class. The tables also summarize of the kinds of teacher commentary that informed each theme.

Because the semi-structured focus group format allowed teachers to raise a great variety of issues, we decided that a minimum of nine teachers—one-third of participants—was an adequate level of agreement for reporting results. If at least half of the teachers in both focus groups for a region agreed with a particular theme, then this preliminary regional patterning is noted in the results using the term “agreement”. However, absence of a pattern does not imply absence of the perspective, and so regionality in teachers’ experiences in the program must be judged based on their development of detailed commentary on a particular theme.

4.2. Was There Regional Patterning in Teachers’ Responses?

Overall, there was less regionality than we expected. In the first place, regional distinctiveness was reduced by broad agreement across regions on several important features of the CIS algebra course and program, including observations of positive change in students’ attitudes, the role that writing plays in students’ growth, and teachers’ use of social identity descriptors in the equity criteria—race, class, language status, and family history—for students who enroll in their classes.

In a few cases, teachers offered detailed enough responses to tentatively consider that there are regional differences in experiences. Table 1, theme 3 on rewriting models for greater local relevance is a possible regional difference. Teachers are welcome and encouraged to rewrite models or select more appropriate ones as long as they address algebra class topics, and they note them in their course syllabus. Teachers in Inner Metropolitan and in rural schools found that University-developed models were sometimes culturally biased because they represented urban situations, such as “traffic jams”, or middle- and upper-class experiences, such as maximizing profit in a “historic hotel”. It is possible that some of these widely shared models seem culturally less problematic in the Outer Metropolitan schools, and therefore require less rewriting.

Several results from Table 2 are likely to represent actual regional differences. While all teachers would probably value the free university credit, teachers in rural communities commented that travel distances to postsecondary institutions limited students’ options for concurrent enrollment experiences. Two additional themes are especially relevant to UDL and are discussed in Section 5: theme 3 on the use of the term “academic middle” for students enrolled in the class and theme 5 on gender in Greater Minnesota.

4.3. Teachers’ Concerns about the Program or Pedagogy

We compiled teachers’ statements of concern about their participation in the program in

Table 3. Teachers’ concerns about concurrent enrollment algebra participation.

Teacher Concerns about Pedagogy

Writing can be a barrier for ELL students. Writing is difficult for all students. Students request fewer models. Students request direct, non-inquiry teaching. The workload for teachers is very high. Teacher does not enjoy grading writing. Teacher reports difficulty in grading mathematical and written content of models. Teacher reports difficulty in learning to grade models.

Teacher Concerns about Program Structure

Inclusion criteria should value women’s access to science, technology, engineering, and mathematics (STEM) education. Teacher is concerned that college credits might not transfer to the students’ universities. Teacher was selected by school administration to teach, with some sense of negativity.

. None were expressed commonly enough to be reported in Table 1 and Table 2. In some cases, only one teacher expressed the concern, but because teachers tended to express enthusiasm for the class and for the program, we wanted to amplify their negative comments. Most of these comments arise commonly in our professional development workshops, and so we believe that they would be acknowledged by multiple teachers if they were asked directly about them. Several of these concerns are relevant for UDL and are discussed in Section 5.

5. Discussion and Implications for UDL

In this section, we use Katz’ three-block framework for UDL [16] to organize teachers’ successes, dilemmas, and concerns in providing inclusive higher education experiences in mathematics to their students. Teachers’ experiences with the concurrent enrollment algebra course were generally positive. They raised many issues that resonate with the goals of UDL. However, merely offering a university course through concurrent enrollment does not mean that it will achieve inclusive educational goals. Teachers’ commentary provides a deeper understanding of the features of our program that support UDL goals and areas in which it could improve.

Teachers’ comments are lightly edited to remove vocalized pauses, such as “um”, “you know”, “okay”, or short repetitive phrases. Pseudonyms have been used for personal or school names.

5.1. Block One Results: Social and Emotional Development through Concurrent Enrollment Algebra

One of teachers’ most common lines of commentary was to describe students’ change in attitudes towards mathematics and towards their potential for educational success. Teachers described this social and emotional growth as fundamentally situated in the concurrent enrollment framework through students’ success in a challenging but flexible and supported curriculum. Many teachers noted a change in students’ understanding of the breadth of mathematics, that the modeling was more enjoyable than the more familiar textbook components of the class.

...I have kids every year who said, “I enjoy the model part, or the modeling part, better than I enjoy the actual chapter work we are doing.”

[Outer Metro]

Teachers also commented that learning to work on a challenging curriculum prepares students for college in a broader sense:

All of my students that do this class walk away believing that they can do college.

[Outer Metro]

Several teachers identified the most challenging aspect of the class, the Extend stage of modeling, as the feature of the class that changes student attitudes towards mathematics:

...when they can bring their own models to it, like in the Extend, I think that is the power of this program, and I remember specifically when we were sharing our Extends for that model this year for the class, the kids were really excited and some of them were saying things like, “I never knew math could be fun.”

[Inner Metro]

The Extend stage of mathematical modeling requires students to pose a new, slightly more difficult question compared to the original task posed by the teacher, and to answer it using mathematics. The UDL principle of offering some student control over the demonstration of their learning can sometimes give students a new sense of enjoyment and understanding of a discipline.

Because concurrent enrollment represents university perspectives on learning, it is not responsible to secondary school curriculum standards, which in the United States can severely constrain secondary teachers’ decision-making in teaching. Concurrent enrollment can create a space for a challenging, creative curriculum that is different from a typical secondary school curriculum. As one teacher commented, this creative thinking in mathematics prepares one for lifelong social and emotional development:

I had a student tell me, that’s not in the class, that, “Oh I am just going to drive a truck. I am not going to have to learn about computers.” And I am going, “Uh, my father-in-law drove truck for a very, very long time, and he quit just as they were bringing in the computer log. So you are going to end up having to deal with this.”

[Greater Minnesota]

A second result that is relevant to UDL is that teachers feel they develop close connections with their students. Building relationships among students, teachers, and academic support staff is a goal of UDL [15,30]. Sometimes, teachers compare their close relationships with the teachers’ other classes, and sometimes with the student’s expected relationship with university professors.

This course here [is] in a setting that is much more comfortable to you. You do not have to feel intimidated because we all know each other here [...] You do not have to be afraid to raise your hand and ask a question. You can get much more individual help and guidance from me in this setting than you would probably be comfortable doing from a college professor.

[Outer Metro]

The concurrent enrollment algebra course facilitated relationship-building through several factors. Teachers’ need to coach students through a difficult curriculum helped the teacher understand students and their individual learning needs better. In some schools, the student eligibility criteria results in classes that are smaller than typical classes in the school. In other cases, the feeling of closeness to students was due to the year-long format of most of the concurrent enrollment algebra classes.

A last feature of students’ social and emotional development through concurrent enrollment is the opportunity to learn about the “hidden curriculum” of expectations and attitudes at universities [31]. An African-American teacher, whose class that year was mostly first generation, African-American students, noted that the concurrent enrollment setting encouraged these kinds of questions.

I think something that is different in my CIS course is they ask a lot of college questions [...] and we can just talk about, okay, they say, “What if we were at the U [University of Minnesota] right now, what would this be like?” And so we really stop, and we have a lot of questions, like questions about college. And things I do not get to talk about with students often. But like, “What would it be like if you turned this in late in college?” You know, that kind of thing.

[Inner Metro]

In this teacher’s story, the concurrent enrollment setting empowers students to initiate “anticipatory socialization” discussions in their classroom [14]. Several other teachers commented on students’ growth in academic responsibility through engaging university expectations.

While teachers’ commentary on students’ growth was overwhelmingly positive, a few teachers noted that students do not always complete the class with a high level of achievement, which in our grading system is an A or B:

I will say this. I have a lot of kids who get Cs and a fair number who get Ds. And kids are not too thrilled with that, because they do not want to start their college transcript off with a C or a D. But the reality is the kids that I am getting into the course, and the work that they are producing, you know, I would love to give them As and Bs, but it really is not there as often as I would like to see it.

[Outer Metro]

This quote represents the reality of student experience in a challenging class and the complexity of school organization. In our concurrent enrollment system, the classroom teacher should have control over the student roster, but the sense expressed here is that the teacher “gets students” instead of choosing them. Our program seeks to empower teachers in their schools, but this is not always fully achieved.

The strength of this commentary on students’ social and emotional development was somewhat surprising. We would have expected that teachers would spend more time discussing the practical feature of free university credit. The concurrent enrollment format allows for a challenging, distinctive curriculum, in a year-long format with small class sizes, that encourages conversations that extend students’ understanding of what it means to do mathematics and to be a university student.

5.2. Block Two Results on Inclusive Instructional Practice

Extending UDL principles through concurrent enrollment must begin with an on-campus class that is organized around a disciplinary-based inclusive pedagogy. Students’ responsibility to create mathematical methods and explain them is the most important feature of inclusive pedagogy in our class. Many teachers narrated students’ changing attitude towards mathematics in terms of this feature of the pedagogy:

Well, they are used to that traditional model where there is a single answer at the end, and I find that kids at the beginning are very uncomfortable with the models [...] most of our models do have multiple levels of entry, which is awesome. They eventually really love that, but it is a very difficult thing early on. You are constantly reminding them, “Just explain why. Just explain why.”

[Outer Metro]

Several teachers commented that the creative aspect of the class contributed to their own satisfaction as teachers compared to their secondary courses:

I love the creative aspect of the class. And I like how I feel a little bit more free in what I can do and choose to do.

[Outer Metro]

Another teacher shared a story from her first year teaching, when the first author visited her class and asked students:

“Does she give you the answers?” And normally in my other classes, they would be so mad at me if I did not give them the answers, but my class goes, “No, no, nope, she is not going to give the answers, so you just have to work it out.” I was like (gasps). So it was okay that I was not giving them the answers. That was like, “Okay. I think I am doing this okay.”

[Inner Metro]

Seven teachers (just under the bar for formal reporting of results) mentioned that they had incorporated modeling pedagogy into other classes, or had learned new non-lecture teaching techniques through their work with the class:

I liked the questioning end of it, too. They question each other and even, myself, you can listen to them and say, “Well, what would you think of, you know, how about this? Or, how about this?” The questioning part of it, which I have had to learn better to do, because, obviously, I am older, and so I am very traditional in how I do. So, this class was a challenge for me to begin with.

[Greater Minnesota]

Block two of UDL values multiple forms of assessment that provide student choice in their presentation of learning. Mathematical modeling pedagogy incorporates this through writing, because students must use text alongside mathematical equations, graphs, and numerical tables to explain their methods. One of the most widely shared perspectives was that mathematical writing supported students who were not positioned, by themselves or by teachers, as previously successful math students. For example, a student who “hated math” at the beginning of the class found success through writing:

... At the end of the year, she is like, “I cannot wait to write my paper.” She was so creative, and she would make like a story out of it. And her Extends were just like short stories. And she could not wait to turn those papers in so that I could read them, and she could show me how she related her solution to whatever thing she came up with. So [...] at the end of the year, she was like, “This is the best math class I have ever taken,” just because it was so different than a traditional math class. And she could see her learning throughout the year, too.

[Outer Metro]

The teacher who gives out fewer high grades than he would like offered a similar reflection about a student who found the textbook component of the class difficult:

...this was a golden course for her [...] the modeling allowed her to take the time to really dig in, think about it, and put it in her own words. And she happened to be an A plus level writer. That’s where her true strength was. [...] Boy, was she incredible on those models. And for her, she could not wait for the next model. She hated any time we were in those books, that traditional style.

[Outer Metro]

Some teachers focus on developing writing skill through the models because they believe it will strengthen their students’ work in non-mathematical university classes:

But I have really put a big emphasis on their writing skills [...] And so besides getting the math credit, they feel that they are more comfortable going into those classes that need a written paper for college.

[Outer Metro]

A strong majority of teachers commented positively on writing as a means of capturing students’ mathematical thinking. Several teachers, however, commented on how difficult it was to learn to grade writing, and that they do not enjoy this aspect of the class. Rating student explanations that are different from each other, and that are presented in writing, is a long-standing challenge for teachers using mathematical modeling pedagogy, but several useful guides for grading written mathematical reports exist (see [18,32]). Three teachers also noted that the writing component of the course could be a barrier for English Language Learners:

I think the write-up part is hard for some of my ELL students. The actual going through the procedure, the hands on, the working together is a good thing. But then when they have to go and write a paper for it, that gets to be a difficulty.

[Outer Metro]

A teacher whose class often includes many Spanish speakers developed a workaround for this problem:

when they turn their models in, sometimes they turn them in, in Spanish first, and then they work with the ESL [English as a Second Language] teacher to get it translated [...] It sort of depends on how recently they have been in the country. And their literacy in their primary language.

[Inner Metro]

A final pedagogical feature of our concurrent enrollment course is that teachers are encouraged to rewrite mathematical modeling assignments to create greater local relevance. This seemed to be most important to teachers in the Inner Metro or Greater Minnesota Regions, who found cultural bias in some of the models presented in the university professional development sessions:

...some of the ones like “Traffic Jam”? (laughter) I think, “What do you mean, having to wait for the train?”

[Greater Minnesota]

One specific model change that I do is the “Historic Hotels” which I think is a great model, but my students have absolutely no connection to historic hotels, it has not worked at all. So a few years ago, Sue helped me make a “Selling Tamales” one, where we got a tamale recipe from one of the students, and we just changed it, and it works great and they love it, because they can compare tamale recipes before we start.

[Inner Metro]

...sometimes I try and pick things that represent not just my scientific background, but more of the social kinds of, like opioid addiction for babies, and things like that, that some of the kids seem to have more of a caring kind of response to.

[Inner Metro]

Teachers’ commentary on block two, inclusive pedagogy, highlights deeper issues in promoting inclusive teaching through concurrent enrollment. The concurrent enrollment framework for the algebra class allows teachers to present a curriculum that seems distinctive and more challenging than secondary classes that present similar types of mathematics. Teachers value students’ enjoyment of mathematical creativity, and teachers also value the opportunity to make curricular decisions that they believe will connect better with students’ interests. Many teachers enjoy these features of the course even though it depends on evaluating writing assignments, work that is more difficult and more ambiguous than other aspects of mathematics teaching.

It is important to note that this approach to concurrent enrollment mathematics courses might not be typical. Mathematical modeling classes, while not rare, are under-utilized in early undergraduate mathematics. A concurrent enrollment algebra class that relies on a more common procedurally based pedagogy would probably be experienced differently by students and teachers. The level of supported teacher choice in our program may also be unusual in concurrent enrollment programs. The most fundamental requirement of concurrent enrollment programs is the equivalence of on-campus and school courses in content and pedagogy. Our on-campus curriculum allows some flexibility for instructors, and so this bounded flexibility extends to secondary teachers, too, but we work every year to satisfy the requirement of university and school equivalency. For example, teachers often use our professional development sessions to present models that they have developed or that they have learned elsewhere. Most importantly, our use of a shared framework for expressing modeling tasks (Figure 1) helps preserve a shared pedagogical value system.

Just as UDL offers students the opportunity to introduce their knowledge and interests into course assignments, our approach to concurrent enrollment algebra offers teachers the opportunity to develop and grow in their enjoyment of teaching mathematics. Teachers’ commentary on UDL’s block two points towards the need to redesign potential concurrent enrollment classes around inclusive pedagogical practices, but also to intentionally negotiate the fine line between teacher creativity and maintaining equivalence with on-campus curriculum.

5.3. Block Three Results on Inclusivity through Program and Administrative Structure

An early article on UDL in higher education recommends that organizations “develop mission statements that include diverse learners as members of the educational community” [33] (p. 50). Our concurrent enrollment algebra course is framed in this way, focusing on underserved social identities or middle-range academic performance. While we agree that making the equity focus explicit is necessary, it does not remove challenges of implementation. Teachers’ commentary on block three, program administration and structure, highlights dilemmas in how to identify the students that the program intends to serve, and the high degree of program advocacy that teachers shoulder in their schools.

In our program, there is a tension between the description of “academic middle”, a measure of academic performance in a particular school setting, and the descriptions of social identities that students will likely carry with them as they move through later stages in their lives: race, ethnicity, class, multilingual status, and family history of immigration or of university attendance. Historically in the U.S., students in both categories have fewer college readiness opportunities in their schools and lower levels of enrollment in postsecondary settings. Both descriptions, however, pose quandaries for teachers trying to create equitable pathways at their schools.

One dilemma of implementation of the equity criteria is that the concurrent enrollment algebra class is offered in extremely varied communities. Publicly available school data shows that some schools have few non-White students, some are highly variable from year to year, and some have increased their non-White student body tremendously in the last decade, especially schools in the Outer Metropolitan area and the outer edge of the Inner Metropolitan area [11]. Two of the teachers in Outer Metropolitan schools described their concurrent enrollment algebra classes in comparison to their school’s broader racial and ethnic composition, as in this comment:

I would say racial and ethnical (sic)—ethnic diversity is probably stronger in my class than it is in the general population of Vermilion High School, along with private (sic) low income students. Things I have question marks about would be multilingual and ELL. I do not know if the percentages in my class are at or below the rest of Vermilion High School. And first gen (first generation)—I do not know that, I do not really survey students about that or anything.

[Outer Metro]

This teacher was trying to reflect in detail on how well the equity mission was being achieved at his school, but information on students’ family history and on the school’s multilingual student population was not readily available to him.

Teachers in several Greater Minnesota schools commented that the race and ethnicity categories of the equity criteria were less relevant to them because their school is comprised mostly of White students:

...and you know, we do not have any, you know, ethnicity. [...] Not much there. All farmers there for the most part. But it is, you know, low to moderate income.

[Greater Minnesota]

Our position is that Whiteness is an ethnicity. However, the intent of this comment was typical of most Greater Minnesota teachers, who rely more on the income and first generation categories instead of the race, ethnicity, and language categories. Even so, in Greater Minnesota, income is also a fraught category for student enrollment in educational support programs. Three teachers in Greater Minnesota agreed that families in their school qualify for, but do not participate in, a federal program that provides free lunches to low-income students.

Teacher 1:

But we also have a lot of kids whose families qualify but they do not take it.

Teacher 2:

Right. They do not wanna fill out the forms.

Lori:

Really?

Teacher 2:

It is a status thing.

Teacher 3:

Yeah.

Teacher 1:

Some of them do not—like, the parents just do not want extra help. They are just like, “We are gonna do this on our own. We are not taking any hand out.”

Teacher 2:

“I do not need that.”

Teacher 3:

Yeah.

Lori:

Wow. That is interesting.

Teacher 1:

We are a pretty strong red county. “No government handouts.”

Teacher 1’s comment about being a “red county” refers to his municipality’s tendency to vote for Republican political candidates. In this context, the three teachers in Greater Minnesota schools used this example to explain that they cannot always identify low income students because their families might not participate in the identifying program.

Teachers in the Inner Metropolitan schools usually commented that the social identity labels described many students in their schools and in the classes that they taught. Only two Outer Metropolitan teachers commented that the academic middle was the primary criteria used at their schools. Most of the teachers who used the “academic middle” terminology work in the Outer Metropolitan and Greater Minnesota regions, schools that either still serve, or until very recently served, predominately White students. However, these teachers almost always used additional social identity descriptions of the students in their concurrent enrollment class.

Two teachers in the Inner Metro region offered an important criticism of our equity criteria. Because women are underrepresented in science, engineering, and other mathematical fields, they felt surprised that our equity criteria do not mention gender. The equity criteria were developed to represent classes in several different disciplines: writing, education, and sociology, in which women are well-represented in higher education, as well as algebra and physics. Teachers in Greater Minnesota did not raise the issue of program criteria directly, but several mentioned that their concurrent enrollment algebra class tends to predominantly enroll young women. They explained that young men might be more likely to chart a course towards trade schools, programs that would require only a lower-level mathematics course, or alternatively towards engineering, which would require a higher-level course, such as calculus. In some schools, young women choose careers, such as nursing or education, in which a single university algebra class is the typical academic requirement, so that the concurrent enrollment algebra class contributes well to their career plans.

Teachers commonly contribute a variety of administrative and program advocacy work for the concurrent enrollment algebra course that goes beyond interpreting the equity criteria at their schools (Table 2, theme 2). The level of hidden work that teachers do to support and administer the concurrent enrollment program at their schools was somewhat unexpected. Several teachers noted that they advocated to initiate concurrent enrollment algebra in their schools, sometimes with school support and sometimes with less support:

It took me two years to get my department to agree to have the course. They were worried that it would take away enrollment from some of the upper level courses.

[Outer Metro]

If the class sizes are very low for a few years, teachers may need to advertise benefits of the class in order to maintain it at the school. One teacher recounted using concurrent enrollment data compiled at the university in her advocacy for the course:

We just got it a week or so ago from the university that, “This is how much your students save by being in a CIS class,” and stuff like that. And I always forward that on to my superintendent. And he then takes it to the school board.

[Greater Minnesota]

Several teachers mentioned that they felt concerned that maintaining adequate class sizes that are acceptable at their schools would put them in violation of the university requirement of maintaining 60% of the seats for students in underrepresented groups.

I have never filled my classroom. So I feel like I am not going to turn a kid away from it when I have 17 kids in my class this year. If I have 18, that is fine. I do not have 35 kids in my class.

[Outer Metro]

Thus, teachers navigate a variety of tensions to help maintain the course and ensure proper placement of students.

Outer Metropolitan communities tend to have large schools with multiple mathematical pathways. Sorting out which students should enroll in which math course is another aspect of teachers’ hidden advocacy for the class. For example, a teacher commented that the school offers a second concurrent enrollment algebra class with a more traditional, procedurally oriented pedagogy. He feels that stronger algebra students are placed into the traditional algebra class and weaker students are placed into his math modeling class:

...I have had several discussions about, you know, “Wait a minute, we have got to think carefully before we just label one as the upper college algebra and the lower college algebra,” [...] I think long term, the modeling idea is going to stick with the kids far more than any rudimentary procedural skill type that you would see in your standard college algebra course.

[Outer Metro]

As we noted in Section 5.2, the mathematical modeling pedagogy seems difficult at first, but ends up making mathematics accessible to a wider range of students. Teachers sometimes need to educate their administrators that inclusive pedagogy does not make a class less challenging or of lower status.

We appreciate the explicitness of the equity criteria of our program, but we recognize that it is sometimes difficult for teachers to implement. The terminology of the “academic middle” is especially fraught. On the one hand, the concept of “academic middle” has less utility than we expected, because nearly all teachers referred to students’ social identities in their descriptions of the way the equity mission of the school functions at their schools. The concept of “academic middle” could potentially shield schools against naming, identifying, and engaging the broad patterns of inequality in education that inspired the change in the concurrent enrollment program’s focus. On the other hand, focus group discussions uncovered the potential that low-income White parents may disavow participation in programs framed by income, race, ethnicity, and other social identities, even if their students have reduced access to higher education. The “academic middle” may encourage continued program participation among these families. More immediately, the teachers noted that they do not always have access to information, such as language status or family educational history, that are included in the program equity criteria.

6. Conclusions

Increasingly, concurrent enrollment programs position themselves as a way to strengthen pathways of underserved students into higher education. The UDL movement in higher education shares this goal, with similar interest in periods of educational transitions [15]. However, very few scholarly reports address concurrent enrollment through UDL frameworks. This paper contributes to this research need by identifying secondary teachers’ experiences in implementing UDL features of a concurrent enrollment algebra course, in particular, their perceptions of the impacts of the course and its pedagogy and the work they do to interpret and implement the equity mission.

Teachers’ experiences with the program were not always positive or fully coordinated with their settings. Teachers expressed some discomfort with the ambiguity and workload concomitant with mathematical modeling pedagogy. They grappled with assignments and with program criteria that do not always speak to their settings. After engaging in an enormous learning curve to teach the class, they often have to advocate in their schools for its continuance or for its appropriate positioning in curricular flows. However, at the same time, teachers expressed a great deal of enjoyment in teaching and in nurturing students’ growth through the course. Their positive comments resonate with UDL goals. Teachers believe that many of their students improve their self-concept and academic skills, such as writing and critical thinking. Teachers value a class that allows them to share their knowledge of university life and expectations and to make significant decisions in their manner of teaching students.

The most important conclusion to draw from this paper is that higher education faculty who work in equity-focused concurrent enrollment programs should redesign their classes using inclusive pedagogies. Learning experiences should go beyond routine skills to engage students in a creative activity appropriate to the discipline. Conversely, concurrent enrollment programs with equity missions should select participating university courses that are committed to UDL principles. These actions are necessary to align the equity focus of many concurrent enrollment programs with the actual experience of secondary teachers and students in the courses. It is worth recalling that in recent years, 82% of secondary schools in the U.S. offered some form of concurrent enrollment through postsecondary educational partnerships, encompassing over 2 million student registrations [2]. Beyond the particular circumstances of our mathematical modeling algebra program, the potential national impact of redesigning all concurrent enrollment courses around UDL design features is substantial.

This call to action will not be easy to achieve. Our commentary highlights dilemmas that faculty and concurrent enrollment administrators will need to consider. One dilemma is the decision of naming the learners who are the focus of the equity mission. We feel it is important to explicitly name the longstanding social categories of exclusion: race, ethnicity, class, language status, family history, disability status, and in mathematics curricula, gender. The terminology of the “academic middle” is ambiguous. It may facilitate program participation in some cultural or political settings, but it can also become a shield that prevents direct engagement with social structures of exclusion. Without clearly articulated equity missions, incorporation of inclusive pedagogies, and continuous monitoring of equity outcomes, concurrent enrollment programs may merely support access for students who already enjoy many opportunities [9]. Assessment of equity in concurrent enrollment programs will be substantially enhanced by using a broad framework UDL that promotes understanding of the many entanglements of educational structures, pedagogies, and student emotional and social development [16].

A second dilemma involves the equivalency principle of concurrent enrollment, that the secondary classes must convey the same disciplinary content through the same pedagogy as on-campus classes, as determined by the faculty coordinator. In the concurrent enrollment algebra course, we use a common format for writing major assignments (Figure 1) and we share and study new assignments together during professional development meetings. This ability to experiment within boundaries, or to redesign assignments for local needs, appears to be a feature of our course that teachers enjoy a great deal. This combination of regimentation, experimentation, and in-depth communication allows us to fulfill UDL principles along with the university oversight that is fundamental to the equivalency principle. Concurrent enrollment faculty and administrators will need to grapple with similar issues of defining the meaning of equitable concurrent enrollment and critically investigating how teachers enact it in the varying social landscapes of their schools.