Analyzing Characteristics of Experts in the Context of Stoichiometric Problem-Solving
Abstract
:1. Introduction
2. Methodology
2.1. Research Questions
- (1)
- How does different expert groups’ success with sub-problems differ from that of overall problem?
- (2)
- What characteristics do experts show while dealing with a wide range of stoichiometry questions?
2.2. Participants and Settings
2.3. Instruments and Design
3. Results and Discussions
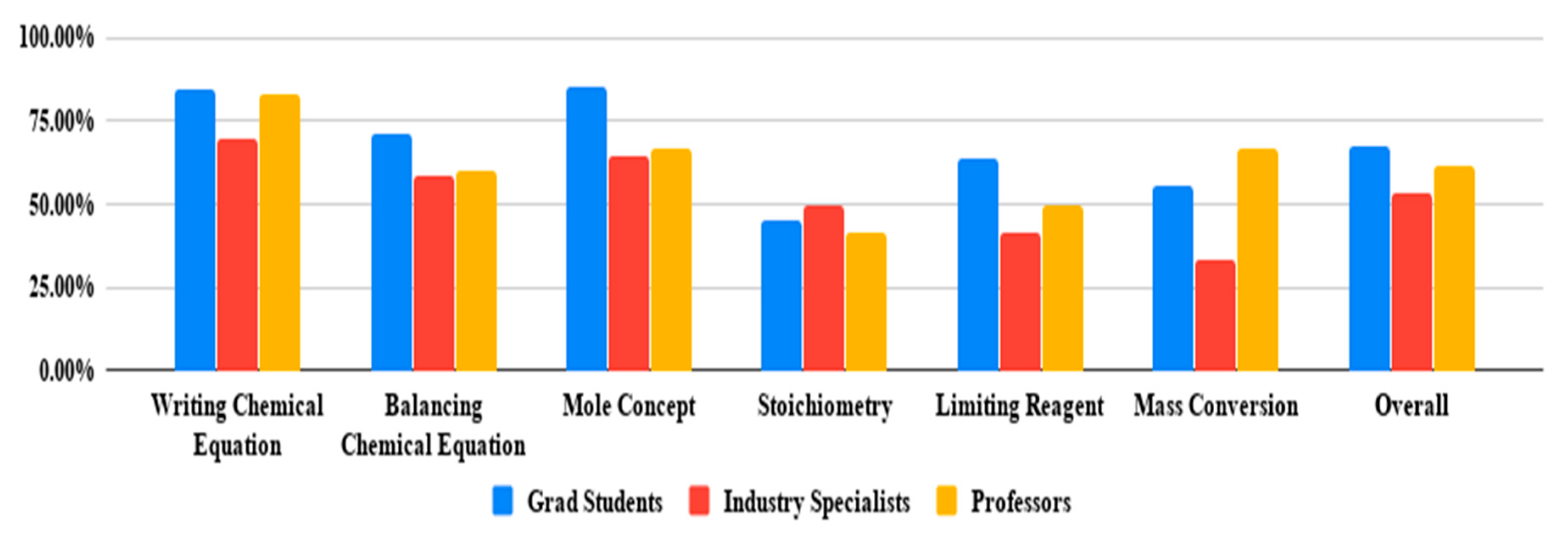
3.1. Analyzing Experts’ Success with Sub-problems Involving Individual Stoichiometric Topics:
3.2. Identifying the Characteristics of Experts in the Context of Stoichiometric Problem-Solving
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Candy, P.C.; Crebert, R.G. Ivory Tower to Concrete Jungle: The Difficult Transition from the Academy to the Workplace as Learning Environments. J. High. Educ. 1991, 62, 570–592. [Google Scholar] [CrossRef]
- Gabel, D.L.; Bunce, D.M. Research on problem solving: Chemistry. In Handbook of Research on Science Teaching and Learning; Gabel, D.L., Ed.; Macmillan: New York, NY, USA, 1994; p. 26. [Google Scholar]
- Sawrey, B.A. Concept Learning versus Problem Solving: Revisited. J. Chem. Educ. 1990, 67, 253–254. [Google Scholar] [CrossRef]
- Bhattacharyya, G.; Bodner, G.M. A cultural approach to problem solving. Educ. Química 2018, 16, 222. [Google Scholar] [CrossRef]
- Bodner, G.M.; Herron, J.D. Problem-Solving in Chemistry. In Chemical Education: Towards Research-Based Practice; Gilbert, J.K., De Jong, O., Justi, R., Treagust, D.E., Van Driel, J.H., Eds.; Kluwer: Dordrecht, The Netherlands, 2002; pp. 235–266. [Google Scholar]
- Nurrenbern, S.C.; Pickering, M. Concept Learning versus Problem Solving: Is There a Difference? J. Chem. Educ. 1987, 64, 508–510. [Google Scholar] [CrossRef]
- Bodner, G.M.; McMillen, T.L. Cognitive Restructuring as an Early Stage in Problem Solving. J. Res. Sci. Teach. 1986, 23, 727–737. [Google Scholar] [CrossRef]
- Pestel, B.C. Teaching Problem Solving without Modeling through “Thinking Aloud Pair Problem Solving”. Sci. Educ. 1993, 77, 83–94. [Google Scholar] [CrossRef]
- Yuriev, E.; Naidu, S.; Schembri, L.S.; Short, J.L. Scaffolding the development of problem-solving skills in chemistry: Guiding novice students out of dead ends and false starts. Chem. Educ. Res. Pract. 2017, 18, 486–504. [Google Scholar] [CrossRef]
- Broman, K.; Bernholt, S.; Parchmann, I. Using model-based scaffolds to support students solving context-based chemistry problems. Int. J. Chem. Educ. 2018, 40, 1176–1197. [Google Scholar] [CrossRef] [Green Version]
- Cooper, M.M.; Cox, C.T., Jr.; Nammouz, M.; Case, E.; Stevens, R. An Assessment of the Effect of Collaborative Groups on Students’ Problem-Solving Strategies and Abilities. J. Chem. Educ. 2008, 85, 866–872. [Google Scholar] [CrossRef]
- Smith, A.L.; Paddock, J.R.; Vaughan, J.M.; Parkin, D.W. Promoting Nursing Students’ Chemistry Success in a Collegiate Active Learning Environment: “If I Have Hope, I Will Try Harder”. J. Chem. Educ. 2018, 95, 1929–1938. [Google Scholar] [CrossRef]
- Frey, R.F.; Fink, A.; Cahill, M.J.; McDaniel, M.A.; Solomon, E.D. Peer-Led Team Learning in General Chemistry I: Interactions with Identity, Academic Preparation, and a Course-Based Intervention. J. Chem. Educ. 2018, 95, 2103–2113. [Google Scholar] [CrossRef]
- Richards-Babb, M.; Curtis, R.; Ratcliff, B.; Roy, A.; Mikalik, T. General Chemistry Student Attitudes and Success with Use of Online Homework: Traditional-Responsive versus Adaptive-Responsive. J. Chem. Educ. 2018, 95, 691–699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Talanquer, V. Concept Inventories: Predicting the Wrong Answer May Boost Performance. J. Chem. Educ. 2017, 94, 1805–1810. [Google Scholar] [CrossRef]
- Casselman, B.L.; Atwood, C.H. Improving General Chemistry Course Performance through Online Homework-Based Metacognitive Training. J. Chem. Educ. 2017, 94, 1811–1821. [Google Scholar] [CrossRef]
- Lysne, S.J.; Miller, B.G. Research and Teaching: A Comparison of Long-Term Knowledge Retention between Two Teaching Approaches. J. Coll. Sci. Teach. 2017, 46, 100–107. [Google Scholar] [CrossRef]
- Shadreck, M.; Enunuwe, O.C. Problem solving instruction for overcoming students’ difficulties in stoichiometric problems. Acta Didact. Napocensia 2017, 10, 69–78. [Google Scholar] [CrossRef]
- Huddle, P.A.; Pillay, A.E. An In-Depth Study of Misconceptions in Stoichiometry and Chemical Equilibrium at a South African University. J. Res. Sci. Teach. 1996, 33, 65–77. [Google Scholar] [CrossRef]
- Sankowsky, D.A. Expert Strategies for Poor-Performing Students in Technical Courses. J. Manag. Educ. 2001, 25, 379–393. [Google Scholar] [CrossRef]
- Bogard, T.; Liu, M.; Chiang, Y.-H.V. Thresholds of Knowledge Development in Complex Problem Solving: A Multiple-Case Study of Advanced Learners’ Cognitive Processes. Educ. Tech. Res. Dev. 2013, 61, 465–503. [Google Scholar] [CrossRef]
- Dixon, R.A.; Johnson, S.D. Experts vs. Novices: Differences in How Mental Representations Are Used in Engineering Design. J. Technol. Educ. 2011, 23, 47–65. [Google Scholar] [CrossRef]
- Chiou, G.-L. Reappraising the Relationships between Physics Students’ Mental Models and Predictions: An Example of Heat Convection. Phys. Rev. Spec. Top.-Phys. Educ. Res. 2013, 9, 010119. [Google Scholar] [CrossRef]
- Randles, A.C.; Overton, L.T. Expert “vs.” Novice: Approaches Used by Chemists When Solving Open-Ended Problems. Chem. Educ. Res. Pract. 2015, 16, 811–823. [Google Scholar] [CrossRef]
- Espinosa, A.A.; España, R.C.N.; Marasigan, A.C. Investigating Pre-service Chemistry Teachers’ Problem Solving Strategies: Towards Developing a Framework in Teaching Stoichiometry. J. Educ. Sci. Environ. Health (JESEH) 2016, 2, 104–124. [Google Scholar] [CrossRef]
- National Research Council; Committee on Learning Reaearch; Educational Practice; Bransford, J.; Pellegrino, J.W.; Donovan, S. How People Learn: Bridging Research and Practice; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Day, E.A.; Arthur, W.; Gettman, D. Knowledge structures and the acquisition of a complex skill. J. Appl. Psychol. 2001, 86, 1022–1033. [Google Scholar] [CrossRef] [PubMed]
- Burrows, N.L.; Mooring, S.R. Using concept mapping to uncover students’ knowledge structures of chemical bonding concepts. Chem. Educ. Res. Pract. 2015, 16, 53–66. [Google Scholar] [CrossRef]
- Gulacar, O.; Overton, T.L.; Bowman, C.R.; Fynewever, H. A novel code system for revealing sources of students’ difficulties with stoichiometry. Chem. Educ. Res. Pract. 2013, 14, 507–515. [Google Scholar] [CrossRef]
- Yin, Y.; Vanides, J.; Ruiz-Primo, M.A.; Ayala, C.C.; Shavelson, R.J. Comparison of Two Concept-Mapping Techniques: Implications for Scoring, Interpretation, and Use. J. Res. Sci. Teach. 2005, 42, 166–184. [Google Scholar] [CrossRef]
- Bradley, J.H.; Paul, R.; Seeman, E. Analyzing the structure of expert knowledge. Inf. Manag. 2006, 43, 77–91. [Google Scholar] [CrossRef]
- Swanson, L.H.; Fung, W. Working Memory Components and Problem-Solving Accuracy: Are There Multiple Pathways? J. Educ. Psychol. 2016, 108, 1153–1177. [Google Scholar] [CrossRef]
- St Clair-Thompson, H.; Overton, T.; Bugler, M. Mental Capacity and Working Memory in Chemistry: Algorithmic “versus” Open-Ended Problem Solving. Chem. Educ. Res. Pract. 2012, 13, 484–489. [Google Scholar] [CrossRef]
- Bodé, N.E.; Flynn, A.B. Strategies of Successful Synthesis Solutions: Mapping, Mechanisms, and More. J. Chem. Educ. 2016, 93, 593–604. [Google Scholar] [CrossRef] [Green Version]
- Clement, J.; Brown, D. Using Analogical Reasoning to Deal with “Deep” Misconceptions in Physics; ERIC: Columbus, OH, USA, 1984. [Google Scholar]
- Kahveci, M.; Orgill, M. Affective Dimensions in Chemistry Education; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Tjoe, H. Giftedness and Aesthetics: Perspectives of Expert Mathematicians and Mathematically Gifted Students. Gift. Child Q. 2015, 59, 165–176. [Google Scholar] [CrossRef]
- Voss, J.F.; Greene, T.R.; Post, T.A.; Penner, B.C. Psychology of Learning and Motivation; Bower, G.H., Ed.; Academic Press: Cambridge, MA, USA, 1983; Volume 17, pp. 165–213. [Google Scholar]
- Schoenfeld, A.H.; Herrmann, D.J. Problem Perception and Knowledge Structure in Expert and Novice Mathematical Problem Solvers. J. Exp. Psychol. Learn. Mem. Cogn. 1982, 8, 484–494. [Google Scholar] [CrossRef]
- Hoffman, B.; McCrudden, M.T.; Schraw, G.; Hartley, K. The Effects of Informational Complexity and Working Memory on Problem-Solving Efficiency. Asia Pac. Educ. Rev. 2008, 9, 464–474. [Google Scholar] [CrossRef]
- Van Merrienboer, J.J.; Sweller, J. Cognitive Load Theory and Complex Learning: Recent Developments and Future Directions. Educ. Psychol. Rev. 2005, 17, 147–177. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load theory, learning difficulty, and instructional design. Learn. Instr. 1994, 4, 295–312. [Google Scholar] [CrossRef]
- Kalyuga, S. Rapid cognitive assessment of learners’ knowledge structures. JLI Learn. Instr. 2006, 16, 1–11. [Google Scholar] [CrossRef]
- Gulacar, O.; Eilks, I.; Bowman, C.R. Differences in General Cognitive Abilities and Domain-Specific Skills of Higher- and Lower-Achieving Students in Stoichiometry. J. Chem. Educ. 2014, 91, 961–968. [Google Scholar] [CrossRef]
- Gulacar, O.; Bowman, C.R.; Feakes, D.A. Observational Investigation of Student Problem Solving: The Role and Importance of Habits. Sci. Educ. Int. 2013, 24, 344–360. [Google Scholar]
- Artistico, D.; Cervone, D.; Pezzuti, L. Perceived Self-Efficacy and Everyday Problem Solving Among Young and Older Adults. Psychol. Aging 2003, 18, 68–79. [Google Scholar] [CrossRef]
- Hunter, S.T.; Bedell-Avers, K.E.; Hunsicker, C.M.; Mumford, M.D.; Ligon, G.S. Applying multiple knowledge structures in creative thought: Effects on idea generation and problem-solving. Creat. Res. J. 2008, 20, 137–154. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulacar, O.; Tan, A.; Cox, C.T., Jr.; Bloomquist, J.; Jimmy, O.; Cao, N. Analyzing Characteristics of Experts in the Context of Stoichiometric Problem-Solving. Educ. Sci. 2019, 9, 219. https://doi.org/10.3390/educsci9030219
Gulacar O, Tan A, Cox CT Jr., Bloomquist J, Jimmy O, Cao N. Analyzing Characteristics of Experts in the Context of Stoichiometric Problem-Solving. Education Sciences. 2019; 9(3):219. https://doi.org/10.3390/educsci9030219
Chicago/Turabian StyleGulacar, Ozcan, Alexandra Tan, Charles T. Cox, Jr., Jennifer Bloomquist, Okechukwu Jimmy, and Nguyen Cao. 2019. "Analyzing Characteristics of Experts in the Context of Stoichiometric Problem-Solving" Education Sciences 9, no. 3: 219. https://doi.org/10.3390/educsci9030219





