Next Article in Journal
Fluorescent “OFF–ON” Sensors for the Detection of Sn2+ Ions Based on Amine-Functionalized Rhodamine 6G
Next Article in Special Issue
Preparation of Au@ZnO Nanofilms by Combining Magnetron Sputtering and Post-Annealing for Selective Detection of Isopropanol
Previous Article in Journal
Au Nanoparticles Decorated Graphene-Based Hybrid Nanocomposite for As(III) Electroanalytical Detection
Previous Article in Special Issue
High-Sensitivity Metal Oxide Sensors Duplex for On-the-Field Detection of Acetic Acid Arising from the Degradation of Cellulose Acetate-Based Cinematographic and Photographic Films
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemosensors
Volume 10
Issue 2
10.3390/chemosensors10020068
chemosensors-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Semiquantitative Classification of Two Oxidizing Gases with Graphene-Based Gas Sensors

by
Martin Lind
1,
Valter Kiisk
1,
Margus Kodu
1,
Tauno Kahro
1,
Indrek Renge
1,
Tea Avarmaa
1,
Prashanth Makaram
2,
Amaia Zurutuza
3 and
Raivo Jaaniso
1,*
1
Institute of Physics, University of Tartu, W. Ostwaldi 1, 50411 Tartu, Estonia
2
Infineon Technologies AG, 81726 Munich, Germany
3
Graphenea, Paseo Mikeletegi 83, 20009 Donostia-San Sebastian, Spain
*
Author to whom correspondence should be addressed.
Chemosensors 2022, 10(2), 68; https://doi.org/10.3390/chemosensors10020068
Submission received: 15 December 2021 / Revised: 3 February 2022 / Accepted: 6 February 2022 / Published: 8 February 2022
(This article belongs to the Special Issue High-Sensitivity and -Selectivity Gas Sensors with Nanoparticles, Nanostructures, and Thin Films)
Browse Figures
Versions Notes

Abstract

:
Miniature and low-power gas sensing elements are urgently needed for a portable electronic nose, especially for outdoor pollution monitoring. Hereby we prepared chemiresistive sensors based on wide-area graphene (grown by chemical vapor deposition) placed on Si/Si3N4 substrates with interdigitated electrodes and built-in microheaters. Graphene of each sensor was individually functionalized with ultrathin oxide coating (CuO-MnO2, In2O3 or Sc2O3) by pulsed laser deposition. Over the course of 72 h, the heated sensors were exposed to randomly generated concentration cycles of 30 ppb NO2, 30 ppb O3, 60 ppb NO2, 60 ppb O3 and 30 ppb NO2 + 30 ppb O3 in synthetic air (21% O2, 50% relative humidity). While O3 completely dominated the response of sensors with CuO-MnO2 coating, the other sensors had comparable sensitivity to NO2 as well. Various response features (amplitude, response rate, and recovery rate) were considered as machine learning inputs. Using just the response amplitudes of two complementary sensors allowed us to distinguish these five gas environments with an accuracy of ~ 85%. Misclassification was mostly due to an overlap in the case of the 30 ppb O3, and 30 ppb O3 + 30 ppb NO2 responses, and was largely caused by the temporal drift of these responses. The addition of recovery rates to machine learning input variables enabled us to very clearly distinguish different gases and increase the overall accuracy to ~94%.

Graphical Abstract

1. Introduction

Low-cost gas sensors of air pollution, which can be embedded in smartphones or other consumer and Internet-of-Things (IoT) devices, can help to reduce the adverse effects of polluting gases worldwide. The main polluting and health-affecting gases in the outdoor air are NO2, O3, SO2, and CO. In urban environments, nitrogen oxides (NO and NO2; commonly NOx) are emitted primarily from vehicle exhausts. Nitrogen dioxide is especially detrimental to health, producing nitric acid after inhalation and diffusion into the lungs. Ground-level ozone is very harmful to human health even at very low concentrations because of its strong oxidizing effect. O3 is a secondary pollutant emerging in atmospheric reactions involving NOx and volatile organic compounds under sunlight [1]. The US and EU standards of concentration limits for these two gases are similar, below 60–70 ppbv levels [2,3]. New World Health Organization (WHO) recommendations (2021) are even stricter with short- (long-) term target values of 13.3 (5.3) ppbv and 50 (30) ppbv for NO2 and O3 concentrations, respectively [4].
Ozone and NO2 are the most important pollutants, besides particulate matter, in terms of health risks [5]. As the traffic density in the urban environment depends largely on the exact location and time, monitoring of both gases with a large spatial and temporal resolution is essential. This is possible with a network of miniature sensors that can be fixed [6], transported [7], or carried in mobile devices. The miniaturization and low power consumption requirements should be met in the latter case without losing sensitivity. In turn, new materials have to be developed for this purpose, with lower working temperatures and compatible with the mass production technologies of microsensors.
Semiconducting metal oxides and other wide bandgap materials have been used for developing chemiresistive gas sensors [8,9]. Nanostructured metal oxides and other new nanomaterials have been demonstrated to be highly sensitive to NO2 or O3 [10,11,12,13]. Although various materials, device architectures, and readout strategies were proposed and investigated, only partial selectivity of the gas responses could be achieved [14]. NO2 is probably the most explored gas; several recent reviews cover its sensing with nanomaterials [15,16]. These studies generally do not include comparative results for ozone. Unfortunately, both electrochemical and conductometric sensors are known to have strong cross-sensitivity to these oxidizing gases [17,18].
In the case of metal-oxide-based conductometric sensors, a significant difference in the sensing mechanism of NO2 and O3 appears only at higher temperatures (above 200 °C) when ozone starts to dissociate on the surface of sensor material [19]. One possible solution for differentiating these gases at lower temperatures is the use of filters that deactivate ozone [20,21]. Another fundamental way to distinguish between gases is to use the principle of the electronic nose [22]. Here the different response patterns from partially selective sensors are fed into machine learning algorithms, which are then trained to predict the concentrations of individual gases [23,24,25,26].
Quantitative detection of formaldehyde and ammonia in the concentration range of 5–200 ppm was successfully demonstrated with a small array based on composites of metal oxides (SnO2 or CuO) and reduced graphene oxide with an artificial neural network (ANN) [27]. In Ref. [28], multiple linear regression and ANN algorithms were used to predict the concentrations of individual gases in the mixtures of NO2 and SO2 (in 50 ppb to 1 ppm range) with an array consisting of six commercial electrochemical sensors. The array of similar size, based on metal-oxide sensors, was demonstrated for semiquantitative detection of carbon monoxide and methane, with additional interference of hydrogen and formaldehyde; different models were utilized and evaluated, including principal components analysis (PCA), linear discriminant analysis (LDA) and ANN, whereas the ANN models had the best performance [26]. Using the dataset recorded for ethylene and CO mixture with 16 metal-oxide sensors (TGS2600, TGS2602, TGS2610, and TGS2620 by Figaro Engineering Inc.; four units of each type), the prediction accuracy of gas concentration via machine learning, based on a support vector machine model was studied in Ref. [29]. It was shown, in particular, that only two properly selected sensors were able to predict the concentrations of two gases with high accuracy.
For distinguishing only two gases, the responses of a few sensors are needed, their exact number depending on the quality of the signal and the required accuracy in gas determination. The simplest task is the classification of gases when the sensor system’s output is just an indication stating which gases are present. At the next complexity level, values of the gas concentrations are also provided. In the simplest form, it may be an air quality index (AQI) scale, extending from good to dangerous, coded by colors from green to red, respectively (see, e.g. [30,31]). Such classification is sufficient for consumer devices where numerical information about the concentrations of different gases is not needed and can even be distracting.
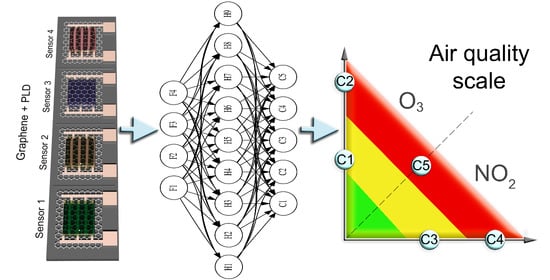
The goal of the present work is the semiquantitative classification of NO2 and O3 in the actual concentration range for outdoor air below ~100 ppb. The AQI scale used is shown in Figure 1. It is a simplified and fictional version for proof-of-principle, using somewhat lower limits for the medium and unhealthy situations than the current actual limit values to demonstrate the feasibility of our approach in light of recent WHO recommendations. The air quality scale has three zones, and the gas responses of different sensors are investigated for five gas compositions in the air: 30 and 60 ppb of NO2, 30 and 60 ppb of O3, and a mixture of 30 ppb of NO2 and 30 ppb of O3.
We are using graphene-based devices functionalized with different metal oxide layers to render the sensors different in terms of partial selectivity. Graphene-based chemiresistors can be extremely sensitive because of the large surface to volume and signal-to-noise ratios. With optimized signal recording, adsorption and desorption events of single gas molecules have been detected [32]. However, for distinguishing different gases, one has to create on the surface of graphene specific adsorption centers for the sake of selectivity to different molecules. In the chemiresistive sensors built on a large area CVD (chemical vapor deposition) or epitaxial graphene, the highly conducting carbon layer acts as an effective electrical transducer, and the functionalizing layers (or defects, particles, atomic groups) provide receptors for different molecules. The enhanced sensitivity and selectivity of graphene functionalized by pulsed laser deposited layers were previously demonstrated for NO2 and NH3 gases and some volatile compounds [33,34,35].

2. Materials and Methods

Single-layer CVD graphene was grown on a polycrystalline copper foil and transferred onto sensor array substrates using a wet transfer procedure. Each element on a sensor array was individually functionalized with a thin oxide coating by pulsed laser deposition (PLD). Three ceramic targets consisting of pressed and sintered metal oxides were used in the PLD process for functionalization: two single-metal oxide targets In2O3 (CAS No. 1312-43-2, 99.99 % pure, Kurt J. Lesker) and Sc2O3, (CAS No. 12060-08-1, 99.9 % pure, JV “New Materials and Technologies”, Ukraine) and a CuO-MnO2 (CuO: CAS No.-s 1317-38-0, 99.995 % pure, Alfa Aesar and MnO2: CAS No. 1313-13-9, 99 % pure, Reakhim) mixed-oxide target with the nominal Cu/Mn atomic ratio of 1/3. The routine PLD process of graphene functionalization was described in Ref. [34]. Briefly, a KrF excimer laser (Coherent COMPexPro 205, wavelength 248 nm, pulse width ~25 ns, repetition rate 5 Hz, energy density on the target 3.0 ± 0.3 J/cm2) was used for deposition in dilute oxygen atmosphere (CAS No. 7782-44-7, 99.999 % pure, AS Linde Gas) while the distance between the substrate and the target was 75 ± 3 mm. Specific process parameters for the functionalization of individual sensors are summarized in Table 1. A shadow mask attached to a linear actuator was used for selecting individual sensors during successive deposition of functionalizing layers. The growth rate of the oxide layer was estimated to be approximately 0.5 ± 0.1 nm per 100 laser pulses. The functionalization by PLD was followed by mounting the sensor substrates to the printed circuit board (PCB) and wire bonding of electrodes of each sensor to the PCB electrode patches. The scheme of an individual sensor on the substrate is depicted in Figure 3 (inset). The sensor substrate contains several sensors, each consisting of a pair of interdigitated metal electrodes (nominal gap width 20 μm) and a separate micro-heater underneath.
The Raman spectra were recorded with Renishaw inVia micro-Raman spectrometer (excitation wavelength 514 nm, spot size ~1 µm, incident power ~1 mW). The spectral resolution of the Raman spectrometer was approximately 2 cm−1 and the wavenumber calibration error ±1 cm−1. The SEM images were obtained using a FEI Helios NanoLab 600 (FIB/SEM) electron microscope. Image acquisition parameters were as follows: electron beam acceleration voltage 2 kV, beam current 8.6 × 10−11 A; a through-the-lens detector was used.
Figure 2 depicts a scheme of the experimental setup for gas sensitivity measurements. The gas mixture was prepared from cylinder gases passing through mass flow controllers into a mixer. The sensors were placed in a small test chamber (internal volume 15 ± 0.5 cm3). The total gas flow through the chamber was kept constant at 200 ± 2 sccm, while the flow rates of individual gases (N2 CAS No. 7727-37-9, O2 CAS No. 7782-44-7, NO2/N2 mixture, all 99.999% pure and all from AS Linde Gas) were varied by mass flow controllers (Brooks SLA5820). The content of NO2 in the gas cylinder with NO2/N2 mixture was 70 ppm (certified by AS Linde Gas) and this gas was fed into the system with an accuracy of 15 μl/min. Ozone was produced with a UV-lamp-based generator (SOG-1, UPV/Analytic Jena), and the resulting O3 concentration was continuously monitored with an analyzer (Teledyne, model 430). The analyte gas concentrations and their estimated accuracies are as follows: 30.0 ± 2.5 and 60.0 ± 2.5 ppb of NO2, 30 ± 2 and 60 ± 2 ppb of O3. The dioxygen content in the gas mixture was always kept constant at 21% to simulate typical atmospheric composition. For the same reason, during the sensor measurements, the relative humidity of testing gas was held at 50%, achieved by passing a part of N2 flow through the water bubbler. Since the testing was performed in the flow-through regime, the gas pressure in the test chamber was equal to atmospheric pressure. The composition of the gas flow was computer-controlled with LABVIEW-based software.
The resistance of sensors was recorded (sampled once per second) with a special lab-built data acquisition system based on Arduino NANO microprocessor and 12-bit A/D-converters. This device also controlled the temperature of sensors via the voltage applied to microheaters.
All sensor elements were kept at approximately 140 °C throughout the measurements. Although the used sensors responded to NO2 and O3 at room temperature, the recovery times were too long (over 1 hour) for meaningful applications. At the higher temperature, both the response and recovery rates increase, as demonstrated in Ref. [35] for PLD functionalized graphene gas sensors. However, with growing sensor temperature, the sensitivity decreases [35], and therefore, 140 °C was chosen as the optimum measurement temperature considering both the sensor speed and response magnitude.
Machine learning studies were conducted in the Python programming language. As a universal nonlinear classifier, we used a feed-forward artificial neural network (ANN). ReLU was used as an activation function in the hidden layers, and the log-loss function was optimized with the Adam method (with backpropagation). Typically, ReLU is preferred over other activation functions (tanh or sigmoid), as it may improve the sparsity of the model, avoid the issue of vanishing gradient, and is very efficient computationally. Such ANN was implemented by the MLPClassifier of the Scikit-Learn library. Due to the limited amount of data (~100 data points), it was split in a 50:50 ratio for training and testing. Moreover, the initial order of data points was retained to reflect the potential temporal drift of the sensors, which could severely affect the result in a real sensing scenario. The performance of the trained ANN is characterized by the F1 score metric, evaluated as a harmonic mean of the precision and recall.

3. Results and Discussion

A typical Raman spectrum of pristine CVD graphene transferred onto the sensor array substrate is depicted in Figure 3 (left). The spectrum is characteristic for a single layer CVD graphene with a low defect density. The two bands peaking at 1585 cm−1 and 2684 cm−1, denoted as G- and 2D-bands, respectively [36,37], are the main features in the graphene Raman spectrum. Two very minor bands appear at 2458 (D + D″) and 3250 cm−1. According to Ferrari et al. [37], the G band belongs to the high-frequency E2g phonon that is due to the in-plane stretching motion of sp2 carbon atoms. The D band corresponds to breathing modes of six-atom rings and requires a defect for its activation. By contrast, the D band overtone 2D does not require the presence of symmetry breaking defects. In the case of single-layer graphene, the 2D band has the largest intensity; it broadens and loses intensity in multi-layer graphene. High-quality single-layer graphene would have only G and 2D bands, whereas defective graphene has D, D′ and D + D′ peaks in addition to the main bands.
A very faint defect-related D-band located at 1345 cm−1 indicates low defect density in the pristine CVD graphene sample. Figure 3 also shows a typical spectrum of graphene after functionalization. The emergence of defect-related D bands, and a simultaneous decrease of the 2D band intensity, as compared to G band, indicate that the point defect density in graphene increases during the PLD, caused by the bombardment with high energy particles present in plasma [38].
An SEM image of the graphene layer on top of interdigitated sensor electrodes is presented in the right panel of Figure 3. The smaller, darker contrasting features belong to the regions of double or/and triple layer graphene. The graphene film grown on polycrystalline copper foil by CVD is typical > 95% single layer and <5% bi/three-layer, the exact proportions depending on the growth conditions [39,40,41]. A layer of nanostructured thin metal oxide material is typically seen in the SEM images after the PLD (not shown). For examples of both a sub-nanometer layer and a few-nanometers-thick layer, see our previous publications [34] and [33], respectively.
Figure 4 shows an overview of time-dependent conductivities for the four sensors on a micro-hotplate substrate during an experimental run. The gas exposure period (ON) lasted for 15 min. and the recovery period (OFF) for 30 min. Considering the goal of semiquantitative gas analysis, two concentrations of pure NO2 and O3 (30 and 60 ppb) and their mixture (30 ppb of NO2 + 30 ppb of O3) were chosen for gas sensing and machine learning studies. Thus, the sensors were randomly exposed to five different gaseous environments. Overall, the sensor array was subjected to nearly 100 such gas concentration cycles over a period of 72 h. Under real sensing conditions, the gas composition generally changes more gradually. However, such an ON-OFF gas exchange protocol can be implemented in real sensors by flow modulation (sniffing [42,43] or by releasing the gases from a pre-concentrator).
In terms of conductance, the overall response amplitudes (defined as the difference between the maximum and minimum values) of sensors S1, S3 and S4 to O3 were comparable; the response of sensor S2 was 2.5 times smaller (Table 2). The baselines, and thereby the relative responses, vary considerably. Sensor S1 had the highest relative response, with the amplitudes changing up to 55%. One can also observe a small baseline drift of less than 10% over the 72 h period. In this regard, sensors S1 and S3 were the most stable and had the largest relative response.
Both the sensitivity (response amplitude per unit gas concentration) and baseline were affected by functionalization (PLD target material and process parameters). As compared to high quality pristine graphene that has very little gas sensitivity [44,45,46], the sensitivity is increased significantly after PLD due to the creation of effective adsorption centers [33]. The conductance of pristine graphene samples before the PLD was 25–30 mS. Different initial conductance of sensors S1–S4 is caused by the defects formed in the laser deposition process. The number of defects created in the graphene depends on the kinetic energy of laser-ablated particles as they hit the surface, which is the function of the target material, the laser energy density, and, most importantly, gas pressure in the deposition chamber [38]. For example, the conductivity of sample S1 (made at 5 Pa of O2) is lower than the conductivity of sample S4 (made at 10 Pa), although the number of laser pulses is higher for the last coating.
Similar combinations of graphene with ultra-thin oxide layers have been extensively studied [33,34,35]. A large (almost 100-fold) increase in gas sensitivity was found after the PLD of oxide layers. The effect was always accompanied by an increase of the D-line in the Raman spectrum and a decrease in electrical conductivity, indicating defect formation in graphene. The density of new gas adsorption centers created by the PLD process was shown to be proportional to the density of point defects [33], whereas the proportionality factor would depend on the gas pressure in the PLD chamber [34].
Figure 5 shows the gas responses in a smaller time scale, where typical individual transient responses to five gas compositions are presented for all sensors in sequence. Ozone generally dominated in the responses, especially for sensors S1 and S3. Sensors S2 and S4, on the other hand, had a reasonably strong response to NO2 as well. For sensor S4, in particular, the response amplitude to NO2 reached about 60% of the response to O3 (at 30 ppb). On the other hand, the response rates of sensors S1 and S3 were by a factor of 2.7 times faster, with a characteristic response time of 125 s.
Figure 6 shows an enlarged view of a typical transient response when exposed to ppb-levels of gas. Several characteristic features derived from such transient response can potentially be utilized for the subsequent machine learning [47]. In the case of two gas components, either a pair of reasonably different sensors or two complementary features of a single sensor are needed at least. Hereby, we considered three types of features having the most straightforward physical interpretation: the response amplitude (difference between the maximum and minimum values of the recorded signal over one cycle), the response rate (inverse rise time) and the recovery rate (inverse recovery time). The first two quantities are directly related to the concentration of the respective gases, whereas the recovery rate is determined by the adsorption energy of gas molecules [8,9]. Curve fitting was exclusively used to derive the feature values (Figure 6). The rate constants were obtained by fitting the initial rising and decaying parts of the transient response curve with the function ae−kt + b (where the parameter k represents either the response rate or the recovery rate), because effectively a first-order kinetics can be assumed over a limited time span. To reduce the effect of noise and other minor irregularities, the terminal value of the conductivity (at the end of the response or recovery period) was determined from the endpoint of a second order polynomial fitted through a preceding section of the curve.
As already seen from Figure 5, the response amplitudes of all sensors were well correlated to the gas concentration. The recovery rates of the sensors S1 and S2 also provided useful inputs for the discrimination of gases. The inclusion of the response rates, however, did not increase the prediction accuracy of machine learning. In part, this may be due to limited resolution of the signal or signal-to-noise ratio because derivative-like quantities acquire more noise than the primary data. Moreover, the adsorption may be a complex phenomenon involving several types of adsorption centers and competitive processes between different oxidizing gases (including dioxygen). In both cases, the signal kinetics cannot be described with a single rate constant.
Figure 7 shows a couple of examples of how the data points cluster in 2D feature space. In terms of the response amplitudes of complementary sensors (such as S1 and S2), the data points remain sufficiently well localized and segregated so that there is only minor overlapping of the domains corresponding to different gas environments. However, the recovery rates do not show such clustering. The regions of 30 ppb NO2 and 60 ppb NO2 are completely overlapping, whereas O3-related data points are significantly shifted along one coordinate.
It is possible that the segregation would improve further in a higher-dimensional feature space. On the contrary, the temporal drift may severely degrade the result. These issues cannot be easily assessed visually and require machine learning. We used a classifier based on a simple feed-forward artificial neural network. An advantage of an ANN is its potentially very large learning capacity, and it is only limited by the number of hidden layers and the number of neurons in each layer. On the other hand, if the amount of training data is small, a large ANN is susceptible to overtraining and fails to generalize the data. This can be counteracted by various regularization techniques, such as constraining the parameter space, typically penalizing overly large parameter values. We tested various ANN configurations. It was found that one hidden layer was sufficient for this task. Distributing the neurons in multiple layers reduced the prediction accuracy even if the overall number of neurons remained small. With no regularization applied, about nine neurons in a single layer provided optimal results. A regularized (using non-zero L2 penalty) ANN was also considered, in which case more neurons were required in the hidden layer, but the classification performance was nearly identical.
Table 3 shows the obtained accuracy when applying a trained ANN to the test data, for a variety of chosen gas response features. Using just two response amplitudes allowed for the distinguishing of the five environments with an accuracy of ~85%. Further improvement was gained (accuracy ~94%) by incorporating both amplitudes and recovery rates of sensors S1 and S2 (the results are also illustrated in Figure 1). One can see that the accuracy is essentially the same for an unregularized 9-neuron network and regularized 100-neuron network. In both cases, only the data for the final optimized network configuration are shown in Table 3.
An obvious conclusion is that for the current problem, the best classifier in terms of simplicity and accuracy is ANN with a single hidden layer and without the penalty parameter. Figure 8 illustrates the performance of such a classifier as applied to time-sequential data. The few mistakes are in the assignment of 30 ppb O3 and 30 ppb O3 + ppb NO2. It is indeed these two gas compositions that are most likely to be confused when looking at the data in Figure 7.
We also see the tendency that the mistakes become more frequent as time progresses. The reason becomes evident when we replot the data in Figure 7 in a manner that also indicates the time coordinate (Figure 9). We can see that within each cluster there is, in addition to the random scatter, also some preferred direction of movement over time. Potentially, without such temporal drift of the responses, the sensors could consistently distinguish the gases with an accuracy approaching 100%. It requires further studies over longer time periods to assess the origin and persistence of this drift. Because of the temporal drift, it is meaningful for machine learning to retain the temporal order of the data points for a more realistic outcome.
The results are comparable to similar experiments (albeit for different gas combinations) described by the literature, for example, [24] and [26]. However, there are plenty of publications on NO2 and O3 sensors separately (see the Refs. discussed in the introduction [10,11,12,13,15,16], the distinctive co-detection of these gases has been underexplored. In Ref [48], a sensor array based on MoS2 nanosheets has been used and the distinction between NO2 and O3 by PCA has been demonstrated. However, the sensitivities and detection limits (215 ppb for NO2 and 17 ppb for O3) achieved in Ref [48] were insufficient for environmental applications.

4. Conclusions

The resistivity of CVD graphene, functionalized with different nanometer-thin metal oxide coatings by pulsed laser deposition, generally shows an excellent response to ppb-levels of NO2 and O3 in the air. At comparable concentrations, O3 typically predominates in the sensors’ responses. Still, heated sensors based on In2O3 and Sc2O3 coatings showed a relatively strong NO2 response when O3 was present. By contrast, CuO-MnO2-based sensors had a weaker response to NO2 and were easily saturated by O3. Using the response amplitudes of two complementary sensors and applying a basic feed-forward neural network for machine learning, it was possible to distinguish between 30 ppb and 60 ppb NO2 and O3, and their mixture, with an accuracy of ~85%. The classification errors were mostly associated with an overlapping of the 30 ppb O3 and 30 ppb O3 + 30 ppb NO2 responses and largely caused by the temporal drift of the sensors’ responses. Further improvement was gained (accuracy ~94%) by including the recovery rates from sensors functionalized with CuO-MnO2 and In2O3. This is explained by the fact that the recovery rate is determined by the binding energy, and hence distinguishes primarily different gases rather than their concentrations.
The model contained only one hidden layer (with ReLU as activation function), and distributing the neurons in multiple layers reduced the prediction accuracy. With no regularization applied, about 9 neurons provided optimal results. A regularized (using non-zero L2 penalty) ANN was also considered, in which case more neurons were required in the hidden layer, but the classification performance was nearly identical.
To conclude, the viability of graphene-based sensors was demonstrated for an important environmental application, monitoring the principal harmful gases, ozone and NOx, in the polluted city air with a cost-effective miniature device, in terms of suitable sensitivity and selectivity. Further studies are needed to take into account the effects of long-term stability and humidity.

Author Contributions

Conceptualization, R.J., V.K. and I.R.; methodology, V.K., M.K., M.L. and P.M.; formal analysis, M.L. and V.K.; investigation, T.A., T.K. and M.K.; resources, P.M and A.Z.; writing—original draft preparation, V.K., M.K, M.L. and R.J.; writing—review and editing, I.R. and A.Z.; supervision, V.K. and R.J.; funding acquisition, A.Z. and R.J. All authors have read and agreed to the published version of the manuscript.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation program under Graphene Flagship grant agreement No 881603.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This work was supported by ERDF project Centre of Technologies and Investigations of Nanomaterials (NAMUR+, project number 2014-2020.4.01.16-0123). The authors are grateful to Riho Raabe and Agu Anijalg for their help with the data acquisition system and Jekaterina Kozlova for the SEM image.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  1. Atkinson, R. Atmospheric chemistry of VOCs and NOx. Atmos. Environ. 2000, 34, 2063–2101. [Google Scholar] [CrossRef]
  2. Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe. OJ L 152, 11.6.2008, p. 1–44. Available online: https://www.eea.europa.eu/themes/air/air-quality-concentrations/AirQlimitvalues.png (accessed on 15 December 2021).
  3. US National Ambient Air Quality Standards. Available online: https://www.epa.gov/criteria-air-pollutants/naaqs-table (accessed on 15 December 2021).
  4. WHO Global Air Quality Guidelines. Particulate Matter (PM2.5 and PM10), Ozone, Nitrogen Dioxide, Sulfur Dioxide and Carbon Monoxide; World Health Organization: Geneva, Switzerland, 2021; ISBN 9789240034228. [Google Scholar]
  5. Huangfu, P.; Atkinson, R. Long-term exposure to NO2 and O3 and all-cause and respiratory mortality: A systematic review and meta-analysis. Environ. Int. 2020, 144, 105998. [Google Scholar] [CrossRef] [PubMed]
  6. Castell, N.; Schneider, P.; Grossberndt, S.; Fredriksen, M.F. Localized real-time information on outdoor air quality at kindergartens in Oslo, Norway using low-cost sensor nodes. Environ. Res. 2018, 165, 410–419. [Google Scholar] [CrossRef] [PubMed]
  7. Mueller, M.; Meyer, J.; Hueglin, C. Design of an ozone and nitrogen dioxide sensor unit and its long-term operation within a sensor network in the city of Zurich. Atmos. Meas. Tech. 2017, 10, 3783–3799. [Google Scholar] [CrossRef] [Green Version]
  8. Barsan, N.; Schierbaum, K. (Eds.) Gas Sensors Based on Conducting Metal Oxides: Basic Understanding, Technology and Applications; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128112243. [Google Scholar]
  9. Jaaniso, R.; Tan, O.K. (Eds.) Semiconductor Gas Sensors, 2nd ed.; Elsevier/Woodhead Publ.: Amsterdam, The Netherlands, 2020; ISBN 9780081025598. [Google Scholar]
  10. Llobet, E. (Ed.) Advanced Nanomaterials for Inexpensive Gas Microsensors: Synthesis, Integration and Applications; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128148273. [Google Scholar]
  11. Meng, Z.; Stolz, R.M.; Mendecki, L.; Mirica, K.A. Electrically-transduced chemical sensors based on two-dimensional nanomaterials. Chem. Rev. 2019, 119, 478–598. [Google Scholar] [CrossRef]
  12. Malik, R.; Tomer, V.K.; Mishra, Y.K.; Lin, L. Functional gas sensing nanomaterials: A panoramic view. Appl. Phys. Rev. 2020, 7, 021301. [Google Scholar] [CrossRef] [Green Version]
  13. Korotcenkov, G. Current trends in nanomaterials for metal oxide-based conductometric gas sensors: Advantages and limitations. Part 1: 1D and 2D nanostructures. Nanomaterials 2020, 10, 1392. [Google Scholar] [CrossRef]
  14. Hunter, G.W.; Akbar, S.; Bhansali, S.; Daniele, M.; Erb, P.D.; Johnson, K.; Liu, C.-C.; Miller, D.; Oralkan, O.; Hesketh, P.J.; et al. A critical review of solid state gas sensors. J. Electrochem. Soc. 2020, 167, 037570. [Google Scholar] [CrossRef]
  15. Lee, S.W.; Lee, W.; Hong, Y.; Lee, G.; Yoon, D.S. Recent advances in carbon material-based NO2 gas sensors. Sens. Actuators B Chem. 2018, 255, 1788–1804. [Google Scholar] [CrossRef]
  16. Kumar, S.; Pavelyev, V.; Mishra, P.; Tripathi, N.; Sharma, P.; Calle, F. A review on 2D transition metal di-chalcogenides and metal oxide nanostructures based NO2 gas sensors. Mater. Sci. Semicond. Processing 2020, 107, 104865. [Google Scholar] [CrossRef]
  17. Isiugo, K.; Newman, N.; Jandarov, R.; Grinshpun, S.A.; Reponen, T. Assessing the accuracy of commercially available gas sensors for the measurement of ambient ozone and nitrogen dioxide. J. Occup. Environ. Hyg. 2018, 15, 782–791. [Google Scholar] [CrossRef] [PubMed]
  18. Ivanovskaya, M.; Gurlo, A.; Bogdanov, P. Mechanism of O3 and NO2 detection and selectivity of In2O3 sensors. Sens. Actuators B Chem. 2001, 77, 264–267. [Google Scholar] [CrossRef]
  19. Korotcenkov, G.; Brinzari, V.; Cho, B.K. In2O3- and SnO2-based thin film ozone sensors: Fundamentals. J. Sens. 2016, 3816094. [Google Scholar] [CrossRef] [Green Version]
  20. Hossain, M.; Saffell, J.; Baron, R. Differentiating NO2 and O3 at low cost air quality amperometric gas sensors. ACS Sens. 2016, 1, 1291–1294. [Google Scholar] [CrossRef]
  21. Othman, M.; Théron, C.; Bendahan, M.; Caillat, L.; Rivron, C.; Bernardini, S.; Le Chevallier, G.; Chevallier, E.; Som, M.-P.; Aguir, K.; et al. Efficiency of new ozone filters for NO2 sensing and air depollution. Sens. Actuators B Chem. 2018, 265, 591–599. [Google Scholar] [CrossRef]
  22. Pearce, T.C.; Schiffman, S.S.; Nagle, H.T.; Gardner, J.W. (Eds.) Handbook of Machine Olfaction: Electronic Nose Technology; Wiley: Weinheim, Germany, 2003; ISBN 9783527303588. [Google Scholar]
  23. Marco, S.; Gutierrez-Galvez, A. Signal and data processing for machine olfaction and chemical sensing: A review. IEEE Sens. J. 2012, 12, 3189–3214. [Google Scholar] [CrossRef]
  24. Chen, Z.; Chen, Z.; Song, Z.; Ye, W.; Fan, Z. Smart gas sensor arrays powered by artificial intelligence. J. Semicond. 2019, 40, 111601. [Google Scholar] [CrossRef]
  25. Feng, S.; Farha, F.; Li, Q.; Wan, Y.; Xu, Y.; Zhang, T.; Ning, H. Review on smart gas sensing technology. Sensors 2019, 19, 3760. [Google Scholar] [CrossRef] [Green Version]
  26. Zhang, J.; Xue, Y.; Sun, Q.; Zhang, T.; Chen, Y.; Yu, W.; Xiong, Y.; Wei, X.; Yu, G.; Wan, H.; et al. A miniaturized electronic nose with artificial neural network for anti-interference detection of mixed indoor hazardous gases. Sens. Actuators B Chem. 2021, 326, 128822. [Google Scholar] [CrossRef]
  27. Zhang, D.; Liu, J.; Jiang, C.; Liu, A.; Xia, B. Quantitative detection of formaldehyde and ammonia gas via metaloxide-modified graphene-based sensor array combining with neural network model. Sens. Actuators B Chem. 2017, 240, 55–65. [Google Scholar] [CrossRef]
  28. Dmitrzak, M.; Jasinski, P.; Jasinski, G. Limited selectivity of amperometric gas sensors operating in multicomponent gas mixtures and methods of selectivity improvement. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1257–1282. [Google Scholar] [CrossRef]
  29. Bae, G.; Kim, M.; Song, W.; Myung, S.; Lee, S.S.; An, K.-S. Impact of a diverse combination of metal oxide gas sensors on machine learning-based gas recognition in mixed gases. ACS Omega 2021, 6, 23155–23162. [Google Scholar] [CrossRef] [PubMed]
  30. Tan, X.; Han, L.; Zhang, X.; Zhou, W.; Li, W.; Qian, Y. A review of current air quality indexes and improvements under the multi-contaminant air pollution exposure. J. Environ. Manag. 2021, 279, 111681. [Google Scholar] [CrossRef] [PubMed]
  31. Spyropoulos, G.C.; Nastos, P.T.; Moustris, K.P. Performance of Aether low-cost sensor device for air pollution measurements in urban environments. Accuracy evaluation applying the Air Quality Index (AQI). Atmosphere 2021, 12, 1246. [Google Scholar] [CrossRef]
  32. Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed]
  33. Kodu, M.; Berholts, A.; Kahro, T.; Avarmaa, T.; Kasikov, A.; Niilisk, A.; Alles, H.; Jaaniso, R. Highly sensitive NO2 sensors by pulsed laser deposition on graphene. Appl. Phys. Lett. 2016, 109, 113108. [Google Scholar] [CrossRef] [Green Version]
  34. Kodu, M.; Berholts, A.; Kahro, T.; Eriksson, J.; Yakimova, R.; Avarmaa, T.; Renge, I.; Alles, H.; Jaaniso, R. Graphene-based ammonia sensors functionalized with sub-monolayer V2O5: A comparative study of chemical vapour deposited and epitaxial graphene. Sensors 2018, 19, 951. [Google Scholar] [CrossRef] [Green Version]
  35. Rodner, M.; Icardi, A.; Kodu, M.; Jaaniso, R.; Schutze, A.; Eriksson, J. Metal oxide nanolayer-decorated epitaxial graphene: A gas sensor study. Nanomaterials 2020, 11, 2169. [Google Scholar] [CrossRef]
  36. Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401–187404. [Google Scholar] [CrossRef] [Green Version]
  37. Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nature Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef] [Green Version]
  38. Eason, R. (Ed.) Pulsed Laser Deposition of Thin Films: Application-Led Growth of Functional Materials; Wiley-Interscience (Online Service): Hoboken, NJ, USA, 2006; ISBN 9780470052129. [Google Scholar] [CrossRef]
  39. Liu, W.; Li, H.; Xu, C.; Khatami, Y.; Banerjee, K. Synthesis of high-quality monolayer and bilayer graphene on copper using chemical vapor deposition. Carbon 2011, 49, 4122–4130. [Google Scholar] [CrossRef]
  40. Nie, S.; Wu, W.; Xing, S.; Yu, Q.; Bao, J.; Pei, S.-S.; McCarty, K.F. Growth from below: Bilayer graphene on copper by chemical vapor deposition. N. J. Phys. 2012, 14, 093028. [Google Scholar] [CrossRef]
  41. Zhang, X.; Wang, L.; Xin, J.; Yakobson, B.I.; Ding, F. Role of hydrogen in graphene chemical vapor deposition growth on a copper surface. J. Am. Chem. Soc. 2014, 136, 3040–3047. [Google Scholar] [CrossRef] [PubMed]
  42. Staymates, M.E.; MacCrehan, W.A.; Staymates, J.L.; Kunz, R.R.; Mendum, T.; Ong, T.-H.; Geurtsen, G.; Gillen, V.; Craven, B.A. Biomimetic sniffing improves the detection performance of a 3D printed nose of a dog and a commercial trace vapor detector. Sci. Rep. 2016, 6, 36876. [Google Scholar] [CrossRef]
  43. Spencer, T.L.; Clark, A.; Fonollosa, J.; Virot, E.; Hu, D.L. Sniffing speeds up chemical detection by controlling air-flows near sensors. Nature Commun. 2021, 12, 1232. [Google Scholar] [CrossRef] [PubMed]
  44. Kumar, B.; Min, K.; Bashirzadeh, M.; Farimani, A.B.; Bae, M.-H.; Estrada, D.; Kim, Y.D.; Yasei, P.; Park, Y.D.; Pop, E.; et al. The role of external defects in chemical sensing of graphene field-effect transistors. Nano Lett. 2013, 13, 1962–1968. [Google Scholar] [CrossRef]
  45. Ricciardella, F.; Vollebregt, S.; Polichetti, T.; Miscuglio, M.; Alfano, B.; Miglietta, M.L.; Massera, E.; Di Francia, G.; Sarro, P.M. Effects of graphene defects on gas sensing properties towards NO2 detection. Nanoscale 2017, 9, 6085–6093. [Google Scholar] [CrossRef] [Green Version]
  46. Fu, W.; Jiang, L.; van Greet, E.P.; Lima, L.M.C.; Schneider, G.F. Sensing at the surface of graphene field-effect transistors. Adv. Mater. 2017, 29, 1603610. [Google Scholar] [CrossRef] [Green Version]
  47. Yan, J.; Guo, X.; Duan, S.; Jia, P.; Wang, L.; Peng, C.; Zhang, S. Electronic nose feature extraction methods: A review. Sensors 2015, 15, 27804–27831. [Google Scholar] [CrossRef]
  48. Shao, L.; Wu, Z.; Duan, H.; Shaymurat, T. Discriminative and rapid detection of ozone realized by sensor array of Zn2+ doping tailored MoS2 ultrathin nanosheets. Sens. Actuators B Chem. 2018, 258, 937–946. [Google Scholar] [CrossRef]
Chemosensors 10 00068 g001 550
Figure 1. Air quality scale with discrete gas concentration points used in the study. The F1 scores shown are figures of merit for a concrete sensor array and machine learning algorithm described in the Results section. The model used was artificial neural network (ANN) using four sensors (see Table 1).
Figure 1. Air quality scale with discrete gas concentration points used in the study. The F1 scores shown are figures of merit for a concrete sensor array and machine learning algorithm described in the Results section. The model used was artificial neural network (ANN) using four sensors (see Table 1).
Chemosensors 10 00068 g001
Chemosensors 10 00068 g002 550
Figure 2. The experimental setup used for gas sensitivity measurements. MFC—mass flow controller, M—gas mixer, O3 Gen—ozone generator, H2O—water bubbler.
Figure 2. The experimental setup used for gas sensitivity measurements. MFC—mass flow controller, M—gas mixer, O3 Gen—ozone generator, H2O—water bubbler.
Chemosensors 10 00068 g002
Chemosensors 10 00068 g003 550
Figure 3. Left—Raman spectra of CVD graphene in sensor device, recorded before (pristine) and after PLD process (a.u. means arbitrary intensity units of the Raman instrument; the spectrum of pristine graphene is shifted upwards by 650 units). Inset: Scheme of the sensor based on PLD-functionalized CVD graphene on the micro-hotplate sensor substrate. Right—SEM image of single-layer graphene on top of interdigitated electrodes of the sensor substrate.
Figure 3. Left—Raman spectra of CVD graphene in sensor device, recorded before (pristine) and after PLD process (a.u. means arbitrary intensity units of the Raman instrument; the spectrum of pristine graphene is shifted upwards by 650 units). Inset: Scheme of the sensor based on PLD-functionalized CVD graphene on the micro-hotplate sensor substrate. Right—SEM image of single-layer graphene on top of interdigitated electrodes of the sensor substrate.
Chemosensors 10 00068 g003
Chemosensors 10 00068 g004 550
Figure 4. Responses of the four sensors to ~100 cycles of various NO2 and O3 combinations (30 or 60 ppb) over the course of several days. For better visibility, the signal of sensor S2 has been multiplied by factor of three.
Figure 4. Responses of the four sensors to ~100 cycles of various NO2 and O3 combinations (30 or 60 ppb) over the course of several days. For better visibility, the signal of sensor S2 has been multiplied by factor of three.
Chemosensors 10 00068 g004
Chemosensors 10 00068 g005 550
Figure 5. Extracts from the sensor responses (solid red lines, from Figure 5) as a function of gas composition, highlighted by yellow and blue bars for NO2 and O3, respectively.
Figure 5. Extracts from the sensor responses (solid red lines, from Figure 5) as a function of gas composition, highlighted by yellow and blue bars for NO2 and O3, respectively.
Chemosensors 10 00068 g005
Chemosensors 10 00068 g006 550
Figure 6. Enlarged view of typical transient response of a graphene-based sensor (S2) to 60 ppb of O3. Curve fitting (as indicated) was applied to certain sections of the data to extract characteristic features for machine learning.
Figure 6. Enlarged view of typical transient response of a graphene-based sensor (S2) to 60 ppb of O3. Curve fitting (as indicated) was applied to certain sections of the data to extract characteristic features for machine learning.
Chemosensors 10 00068 g006
Chemosensors 10 00068 g007 550
Figure 7. Clustering of the data points in 2D feature space of the response amplitudes (left) or the recovery rates (right) of sensors S1 and S2.
Figure 7. Clustering of the data points in 2D feature space of the response amplitudes (left) or the recovery rates (right) of sensors S1 and S2.
Chemosensors 10 00068 g007
Chemosensors 10 00068 g008 550
Figure 8. Performance of a trained ANN (9 neurons in 1 hidden layer) on the test data. Red circles represent the expected result; blue crosses represent the predicted result.
Figure 8. Performance of a trained ANN (9 neurons in 1 hidden layer) on the test data. Red circles represent the expected result; blue crosses represent the predicted result.
Chemosensors 10 00068 g008
Chemosensors 10 00068 g009 550
Figure 9. A diagram from Figure 7, redrawn so that the color indicates the time passed since the start of the experiment.
Figure 9. A diagram from Figure 7, redrawn so that the color indicates the time passed since the start of the experiment.
Chemosensors 10 00068 g009
Table
Table 1. PLD functionalization parameters for the sensors used in the experiments.
Table 1. PLD functionalization parameters for the sensors used in the experiments.
Sensor LabelTargetO2 Pressure (Pa)No. of Pulses
S1CuO-MnO25.0 ± 0.1160
S2In2O35.0 ± 0.1160
S3CuO-MnO210.0 ± 0.21000
S4Sc2O310.0 ± 0.21000
Table
Table 2. Sensitivities of the sensors to the individual gases at 30 ppb concentration (average over all cycles, uncertainties indicated in the brackets as double standard deviation).
Table 2. Sensitivities of the sensors to the individual gases at 30 ppb concentration (average over all cycles, uncertainties indicated in the brackets as double standard deviation).
Sensor LabelSensitivity to NO2 (µS/ppb)Sensitivity to O3 (µS/ppb)Baseline (mS)
S14.9 (0.9)26.5 (5.1)2.48 (0.19)
S24.6 (1.3)11.3 (1.7)6.85 (0.28)
S34.4 (3.2)29.6 (6.0)8.36 (0.19)
S414.5 (4.4)27.7 (6.9)23.73 (0.90)
Table
Table 3. Prediction accuracy of a trained ANN model (using the indicated features), when applied to the test data.
Table 3. Prediction accuracy of a trained ANN model (using the indicated features), when applied to the test data.
Number of NeuronsL2 Penalty
Parameter		FeaturesF1 Score
90Amplitudes of S1 and S2~0.84
Amplitudes of S3 and S4~0.65
Amplitudes of all sensors~0.74
Amplitudes and recovery times of S1 and S2~0.94
1000.0001Amplitudes of S1 and S2~0.86
Amplitudes of S3 and S4~0.69
Amplitudes of all sensors~0.76
Amplitudes and recovery times of S1 and S2~0.94
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lind, M.; Kiisk, V.; Kodu, M.; Kahro, T.; Renge, I.; Avarmaa, T.; Makaram, P.; Zurutuza, A.; Jaaniso, R. Semiquantitative Classification of Two Oxidizing Gases with Graphene-Based Gas Sensors. Chemosensors 2022, 10, 68. https://doi.org/10.3390/chemosensors10020068

AMA Style

Lind M, Kiisk V, Kodu M, Kahro T, Renge I, Avarmaa T, Makaram P, Zurutuza A, Jaaniso R. Semiquantitative Classification of Two Oxidizing Gases with Graphene-Based Gas Sensors. Chemosensors. 2022; 10(2):68. https://doi.org/10.3390/chemosensors10020068

Chicago/Turabian Style

Lind, Martin, Valter Kiisk, Margus Kodu, Tauno Kahro, Indrek Renge, Tea Avarmaa, Prashanth Makaram, Amaia Zurutuza, and Raivo Jaaniso. 2022. "Semiquantitative Classification of Two Oxidizing Gases with Graphene-Based Gas Sensors" Chemosensors 10, no. 2: 68. https://doi.org/10.3390/chemosensors10020068

APA Style

Lind, M., Kiisk, V., Kodu, M., Kahro, T., Renge, I., Avarmaa, T., Makaram, P., Zurutuza, A., & Jaaniso, R. (2022). Semiquantitative Classification of Two Oxidizing Gases with Graphene-Based Gas Sensors. Chemosensors, 10(2), 68. https://doi.org/10.3390/chemosensors10020068

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop