Origin of Baseline Drift in Metal Oxide Gas Sensors: Effects of Bulk Equilibration
Abstract
:1. Introduction
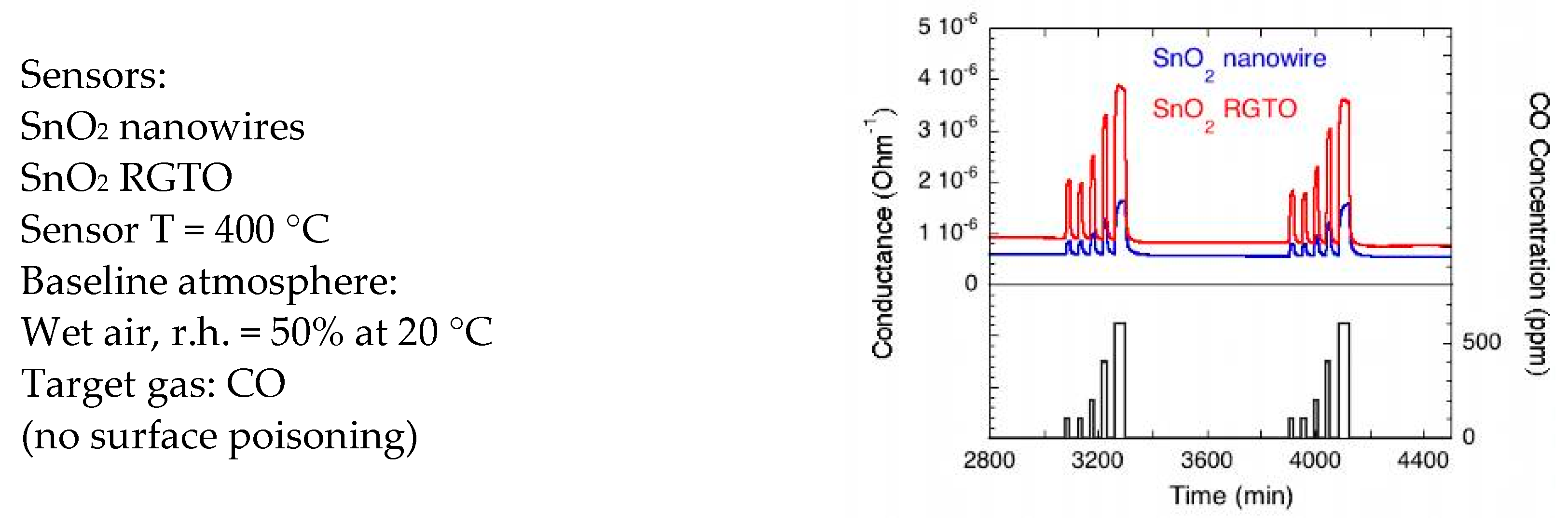
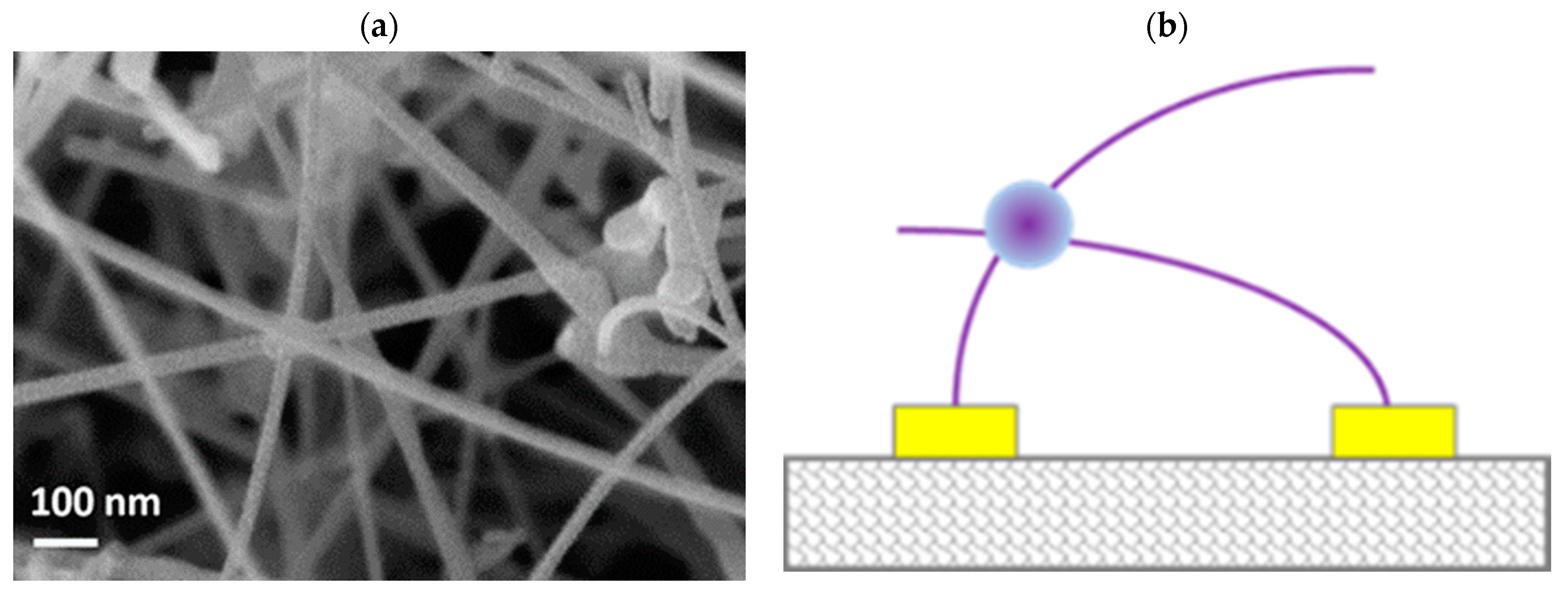
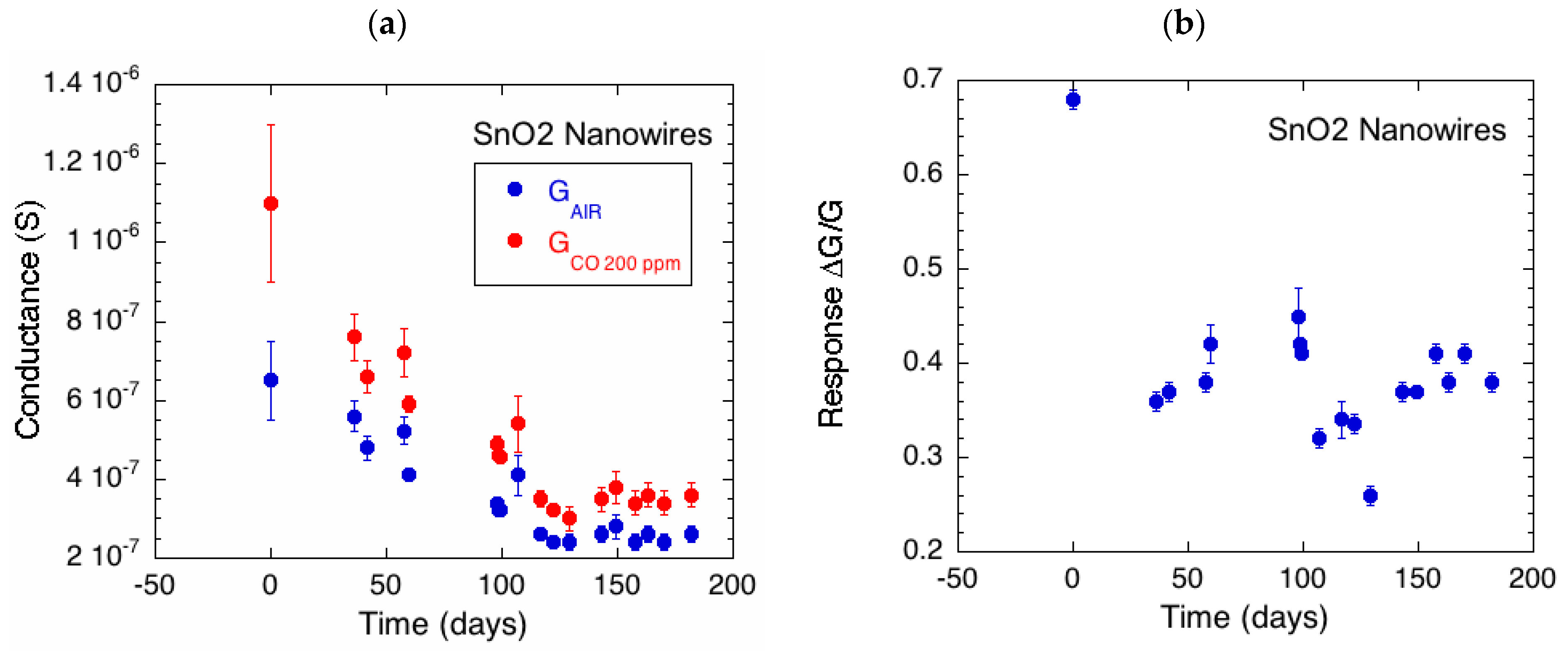
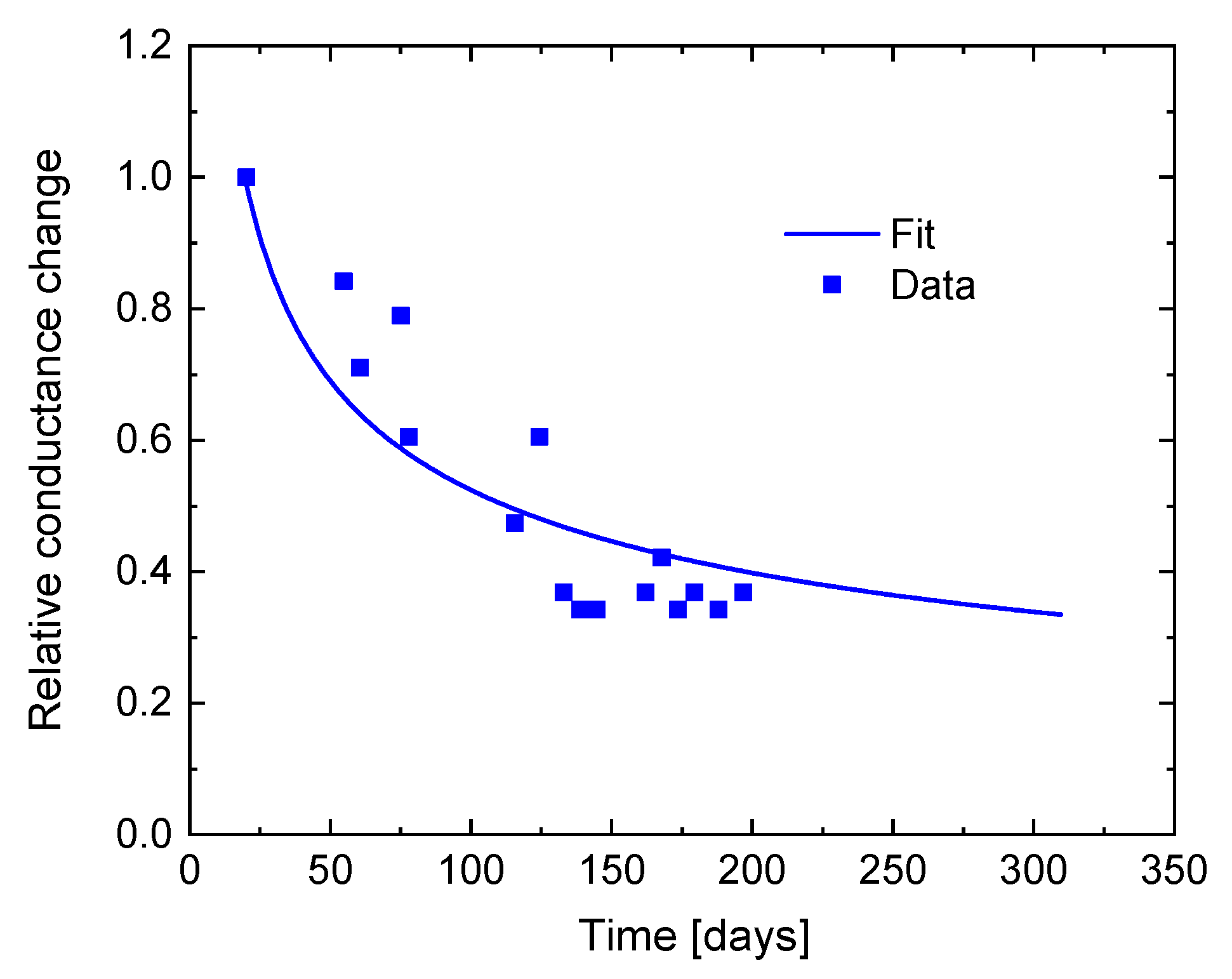
2. Experimental Evidence for Sensor Drift
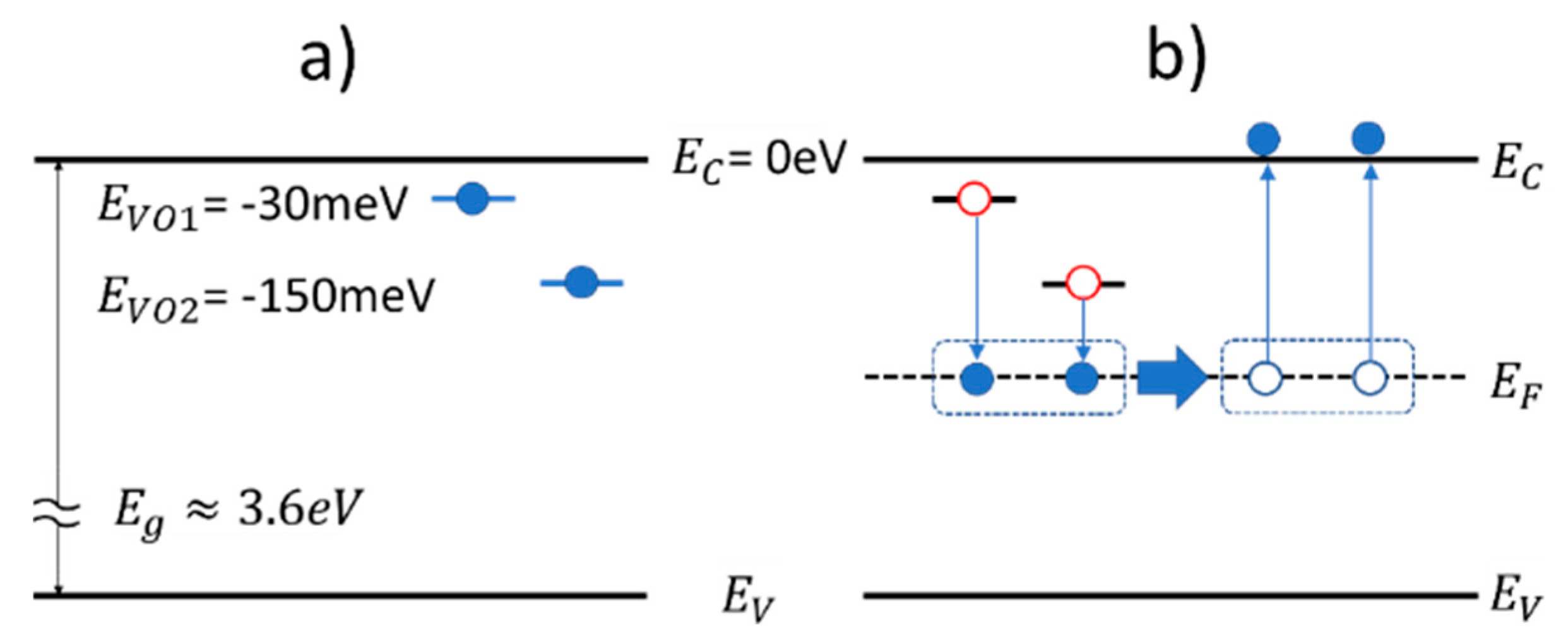
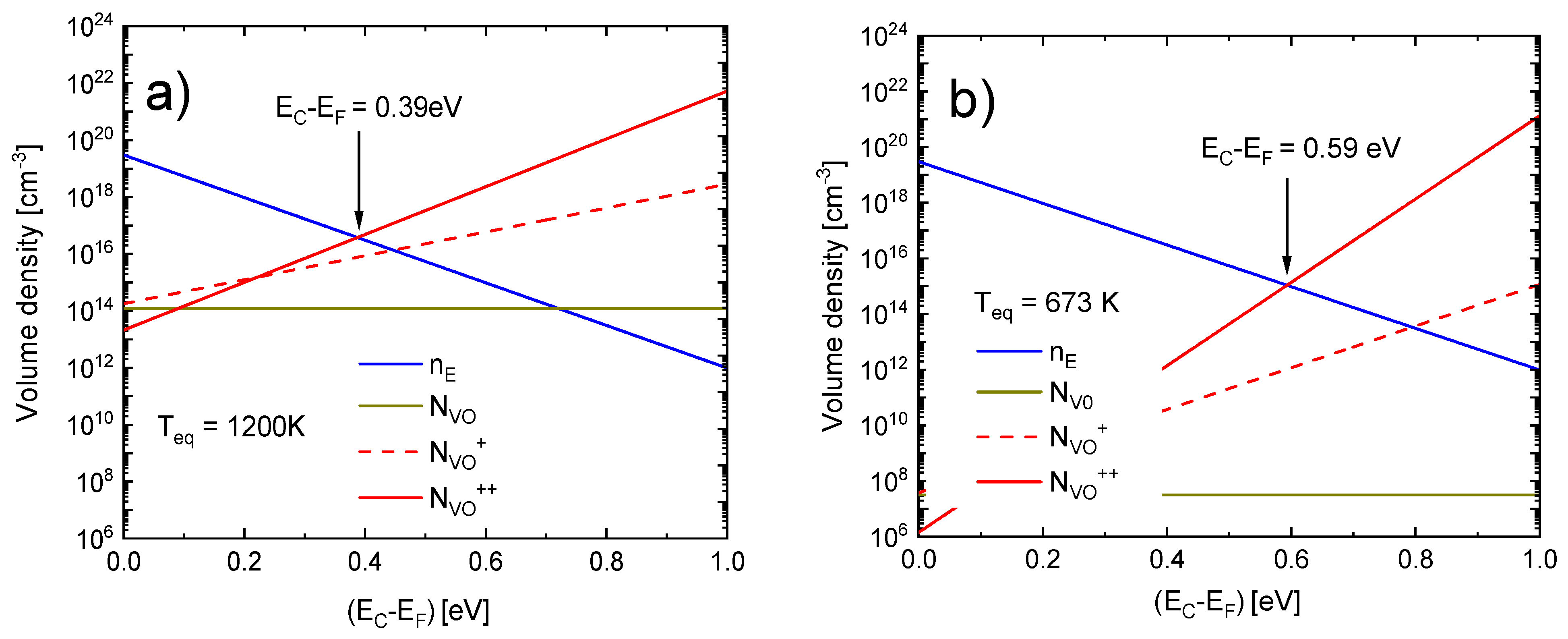
3. Oxygen Vacancy Donors and Electrical Conductivity in n-Type Metal Oxides
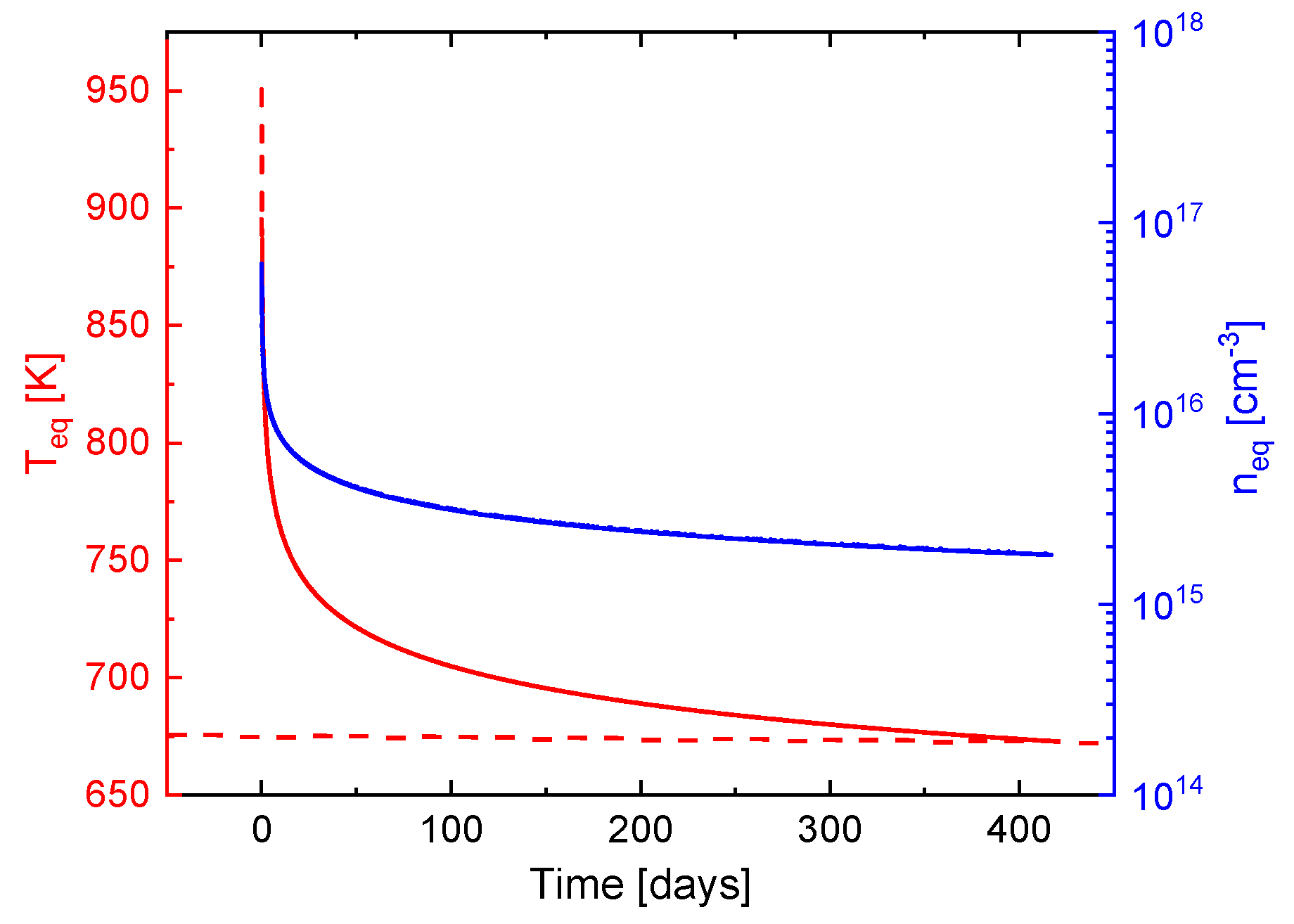
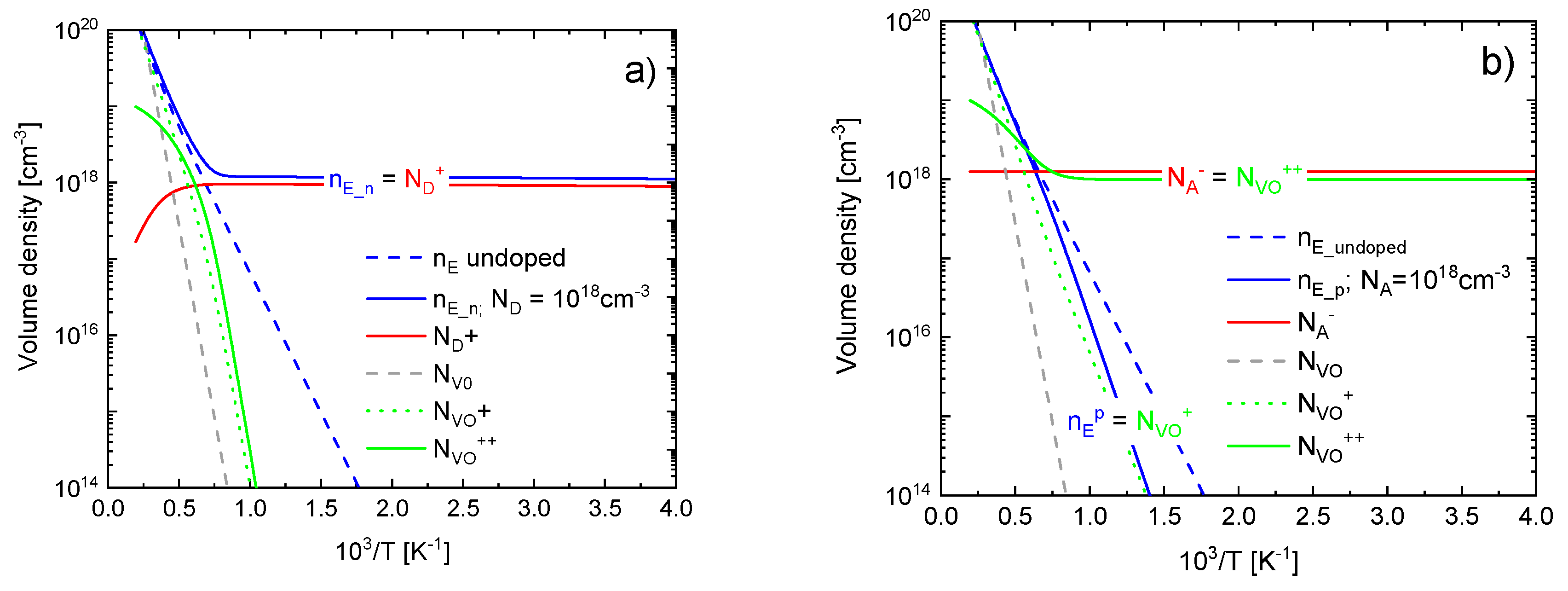
4. Thermal Quenching of Electrical Conductivity and Conductivity Relaxation
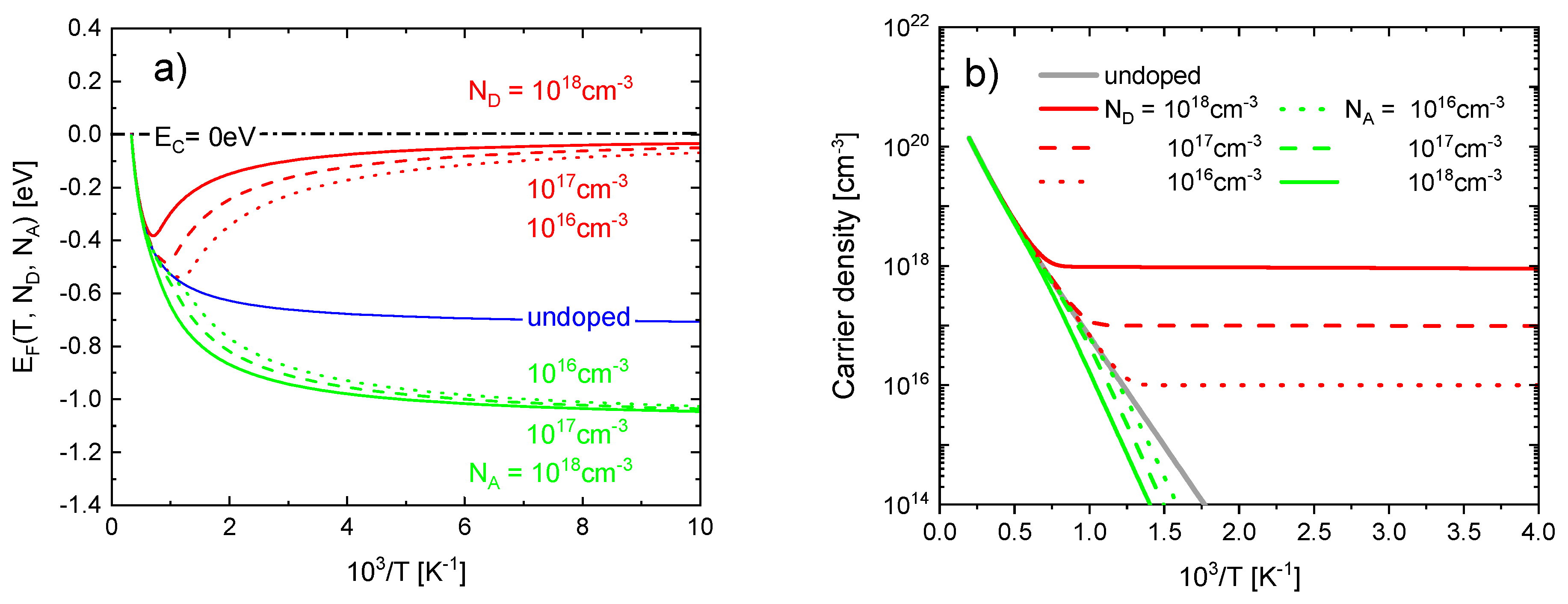
5. Impurity Doping, Mitigation and Suppression of Sensor Drift
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
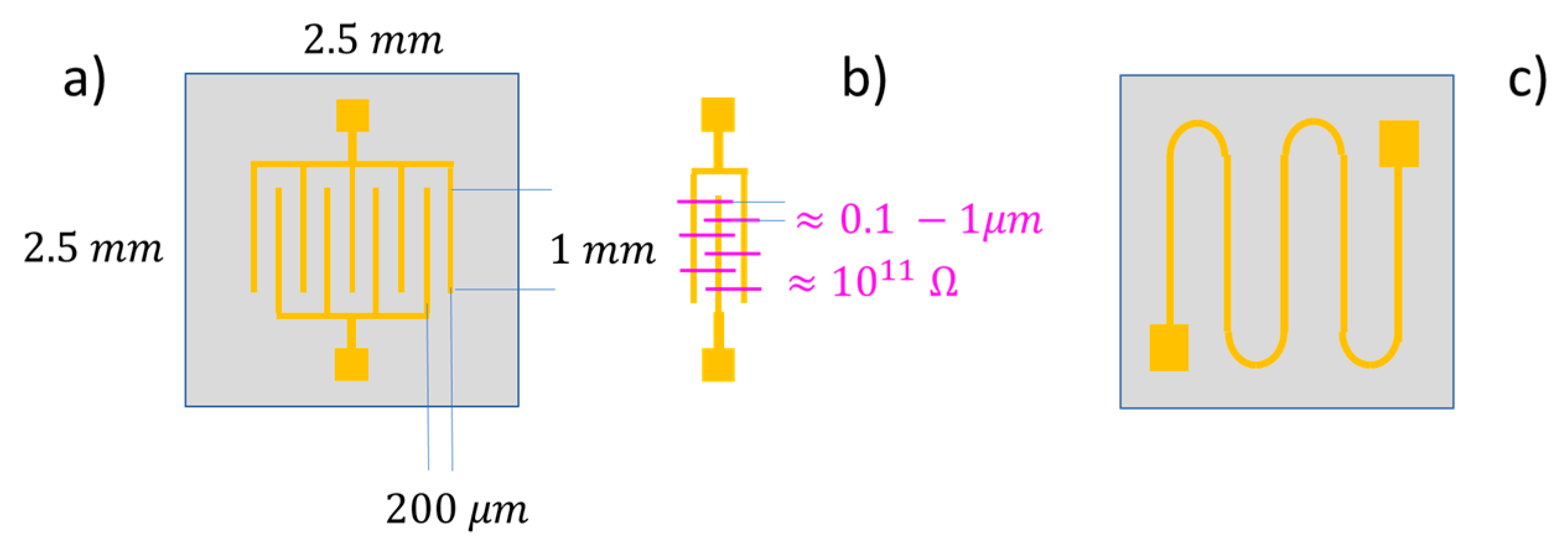
Appendix A. Materials Preparation and Long-Term Tests
Appendix B. Oxygen Vacancies as Elements of Thermal Disorder in MOX Materials

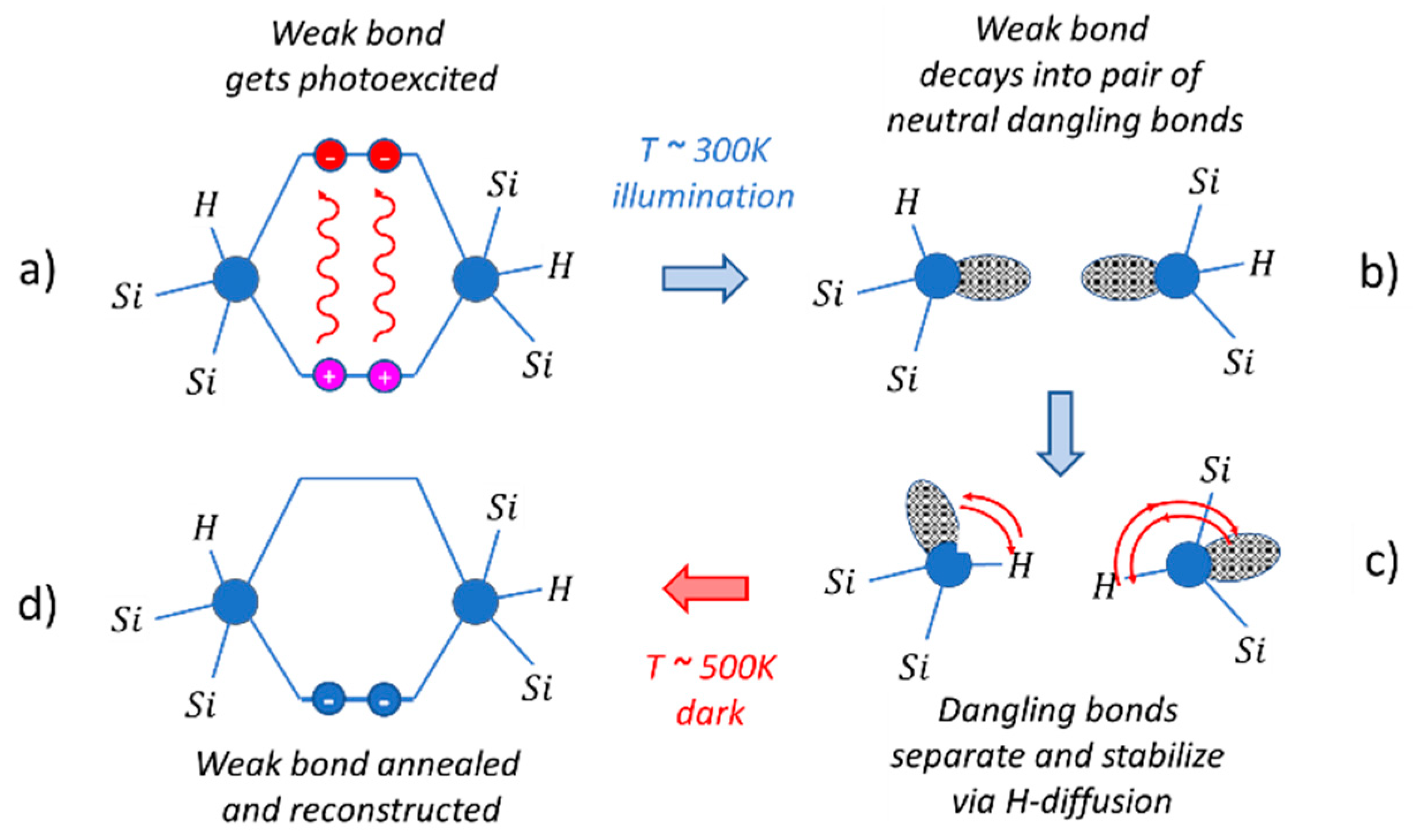
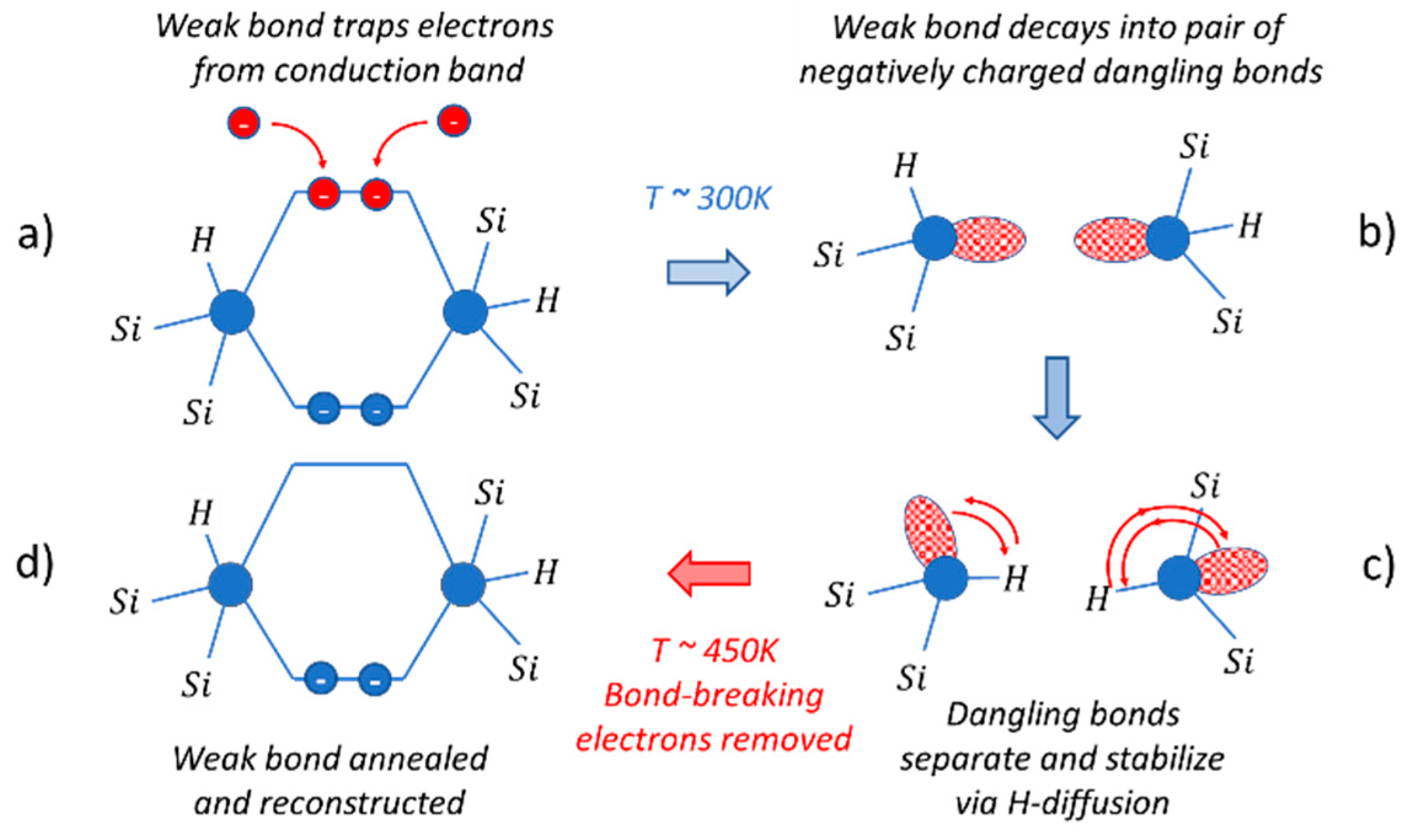
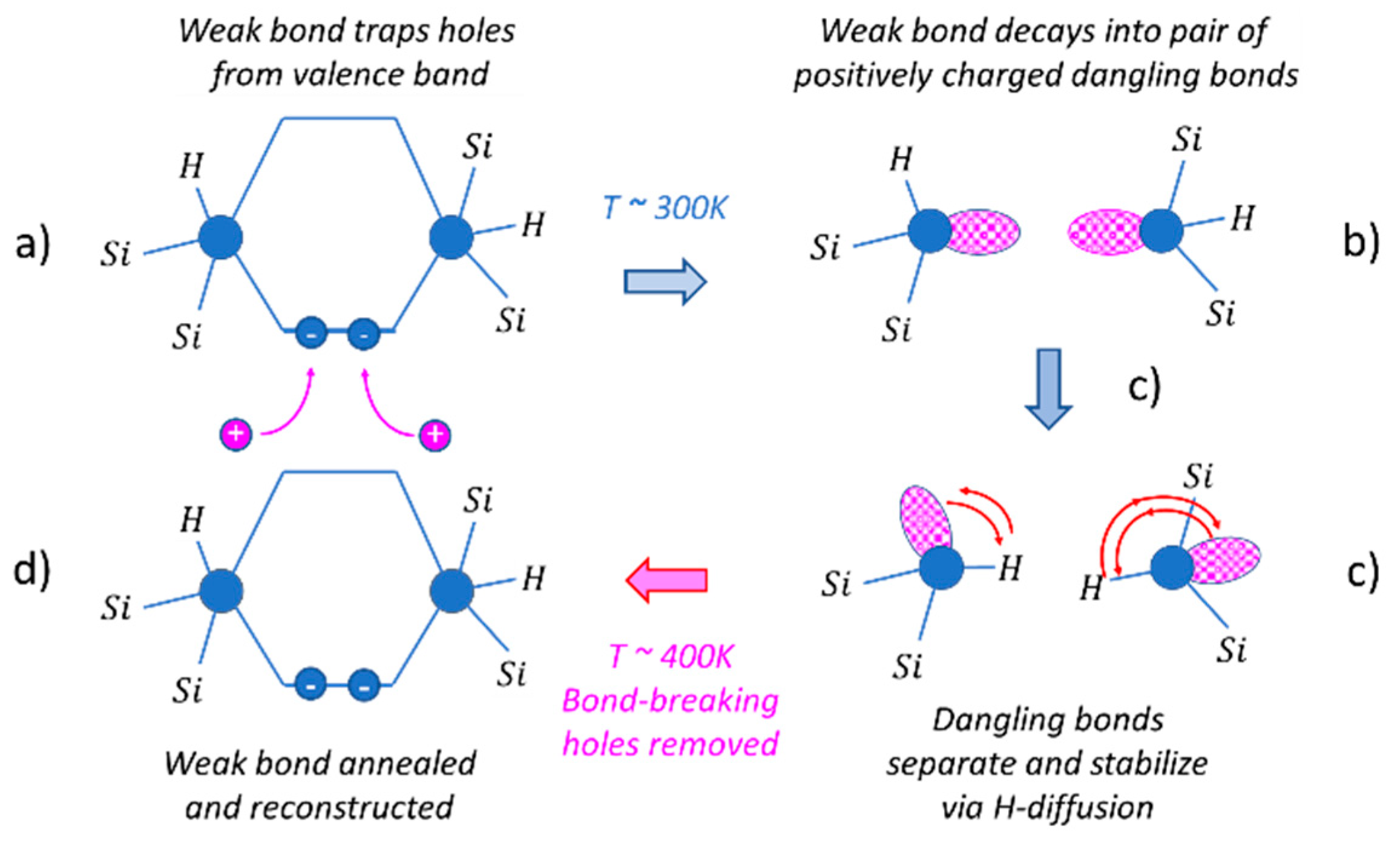
Appendix C. Electronically Induced Metastability and Drift in Amorphous Semiconductors

References
- Gardner, J.W.; Bartlett, P.N. Electronic Noses: Principles and Application; Oxford University Press: Oxford, UK, 1999; ISBN 0-19-855955-0. [Google Scholar]
- Jaeschke, C.; Gonzalez, O.; Padilla, M.; Richardson, K.; Glöckler, J.; Mitrovics, J.; Mizaikoff, B. A Novel Modular System for Breath Analysis Using Temperature Modulated MOX Sensors. Proceedings 2019, 14, 49. [Google Scholar] [CrossRef] [Green Version]
- Danesh, E.; Dudeney, R.; Tsang, J.-H.; Blackman, C.; Covington, J.; Smith, P.; Saffell, J. A Multi-MOx Sensor Approach to Measure Oxidizing and Reducing Gases. Proceedings 2019, 14, 50. [Google Scholar] [CrossRef] [Green Version]
- Shaposhnik, A.; Moskalev, P.; Vasiliev, A. Selective Detection of Hydrogen and Hydrogen Containing Gases with Metal Oxide Gas Sensor Operating in Non-Stationary Thermal Regime. Proceedings 2019, 14, 2. [Google Scholar] [CrossRef] [Green Version]
- Byun, H.-G.; Yu, J.-B.; Kang, C.-Y.; Jang, B.K.; Lee, H.-R. Comparative Analysis between Blood Test and Breath Analysis Using sensors Array for Diabetic Patients. Proceedings 2019, 14, 22. [Google Scholar] [CrossRef] [Green Version]
- Astolfi, M.; Zonta, G.; Landini, N.; Gherardi, S.; Rispoli, G.; Anania, G.; Benedusi, M.; Guidi, V.; Palmonari, C.; Secchiero, P.; et al. Chemoresistive Nanostructured sensors for Tumor Pre-Screening. Proceedings 2019, 14, 29. [Google Scholar] [CrossRef] [Green Version]
- Abbatangelo, M.; Duina, G.; Comini, E.; Sberveglieri, G. MOX sensors to Ensure Suitable Parameters of Grated Parmigiano Reggiano Cheese. Proceedings 2019, 14, 38. [Google Scholar] [CrossRef] [Green Version]
- Izawa, K. SnO2-Based Gas Sensor for Detection of Refrigerant Gases. Proceedings 2019, 14, 32. [Google Scholar] [CrossRef] [Green Version]
- Portalo-Calero, F.; Lozano, J.; Meléndez, F.; Arroyo, P.; Suárez, J.I. Identification of Poisonous Mushrooms by Means of a Hand-Held Electronic Nose. Proceedings 2019, 14, 33. [Google Scholar] [CrossRef] [Green Version]
- Landini, N.; Anania, G.; Astolfi, M.; Fabbri, B.; Gaiardo, A.; Gherardi, S.; Giberti, A.; Guidi, V.; Rispoli, G.; Scagliarini, L.; et al. Nanostructured Chemoresistive sensors for Oncological Screening: Preliminary Study with Single Sensor Approach on Human Blood Samples. Proceedings 2019, 14, 34. [Google Scholar] [CrossRef] [Green Version]
- Zonta, G.; Astolfi, M.; Gaiardo, A.; Gherardi, S.; Giberti, A.; Guidi, V.; Landini, N.; Malagù, C. Semiconductor Gas sensors to Analyze Fecal Exhalation as a Method for Colorectal Cancer Screening. Proceedings 2019, 14, 35. [Google Scholar] [CrossRef] [Green Version]
- Reidt, U.; Helwig, A.; Müller, G.; Lenic, J.; Grosser, J.; Fetter, V.; Kornienko, A.; Kharin, S.; Novikova, N.; Hummel, T. Detection of Microorganisms with an Electronic Nose for Application under Microgravity Conditions. Gravit. Space Res. 2020, 8, 1–17. [Google Scholar] [CrossRef]
- Reidt, U.; Helwig, A.; Müller, G.; Plobner, L.; Lugmayr, V.; Kharin, S.; Smirnov, Y.; Novikova, N.; Lenic, J.; Fetter, V.; et al. Detection of Microorganisms Onboard the International Space Station Using an Electronic Nose. Gravit. Space Res. 2017, 5, 89–111. [Google Scholar] [CrossRef]
- Helwig, A.; Müller, G.; Wassner, T.; Eickhoff, M.; Sberveglieri, G.; Faglia, G. Analysis of the baseline drift phenomenon in nano crystalline SnO2 gas sensing layers. In Proceedings of the 11th International Meeting on Chemical Sensors, Brescia, Italy, 16–19 July 2006; Available online: https://www.researchgate.net/publication/259361252_Analysis_of_the_baseline_drift_phenomenon_in_nano-crystalline_SnO2_gas_sensing_layers (accessed on 13 March 2022).
- S3 Project: FP7-NMP-2009-EU-Russia: Surface Ionization and Novel Concepts in Nano-MOX Gas sensors with Increased Selectivity, Sensitivity and Stability for Detection of Low Concentrations of Toxic and Explosive Agents. Contract Number 247768. Available online: https://cordis.europa.eu/project/id/247768/de (accessed on 1 May 2022).
- Korotcenkov, G.; Cho, B. Instability of metal oxide-based conductometric gas sensors and approaches to stability improvement (short survey). Sens. Actuators B Chem. 2011, 156, 527–538. [Google Scholar] [CrossRef]
- Hrichi, S.; Chaabane-Banaoues, R.; Bayar, S.; Flamini, G.; Oulad El Majdoub, Y.; Mangraviti, D.; Mondello, L.; El Mzoughi, R.; Babba, H.; Mighri, Z.; et al. Botanical and Genetic Identification Followed by Investigation of Chemical Composition and Biological Activities on the Scabiosa atropurpurea L. Stem from Tunisian Flora. Molecules 2020, 25, 5032. [Google Scholar] [CrossRef] [PubMed]
- Beer, S. Personal Communication; University of Freiburg: Freiburg, Germany, 28 March 2012. [Google Scholar]
- Holmberg, M.; Winquist, F.; Lundström, I.; Davide, F.; DiNatale, C.; D’Amico, A. Drift counteraction for an electronic nose. Sens. Actuators B Chem. 1996, 36, 528–535. [Google Scholar] [CrossRef]
- Artursson, T.; Ekl, T.; Lundström, I.; Martensson, P.; Sjöström, M.; Holmberg, M. Drift correction for gas sensors using multivariate methods. J. Chemom. 2000, 14, 711–723. [Google Scholar] [CrossRef]
- Ziyatdinov, A.; Marco, S.; Chaudry, A.; Persaud, K.; Caminal, P.; Perera, A. Drift compensation of gas sensor array data by common principal component analysis. Sens. Actuators B Chem. 2010, 146, 460–465. [Google Scholar] [CrossRef] [Green Version]
- Vergara, A.; Vembu, S.; Ayhan, T.; Ryan, M.A.; Homer, M.L.; Huerta, R. Chemical gas sensor drift compensation using classifier ensembles. Sens. Actuators B Chem. 2012, 166–167, 320–329. [Google Scholar] [CrossRef]
- Abidin, M.Z.; Asmat, A.; Hamidon, M.N. Identification of initial drift in semiconductor gas sensors caused by temperature variation. In Proceedings of the IEEE 9th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 8–10 March 2013; pp. 285–288. [Google Scholar] [CrossRef]
- Liu, H.; Chu, R.; Tang, Z. Metal Oxide Gas Sensor Drift Compensation Using a Two-Dimensional Classifier Ensemble. Sensors 2015, 15, 10180–10193. [Google Scholar] [CrossRef] [Green Version]
- Verma, M.; Asmita, S.; Shukla, K.K. A Regularized Ensemble of Classifiers for Sensor Drift Compensation. IEEE Sens. J. 2016, 16, 1310–1318. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, H.; Liu, F. Time Series Prediction of E-nose Sensor Drift Based on Deep Recurrent Neural Network. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 479–3484. [Google Scholar] [CrossRef]
- Das, P.; Manna, A.; Ghoshal, S. Gas Sensor Drift Compensation by Ensemble of Classifiers Using Extreme Learning Machine. In Proceedings of the 2020 International Conference on Renewable Energy Integration into Smart Grids: A Multidisciplinary Approach to Technology Modelling and Simulation (ICREISG), Bhubaneswar, India, 14–15 February 2020; pp. 197–201. [Google Scholar] [CrossRef]
- Dennler, N.; Rastogi, S.; Fonollosa, J.; van Schaik, A.; Schmuker, M. Drift in a popular metal oxide sensor dataset reveals limitations for gas classification benchmarks. Sens. Actuators B Chem. 2022, 361, 131668. [Google Scholar] [CrossRef]
- Perera, A.; Montoliu, I.; Chaudry, A.; Persaud, K.; Marco, S.; Padilla, M. Drift compensation of gas sensor array data by Orthogonal Signal Correction. Chemom. Intell. Lab. Syst. 2010, 100, 28–35. [Google Scholar]
- Comini, E.; Faglia, G.; Sberveglieri, G.; Pan, Z.; Wang, Z.L. Stable and highly sensitive gas sensors based on semiconducting oxide nanobelts. Appl. Phys. Lett. 2002, 81, 1869–1871. [Google Scholar] [CrossRef]
- Kaur, N.; Singh, M.; Comini, E. One-Dimensional Nanostructured Oxide Chemoresistive Sensors. Langmuir 2020, 36, 6326–6344. [Google Scholar] [CrossRef] [PubMed]
- Sberveglieri, G.; Faglia, G.; Groppelli, S.; Nelli, P.; Taroni, A. A novel PVD technique for the preparation of SnO2 thin films as C2H5OH sensors. Sens. Actuators B Chem. 1992, 7, 721–726. [Google Scholar] [CrossRef]
- Sberveglieri, G. Classical and novel techniques for the preparation of SnO2 thin-film gas sensors. Sens. Actuators B Chem. 1992, 6, 239–247. [Google Scholar] [CrossRef]
- Müller, G.; Sberveglieri, G. Origin of Sensor Drift in Metal Oxide Gas Sensors: Effects of Adsorption and Surface Band Bending. Chemosensors, in press.
- Moseley, P.T.; Tofield, B.C. Solid State Gas Sensors; Adam Hilger: Bristol, UK, 1987. [Google Scholar] [CrossRef]
- Moseley, P.T.; Norris, J.; Williams, D.E. Techniques and Mechanisms in Gas Sensing; Adam Hilger: Bristol, UK, 1991; ISBN 0750300744. [Google Scholar]
- Henzler, M.; Göpel, W. Oberflächenphysik des Festkörpers. In Teubner Studienbücher Physik; Springer International Publishing: Cham, Switzerland, 1991; ISBN 3-519-03047-0. [Google Scholar] [CrossRef]
- Sze, S.M. Semiconductor Sensors; John Wiley & Sons: Hoboken, NJ, USA, 1994; ISBN 0-471-54609-7. [Google Scholar]
- Sze, S.M. Semiconductor Devices; Physics and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 79–124. [Google Scholar] [CrossRef] [Green Version]
- Ahlers, S.; Müller, G.; Doll, T. A rate equation approach to the gas sensitivity of thin-film SnO2. Sens. Actuators 2005, B107, 587–599. [Google Scholar] [CrossRef]
- Ahlers, S.; Müller, G.; Becker, T.; Doll, T. Factors Influencing the Gas Sensitivity of Metal Oxide Materials. Encyclopedia of Sensors; Grimes, C.A., Dickey, E.C., Pishko, M.V., Eds.; The Pennsylvania State University: University Park, PA, USA, 2005; ISBN 1-58883-056-X. [Google Scholar]
- Comini, E.; Faglia, G.; Sberveglieri, G. Solid State Gas Sensing; Springer Science and Business Media: Berlin, Germany, 2009. [Google Scholar]
- Madelung, O. Festkörpertheorie III; Springer-Verlag: Berlin/Heidelberg, Germany; New York, NY, USA, 2013; ISBN 9783642654138. (In German) [Google Scholar]
- Kröger, F.A.; Vink, H.J. Solid State Physics: Advances in Research and Applications; Seitz, F., Turnbull, D., Eds.; Academic: New York, NY, USA, 1956; p. 307. [Google Scholar]
- Kim, S.S.; Na, H.G.; Kim, H.W.; Kulish, V.; Wu, P. Promotion of acceptor formation in SnO2 nanowires by e-beam bombardment and impacts to sensor application. Sci. Rep. 2015, 5, srep10723. [Google Scholar] [CrossRef] [Green Version]
- Westbrook, M.H.; Turner, J.D. Automotive Sensors; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 1994; ISBN 0-7503-0293-3. [Google Scholar]
- Hellmich, W.; Braunmühl, C.B.-V.; Müller, G.; Sberveglieri, G.; Berti, M.; Perego, C. The kinetics of formation of gas-sensitive RGTO-SnO2 films. Thin Solid Films 1995, 263, 231–237. [Google Scholar] [CrossRef]
- Makeeva, E.A.; Rumyantseva, M.; Gas’Kov, A.M. Kinetics of Interaction of Thick Nanocrystalline SnO2 Films with Oxygen. Inorg. Mater. 2004, 40, 161–165. [Google Scholar] [CrossRef]
- Kamp, B.; Merkle, R.; Lauck, R.; Maier, J. Chemical diffusion of oxygen in tin dioxide: Effects of dopants and oxygen partial pressure. J. Solid State Chem. 2005, 178, 3027–3039. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Wu, X.; Jin, G.; Zhai, Z.; Liu, H. Inhomogeneous Oxygen Vacancy Distribution in Semiconductor Gas Sensors: Formation, Migration and Determination on Gas Sensing Characteristics. Sensors 2017, 17, 1852. [Google Scholar] [CrossRef] [PubMed]
- Spannhake, J.; Helwig, A.; Müller, G.; Faglia, G.; Sberveglieri, G.; Doll, T.; Wassner, T.; Eickhoff, M. SnO2:Sb—A new material for high-temperature MEMS heater applications: Performance and limitations. Sens. Actuators B Chem. 2007, 124, 421–428. [Google Scholar] [CrossRef]
- Cavicchi, R.E.; Semancik, S.; Walton, R.M.; Panchapakesan, B.; DeVoe, D.L.; Aquino-Class, M.I.; Allen, J.D.; Suehle, J.S. Microhotplate gas sensor arrays. In Chemical Microsensors and Applications IIOK; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; pp. 38–49. [Google Scholar] [CrossRef]
- Schütze, A.; Sauerwald, T. Dynamic operation of semiconductor sensors. In Semiconductor Gas Sensors; Woodhead Publishing: Sawston, UK, 2019; pp. 385–412. [Google Scholar] [CrossRef]
- Street, R.A. Doping and the Fermi Energy in Amorphous Silicon. Phys. Rev. Lett. 1982, 49, 1187–1190. [Google Scholar] [CrossRef]
- Müller, G.; Kalbitzer, S.; Mannsperger, H. A chemical-bond approach to doping, compensation and photo-induced degradation in amorphous silicon. Appl. Phys. A 1986, 39, 243–250. [Google Scholar] [CrossRef]
- Stutzmann, M. Weak bond-dangling bond conversion in amorphous silicon. Philos. Mag. Part B 1987, 56, 63–70. [Google Scholar] [CrossRef]
- Müller, G. On the generation and annealing of dangling bond defects in hydrogenated amorphous silicon. Appl. Phys. A 1988, 45, 41–51. [Google Scholar] [CrossRef]
- Müller, G. Equilibrium dangling bond densities and its related thin-film alloys. Appl. Phys. A 1988, 45, 103–107. [Google Scholar] [CrossRef]
- Krötz, G.; Wind, J.; Stitzl, H.; Müller, G.; Kalbitzer, S.; Mannsperger, H. Experimental tests of the auto compensation model of doping. Philos. Mag. 1991, 63, 101–121. [Google Scholar] [CrossRef]
- Street, R.A. Hydrogenated Amorphous Silicon; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hellmich, W.; Müller, G.; Braunmühl, C.-V.; Doll, T.; Eisele, I. Field-effect-induced gas sensitivity changes in metal oxides. Sens. Actuators B Chem. 1997, 43, 132–139. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, G.; Sberveglieri, G. Origin of Baseline Drift in Metal Oxide Gas Sensors: Effects of Bulk Equilibration. Chemosensors 2022, 10, 171. https://doi.org/10.3390/chemosensors10050171
Müller G, Sberveglieri G. Origin of Baseline Drift in Metal Oxide Gas Sensors: Effects of Bulk Equilibration. Chemosensors. 2022; 10(5):171. https://doi.org/10.3390/chemosensors10050171
Chicago/Turabian StyleMüller, Gerhard, and Giorgio Sberveglieri. 2022. "Origin of Baseline Drift in Metal Oxide Gas Sensors: Effects of Bulk Equilibration" Chemosensors 10, no. 5: 171. https://doi.org/10.3390/chemosensors10050171
APA StyleMüller, G., & Sberveglieri, G. (2022). Origin of Baseline Drift in Metal Oxide Gas Sensors: Effects of Bulk Equilibration. Chemosensors, 10(5), 171. https://doi.org/10.3390/chemosensors10050171






