Design of Christmas-Tree-like Microfluidic Gradient Generators for Cell-Based Studies
Abstract
:1. Introduction
2. Materials and Methods
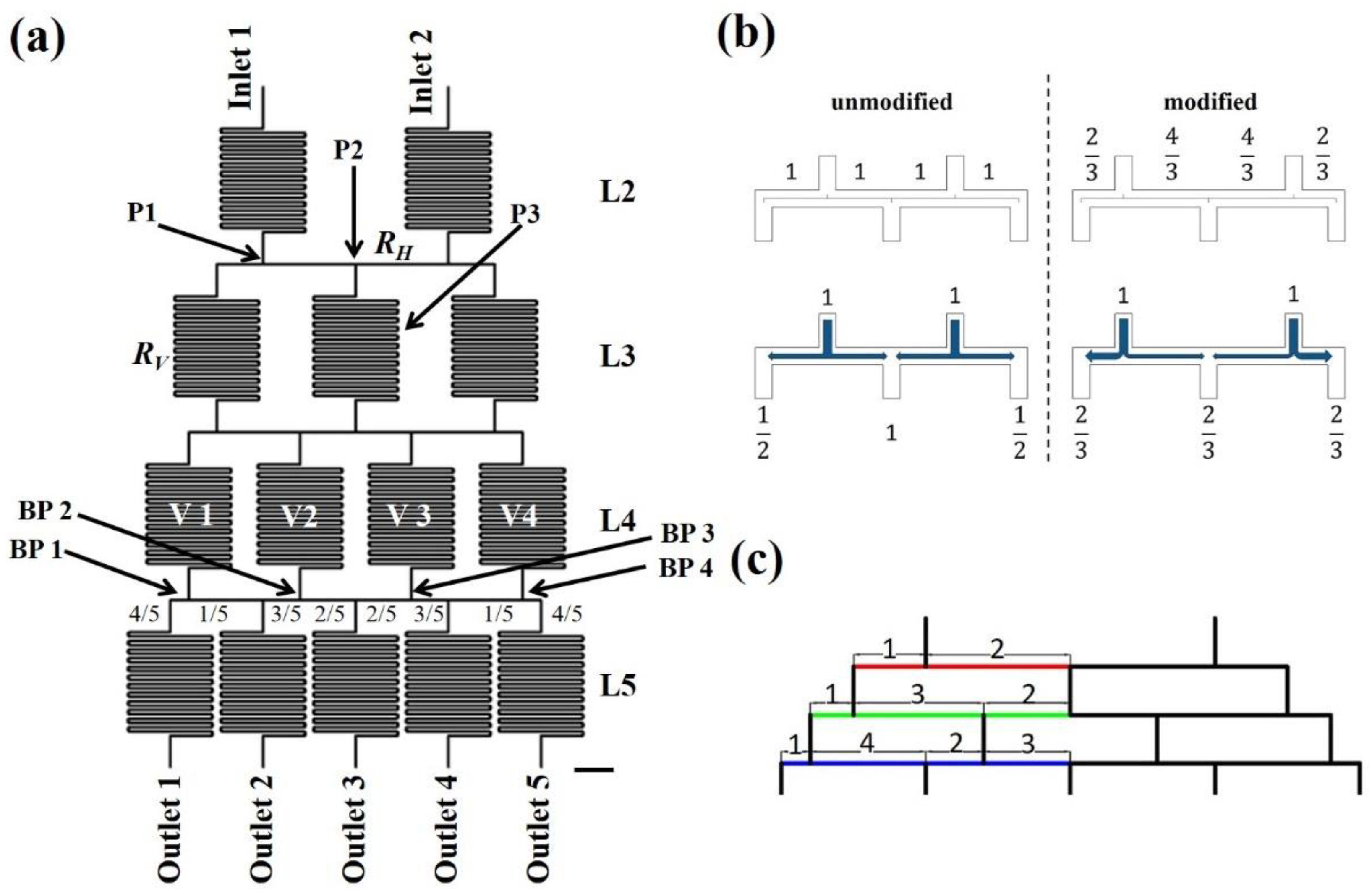
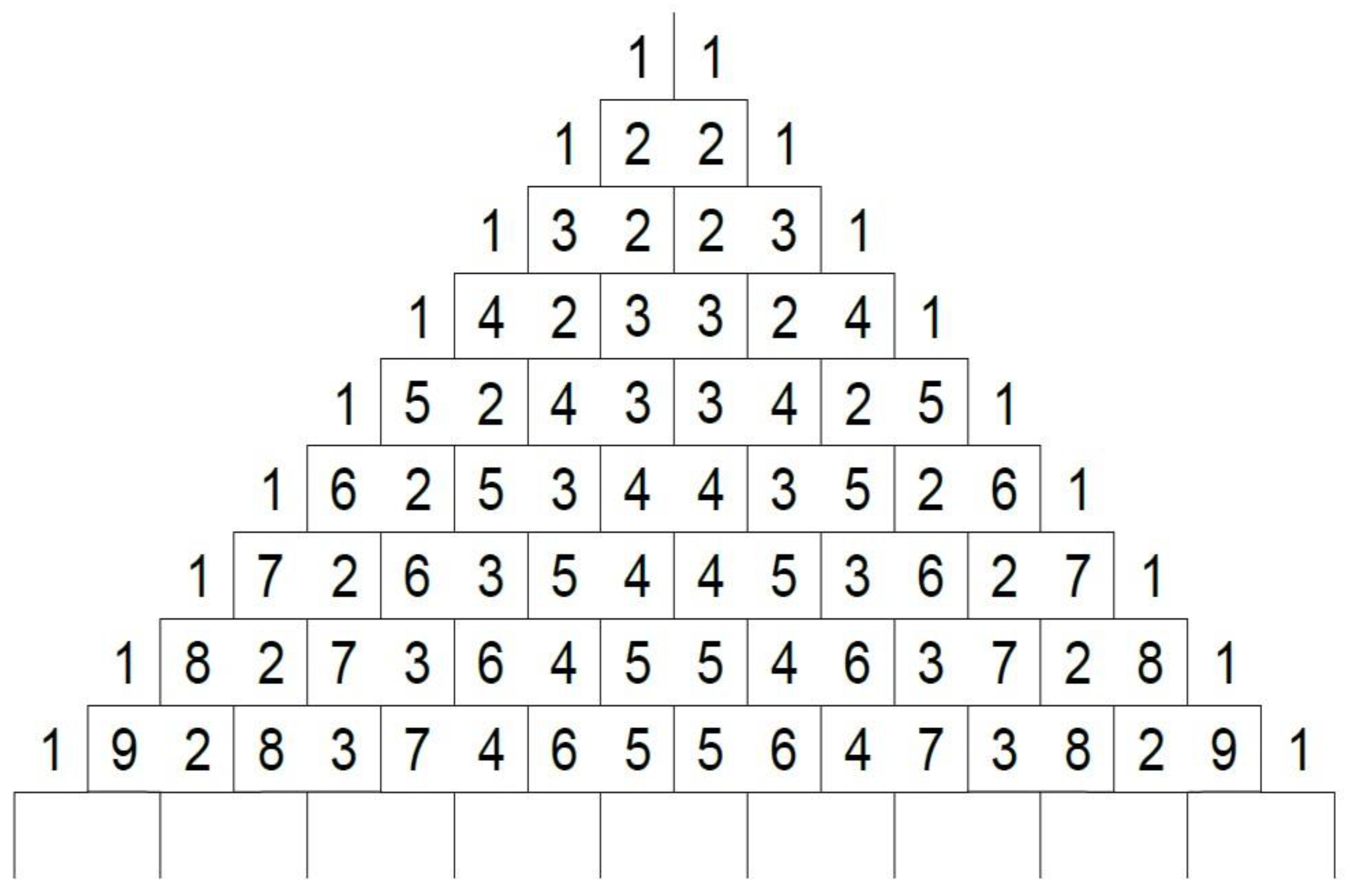
2.1. Design Rationale
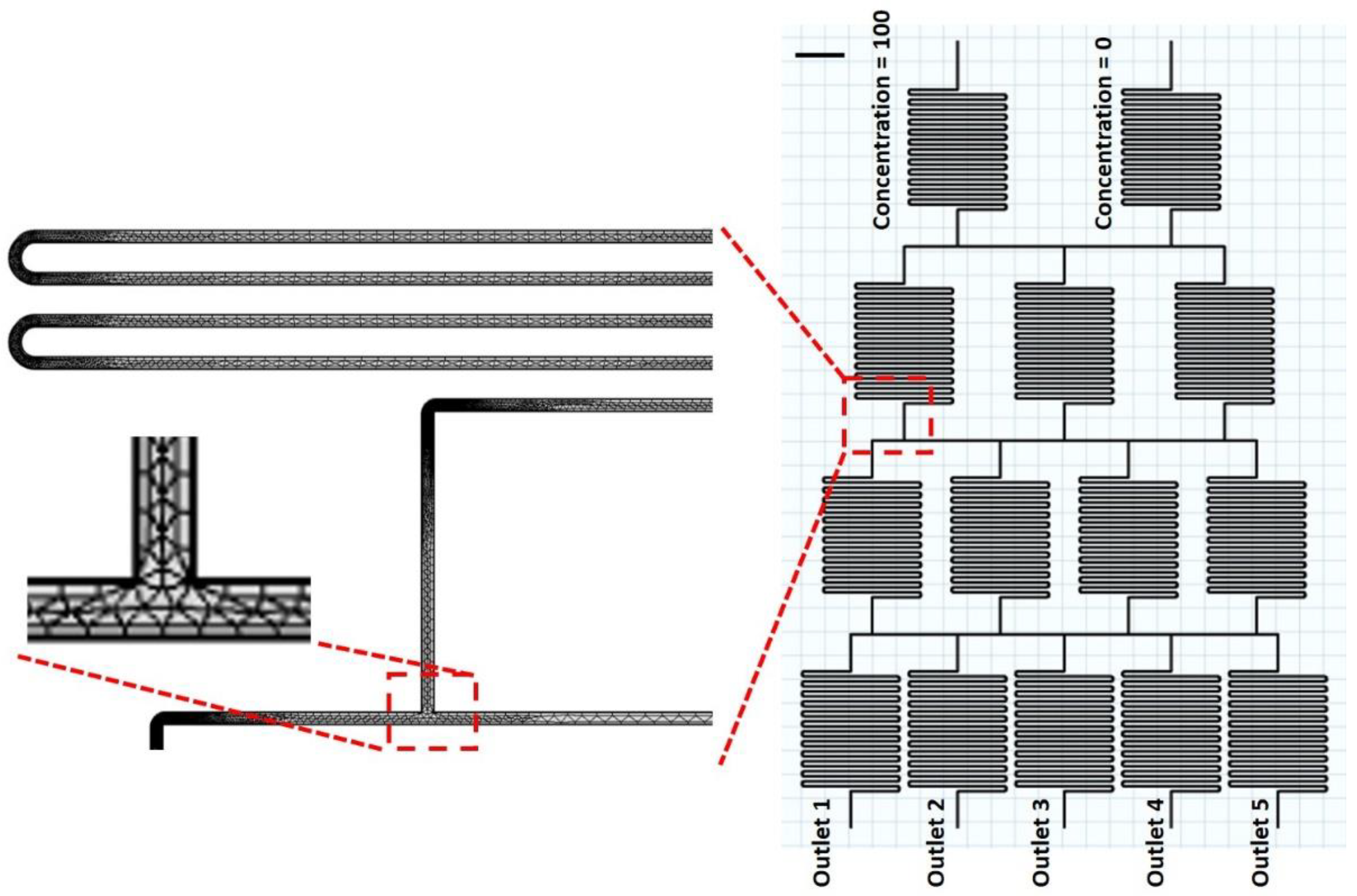
2.2. COMSOL Simulation
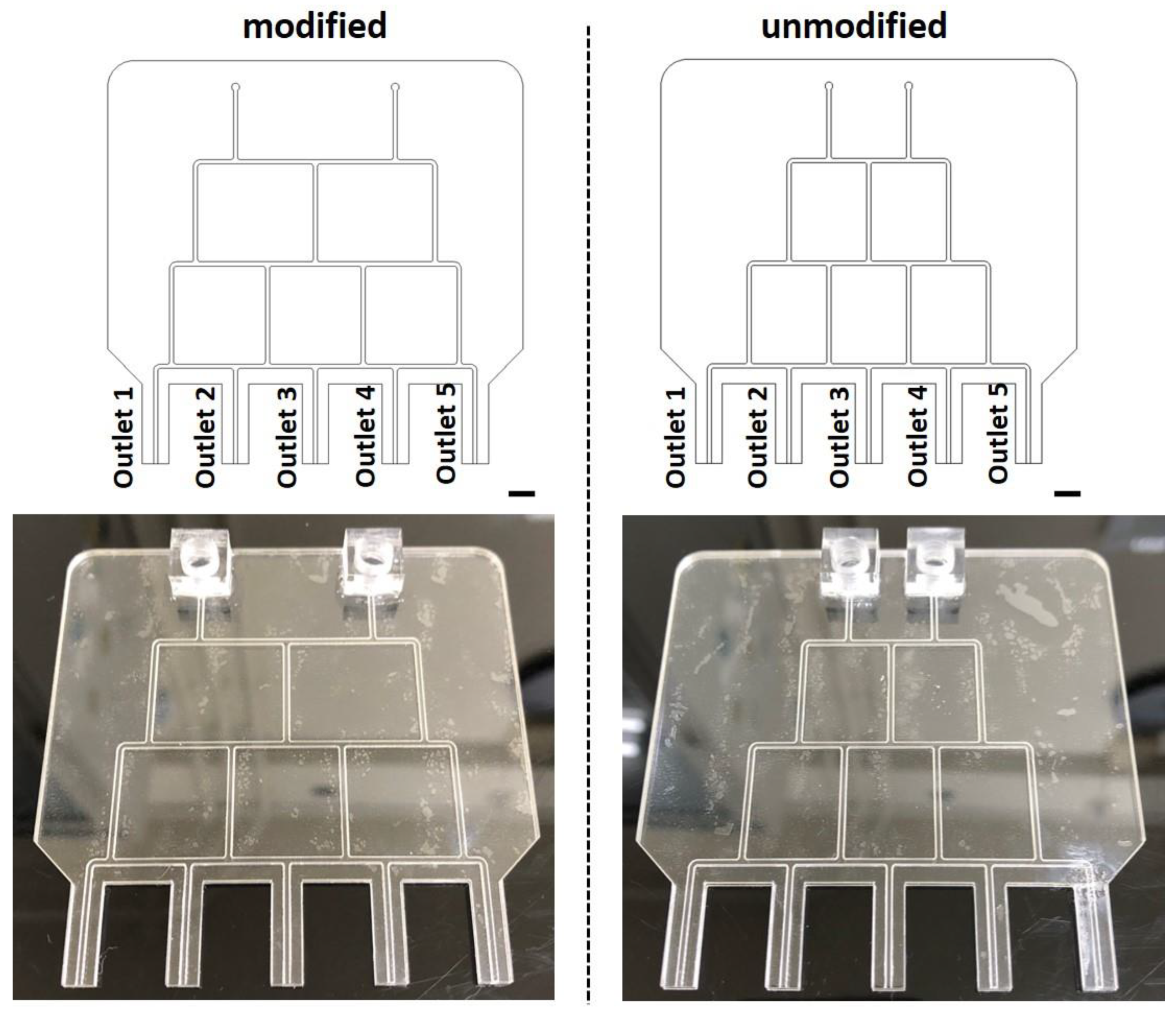
2.3. Chip Fabrication and Experimental Procedure
3. Results and Discussion
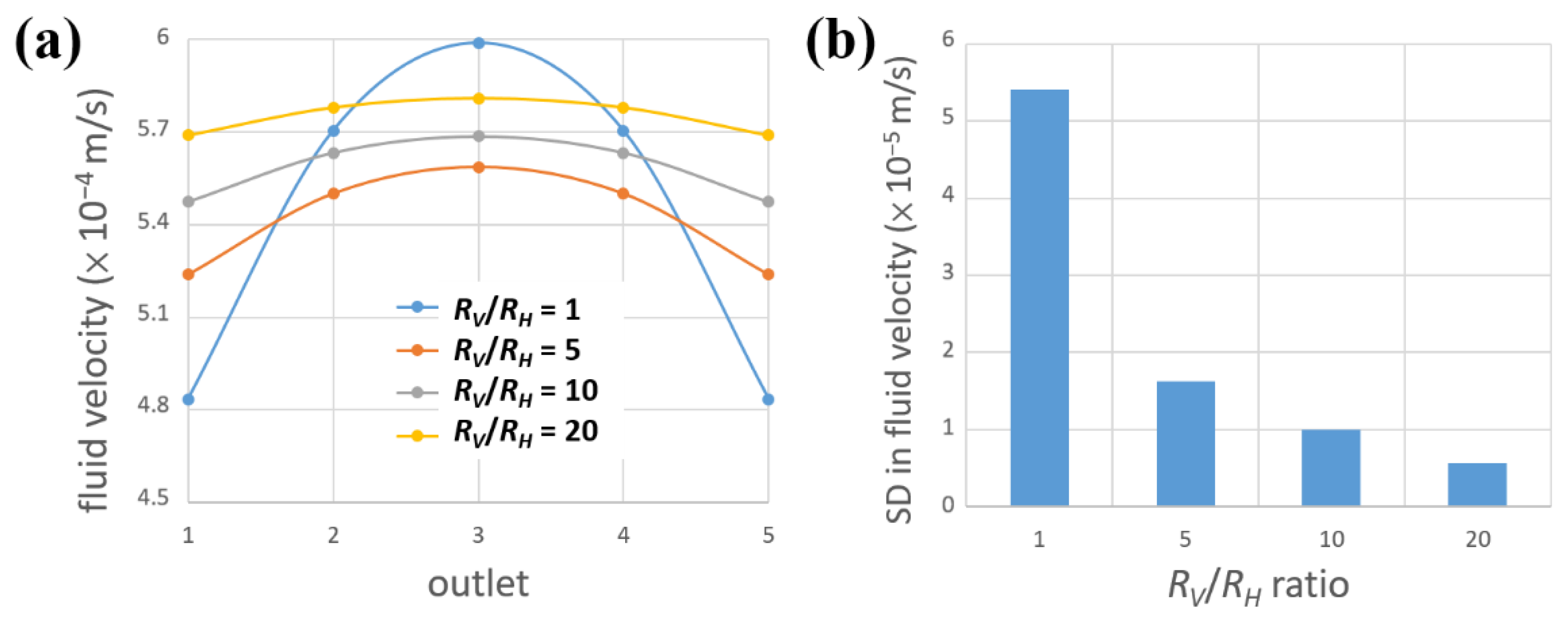
3.1. Simulation of Fluid Velocities
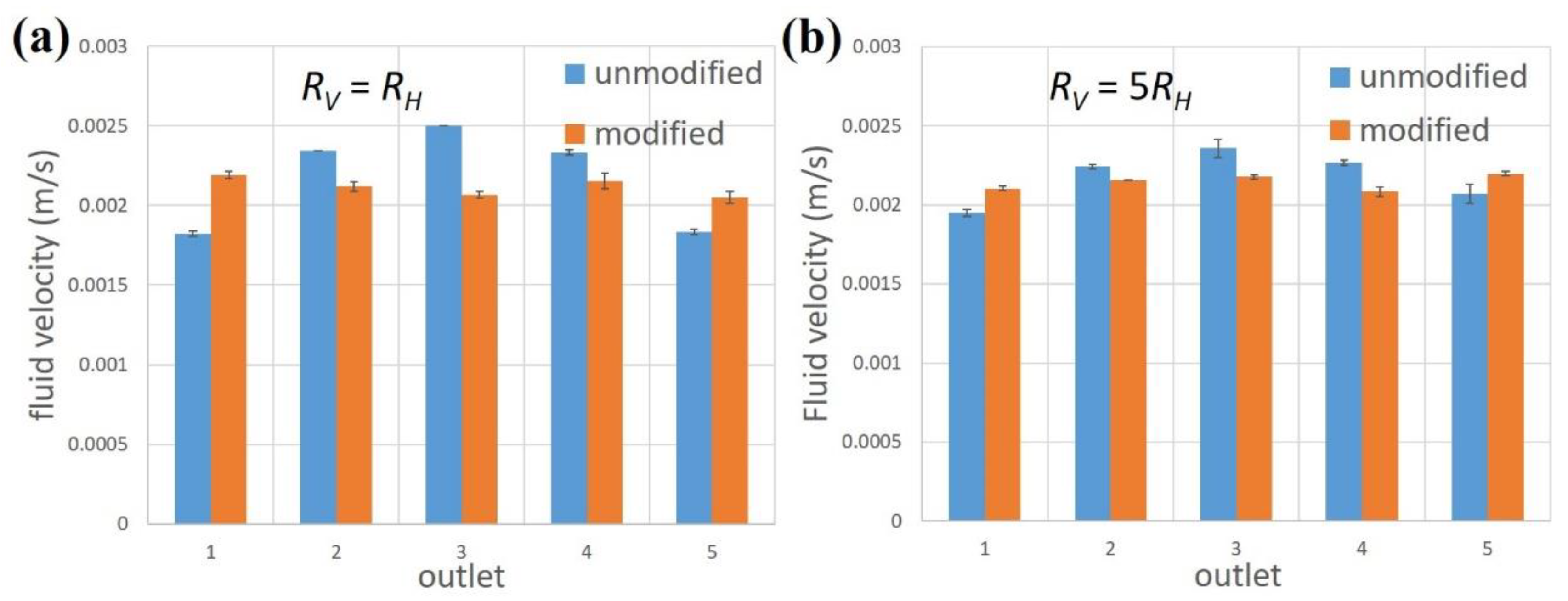
3.2. Experiments
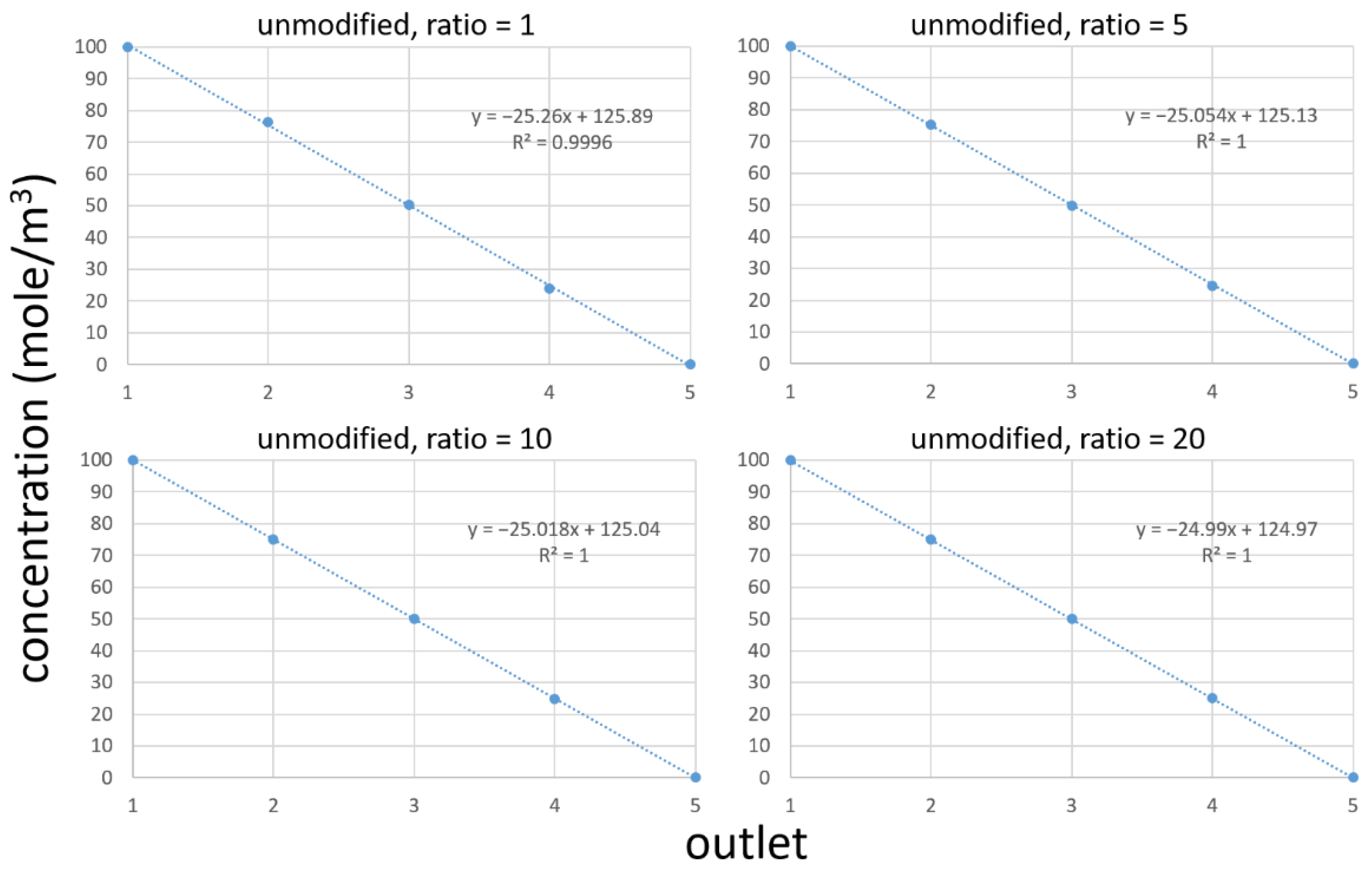
3.3. Simulation of Chemical Concentrations
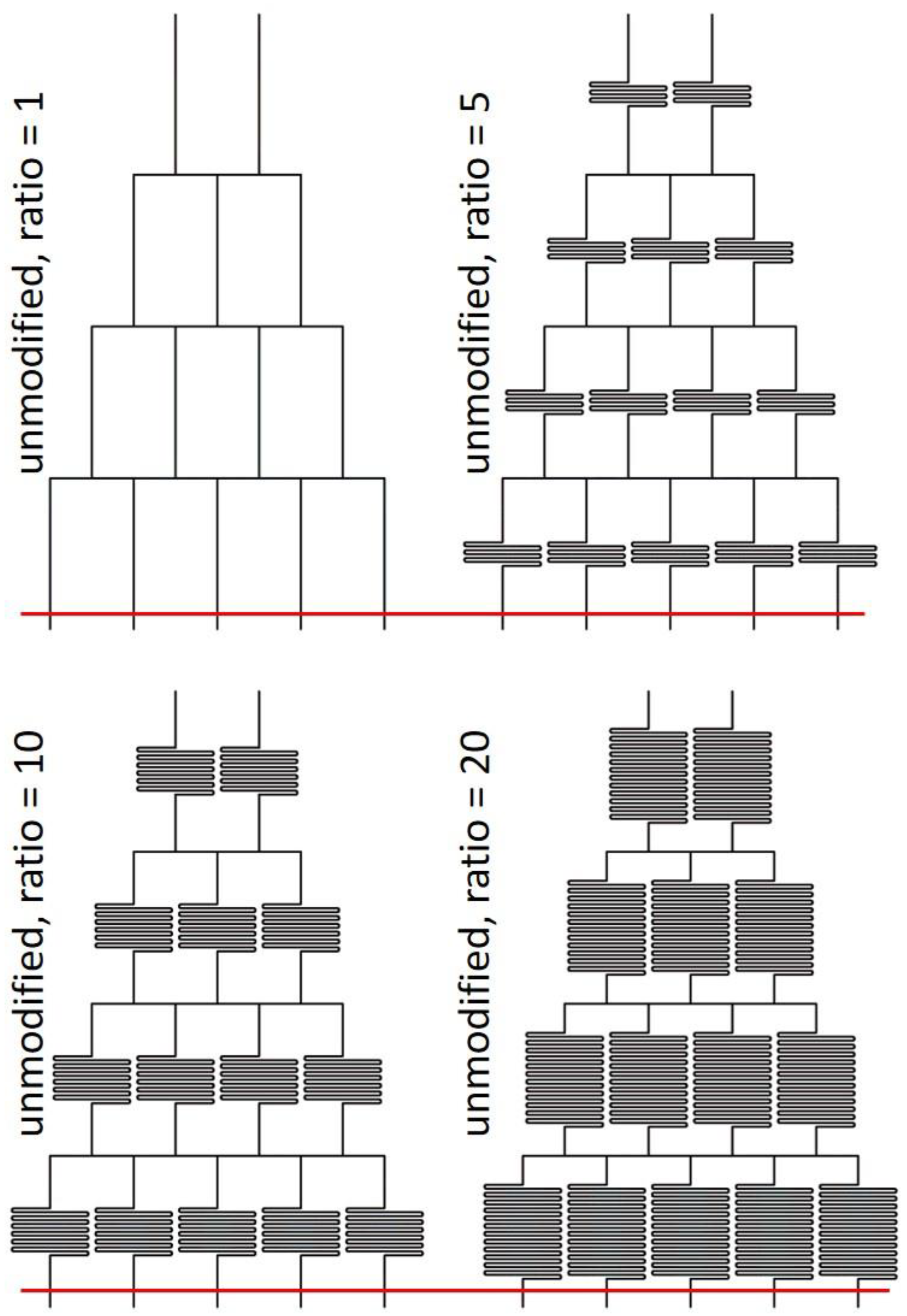
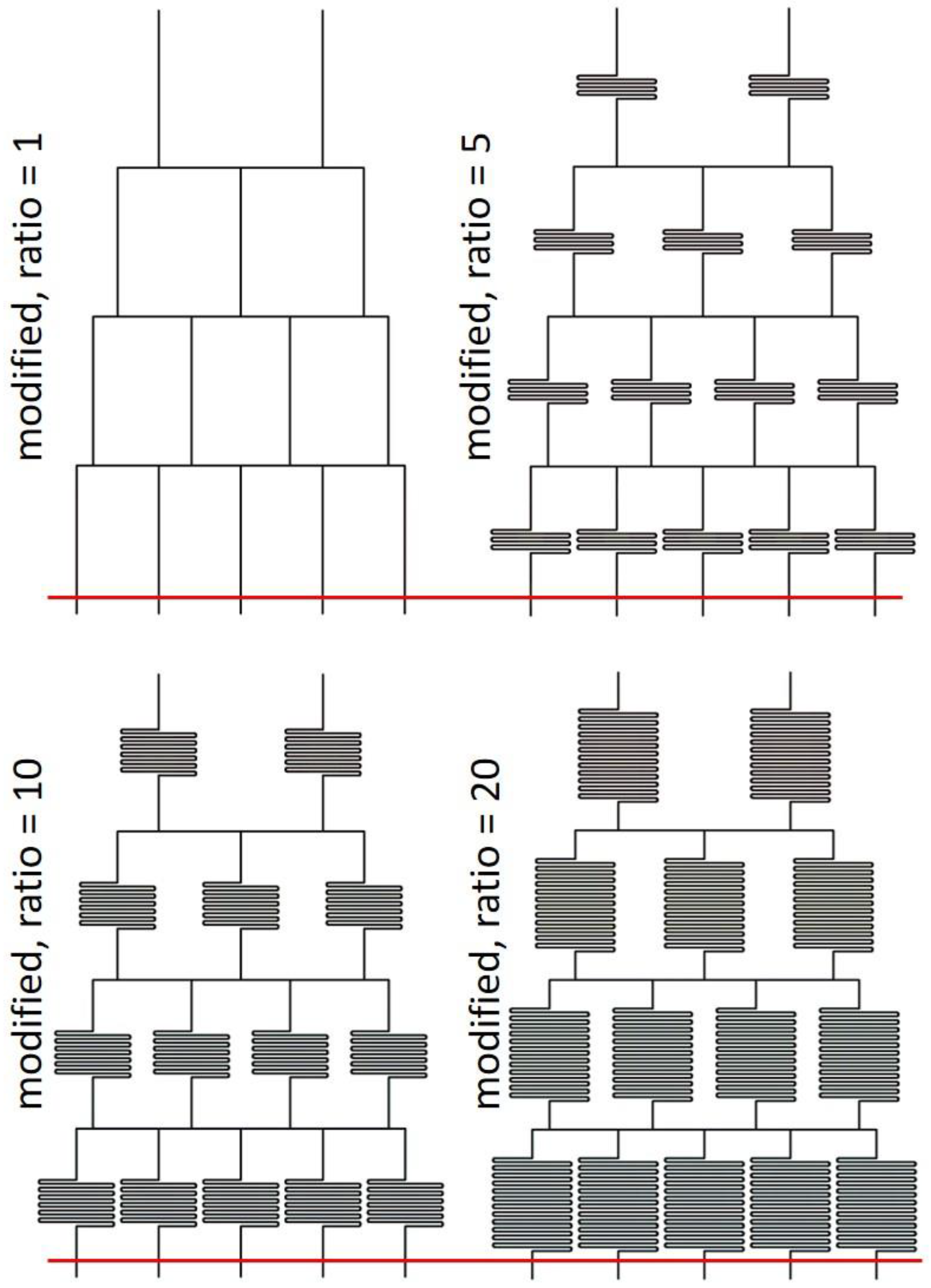
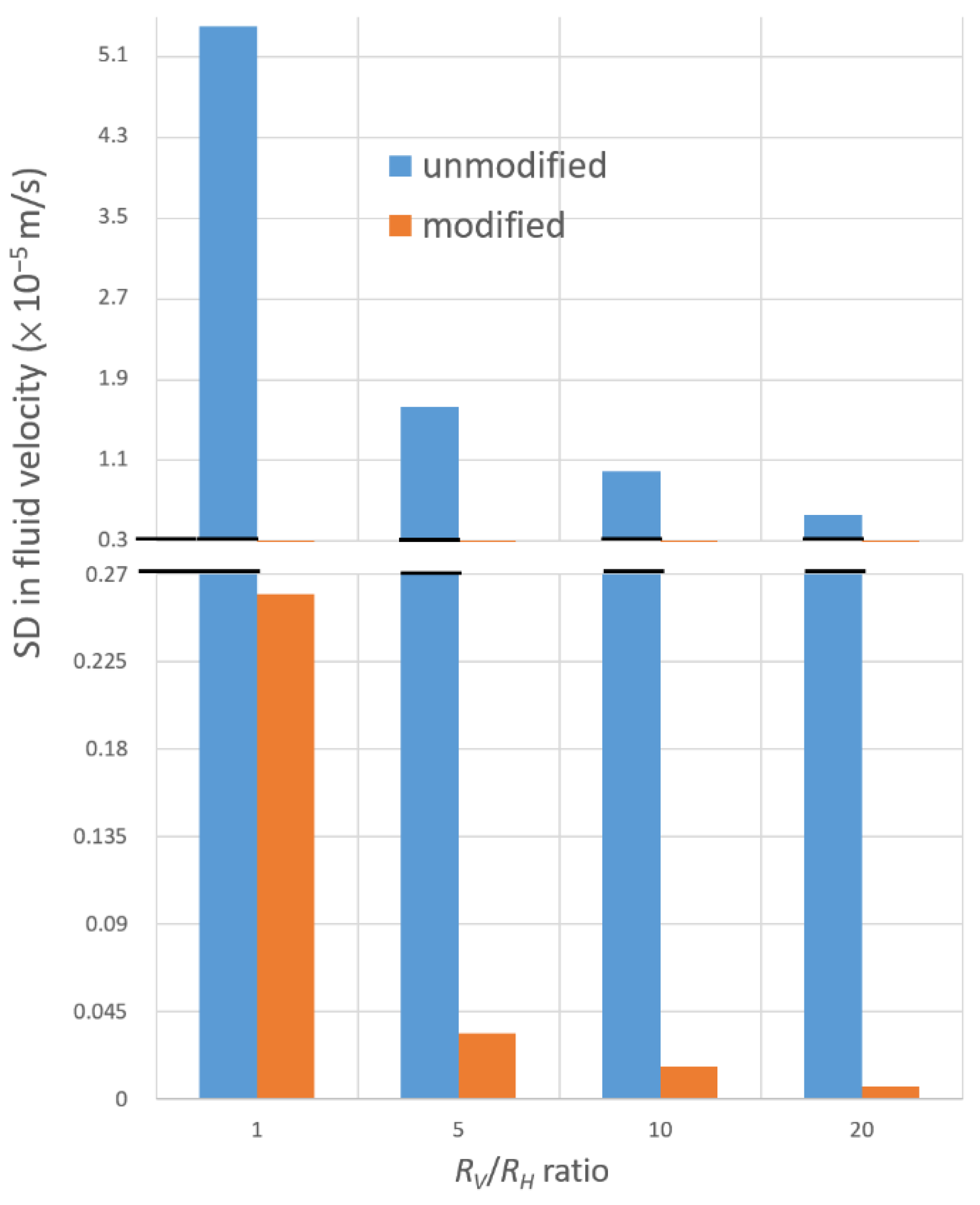
3.4. Extension to MGGs with Multiple Outlets
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wadhams, G.H.; Armitage, J.P. Making sense of it all: Bacterial chemotaxis. Nat. Rev. Mol. Cell Bio. 2004, 5, 1024–1037. [Google Scholar] [CrossRef] [PubMed]
- Cortese, B.; Palama, I.E.; D’Amone, S.; Gigli, G. Influence of electrotaxis on cell behaviour. Integr. Biol.-UK 2014, 6, 817–830. [Google Scholar] [CrossRef] [PubMed]
- Niculescu, A.G.; Chircov, C.; Birca, A.C.; Grumezescu, A.M. Fabrication and applications of microfluidic devices: A review. Int. J. Mol. Sci. 2021, 22, 2011. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Butcher, E.C. T cell chemotaxis in a simple microfluidic device. Lab. Chip. 2006, 6, 1462–1469. [Google Scholar] [CrossRef]
- Li, J.; Nandagopal, S.; Wu, D.; Romanuik, S.F.; Paul, K.; Thomson, D.J.; Lin, F. Activated t lymphocytes migrate toward the cathode of dc electric fields in microfluidic devices. Lab. Chip. 2011, 11, 1298–1304. [Google Scholar] [CrossRef]
- Sia, S.K.; Whitesides, G.M. Microfluidic devices fabricated in poly(dimethylsiloxane) for biological studies. Electrophoresis 2003, 24, 3563–3576. [Google Scholar] [CrossRef]
- Wheeler, A.R.; Throndset, W.R.; Whelan, R.J.; Leach, A.M.; Zare, R.N.; Liao, Y.H.; Farrell, K.; Manger, I.D.; Daridon, A. Microfluidic device for single-cell analysis. Anal. Chem. 2003, 75, 3581–3586. [Google Scholar] [CrossRef]
- Shin, Y.S.; Cho, K.; Lim, S.H.; Chung, S.; Park, S.J.; Chung, C.; Han, D.C.; Chang, J.K. Pdms-based micro pcr chip with parylene coating. J. Micromech. Microeng. 2003, 13, 768–774. [Google Scholar] [CrossRef]
- Sun, Y.S. Studying electrotaxis in microfluidic devices. Sensors 2017, 17, 2048. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.Y.; Lo, K.Y.; Sun, Y.S. A microfluidics-based wound-healing assay for studying the effects of shear stresses, wound widths, and chemicals on the wound-healing process. Sci. Rep.-UK 2019, 9, 20016. [Google Scholar] [CrossRef]
- Sun, Y.; Kwok, Y.C.; Nguyen, N.T. Low-pressure, high-temperature thermal bonding of polymeric microfluidic devices and their applications for electrophoretic separation. J. Micromech. Microeng. 2006, 16, 1681–1688. [Google Scholar] [CrossRef]
- Hashimoto, M.; Barany, F.; Soper, S.A. Polymerase chain reaction/ligase detection reaction/hybridization assays using flow-through microfluidic devices for the detection of low-abundant DNA point mutations. Biosens. Bioelectron. 2006, 21, 1915–1923. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, L.Y.; Chen, G. Fabrication, modification, and application of department of analytical poly(methyl methacrylate) microfluidic chips. Electrophoresis 2008, 29, 1801–1814. [Google Scholar] [CrossRef] [PubMed]
- Gurdon, J.B.; Dyson, S.; St Johnston, D. Cells’ perception of position in a concentration gradient. Cell 1998, 95, 159–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, S.; Zhang, X.; Zhang, F.; Wang, D.; Long, D.; Niu, Y. Three-gradient constructions in a flow-rate insensitive microfluidic system for drug screening towards personalized treatment. Talanta 2020, 208, 120477. [Google Scholar] [CrossRef]
- Dai, W.; Zheng, Y.Z.; Luo, K.Q.; Wu, H.K. A prototypic microfluidic platform generating stepwise concentration gradients for real-time study of cell apoptosis. Biomicrofluidics 2010, 4, 024101. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Liu, W.M.; Wang, Y.L.; Wang, J.C.; Tu, Q.; Liu, R.; Wang, J.Y. Construction of oxygen and chemical concentration gradients in a single microfluidic device for studying tumor cell-drug interactions in a dynamic hypoxia microenvironment. Lab. Chip. 2013, 13, 695–705. [Google Scholar] [CrossRef]
- Atencia, J.; Cooksey, G.A.; Locascio, L.E. A robust diffusion-based gradient generator for dynamic cell assays. Lab. Chip. 2012, 12, 309–316. [Google Scholar] [CrossRef]
- Dravid, A.; Raos, B.; Aqrawe, Z.; Parittotokkaporn, S.; O’Carroll, S.J.; Svirskis, D. A macroscopic diffusion-based gradient generator to establish concentration gradients of soluble molecules within hydrogel scaffolds for cell culture. Front. Chem. 2019, 7, 638. [Google Scholar] [CrossRef]
- Skolimowski, M.; Nielsen, M.W.; Emneus, J.; Molin, S.; Taboryski, R.; Sternberg, C.; Dufva, M.; Geschke, O. Microfluidic dissolved oxygen gradient generator biochip as a useful tool in bacterial biofilm studies. Lab. Chip. 2010, 10, 2162–2169. [Google Scholar] [CrossRef]
- Jeon, H.; Lee, Y.; Jin, S.; Koo, S.; Lee, C.S.; Yoo, J.Y. Quantitative analysis of single bacterial chemotaxis using a linear concentration gradient microchannel. Biomed Microdevices 2009, 11, 1135–1143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, H.B.; Cremer, P.S.; Manson, M.D. A sensitive, versatile microfluidic assay for bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 2003, 100, 5449–5454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lo, K.Y.; Wu, S.Y.; Sun, Y.S. A microfluidic device for studying the production of reactive oxygen species and the migration in lung cancer cells under single or coexisting chemical/electrical stimulation. Microfluid Nanofluid 2016, 20, 15. [Google Scholar] [CrossRef]
- Lo, K.Y.; Zhu, Y.; Tsai, H.F.; Sun, Y.S. Effects of shear stresses and antioxidant concentrations on the production of reactive oxygen species in lung cancer cells. Biomicrofluidics 2013, 7, 064108. [Google Scholar] [CrossRef] [Green Version]
- Jeon, N.L.; Dertinger, S.K.W.; Chiu, D.T.; Choi, I.S.; Stroock, A.D.; Whitesides, G.M. Generation of solution and surface gradients using microfluidic systems. Langmuir 2000, 16, 8311–8316. [Google Scholar] [CrossRef]
- Wang, S.Y.; Yue, F.; Zhang, L.C.; Wang, J.R.; Wang, Y.Y.; Jiang, L.; Lin, B.C.; Wang, Q. Application of microfluidic gradient chip in the analysis of lung cancer chemotherapy resistance. J. Pharmaceut. Biomed. 2009, 49, 806–810. [Google Scholar]
- Ye, N.N.; Qin, J.H.; Shi, W.W.; Liu, X.; Lin, B.C. Cell-based high content screening using an integrated microfluidic device. Lab Chip 2007, 7, 1696–1704. [Google Scholar] [CrossRef]
- Cucina, A.; Sterpetti, A.V.; Pupelis, G.; Fragale, A.; Lepidi, S.; Cavallaro, A.; Giustiniani, Q.; Santoro D’Angelo, L. Shear stress induces changes in the morphology and cytoskeleton organisation of arterial endothelial cells. Eur. J. Vasc. Endovasc. Surg. 1995, 9, 86–92. [Google Scholar] [CrossRef] [Green Version]
- Feugier, P.; Black, R.A.; Hunt, J.A.; How, T.V. Attachment, morphology and adherence of human endothelial cells to vascular prosthesis materials under the action of shear stress. Biomaterials 2005, 26, 1457–1466. [Google Scholar] [CrossRef]
- Chang, S.F.; Chang, C.A.; Lee, D.Y.; Leet, P.L.; Yeh, Y.M.; Yeh, C.R.; Cheng, C.K.; Chien, S.; Chiu, J.J. Tumor cell cycle arrest induced by shear stress: Roles of integrins and smad. Proc. Natl. Acad. Sci. USA 2008, 105, 3927–3932. [Google Scholar] [CrossRef] [Green Version]
- Sakota, D.; Sakamoto, R.; Yokoyama, N.; Kobayashi, M.; Takatani, S. Glucose depletion enhances sensitivity to shear stress-induced mechanical damage in red blood cells by rotary blood pumps. Artif. Organs 2009, 33, 733–739. [Google Scholar] [CrossRef] [PubMed]
- Braddock, M.; Schwachtgen, J.L.; Houston, P.; Dickson, M.C.; Lee, M.J.; Campbell, C.J. Fluid shear stress modulation of gene expression in endothelial cells. News Physiol. Sci. 1998, 13, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Stolberg, S.; McCloskey, K.E. Can shear stress direct stem cell fate? Biotechnol Progr 2009, 25, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Albuquerque, M.L.C.; Waters, C.M.; Savla, U.; Schnaper, H.W.; Flozak, A.S. Shear stress enhances human endothelial cell wound closure in vitro. Am. J. Physiol.-Heart C 2000, 279, H293–H302. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-H.; Ping, C.-H.; Sun, Y.-S. Design of Christmas-Tree-like Microfluidic Gradient Generators for Cell-Based Studies. Chemosensors 2023, 11, 2. https://doi.org/10.3390/chemosensors11010002
Wang Y-H, Ping C-H, Sun Y-S. Design of Christmas-Tree-like Microfluidic Gradient Generators for Cell-Based Studies. Chemosensors. 2023; 11(1):2. https://doi.org/10.3390/chemosensors11010002
Chicago/Turabian StyleWang, Yu-Hsun, Chi-Hung Ping, and Yung-Shin Sun. 2023. "Design of Christmas-Tree-like Microfluidic Gradient Generators for Cell-Based Studies" Chemosensors 11, no. 1: 2. https://doi.org/10.3390/chemosensors11010002
APA StyleWang, Y.-H., Ping, C.-H., & Sun, Y.-S. (2023). Design of Christmas-Tree-like Microfluidic Gradient Generators for Cell-Based Studies. Chemosensors, 11(1), 2. https://doi.org/10.3390/chemosensors11010002








