Gas Sensing with Nanoporous In2O3 under Cyclic Optical Activation: Machine Learning-Aided Classification of H2 and H2O
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Characterization of Ordered Mesoporous In2O3
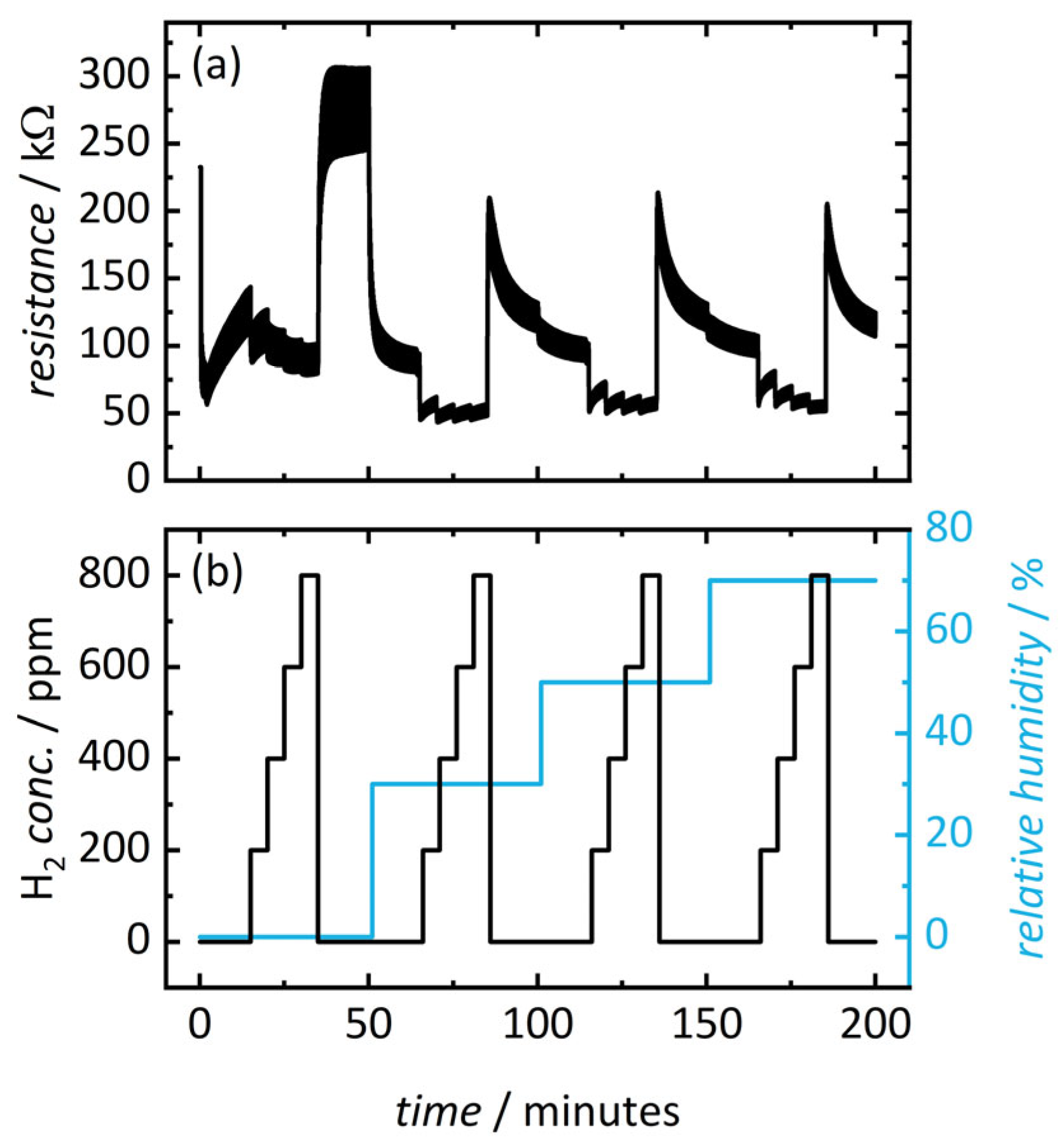
3.2. Resistance Changes during Cyclic Optical Activation and Gas Exposure
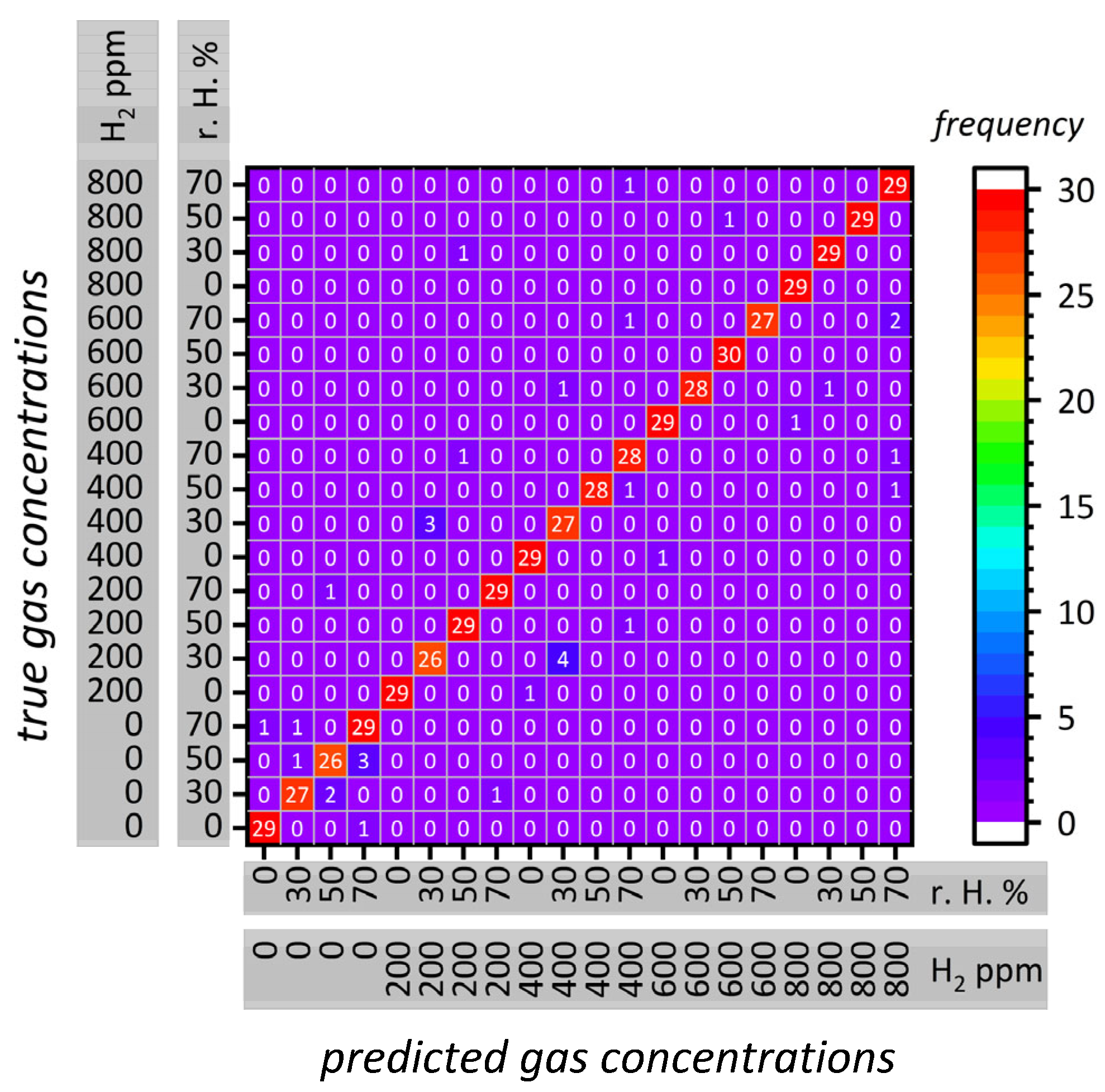
3.3. Gas Concentration Classification
| Faleh et al. [65] | Tonezzer, Van Duy et al. [27] | Kim, Shin et al. [66] | Ge et al. [50] | Yoon, Park et al. [13] | This Study | |
| material | WO3 | SnO2 + Ag, Pt | ZnO | commercial | In2O3 + Au | In2O3 |
| no. sensor(s) | 4 | 4 | 1 | 1 | 1 | 5 |
| operation mode | static T a | static T a | cyclic T a | cyclic T a | time-variant illumination | cyclic illumination |
| data analysis | SVM | SVM | CNN b | SVM | CNN b | SVM |
| data preprocessing | yes | no | yes | yes | yes | no |
| classification rate/% | 93.03 | 100 | 93.9 | 95.4 | 96.53 | 92.0 |
3.4. Single-Gas Concentration Classification and Cycle Normalization
3.5. Classification Success for Different Stages of the Optical Activation Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Commission. Communication from the Commision to the European Parliament, the Council, the European Economics and Social Committee and the Committee of the Regions: A Hydrogen Strategy for Climate-Neutral Europe. Available online: https://ec.europa.eu/energy/sites/ener/files/hydrogen_strategy.pdf (accessed on 3 July 2024).
- Xu, F.; HO, H.-P. Light-Activated Metal Oxide Gas Sensors: A Review. Micromachines 2017, 8, 333. [Google Scholar] [CrossRef]
- Li, Z.; Yan, S.; Wu, Z.; Li, H.; Wang, J.; Shen, W.; Wang, Z.; Fu, Y. Hydrogen gas sensor based on mesoporous In2O3 with fast response/recovery and ppb level detection limit. Int. J. Hydrogen Energy 2018, 43, 22746–22755. [Google Scholar] [CrossRef]
- Wagner, T.; Haffer, S.; Weinberger, C.; Klaus, D.; Tiemann, M. Mesoporous materials as gas sensors. Chem. Soc. Rev. 2013, 42, 4036–4053. [Google Scholar] [CrossRef] [PubMed]
- Gu, D.; Schüth, F. Synthesis of non-siliceous mesoporous oxides. Chem. Soc. Rev. 2014, 43, 313–344. [Google Scholar] [CrossRef] [PubMed]
- Kohl, C.-D.; Wagner, T.; Dickert, F.L.; Dickert, F.L. (Eds.) Gas Sensing Fundamentals; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-54518-4. [Google Scholar]
- Shah, S.; Hussain, S.; Din, S.T.U.; Shahid, A.; Amu-Darko, J.N.O.; Wang, M.; Tianyan, Y.; Liu, G.; Qiao, G. A review on In2O3 nanostructures for gas sensing applications. J. Environ. Chem. Eng. 2024, 12, 112538. [Google Scholar] [CrossRef]
- Xirouchaki, C.; Kiriakidis, G.; Pedersen, T.F.; Fritzsche, H. Photoreduction and oxidation of as-deposited microcrystalline indium oxide. J. Appl. Phys. 1996, 79, 9349–9352. [Google Scholar] [CrossRef]
- Matino, F.; Persano, L.; Arima, V.; Pisignano, D.; Blyth, R.I.R.; Cingolani, R.; Rinaldi, R. Electronic structure of indium-tin-oxide films fabricated by reactive electron-beam deposition. Phys. Rev. B 2005, 72, 85437. [Google Scholar] [CrossRef]
- Spencer, J.A.; Mock, A.L.; Jacobs, A.G.; Schubert, M.; Zhang, Y.; Tadjer, M.J. A review of band structure and material properties of transparent conducting and semiconducting oxides: Ga2O3, Al2O3, In2O3, ZnO, SnO2, CdO, NiO, CuO, and Sc2O3. Appl. Phys. Rev. 2022, 9, 011315. [Google Scholar] [CrossRef]
- Wagner, T.; Kohl, C.D.; Morandi, S.; Malagù, C.; Donato, N.; Latino, M.; Neri, G.; Tiemann, M. Photoreduction of Mesoporous In2O3: Mechanistic Model and Utility in Gas Sensing. Chem. Eur. J. 2012, 18, 8216–8223. [Google Scholar] [CrossRef]
- Espid, E.; Taghipour, F. UV-LED Photo-activated Chemical Gas Sensors: A Review. Crit. Rev. Solid State Mater. Sci. 2017, 42, 416–432. [Google Scholar] [CrossRef]
- Cho, I.; Lee, K.; Sim, Y.C.; Jeong, J.-S.; Cho, M.; Jung, H.; Kang, M.; Cho, Y.-H.; Ha, S.C.; Yoon, K.-J.; et al. Deep-learning-based gas identification by time-variant illumination of a single micro-LED-embedded gas sensor. Light Sci. Appl. 2023, 12, 95. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Shao, L.; Deng, S.; Lu, Z.; Yan, R.; Ren, D.; Huang, Y.; Liu, H. Synthesis of C-In2O3/BiOI composite and its enhanced photocatalytic degradation for methyl blue. Inorg. Chem. Commun. 2019, 100, 56–59. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Balogun, M.-S.; Tong, Y.; Huang, Y. Oxygen vacancy–based metal oxides photoanodes in photoelectrochemical water splitting. Mater. Today Sustain. 2022, 18, 100118. [Google Scholar] [CrossRef]
- Eranna, G.; Joshi, B.C.; Runthala, D.P.; Gupta, R.P. Oxide Materials for Development of Integrated Gas Sensors—A Comprehensive Review. Crit. Rev. Solid State Mater. Sci. 2004, 29, 111–188. [Google Scholar] [CrossRef]
- Schultealbert, C.; Amann, J.; Baur, T.; Schütze, A. Measuring Hydrogen in Indoor Air with a Selective Metal Oxide Semiconductor Sensor. Atmosphere 2021, 12, 366. [Google Scholar] [CrossRef]
- van den Broek, J.; Weber, I.C.; Güntner, A.T.; Pratsinis, S.E. Highly selective gas sensing enabled by filters. Mater. Horiz. 2021, 8, 661–684. [Google Scholar] [CrossRef]
- Dey, A. Semiconductor metal oxide gas sensors: A review. Mater. Sci. Eng. B 2018, 229, 206–217. [Google Scholar] [CrossRef]
- Ueda, T.; Boehme, I.; Hyodo, T.; Shimizu, Y.; Weimar, U.; Barsan, N. Enhanced NO2-Sensing Properties of Au-Loaded Porous In2O3 Gas Sensors at Low Operating Temperatures. Chemosensors 2020, 8, 72. [Google Scholar] [CrossRef]
- Weber, I.C.; Güntner, A.T. Catalytic filters for metal oxide gas sensors. Sens. Actuators B 2022, 356, 131346. [Google Scholar] [CrossRef]
- Sauerwald, T.; Skiera, D.; Kohl, C.-D. Selectivity enhancement of gas sensors using non-equilibrium polarisation effects in metal oxide films. Appl. Phys. A 2007, 87, 525–529. [Google Scholar] [CrossRef]
- Gramm, A.; Schütze, A. High performance solvent vapor identification with a two sensor array using temperature cycling and pattern classification. Sens. Actuators B 2003, 95, 58–65. [Google Scholar] [CrossRef]
- Lee, A. Temperature modulation in semiconductor gas sensing. Sens. Actuators B 1999, 60, 35–42. [Google Scholar] [CrossRef]
- Semancik, S.; Cavicchi, R.E.; Wheeler, M.C.; Tiffany, J.E.; Poirier, G.E.; Walton, R.M.; Suehle, J.S.; Panchapakesan, B.; DeVoe, D.L. Microhotplate platforms for chemical sensor research. Sens. Actuators B 2001, 77, 579–591. [Google Scholar] [CrossRef]
- Leidinger, M.; Sauerwald, T.; Reimringer, W.; Ventura, G.; Schütze, A. Selective detection of hazardous VOCs for indoor air quality applications using a virtual gas sensor array. J. Sens. Sens. Syst. 2014, 3, 253–263. [Google Scholar] [CrossRef]
- Thai, N.X.; Tonezzer, M.; Masera, L.; Nguyen, H.; van Duy, N.; Hoa, N.D. Multi gas sensors using one nanomaterial, temperature gradient, and machine learning algorithms for discrimination of gases and their concentration. Anal. Chim. Acta 2020, 1124, 85–93. [Google Scholar] [CrossRef]
- Smulko, J.; Trawka, M.; Ionescu, R.; Annanouch, F.E.; ETSE-DEEEA, E.L.; Granqvist, C.G.; Kish, L.B. New approaches for improving selectivity and sensitivity of resistive gas sensors: A review. Int. J. Smart Sens. Intell. Syst. 2014, 7, 1–6. [Google Scholar] [CrossRef]
- Güney, S.; Atasoy, A. Multiclass classification of n-butanol concentrations with k-nearest neighbor algorithm and support vector machine in an electronic nose. Sens. Actuators B 2012, 166–167, 721–725. [Google Scholar] [CrossRef]
- Reimann, P.; Schütze, A. Sensor Arrays, Virtual Multisensors, Data Fusion, and Gas Sensor Data Evaluation. In Gas Sensing Fundamentals; Kohl, C.-D., Wagner, T., Dickert, F.L., Dickert, F.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 67–107. ISBN 978-3-642-54518-4. [Google Scholar]
- Dorst, T.; Schneider, T.; Eichstädt, S.; Schütze, A. Influence of measurement uncertainty on machine learning results demonstrated for a smart gas sensor. J. Sens. Sens. Syst. 2023, 12, 45–60. [Google Scholar] [CrossRef]
- Ankara, Z.; Kammerer, T.; Gramm, A.; Schütze, A. Low power virtual sensor array based on a micromachined gas sensor for fast discrimination between H2, CO and relative humidity. Sens. Actuators B 2004, 100, 240–245. [Google Scholar] [CrossRef]
- Prades, J.D.; Jimenez-Diaz, R.; Hernandez-Ramirez, F.; Barth, S.; Cirera, A.; Romano-Rodriguez, A.; Mathur, S.; Morante, J.R. Equivalence between thermal and room temperature UV light-modulated responses of gas sensors based on individual SnO2 nanowires. Sens. Actuators B 2009, 140, 337–341. [Google Scholar] [CrossRef]
- Njio, G.; Wagner, T. P2AR.3—Virtual Gas Sensor Array by Cyclic Optical Activation: Optimization of Activation Profile by Machine Learning. In Proceedings of the 17th International Meeting on Chemical Sensors—IMCS 2018, Vienna, Austria, 15–19 July 2018; AMA Service GmbH: Wunstorf, Germany, 2018; pp. 905–906. [Google Scholar]
- Agoston, P.; Albe, K. Formation entropies of intrinsic point defects in cubic In2O3 from first-principles density functional theory calculations. Phys. Chem. Chem. Phys. 2009, 11, 3226–3232. [Google Scholar] [CrossRef] [PubMed]
- Bender, M.; Katsarakis, N.; Gagaoudakis, E.; Hourdakis, E.; Douloufakis, E.; Cimalla, V.; Kiriakidis, G. Dependence of the photoreduction and oxidation behavior of indium oxide films on substrate temperature and film thickness. J. Appl. Phys. 2001, 90, 5382–5387. [Google Scholar] [CrossRef]
- Klaus, D.; Klawinski, D.; Amrehn, S.; Tiemann, M.; Wagner, T. Light-activated resistive ozone sensing at room temperature utilizing nanoporous In2O3 particles: Influence of particle size. Sens. Actuators B 2015, 217, 181–185. [Google Scholar] [CrossRef]
- Chizhov, A.; Rumyantseva, M.; Gaskov, A. Light Activation of Nanocrystalline Metal Oxides for Gas Sensing: Principles, Achievements, Challenges. Nanomaterials 2021, 11, 892. [Google Scholar] [CrossRef] [PubMed]
- Nasriddinov, A.; Tokarev, S.; Fedorova, O.; Bozhev, I.; Rumyantseva, M. In2O3 Based Hybrid Materials: Interplay between Microstructure, Photoelectrical and Light Activated NO2 Sensor Properties. Chemosensors 2022, 10, 135. [Google Scholar] [CrossRef]
- Nasriddinov, A.; Rumyantseva, M.; Konstantinova, E.; Marikutsa, A.; Tokarev, S.; Yaltseva, P.; Fedorova, O.; Gaskov, A. Effect of Humidity on Light-Activated NO and NO2 Gas Sensing by Hybrid Materials. Nanomaterials 2020, 10, 915. [Google Scholar] [CrossRef] [PubMed]
- Rumyantseva, M.; Nasriddinov, A.; Krivetskiy, V.; Gaskov, A. Light—Assisted Low Temperature Formaldehyde Detection at Sub-ppm Level Using Metal Oxide Semiconductor Gas Sensors. Proceedings 2019, 14, 37. [Google Scholar] [CrossRef]
- Rumyantseva, M.; Nasriddinov, A.; Vladimirova, S.; Tokarev, S.; Fedorova, O.; Krylov, I.; Drozdov, K.; Baranchikov, A.; Gaskov, A. Photosensitive Organic-Inorganic Hybrid Materials for Room Temperature Gas Sensor Applications. Nanomaterials 2018, 8, 671. [Google Scholar] [CrossRef]
- Lee, D.-Y.; Yu, J.-B.; Byun, H.-G.; Kim, H.-J. Chemoresistive Sensor Readout Circuit Design for Detecting Gases with Slow Response Time Characteristics. Sensors 2022, 22, 1102. [Google Scholar] [CrossRef]
- Dulhare, U.; Ahmad, K.; Bin Ahmad, K. Machine Learning and Big Data, 1st ed.; Wiley-Scrivener; Safari: Boston, MA, USA, 2020; ISBN 9781119654742. [Google Scholar]
- Yaqoob, U.; Younis, M.I. Chemical Gas Sensors: Recent Developments, Challenges, and the Potential of Machine Learning—A Review. Sensors 2021, 21, 2877. [Google Scholar] [CrossRef]
- Ferguson, A.L.; Hachmann, J.; Miller, T.F.; Pfaendtner, J. The Journal of Physical Chemistry A / B / C Virtual Special Issue on Machine Learning in Physical Chemistry. J. Phys. Chem. C 2020, 124, 24033–24038. [Google Scholar] [CrossRef]
- Prezhdo, O.V. Advancing Physical Chemistry with Machine Learning. J. Phys. Chem. Lett. 2020, 11, 9656–9658. [Google Scholar] [CrossRef] [PubMed]
- Dennler, N.; Rastogi, S.; Fonollosa, J.; van Schaik, A.; Schmuker, M. Drift in a popular metal oxide sensor dataset reveals limitations for gas classification benchmarks. Sens. Actuators B 2022, 361, 131668. [Google Scholar] [CrossRef]
- Vergara, A.; Fonollosa, J.; Mahiques, J.; Trincavelli, M.; Rulkov, N.; Huerta, R. On the performance of gas sensor arrays in open sampling systems using Inhibitory Support Vector Machines. Sens. Actuators B 2013, 185, 462–477. [Google Scholar] [CrossRef]
- Ge, H.; Liu, J. Identification of gas mixtures by a distributed support vector machine network and wavelet decomposition from temperature modulated semiconductor gas sensor. Sens. Actuators B Chem. 2006, 117, 408–414. [Google Scholar] [CrossRef]
- Laref, R.; Losson, E.; Sava, A.; Siadat, M. Support Vector Machine Regression for Calibration Transfer between Electronic Noses Dedicated to Air Pollution Monitoring. Sensors 2018, 18, 3716. [Google Scholar] [CrossRef]
- Wang, T.; Ma, H.; Jiang, W.; Zhang, H.; Zeng, M.; Yang, J.; Wang, X.; Liu, K.; Huang, R.; Yang, Z. Type discrimination and concentration prediction towards ethanol using a machine learning-enhanced gas sensor array with different morphology-tuning characteristics. Phys. Chem. Chem. Phys. 2021, 23, 23933–23944. [Google Scholar] [CrossRef] [PubMed]
- Boon-Brett, L.; Bousek, J.; Black, G.; Moretto, P.; Castello, P.; Hübert, T.; Banach, U. Identifying performance gaps in hydrogen safety sensor technology for automotive and stationary applications. Int. J. Hydrogen Energy 2010, 35, 373–384. [Google Scholar] [CrossRef]
- Kleitz, F.; Hei Choi, S.; Ryoo, R. Cubic Ia3d large mesoporous silica: Synthesis and replication to platinum nanowires, carbon nanorods and carbon nanotubes. Chem. Commun. 2003, 17, 2136–2137. [Google Scholar] [CrossRef]
- Klaus, D.; Amrehn, S.; Tiemann, M.; Wagner, T. One-step synthesis of multi-modal pore systems in mesoporous In2O3: A detailed study. Microporous Mesoporous Mater. 2014, 188, 133–139. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Rouquerol, J.; Llewellyn, P.; Rouquerol, F. Is the BET equation applicable to microporous adsorbents? In Studies in Surface Science and Catalysis Characterization of Porous Solids VII, Proceedings of the 7th International Symposium on the Characterization of Porous Solids (COPS-VII), Aix-en-Provence, France, 26–28 May 2005; Llewellyn, P.L., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 49–56. ISBN 0167-2991. [Google Scholar]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The Determination of Pore Volume and Area Distributions in Porous Substances. I. Computations from Nitrogen Isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Evans, J.D.; Bon, V.; Senkovska, I.; Kaskel, S. A Universal Standard Archive File for Adsorption Data. Langmuir 2021, 37, 4222–4226. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.W.; Solovyov, L.A. Synthesis and characterization of large-pore ordered mesoporous carbons using gyroidal silica template. J. Mater. Chem. 2006, 16, 1445–1455. [Google Scholar] [CrossRef]
- Haffer, S.; Waitz, T.; Tiemann, M. Mesoporous In2O3 with Regular Morphology by Nanocasting: A Simple Relation between Defined Particle Shape and Growth Mechanism. J. Phys. Chem. C 2010, 114, 2075–2081. [Google Scholar] [CrossRef]
- Suematsu, K.; Ma, N.; Watanabe, K.; Yuasa, M.; Kida, T.; Shimanoe, K. Effect of Humid Aging on the Oxygen Adsorption in SnO2 Gas Sensors. Sensors 2018, 18, 254. [Google Scholar] [CrossRef]
- Jia, W.; Sun, M.; Lian, J.; Hou, S. Feature dimensionality reduction: A review. Complex Intell. Syst. 2022, 8, 2663–2693. [Google Scholar] [CrossRef]
- Faleh, R.; Gomri, S.; Aguir, K.; Kachouri, A. A new combined transient extraction method coupled with WO3 gas sensors for polluting gases classification. Sens. Rev. 2021, 41, 437–448. [Google Scholar] [CrossRef]
- Kim, T.; Kim, Y.; Cho, W.; Kwak, J.-H.; Cho, J.; Pyeon, Y.; Kim, J.J.; Shin, H. Ultralow-Power Single-Sensor-Based E-Nose System Powered by Duty Cycling and Deep Learning for Real-Time Gas Identification. ACS Sens. 2024, 9, 3557–3572. [Google Scholar] [CrossRef]
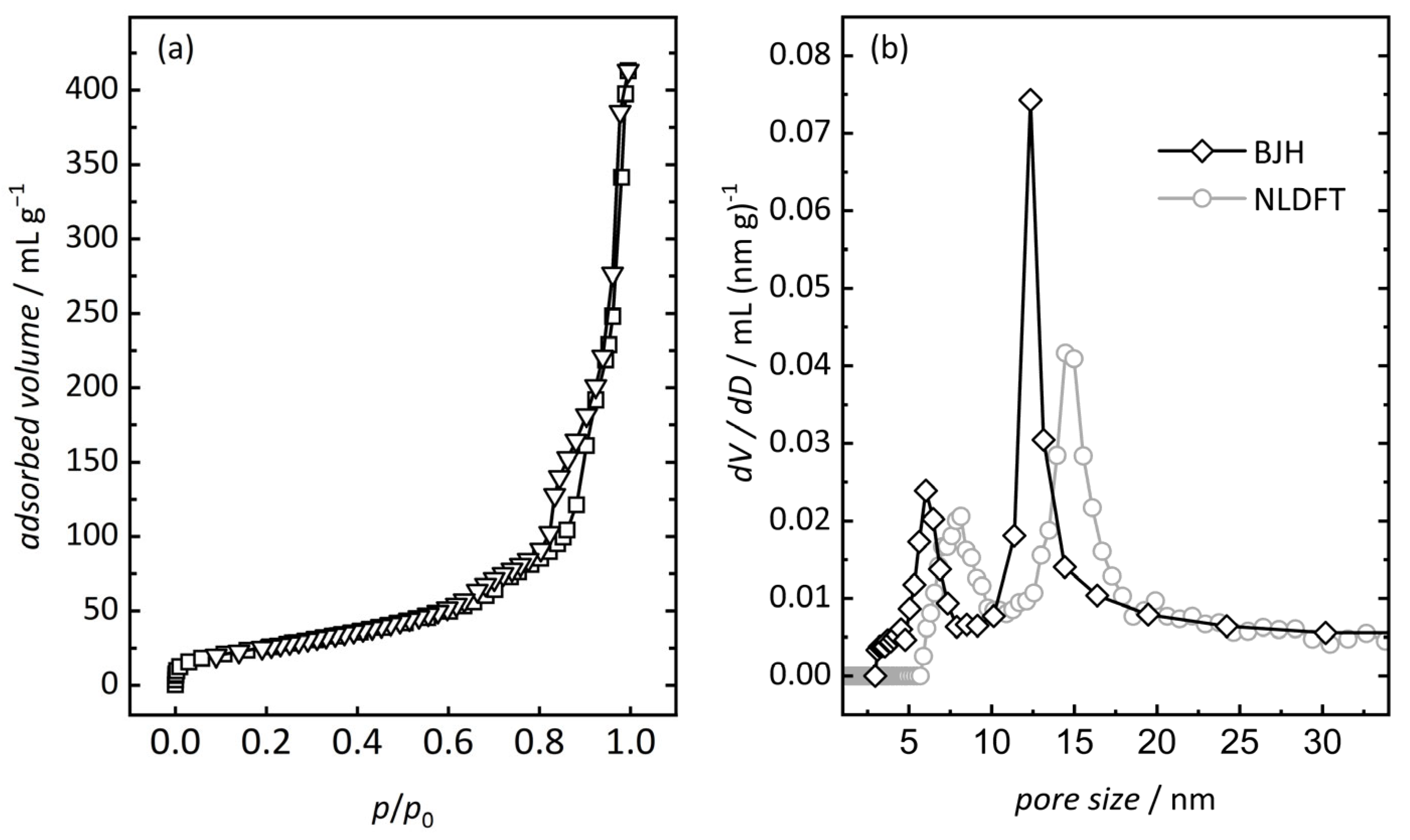
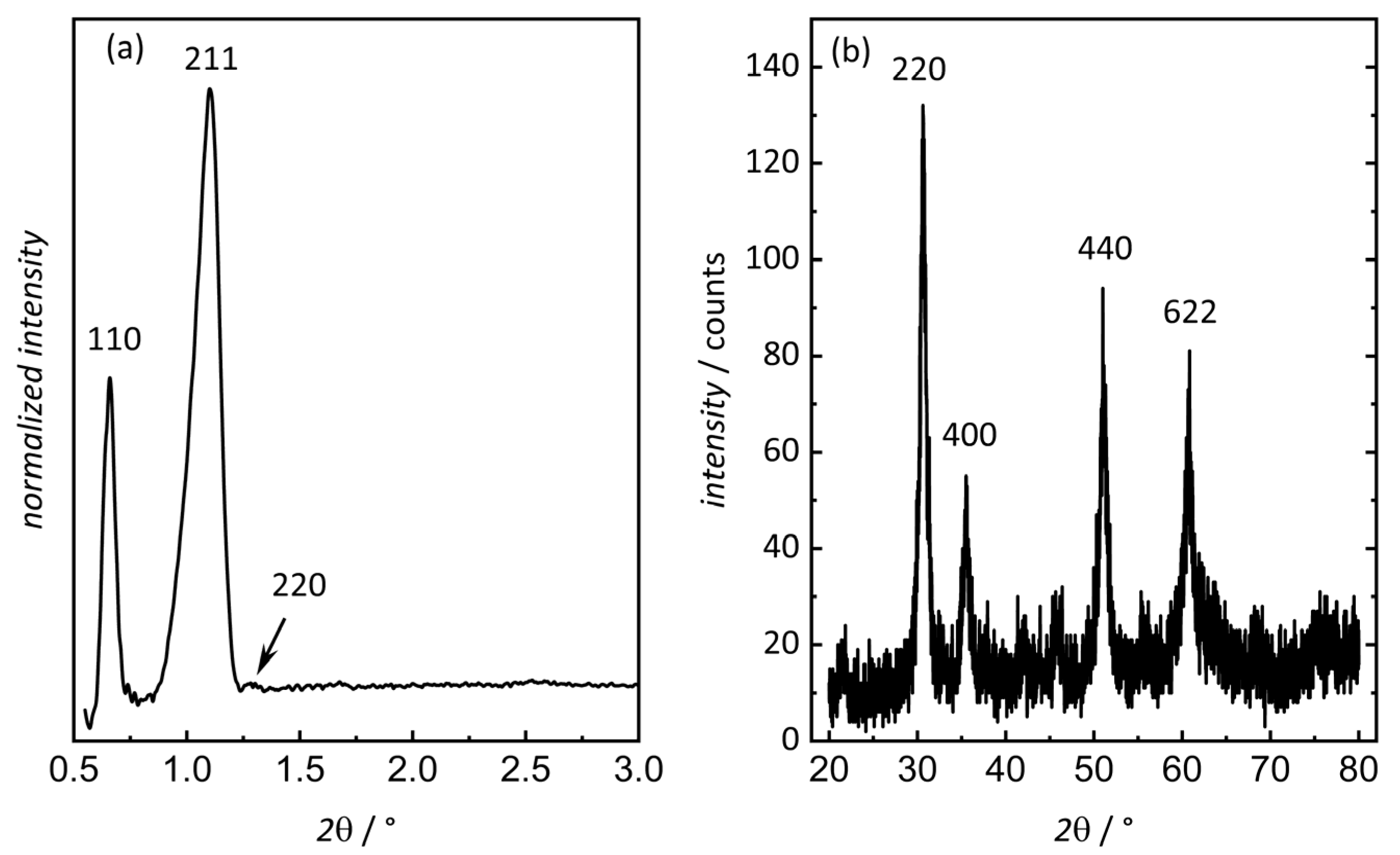



| Sample | Pore Size (a) nm | Pore Size (b) nm | Surface Area (c) m2 g−1 | Pore Volume (d) mL g−1 |
|---|---|---|---|---|
| silica | 5.1 | 6.6 | 550 | 0.83 |
| In2O3 | 6.0; 12.3 | 8.1; 14.5 | 95 | 0.62 |
| constant H2 concentration [ppm] | 0 | 200 | 400 | 600 | 800 |
| H2O classification | 79.8 ± 8.5 | 96.6 ± 1.7 | 96.2 ± 1.5 | 99.0 ± 1.3 | 99.4 ± 0.8 |
| constant H2O concentration [%] | 0 | 30 | 50 | 70 |
| H2 classification | 97.8 ± 1.7 | 96.4 ± 0.8 | 97.0 ± 1.7 | 95.1 ± 1.0 |
| Dataset | LED Status | Duration of ... s | Classification Rate % | ||
|---|---|---|---|---|---|
| Illumination | Darkness | Dataset | |||
| (a) | on-off | 5 | 5 | 10 | 88.4 ± 3.0 |
| (b) | on | 5 | 0 | 5 | 80.4 ± 4.5 |
| (c) | off | 0 | 5 | 5 | 81.2 ± 6.0 |
| (d) | off-on | 2.5 | 2.5 | 5 | 86.6 ± 4.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baier, D.; Krüger, A.; Wagner, T.; Tiemann, M.; Weinberger, C. Gas Sensing with Nanoporous In2O3 under Cyclic Optical Activation: Machine Learning-Aided Classification of H2 and H2O. Chemosensors 2024, 12, 178. https://doi.org/10.3390/chemosensors12090178
Baier D, Krüger A, Wagner T, Tiemann M, Weinberger C. Gas Sensing with Nanoporous In2O3 under Cyclic Optical Activation: Machine Learning-Aided Classification of H2 and H2O. Chemosensors. 2024; 12(9):178. https://doi.org/10.3390/chemosensors12090178
Chicago/Turabian StyleBaier, Dominik, Alexander Krüger, Thorsten Wagner, Michael Tiemann, and Christian Weinberger. 2024. "Gas Sensing with Nanoporous In2O3 under Cyclic Optical Activation: Machine Learning-Aided Classification of H2 and H2O" Chemosensors 12, no. 9: 178. https://doi.org/10.3390/chemosensors12090178
APA StyleBaier, D., Krüger, A., Wagner, T., Tiemann, M., & Weinberger, C. (2024). Gas Sensing with Nanoporous In2O3 under Cyclic Optical Activation: Machine Learning-Aided Classification of H2 and H2O. Chemosensors, 12(9), 178. https://doi.org/10.3390/chemosensors12090178








