RH Sensing by Means of TiO2 Nanoparticles: A Comparison among Different Sensing Techniques Based on Modeling and Chemical/Physical Interpretation
Abstract
:1. Introduction
2. Theoretical Background
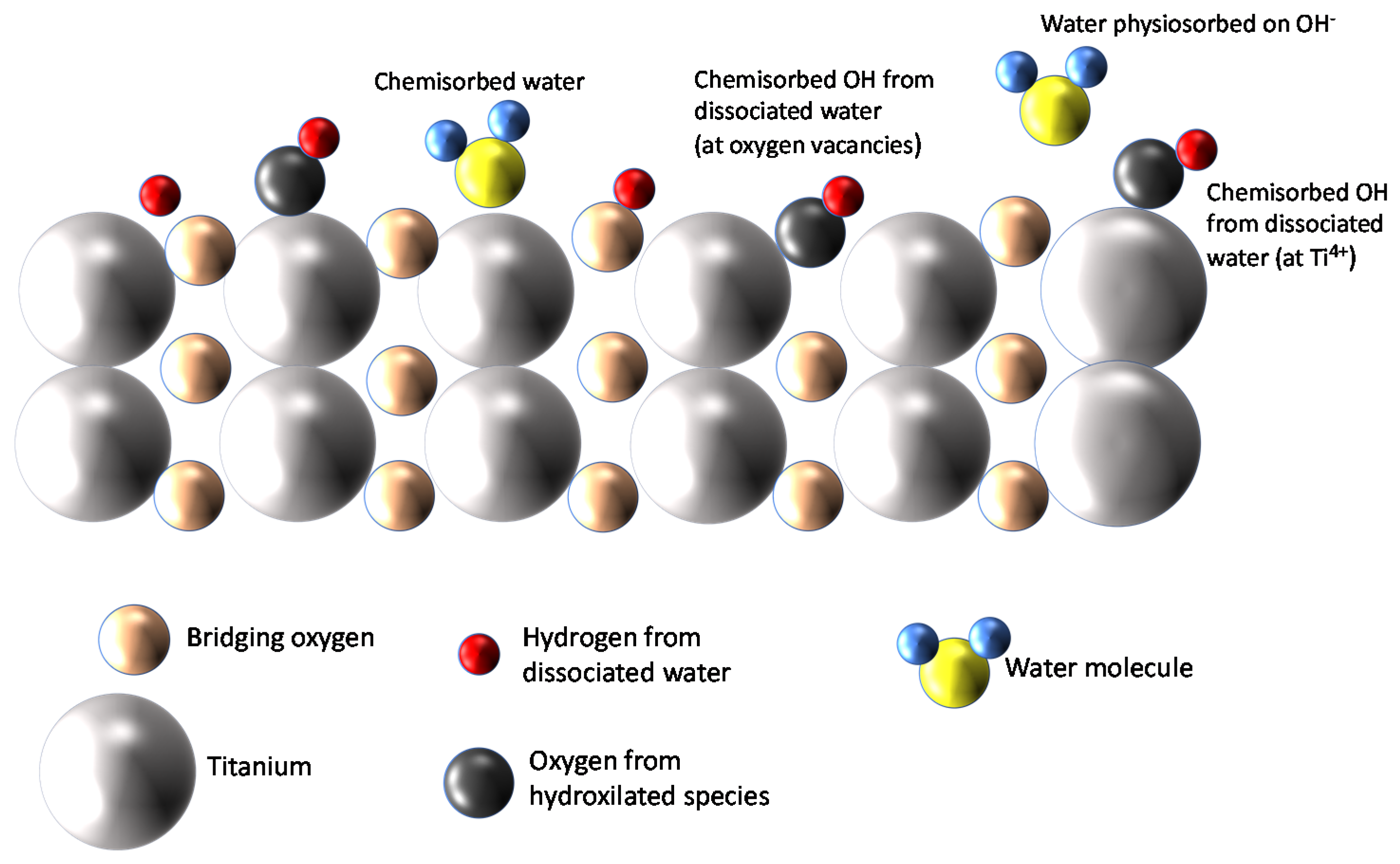
2.1. Modeling of Water Adsorption on TiO2
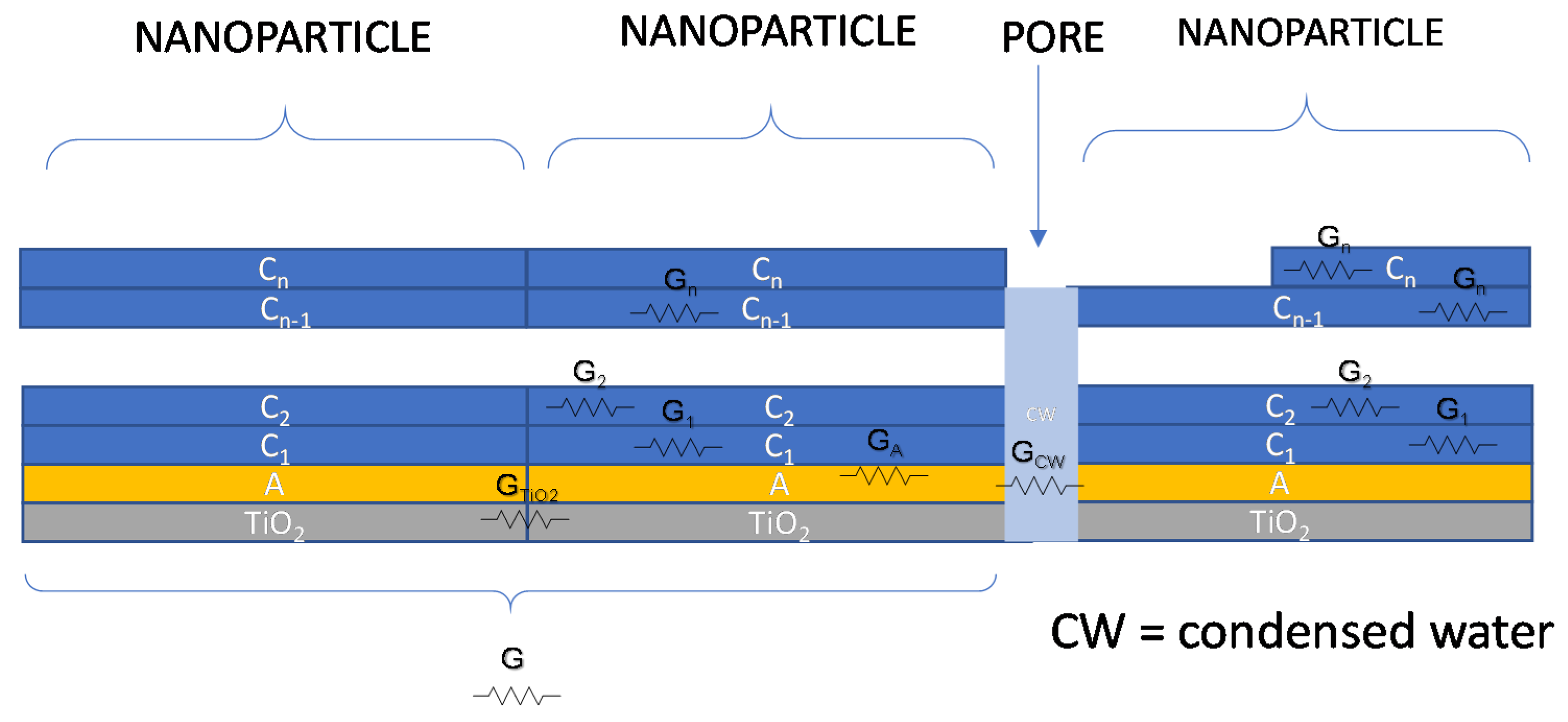
2.2. Influence of Adsorbed Water on the TiO2 Film Impedance
3. Materials and Material Characterization
3.1. Water Adsorption on TiO2: Sensing Devices and Measurement Methods
3.1.1. The QCM Sensor and Sensing System
3.1.2. The Cantilever-Based Sensor and Sensing System
3.1.3. The Impedance Sensor and Sensing System
4. Experimental Results and Discussion
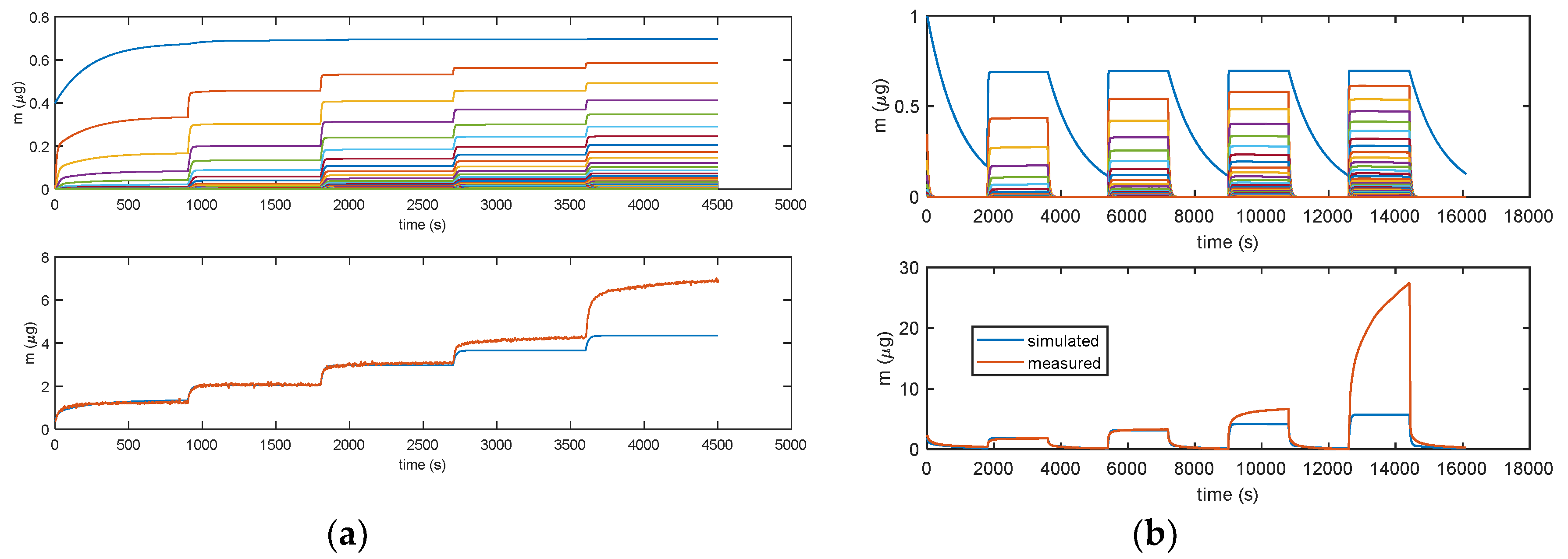
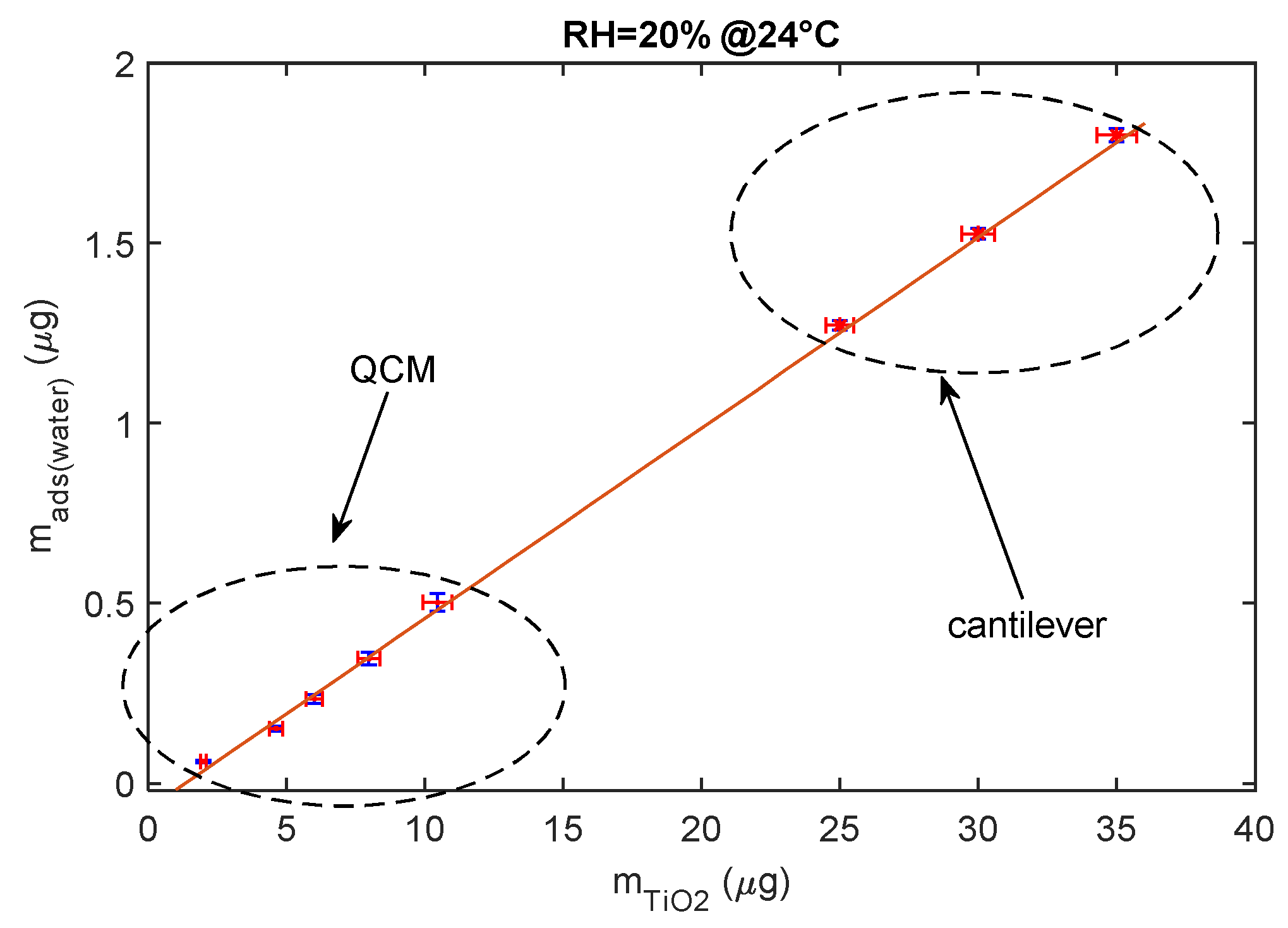
4.1. Water Adsorption on TiO2 Nanoparticle Films
4.2. Impedance of the TiO2 Nanoparticle Film
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cambra, C.; Sendra, S.; Lloret, J.; Garcia, L. An IoT service-oriented system for agriculture monitoring. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zhou, S.; Deng, F.; Yu, L.; Li, B.; Wu, X.; Yin, B. A Novel Passive Wireless Sensor for Concrete Humidity Monitoring. Sensors 2016, 16, 1535. [Google Scholar] [CrossRef]
- Al-Hamry, A.; Panzardi, E.; Mugnaini, M.; Kanoun, O. Health Monitoring of Human Breathing by Graphene Oxide Based Sensors. In Proceedings of the Sensors and Measuring Systems; 19th ITG/GMA-Symposium, Nuremberg, Germany, 26–27 June 2018; pp. 185–188. [Google Scholar]
- Faia, P.M.; Furtado, C.S.; Ferreira, A.J. Humidity sensing properties of a thick-film titania prepared by a slow spinning process. Sens. Actuators B Chem. 2004, 101, 183–190. [Google Scholar]
- Lensch, H.; Doerr, J.; Schutze, A.; Sauerwald, T. Selective high temperature humidity sensing using fast impedance spectroscopy on Titania sensors. Sens. Actuators B Chem. 2020, 321, 128497. [Google Scholar] [CrossRef]
- Ghadiry, M.; Gholami, M.; Kong, L.C.; Yi, C.W.; Ahmad, H.; Alias, Y. Nano-Anatase TiO2 for High Performance Optical Humidity Sensing on Chip. Sensors 2016, 16, 39. [Google Scholar] [CrossRef] [Green Version]
- Pomoni, K.; Vomvas, A.; Trapalis, C. Electrical conductivity and photoconductivity studies of TiO2 sol–gel thin films and the effect of N-doping. J. Non-Cryst. Solids 2008, 354, 4448–4457. [Google Scholar] [CrossRef]
- Cedillo-González, E.I.; Mugoni, C.; Montorsi, M.; Siligardi, C. Evaluation of the correlations between temperature, humidity, incident UV light and the photocatalytic activity of TiO2 films using a rationale approach. Appl. Surf. Sci. 2016, 378, 73–79. [Google Scholar] [CrossRef]
- Ciani, L.; Farina, A.; Catelani, M.; Pacini, L.; Baldi, A.; Calastrini, S.; Carnevale, E.; Bruzzi, M.; Signorini, L. Self-cleaning of Si photovoltaic modules by a nanostructured TiO2 spray-coating. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–5. [Google Scholar]
- Fort, A.; Panzardi, E.; Vignoli, V.; Landi, E.; Trigona, C.; Mugnaini, M. Performance Analysis of a Humidity Sensor based on a micro-resonator functionalized with TiO2 nanoparticles. IEEE Trans. Instrum. Meas. 2020, 69, 7999–8008. [Google Scholar]
- Addabbo, T.; Fort, A.; Mugnaini, M.; Vignoli, V.; Baldi, A.; Bruzzi, M. Quartz-Crystal Microbalance Gas Sensors Based on TiO2 Nanoparticles. IEEE Trans. Instrum. Meas. 2018, 67, 722–730. [Google Scholar] [CrossRef]
- Cappelli, I.; Fort, A.; Mugnaini, M.; Panzardi, E.; Pozzebon, A.; Tani, M.; Vignoli, V. Battery-less HF RFID sensor tag for humidity measurements based on TiO2 nanoparticles. In 2020—International Instrumentation and Measurement Technology Conference (I2MTC); IEEE: Dubrovnik, Croatia, 2020. [Google Scholar]
- Faia, P.M.; Ferreira, A.; Furtado, C. Establishing and interpreting an electrical circuit representing a TiO2–WO3 series of humidity thick film sensors. Sens. Actuators B Chem. 2009, 140, 128–133. [Google Scholar] [CrossRef]
- Benkoula, S.; Sublemontier, O.; Patanen, M.; Nicolas, C.; Sirotti, F.; Naitabdi, A.; Gaie-Levrel, F.; Antonsson, E.; Aureau, D.; Ouf, F.-X.; et al. Water adsorption on TiO2 surfaces probed by soft X-ray spectroscopies: Bulk materials vs. isolated nanoparticles. Sci. Rep. 2015, 5, 15088. [Google Scholar] [CrossRef]
- Maier, K.; Helwig, A.; Müller, J.G.; Hille, P.; Eickhoff, M. Effect of Water Vapor and Surface Morphology on the Low Temperature Response of Metal Oxide Semiconductor Gas Sensors. Materials 2015, 8, 6570–6588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scheufele, F.B.; Módenes, A.N.; Borba, C.E.; Ribeiro, C.; Espinoza-Quiñones, F.R.; Bergamasco, R.; Pereira, N.C. Monolayer–multilayer adsorption phenomenological model: Kinetics, equilibrium and thermodynamics. Chem. Eng. J. 2016, 284, 1328–1341. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Shirai, K.; Sugimoto, T.; Watanabe, K.; Haruta, M.; Kurata, H.; Matsumoto, Y. Effect of Water Adsorption on Carrier Trapping Dynamics at the Surface of Anatase TiO2 Nanoparticles. Nano Lett. 2016, 16, 1323–1327. [Google Scholar] [CrossRef]
- Shiraiwa, M.; Pfrang, C.; Koop, T.; Pöschl, U. Kinetic multi-layer model of gas-particle interactions in aerosols and clouds (KM-GAP): Linking condensation, evaporation and chemical reactions of organics, oxidants and water. Atmos. Chem. Phys. Discuss. 2012, 12, 2777–2794. [Google Scholar] [CrossRef] [Green Version]
- Tai, W.-P.; Kim, J.-G.; Oh, J.-H. Humidity sensitive properties of nanostructured Al-doped ZnO:TiO2 thin films. Sens. Actuators B Chem. 2003, 96, 477–481. [Google Scholar] [CrossRef]
- Torún, B.; Kunze, C.; Zhang, C.; Kuhne, T.D.; Grundmeier, G. Study of water adsorption and capillary bridge formation for SiO2 nanoparticle layers by means of a combined in situ FT-IR reflection spectroscopy and QCM-D set-up. Phys. Chem. Chem. Phys. 2014, 16, 7377–7384. [Google Scholar] [CrossRef] [Green Version]
- Biju, K.P.; Jain, M.K. Sol–gel derived TiO2:ZrO2 multilayer thin films for humidity sensing application. Sens. Actuators B Chem. 2008, 128, 407–413. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, S.; Ren, W.; Wu, R. Development of High Sensitivity Humidity Sensor Based on Gray TiO₂/SrTiO₃ Composite. Sensors 2017, 17, 1310. [Google Scholar] [CrossRef] [Green Version]
- Geng, W.; Yuan, Q.; Jiang, X.; Tu, J.; Duan, L.; Gu, J.; Zhang, Q. Humidity sensing mechanism of mesoporous MgO/KCl–SiO2 composites analyzed by complex impedance spectra and bode diagrams. Sens. Actuators B Chem. 2012, 174, 513–520. [Google Scholar] [CrossRef]
- Fort, A.; Panzardi, E.; Vignoli, V.; Landi, E.; Mugnaini, M.; Carlo, T. Performance Analysis of an AlN Humidity Sensor based on TiO2 nanoparticles. In Proceedings of the 2019 IEEE International Symposium on Measurements & Networking (M&N), Catania, Italy, 8–10 July 2019; pp. 1–5. [Google Scholar]
- Fort, A.; Trigona, C.; Panzardi, E.; Vignoli, V.; Addabbo, T.; Mugnaini, M. An AlN Micromachined Mass Sensor: Modeling and Characterization. IEEE Trans. Instrum. Meas. 2020, 1. [Google Scholar] [CrossRef]
- Du, B.; König, A.M.; Johannsmann, D. On the role of capillary instabilities in the sandcastle effect. New J. Phys. 2008, 10, 053014. [Google Scholar] [CrossRef]
- Dybwad, G.L. A sensitive new method for the determination of adhesive bonding between a particle and a substrate. J. Appl. Phys. 1985, 58, 2789–2790. [Google Scholar] [CrossRef]












© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappelli, I.; Fort, A.; Lo Grasso, A.; Panzardi, E.; Mugnaini, M.; Vignoli, V. RH Sensing by Means of TiO2 Nanoparticles: A Comparison among Different Sensing Techniques Based on Modeling and Chemical/Physical Interpretation. Chemosensors 2020, 8, 89. https://doi.org/10.3390/chemosensors8040089
Cappelli I, Fort A, Lo Grasso A, Panzardi E, Mugnaini M, Vignoli V. RH Sensing by Means of TiO2 Nanoparticles: A Comparison among Different Sensing Techniques Based on Modeling and Chemical/Physical Interpretation. Chemosensors. 2020; 8(4):89. https://doi.org/10.3390/chemosensors8040089
Chicago/Turabian StyleCappelli, Irene, Ada Fort, Anna Lo Grasso, Enza Panzardi, Marco Mugnaini, and Valerio Vignoli. 2020. "RH Sensing by Means of TiO2 Nanoparticles: A Comparison among Different Sensing Techniques Based on Modeling and Chemical/Physical Interpretation" Chemosensors 8, no. 4: 89. https://doi.org/10.3390/chemosensors8040089
APA StyleCappelli, I., Fort, A., Lo Grasso, A., Panzardi, E., Mugnaini, M., & Vignoli, V. (2020). RH Sensing by Means of TiO2 Nanoparticles: A Comparison among Different Sensing Techniques Based on Modeling and Chemical/Physical Interpretation. Chemosensors, 8(4), 89. https://doi.org/10.3390/chemosensors8040089







