3.2. Algal Identidication
Of all eight target HAB species, four of each phyla, CM (from
Raphidophyta), PG (from
Haptophyta), AC (from
Dinophyta), and SC (from
Bacillariophyta) were first selected and their initial spectra are shown in
Figure 3 with unique pigmentation composition (
Table 1). In these spectra, excitation wavelengths of 435 nm (Chl
a), 460 nm (Chl
c1-c3), 470 nm (Peridinin), 490 nm (Fucoxanthin), 495 nm (Diadinoxanthin, Zeaxanthin and β,β-carotene) and 520 nm (19′Butanoyloxyfucoxanthin and 19′ Hexanoyloxyfucoxanthin) are included. Moreover, a range of ±5 nm was considered for each wavelength (
Figure 3a–d).
Chl
a plays a fundamental role in peripheral antennas of PS II [
27], which exists in all these algae. In prior research, the level of Chl
a was widely used to measure the degree of eutrophication [
28,
29]. Additionally, its position is distinguishable in the spectra. Therefore, 435 nm, corresponding with Chl
a, was chosen first.
Peridinin (470nm) is the marker pigment of Dinophyta and its position is separate from other phyla; therefore, 470 nm was selected. Zeaxanthin (460 nm and 495 nm) was used as marker pigment for Raphidophyta, and 19’ Hex and 19′ But. However, (490 nm and 520 nm) were used as marker pigments of Haptophyta. The positions of characteristic peaks of multiple pigments were very close and even overlapped, e.g., in Diadinoxanthin (460 nm and 495 nm) and Zeaxanthin (460 nm and 495 nm), Fucoxanthin (490 nm), and 19’ Hex (490 nm). Therefore, it was difficult to match all positions of marker pigments with the excitation wavelengths one-to-one, making it difficult to select typical wavelengths merely based on the position of marker pigments.
Fortunately, the proportions of these pigments are different, which is reflected in the changing trend of the excitation fluorescence spectra, e.g., the position shifts of peaks and troughs of excitation fluorescence spectra. These features can also be utilized to determine typical excitation wavelengths. Here, a peak-finding algorithm based on the difference function was used to search and determine peaks and troughs of the excitation fluorescence spectra of these eight species. The two toxic algae, AC and AT, from the same phylum are compared, and the peaks and troughs are marked with a positive triangle and inverted triangle, respectively, in
Figure 4a,b. Although these two species of algae share a similar composition, the fluctuating trends of the curves, as well as the position of peaks and troughs, may differ.
After combining all peak and trough positions with the wavelengths of Chl
a and Peridinin (435 nm and 470 nm), the following 17 different excitation wavelengths were initially selected: 405, 415, 420, 435, 445, 450, 465, 470, 490, 505, 525, 530, 535, 555, 560, 570, and 590 nm. To further reduce the number of excitation wavelengths, the shortest distance hierarchical clustering method [
30] was used to reflect the correlation of these 17 different wavelengths. Wavelengths with strong correlation with others were removed. As shown in the hierarchical clustering graph (
Figure 4c), the 11th and 12th wavelengths (525 nm and 530 nm, respectively) were categorized into one category first, which means that they had the strongest correlation. Furthermore, the 12th wavelength also had a strong correlation with the 13th wavelength (535 nm). Therefore, 530 nm was deleted first. At each step, one wavelength was deleted, and new discrete characteristic excitation spectra were established with the remaining excitation wavelengths only.
The new discrete characteristic excitation spectra were set as feature spectra for training the Softmax Classifier model. To train and test the model, 80 monocultures of each species were cultured in the same environmental conditions and were randomly classified into training sets and validation sets according to a ratio of 7:1. Another eight pure samples of each were used as testing sets. In total, there were 560 training samples, 80 validation samples and 64 testing samples. The number of excitation wavelengths was reduced each time. When the number of wavelengths had been reduced to seven, the identification accuracy of the validation sets of monocultures exceeded 90%, and the accuracy of the test sets of monocultures reached 88.2%. This represents a comparatively improved recognition result. Therefore, discrete excitation wavelengths of 405, 435, 470, 490, 535, 555, and 590 nm were selected for establishing feature spectra (
Figure 4d).
The overall accuracy of identifying dominant HAB species from the mixed culture was 67.7%. To increase the accuracy of dominant algae identification in mixtures, further features were obtained based on other methods. The ratios of the relative fluorescence intensity between 435 and 470 nm, 470 and 490 nm, as well as 535 and 555 nm in discrete excitation fluorescence spectra were selected (
Figure 4e). To evaluate the quality of the added features, the discriminative probability values were compared. These were the output of the Softmax classifier and could reflect the probability that test samples would be discriminated as each species of algae. In this study, each test sample was assigned eight discriminative probabilities corresponding to eight species of algae. The largest probability would be accepted as the corresponding label. With the seven-wavelength discrete excitation fluorescence spectra as standard spectra for training, the average discriminative probabilities were 54.3–88.9%. After adding new features, the average probability increased to 75.8–98.1% (
Table 4).
For all eight species of algae, the probability increased by different degrees, except for PP. Therefore, by adding new features, 10 new features of eight species of algae were set as standard feature spectra for the training and testing of the classification model. The identification accuracy for the pure test set exceeded 95%. The identification accuracy indicates the proportion of the number of predicted samples in the total number of testing samples. Moreover, for each species of pure testing algae, the
precision,
recall, and
f1−score were calculated to evaluate the model. The details of these evaluation indexes are expressed in the following:
where
TP is the number of positive samples that were correctly predicted,
FP is the number of samples belonging to negative samples that were predicted to be positive, and
FN is the number of samples belonging to positive samples that were predicted to be negative. In general,
precision represents how exactly the respective species are predicted and
recall implies whether all species have been identified. For example, there is a total of eight samples of AC among the testing samples, seven samples are accurately predicted as AC, but one sample is misidentified as a different species; then, the
precision would be “7/(7 + 0)” and the
recall would be “7/(7 + 1)”. A higher
precision is always accompanied by a lower
recall. Sometimes the
f1−score that combines
precision and
recall with the harmonic mean can produce a balanced result to better evaluate the classifier.
In
Table 5, the
precision and
recalls of SC, PD, PG, and PP reached 1.00, indicating that their features could be easily distinguished from others. Regarding the other four species of algae, the
precision of AC was 1.00, but the
recall was 0.88, and
recall of AT was 1.00, but the
precision was 0.89. This implies that wrong classification existed between AC and AT.
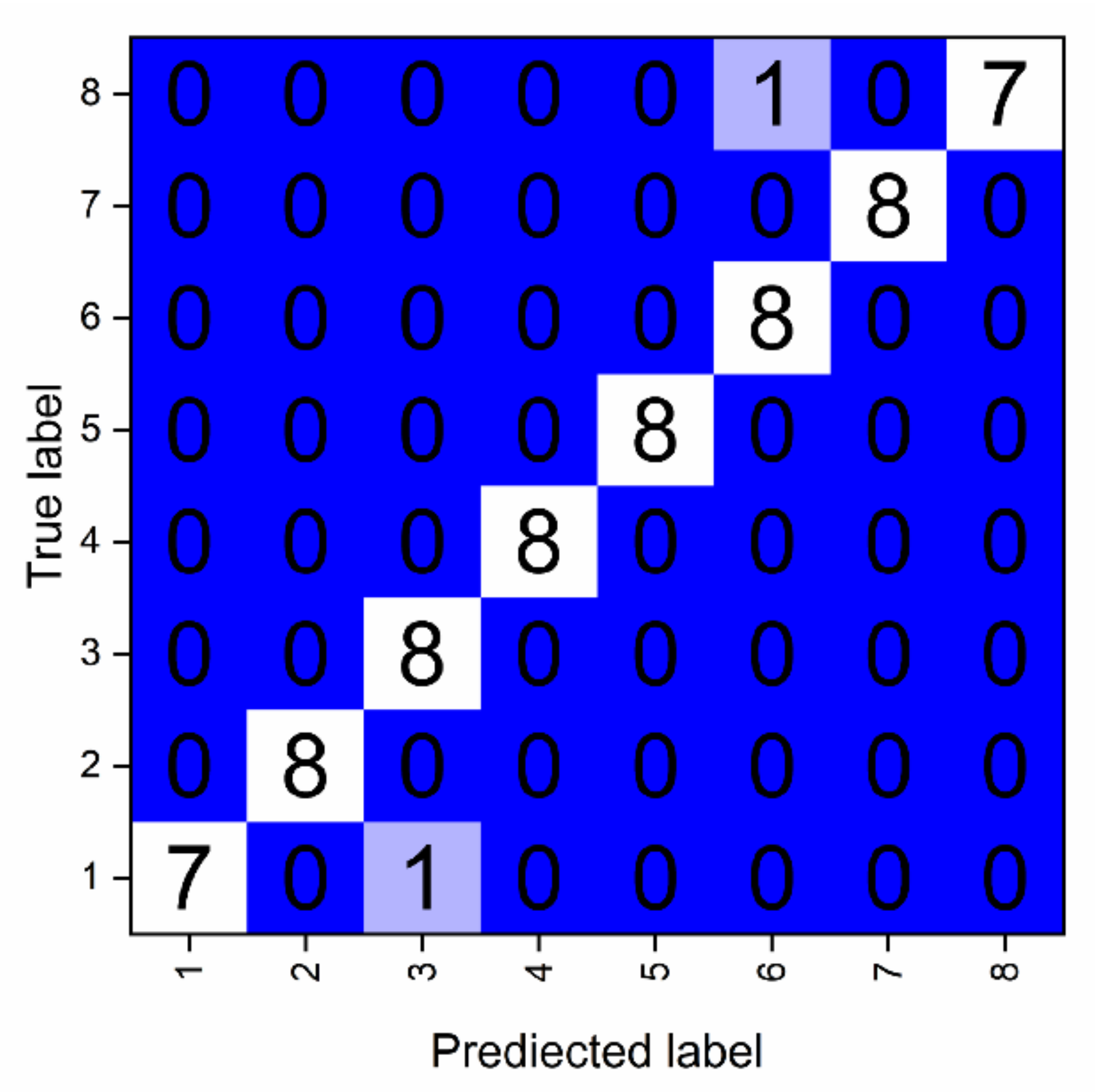
Specifically, the confusion matrix was used to compare classification results with actual values (
Figure 5). One sample of AC was erroneously classified as AT, leading to a decrease in the
precision of AT and the
recall of AC. Although
Figure 4a,b show that their feature points are different, sometimes, because of changes in the cell densities, there may be a shift in position of feature areas, especially in the range of 470–535nm. Moreover, AT and AC belong to the same phylum and share a similar pigment composition. Because of these factors, their feature spectra are quite similar, and can thus be easily confused. Similarly, one sample of CM was erroneously identified as Ha for similar reason. Generally, 100% accuracy was achieved among different phyla.
After adding features, the overall identification accuracy rate of the dominant species in mixed test samples increased from 67.7–77.4%. The specific identifying results of each species of algae are shown in
Table 6. The identification accuracy rates vary in different species of algae, and the results were greatly affected by the size of algae. For example,
Chattonella is the largest among all the algae, and even if its ratio only accounts for 1/3, a good identification can still be obtained. However, smaller algae, such as PG, PP, and SC, can only be identified when the ratio well exceeds 50%. This can be explained because in a mixture, smaller algae are easily obstructed by the larger algae. Furthermore, the disparity of pigment content inside each cell also plays a key role. In summary, this model performed well for all these eight species of algae if the relative content of the dominant algal species exceeded 50%.
Generally, identification based on pigment contents enables relatively high accuracy. However, this method may be limited to changes of external factors. Sometimes, because of changes in the environment (e.g., temperature and salinity), the content of certain pigments may also change, which may make discrimination more difficult. Fortunately, such variety in environmental factors is limited. Especially for AC and PD, the total pigment ratio remains almost unchanged [
31,
32].
3.3. Concentration Prediction
The concentration model based on non-negative least squares was used to calculate the corresponding cell density. Two toxic algae and two non-toxic algae were used for the experiment: Amphidinium carterae and Phaeocystis globose, and VS Skeletonema costatum and Prorocentrum donghaiensis. Their outbreaks are frequent and their biomass is difficult to calculate. Different concentrations of algae were prepared by diluting the pure culture with artificial sea water. Because this research focuses on the period before algal bloom, the species involved were only collected at the exponential growth phase.
The linear relationship between fluorescence intensity and cell density at each excitation wavelength (405, 435, 470, 490, 535, 555, and 590 nm) was assessed first (
Figure 6). The result shows that the R2 value in all linear models for these four species of algae exceeded 0.99 (
p < 0.05), indicating good linearity at all seven wavelengths. Therefore, norm spectra were constructed based on the seven-wavelength discrete excitation fluorescence spectra for four species of algae (
Figure 4f).
After confirming species, the norm spectrum was used to calculate the cell density by the model. With all designed concentration ratios, only the dominant species were targeted (
Figure 7). The black line was fitted by standard concentration and the red circles indicate measured concentrations. In general, the red circles are quite close to the standard, especially at the initial part of the axis where the cell densities are below 5.35 × 10
4 cells/mL. More details of the results are shown in
Table 7.
Relative error (RE) and average and absolute relative error (ARE) were used to evaluate the accuracy of the concentration predictions. The ARE of the monocultures of AC, PG, PD, and SC was 22.4%, 13.3%, 10.3% and 11.0%, respectively. Large errors were found when cell concentrations were high, except for Sc. Moreover, the recovery rates of most samples were around 100%, especially at low concentrations. In mixed samples, the measured cell density tended to be larger than the standard cell density. This can be explained because all fluorescence received was considered to be emitted by the dominant algae when using the corresponding model to calculate the cell density. Because the entered fluorescence intensity value was larger than the real value, the calculated density was also higher than the standard value.