Optimization of Obstructive Sleep Apnea Management: Novel Decision Support via Unsupervised Machine Learning

Abstract

This study addresses Obstructive Sleep Apnea (OSA), which impacts around 936 million adults globally. The research introduces a novel decision support method named Communalities on Ranking and Objective Weights Method (CROWM), which employs principal component analysis (PCA), unsupervised Machine Learning technique, and Multicriteria Decision Analysis (MCDA) to calculate performance criteria weights of Continuous Positive Airway Pressure (CPAP—key in managing OSA) and to evaluate these devices. Uniquely, the CROWM incorporates non-beneficial criteria in PCA and employs communalities to accurately represent the performance evaluation of alternatives within each resulting principal factor, allowing for a more accurate and robust analysis of alternatives and variables. This article aims to employ CROWM to evaluate CPAP for effectiveness in combating OSA, considering six performance criteria: resources, warranty, noise, weight, cost, and maintenance. Validated by established tests and sensitivity analysis against traditional methods, CROWM proves its consistency, efficiency, and superiority in decision-making support. This method is poised to influence assertive decision-making significantly, aiding healthcare professionals, researchers, and patients in selecting optimal CPAP solutions, thereby advancing patient care in an interdisciplinary research context.

1. Introduction

According to the scientific journal The Lancet [1] and Yasir et al. [2], there are about 936 million adults between the ages of 30 and 69 who suffer from obstructive sleep apnea (OSA) in the world. Given this scenario, effective diagnostic and treatment strategies are needed to minimize negative impacts on health, maximizing cost-effectiveness. According to Mcevoy et al. [3], OSA is associated with an increased risk of cardiovascular events, which can cause patient death if treatment is not adequate. In addition, OSA is characterized by recurrent episodes of partial and complete airway obstruction during sleep [4] and usually presents with excessive daytime sleepiness, loud snoring, observed episodes of respiratory arrest during sleep, morning headaches, and sudden mood swings. As a form of treatment, Continuous Positive Airway Pressure (CPAP) is essential for OSA [5], providing an unobstructed airway, reducing apnea episodes, and significantly improving sleep quality. However, the appropriate selection of CPAP devices is crucial to maximizing clinical benefits and treatment adherence, highlighting the need for analytical and objective decision methods in evaluating these devices, aiming to improve clinical outcomes and maximize patients’ quality of life while considering economic constraints within health management.

This study introduces the Communalities on Ranking and Objective Weights Method (CROWM) to evaluate CPAP devices. It allows a technical analysis of these devices based on their characteristics, allowing the physician or patient to decide based on data. By pinpointing the most effective and technically suitable devices, CROWM streamlines healthcare resources and reduces the costs of treating OSA without sacrificing the quality of care. This method guarantees the selection of devices that provide the best value for investment, aligning treatment choices with the goals of economic sustainability within the healthcare framework. Therefore, our study delivers crucial insights for strategic decision-making, ensuring a balance between the clinical and financial considerations in managing OSA patient care.

Production Engineering, crucial in supporting strategic decision-making, is significant in managing complex operations, including healthcare. Operations Research (OR), a field of Production Engineering, is a vital discipline that encompasses a variety of mathematical methods and advanced analytical techniques to address large-scale and complex operational challenges [6]. This study evaluates nine types of CPAP devices using the CROWM, an OR decision support tool integrated with the unsupervised Machine Learning (ML) technique of principal component analysis (PCA). CROWM analyzed the devices based on six specific performance criteria: resources, warranty, noise, weight, cost, and maintenance.

It is essential to highlight that although this state-of-the-art method can identify the most technically appropriate CPAP according to these criteria, the final selection of the proper device for each patient should be guided by the physician’s clinical evaluation, considering the patient’s needs. Thus, this study recognizes the importance of medical expertise in the decision-making process, complementing it with analytical data for a more informed choice.

In the healthcare setting, decisions are inherently intricate and imply trade-offs between multiple, often conflicting, objectives; applying methodologically structured and explicitly delineated approaches to deal with Multicriteria Decision Analysis (MCDA) is vital to improving the quality of the decision-making process [7]. These methodologies address the complexity inherent in health decisions and provide a systematic and reasonable framework to improve efficiency and effectiveness in formulating informed choices.

In developing this study, the CROWM introduces novel methodologies to advance the evaluation of CPAP devices for OSA management. Unique to CROWM are several innovations: the incorporation of communalities in factor analysis to more accurately assess the performance of alternatives; the consideration of non-beneficial criteria within PCA to delineate devices’ strengths and weaknesses clearly; the automation of weight generation through the MEthod based on the Removal Effects of Criteria (MEREC) [8] and factor loadings [9], promoting an objective, data-driven evaluation process; and the incorporation of PCA validation tests, such as the Bartlett and Kaiser tests, ensuring the analytical rigor and reliability of the evaluation. These methodological advances significantly enhance the MCDA and ML landscape, providing a robust and comprehensive decision support system for selecting CPAP devices. By addressing gaps in the existing literature and offering a methodologically sound and objective approach, CROWM stands out as a pioneering tool designed to optimize patient care through informed, data-backed medical device selection.

The relevance of this article lies in introducing an innovative and integrated approach to the evaluation of medical devices, with a specific focus on CPAPs, used in the treatment of sleep-disordered breathing. The strategic blending of ML represents an evolution in the field, offering a comprehensive solution to address the challenges inherent in complex decision-making, especially in the healthcare setting. Therefore, this article aims to evaluate CPAP devices, aiming at effectiveness in the fight against OSA, emphasizing innovation and analytical accuracy, standing out in the current panorama of medical device evaluation.

2. Literature Review

This chapter provides a comprehensive overview of the methodological approaches to OR, MCDA, and PCA in health, highlighting their significant applications and contributions. The meticulous review of the literature reveals the versatility and effectiveness of these techniques in various health contexts but also points to a notable gap in the specific evaluation of medical devices, such as CPAPs, in treating sleep-disordered breathing.

2.1. OR, PCA, and MCDA in Healthcare

OR is distinguished by its application in mathematical, statistical, and computational techniques. It focuses on practical challenges to enhance decision-making across diverse domains [10] and facilitates communication between medical professionals and health system managers [11].

The imperative of developing decision support systems for resource planning and sizing is widely recognized [12].

Studies on OR in health are diverse. They include literature reviews exploring OR in surgical planning [13]; its role as an optimizing instrument in health [14]; and specific contributions to health systems coordination during disasters [15]. Notably, there is an emphasis on proposing optimal measures to integrate OR into health systems, aiming at more efficient collaboration [16] and identifying care based on the community-based approach to OR [17]. This broad approach highlights the comprehensive relevance of OR, from the surgical scope to systemic management, evidencing its integral role in optimizing and coordinating the medical field.

MCDA, as an extension of OR, transcends disciplines like social sciences, medicine, and engineering. It is a comprehensive method for determining optimal solutions in complex situations [18]. MCDA methods offer valuable techniques for structuring and understanding problems in intricate environments [19], making it easier to define preferences between frequently conflicting alternatives. These methods are crucial for solving selection, classification, and portfolio-related issues and enable organizations to structure decision-making at operational and strategic levels.

MCDA methods are widely employed in the performance evaluation of alternatives, structuring complex problems with multiple criteria, some of which may be conflicting [20]. These methods make it possible to structure the decision-making process, considering technical, socioeconomic, and environmental aspects at operational and strategic levels [21]. PCA, as explained by Fávero and Belfiore [22], also evaluates the performance of alternatives. Concerning the generation of criteria weights, which is essential in this process, it can either apply the Decision-Maker’s (DM) preferences and priorities, which is a subjective process, or evolve to the use of mathematical models or ML algorithms for a more precise and objective allocation of weights, increasing the consistency and reliability of the decision-making process [23].

In addition, studies involving MCDA in healthcare are varied. Notable ones include sustainable supplier selection in the medical industry [24]; strategic analysis of the quality of electronic services in the health sector [25]; guidance for professionals and researchers in the practical application of MCDA methods in decision-making [7]; evaluation of organizational performance indicators in the health area, with emphasis on adaptability [26]; innovative medical device selection process [27]; and assessment of a supply chain in the context of a blood bank system [28].

Prominent studies on MCDA in healthcare include emergency medical facility location analysis [29]; determining the most appropriate location for medical waste disposal centers [30]; development of an evaluation model for health services, focusing on hospitals that provide inpatient services [31]; prioritization of factors that impact the performance of clinical laboratories [32]; and choosing a hospital aid ship to combat the COVID-19 pandemic [33].

In PCA applications for evaluating OSA, significant studies include efficacy evaluation based on a simplified Chinese Pediatric Sleep Questionnaire (PSQ) [34]; assessment of OSA risk in laryngectomy patients using PCA [35]; and identification by PCA of depressive symptom factors that influence the effectiveness of CPAP in the treatment of OSA [36]. Unlike what was presented in the work in this paragraph, the PCA can also be used to generate rankings, as can be seen below: employment of the PCA to establish a ranking order for U.S. Army Pilots [37]; hybrid approach that combined the Analytic Hierarchy Process (AHP) method and the PCA for weapon system selection [9]; and evaluation of third-party logistics companies through the PCA [38].

The literature review underscores the broad application of decision support methods in healthcare. However, a gap is observed in the focused evaluation of medical devices like CPAPs. According to The Lancet [1], it is imperative to develop effective treatment strategies to minimize adverse health impacts while seeking to optimize the cost–benefit ratio. No dedicated studies on CPAP evaluation for healthcare decision-making are found in this context. This gap, critical in the academic landscape, becomes particularly relevant in the context of device selection for treating sleep-disordered breathing. The absence of such investigations highlights a need for in-depth research using these methods to evaluate medical devices, thus promoting advances in informed and personalized healthcare decision-making and optimizing patient therapeutic outcomes.

2.2. Novelty and Contributions of the Study

Given the complexity of variables (criteria) in evaluating medical devices such as CPAP machines for treating OSA, this study develops a new multicriteria framework named CROWM. Recognizing that traditional approaches may not fully capture the multifunctionality and critical variables in CPAP selection, this study aims to bridge the gap in medical device evaluation. The literature review confirms that the approach introduced is innovative, contributing to the current literature in sleep medicine, OR, ML, and healthcare decision-making. The contributions of this paper are:

• To develop an objective weighting method within CROWM to extract the relative importance of evaluation criteria for CPAPs.
• To introduce the PCA technique in CROWM for ranking purposes in MCDA problems, enhancing accuracy and objectivity in medical device selection.
• To provide information and enable efficacy comparisons among different CPAP models, assisting healthcare professionals in choosing the most suitable device.
• To construct a support system to evaluate CPAP device performance, considering multiple criteria aligning with clinical guidelines and patient expectations.

Thus, this study not only presents an innovative method evaluation but also provides a robust and reliable tool for healthcare professionals and DMs in the field of sleep medicine.

3. Methodology

According to the taxonomic structure outlined by Creswell and Creswell [39], the present research adopts a predominantly quantitative approach, amalgamating case study elements and mathematical modeling [40]. This section aims to clarify the essence of the problem that will be investigated in the present study, based on the proposition of a new decision support method to evaluate health services, specifically CPAPs.

By incorporating PCA enriched with multicriteria enhancements, this study contributes to the academic landscape by broadening the scope of application of principal component analysis and enhancing analytical capacity when considering multiple decision criteria. In the global panorama, introducing this decision support method stands out as a contribution, providing a methodology for evaluation while having intrinsic competence to simplify multidimensional data, identify correlations between variables, and generate rankings, allowing it to establish a solid basis in the decision-making process.

Case Study: Evaluation of CPAP Models

This research used the Soft Systems Methodology (SSM) problem-structuring method. SSM is a well-established method in the literature, developed and improved by Checkland and Haynes [41]. It is explored in various research fields, fundamental to structuring problems and facilitating their understanding.

Employing SSM, this study comprehensively addresses the challenges and management of OSA. It begins by recognizing the individual burden of OSA, spotlighting the clinical necessity for effective interventions due to its detrimental health implications. The journey from acknowledging the issue of seeking actionable solutions encapsulates the reflection on accessible treatment modalities. Emphasis is placed on the decision to opt for a CPAP device as a medically endorsed treatment avenue, representing an active step toward lessening the condition [5]. The narrative advances by detailing the methodological adoption of a cutting-edge decision support system to facilitate the CPAP selection process. This approach ensures choices are informed and grounded in robust data analysis. The successful application of this methodology heralds a suite of positive outcomes—enhanced sleep quality, minimized cardiovascular risks, and overall health betterment—reinforcing the value of a systematic and data-driven selection process. This structured progression from problem identification to solution implementation and subsequent realization of health benefits furnishes a comprehension of the strategic and methodological considerations that form the backbone of this study. It underscores the significance of informed decisions in healthcare and the positive repercussions of such methodologically sound choices on patient care.

In addition, Figure 1 presents a CATWOE analysis, a framework for analyzing problems in systems and processes, which helped identify and structure the key elements that make up the situation discussed. It is a tool used mainly in SSM. It aims to address complex and unstructured organizational problems from a comprehensive systemic view, identifying the stakeholders, the necessary transformation processes, the challenges, and the constraints present.

Complementing the proposed methodology, a literature review was conducted to evaluate nine CPAP models based on six operational and logistical criteria. This practical analysis serves as a case study exemplifying the application of the CROWM methodology.

4. The CROWM Method

In recent years, the terminology and application of MCDA methods have expanded, drawing attention to developing an ever-expanding range of ordering methods such as CROWM [43]. This proposed method employs a quantitative approach to ordering alternatives according to the criteria analyzed.

This study employs the CROWM method to evaluate CPAP devices, due to its ability to integrate PCA and MCDA, providing a holistic and objective approach to evaluating complex medical devices. According to the following presentation, CROWM arose from gaps in the literature regarding decision support approaches that employed PCA and MCDA. This chapter outlines the journey toward the development of CROWM, highlighting fundamental studies that collectively inspired its creation, according to

Table 1. Related works.

Method	Objective Weights	Techniques	Communality Assessment	Advantages and Disadvantages	PCA Tests	Non-Beneficial Criteria in PCA	Alternative Evaluation
CROWM	X	PCA and MEREC	X	Removes DM evaluation/Bias-free.	X	X	X
PCA-AHP [44]		PCA and AHP		Considers the evaluation of the DM/Enables bias in the process.	X		X
PCA-AHP-MFA [45]		PCA and AHP		Considers the evaluation of the DM/Enables bias in the process.	X		X
AHP-PCA-GP [9]		PCA, AHP, and Goal Programming (GP)		Considers the evaluation of the DM/Enables bias in the process.			X
AHP-PCA [38]		PCA and AHP		Considers the evaluation of the DM/Enables bias in the process.			X
ELICIT [46]		PCA and Monte Carlo		Considers the evaluation of the DM/Enables bias in the process.
Group AHP-PCA [47]		PCA and AHP		Considers the evaluation of the DM/Enables bias in the process.			X
KPCA-TOPSIS [48]	X	PCA and TOPSIS		Removes DM evaluation/Bias-free.			X
PCA—VIKOR, ANP, DEMATEL [49]		PCA and VIKOR		Considers the evaluation of the DM/Enables bias in the process.	X		X
P-SPCA, P-PFA and P-SRD [50]	X	PCA and PROMETHEE-GAIA		Removes DM evaluation/Bias-free.	X		X
ORME [51]		PCA, ELECTRE III, and IV		Considers the evaluation of the DM/Enables bias in the process.			X
WIRI [52]	X	PCA, CRITIC and TOPSIS		Removes DM evaluation/Bias-free.			X
TAOV [53]		PCA		Considers the evaluation of the DM/Enables bias in the process.			X
PCA-TOPSIS [54]	X	PCA and TOPSIS		Removes DM evaluation/Bias-free.			X
SMART-PCA [55]		PCA		Considers the evaluation of the DM/Enables bias in the process.			X
AHP-PCA and Communalities [56]		PCA and AHP		Considers the evaluation of the DM/Enables bias in the process.	X
PCA-PROMETHEE [57]	X	PCA and PROMETHEE		Removes DM evaluation/Bias-free.	X		X

Source: authors.

.

Table 1 analyzes the related works that have been studied to generate CROWM according to the following characteristics: calculation of weights (objective or not); techniques employed; use of communalities in performance evaluation; advantages and disadvantages; presence or absence of PCA validation tests; consideration of non-beneficial criteria in the PCA; and, finally, whether they can generate performance evaluation of the alternatives. Regarding the generation of criteria weights, the analysis of methods that combine PCA and MCDA can be divided into approaches based on the DM’s assessment and those that use objective weights, like KPCA-TOPSIS [48], PCA-TOPSIS [54], PCA-PROMETHEE [57], WIRI [52] and P-SPCA, P-PFA, and P-SRD [50]. This distinction is crucial, as objective methods focus exclusively on the data, free from subjective influences, which is necessary to ensure an unbiased and evidence-based analysis. In this sense, the CROWM method is distinguished by its rigorously objective approach, not depending on the evaluation of the DM to calculate the weights of the criteria. Table 1 shows that, when validating PCA results, the necessary tests in more than half of the approaches, following Bartlett [58] and Kaiser [59], were not identified. These tests ensure the validity and accuracy of results derived from PCA, which are crucial elements for analytical integrity in quantitative research [60]. Other relevant aspects were the absence of studies that applied the communalities (representing how much a criterion is present in each principal component of PCA) in the evaluation of the performance of the alternatives, and the non-consideration of non-beneficial criteria (the higher, the worse for alternative evaluation) in the PCA. These two approaches are innovative features of CROWM, according to Table 1. It is also noteworthy that only two methods do not evaluate the performance of alternatives: ELICIT [46] and AHP-PCA and Communalities [56], while the disadvantages and advantages column explored, in a macro way, the ability of the methods to measure the opinion of the decision-maker in the evaluation. In addition, Table 1 also shows the approaches, mostly MCDA, that are close to the methods created, according to what is present in the technique’s column.

In summary, to explore the gaps found in the literature and the opportunities for improvement, the merits of the proposed methodology are delineated as follows:

Automation in weight generation: the method focuses on efficiency by automating weight generation, thereby minimizing the cognitive load on DMs. This automation removes subjective elements, ensuring weights assigned to criteria are determined through an objective, data-driven approach, leading to more reliable and replicable outcomes for well-justified decisions;

Application of tests for PCA validation: CROWM incorporates the Kaiser and Bartlett tests, which are fundamental to validating PCA results. This integration ensures greater consistency and robustness in interpreting data from this unsupervised ML technique. The application of these tests, particularly the Bartlett test, as highlighted by Fávero and Belfiore [60], is crucial to verify the adequacy of PCA, reinforcing the reliability and accuracy of the CROWM method;

Incorporation of communalities in factor analysis: the CROWM method utilizes communalities to represent shared variance between variables in extracted factors, an approach not yet explored. This technique contributes to more accurate and complete assessments, enhancing the precision of analysis and offering a new perspective for future research in performance evaluation;

Integration of non-beneficial criteria into PCA: CROWM enhances PCA’s methodology by integrating non-beneficial criteria, effectively delineating the advantages and disadvantages of each alternative. This enhancement ensures larger values, indicating less favorable outcomes are aptly recognized and weighted, aligning PCA more closely with intricate decision-making criteria for a comprehensive evaluation.

These points highlight the comprehensive and innovative aspects of the CROWM methodology, demonstrating its effectiveness in refining performance evaluation and decision-making processes. The following subsections explain some terms of factor analysis.

4.1. Weights of Criteria

The CROWM calculates the importance of the CPAP’s performance criteria by the PCA factor loadings [9] and the MEREC method [8], performing the CPAP’s weights of criteria by considering the combination of these two values [43].

4.1.1. The MEREC Method

MEREC, initially proposed by Keshavarz-Ghorabaee et al. [8], uses the removal effects of each criterion on the aggregate performance of alternatives to calculate the weights. A specific computational process is employed based on the initial data or the decision matrix. As a most relevant advantage, MEREC calculates the criteria weights without the need for the evaluation or opinion of the DM, requiring only the data from the decision matrix. Thus, MEREC is formed by six stages [8]:

• Establishment of the decision matrix, expressing the score of each alternative about each criterion analyzed;
• Determination of the normalized decision matrix. The elements of the normalized matrix are denoted by $n_{\mathrm{i}j}^x$. Below, the first line denotes the set of beneficial criteria, and the second line represents the set of non-beneficial criteria;

  $$n_{\mathrm{i}j}^x=\left\{\begin{array}{c}\frac{\underset{k}{min}{x}_{kj}}{x_{ij}},forbeneficialcriteria\\ \frac{x_{ij}}{\underset{k}{max}{x}_{kj}},non-beneficialcriteria\end{array}\right.$$

  (1)
• Determination of the overall performance of alternatives [$S_i$]:

  $$S_i=\mathit{ln}\left(1+\left(\frac{1}{m}{\sum }_j\left|ln\left(n_{ij}^x\right)\right|\right)\right)$$

  (2)
• Performance of alternatives by removing each criterion [$S_{\mathrm{i}j}^{\prime }$]:

  $$S_{\mathrm{i}j}^{\prime }=\mathit{ln}\left(1+\left(\frac{1}{m}{\sum }_{k,k\ne j}\left|ln\left(n_{ij}^x\right)\right|\right)\right)$$

  (3)
• Calculation of the removal effect of each criterion, through the result of the difference of the modulus sum between the Equations (2) and (3) [$E_j$]:

  $$E_j={\sum }_i\left|S_{\mathrm{i}j}^{\prime }-S_{\mathrm{i}}\right|$$

  (4)
• Calculation of the weight of the criteria [${{\omega }^{\prime }}_j$]:

  $${{\omega }^{\prime }}_j=\frac{E_j}{{\Sigma }_k{E}_k}$$

  (5)

4.1.2. Weight by Factor Loadings

Factor loadings represent each criterion’s importance in forming a PC. For example, ${\alpha }_{ij}$ is the factor loading of ith PC, referring to the jth criterion. As a complementary form of the equation, the shared variance of the ith PC, $w_i$, is used [9]. The improvement implemented by the CROWM method is that only principal components (PCs) with eigenvalues greater than one will be considered, respecting the Kaiser criterion [59]:

• Calculation of the importance of jth criterion by factor loadings [${\phi }_j$]:

  $${\phi }_j={\sum }_{i=1}^k{|\alpha }_{ij}|w_i,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} k \mathrm{i}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{P}\mathrm{C}\mathrm{s} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{e}\mathrm{i}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s} \mathrm{g}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{a}\mathrm{n} \mathrm{o}\mathrm{n}\mathrm{e}$$

  (6)
• Calculating weights by factor loadings [${{\omega }^{″}}_j$]:

  $${{\omega }^{″}}_j=\frac{{\phi }_j}{{\sum }_{j=1}^m{\phi }_j},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} m \mathrm{i}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}$$

  (7)

4.1.3. Calculation of Criteria Weights

From the weights derived of (5) and (7), it is possible to calculate the weights of CROWM (${\omega }_j$):

$${\omega }_j=\frac{{{\omega }^{\prime }}_j+{{\omega }^{″}}_j}{2}$$

(8)

4.2. Evaluation of Alternatives

To calculate the score for each CPAP, CROWM will follow the step-by-step instructions below [60]:

1.

Establishment of a database containing a total of n CPAPs and k evaluation criteria (or variables);

For each CPAP I (where I range from 1 to n), it is necessary to record the values corresponding to the k metric criteria X. To extract factors from these k criteria, defining the matrix of correlations $\mathsf{\rho }$ is imperative. This matrix, called Equation (9), encompasses the values of Pearson’s linear correlations between each pair of variables, presenting itself as a visual representation of their relationships [60].

2.

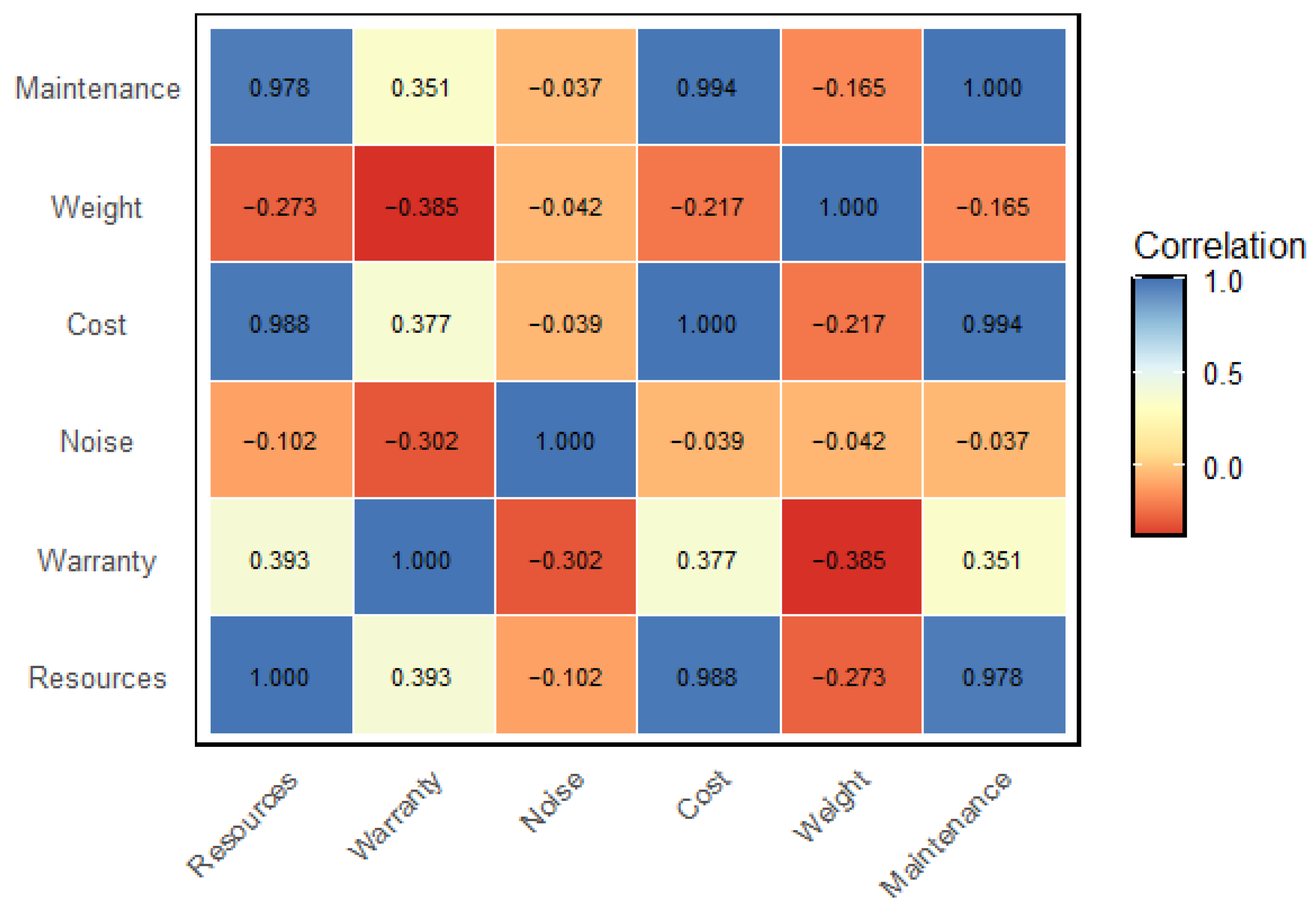
Determination of the correlation matrix $\mathsf{\rho }$:

$$\mathsf{\rho }=\left(\begin{array}{cccc}1& {\mathsf{\rho }}_{12}& \dots & {\mathsf{\rho }}_{1\mathrm{k}}\\ {\mathsf{\rho }}_{21}& 1& \dots & {\mathsf{\rho }}_{2\mathrm{k}}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathsf{\rho }}_{\mathrm{k}1}& {\mathsf{\rho }}_{\mathrm{k}2}& \dots & 1\end{array}\right)$$

(9)

The matrix of correlations $\mathsf{\rho }$ exhibits a symmetry concerning its principal diagonal, in which the values are uniformly equal to 1. As an example, the coefficient ${\mathsf{\rho }}_{12}$ denotes Pearson’s correlation between the variables X₁ and X₂, calculated based on Equation (10):

$${\mathsf{\rho }}_{12}=\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{X}}_{1\mathrm{i}}-\overline{{\mathrm{X}}_1}\right).\left({\mathrm{X}}_{2\mathrm{i}}-\overline{{\mathrm{X}}_2}\right)}{\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{1\mathrm{i}}-\overline{{\mathrm{X}}_1}\right)}^2}.\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{2\mathrm{i}}-\overline{{\mathrm{X}}_2}\right)}^2}}$$

(10)

where $\overline{{\mathrm{X}}_1}$ and $\overline{{\mathrm{X}}_2}$ correspond, respectively, to the means of the evaluation criteria X₁ and X₂.

3.

Elaboration of the Bartlett sphericity test:

The Bartlett test is conducted as specified in [58], comparing Pearson’s correlation matrix with an identity matrix to assess the statistical significance of their discrepancies. If the differences are not statistically significant, factor extraction may be unsuitable for the data. As Fávero and Belfiore [60] note, non-significant Pearson correlations suggest that the data or methodology may be reevaluated. The null H₀ and alternative H₁ hypotheses of the Bartlett sphericity test are defined according to Equations (11) and (12):

$${\mathrm{H}}_0:\mathsf{\rho }=\left(\begin{array}{cccc}1& {\mathsf{\rho }}_{12}& \dots & {\mathsf{\rho }}_{1\mathrm{k}}\\ {\mathsf{\rho }}_{21}& 1& \dots & {\mathsf{\rho }}_{2\mathrm{k}}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathsf{\rho }}_{\mathrm{k}1}& {\mathsf{\rho }}_{\mathrm{k}2}& \dots & 1\end{array}\right)=\mathrm{I}=\left(\begin{array}{cccc}1& 0& \dots & 0\\ 0& 1& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & 1\end{array}\right)$$

(11)

$${\mathrm{H}}_1:\mathsf{\rho }=\left(\begin{array}{cccc}1& {\mathsf{\rho }}_{12}& \dots & {\mathsf{\rho }}_{1\mathrm{k}}\\ {\mathsf{\rho }}_{21}& 1& \dots & {\mathsf{\rho }}_{2\mathrm{k}}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathsf{\rho }}_{\mathrm{k}1}& {\mathsf{\rho }}_{\mathrm{k}2}& \dots & 1\end{array}\right)\ne \mathrm{I}=\left(\begin{array}{cccc}1& 0& \dots & 0\\ 0& 1& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & 1\end{array}\right)$$

(12)

The statistic corresponding to this test is a χ2, represented by Equation (13):

$${\mathsf{\chi }}_{\mathrm{B}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{t}}^2=-⌈\left(\mathrm{n}-1\right)-\left(\frac{2.\mathrm{k}+5}{6}\right)⌉·\ln \left|\mathrm{D}\right|$$

(13)

With $\frac{\mathrm{k}·\left(\mathrm{k}-1\right)}{2}$ degrees of freedom, where n is the sample size, k corresponds to the number of variables, and D is the determinant of the matrix of correlations $\mathsf{\rho }$ [22].

4.

Determination of eigenvalues and their respective shared variances:

The matrix of correlations k × k, Equation (9), shows k eigenvalues λ₂ (λ₂₁ ≥ λ₂₂ ≥ ... ≥ λ_2k), obtained through Equation (14):

$$\det \left({\mathsf{\lambda }}^2·\mathrm{I}-\mathsf{\rho }\right)=0,\mathrm{c}\mathrm{o}\mathrm{m} {\mathsf{\lambda }}_1^2+{\mathsf{\lambda }}_2^2+\cdots +{\mathsf{\lambda }}_{\mathrm{k}}^2=\mathrm{k}$$

(14)

It is the identity matrix, also with dimensions k × k. Expression 14 can be rewritten as follows, according to (14a), resulting in the eigenvalues Λ² contained in (14b):

$$\left(\begin{array}{cccc}{\mathsf{\lambda }}^2-1& -{\mathsf{\rho }}_{12}& \dots & -{\mathsf{\rho }}_{1\mathrm{k}}\\ -{\mathsf{\rho }}_{21}& {\mathsf{\lambda }}^2-1& \dots & -{\mathsf{\rho }}_{2\mathrm{k}}\\ ⋮& ⋮& \ddots & ⋮\\ -{\mathsf{\rho }}_{\mathrm{k}1}& -{\mathsf{\rho }}_{\mathrm{k}2}& \dots & {\mathsf{\lambda }}^2-1\end{array}\right)=0$$

(14a)

$${\mathsf{\Lambda }}^2=\left(\begin{array}{cccc}{\mathsf{\lambda }}_1^2& 0& \dots & 0\\ 0& {\mathsf{\lambda }}_2^2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\mathsf{\lambda }}_{\mathrm{k}}^2\end{array}\right)$$

(14b)

5.

Determination of eigenvectors:

One must solve the equations systems to define the eigenvectors of the matrix $\mathsf{\rho }$ based on the eigenvalues (15) for each eigenvalue λ₂ (λ₂₁ ≥ λ₂₂ ≥ ... ≥ λ_2k):

$$\begin{gathered} \left(\begin{array}{cccc}{\mathsf{\lambda }}_{\mathrm{k}}^2-1& -{\mathsf{\rho }}_{12}& \dots & -{\mathsf{\rho }}_{1\mathrm{k}}\\ -{\mathsf{\rho }}_{21}& {\mathsf{\lambda }}_{\mathrm{k}}^2-1& \dots & -{\mathsf{\rho }}_{2\mathrm{k}}\\ ⋮& ⋮& \ddots & ⋮\\ -{\mathsf{\rho }}_{\mathrm{k}1}& -{\mathsf{\rho }}_{\mathrm{k}2}& \dots & {\mathsf{\lambda }}_{\mathrm{k}}^2-1\end{array}\right).\left(\begin{array}{c}{\mathrm{v}}_{1\mathrm{k}}\\ {\mathrm{v}}_{2\mathrm{k}}\\ ⋮\\ {\mathrm{v}}_{\mathrm{k}\mathrm{k}}\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\end{array}\right) \\ \to \left\{\begin{array}{c}\left({〖\mathsf{\lambda }〗}_{\mathrm{k}}^2-1\right).{\mathrm{v}}_{1\mathrm{k}}-{\mathsf{\rho }}_{12}.{\mathrm{v}}_{2\mathrm{k}}\dots -{\mathsf{\rho }}_{1\mathrm{k}}.{\mathrm{v}}_{\mathrm{k}\mathrm{k}}=0\\ -{\mathsf{\rho }}_{21}.{\mathrm{v}}_{1\mathrm{k}}+({〖\mathsf{\lambda }〗}_2^2-1).{\mathrm{v}}_{2\mathrm{k}}\dots -{\mathsf{\rho }}_{2\mathrm{k}}.{\mathrm{v}}_{\mathrm{k}\mathrm{k}}=0\\ ⋮\\ -{\mathsf{\rho }}_{\mathrm{k}1}.{\mathrm{v}}_{1\mathrm{k}}-{\mathsf{\rho }}_{\mathrm{k}2}.{\mathrm{v}}_{2\mathrm{k}}\dots +\left({〖\mathsf{\lambda }〗}_{\mathrm{k}}^2-1\right).{\mathrm{v}}_{\mathrm{k}\mathrm{k}}=0\end{array}\right. \end{gathered}$$

(15)

6.

Determination of factor scores:

The formulation for the vectors of the factor scores referring to the kth factor can be represented by Equation (16):

$${\mathrm{S}}_{\mathrm{k}}=\left(\begin{array}{c}\begin{array}{c}{\mathrm{S}}_{1\mathrm{k}}\\ {\mathrm{S}}_{2\mathrm{k}}\end{array}\\ \begin{array}{c}⋮\\ {\mathrm{S}}_{\mathrm{k}\mathrm{k}}\end{array}\end{array}\right)=\left(\begin{array}{c}\begin{array}{c}\frac{{\mathrm{v}}_{1\mathrm{k}}}{\sqrt{{\mathsf{\lambda }}_{\mathrm{k}}^2}}\\ \frac{{\mathrm{v}}_{2\mathrm{k}}}{\sqrt{{\mathsf{\lambda }}_{\mathrm{k}}^2}}\end{array}\\ \begin{array}{c}⋮\\ \frac{{\mathrm{v}}_{\mathrm{k}\mathrm{k}}}{\sqrt{{\mathsf{\lambda }}_{\mathrm{k}}^2}}\end{array}\end{array}\right)$$

(16)

7.

Determination of factors:

As the respective eigenvalues standardize the factorial scores of each factor, the factors of the set of equations presented in expression (17) should be obtained by multiplying each factorial score by the corresponding original variable, standardized using the procedure Z-scores:

$$\begin{array}{c}\begin{array}{c}{\mathrm{F}}_{1\mathrm{i}}={\mathrm{s}}_{11}.{\mathrm{X}}_{1\mathrm{i}}+{\mathrm{s}}_{21}.{\mathrm{X}}_{2\mathrm{i}}+\cdots +{\mathrm{s}}_{\mathrm{k}1}.{\mathrm{X}}_{\mathrm{k}\mathrm{i}}\\ {\mathrm{F}}_{2\mathrm{i}}={\mathrm{s}}_{12}.{\mathrm{X}}_{1\mathrm{i}}+{\mathrm{s}}_{22}.{\mathrm{X}}_{2\mathrm{i}}+\cdots +{\mathrm{s}}_{\mathrm{k}2}.{\mathrm{X}}_{\mathrm{k}\mathrm{i}}\end{array}\\ \begin{array}{c}⋮\\ {\mathrm{F}}_{\mathrm{k}\mathrm{i}}={\mathrm{s}}_{1\mathrm{k}}.{\mathrm{X}}_{1\mathrm{i}}+{\mathrm{s}}_{2\mathrm{k}}.{\mathrm{X}}_{2\mathrm{i}}+\cdots +{\mathrm{s}}_{\mathrm{k}\mathrm{k}}.{\mathrm{X}}_{\mathrm{k}\mathrm{i}}\end{array}\end{array}$$

(17)

It should be noted that the extracted factors will be established based on the values of the non-beneficial criteria, which will be multiplied by −1. This operation is carried out to appropriately consider the effects of these criteria within the analytical context. The calculation of the kth factor can be represented by Equation (18).

$${\mathrm{F}}_{\mathrm{k}\mathrm{i}}=\frac{{\mathrm{v}}_{1\mathrm{k}}}{\sqrt{{\mathsf{\lambda }}_{\mathrm{k}}^2}}.{\mathrm{Z}\mathrm{X}}_{1\mathrm{i}}+\frac{{\mathrm{v}}_{2\mathrm{k}}}{\sqrt{{\mathsf{\lambda }}_{\mathrm{k}}^2}}.{\mathrm{Z}\mathrm{X}}_{2\mathrm{i}}+\cdots +\frac{{\mathrm{v}}_{\mathrm{k}\mathrm{k}}}{\sqrt{{\mathsf{\lambda }}_{\mathrm{k}}^2}}.{\mathrm{Z}\mathrm{X}}_{\mathrm{k}\mathrm{i}}$$

(18)

It should be noted that ZX_i represents the value standardized by the Z-scores of each criterion X for a specific CPAP, denoted as i.

8.

Determination of factor loadings and communalities:

Factor loadings shall be calculated using Equation (6) and as proposed by [9,60].

Conversely, a criterion’s communality is calculated as the sum of its factor loadings’ squared values, indicating its contribution in each PC with eigenvalues over one. This relationship is defined in Equation (19):

$${\mathsf{\alpha }}_{\mathrm{i}\mathrm{j}}^2=\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{u}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y} {\mathrm{C}}_{\mathrm{i}\mathrm{j}},\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} i \mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{t}\mathrm{o} \mathrm{t}\mathrm{h}\mathrm{e} i\mathrm{t}\mathrm{h} \mathrm{P}\mathrm{C} \mathrm{a}\mathrm{n}\mathrm{d} j \mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{t}\mathrm{o} \mathrm{t}\mathrm{h}\mathrm{e} j\mathrm{t}\mathrm{h} \mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}$$

(19)

9.

Performance evaluation:

Finally, it is possible to establish a performance rating between the CPAPs. Notably, the adopted formulation derives from the proposition outlined by Fávero and Belfiore [60], incorporating specific improvements, including the values of the communalities, the weight derived from Equation (8), and the non-beneficial criteria. It is reiterated that the Kaiser [60] criterion was used, and only PCs with eigenvalues greater than one were considered.

$$P_n={\sum }_{i=1}^{k_{max}}{\sum }_{j=1}^m{\mathrm{F}}_{in}{\mathrm{C}}_{ji}{\omega }_j$$

(20)

On Equation (20), $P_n$ represents the score (performance evaluation) of the nth CPAP; $k_{max}$ represents the maximum number of PCs with an eigenvalue greater than one; ${\mathrm{F}}_{in}$ represents the factor referring to the ith PC and nth CPAP; ${\mathrm{C}}_{ji}$ represents the communality of the ith PC and jth criteria; and ${\omega }_j$ the weight of the jth criteria according to Equation (8).

To facilitate the understanding of the CROWM method, Figure 2 is proposed, which outlines the analysis of a dataset with alternatives and criteria, which the PCA will process through analysis and validation by the Bartlett and Kaiser tests. Next, it is on to the formation of the criteria weights, which is done automatically (there is no consideration of the evaluation of the DM) by MEREC and the factor loadings. In the next step, the weights generated are weighted by the communalities to identify each criterion’s presence correctly and precisely in the respective PCs. Finally, the performance of the CPAPs is evaluated, which explains the consideration of the weights generated by the communalities within each factor with an eigenvalue greater than one.

4.3. Hypothesis and Limitations

The hypotheses underscore the innovative and potential contributions of the CROWM model to data analysis in complex decision-making scenarios. The proposed approach is promising, highlighting its effectiveness and efficiency with a novel conceptual framework. This framework offers an integrated methodology for evaluating alternatives and criteria, enhancing the analytical capabilities in decision-making processes. The emphasis on generating criteria weights, performance evaluation of alternatives based on communalities, incorporation of non-beneficial criteria through PCA, and the validation of PCA results via established tests suggests a rigorous and methodologically robust approach. It underscores the value of CROWM as a powerful and versatile analytical tool.

Furthermore, the model is posited to integrate methods from existing approaches and introduce new analyses not yet explored in the literature. This represents a significant advancement in the research area, providing new insights and tools for decision-making. This comprehensive approach aims to enrich decision-making processes by offering a complete analysis of outcomes, leveraging the strengths of various methods to create innovative analyses, and facilitating more informed decision-making in healthcare and beyond.

As a limitation, the CROWM method adopts an objective approach to data evaluation, excluding subjective decision-maker intervention. While this ensures an impartial analysis strictly based on data, it is recognized that such an approach limits the ability to incorporate qualitative evaluations directly into the decision-making process. Furthermore, given its mathematical complexity and the integration of sophisticated MCDA and ML techniques, it benefits from specialized software support to optimize accessibility and enhance the user experience. This requirement underscores the method’s sophistication and deep analytical capability, turning mathematical complexity into a strategic advantage for detailed analyses. Another limitation pertains to the method’s dependence on data correlation, a fundamental characteristic of PCA, which requires rigorous verification, such as the Bartlett test, to confirm the suitability of the analysis. These limitations are acknowledged and present opportunities for future research to refine the methodology and expand its applicability.

5. Results and Analysis

This study uses a bifurcated methodology to assess CPAP devices. Initially, it involves deriving criteria weights and establishing the ranking order for the CPAPs.

A meticulous literature review was carried out to acquire data pertinent to CPAP devices, enriched by the information contained in the manuals of these devices and through consultations with ten health professionals with extensive experience in treating OSA. Notably, the primary purpose of the data collected is to facilitate a meticulous comparative evaluation of CPAP devices, constituting a fundamental pillar to guide decisions regarding its recommendation. This analysis, however, does not replace the essential individualized clinical evaluation, considering the singularities of each patient, and respects the diagnostic understanding of the specialist for selecting the evaluation criteria for CPAP devices; a comprehensive and relevant set of factors that reflect both the effectiveness and usability of the devices was considered, ensuring a thorough evaluation that addresses both the technical characteristics and the practical considerations of the devices.

Thus, the evaluation criteria are listed below, with their respective definitions:

• Resources: scale from 1 to 7, which represents the number of resources available for each CPAP;
• Warranty (months): warranty period offered for each CPAP, expressed in months;
• Noise (decibels—db): the level of noise produced by CPAP, measured in decibels;
• Cost (real): the monetary cost associated with each CPAP, expressed in real (approximately 5 BRL is equivalent to 1 USD);
• Weight (g): CPAP weight, measured in grams;
• Maintenance: rating from 1 to 7, representing each CPAP’s ease of maintenance.

The values for the resources and maintenance criteria were obtained from evaluating ten physicians who specialized in CPAPs, as cited above.

Table 2. Decision Matrix.

CPAPs\Criterion		Resources	Warranty	Noise	Cost	Weight	Maintenance
CP1	S10 AutoSet	5	24	−26	−5200	−1248	5.3
CP2	AirSense 10 Elite	3	24	−26	−3500	−1248	3.6
CP3	CPAP XT-I	3	12	−30	−3800	−1800	4
CP4	AirMini AutoSet	7	24	−30	−7000	−300	7
CP5	SleepStyle	6	24	−28	−6000	−1700	6
CP6	VPAP Aircurve 10 VAauto	6	24	−28	−6600	−1300	6.4
CP7	SleepLive	3	3	−32	−3673	−1500	3.7
CP8	Dreamstation	4	3	−26	−4123	−1300	4
CP9	Ecostar	2	24	−29	−2400	−800	2

Source: authors.

shows the decision matrix, which consists of nine alternatives and six criteria. The CPAPs, for better explanation and development of the step-by-step methodology presented, will be named CPs, ranging from 1 to 9. A programming code in R was used to elaborate the results and to consider the non-beneficial criteria values in the PCA; the CROWM enters this data in the code in R multiplied by −1:

5.1. Determination of Criteria Weights by CROWM

The values of the non-beneficial criteria were entered with a negative value to correctly weigh the criteria that, the higher, are the worse for a respective CPAP, such as cost, noise, and weight. Before the presentation of the data obtained, it is essential to evidence the consistency of the analysis performed. In this context, the observations outlined in Table 2 were submitted to a Bartlett sphericity test, a crucial step for validating the analysis. The results of the Bartlett test [58], calculated based on Equations (11)–(13) and performed with a significance level of 5% and 15 degrees of freedom, indicated that the Pearson correlation matrix differs significantly from the identity matrix of the same dimension. The p-value (2.42 × 10⁻⁵) presents a value below the significance level of 5%, culminating in rejecting the null hypothesis. Therefore, there is a statistically significant correlation between the observed variables. Thus, Table 2 can proceed with PCA.

The heatmap analysis (Figure 3) indicates that CPAP devices with more features tend to be more expensive, showing a direct correlation (0.988) between cost and resources. Furthermore, costlier and more advanced devices are correlated with maintenance (0.994), likely due to their complexity and superior quality, suggesting enhanced maintenance justifies the higher investment. Weight and warranty display a negative correlation (−0.385), hinting that lighter CPAPs may come with more extended warranties, possibly highlighting strategies to enhance confidence in durability. Meanwhile, noise negatively correlates with warranty (−0.302), implying quieter devices are perceived as higher quality, warranting better warranty terms.

In the proposed framework’s foundational stage, each criterion’s priority weighting is ascertained by integrating factor loadings and the MEREC approach. The computation of criteria weights leverages Equations (1)–(8), with the initial phase employing Equations (1)–(5) for MEREC outcomes, supplemented by factor loadings under Equations (6) and (7). Further, the CROWM methodology amalgamates these techniques, utilizing Equation (8) to calculate the weights for CPAP performance criteria.

Table 3. Criteria weights.

	Weights
Criteria	MEREC	Factor Loadings	CROWM
Resources	0.168	0.196	0.182
Warranty	0.383	0.153	0.268
Noise	0.030	0.110	0.070
Cost	0.119	0.199	0.159
Weight	0.108	0.140	0.124
Maintenance	0.193	0.201	0.197

Source: authors.

shows the criteria weights calculated by MEREC and factor loadings, resulting in the CROWM weights. Notably, the warranty criterion obtained the highest value with a score of 0.268, indicating its importance in selecting CPAP devices. The maintenance criterion, with a weight of 0.197, is also significant, reflecting its relevance in evaluating the devices’ performance. On the other hand, noise, with a value of 0.07, assumes a position of lesser importance relative to the different criteria.

5.2. Performance Evaluation by CROWM

After obtaining the criteria weights, each CPAP’s scores are calculated, with their subsequent ranking, and Equations (14)–(20) are used.

Table 4. Eigenvalues and their variances.

	PC1	PC2	PC3	PC4	PC5	PC6
Eigenvalues	3.281	1.208	1.020	0.475	0.013	0.004
Shared variance	0.547	0.201	0.17	0.079	0.002	0.001
Cumulative shared variance	54.70%	74.80%	91.80%	99.70%	99.90%	100.00%

Source: authors.

delineates the eigenvalues and shared variance of the principal components derived from PCA, foundational to the CROWM methodology. The first principal component (PC1) possesses the highest eigenvalue of 3.281, explaining 54.7% of the variance alone, while the first three components together account for a substantial 91.8% of the total variance. This significant cumulative variance illustrates the effectiveness of PCA in capturing the essence of the data, thereby confirming the robustness of the CROWM method in evaluating CPAP device performance based on a comprehensive dataset. Upon calculating eigenvalues by Equation (14), the Kaiser criterion [60] is applied to selectively identify factors with eigenvalues surpassing one, resulting in the first three factors (PC1, PC2, and PC3) achieving respective values of 3.281, 1.2, and 1.02. Consequently, only these factors were incorporated into subsequent PCA phases.

Thus, only the factors’ values remain to apply the performance evaluation equations, as represented in Table 4, and these are calculated by Equations (15)–(18).

Table 5. Factors.

CPAPs	PC1	PC2	PC3
CP1	0.479	0.776	−0.724
CP2	−0.493	1.348	−0.449
CP3	−0.800	−0.919	−0.333
CP4	1.622	−0.168	1.719
CP5	0.776	−0.365	−0.987
CP6	1.060	−0.186	−0.395
CP7	−1.008	−1.690	0.671
CP8	−0.525	−0.090	−0.869
CP9	−1.113	1.294	1.368

Source: authors.

presents the factor scores for PC1, PC2, and PC3. These scores represent the relative contribution of each CPAP device to the components identified after the Kaiser test. They also reflect the multidimensional characteristics of the evaluated devices and the defined criteria for this study. This approach to dimensionality reduction preserves essential information, enabling detailed and comparative analyses of CPAP devices within the context of the CROWM methodology.

Then,

Table 6. Factor loadings and communalities of criteria.

	Factor Loadings			Communalities
Criteria	PC1	PC2	PC3	PC1	PC2	PC3
Resources	0.978	−0.156	−0.069	0.956	0.024	0.005
Warranty	0.558	0.646	0.109	0.311	0.417	0.012
Noise	0.143	0.690	−0.643	0.020	0.476	0.413
Cost	−0.970	0.223	0.075	0.942	0.050	0.006
Weight	0.370	0.419	0.756	0.137	0.175	0.572
Maintenance	0.957	−0.256	−0.114	0.915	0.065	0.013

Source: authors.

calculates the factor loadings and communalities based on Equations (6) and (19), respectively.

Table 6 showcases the factor loadings and communalities across PC1, PC2, and PC3, illustrating the influence and representation of each criterion in the identified components. Resources and maintenance exhibit high loadings in PC1, indicating their significant contribution to this component. Conversely, noise shows a distinct pattern with a strong negative loading in PC3, suggesting a differentiating factor in device assessment; cost is negatively loaded in PC1, highlighting its inverse relationship with the primary component of variance. When considered across all three PCs, the communalities for resources, maintenance, and cost cumulatively exceed 90%, emphasizing the considerable shared variance of these criteria and their critical role in the CROWM methodology’s comprehensive analysis. This highlights the essential nature of these criteria in the PCA performed, underscoring their significance in the holistic assessment of CPAP devices facilitated by CROWM.

The loading plot analysis (graphical depiction illustrating each variable’s influence on the principal components in PCA—Figure 4) for PCs 1 and 2, which account for approximately 75% of the shared variance, unveils significant relationships among the variables examined. Along the PC1 axis, resources, maintenance, and cost align positively, suggesting a concurrent variation indicative of CPAP devices with superior quality and an extensive set of features. Intriguingly, warranty is oppositely situated, implying an inverse variation with resources and cost. This might point to a compensatory mechanism in devices with fewer features or lower costs through extended warranties.

On the PC2 axis, weight is prominently negative, underscoring specific functional factors such as portability and ease of handling, distinct from conventional criteria of cost and features that primarily focus on operational efficacy. Thus, the emphasis on weight suggests its independent significance in user preferences and satisfaction. Noise stands alone in the upper quadrant, indicating a less defined association or a distinct pattern of variation compared to quality and cost criteria typically related to resources and maintenance. The distribution of these variables in a two-dimensional space provides an intuitive understanding of the underlying dimensions shaping the evaluation of CPAP devices. It is important to note that the analysis of the loading plots (Figure 4) and heatmap (Figure 3) was conducted without the inversion of non-beneficial criteria, a specific approach reserved for the application of the CROWM method in performance evaluation [60].

Finally, the score of each CPAP is generated by Equation (20), and it is possible to rank the devices by CROWM. In this sense, to establish a sensitivity analysis of the results, three methods renowned in the literature were used: the PCA, using the weighted rank-sum criterion method [60]; the Combined Compromise Solution (CoCoSo) method [61] with the weights generated by CROWM (Table 3); and the Gaussian AHP [62].

According to

Table 7. Comparison of proposed method ranking and variations.

Ranking	CROWM		PCA		CoCoSo		Gaussian AHP
1º	CP4	1.134	CP4	1.145	CP4	2.722	CP4	0.208
2º	CP6	0.564	CP6	0.475	CP1	2.704	CP9	0.119
3º	CP1	0.362	CP1	0.295	CP6	2.679	CP6	0.115
4º	CP5	0.294	CP5	0.183	CP5	2.61	CP1	0.112
5º	CP2	−0.087	CP2	−0.074	CP2	2.51	CP5	0.109
6º	CP9	−0.278	CP9	−0.115	CP9	2.009	CP2	0.105
7º	CP8	−0.428	CP8	−0.453	CP8	1.837	CP3	0.080
8º	CP3	−0.696	CP3	−0.679	CP3	1.778	CP8	0.079
9º	CP7	−0.863	CP7	−0.778	CP7	1.316	CP7	0.072

Source: authors.

, the sensitivity analysis highlights the remarkable stability and consistency of the CROWM method compared to the other rankings. The preservation (mainly) of the original positions evidences the intrinsic robustness of the proposed method in the evaluation and classification of medical devices. Regarding the ranking generated by the PCA, no changes were observed. In contrast, only one change was recorded when compared to the CoCoSo method, and for the Gaussian AHP, some positions were swapped, but the first and last CPAP were the same in both methods.

The inherent robustness of the CROWM method, as highlighted in the sensitivity analysis, derives from its integrated approach that effectively combines PCA and MCDA techniques. This fusion provides a holistic and objective assessment, essential in highly complex contexts. Such integration ensures a comprehensive criteria analysis, reflecting a deeper understanding of the dataset. Still, automation in generating weights significantly reduces subjective influences, leading to more balanced and unbiased assessments. In addition, the rigorous application of statistical tests, such as the Kaiser and Bartlett criteria, increases analytical accuracy, ensuring that only significant components are covered. Additionally, the incorporation of communalities in the factor analysis and the innovative inclusion of monotonous cost criteria enrich the method, providing a more detailed view of the shared variation between the variables and ensuring the proper evaluation of all relevant factors, including those with potentially negative impacts on a given CPAP performance.

Table 7 presents a comparative ranking of CPAP devices based on the results obtained by the CROWM method alongside three alternative analytical methods: PCA, CoCoSo, and Gaussian AHP. Moreover, Table 7 highlights the effectiveness of the CROWM method in evaluating CPAP devices, singling out the CP4 as the top-performing device with a score of 1.134, underscoring its exceptional performance across nearly all criteria being assessed. This analysis not only underlines the superiority of CP4 in terms of efficacy and versatility but also emphasizes the robust methodology of CROWM in providing consistent and comparable results with other analytical methods. The consistency of CP4 in maintaining the lead position across different methodologies bolsters its recommendation as a standout option for patients, demonstrating the practical applicability and precision of the CROWM method in selecting CPAP devices.

The CP1, despite its lower price point, demonstrates a commendable balance across various criteria, earning it the third rank. This finding highlights its cost-effectiveness, suggesting that, upon medical recommendation, the CP1 could be a reasonable choice for patients seeking quality treatment aligned with economic considerations. Moving beyond mere cost analysis, employing the CP1 in OSA treatment introduces significant financial considerations for healthcare. While the CP4 leads in performance metrics, the CP1 distinguishes itself through its optimal cost-effectiveness balance. Utilizing the CROWM method, this analysis advocates for the CP1 as a model of efficient resource allocation in healthcare, particularly in managing complex conditions like OSA within economically constrained environments.

In the study, Spearman’s correlation analysis [63] compares the rankings generated by the CROWM method with the established PCA, CoCoSo, and Gaussian AHP methods. Spearman’s correlation, a nonparametric statistical test used to measure the strength and direction of association between two rankings, revealed the following results: between CROWM and PCA, a value of 1000; between CROWM and CoCoSo, 0.983; and between CROWM and Gaussian AHP, 0.817.

Corroborating these results, Figure 5 shows the variations in the positions of the CPs according to the evaluation methods, denoting stability of the analyses between the proposed method and the PCA and CoCoSo, but with slight variations concerning the Gaussian AHP. Notably, CP4 was the first in the three rankings, while CP7 was last in all methods. According to Mukaka’s [64] explanation, a solid positive correlation is evidenced by Spearman’s correlation values greater than 0.9, while values between 0.7 and 0.9 suggest a high correlation, reinforcing the validity of the CROWM as a reliable method and in line with established approaches. These high correlation values indicate a strong agreement between the rankings generated by CROWM and the other methods and suggest the consistency and robustness of the method.

5.3. Advantages and Disadvantages of the CROWM Method

As a drawback, the CROWM method does not allow for the inclusion of the DM opinion in the evaluation process, making the analysis dependent on the evaluated data, resulting in the criteria weights in Table 3. This can limit the method’s flexibility in situations where the DM’s intuition or experience could be valuable. Another point to consider is the complexity of the technique, which requires computational support for its implementation. Moreover, for CROWM to yield consistent and reliable results, the dataset must exhibit a correlation among its data, typically analyzed at a significance level of 5% by the Bartlett test [58]. After applying the Bartlett test, the p-value (2.42 × 10⁻⁵) presents a value below the significance level of 5%; if this had not happened, the correlation between the variables would not have been justified, and the CROWM might not have presented robust results.

A vital advantage of the CROWM method lies in its robust data analytics capabilities, notably through the application of PCA validation tests, which are often overlooked in the literature. A unique characteristic of this method is its use of communalities to accurately represent the shared variance between variables in extracted factors. This approach enables a precise representation of specific criteria within the PCs, facilitating a correct scoring of each alternative by considering this weighting in each PC. Another advantage is integrating non-beneficial criteria into PCA, allowing for a more comprehensive understanding of each alternative’s advantages and disadvantages, and providing a reliable evaluation by correctly positioning their characteristics within the decision-making process. Furthermore, leveraging the inherent features of PCA, CROWM benefits from this ML technique’s efficiency and ability to generate objective rankings. This is achieved by simplifying data complexity through dimensionality reduction, which retains only essential information. Unlike some traditional decision support and multicriteria methods, PCA minimizes ambiguities and subjectivities by automatically weighting variables based on their shared variance. This methodological approach results in precise rankings grounded on robust statistical criteria, dynamically adapting to the data and faithfully reflecting the performance of alternatives.

These advantages are explained by the consistent results, which were validated by renowned methods in the literature, as shown in Table 7, Figure 5, and by Spearman’s coefficient [63,64].

6. Conclusions

Fulfilling its objective, this research presented a methodology for evaluating CPAP devices in healthcare, particularly in managing sleep quality. By employing the CROWM method, the study highlights its capacity to provide personalized CPAP therapies that optimize the treatment of respiratory disorders and improve patients’ quality of life, while minimizing associated risks.

The findings of this study underscore the AirMini AutoSet, CP4, as the frontrunner with a score of 1.134, highlighting its superiority across evaluated criteria. The CP1, S10 AutoSet, despite its lower price point, demonstrates a commendable balance across various criteria, earning it the third rank. This underscores its cost-effectiveness, suggesting it is a viable option for quality treatment aligned with economic considerations. Conversely, the SleepLive device, CP7, ranks at the bottom with a score of −0.863, indicating areas for improvement. These results elucidate the distinct performance spectrum of CPAP devices, guiding optimal selection based on comprehensive evaluations.

Sensitivity analysis revealed the remarkable stability and consistency of the CROWM method, especially when compared to other methodologies like CoCoSo and Gaussian AHP, with high Spearman correlation values, 0.983 and 0.817, respectively. This robustness and consistency are critical in analyzing complex variables and confirm the value of this innovative method for informed decision-making in the selection of medical devices.

The study also provides practical guidance for both healthcare professionals and CPAP manufacturers. It underscores the importance of balancing efficacy, convenience, and technical features in treating sleep apnea. Healthcare professionals are advised to familiarize themselves with the evaluation criteria for more informed decision-making. Concurrently, CPAP manufacturers are urged to prioritize a balance between technical quality, cost, usability, and maintenance, aiming to develop affordable and easy-to-use devices.

Finally, the potential extension of the CROWM method to other applications in health and society is highlighted, serving as a reference for high-impact decisions across various contexts. This method is expected to contribute to assertive decision-making, assisting healthcare professionals, researchers, and patients in the practical and reasonable choice of these essential devices. The goal is to provide a valuable tool that positively impacts the quality of medical care offered to patients with specific needs, reinforcing this study’s position as an essential milestone in healthcare.

Future research should explore the development of decision support methodologies that integrate the subjective opinions of DMs, especially in evaluating medical devices like CPAPs. This approach could incorporate expert opinions, patient preferences, and clinical insights to enhance decision-making. Such methodologies could utilize advanced techniques like fuzzy logic, AHP, or ML algorithms to process and synthesize these subjective inputs. This integration would add a human-centric dimension to the decision-making process and increase the accuracy and relevance of the evaluations. Such research would represent a step forward in personalized medicine, ensuring that the selection of medical devices aligns more closely with individual patient needs and preferences, as well as the expertise of healthcare professionals.