Innovative Methods of Centrifugal Separation

Abstract

Considered are: (i) separation of gaseous molecules of different weight by the Ultra Centrifuge with application to large scale uranium enrichment to fuel nuclear power plants; (ii) separation of micron-sized particulate matter from fluids in mechanical devices in which use is made of inertial and centrifugal forces; (iii) separation of gaseous mixtures by fast expansion and cooling such that one of the gaseous components forms a mist of micron-sized droplets which are separated by centrifugation; and (iv) separation of components from gases by absorbing liquid films in small sized rotating channels. For each of these technologies we consider: physics of the separation process, assessment of the influence of fluid flow in the separation device, identification of leading parameters and their effect on design, experimental evidence, status of development, areas of application, position compared to other technologies, and economic value.

1. Introduction

A simple method to separate mixtures with components having different mass density is to make use of the action of the earth’s gravitation. It provides, for example, the driving force to separate of mixtures of oil, gas, and/or water in settling chambers used in the oil and gas industry. For cases where the substances which are to be separated are very small or differ only slightly in mass density, the time needed for settlement and separation becomes correspondingly larger. It leads to disproportionally sized devices of gravitational separation. A significant reduction in size can be achieved by employing centrifugation instead of gravitation. In practical devices of centrifugation the acceleration of centrifugation can be orders of magnitude larger than that of gravitation. It results in much more compact devices capable of separating mixtures of various kinds. Traditional applications are milk centrifuges in dairy industry, blood separators in hospitals, and tumble dryers at home. In this paper, attention is focused on four innovations in centrifugal separation:

(i)

Separation of gaseous molecules of different weight by the Ultra Centrifuge with application to large scale uranium enrichment to serve for peaceful use as fuel for nuclear power plants;

(ii)

Separation of micron-sized particulate matter from fluids by mechanical separators based on centrifugation with special attention to the device of the Rotational Particle Separator RPS for dedusting and demisting gases in industry and domestic environment;

(iii)

Separation of mixtures of gases by Condensed Rotational Separation CRS, i.e., fast cooling by expansion leading to preferential condensation of one of the gaseous components in the form of micron-sized droplets which are separated by the RPS. Applications range from large scale upgrading of sour and acid natural gas to purification and liquefaction of the greenhouse gas CO₂ emitted from carbon-based conversion processes;

(iv)

Separation of components from gases by applying absorbing liquid films in the rotating channels of the RPS. Applications range from H2S and CO₂ removal from gases to separation and elimination of contagious aerosols such as aerosols containing harmful bacteria and viruses present in air.

For each of these technologies we consider physics of the separation process, assessment of the influence of fluid flow in the separation device, identification of leading parameters and their effect on design, experimental evidence, status of development, areas of application, position compared to other technologies, and economic value.

2. The Ultra Centrifuge for Separation of Gas Mixtures

The density $\rho$ of air decreases exponentially with height h from the earth’s surface according to the barometric density formula: Cohen [1].

$$p_1=p_1\left(0\right)exp\left(-\frac{M_{1}gh}{R_{0}T}\right),$$

(1)

where M is molecular weight of the gas, g gravitational acceleration, $R_0$ universal gas constant, and T temperature. In case of a binary mixture of gases with different molecular weights $M_1$ and $M_2$, the density distributions will be different and this can be used as a means for separation [1]. If we put the mixture in a chamber of height h and wait for some time, the ratio of both concentrations $N/(1-N)$ will have changed. At the top there will be a higher ratio for the lighter component, at the bottom for the heavier component. The separation factor $\alpha$ defined as

$$\alpha =\frac{{\left(\frac{N}{1-N}\right)}_h}{{\left(\frac{N}{1-N}\right)}_0}=\frac{\frac{p_1\left(h\right)}{p_2\left(h\right)}}{\frac{p_1\left(0\right)}{p_2\left(0\right)}},$$

(2)

will amount to

$$\alpha =exp\left(-\frac{(M_1-M_2)gh}{R_{0}T}\right),$$

(3)

where N is molecular concentration of component 1 and $1-N$ of component 2. The separation factor can be substantially increased by applying centrifugation instead of gravitation as separation force. The appropriate formula is simply obtained by replacing $gh$ by ${\omega }^2{r}_o^2$ where $\omega$ is angular speed and $r_o$ is radius of the centrifuge:

$$\alpha =\frac{{\left(\frac{N}{1-N}\right)}_{r_o}}{{\left(\frac{N}{1-N}\right)}_0}=\frac{\frac{p_1\left(r_o\right)}{p_2\left(r_o\right)}}{\frac{p_1\left(0\right)}{p_2\left(0\right)}}=exp\left(-\frac{(M_1-M_2){\omega }^2{r}_o^2}{R_{0}T}\right),$$

(4)

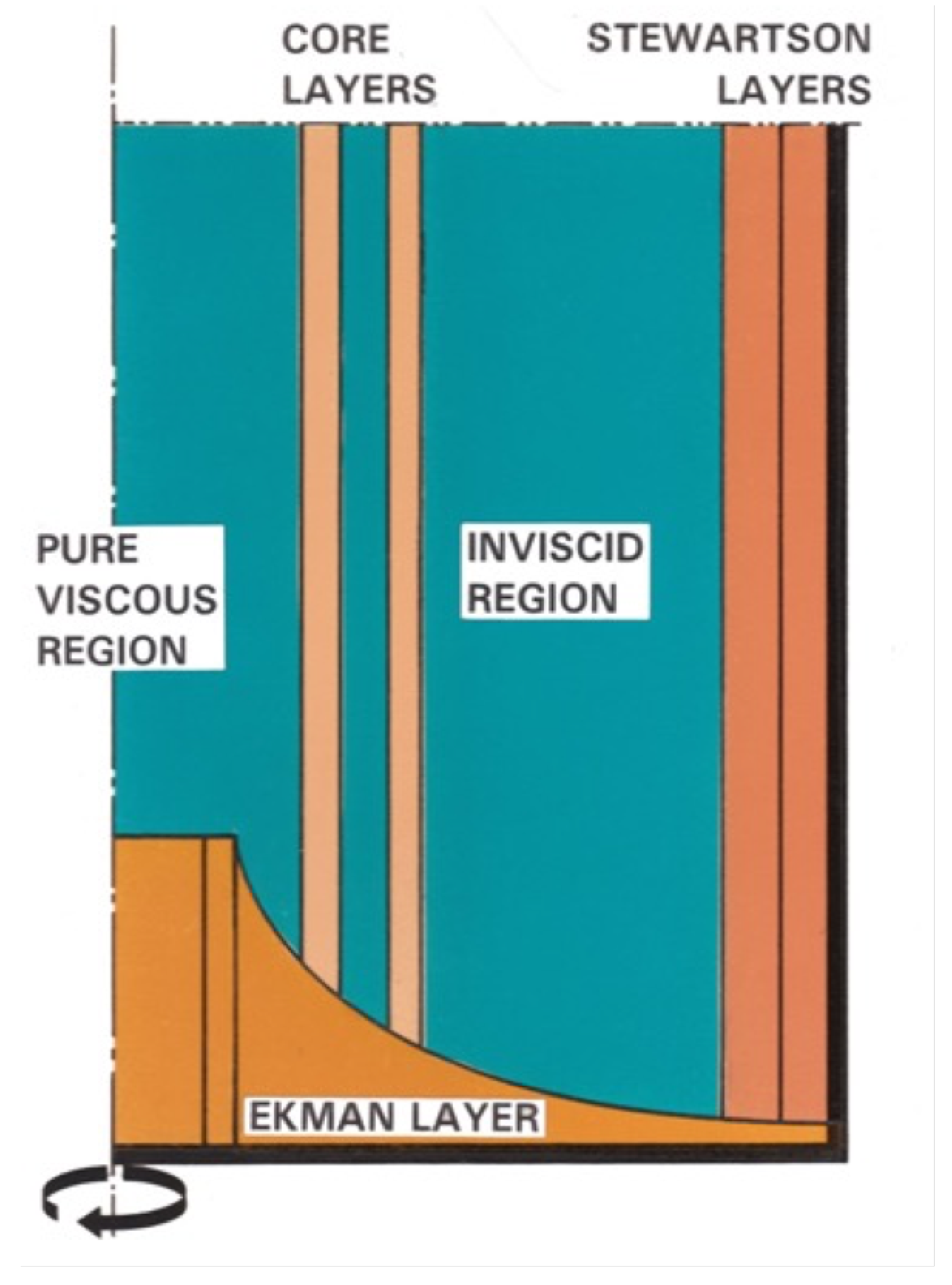
2.1. Working of the Centrifuge

Centrifuges used for uranium enrichment are usually designed according to the three-pole principle or Zippe-type centrifuge named after the German engineer Zippe. A schematic drawing is given in Figure 1: Delbeke et al. [2].

The centrifuge consists of a thin-walled rotor which rotates at high speeds in a housing. The area between rotor and housing is kept at near vacuum to minimize friction between rotor and housing. The working fluid is gaseous UF${}_6$ which fills the interior of the rotor. Gas is fed about halfway in the center of the rotor. Extraction of enriched and depleted fraction takes place at top and bottom, respectively. Inside the rotor there exists a counter-current flow. It converts a centrifugally induced radial concentration gradient into a large axial component. In the upward inner flow the concentration of the light fraction increases with distance from the bottom, while the concentration of the heavier fraction increases with distance from the top in the outer part of the counter-current [1,2].

Consider an example which is appropriate for Ultra Centrifuges for uranium enrichment: $M_2-M_1=3$ gmol⁻¹, $R_0=8.3$ Jmol⁻¹K⁻¹, $T=300$ K, $\omega r_0=400$ ms⁻¹. In this case one calculates for the elementary radial enrichment factor ${\alpha }_0$ the value 1.10. Uranium suited as fuel for a nuclear power plant should contain the Isotope U${}^{235}$ at a concentration of about 3% while its concentration in nature is around 0.7%. The required enrichment factor amounts to $3/0.7=4.3$. It can be achieved by placing 15 separation elements each having a separation factor of 1.10 in series ($1.1^{15}=4.3$). In the case of the centrifuge, the radial enrichment factor is increased by the counter-current inside the centrifuge. It can amplify the exponent of elementary enrichment of the centrifuge according to Equation (4) by $L/\left(2r_0\right)$ where L is rotor length [1].

Despite enhancement by the internal counter-current flow, the elementary separation of a single Ultra Centrifuge is usually not enough to bridge the gap between the natural concentration of U${}^{235}$ of 0.7% and the concentration of 3% needed in fuel of nuclear power plants. It results in the cascade formation of separation elements used in enrichment plants [1,2] and shown in elementary form in Figure 2.

The cascade consists of elements placed in series whereby the enriched fraction of one element is fed as feed to the next while the depleted fraction is fed as feed to the previous element. Elements are placed in parallel to meet the full demand of enriched product. A picture of a centrifuge plant in practice is shown in Figure 3.

2.2. Separative Power

It is not only the degree of separation achieved by a single element which is important for a separation duty but also the amount of flow handled by the element. During the Manhattan Project [1] Dirac was able to derive an expression known as Separative Power which combines flow and separation factor in unique fashion [1]. The expression can be applied to the cascade as a whole as well as to the individual separation element. The ratio of the two defines the number of elements. Given a required duty for a cascade in terms of concentration of enriched fraction and amount of flow, one can calculate its Separative Power. The number of separation elements necessary to perform this duty is then specified by the Separative Power of the elements constituting the cascade. This Separative Power is determined by the physics of the element. If the Separative Power of the individual elements can be doubled the number of elements to perform the duty required for the cascade can be halved. The objective of centrifuge development is to enlarge its Separative Power while keeping costs for building in control.

The maximum Separative Power of a centrifuge according to Dirac [1] is given by

$$\delta U_D=\frac{\pi }{2}\rho DL{\left(\frac{\Delta M{\omega }^2{r}_o^2}{R_{0}T}\right)}^2$$

(5)

where $\rho$ is gas density, D is diffusion coefficient ($\rho D$ is almost constant and varies only with gas temperature T), L is rotor length, and $\Delta M=M_1-M_2$. Los, in his PhD thesis (1963), [3] extended the above formula for the three-pole centrifuge according to

$$\delta U_{max}=0.81E_f\delta U_D$$

(6)

where $E_f$ is the flow pattern efficiency. Los [3,4] also developed analytical formulae for separation performance versus feed flow with as parameters the axial position of the feed inside the rotor, the ratio of product flow and waste flow, and the magnitude of the internal circulation. These formulas are of great help when testing and optimizing the performance of a single centrifuge.

It can be shown for which spatial distribution of the internal flow circulation the flow pattern efficiency reaches a value of 100% [1,4]. However, the actual value is determined by internal flow dynamics. Its value was unknown. This problem was tackled by Brouwers in his PhD thesis (1976) [5]. The solution approach was an analytical one applied to the Navier–Stokes equations for laminar gas flow. The laminar treatment was permitted because of a low value of the Reynolds number based on internal flow magnitude. The differences in molecular weights are small so that the gas could be treated as a uniform mixture. It is well described by the ideal gas law. The analytical solution procedure consisted of the following steps:

(i)

The internal flow field represents a small perturbation on isothermal solid body rotation:

Isothermal solid body rotation:

$$\mathbf{v}=\mathbf{\omega }\times \mathbf{r},T=T_0,\frac{{\rho }_0}{{\rho }_{\mathbf{r}=0}}=\frac{p_0}{p_{\mathbf{r}=0}}=exp\left(\frac{1}{2}\frac{{M|\mathbf{\omega }\times \mathbf{r}|}^2}{R_0{T}_0}\right)$$

(7)

Small perturbation:

$$\mathbf{v}=\mathbf{\omega }\times \mathbf{r}+ϵ{\mathbf{v}}^{\prime },\frac{T}{T_0}=1+ϵ{\theta }^{\prime },\frac{\rho }{{\rho }_0}=1+ϵ{\rho }^{\prime },\frac{p}{p_0}=1+ϵp^{\prime }$$

(8)

where v is gas velocity, r is radial position inside the rotor, p is gas pressure, M is average molecular weight, $ϵ$ is small dimensionless parameter representing the perturbation on isothermal rigid body rotation, $v^{\prime }$ is perturbed velocity, ${\theta }^{\prime }$ is perturbed temperature, ${\rho }^{\prime }$ perturbed density, and $p^{\prime }$ perturbed pressure.

(ii)

The Navier–Stokes equations can be linearized by retaining terms linear in $ϵ$ with the result that:

Conservation of mass:

$$\nabla ·{\rho }_0{\mathbf{v}}^{\prime }=0$$

(9)

Conservation of momentum:

$$2\mathbf{\omega }\times {\mathbf{v}}^{\prime }+\frac{1}{2}{\theta }^{\prime }\nabla {|\mathbf{\omega }\times \mathbf{r}|}^2=-\frac{R_0{T}_0}{M}\nabla p^{\prime }+{\rho }_0^{-1}\eta \left({\nabla }^2{\mathbf{v}}^{\prime }+\frac{1}{3}\nabla \nabla ·{\mathbf{v}}^{\prime }\right)$$

(10)

Conservation of energy:

$$-\frac{1}{2}{\mathbf{v}}^{\prime }·\nabla {|\mathbf{\omega }\times \mathbf{r}|}^2={\rho }_0^{-1}\lambda {\nabla }^2{\theta }^{\prime }$$

(11)

where $\eta$ is dynamic viscosity, $\lambda$ is heat conductivity, and ∇ is nabla operator. In total there are five equations for five variables: ${\theta }^{\prime }$, $p^{\prime }$, and ${\mathbf{v}}^{\prime }=(v^{\prime },u,w)$ where $v^{\prime }$ is perturbed tangential velocity, u is radial velocity, and w is axial velocity.

(iii)

Analytical solutions from the linearized Navier–Stokes equations can be derived by making use of a large value of the Reynolds number based on peripheral speed $Re$ and a large value of the speed parameter A because of high peripheral speed and large molecular weight of the gas [5,6].

$$Re={\rho }_0\omega r_o^2/\mu ,A=\frac{1}{2}M{\omega }^2{r}_o^2/R_0{T}_0$$

(12)

In this way a variety of flow regimes can be identified; see Figure 4.

In a region in the outer radial part of the rotor the flow behaves in an almost inviscid manner because of the large value of $Re$ near the wall. The inviscid region connects to the top and bottom cap via Ekman layers and at the outer cylindrical wall by two Stewartson layers; the thicker one to adjust tangential velocities of the inviscid interior to those of the wall and the thinner one to adjust axial and radial velocities. Because of high values of A, the density ${\rho }_0$ rapidly decreases with distance from the cylinder wall: c.f. Equation (7). As a result viscous forces and heat conduction represented by the terms on the right hand side of Equations (10) and (11) become more and more important with decreasing radial position inside the rotor. At a certain position viscous forces and heat condition become in balance with inertial forces on the left hand sides of Equations (10) and (11). The positions mark two layers referred two as core layers. The double structure is similar to the double structure of the two Stewartson layers. Descriptions for the flow in these regions have been derived using a Pohlhausen method [7]. Further inwards of the core layers viscous forces and heat conduction will dominate.

From a standpoint of flow efficiency the inviscid region is the preferred one. Here an ideal radial flow profile of constant axial velocity can be created by well suited boundary conditions imposed at the ends of the rotor. The axial velocity returns via Ekman layers and Stewartson layers at the walls. The viscous core is an area where the product of density and axial velocity decreases exponentially in strength with radial distance from the wall. Here the contribution to the efficiency is minimal. All this means that the maximum value of the efficiency highly depends on the radial position of the core layers. The larger the inviscid region, the larger the efficiency of the centrifuge can be. The position of the core layers is specified by a number of parameters [2,7]. Using the information of this dependency a general graph on efficiency as a function of two dimensionless combinations of parameters A and B defined in [7] can be produced. It has been shown in Figure 5 [2].

From the graph it is seen that for constant B the efficiency drops considerably with increasing value of the speed parameter A. The net effect is that the increase in separative power with peripheral speed is much less than the increase expected according to the proportionality with ${\left(\omega r_o\right)}^4$ following Dirac. This effect is arrested by increasing B.

The analytical solutions of Brouwers [5,6,7] have largely been confirmed by the numerical works of Dickinson and Jones [8] and Van Ommen [9]. The insights have been used in the development of advanced centrifuges used in today’s plants of Urenco. They exhibit centrifuge technology with high performance at low footprint [2]. Plants have been erected in the United Kingdom, The Netherlands, Germany, France, and the United States of America.

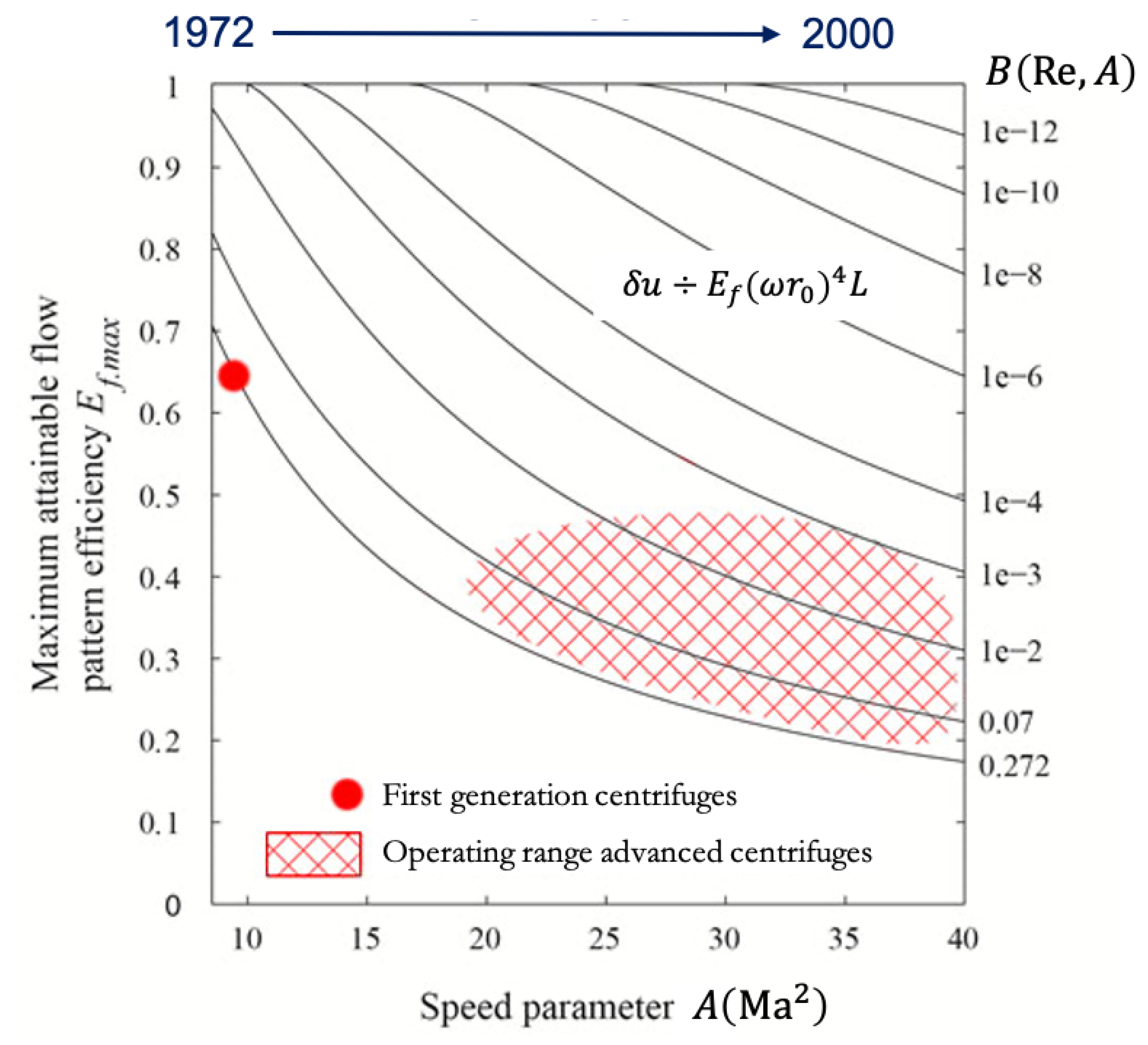
2.3. Limitations of Centrifugal Separation of Gas Mixtures

The concentration of the light isotope molecules in the UF${}_6$ mixture is small. Their motion in a centrifugal field can be described by a Langevin equation whose form follows from the diffusion equation described by Cohen [1] under the assumption of small concentration of one component. The mean radial motion $<(d/dt)r>$ of the lighter molecules particles which is inwards can be derived from the Langevin equation as

$$\frac{d<r>}{dt}=\frac{\mathcal{D}\Delta M{\omega }^2<r>}{R_{0}T}$$

(13)

where $\mathcal{D}$ is diffusion coefficient of the gas. From this equation one can obtain an approximate description for the time needed for separation

$$t\approx \frac{R_{0}T}{\mathcal{D}\Delta M{\omega }^2}$$

(14)

The volume of all centrifuge rotors together V equals ${\varphi }_{m}t/\rho$ where ${\varphi }_m$ is mass flow. With the help of Equation (14) we have

$$V=\frac{{\varphi }_m{R}_0{T}_0}{\rho \mathcal{D}\Delta M{\omega }^2}$$

(15)

A nuclear power plant of 1000 MW needs about 10${}^{-3}$ kg/s of UF${}_6$. Furthermore, I note that for UF${}_6$ gas $\rho D$ is about 2 × 10${}^{-5}$ kg/ms, $\Delta M=3$ g/mol, $\omega$ of centrifuges is about ${10}^3$ s${}^{-1}$, $T_0=300$ K, and $R_0=8314$ gm²/(s²Kmol). From Equation (15) one then calculates a total volume of centrifuge rotors of about 40 m³. A relatively small centrifuge plant can already feed the fuel for a 1000 MW nuclear power plant.

To mitigate carbon emissions it has sometimes been suggested to use gas centrifuges to separate CO₂ from the exhaust gases of fossil fired power plants. An advantage is that $\Delta M$ in case of CO₂/N₂ mixtures amounts to 16 g/mol whereas in case of uranium Isotopes this is only 3 g/mol. However, the exhaust flow of fossil fired power plants is very large. A coal fired power plant of 1000 MW has an exhaust flow of about 10${}^3$ kg/s. The total rotor volume will be about 2 × 10${}^5$ m${}^3$. A very large centrifuge plant is thus needed to do the job. Other methods for CO${}_2$ separation are more appropriate (e.g., the methods of Section 4 and Section 5).

3. Centrifugal Particle Separation

A classical way to separate particles whose density is larger than the density of the fluid in which they are embedded is to use settling tanks. Due to gravity the particles sink to the bottom where they are removed. The time to sink to the bottom depends on size and weight of the particles. If they are small or light it will take a long time to settle at the bottom. To speed up this process a curved flow can be created whereby the particle experiences an external force. An example is the force which is created when sending the gas through a bend, while flowing through the bend the particle experiences an outwardly directed force which equals the centrifugal force based on radius of curvature and gas velocity. The principle is applied in vane packs and is illustrated in Figure 6.

Another method for creating a separating force is by the swirl in a cyclone. Gas with particles in it is tangentially fed into a cylindrical pipe. The flow in the pipe goes axially through the pipe while exhibiting a tangential swirl. The swirl leads to an outwardly directed force which causes the particle to move to the wall of the cylinder: see Figure 6.

In the cases of the vane type separator and the cyclone a separating force is created which can be related to a centrifugal effect without applying a rotating mechanical structure. This in contrast with the method of the Rotational Particle Separator invented in 1987: Brouwers [10,11]. It can be conceived as an extension of the cyclone, see Figure 6. Inside a cylindrical housing a rotating element is placed, Figure 7. It consists of a large number of axially oriented channels of small height. Because the small height particles only have to move a small distance before being collected. In this way particles which are about ten times smaller than those of the corresponding cyclone have a similar external size, flow capacity, and pressure drop. In practice these advantages should work against the higher costs of the device compared to that of the non-rotating cyclone. Vane type separators, cyclones, and Rotational Particle Separators applied in industry typically separate particles larger than 20, 5, and 0.5 micron (10${}^{-6}$ m), respectively.

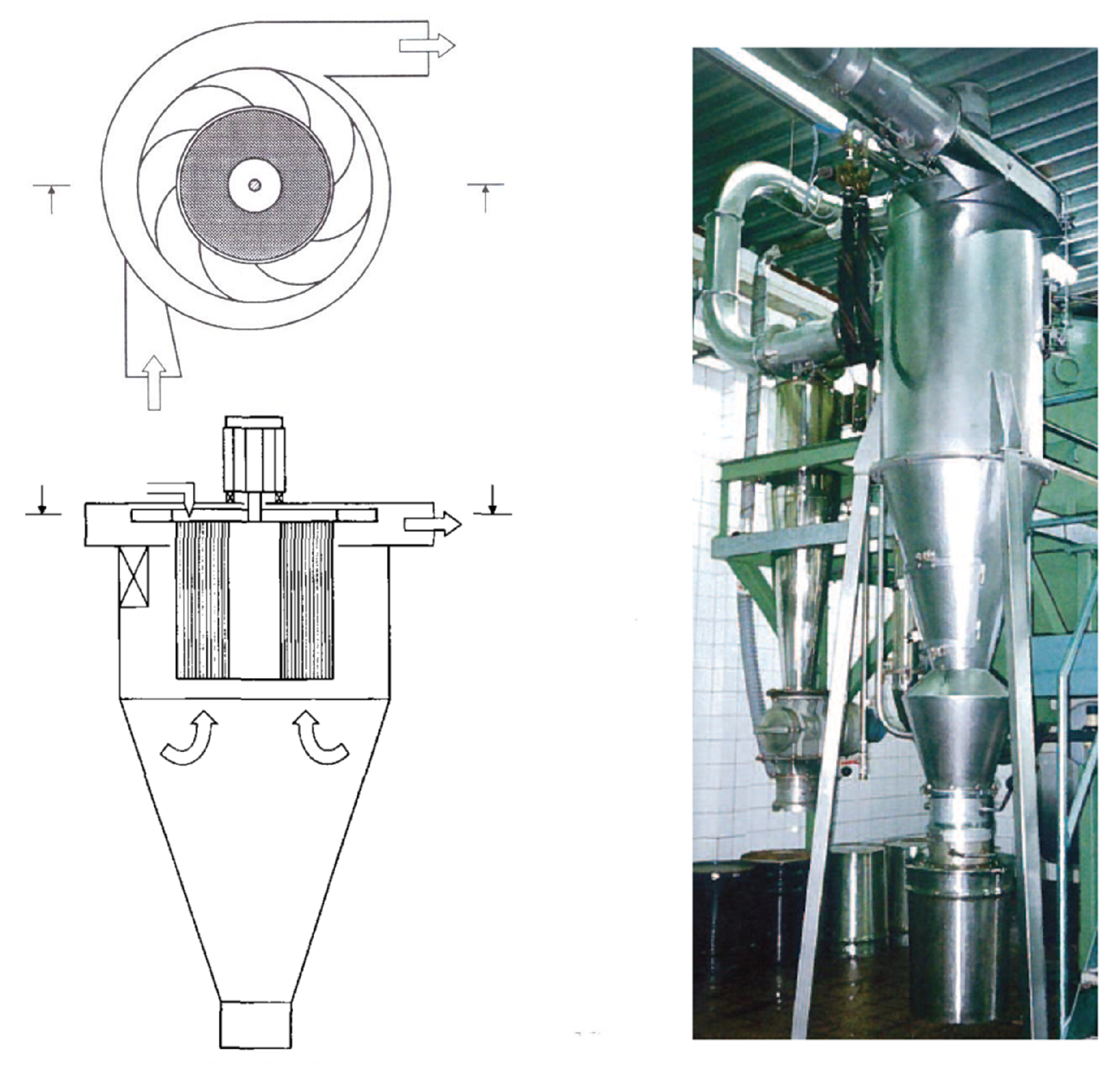
3.1. The Rotational Particle Separator

When a gas with particles entrained in it flows through a channel of the Rotational Particle Separator (RPS) the particles will be subjected to a centrifugal force caused by the rotation of the device: Figure 7.

The centrifugal force $F_c$ can be described by

$$F_c=\frac{\pi }{6}({\rho }_c-\rho )d_p^3{\omega }^{2}r$$

(16)

$d_p$ is particle diameter ${\rho }_p$ particle density, $\rho$ gas density, $\omega$ angular speed, and r radial position. Due to this force the particle will move radially leading to a resistance force caused by the gas. For particles with diameters in the range 0.5–5 micron Stokes force $F_s$ can be used to describe the resistance to motion relative to the gas: Fuchs [12], Hinds [13].

$$F_s=3\pi \eta d_p{u}_p$$

(17)

where $\eta$ is dynamic viscosity of the gas and $u_p$ radial velocity of the particle. Soon after entrance in the channel the radial velocity of the particle will reach a value according to a balance between centrifugal and Stokes’ force. It is given by

$$u_p=\frac{({\rho }_p-\rho )d_p^2{\omega }^{2}r}{18\eta }$$

(18)

Particles which will be collected by 50% or more are those which start at entrance halfway the height of the channel and reach the wall at the exit of the channel. These particles have the velocity

$$u_{p50\%}=\frac{1}{2}{w}_g{D}_c/L$$

(19)

where $w_g$ is velocity of the gas in the channel which is also the axial velocity of the particles $D_c$ is height of the channel and L is length of the channel. From Equations (18) and (19) an expression is obtained which describes the diameter of the particles which have an average collection rate of 50%.

$$d_{p50\%}={\left(\frac{9\eta w_g{d}_c}{({\rho }_p-\rho ){\omega }^{2}rL}\right)}^{1/2}$$

(20)

From this formula it is noted that for constant values of $d_c$, $w_g$, and L, $d_{p50\%}$ increases with decreasing distance r from the rotation axis. This increase in $d_{p50\%}$ can be avoided by designing an axial gas velocity $w_g$ which increases linearly with distance r from the rotation axis. The reduction in centrifugal force with decreasing r is then compensated by an increase in residence time in the channel. The result is that the degree of particles separation will be the same for all channels. The desired distribution of the axial gas velocity can be accomplished by appropriate dimensioning of the inlet and outlet configuration upstream and downstream of the filter element.

In case of an optimum distribution of the axial gas velocity, i.e., $w_g$ is proportional to r, an expression for $d_{p50\%}$ can be derived which is applicable to the entire filter element:

$$d_{p50\%}={\left(\frac{27\eta \varphi d_c}{{\rho }_p{\omega }^{2}L\pi (1-ϵ)(r_o^3-r_i^3)}\right)}^{1/2}$$

(21)

where $\varphi$ is the gas flow through the filter element, $ϵ$ the reduction in the effective cross-sectional area of the element due to wall thickness of the channels, $r_o$ the outer radius of the element, and $r_i$ the inner radius.

Consider the following example:

$$\begin{array}{cc}\hfill \varphi & =1{\mathrm{m}}^3/\mathrm{s}\hfill \\ \hfill d_c& =2\times {10}^{-3}\mathrm{m}\hfill \\ \hfill \omega & =150\mathrm{rad}/\mathrm{s}\hfill \\ \hfill L& =0.6\mathrm{m}\hfill \\ \hfill ϵ& =0.1\hfill \\ \hfill r_o& =0.3\mathrm{m}\hfill \\ \hfill r_i& =0.1\mathrm{m}\hfill \\ \hfill {\rho }_p& =2000{\mathrm{kg}/\mathrm{m}}^3\hfill \\ \hfill \eta & =1.8\times {10}^{-5}\mathrm{kg}/\mathrm{ms}\hfill \end{array}$$

(22)

In this case one calculates:

$$d_{p50\%}=5\times {10}^{-7}\mathrm{m}$$

(23)

In other words, under the given conditions particles with a diameter of 0.5 $\mathsf{\mu }$m are separated by 50%. This result is obtained with relatively small element: the residence time is less than 0.2 s. Furthermore, the circumferential speed of the element is limited to 45 m/s, implying low friction and mechanical loading. According to the Hagen–Poiseulle formula for circular tubes, the pressure drop over the channels is assessed as 320 Pa.

Theoretical descriptions for the distribution of particle collection rate as a function of particle diameter can be derived by considering the path of particles for different starting positions in the channel [14]. This can be conducted for different shapes of the channels (circular, triangular, concentric, and sinusoid) as well as for uniform and parabolic velocity profiles of the gas in the channel. Furthermore, the effect of non-optimum velocity distributions over the rotor as a whole can be determined [14]. The distributions have been confirmed by many experiments executed over the past 30 years. A version of the RPS in which turbulent flow in the channels occurs was patented in 2009: Hoijtink et al. [15]. Measured efficiency distributions of the turbulent RPS have been found to differ slightly from the measured and theoretical ones for laminar channel flow: Kroes [16]. A summary of measured efficiency distributions in case of laminar flow has been presented in Figure 8.

3.2. RPS Designs

Since its inception several designs have been built, tested, and brought onto the market [17]. In Figure 9, a drawing and a picture of a practical design are shown of an RPS integrated with a reverse cyclone.

Gas with particles in it enters the cyclone in tangential direction and follows a spiral motion to the bottom to reverse in the inner part. Here it flows upwards to enter the channels of the rotating element of the RPS. The gas leaves the RPS element tangentially at the top via blades of an impeller which drives the flow through the separation unit. In the cyclone section downstream of the RPS element larger particles with diameters typically larger than 5 micron are separated. They are propelled to the cyclone wall and leave the apparatus at the bottom. All this is common in reverse cyclones. The RPS element subsequently separates the smaller particle typically 0.5 micron in diameter and larger. When the element rotates particles will be stuck against the outwardly oriented sides of the channels. They accumulate in a layer which can be removed by blowing downwards from time to time gas at high pressure at the top side of the rotating element. The channel cleaning can happen under rotation. With intermittent blowing with short periods of time the process of separation is only slightly disturbed. Particles which are blown out of the filter element are by rotation thrown to the cyclone wall and leave the apparatus at the bottom. The apparatus can be fabricated from stainless steel, making it well suited for high temperature applications with temperatures up to 600 ${}^{\circ }$C. The stainless steel version is also suited for separating ultra-fine particles in areas where high requirements on hygiene exist such as in food and pharmaceutical production.

Another design of the RPS is the RPS Demister (Figure 10).

It serves to separate small liquid droplets from gas at pressures as high as 200 bar. Gas with droplets enters tangentially into a cylindrical housing where the larger droplets are propelled outwards to leave the apparatus at the first liquid outlet at the top. Gas with finer droplets enters the channels of the rotating element. The finer droplets are propelled to channel walls where they form a film which flows downwards. The liquid leaves the channels at the bottom where it breaks up in relatively large droplets which are propelled to the chamber of the second liquid outlet. The RPS Demister is particularly suited for applications at high gas pressure as in this case the size of the apparatus is small while mass flows are large. A picture of an RPS Demister which separates simultaneously liquid droplets and fine sand particles is shown in Figure 11.

A version suited for application in the consumer market has been shown in Figure 12. The function of the RPS filter element is here rather limited, it is only a pre-filter upstream of a fan and a porous filter medium. The combination allows for a longer life time of the porous filter medium. In a recent tested design aimed at domestic applications the RPS Filter separates down to 0.5 micron without filter media. It removes almost all particles and aerosols from the air. The RPS element is flushed by a liquid which decontaminates harmful bacteria and viruses separated from the gas [18].

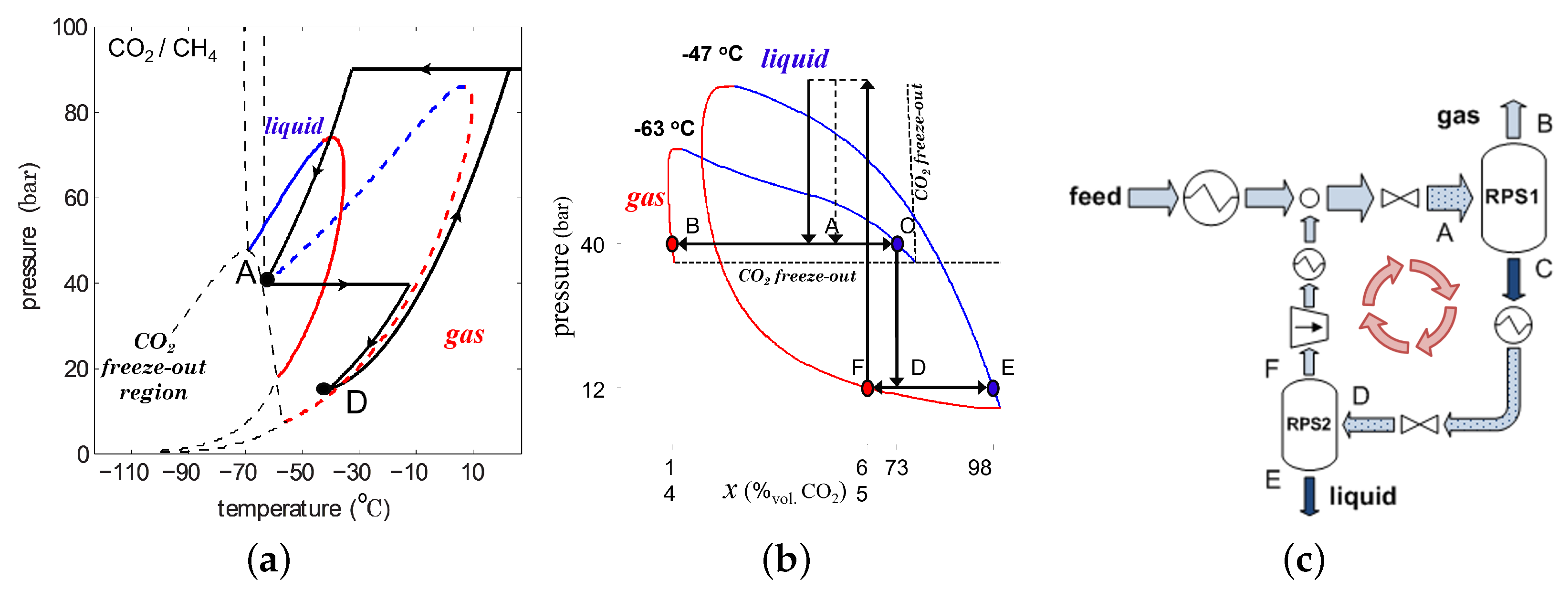
4. Condensed Rotational Separation

Centrifugal separation of mixtures of gases on the basis of different molecular weight is not feasible in most cases of industrial application. For centrifugal separation to be an option the component which is to be separated must be much significantly larger in size than that of the molecules in which it is embedded. To show this, consider the equation of radial velocity of a particle in a centrifugal field according to Equation (24) which is written as

$$\frac{dr}{dt}=\frac{(\delta M/M)\rho d_p^2{\omega }^{2}r}{\left(18\eta \right)}$$

(24)

where ${\rho }_p-\rho$ was replaced by $(\delta M/M)\rho$. The residence time for a channel with inner radius $r_i$ and outer radius $r_o$ is now approximately equal to

$$t=\frac{18\eta (r_o-r_i)}{(\delta M/M)\rho d_p^2{\omega }^{2}r}$$

(25)

The difference between Equations (25) and (18) is due to application of Stokes law. For particles smaller than 0.5 micron the formula of Stokes has to be amended by the Cunningham factor [12,13]. For particles down to molecular size Equation (25) becomes equal to (18).

From Equation (25) it is seen that residence times reduce with increased particle diameter, with increased density of the gas and with reduced separation distance $r_o-r_i$; the latter being the case in the channels of the RPS. Decrease in temperature and pressure produces a mist of small particles which are of sub-micron size but many times larger in diameter than the molecules of the gas they originate from. The formation of fog in air undergoing cooling and pressure decrease is a well-known example of this phenomenon: Figure 13. The deliberate reduction in temperature and pressure by coolers and Joule Thomson valves and subsequent separation of the droplets by the RPS is the central idea behind Condensed Rotational Separation CRS. Installations based on CRS have small footprint: Van Kemenade et al. [19,20], Hoijtink et al. [21], Van Wissen [22], Willems [23], and Bansal [24].

4.1. Liquefaction of Gases by CRS

Liquefying a gas consisting of a single component is straightforward. The gas is brought on pressure and from here is cooled by a heat exchanger and subsequently flashed to a desired pressure and temperature. Part of the gas becomes liquid in the form of mist and is separated by the RPS. The non-liquefied gas coming from the RPS is re-looped to the inlet of the process and undergoes the previous steps once again. The process thus involves an internal circulation. The strength of this circulation becomes smaller if the temperature after flashing is lower. In this case there will be less gas after the flash which needs to be recirculated. However, the energy required for cooling and higher pressure will be larger. In practice one will look for a balance between these opposing effects, more liquid after the flash against more circulating flow. A flow diagram of the process is shown in Figure 14.

The described CRS process differs from a more conventional process whereby the gas is brought in liquid phase by external cooling only. In case of methane liquefaction there is often some CO₂ present in the gas. Gas of pipeline quality, for example, is generally allowed to contain 2% of CO₂. The CO₂ freezes out at about −50 °C while methane liquefies at below −100 °C. It will cause blocking of the heat exchanger in the part where temperatures are below −50 °C. To avoid this from happening a separate process of CO₂ removal prior to liquefaction is used. In the CRS process this extra step is not needed. The flash is designed to take place at temperatures above the freeze out point of CO₂. The CO₂ particle created in the flash will be embedded in methane liquid droplets. They cause no blockage of the RPS and are carried by the liquid methane.

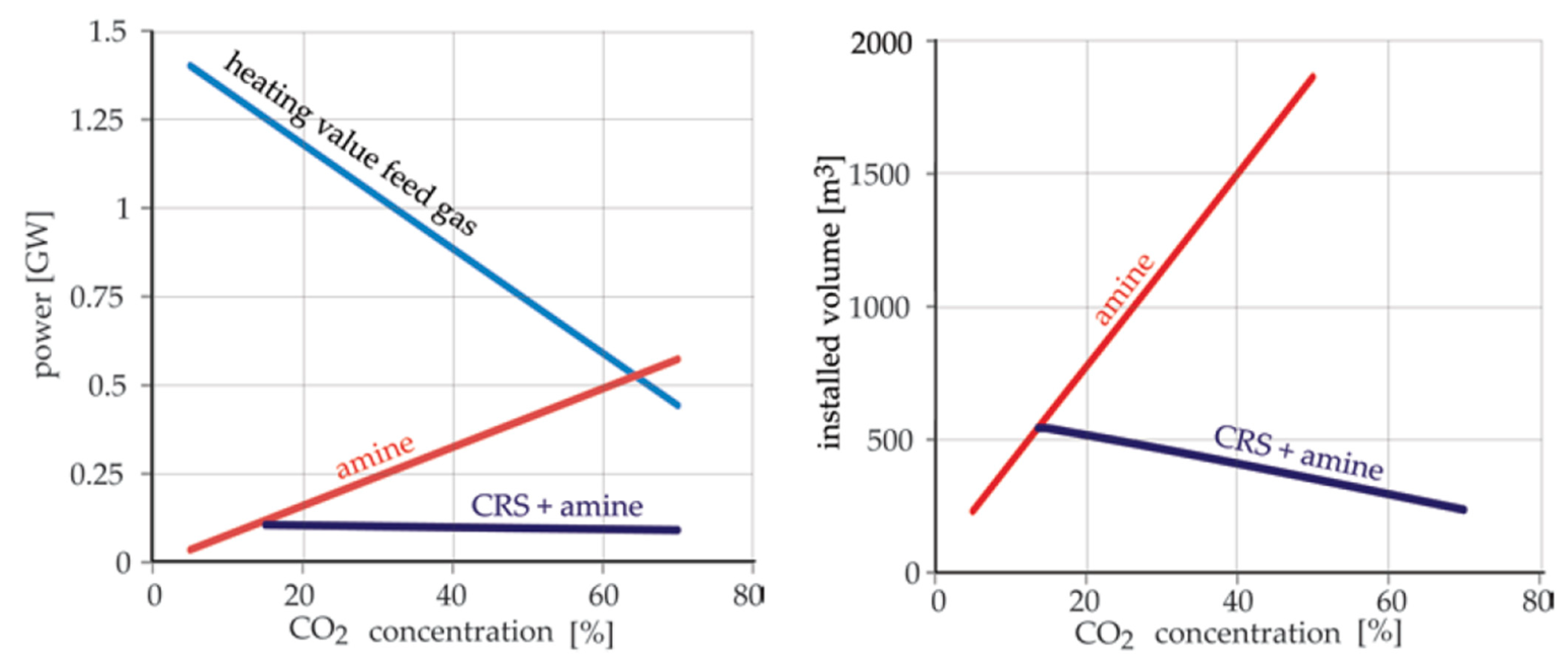
4.2. Upgrading a Sour Gas

Separation of mixtures of gases of different components is an issue in various energy related processes. Examples are the separation of H2S and CO₂ from methane to upgrade sour gas fields and the capture of CO₂ from coal fired power plants to reduce the emissions of greenhouse gases. Mature industrial methods for these applications are amine absorption and fractional distillation: Kohl et al. [25]. Disadvantages of these technologies are high energy consumption and equipment size, in particular when sour gas concentrations are large. CRS provides an improvement.

The CRS process for separating a mixture of two gases consists of two separation steps. It is illustrated by flow diagrams, pressure concentration diagrams and pressure temperature diagrams in Figure 15a–c for a mixture of CO₂/CH₄. An incoming mixture of CO${}_2$/CH${}_4$ which is at 90 bar is chilled by a combination of external cooling and expansion to point A close to the solid boundary of the vapor–liquid phase. The mixture of mist and gas is separated by RPS 1 in accordance with points B and C. The concentration CH${}_4$ in the gas phase is at a maximum at point B. The mist at point C constitutes a liquid stream which is heated and expanded to point D The resulting mixture of mist and gas is separated by RPS2. The liquid from RPS2 has maximum CO${}_2$ concentration: point E. The gas leaving RPS2 (point F) is compressed, cooled, and re-fed in the incoming stream. The result is maximum purities in both phases at both exits.

A disadvantage of the presented process is that methane concentrations in the gas outlet are limited to about 88% at about −50 °C. Lower temperatures to arrive at higher methane concentrations are not possible if one wants to avoid ice formation of CO₂. It would lead to blockages in the particles separator. However, for much higher field concentrations of CO₂ CRS becomes an interesting option when applied upstream of a conventional amine scrubber. CRS is handling the bulk by reducing sour gas concentrations to about 12%. The rest is performed by the amine scrubber. Energy consumption and footprint of the combination are significantly less than those of stand-alone amine scrubber [20]: Figure 16.

The freeze out point of H2S in methane is at lower temperature and leads to lower H2S concentrations in the gas outlet of CRS: [19]. Furthermore, in combination with CO₂ contamination, the purity of gas outlet achieved by CRS can be significantly lower than in case of CO₂ alone: [19]. In general the two step CRS process is an interesting option for upgrading gases in cases where the phase diagrams favors the condensation process.

The first step in the CRS process consisting of compression, cooling, J-T expansion, and separating gas and mist has been tested at lab scale in the Shell Laboratory in Amsterdam [22,23,24]. Both CH₄-CO₂ mixtures and N₂-CO₂ mixtures were considered. The latter with a view of application in processes of mitigation of greenhouse gases from fossil fueled power plants: Van Benthum [26].

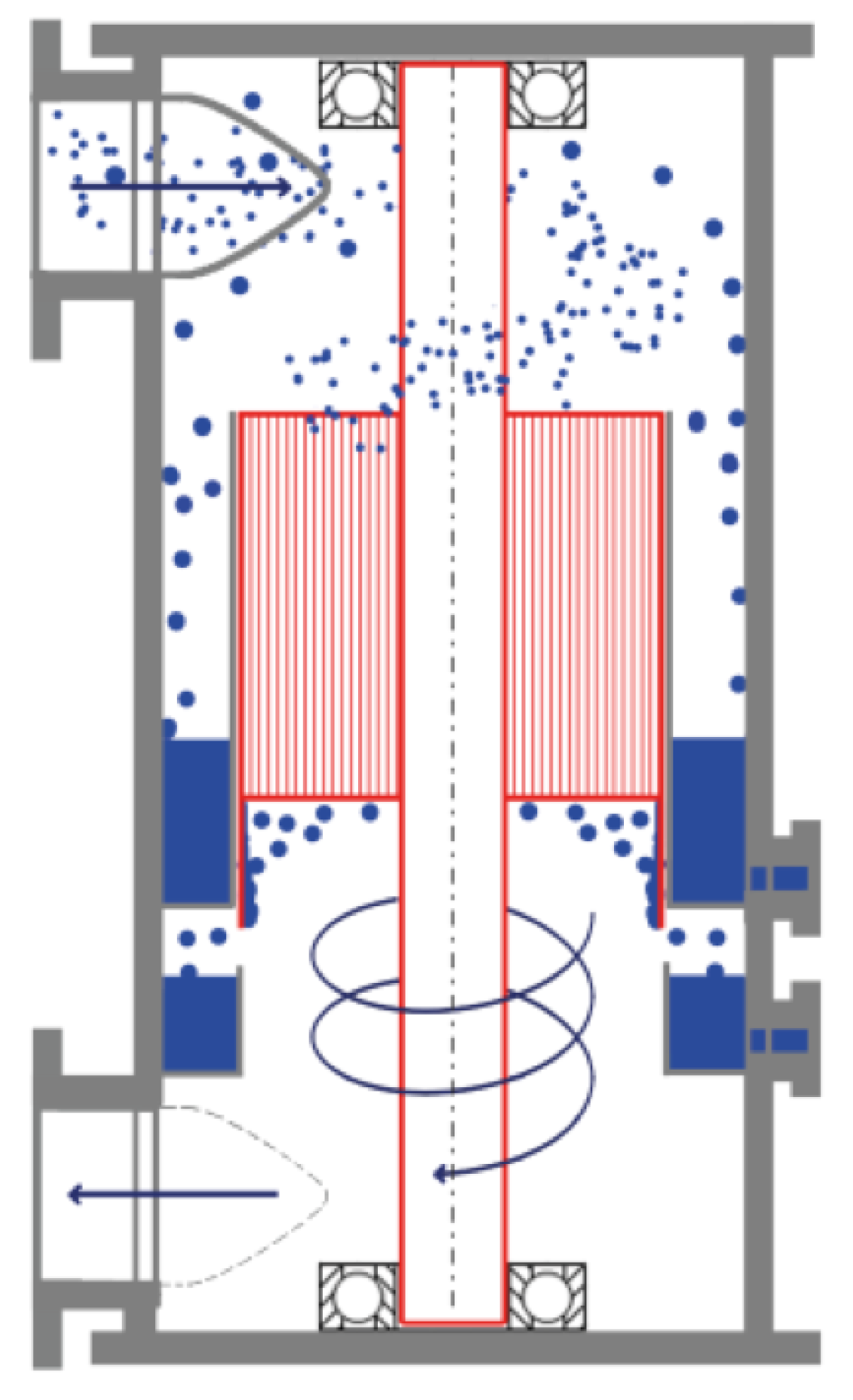
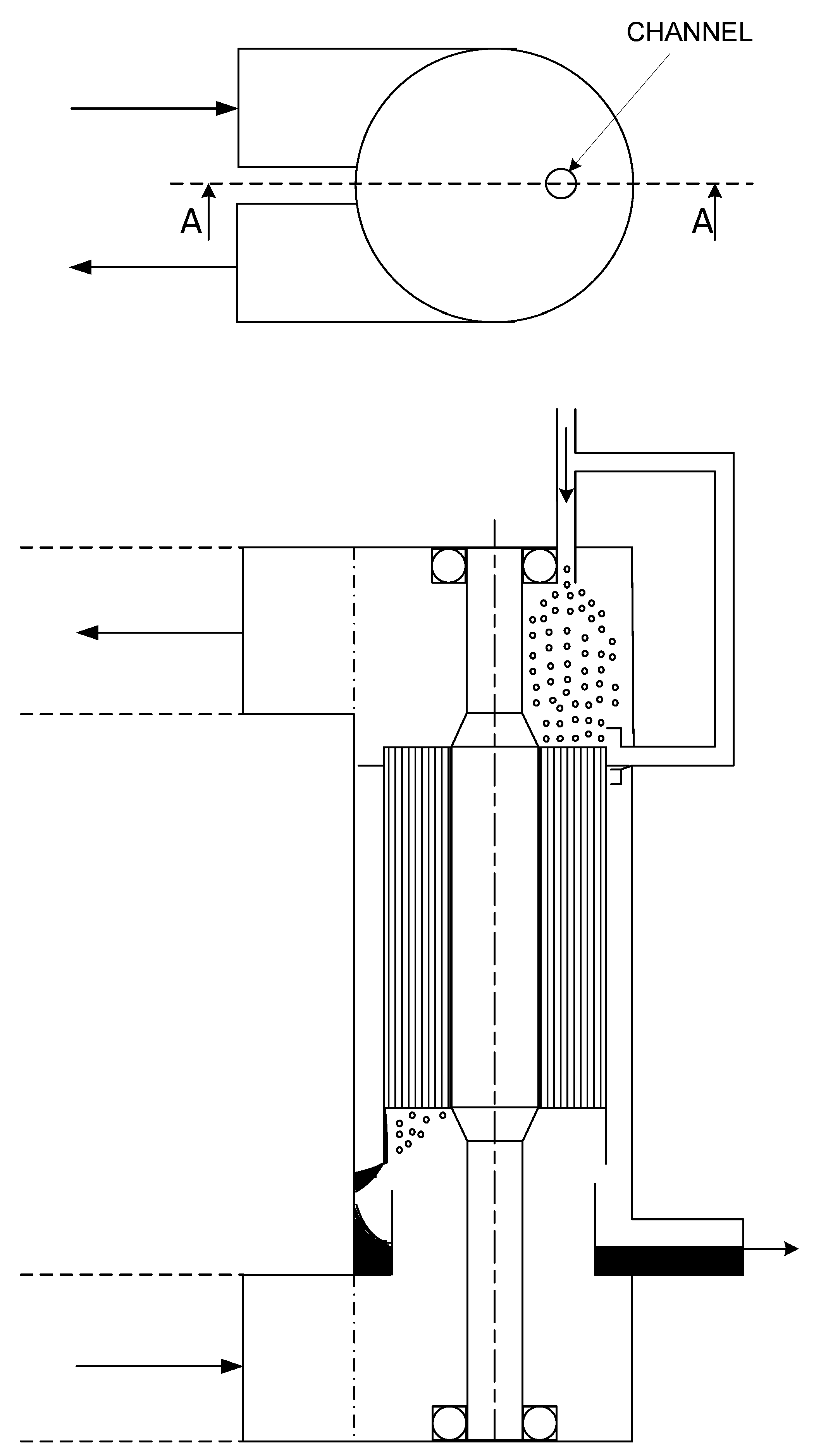
5. The Rotational Absorber Device

Scrubbing a waste gas from unwanted components (the absorbate) has been performed for many years. Typical scrubbing treatment installations bring a gas stream into contact with a so-called absorbent liquid with the aim of allowing the absorbate in the form of certain gaseous components to pass from the gas to the liquid. Scrubbing can for instance be used to limit emissions. Scrubbing is also referred to as absorption. Conventional ways of scrubbing a gas are by liquid spraying, wetted tray columns, and wetted packed columns [26]. Although the known devices may operate satisfactorily, they are prone to improvements, in particular regarding their efficiency and footprint. An alternative is provided by the Rotational Absorber Device RAD patented in 2021 [27]. In this device scrubbing takes place by injecting absorber liquid into the channels of the RPS. A schematic drawing of the RDA is shown in Figure 17.

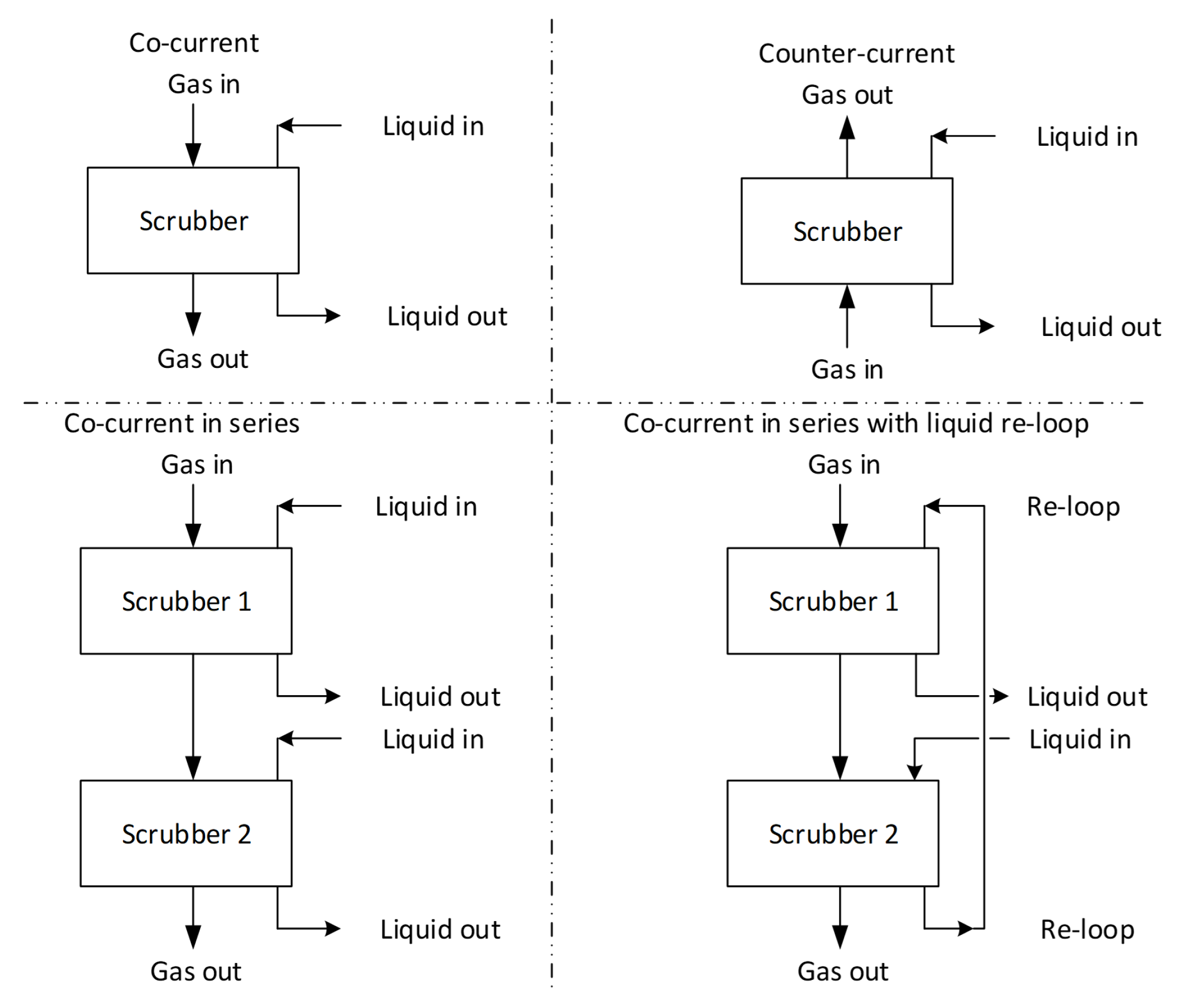
5.1. Design Layouts

The RAD can be designed as co-current scrubber or counter-current scrubber: Figure 18.

The rate or ratio by which the concentration of constituent in the gas is absorbed by the liquid is given by

$$R=\frac{C_g^M\left(L\right)}{C_g^M\left(0\right)}$$

(26)

where $C_g^M\left(L\right)$ and $C_g^M\left(0\right)$ are the molar concentrations of constituent in the gas at gas outlet and gas inlet, respectively, and L is channel length. For the co-current design and counter-current design general formulae for R can be given. They are not just limited to the RDA but are valid for any other scrubber as well [25]. They follow from a balance between the molecular or mass flows of the absorbate constituent from gas to liquid at every axial position at the surface where the transfer takes place.

Co-current:

$$R={(1+C_R)}^{-1}\left[C_R+exp(-NTU(1+C_R))\right]$$

(27)

Counter-current:

$$R=\frac{(1-C_R)exp(-NTU(1-C_R))Q}{1-C_{R}exp(-NTU(1-C_R))}$$

(28)

where

$$C_R=\frac{Q_g^M}{H{Q}_t^M}$$

(29)

$Q_g^M$ and $Q_t^M$ are molar gas and liquid flows (mol/s) and H is Henry’s constant. Henry’s constant equals the ratio of molar concentrations of absorbate in liquid and gas when there is equilibrium which is achieved when liquid and gas are very long together. Its value can be obtained from a flash program or literature. $NTU$ stands for normalized transfer units; it is dimensionless and its value is determined by the internal parameters and dimensions of the scrubber.

In Figure 19 and Figure 20 we have shown the reductions in gas concentration of the constituent obtained with the co-current and counter-current scrubber versus NTU for decreasing values of $C_R^{-1}$, that is, with increasing liquid flow. Furthermore we have shown the performance of two co-current scrubbers in series and two co-current scrubbers in series with a re-loop of the liquid flow from the outlet of the second scrubber to the inlet of the first scrubber: see Figure 21. The formulae for these two co-current scrubbers in series are:

Two co-current scrubbers in series:

$$R={\left({(1+C_R)}^{-1}\left[C_R+exp(-NTU(1+C_R))\right]\right)}^2$$

(30)

Two co-current scrubbers in series with liquid re-loop:

$$\begin{array}{cc}\hfill R& ={\left({(1+C_R)}^{-1}\left[C_R+exp(-NTU(1+C_R))\right]\right)}^2(1+b)\hfill \\ \hfill b& =\frac{C_R{\left[1-exp(-NTU(1+C_R))\right]}^2}{\left[C_R+exp(-NTU(1+C_R))\right]\left[1+2C_R-C_{R}exp(-NTU(1+C_R))\right]}\hfill \end{array}$$

(31)

For two co-current scrubbers in series the reduction in concentration becomes equal to the square of the single unit. For two co-current in series with liquid re-loop the reduction becomes somewhat less because already used “dirty” liquid from the second scrubber is used as new scrubbing liquid in the first. The reduction in performance is described by the factor b in the above equation. Its effect on performance degradation is limited. The advantage of the re-loop is that the amount of liquid used for scrubbing is only half of that without re-loop. Moreover, the concentration of absorbate in the liquid will be higher which will be an advantage in those cases where the absorbate is a useful product which is to be recovered from the absorber liquid.

From Figure 19 and Figure 20 it is seen that scrubber performance increases with increasing $C_R^{-1}$ and $NTU$. At lower values of $NTU$, which corresponds to smaller sized scrubbers, the performance of the co-current and counter-current scrubber are comparable but at larger $NTU$ the counter-current scrubber becomes better. The performance of the co-current units in series is better than that of the counter-current unit for not too large values of $NTU$. However, it should be noted that two units in series have a $NTU$ which is double of that of the single one and this double value should be compared with that of the counter-current unit to understand presented performances versus $NTU$. Taking this effect into account, it is still true that two co-current RDA units compete in performance and size with a counter-current RDA units, assuming that the counter-current configuration is possible, i.e., for laminar gas flow in the channels; see Section 5.3. The multiple series design of the co-current RDA consists of multiple rotating elements mounted on a single shaft in a single housing. It will be of similar size and similar performance as that of a counter-current version. So the limitation of RPS Scrubbers to co-current designs when the internal turbulent gas flow is turbulent, i.e., under high pressure operation, is not a serious drawback. The limitation is circumvented by the series design with liquid re-loop. At the same time it is to be noted that the RDA whether it is counter-current or co-current in series, is much smaller in size than all other scrubbing units which are on the market and having similar scrubbing performance. It is a consequence of the different physical principles employed in the RPS Scrubber.

5.2. Definition of $C_R$

From the formulae for concentration reduction it is seen that absorber performance is determined by $C_R$ and NTU; $C_R$ is determined by ratio of gas and liquid flow and Henry constant:

$$C_R=\frac{Q_g^M}{H{Q}_l^M}=\frac{Q_g{\rho }_g{M}_l}{H{Q}_l{\rho }_l{M}_g}=\frac{Q_g}{H_v{Q}_l}$$

(32)

where $Q_g$ and $Q_l$ are volume flows of gas and liquid at actual pressure and temperature (m${}^3$/s), $\rho g$ and $\rho l$ are gas and liquid densities (kg/m${}^3$), and $M_g$ and $M_l$ are molecular weights of gas and liquid (kg/mol); $H_v$ is Henry’s constant based on volume concentrations of absorbate in liquid and gas when there is equilibrium between concentrations in liquid and gas. Note that $C_R$ does not depend on the dimensions and form of the RDA or other scrubber design. It is entirely determined by external flows and Henry constant. In case of the single co-current scrubber $C_R$ needs to be small to obtain good performance. This becomes apparent if we write the formula for the co-current unit, c.f. Equation (27), in the form

$$R=\frac{C_g^M\left(L\right)}{C_g^M\left(0\right)}={(1+C_R)}^{-1}{C}_R+{(1+C_R)}^{-1}exp[-NTU(1+C_R)]$$

(33)

The two terms on the right hand side add up whereby the first term is determined by $C_R$ and the second mainly by $NTU$. Both terms need to be small to obtain good performance, implying that CR needs to be small and $NTU$ reasonably large ( as it occurs in the exponential). For example, to achieve a reduction in concentration of constituent in the gas of a factor 10 one can opt for $C_R=0.05$ and $NTU=3$ leading to $C_g^M\left(L\right)/C_g^M\left(0\right)=0.05+0.05=0.1$. How much larger H is dictates how much less liquid is needed. Large values of H occur, e.g., for methanol in water, water vapor in glycol, SO${}_2$ in caustic soda, etc. In general H is proportional to pressure, so scrubbing under pressure requires less scrubbing liquid. The counter-current design and the co-current design in series with liquid re-loop require less scrubbing liquid to achieve good performance.

Henry’s constant H equals the ratio of molar concentrations in liquid and gas when equilibrium is reached. The term $(1+C_R)-1C_R$ in Equation (27) equals the ratio of molar concentration in the gas at equilibrium to the molar concentration in the gas at inlet of the absorber. This is the smallest possible value which can be obtained for $C_g^M\left(L\right)/C_g^M\left(0\right)$ in a single co-current unit and is reached when $NTU$ is very large such that the second term on the right hand side of Equation (27) has become small. This behaviour is seen in the horizontal asymptote of the curves for the single co-current unit shown in Figure 19 and Figure 20 when $NTU$ becomes large.

5.3. Definition of $NTU$

$NTU$ is defined by

$$NTU=\frac{A_{tot}K}{Q_{gtot}^M}=\frac{A_{ch}K}{Q_{gch}^M}$$

(34)

where $Q_{gtot}^M$ and $Q_{gch}^M$ are molecular gas flows through the entire absorber element and through a single channel of the element, respectively, (mol/s), while $A_{tot}$ is the total contact area between gas and liquid in the absorber element, and $A_{ch}$ the contact area in a single channel of the element [m${}^2$]. K is overall mass transfer coefficient defined as

$$K=\frac{1}{M_g/\left({\rho }_g{k}_g\right)+M_l/\left({\rho }_l{k}_{l}H\right)}$$

(35)

where $k_g$ and $k_l$ are the mass transfer coefficients of gas and liquid in the channel (m/s), $M_g$ and $M_l$ are the molecular weights of gas and liquid (kg/mol), and ${\rho }_g$ and ${\rho }_l$ are the densities of gas and liquid (kg/m${}^3$), respectively. We have

$$\frac{A_{tot}}{A_{ch}}=\frac{Q_{gtot}^M}{Q_{gch}^M}=N$$

(36)

where N is number of channels. From the above formula we can see that the value of $NTU$ can be related to the properties of a single channel, that is, the dimensions of and flow in the channel. We obtain from the above equations for $NTU$

$$NTU=k_g{A}_{ch}{Q}_{gch}^{-1}{(1+\alpha )}^{-1};\alpha =\frac{{\rho }_g{k}_g{M}_l}{H{\rho }_l{k}_l{M}_g}=\frac{k_g}{H_v/k_l}$$

(37)

The value of $\alpha$ determines how far mass transfer in the gas phase or in the liquid phase is limiting the process of overall transfer. If $\alpha <<1$ the gas phase is determining and for $\alpha >>1$ transfer in the liquid phase determines the outcome. The values of the mass transfer coefficients $k_g$ and $k_l$ will depend on the type of flow in the channels, viz. turbulent or laminar and co-current or counter-current. These aspects are discussed in the subsequent section.

5.4. Mass Transfer Coefficients

The internal flow conditions according to the co-current design can always be realized. Liquid and gas flow parallel to each other from top to bottom. Due to centrifugation liquid which is injected at the top is thrown to the outer channel wall and forms a film. It flows downward being driven by gravity and the shear flow executed by the gas [20,28]. For counter-current flow, however, there are limitations, while the gas flow is now upwards, the liquid flow driven by gravity is downwards. The shear force executed by the gas can be so high that the liquid flow is upwards against gravity. This is particularly the case under high gas pressure where the shear force is large. The counter-current design is then impossible. The conditions under which this happens follow from the theory of the liquid film: Willems [23] and Mondt [28]. When the counter-current version is not possible one can resort to the co-current design in series with similar performance (Section 5.1).

The centrifugal force plays no role in the mas transfer at the surface between the two phases. It implies that for the transfer coefficient of the gas kg one can resort to the transfer coefficients known for gas at channel walls. These are known for both turbulent and laminar flow [29]. The liquid film will only wet part of the circumference of the channel. However, transfer is concentrated in a relatively thin area near the wall. Curvature of the channel will be a secondary parameter and the effect of partial wetting can be treated by the corresponding reduction in transfer surface when using the transfer coefficients known for channels.

The flow in the liquid film is at low Reynolds number and is laminar. Film theory developed for the channels of the RDA [23,28] enables specification of the parameters which determine the liquid transfer coefficient $k_l$ given in the literature [29].

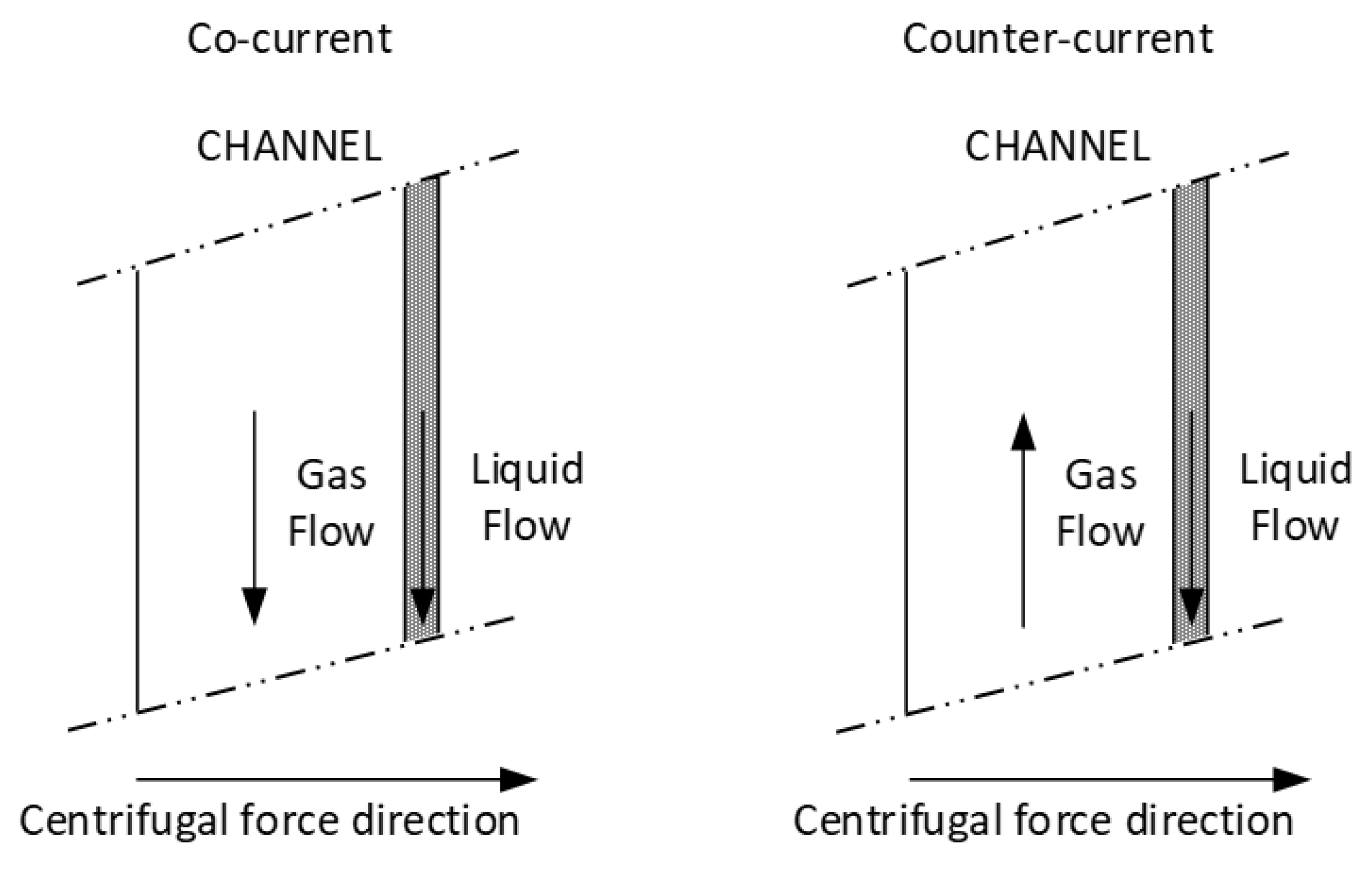
5.5. The Role of Rotation

Rotation plays no role in mass transfer in the channels of the RDA. Its importance is found in the following processes:

(i)

The RAD element consists of a multitude of small channels. Because of rotation each channel receives about an equal amount of liquid from a stationary liquid source positioned above the rotating element. Some variation of injection in the circumference of the element will lead to some variation in time of the feeding of liquid from the stationary source in each channel. The degree of variation depends on rotational speed and inhomogeneity of injection in circumferential direction. The variation will lead to a wave through the liquid film which can be described by that of gravity waves in shallow water [30,31] by replacing g by ${\mathsf{\Omega }}^{2}r$. It enhances mass transfer in the liquid film in the manner described by Villermaux [32]. Its stimulating effect becomes important in case of high liquid loads where film thicknesses are large and mass transfer in the liquid is a limiting factor in the overall transfer process.

(ii)

The centrifugal force pushes the liquid to the outer wall of each channel. It results in the separation of gas flow and liquid film in the channel and a well-defined surface of mass transfer between both phases.

(iii)

Because of rotation, liquid which leaves the channels at the bottom is propelled in the form of relatively large droplets to a liquid collection chamber in the housing of the RAD: Figure 16.

(iv)

The RAD can also be used as a method for separating particles in addition to absorption by the liquid added to the rotating element. If the particles are very small and of micron/submicron size higher rotation speeds are required than those necessary for the functioning of the absorption processes of (i)–(iii). The particles will be transported by the liquid towards the liquid exit chamber. Applying a disinfecting liquid enables elimination of harmful bacteria and viruses [18].

A picture of technology which incorporates the Rotational Absorber Device for SO${}_2$ removal from exhaust gases from ships is shown in Figure 22.

6. Conclusions

Four innovations in centrifugal methods of separation have been analyzed. It was found that by using rotation significant improvements in separation performance can be obtained. Installations in which centrifugally induced separation is applied result in considerable reduction in the footprint. Furthermore, with the presented technology new fields of application can be unlocked. All this exists under the premise that a more complex rotating apparatus can be reliably built at acceptable costs.