Insights into the Adsorption Performance of Emerging Contaminants on Granular Activated Carbon
Abstract
:1. Introduction
2. Experimental
2.1. Adsorbents
2.2. Chemicals and Reagents
2.3. Batch Experiments
2.4. Kinetic Models
2.5. Equilibrium Isotherm Model
2.6. Analysis
3. Results and Discussion
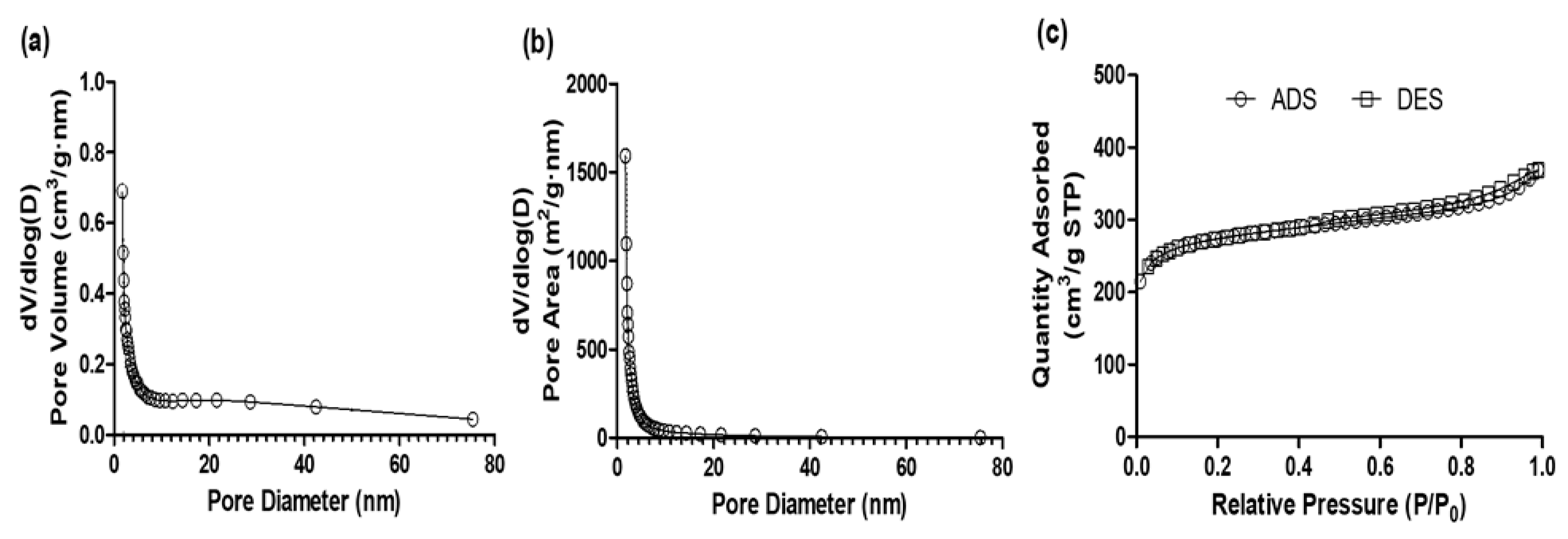
3.1. Characterization of the Adsorbent
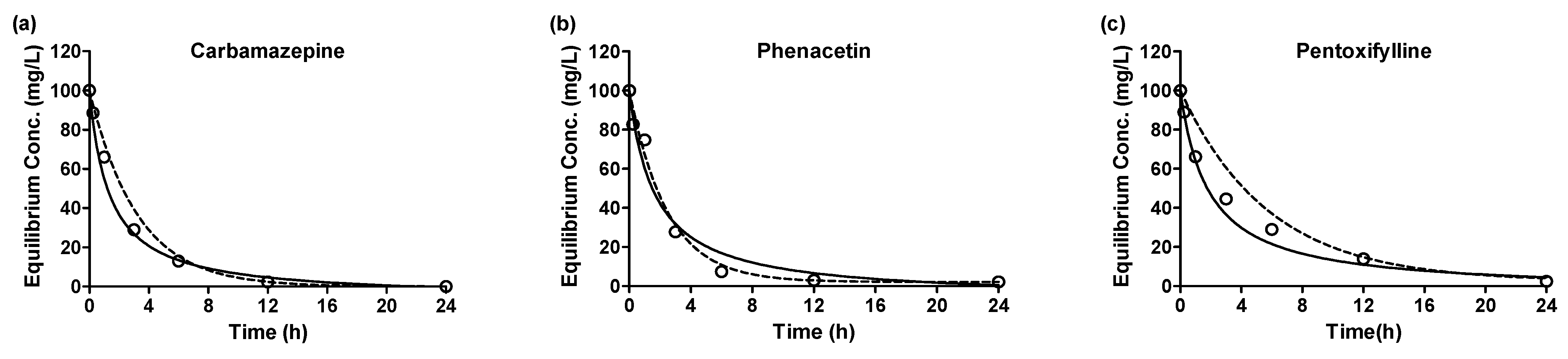
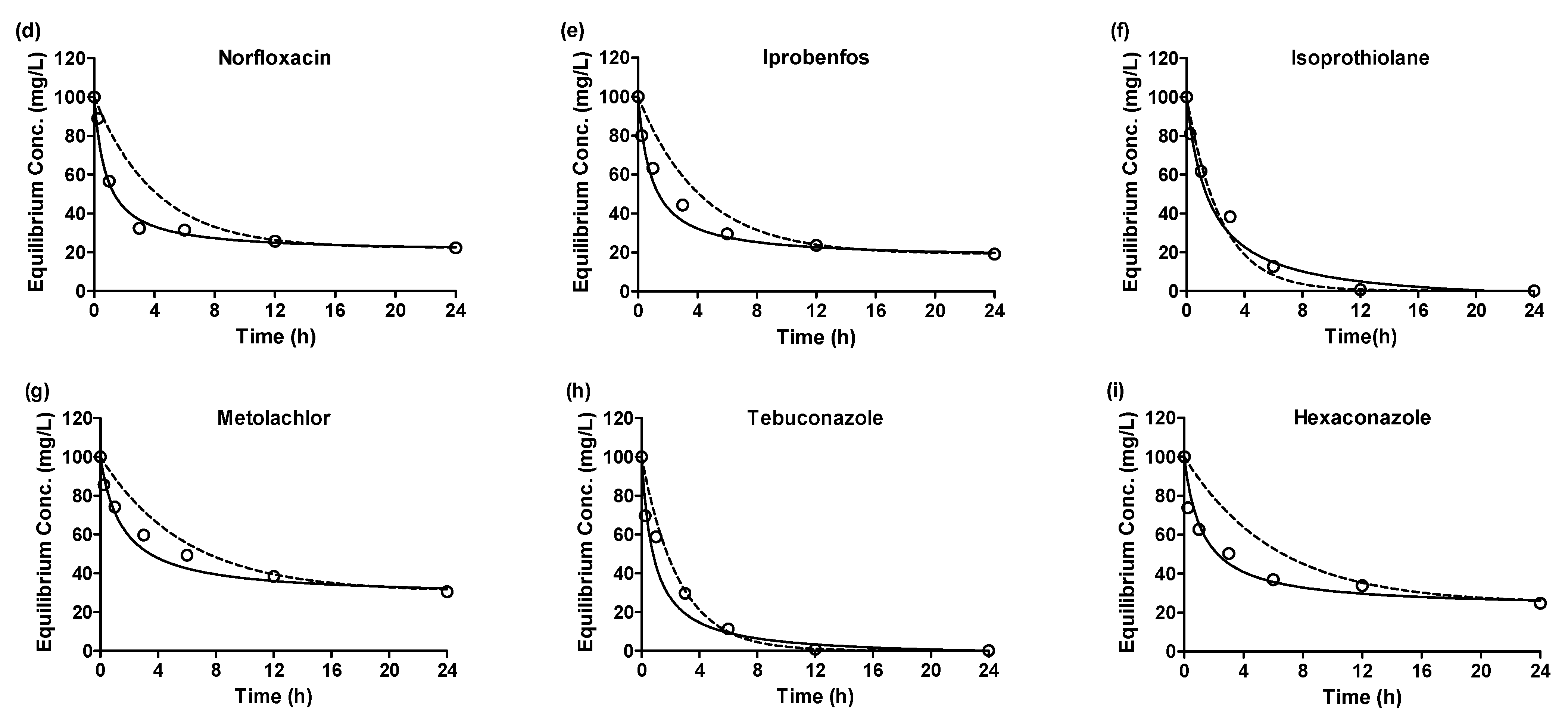
3.2. Adsorption Kinetic Model
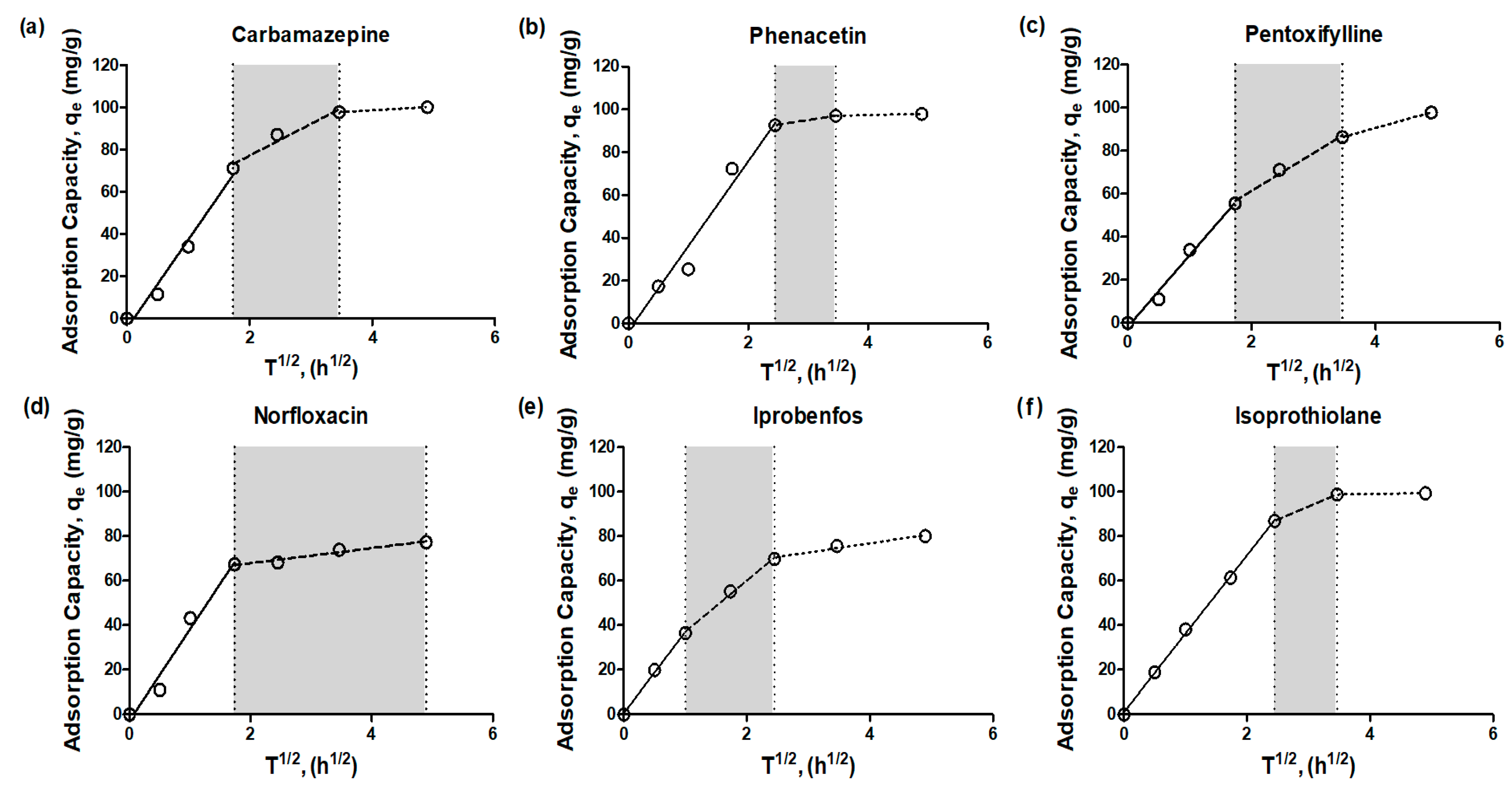
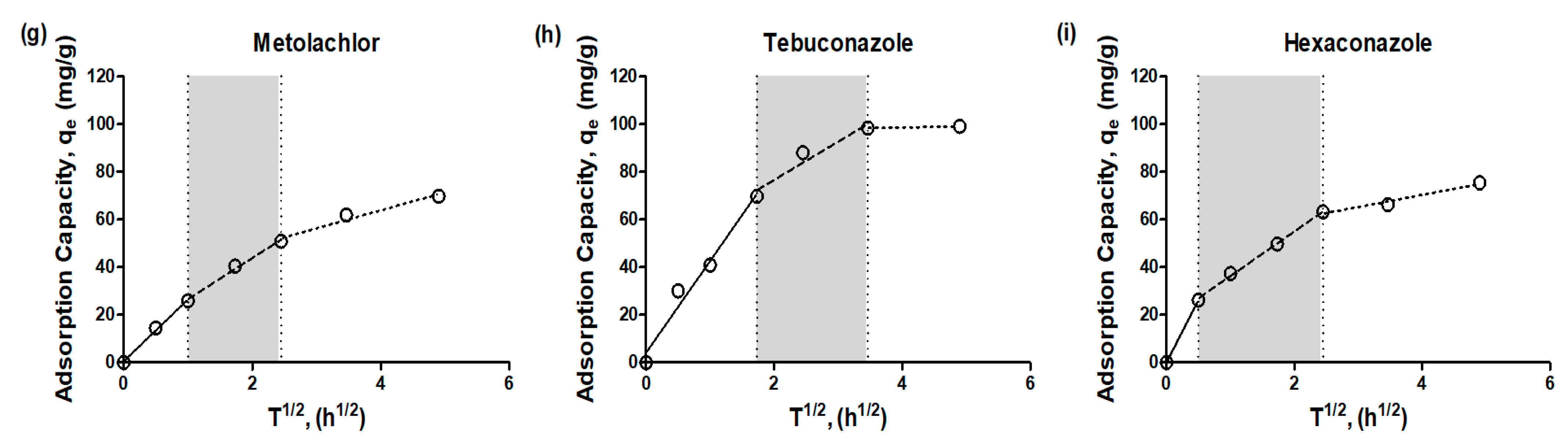
3.3. Diffusion Mechanism
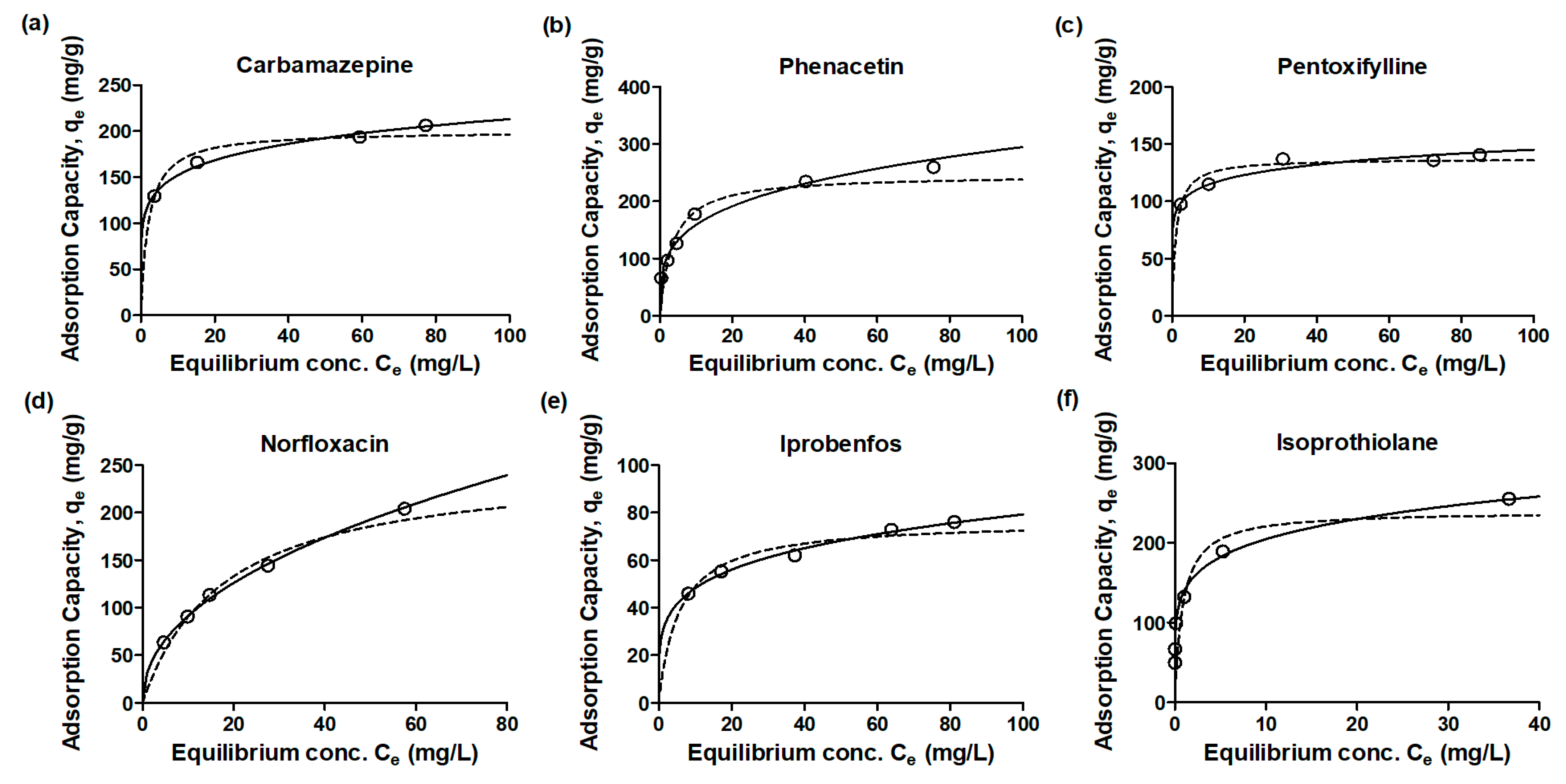
3.4. Equilibrium of Emerging Contaminants
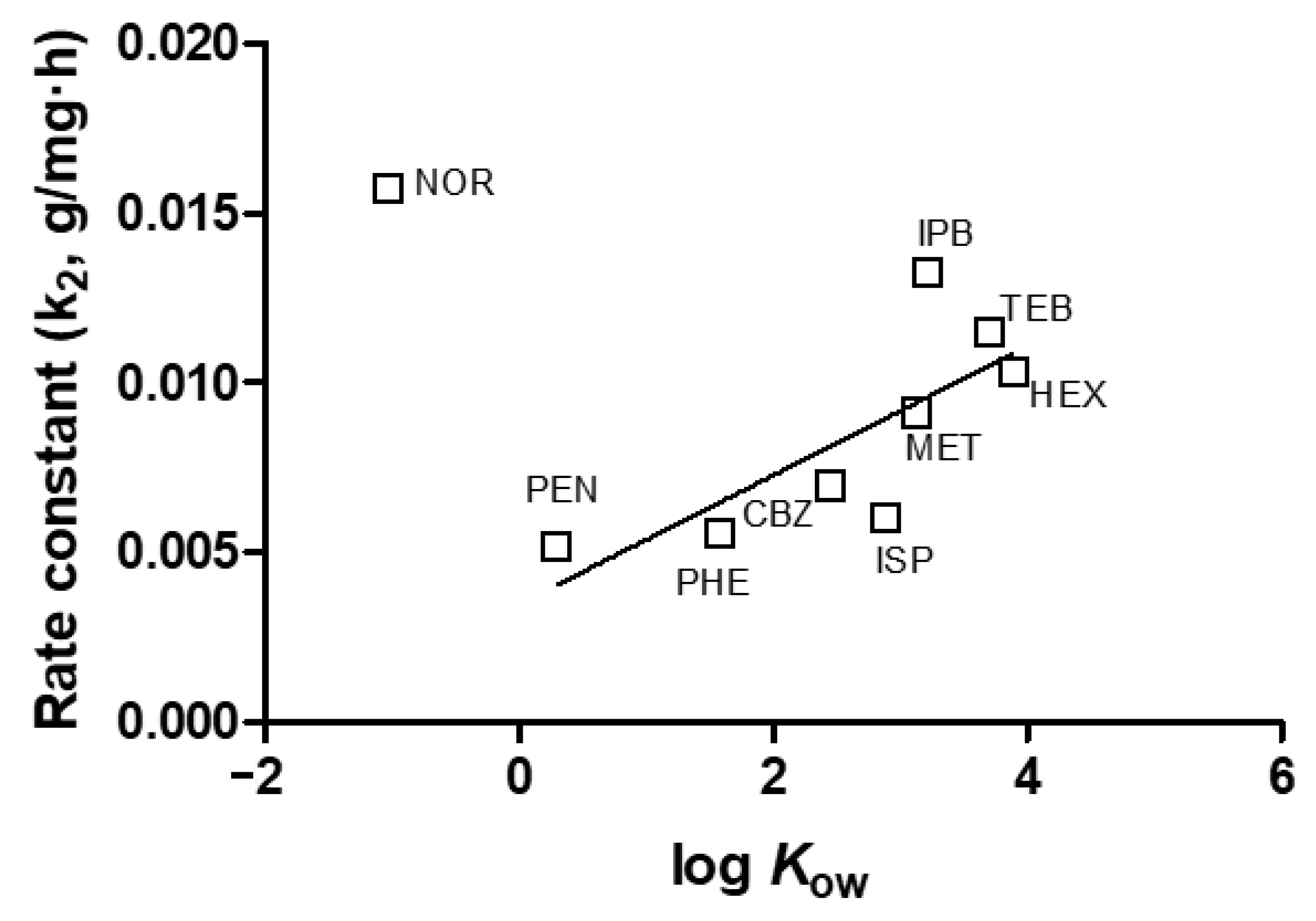
3.5. Relationship of between Emerging Contaminants and Adsorption
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Peldszus, S.; Huck, P.M. Adsorption characteristics of selected pharmaceuticals and an endocrine disrupting compound—Naproxen, carbamazepine and nonylphenol—On activated carbon. Water Res. 2008, 42, 2873–2882. [Google Scholar] [CrossRef] [PubMed]
- Farré, M.L.; Pérez, S.; Kantiani, L.; Barceló, D. Fate and toxicity of emerging pollutants, their metabolites and transformation products in the aquatic environment. TrAC Trends Anal. Chem. 2008, 27, 991–1007. [Google Scholar] [CrossRef]
- Daughton, C.G. Non-regulated water contaminants: Emerging research. Environ. Impact Assess. Rev. 2004, 24, 711–732. [Google Scholar] [CrossRef]
- Schriks, M.; Heringa, M.B.; van der Kooi, M.M.E.; de Voogt, P.; van Wezel, A.P. Toxicological relevance of emerging contaminants for drinking water quality. Water Res. 2010, 44, 461–476. [Google Scholar] [CrossRef] [PubMed]
- Bolong, N.; Ismail, A.F.; Salim, M.R.; Matsuura, T. A review of the effects of emerging contaminants in wastewater and options for their removal. Desal. 2009, 239, 229–246. [Google Scholar] [CrossRef]
- Comerton, A.M.; Andrews, R.C.; Bagley, D.M.; Yang, P. Membrane adsorption of endocrine disrupting compounds and pharmaceutically active compounds. J. Membr. Sci. 2007, 303, 267–277. [Google Scholar] [CrossRef]
- Rakić, V.; Rac, V.; Krmar, M.; Otman, O.; Auroux, A. The adsorption of pharmaceutically active compounds from aqueous solutions onto activated carbons. J. Hazard. Mater. 2015, 282, 141–149. [Google Scholar] [CrossRef]
- Rivera-Utrilla, J.; Sánchez-Polo, M.; Ferro-García, M.Á.; Prados-Joya, G.; Ocampo-Pérez, R. Pharmaceuticals as emerging contaminants and their removal from water. A review. Chemosphere 2013, 93, 1268–1287. [Google Scholar] [CrossRef]
- Rosal, R.; Rodríguez, A.; Perdigón-Melón, J.A.; Petre, A.; García-Calvo, E.; Gómez, M.J.; Agüera, A.; Fernández-Alba, A.R. Occurrence of emerging pollutants in urban wastewater and their removal through biological treatment followed by ozonation. Water Res. 2010, 44, 578–588. [Google Scholar] [CrossRef]
- Rodriquez-Narvaez, O.M.; Peralta-Hernandez, J.M.; Goonetilleke, A.; Bandala, E.R. Treatment technologies for emerging contaminants in water: A review. Chem. Eng. J. 2017, 323, 361–380. [Google Scholar] [CrossRef]
- Ho, Y.S.; McKay, G. Sorption of dye from aqueous solution by peat. Chem. Eng. J. 1998, 70, 115–124. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solution. J. Sanit. Eng. Div. 1963, 89, 31–60. [Google Scholar] [CrossRef]
- Tan, I.A.W.; Hameed, B.H.; Ahmad, A.L. Equilibrium and kinetic studies on basic dye adsorption by oil palm fibre activated carbon. Chem. Eng. J. 2007, 127, 111–119. [Google Scholar] [CrossRef]
- Tseng, R.-L.; Wu, F.-C. Inferring the favorable adsorption level and the concurrent multi-stage process with the freundlich constant. J. Hazard. Mater. 2008, 155, 277–287. [Google Scholar] [CrossRef]
- Khan, M.A.; Lee, S.-H.; Kang, S.; Paeng, K.-J.; Lee, G.; Oh, S.-E.; Jeon, B.-H. Adsorption studies for the removal of methyl tert-butyl ether on various commercially available gacs from an aqueous medium. Sep. Sci. Technol. 2011, 46, 1121–1130. [Google Scholar] [CrossRef]
- Lu, S.; Song, Z.; He, J. Diffusion-controlled protein adsorption in mesoporous silica. J. Phys. Chem. B 2011, 115, 7744–7750. [Google Scholar] [CrossRef]
- Gao, Q.; Zhu, H.; Luo, W.-J.; Wang, S.; Zhou, C.-G. Preparation, characterization, and adsorption evaluation of chitosan-functionalized mesoporous composites. Microporous Mesoporous Mater. 2014, 193, 15–26. [Google Scholar] [CrossRef]
- Vinhal, J.O.; Lage, M.R.; Carneiro, J.W.M.; Lima, C.F.; Cassella, R.J. Modeling, kinetic, and equilibrium characterization of paraquat adsorption onto polyurethane foam using the ion-pairing technique. J. Environ. Manag. 2015, 156, 200–208. [Google Scholar] [CrossRef]
- Saeed, M.M.; Rusheed, A.; Ahmed, N. Modeling of iron adsorption on htta-loaded polyurethane foam using freundlich, langmuir and d-r isotherm expressions. J. Radioanal. Nucl. Chem. 1996, 211, 283–292. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Rogers, H.R. Sources, behaviour and fate of organic contaminants during sewage treatment and in sewage sludges. Sci. Total Environ. 1996, 185, 3–26. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, A.I.; Akanyeti, I.; Semião, A.J.C. Micropollutant sorption to membrane polymers: A review of mechanisms for estrogens. Adv. Colloid Interface Sci. 2011, 164, 100–117. [Google Scholar] [CrossRef]
- Boyd, G.R.; Reemtsma, H.; Grimm, D.A.; Mitra, S. Pharmaceuticals and personal care products (ppcps) in surface and treated waters of Louisiana, USA and Ontario, Canada. Sci. Total Environ. 2003, 311, 135–149. [Google Scholar] [CrossRef] [PubMed]
- Loraine, G.A.; Pettigrove, M.E. Seasonal variations in concentrations of pharmaceuticals and personal care products in drinking water and reclaimed wastewater in southern california. Environ. Sci. Technol. 2006, 40, 687–695. [Google Scholar] [CrossRef] [PubMed]
- Ternes, T.A.; Meisenheimer, M.; McDowell, D.; Sacher, F.; Brauch, H.-J.; Haist-Gulde, B.; Preuss, G.; Wilme, U.; Zulei-Seibert, N. Removal of pharmaceuticals during drinking water treatment. Environ. Sci. Technol. 2002, 36, 3855–3863. [Google Scholar] [CrossRef]
- Vieno, N.M.; Härkki, H.; Tuhkanen, T.; Kronberg, L. Occurrence of pharmaceuticals in river water and their elimination in a pilot-scale drinking water treatment plant. Environ. Sci. Technol. 2007, 41, 5077–5084. [Google Scholar] [CrossRef]
- Westerhoff, P.; Yoon, Y.; Snyder, S.; Wert, E. Fate of endocrine-disruptor, pharmaceutical, and personal care product chemicals during simulated drinking water treatment processes. Environ. Sci. Technol. 2005, 39, 6649–6663. [Google Scholar] [CrossRef]


| Compound Type | Compound (CAS-RN) | Classification | Chemical Formula | Chemical Structure | MOL. MASS | log Kow | pKa |
|---|---|---|---|---|---|---|---|
| Pharmaceutical compounds | Carbamazepine (298-46-4) | Antiepileptic | C15H12N2O |  | 236.27 | 2.45 | 2.3 |
| Phenacetin (62-44-2) | Pain-relieving, Fever-reducing | C10H13NO2 | 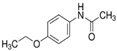 | 179.22 | 1.58 | 2.1 | |
| Pentoxifylline (6493-05-6) | Circulation problem-reducing | C13H18N4O3 | 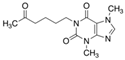 | 278.31 | 0.29 | 0.97 | |
| Norfloxacin (70458-96-7) | Antibiotic | C16H18FN3O3 | 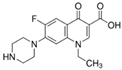 | 319.33 | −1.03 | 6.22 | |
| Pesticide compounds | Iprobenfos (26087-47-8) | Fungicide | C11H17O3PS | 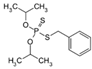 | 260.29 | 3.21 | −8.2 |
| Isoprothiolane (50512-35-1) | Fungicide, Insecticide | C12H18O4S2 |  | 290.40 | 2.88 | −7 | |
| Metolachlor (87392-12-9) | Herbicide | C15H22ClNO2 |  | 283.79 | 3.13 | −1.34 | |
| Tebuconazole (107534-96-3) | Fungicides | C16H22ClN3O | 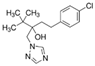 | 307.82 | 3.70 | 2.3 | |
| Hexaconazole (79983-71-4) | Fungicide | C14H17Cl2N3O | 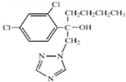 | 314.21 | 3.90 | 2.3 |
| Characteristics | Norit 1240 |
|---|---|
| Source material | Bituminous coal |
| BET Surface area (m2/g) | 930.4871 |
| Micro-pore Surface area (m2/g) | 676.0105 |
| Total pore volume (cm3/g) | 0.5710 |
| Micro-pore volume (cm3/g) | 0.3113 |
| Adsorption average pore width (nm) | 2.4546 |
| BJH Adsorption average pore diameter (nm) | 3.9258 |
| BJH Desorption average pore diameter (nm) | 4.1566 |
| Granulation (mm) | 0.4–1.7 |
| Methylene blue (mL/g) | 153.44 ± 0.76 |
| Iodine number (mg/g) | 680.63 ± 12.10 |
| Hardness (%) | >95% |
| pHpzc | 10.0 |
| Initial Concentration (mg/L) | qe,exp (mg/g) | Pseudo First Order Kinetic Model | Pseudo Second Order Kinetic Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| qe,cal (mg/g) | k1 (h) | r2 | qe,cal (mg/g) | k2 × 103 (g/mg·h) | Initial Sorption Rate (g/mg·h) | r2 | |||
| Carbamazepine | 100 | 97.66 | 89.45 | 0.3104 | 0.9935 | 106.11 | 6.962 | 78.39 | 0.9934 |
| Phenacetin | 100 | 97.91 | 90.03 | 0.403 | 0.9850 | 106.52 | 5.568 | 63.19 | 0.9912 |
| Pentoxifylline | 100 | 97.75 | 82.92 | 0.1725 | 0.9735 | 103.13 | 5.197 | 55.27 | 0.9981 |
| Norfloxacin | 100 | 77.32 | 48.66 | 0.2463 | 0.8440 | 79.59 | 15.726 | 99.61 | 0.9987 |
| Iprobenfos | 100 | 80.03 | 59.45 | 0.2343 | 0.9526 | 82.39 | 13.252 | 89.95 | 0.9992 |
| Isoprothiolane | 100 | 99.29 | 106.23 | 0.4193 | 0.9847 | 106.77 | 6.003 | 68.44 | 0.9974 |
| Metolachlor | 100 | 69.77 | 56.69 | 0.1709 | 0.9740 | 72.36 | 9.108 | 47.70 | 0.9947 |
| Tebuconazole | 100 | 99.07 | 91.05 | 0.3903 | 0.9931 | 102.67 | 11.504 | 121.27 | 0.9982 |
| Hexaconazole | 100 | 75.37 | 49.83 | 0.1636 | 0.8609 | 77.75 | 10.312 | 62.33 | 0.9957 |
| First Stage (Outer Diffusion) | Second Stage (Inner Diffusion) | Third Stage (Adsorption Equilibrium) | ||||
|---|---|---|---|---|---|---|
| Ki,1 (mg/g·h1/2) | r2 | Ki,2 (mg/g·h1/2) | r2 | Ki,3 (mg/g·h1/2) | r2 | |
| Carbamazepine | 41.91 | 0.9779 | 15.02 | 0.9552 | 1.631 | 1.0000 |
| Phenacetin | 39.61 | 0.9700 | 4.317 | 1.0000 | 0.6133 | 1.0000 |
| Pentoxifylline | 33.22 | 0.9870 | 17.54 | 0.9882 | 8.022 | 1.0000 |
| Norfloxacin | 40.96 | 0.9722 | 3.394 | 0.9577 | - | - |
| Iprobenfos | 36.41 | 0.9973 | 22.99 | 0.9958 | 4.136 | 0.9688 |
| Isoprothiolane | 35.17 | 0.9989 | 11.72 | 1.0000 | 0.3833 | 1.0000 |
| Metolachlor | 25.94 | 0.9956 | 17.21 | 0.9924 | 7.565 | 0.9632 |
| Tebuconazole | 38.50 | 0.9734 | 16.06 | 0.9357 | 0.5157 | 1.0000 |
| Hexaconazole | 52.42 | 1.0000 | 18.66 | 0.9976 | 5.064 | 0.9679 |
| qe,exp (mg/g) | Langmuir Model | Freundlich Model | |||||
|---|---|---|---|---|---|---|---|
| qe,cal (mg/g) | bL (L/mg) | r2 | KF (mg/g) (L/mg)1/n | n | r2 | ||
| Carbamazepine | 206.34 | 200.08 | 0.495 | 0.9574 | 108.671 | 6.839 | 0.9901 |
| Phenacetin | 248.89 | 245.87 | 0.293 | 0.9658 | 86.011 | 3.739 | 0.9827 |
| Pentoxifylline | 140.83 | 137.27 | 0.957 | 0.9187 | 90.447 | 9.734 | 0.9411 |
| Norfloxacin | 204.16 | 251.51 | 0.056 | 0.9878 | 31.538 | 2.162 | 0.9980 |
| Iprobenfos | 76.05 | 76.45 | 0.177 | 0.9443 | 29.365 | 4.640 | 0.9905 |
| Isoprothiolane | 255.36 | 239.70 | 1.162 | 0.9537 | 139.324 | 5.976 | 0.9905 |
| Metolachlor | 97.44 | 125.59 | 0.042 | 0.9867 | 13.949 | 2.170 | 0.9848 |
| Tebuconazole | 215.52 | 181.02 | 8.725 | 0.8769 | 123.187 | 5.809 | 0.9623 |
| Hexaconazole | 158.56 | 170.79 | 0.030 | 0.9658 | 10.088 | 1.647 | 0.9715 |
| Compound | Octanol-Water Partition Coefficient (log Kow) | Acid Dissociation Constant (pKa) | Maximum Adsorption Capacity (qmax; mg/g) | Pseudo-2nd-Order Rate Constant (k2; g/mg·h) |
|---|---|---|---|---|
| Carbamazepine | 2.45 | 2.3 | 206.34 | 0.0070 |
| Phenacetin | 1.58 | 2.1 | 248.89 | 0.0056 |
| Pentoxifylline | 0.29 | 0.97 | 140.83 | 0.0052 |
| Norfloxacin | −1.03 | 6.22 | 204.16 | 0.0157 |
| Iprobenfos | 3.21 | −8.2 | 76.05 | 0.0133 |
| Isoprothiolane | 2.88 | −7 | 255.36 | 0.0060 |
| Metolachlor | 3.13 | −1.34 | 97.44 | 0.0091 |
| Tebuconazole | 3.7 | 2.3 | 215.52 | 0.0115 |
| Hexaconazole | 3.9 | 2.3 | 158.56 | 0.0103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-H.; Kim, N.; Park, D. Insights into the Adsorption Performance of Emerging Contaminants on Granular Activated Carbon. Separations 2023, 10, 501. https://doi.org/10.3390/separations10090501
Lee S-H, Kim N, Park D. Insights into the Adsorption Performance of Emerging Contaminants on Granular Activated Carbon. Separations. 2023; 10(9):501. https://doi.org/10.3390/separations10090501
Chicago/Turabian StyleLee, Sang-Hoon, Namgyu Kim, and Donghee Park. 2023. "Insights into the Adsorption Performance of Emerging Contaminants on Granular Activated Carbon" Separations 10, no. 9: 501. https://doi.org/10.3390/separations10090501
APA StyleLee, S.-H., Kim, N., & Park, D. (2023). Insights into the Adsorption Performance of Emerging Contaminants on Granular Activated Carbon. Separations, 10(9), 501. https://doi.org/10.3390/separations10090501







