Theoretical Calculations and Experimental Investigation of Separation of Dy3+, Er3+, Tm3+ and Yb3+ by Cascade Extraction in TOGDA–Kerosene/Hydrochloric Acid System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents and Materials
2.2. Experimental Methods
2.2.1. Liquid–Liquid Extraction
2.2.2. Saturation Concentrations of Dy3+, Er3+, Tm3+ and Yb3+ in TODGA–Kerosene Medium
2.2.3. Theoretical Calculations and Experimental Validation of Cascade Extraction
3. Results and Discussion
3.1. Distribution Ratios of Dy3+, Er3+, Tm3+ and Yb3+ in the TODGA–Kerosene/Hydrochloric Acid System
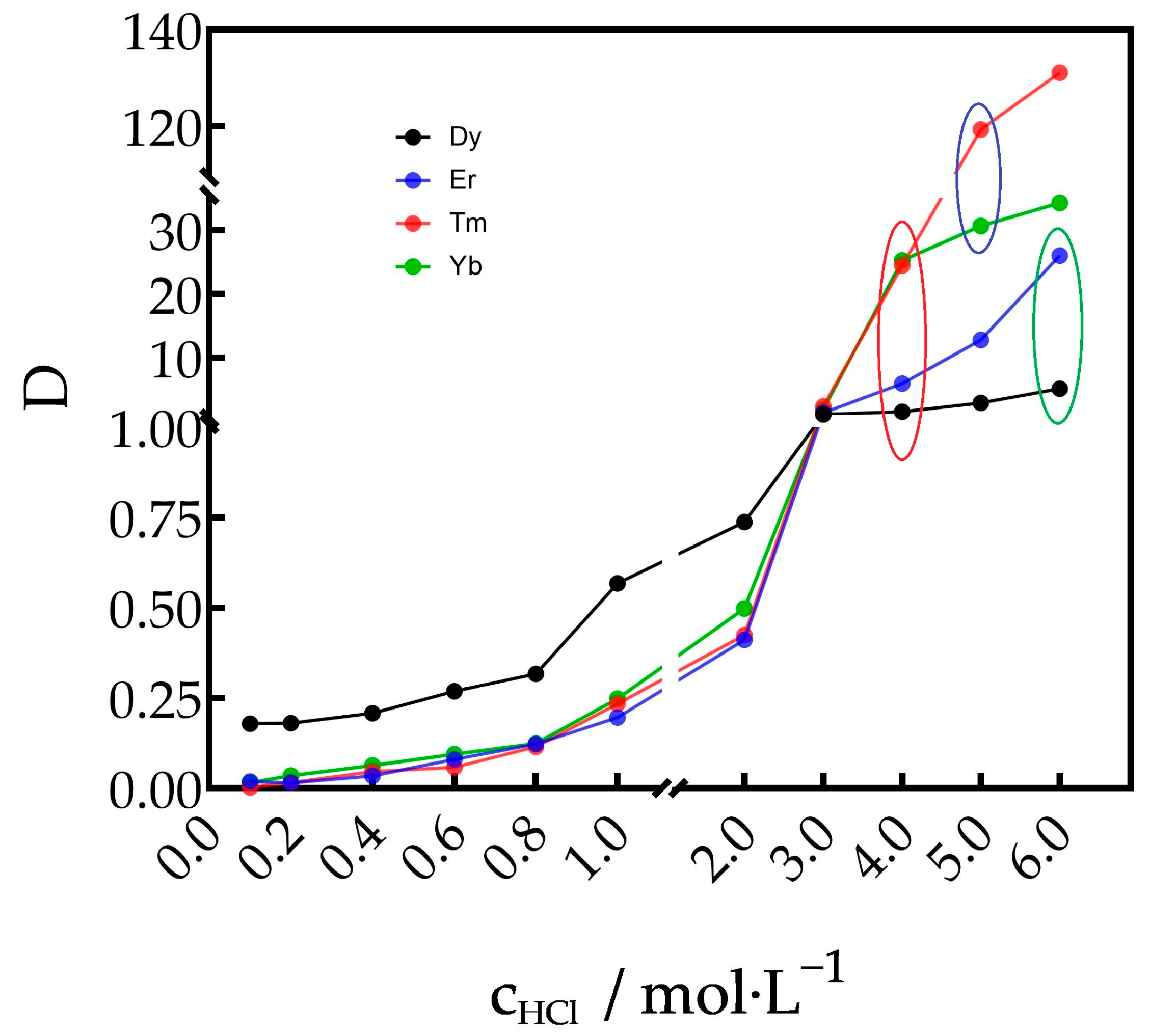
3.1.1. Effect of Acid Concentration
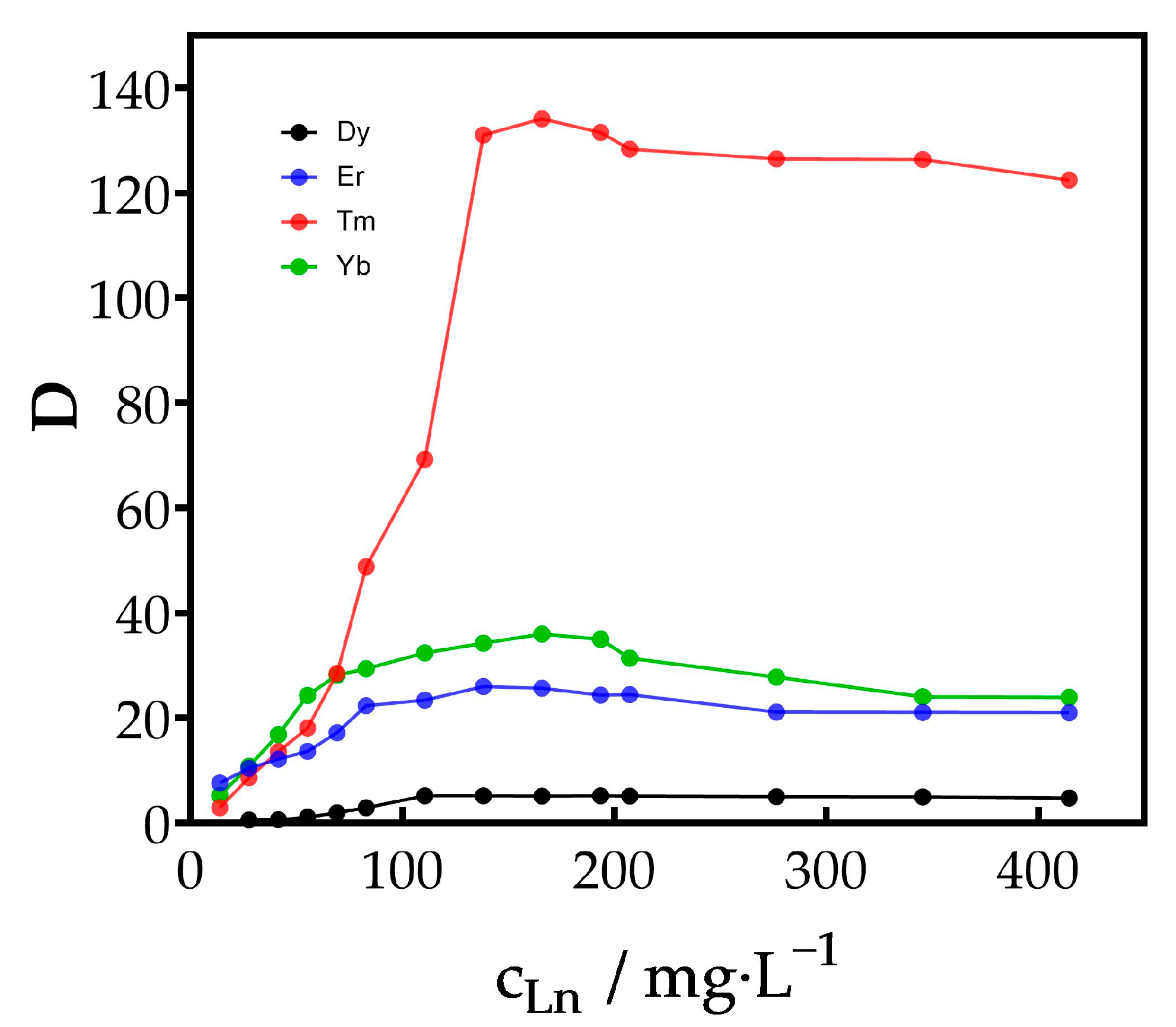
3.1.2. Effect of REE Concentration
3.1.3. Effect of Extraction Temperature
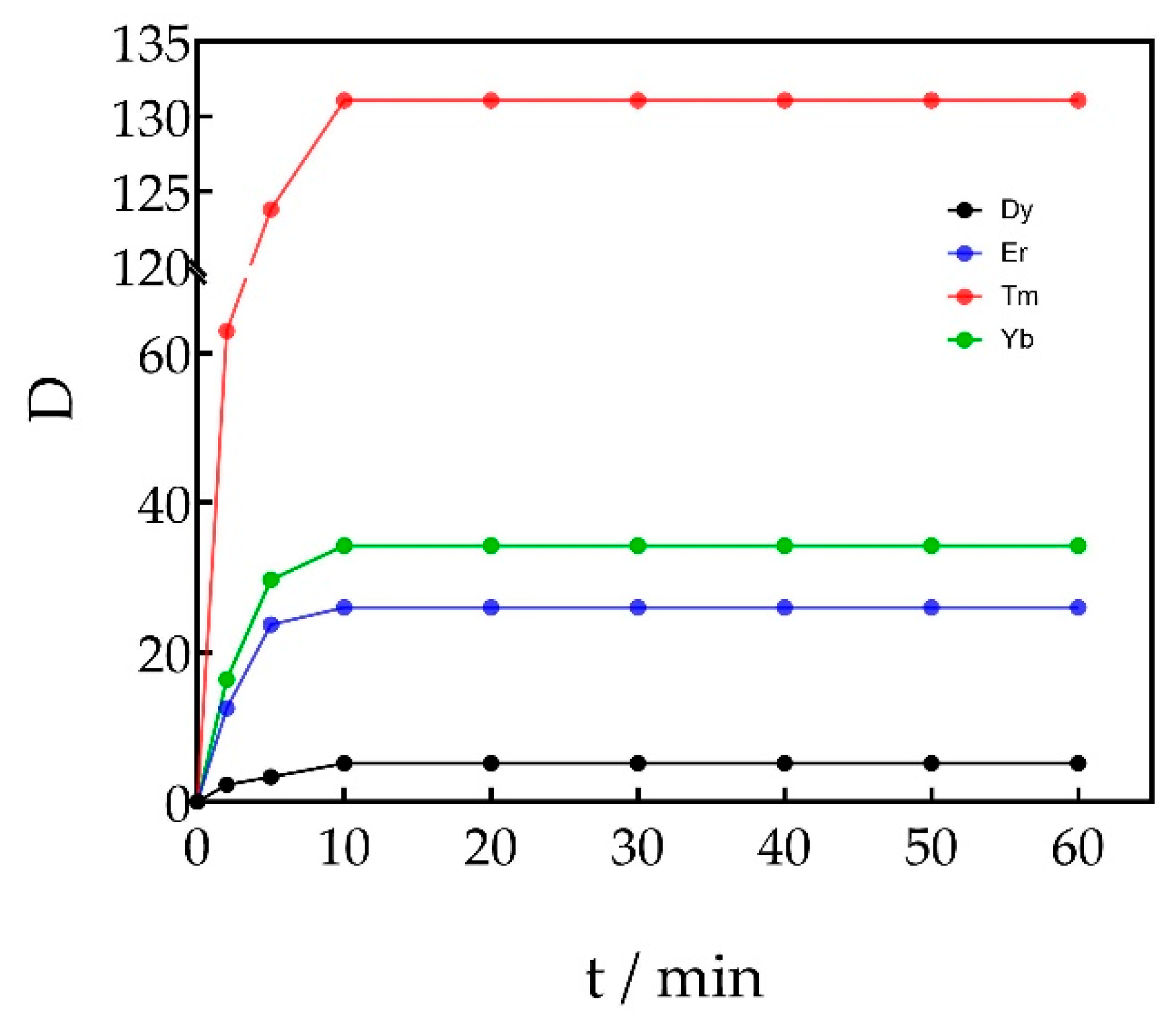
3.1.4. Effect of Extraction Time
3.1.5. Determination of the Process Flow for the Separation of Dy3+, Er3+, Tm3+ and Yb3+ by Fractional Extraction with TODGA
3.2. Saturation Concentrations of Dy3+, Er3+, Tm3+ and Yb3+ in TODGA–Kerosene Medium
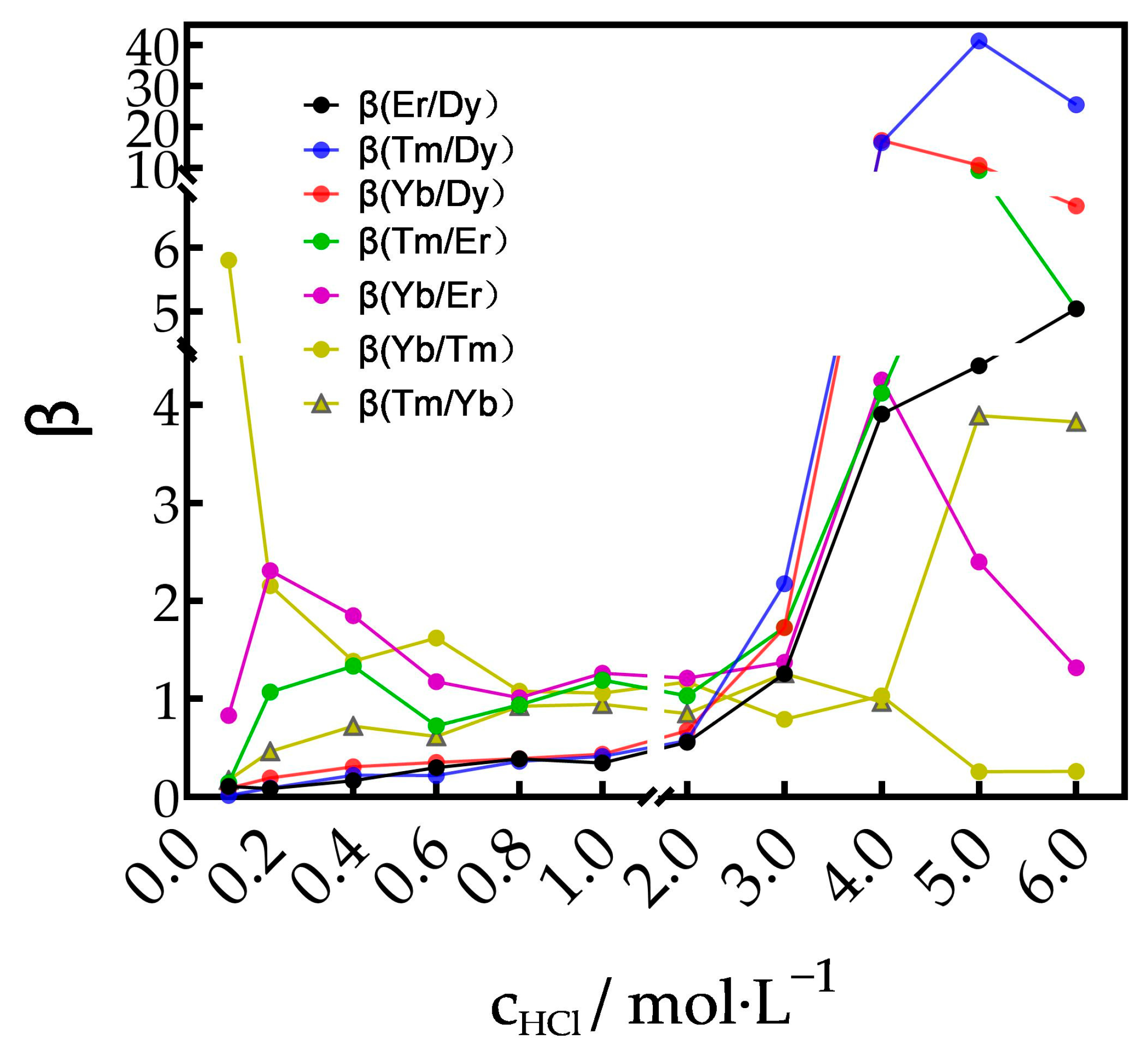
3.3. Theoretical Calculation of Separation Parameters of REEs Using TODGA as Extractant
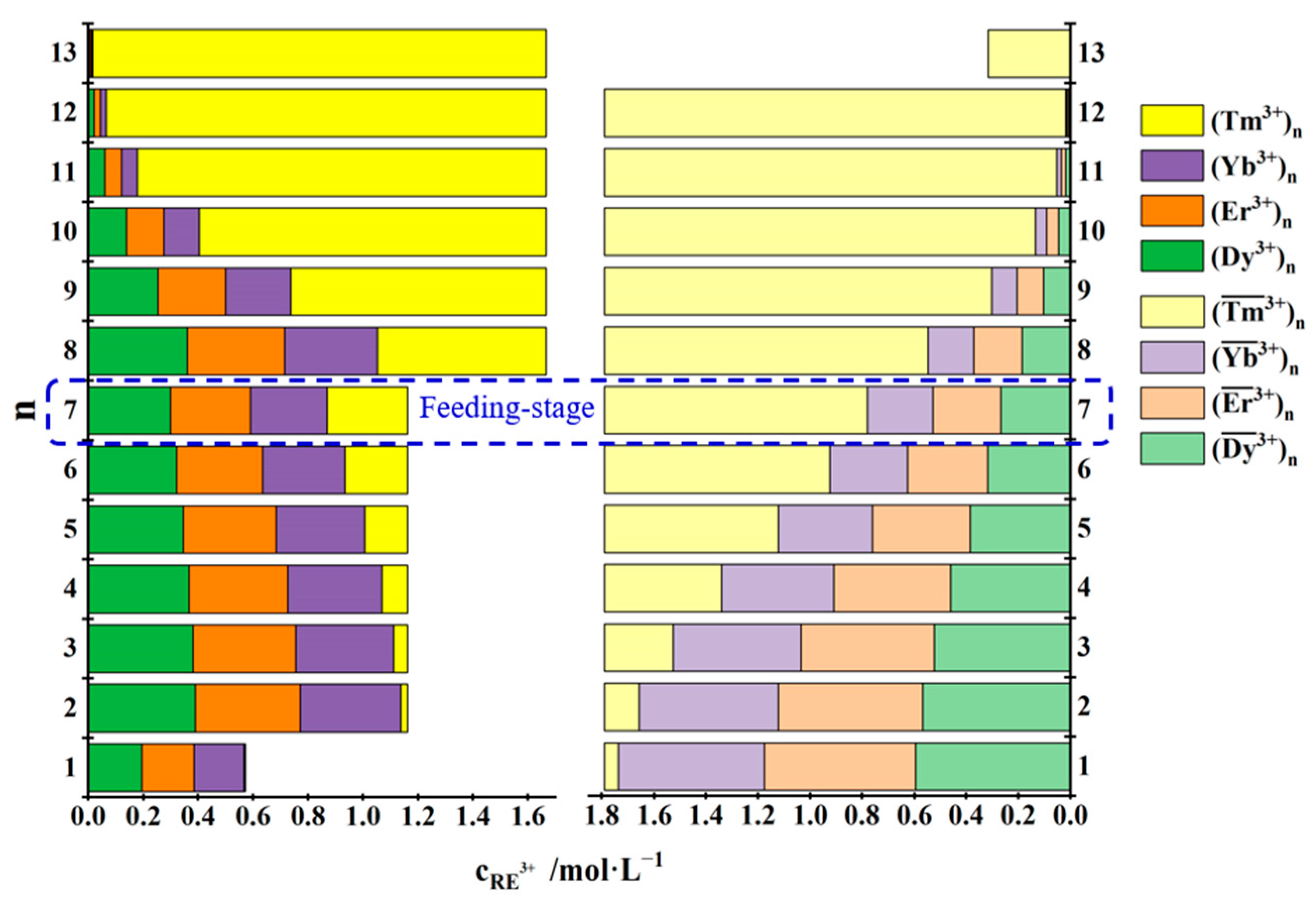
3.3.1. Separation of Tm3+ from Dy3+, Er3+, Tm3+ and Yb3+ Mixtures
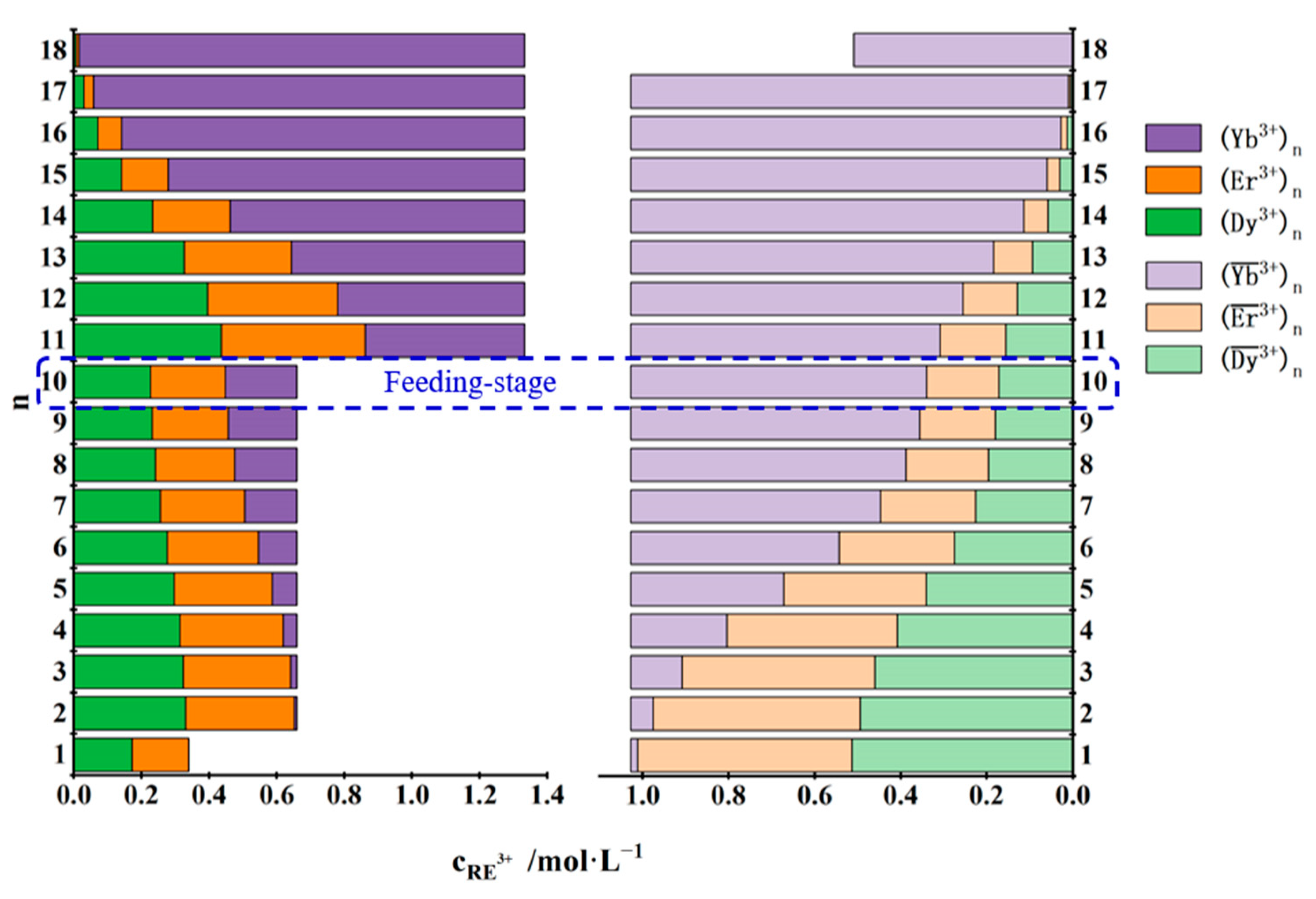
3.3.2. Separation of Yb3+ from Dy3+, Er3+ and Yb3+ Mixtures
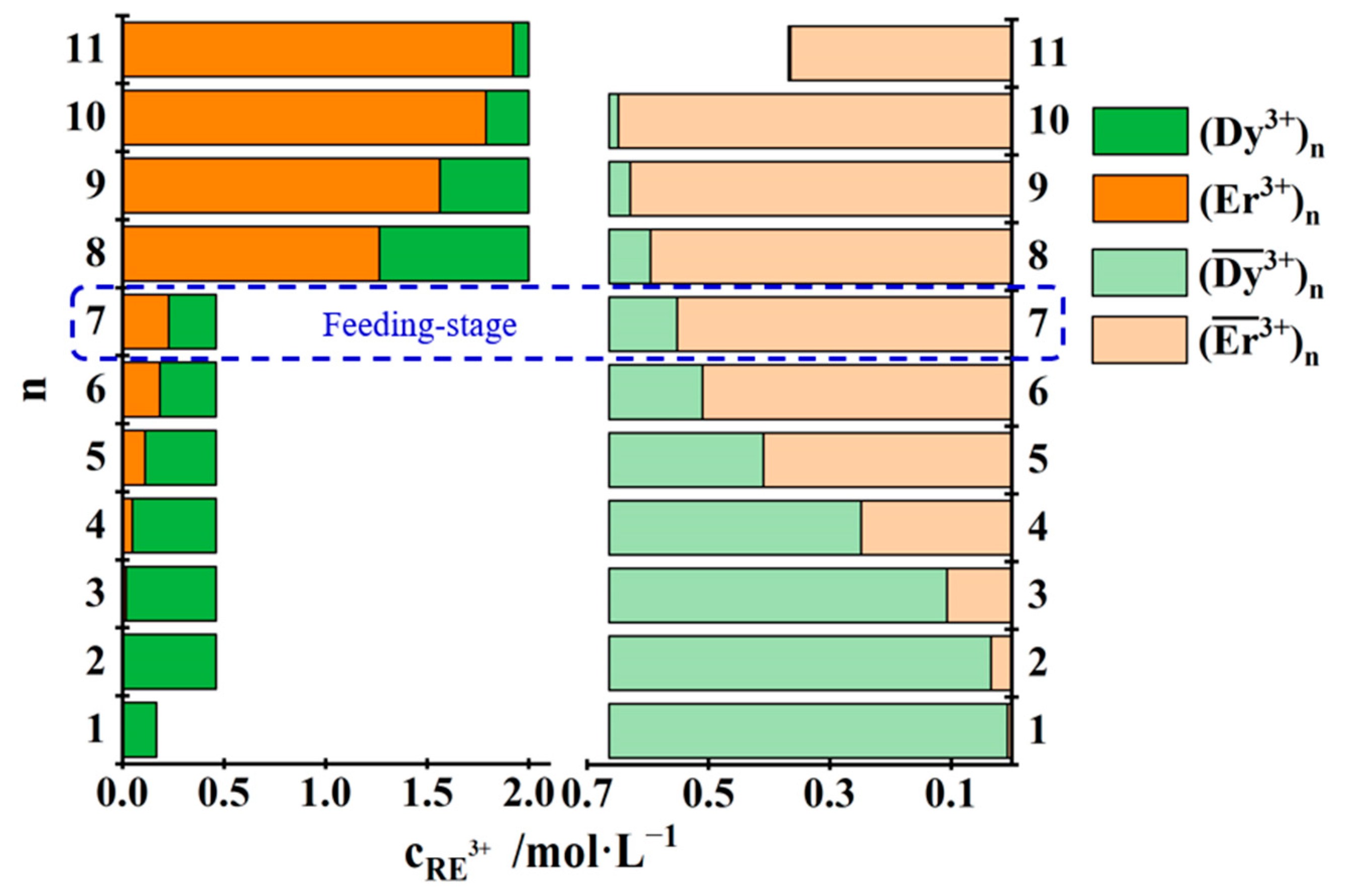
3.3.3. Separation of Yb3+ from Dy3+ and Er3+ Mixtures
3.4. The Mechanism of Separation of Dy3+, Er3+, Tm3+ and Yb3+ Using TODGA as Extractant
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| CN | La | Ce | Pr | Nd | Pm | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 2.303 | 2.255 | 2.256 | 2.227 | 2.214 | 2.201 | 2.161 | 2.139 | 2.124 | 2.106 | 2.138 | 2.053 | 2.079 | 2.067 | 2.060 |
| 7 | 2.243 | 2.206 | 2.199 | 2.201 | 2.180 | 2.158 | 2.066 | 2.154 | 2.121 | 2.095 | 2.047 | 2.080 | 2.068 | 2.041 | 2.018 |
| 8 | 2.222 | 2.236 | 2.184 | 2.185 | 2.173 | 2.160 | 2.144 | 2.115 | 2.098 | 2.101 | 2.117 | 2.084 | 2.067 | 2.049 | 2.054 |
| 9 | 2.261 | 2.244 | 2.224 | 2.177 | 2.169 | 2.161 | 2.165 | 2.160 | 2.137 | 2.138 | 2.126 | 2.101 | 2.087 | 2.109 | 2.082 |
| 10 | 2.260 | 2.240 | 2.218 | 2.221 | 2.200 | 2.178 | 2.197 | 2.174 | 2.179 | 2.147 | 2.148 | 2.134 | 2.139 | 2.114 | 2.084 |
| 11 | 2.303 | 2.266 | 2.225 | 2.331 | 2.289 | 2.246 | 2.215 | 2.184 | 2.181 | 2.165 | 2.154 | 2.139 | 2.127 | 2.120 | 2.098 |
| 12 | 2.316 | 2.321 | 2.246 | 2.297 | 2.280 | 2.262 | 2.258 | 2.208 | 2.211 | 2.196 | 2.185 | 2.173 | 2.158 | 2.155 | 2.132 |
| mean | 2.261 | 2.254 | 2.215 | 2.201 | 2.215 | 2.171 | 2.161 | 2.146 | 2.130 | 2.124 | 2.118 | 2.086 | 2.082 | 2.064 | 2.046 |
| k | j | ||||
| O | N | C | S | Cl | |
| O | 0.0 | −0.015 | −0.176 | 0.418 | 0.400 |
| 1.0 | 1.064 | 1.124 | 1.026 | 1.009 | |
| N | 0.045 | 0.0 | −0.142 | 0.457 | 0.437 |
| 0.925 | 1.0 | 1.047 | 0.953 | 0.937 | |
| C | 0.197 | 0.181 | 0.0 | 0.613 | 0.589 |
| 0.871 | 0.933 | 1.0 | 0.897 | 0.882 | |
| S | −0.400 | −0.450 | −0.637 | 0.0 | −0.019 |
| 0.971 | 1.037 | 1.096 | 1.0 | 0.985 | |
| Cl | −0.335 | −0.381 | −0.565 | 0.060 | 0.0 |
| 0.967 | 1.033 | 1.092 | 0.998 | 1.0 | |
| Symbols | Name | Unit |
|---|---|---|
| Mass flow rate of aqueous phase A | mol·min−1 | |
| Mass flow rate of organic phase A | mol·min−1 | |
| Mass flow rate of A in the aqueous phase feed solution | mol·min−1 | |
| Concentration of A in the aqueous phase feed solution | mol·L−1 | |
| Purification factor of groups A | ||
| Mass flow rate of aqueous phase B | mol·min−1 | |
| Mass flow rate of organic phase B | mol·min−1 | |
| Mass flow rate of B in the aqueous phase feed solution | mol·min−1 | |
| Concentration of B in the aqueous phase feed solution | mol·L−1 | |
| Purification factor of groups B | ||
| Average distribution ratio of component A in extraction section | ||
| Average distribution ratio of component B in extraction section | ||
| Average separation factor in extraction section | ||
| Average separation factor in scrubbing section | ||
| Phase ratio | ||
| Average extraction ratio of component A in extraction section | ||
| Average extraction ratio of component B in extraction section | ||
| Average extraction ratio of component A in scrubbing section | ||
| Average extraction ratio of component B in scrubbing section | ||
| Average mixed extraction ratio in extraction section | ||
| Average mixed extraction ratio in scrubbing section | ||
| Molar fraction of A in the feed solution | ||
| Organic phase outlet fraction | ||
| Molar fraction of B in the feed solution | ||
| Aqueous phase outlet fraction | ||
| Mass flow rate of organic phase feed solution | mol·min−1 | |
| Mass flow rate of aqueous phase feed solution | mol·min−1 | |
| Scrubbing stage number (excluding feed stage) | ||
| Extraction stage number (including feed stage) | ||
| Purity of component A in organic phase export products | ||
| Purity of component B in aqueous phase export products | ||
| Maximum extraction mass flow | mol·min−1 | |
| Volume flow rate of feed solution | ml·min−1 | |
| Volume flow rate of organic solution | ml·min−1 | |
| Volume flow rate of scrubbing solution | ml·min−1 | |
| Maximum scrubbing mass flow | mol·min−1 | |
| Yield of component A | ||
| Yield of component B | ||
| Concentrations of the raffinate aqueous phase | mol·L−1 |
References
- Voncken, J.H.L. The Rare Earth Elements: An Introduction; Springer: New York, NY, USA, 2016. [Google Scholar]
- Lima, I.B.D.; Filho, W.L. Rare Earths Industry: Technological, Economic, and Environmental Implications; Elsevier: New York, NY, USA, 2016. [Google Scholar]
- Goodenough, K.M.; Wall, F. The Rare Earth Elements: Demand, Global Resources, and Challenges for Resourcing Future Generations. Nat. Resour. Res. 2018, 27, 201–216. [Google Scholar] [CrossRef]
- Chen, L.Y.; Deng, B.C.; Kuang, S.T.; Liao, W.P. Efficient extraction and separation of heavy rare earths from chloride medium with N, N′-di(2-ethylhexyl)aminomethyl phosphonic acid mono-2-ethylhexyl ester. Hydrometallurgy 2023, 222, 106173. [Google Scholar] [CrossRef]
- Nemova, G. Radiation-balanced lasers: History, status, potential. Appl. Sci. 2021, 11, 7539. [Google Scholar] [CrossRef]
- Starecki, F.; Braud, A.; Doualan, J.-L.; Ari, J.; Boussard-Pl’edel, C.; Michel, K.; Nazabal, V.; Camy, P. All-optical carbon dioxide remote sensing using rare earth doped chalcogenide fibers. Opt. Lasers Eng. 2019, 122, 328–334. [Google Scholar] [CrossRef]
- Akatsuka, M.; Nakauchi, D.; Kato, T.; Kawaguchi, N.; Yanagida, T. Optical and scintillation properties of YAlO3 doped with rare-earths emitting near-infrared photons. Sens. Mater. 2020, 32, 1373–1380. [Google Scholar] [CrossRef]
- Pinto, I.C.; Rivera, V.A.G.; Falci, R.; Fuertes, V.; LaRochelle, S.; Messaddeq, Y. Tailoring near-infrared luminescence with Er3+/Tm3+/Yb3+ tri-doped tellurite glasses for applications in the C, L and U bands. J. Lumin. 2024, 265, 120206. [Google Scholar] [CrossRef]
- El Ouardi, Y.; Virolainen, S.; Mouele, E.S.M.; Laatikainen, M.; Repo, E.; Laatikainen, K. The recent progress of ion exchange for the separation of rare earths from secondary resources–A review. Hydrometallurgy 2023, 218, 106047. [Google Scholar] [CrossRef]
- Liu, T.C.; Chen, J. Extraction and separation of heavy rare earth elements: A review. Sep. Purif. Technol. 2021, 276, 119263. [Google Scholar] [CrossRef]
- Turra, C. Sustainability of Rare Earth Elements Chain: From Production to Food—A Review. Int. J. Environ. Health Res. 2018, 28, 23–42. [Google Scholar] [CrossRef]
- Krishnamurthy, N.; Gupta, C.K. Extractive Metallurgy of Rare Earth Elements; CRC Press: New York, NY, USA, 2016. [Google Scholar]
- Gschneidner, K.A.; Bünzli, J.C.G.; Pecharsky, V.K. Handbook on the Physics and Chemistry of Rare Earths; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Kuang, S.T.; Liao, W.P. Progress in the Extraction and Separation of Rare Earths and Related Metals with Novel Extractants: A Review. Sci. China Technol. Sci. 2018, 61, 1319–1328. [Google Scholar] [CrossRef]
- Li, D.Q. Development Course of Separating Rare Earths with Acid Phosphorus Extractants: A Critical Review. J. Rare Earths 2018, 37, 468–486. [Google Scholar] [CrossRef]
- Dong, Y.M.; Sun, X.Q.; Wang, Y.L.; Chai, Y.J. The development of an extraction strategy based on EHEHP-type functional ionic liquid for heavy rare earth element separation. Hydrometallurgy 2015, 157, 256–260. [Google Scholar] [CrossRef]
- Wang, W.; Yang, H.L.; Cui, H.M.; Zhang, D.L.; Liu, Y.; Chen, J. Application of bifunctionalionic liquid extractants [A336][CA-12] and [A336][CA-100] to the lanthanum extraction and separation from rare earths in the chloride medium. Ind. Eng. Chem. Res. 2021, 50, 7534–7541. [Google Scholar] [CrossRef]
- Gupta, C.K.; Krishnamurthy, N. Extractive Metallurgy of Rare-Earths; CRC: Boca Raton, FL, USA, 2004; p. 15. [Google Scholar]
- Abreu, R.D.; Morais, C.A. Study on separation of heavy rare earth elements by solvent extraction with organophosphorus acids and amine reagents. Miner. Eng. 2014, 61, 82–87. [Google Scholar] [CrossRef]
- Zhang, X.F.; Li, D.Q. Extraction of rare-earth ions (III) with bis(2,4,4-trimethylpentyl) phosphinic acid. Chin. J. Appl. Chem. 1993, 10, 72–74. [Google Scholar]
- Zhang, C.; Wang, L.S.; Huang, X.W.; Dong, J.S.; Long, Z.Q.; Zhang, Y.Q. Yttrium extraction from chloride solution with a synergistic system of 2-ethylhexyl phosphonic acid mono-(2-ethylhexyl) ester and bis(2,4,4trimethylpentyl) phosphinic acid. Hydrometallurgy 2014, 147–148, 7–12. [Google Scholar] [CrossRef]
- Wang, X.L.; Li, W.; Li, D.Q. Extraction and stripping of REs using mixtures of acidic phosphorus based reagents. J. Res. 2011, 29, 413–415. [Google Scholar]
- Xiong, Y.; Wang, X.L.; Li, D.Q. Synergistic extraction and separation of heavy lanthanide by mixtures of bis(2,4,4-trimethylpentyl) phosphinic acid and 2-ethylhexyl phosphinic acid mono-2-ethylhexyl ester. Sep. Sci. Technol. 2005, 40, 2325–2336. [Google Scholar] [CrossRef]
- Xiong, Y.; Li, W.; Wu, D.B.; Li, D.Q.; Meng, S.L. Kinetics and mechanism of Yb(III) extraction and separation from Y(III) with mixtures of bis(2,4,4-trimethylpentyl)phosphinic acid and 2-ethylhexyl phosphonic acid mono-2-ethylhexyl ester. Sep. Sci. Technol. 2006, 41, 167–178. [Google Scholar] [CrossRef]
- Li, D.Q.; Wang, X.L.; Meng, S.L.; Li, W. A Kind of Technique with Adding Modifier for Extraction and Separation of REs. Chinese Patent Application No. 200510016682.6, 5 April 2005. [Google Scholar]
- Anderson, J.L.; Armstrong, D.W.; Wei, G.-T. Ionic liquids in analytical chemistry. Anal. Chem. 2006, 78, 2893–2902. [Google Scholar] [CrossRef]
- Sun, X.Q.; Ji, Y.; Hu, F.C.; He, B.; Chen, J.; Li, D.Q. The inner synergistic effect of bifunctional ionic liquid extractant for solvent extraction. Talanta 2010, 81, 1877–1883. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.Q.; Ji, Y.; Liu, Y.; Chen, J.; Li, D.Q. An engineering-purpose preparation strategy for ammonium-type ionic liquid with high purity. AICHE J. 2010, 56, 989–996. [Google Scholar] [CrossRef]
- Liu, Y.H.; Chen, J.; Li, D.Q. Application and perspective of ionic liquids on REs green separation. Sep. Sci. Technol. 2012, 47, 223–232. [Google Scholar] [CrossRef]
- Guo, L.; Chen, J.; Shen, L.; Zhang, J.P.; Zhang, D.L.; Deng, Y.F. Highly selective extraction and separation of REs(III) using bifunctional ionic liquid extractant. ACS Sustain. Chem. Eng. 2014, 2, 1968–1975. [Google Scholar] [CrossRef]
- Kuang, S.T.; Zhang, Z.F.; Li, Y.L.; Wei, H.Q.; Liao, W.P. Extraction and separation of heavy rare earths from chloride medium by α-aminophosphonic acid HEHAPP. J. Rare Earths 2018, 36, 304–310. [Google Scholar] [CrossRef]
- GB/T 18882.1–2008; Chemical Analysis Methods of Mixed Rare Earth Oxide of Ion–Absorpted Type RE Ore—Determination of Fifteen REO Relative Content. Standards Press of China: Beijing, China, 2008.
- Zhang, H.; Zhang, X.; Ma, J.G. Chemical Bonding Characteristics of Lanthanide Complexes: A Case of Valence Study. Adv. Mater. Res. 2013, 634–638, 3–6. [Google Scholar] [CrossRef]


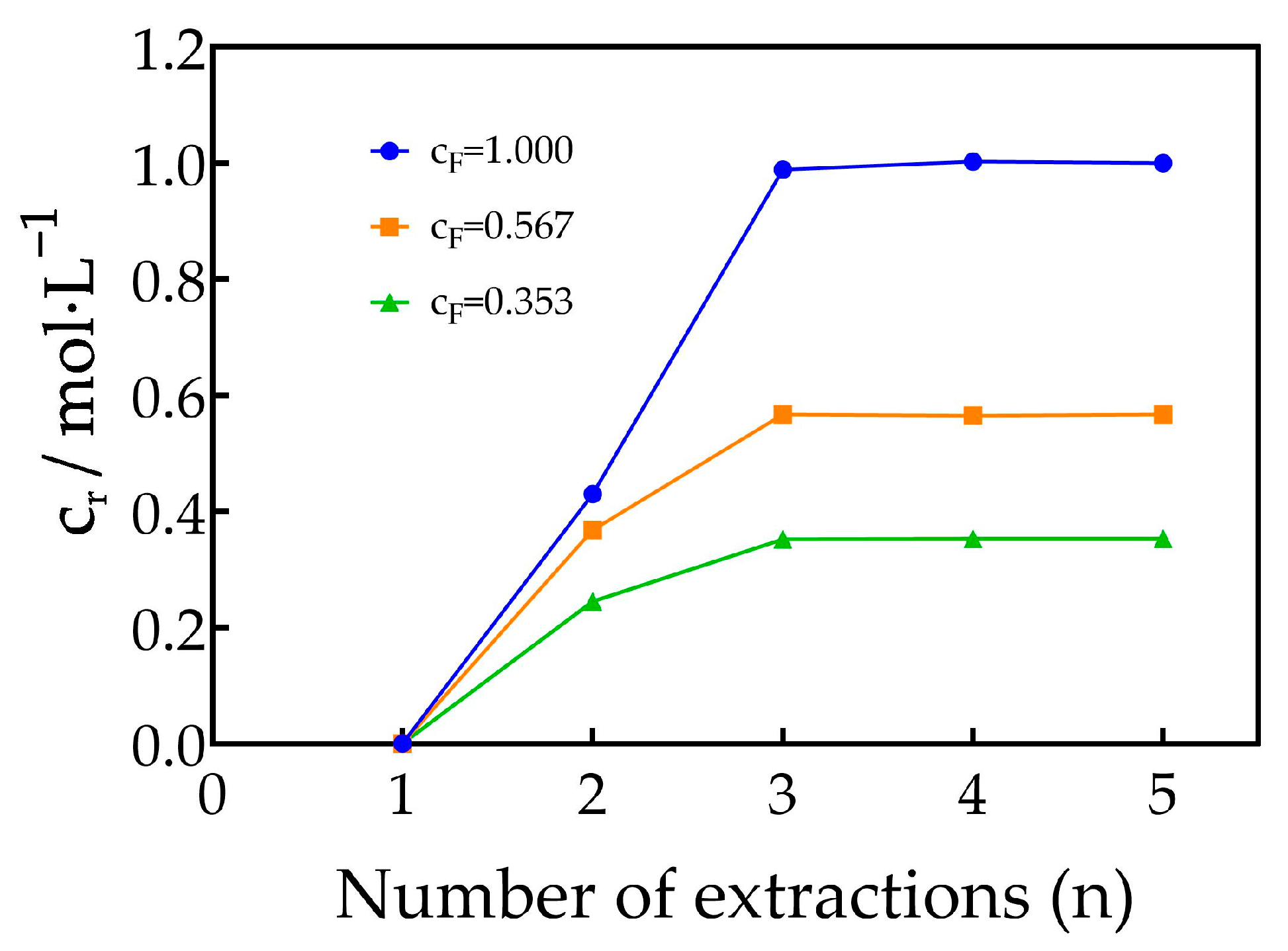

| No. | Concentration of REEs in the Feed Solution /mol·L−1 | Total Concentration of REEs in the Mixed Solution of the First Three Raffinate Aqueous Phases /mol·L−1 | Saturated Concentration of REEs in the TODGA–KS Medium /mol·L−1 |
|---|---|---|---|
| 1 | 1.000 | 0.403 | 1.790 |
| 2 | 0.567 | 0.224 | 1.028 |
| 3 | 0.353 | 0.132 | 0.664 |
| n | A | B | A | PB | EA | EB | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.023 | 0.753 | 0.012 | 1.519 | 0.030 | 0.992 | 1.929 | 0.496 |
| 2 | 0.057 | 0.719 | 0.031 | 1.500 | 0.074 | 0.980 | 1.864 | 0.479 |
| 3 | 0.114 | 0.662 | 0.065 | 1.466 | 0.147 | 0.958 | 1.757 | 0.451 |
| 4 | 0.195 | 0.581 | 0.122 | 1.409 | 0.252 | 0.920 | 1.604 | 0.412 |
| 5 | 0.289 | 0.487 | 0.203 | 1.328 | 0.373 | 0.868 | 1.426 | 0.366 |
| 6 | 0.375 | 0.401 | 0.297 | 1.234 | 0.484 | 0.806 | 1.264 | 0.325 |
| 7 | 0.438 | 0.338 | 0.383 | 1.148 | 0.565 | 0.750 | 1.145 | 0.294 |
| 8 | 0.539 | 0.237 | 0.196 | 0.335 | 0.694 | 0.632 | 2.753 | 0.707 |
| 9 | 0.645 | 0.131 | 0.296 | 0.235 | 0.831 | 0.442 | 2.176 | 0.559 |
| 10 | 0.717 | 0.059 | 0.402 | 0.129 | 0.924 | 0.243 | 1.783 | 0.458 |
| 11 | 0.753 | 0.023 | 0.474 | 0.057 | 0.970 | 0.107 | 1.587 | 0.408 |
| 12 | 0.768 | 0.008 | 0.510 | 0.021 | 0.990 | 0.039 | 1.505 | 0.387 |
| 13 | 0.774 | 0.002 | 0.525 | 0.006 | 0.997 | 0.010 | 1.473 | 0.378 |
| n | A | B | A | PB | EA | EB | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.010 | 0.632 | 0.005 | 1.319 | 0.015 | 0.996 | 2.040 | 0.479 |
| 2 | 0.033 | 0.609 | 0.017 | 1.307 | 0.051 | 0.987 | 1.983 | 0.466 |
| 3 | 0.075 | 0.567 | 0.040 | 1.284 | 0.116 | 0.970 | 1.881 | 0.442 |
| 4 | 0.140 | 0.502 | 0.081 | 1.243 | 0.218 | 0.939 | 1.720 | 0.404 |
| 5 | 0.223 | 0.419 | 0.147 | 1.177 | 0.347 | 0.889 | 1.517 | 0.356 |
| 6 | 0.303 | 0.339 | 0.229 | 1.095 | 0.472 | 0.827 | 1.319 | 0.310 |
| 7 | 0.363 | 0.279 | 0.310 | 1.014 | 0.565 | 0.766 | 1.172 | 0.275 |
| 8 | 0.400 | 0.242 | 0.370 | 0.954 | 0.622 | 0.721 | 1.081 | 0.254 |
| 9 | 0.420 | 0.222 | 0.406 | 0.918 | 0.653 | 0.693 | 1.032 | 0.242 |
| 10 | 0.430 | 0.212 | 0.426 | 0.898 | 0.669 | 0.678 | 1.008 | 0.237 |
| 11 | 0.449 | 0.193 | 0.115 | 0.209 | 0.700 | 0.646 | 3.917 | 0.920 |
| 12 | 0.482 | 0.160 | 0.135 | 0.189 | 0.752 | 0.585 | 3.585 | 0.842 |
| 13 | 0.527 | 0.115 | 0.168 | 0.156 | 0.820 | 0.482 | 3.141 | 0.738 |
| 14 | 0.571 | 0.071 | 0.212 | 0.112 | 0.889 | 0.346 | 2.695 | 0.633 |
| 15 | 0.604 | 0.038 | 0.256 | 0.068 | 0.941 | 0.209 | 2.359 | 0.554 |
| 16 | 0.625 | 0.017 | 0.290 | 0.034 | 0.973 | 0.106 | 2.157 | 0.507 |
| 17 | 0.635 | 0.007 | 0.310 | 0.014 | 0.989 | 0.044 | 2.051 | 0.482 |
| 18 | 0.640 | 0.002 | 0.320 | 0.004 | 0.997 | 0.011 | 1.999 | 0.470 |
| n | A | B | A | PB | EA | EB | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.010 | 0.880 | 0.003 | 1.394 | 0.011 | 0.998 | 3.184 | 0.631 |
| 2 | 0.046 | 0.844 | 0.015 | 1.382 | 0.052 | 0.989 | 3.079 | 0.611 |
| 3 | 0.143 | 0.747 | 0.051 | 1.346 | 0.161 | 0.963 | 2.799 | 0.555 |
| 4 | 0.333 | 0.557 | 0.148 | 1.249 | 0.374 | 0.894 | 2.249 | 0.446 |
| 5 | 0.549 | 0.341 | 0.338 | 1.059 | 0.617 | 0.758 | 1.624 | 0.322 |
| 6 | 0.684 | 0.206 | 0.554 | 0.843 | 0.768 | 0.603 | 1.234 | 0.245 |
| 7 | 0.739 | 0.151 | 0.689 | 0.708 | 0.831 | 0.507 | 1.073 | 0.213 |
| 8 | 0.798 | 0.092 | 0.251 | 0.146 | 0.897 | 0.367 | 3.178 | 0.630 |
| 9 | 0.843 | 0.047 | 0.310 | 0.087 | 0.947 | 0.219 | 2.720 | 0.539 |
| 10 | 0.870 | 0.020 | 0.355 | 0.042 | 0.977 | 0.106 | 2.450 | 0.486 |
| 11 | 0.883 | 0.007 | 0.382 | 0.015 | 0.992 | 0.039 | 2.314 | 0.459 |
| Ligand or REE (III) | ELigand | Complex | EComplex | ΔEComplex |
|---|---|---|---|---|
| TODGA | −1120.5445 | Dy–TODGA | −2734.2309 | −0.5151 |
| Dy3+ | −823.7545 | Er–TODGA | −2858.1644 | −0.4358 |
| Er3+ | −947.8173 | Tm–TODGA | −2925.5679 | −0.5518 |
| Tm3+ | −1014.8049 | Yb–TODGA | −2995.7834 | −0.4917 |
| Yb3+ | −1085.0803 | |||
| NO3− | −280.246872 | |||
| H2O | −76.3910343 |
| Ln–O | Average Bond Lengths (d) | Difference in Bond Lengths for Different Core Ions (Δd) | ||
|---|---|---|---|---|
| TODGA | Dy3+–O | 2.435 | dDy-O-dEr-O | 0.028 |
| Er3+–O | 2.407 | dEr-O-dTm-O | 0.009 | |
| Tm3+–O | 2.398 | dYb-O-dTm-O | 0.014 | |
| Yb3+–O | 2.412 | dYb-O-dEr-O | 0.005 | |
| dDy-O-dYb-O | 0.023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Gong, A.; Qiu, L.; Wang, Y.; Gao, G.; Zhao, W.; Liu, Y.; Yin, J.; Huang, X.; Chen, Y. Theoretical Calculations and Experimental Investigation of Separation of Dy3+, Er3+, Tm3+ and Yb3+ by Cascade Extraction in TOGDA–Kerosene/Hydrochloric Acid System. Separations 2024, 11, 33. https://doi.org/10.3390/separations11010033
Bai Y, Gong A, Qiu L, Wang Y, Gao G, Zhao W, Liu Y, Yin J, Huang X, Chen Y. Theoretical Calculations and Experimental Investigation of Separation of Dy3+, Er3+, Tm3+ and Yb3+ by Cascade Extraction in TOGDA–Kerosene/Hydrochloric Acid System. Separations. 2024; 11(1):33. https://doi.org/10.3390/separations11010033
Chicago/Turabian StyleBai, Yuzhen, Aijun Gong, Lina Qiu, Yiwen Wang, Ge Gao, Weiyu Zhao, Yang Liu, Jiayi Yin, Xinyu Huang, and Yiyang Chen. 2024. "Theoretical Calculations and Experimental Investigation of Separation of Dy3+, Er3+, Tm3+ and Yb3+ by Cascade Extraction in TOGDA–Kerosene/Hydrochloric Acid System" Separations 11, no. 1: 33. https://doi.org/10.3390/separations11010033
APA StyleBai, Y., Gong, A., Qiu, L., Wang, Y., Gao, G., Zhao, W., Liu, Y., Yin, J., Huang, X., & Chen, Y. (2024). Theoretical Calculations and Experimental Investigation of Separation of Dy3+, Er3+, Tm3+ and Yb3+ by Cascade Extraction in TOGDA–Kerosene/Hydrochloric Acid System. Separations, 11(1), 33. https://doi.org/10.3390/separations11010033






