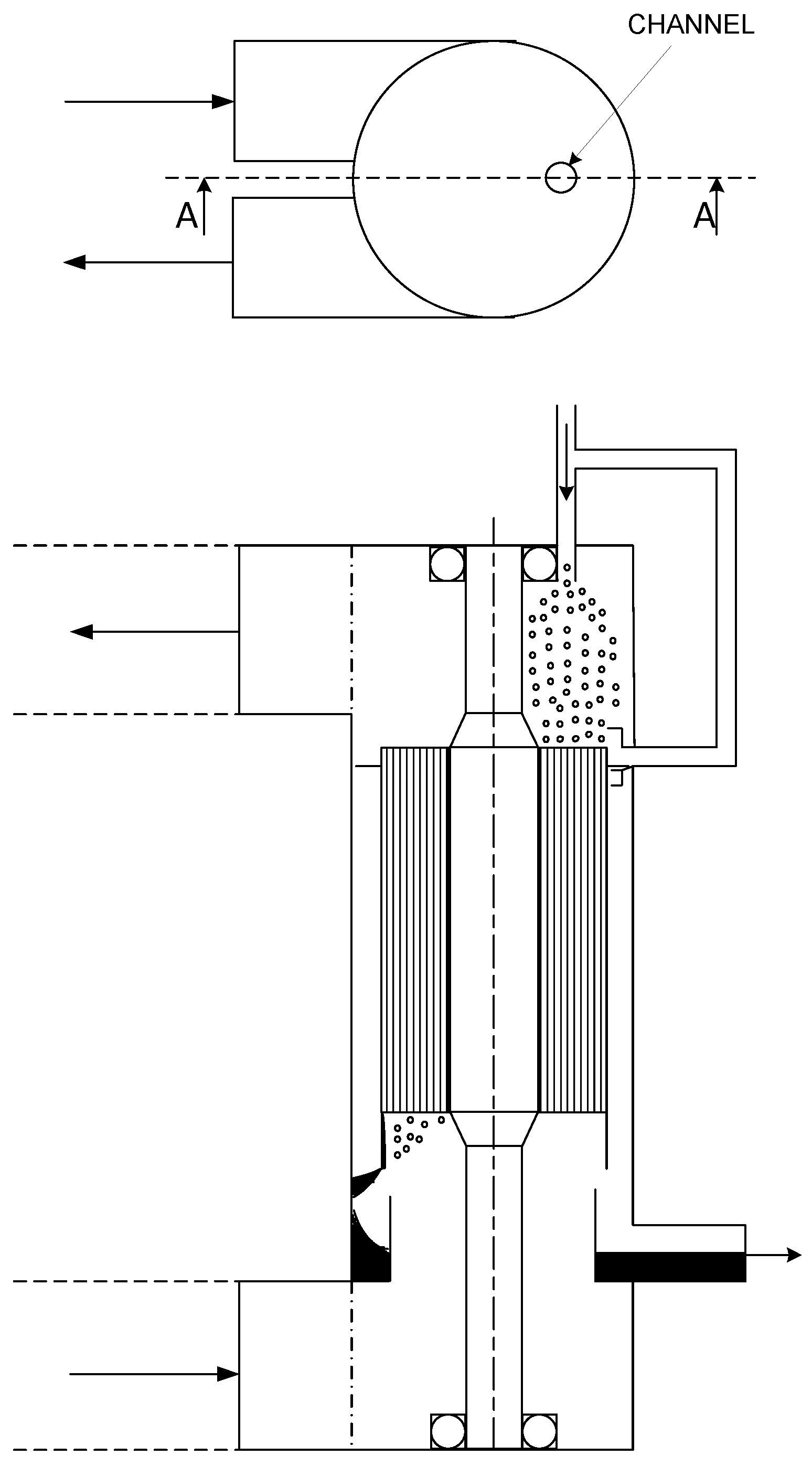
Theory of Gas Purification by Liquid Absorber in Small Rotating Channels with Application to the Patented Rotational Absorber Device
Abstract
1. Introduction
2. Derivation of Absorption Formula
2.1. Co-Current Rotational Absorber Device
2.2. Counter-Current Rotational Absorber Device
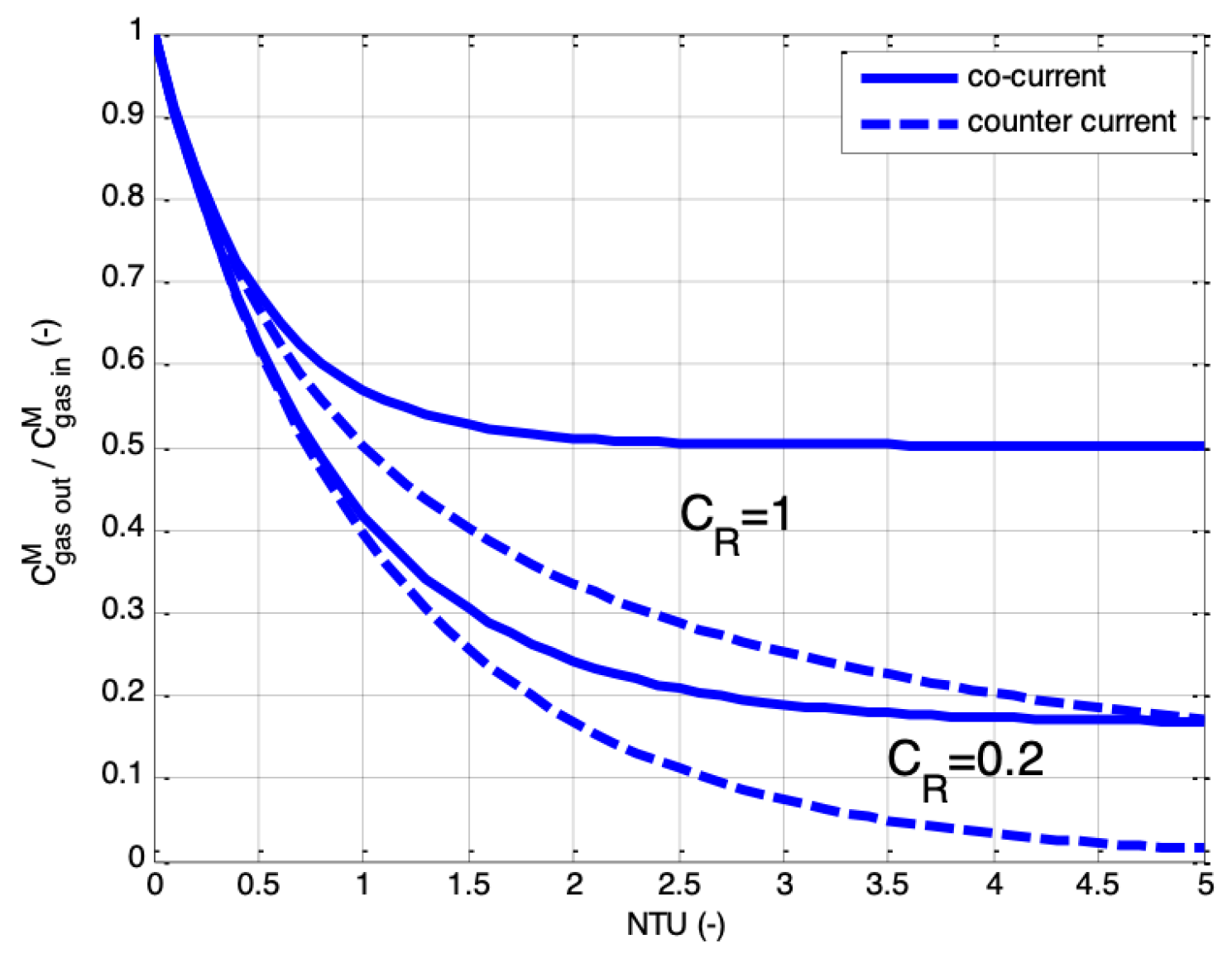
2.3. Co-Current vs. Counter-Current
3. Mass Transfer Coefficients Derived from Diffusion Theory
Comparison with an Exact Result
4. Fluid Flow in the Channels of the Rotational Absorber Device
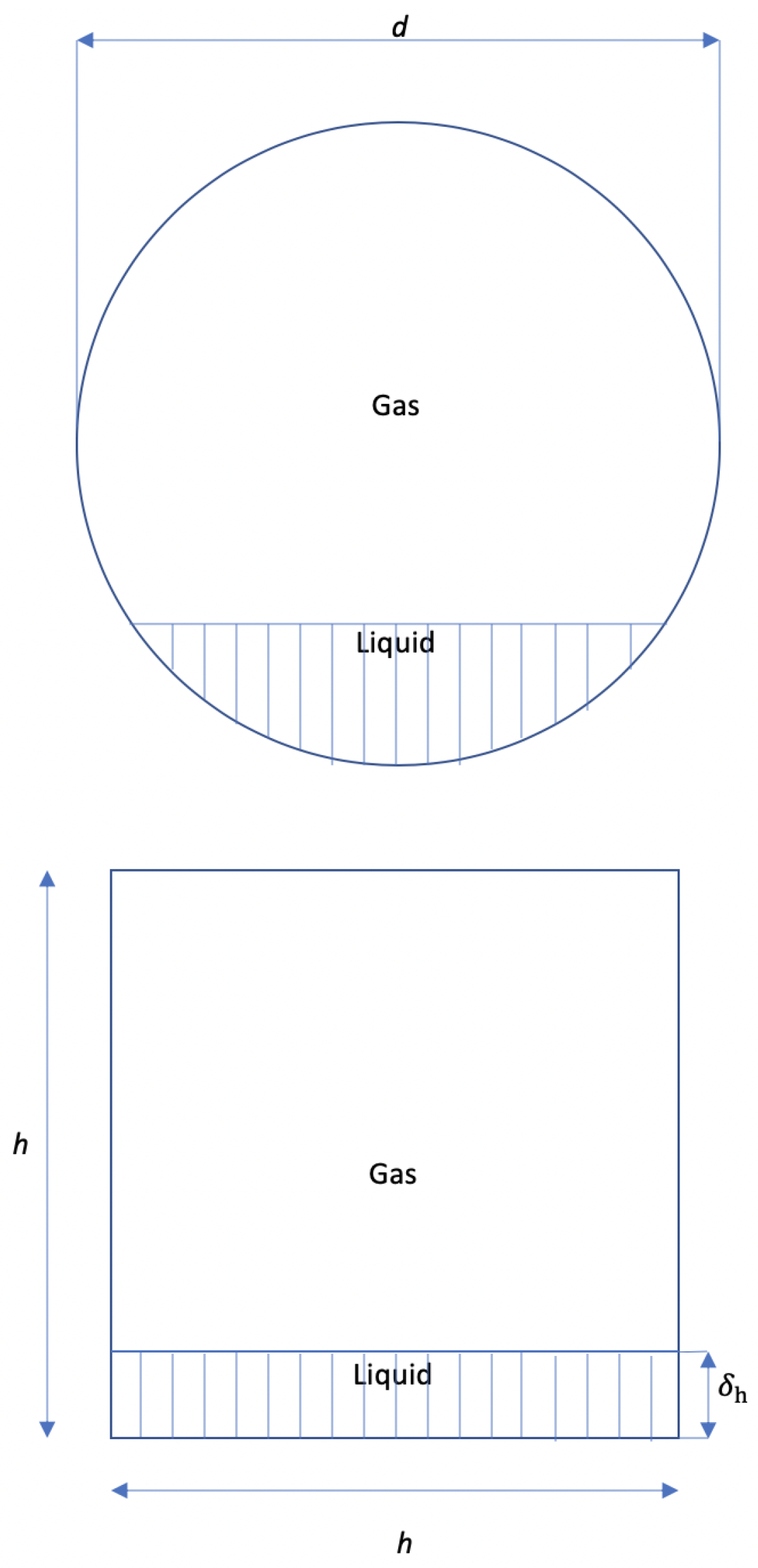
4.1. Laminar Flow in the Gas Section
4.2. Laminar Flow in the Liquid Section
4.3. Turbulent Flow in the Gas Section
- (i)
- For the region , we can writewhere we took andis the Reynolds number based on shear velocity and diffusion coefficient. For turbulent flow at large Reynolds number will also be large. Evaluating the integral using an expansion involving small and disregarding contributions of magnitude directly compared to 1, we obtain
- (ii)
- For the region , we can writewhere we took . Integral (68) can be evaluated again using expansions based on small . Disregarding terms of relative magnitude directly compared to 1, we obtain
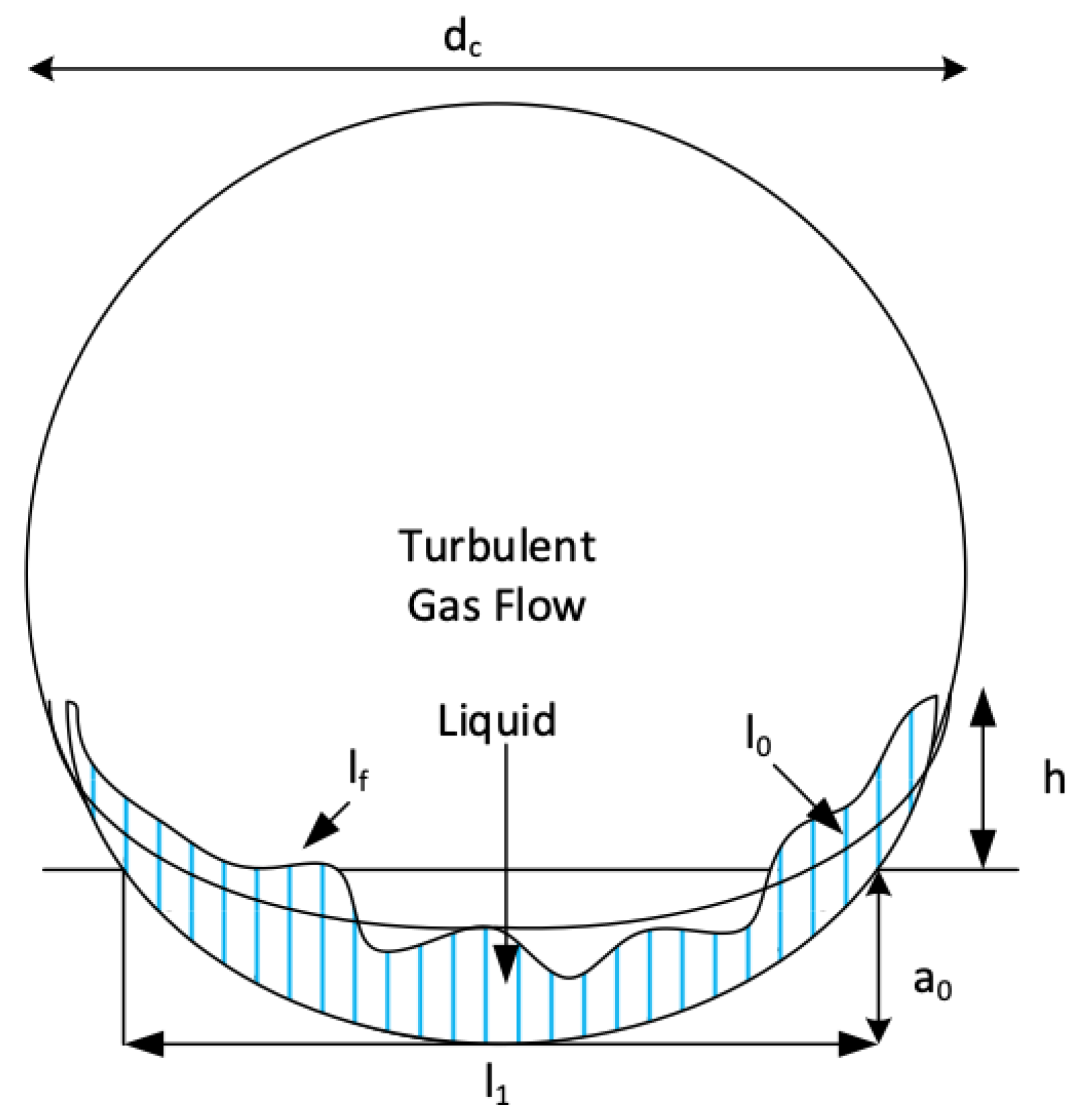
4.4. The Contact Surface in Circular Channels
5. Wave-Enhanced Transfer in the Liquid Film
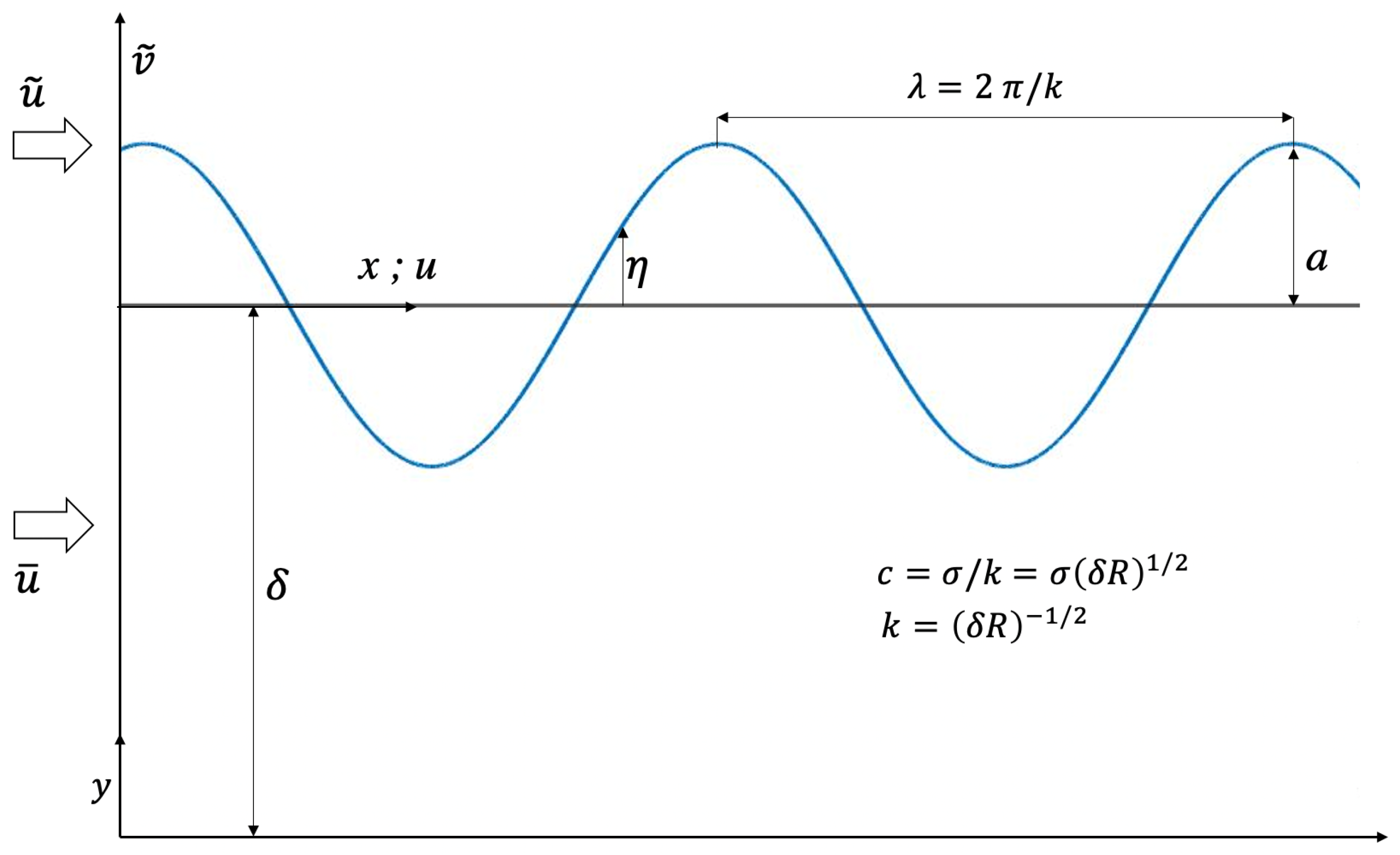
5.1. Generation of Waves
5.2. Wave Motion
5.3. Decay of Wave Motion
5.4. Fluid Particle Path
5.5. Enhanced Diffusion by Wave Motion
6. The Role of Rotation
6.1. Liquid Pressing to Outer Channel Wall
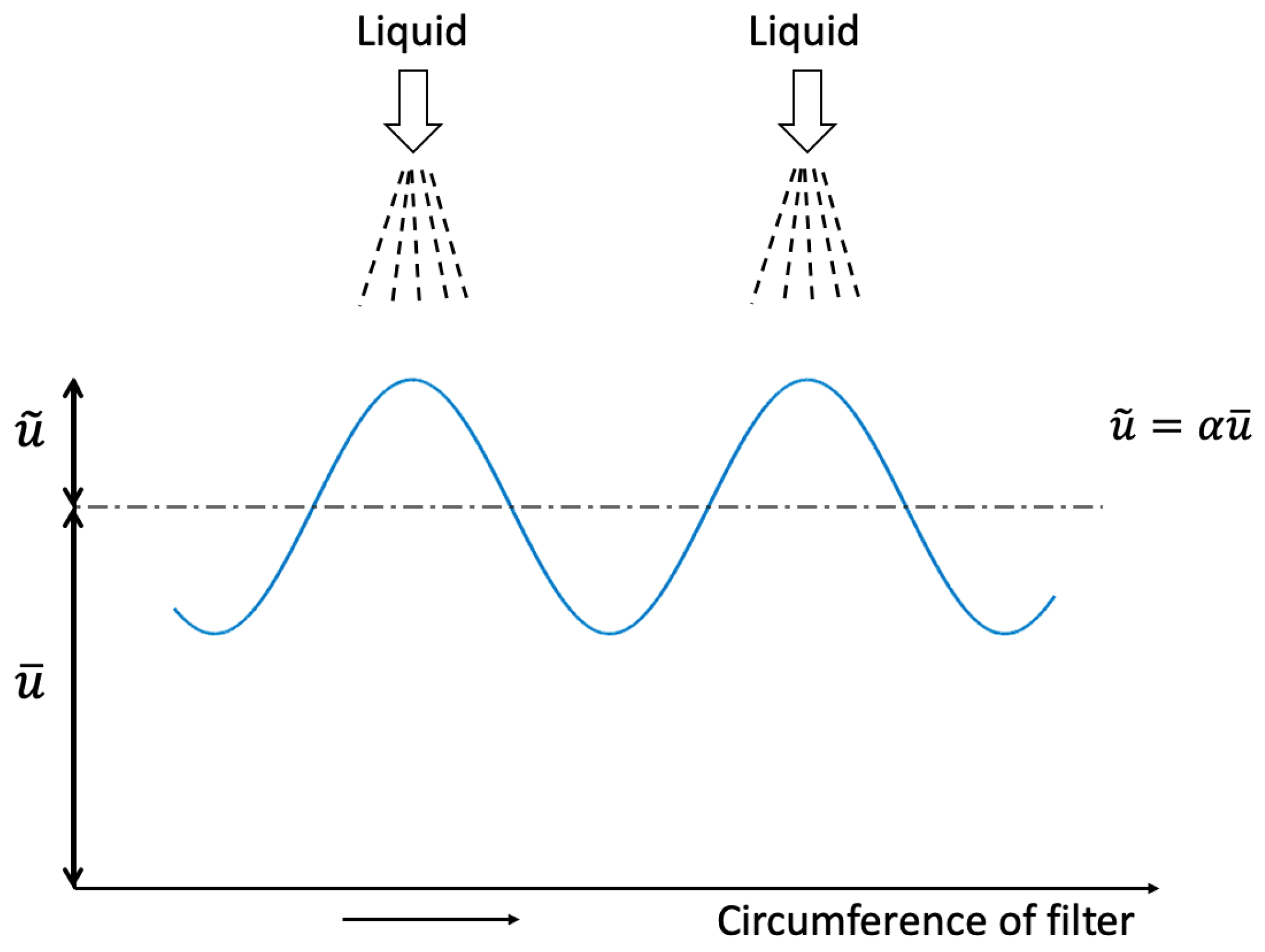
6.2. Wave Motion Generated by Stationary Liquid Injection
6.3. Limitation of the Wave Amplitude of the Liquid Layer
6.4. Liquid Separation from the Gas
6.5. Particle Separation
7. Application in Design
8. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kohl, A.; Nielsen, R. Gas Purification; Gulf Professional Publishing: Houston, TX, USA, 1997. [Google Scholar]
- Brouwers, J.J.H. Rotational Absorber Device and Method for Scrubbing an Adsorbate from a Gas. European Patent EP3624923B1, 14 April 2021. Patent Granted in Countries Worldwide. [Google Scholar]
- Brouwers, J.J.H. Innovative Methods of Centrifugal Separation. Separations 2023, 10, 181. [Google Scholar] [CrossRef]
- Bramley, A. On the Theory of the Separation of Isotopes by Thermal or Centrifugal Methods. Science 1940, 92, 427–428. [Google Scholar] [CrossRef] [PubMed]
- Willems, G.P. Condensed Rotational Cleaning of Natural Gas. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2009. Available online: https://pure.tue.nl/ws/portalfiles/portal/2808690/200911885.pdf (accessed on 1 January 2020).
- Mondt, E. Compact Separator of Dispersed Phases. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2005. Available online: https://pure.tue.nl/ws/files/3339334/200513466.pdf (accessed on 1 January 2020).
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenemena; John Wiley and Sons: New York, NY, USA, 1960. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Lamb, H. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Basset, A.B. A Treatise on Hydrodynamics; Bell and Co., Ltd.: Cambridge, UK, 1888; Volume 2. [Google Scholar]
- Villermaux, E. Mixing Versus Stirring. Annu. Rev. Fluid Mech. 2019, 51, 245–273. [Google Scholar] [CrossRef]
- Brouwers, J.J.H. Separation and Disinfection of Contagious Aerosols From the Perspective of SARS-CoV-2. Separations 2021, 8, 190. [Google Scholar] [CrossRef]
- Koonin, S.E. Unsettled; BenBella Books, Inc.: Dallas, TX, USA.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brouwers, J.J.H. Theory of Gas Purification by Liquid Absorber in Small Rotating Channels with Application to the Patented Rotational Absorber Device. Separations 2024, 11, 338. https://doi.org/10.3390/separations11120338
Brouwers JJH. Theory of Gas Purification by Liquid Absorber in Small Rotating Channels with Application to the Patented Rotational Absorber Device. Separations. 2024; 11(12):338. https://doi.org/10.3390/separations11120338
Chicago/Turabian StyleBrouwers, J. J. H. 2024. "Theory of Gas Purification by Liquid Absorber in Small Rotating Channels with Application to the Patented Rotational Absorber Device" Separations 11, no. 12: 338. https://doi.org/10.3390/separations11120338
APA StyleBrouwers, J. J. H. (2024). Theory of Gas Purification by Liquid Absorber in Small Rotating Channels with Application to the Patented Rotational Absorber Device. Separations, 11(12), 338. https://doi.org/10.3390/separations11120338