Study on Separation Kinetics of Non-Spherical Single Feeding Particle in the Gas–Solid Separation Fluidized Bed
Abstract
1. Introduction
2. Materials and Methods
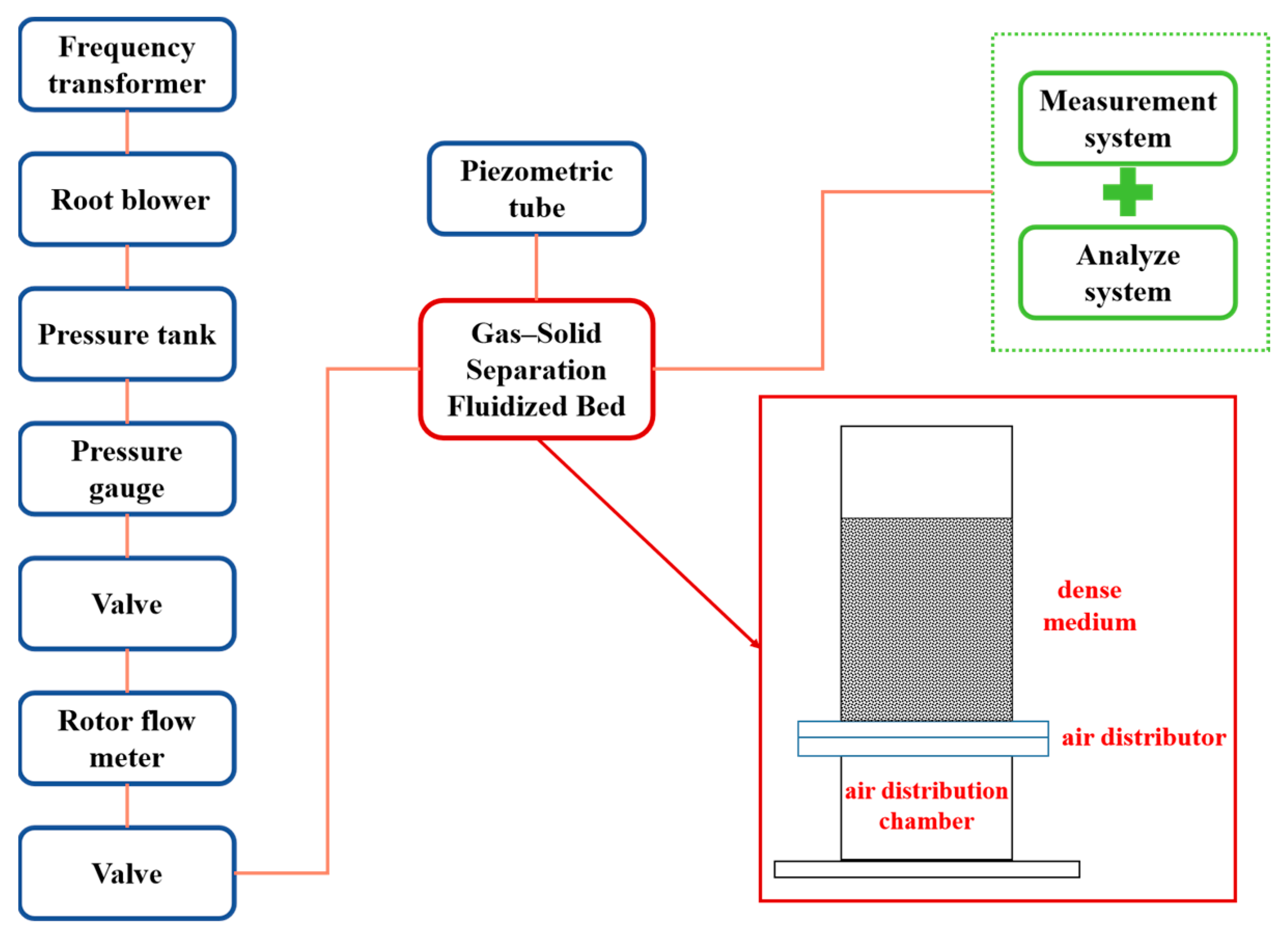
2.1. Apparatus
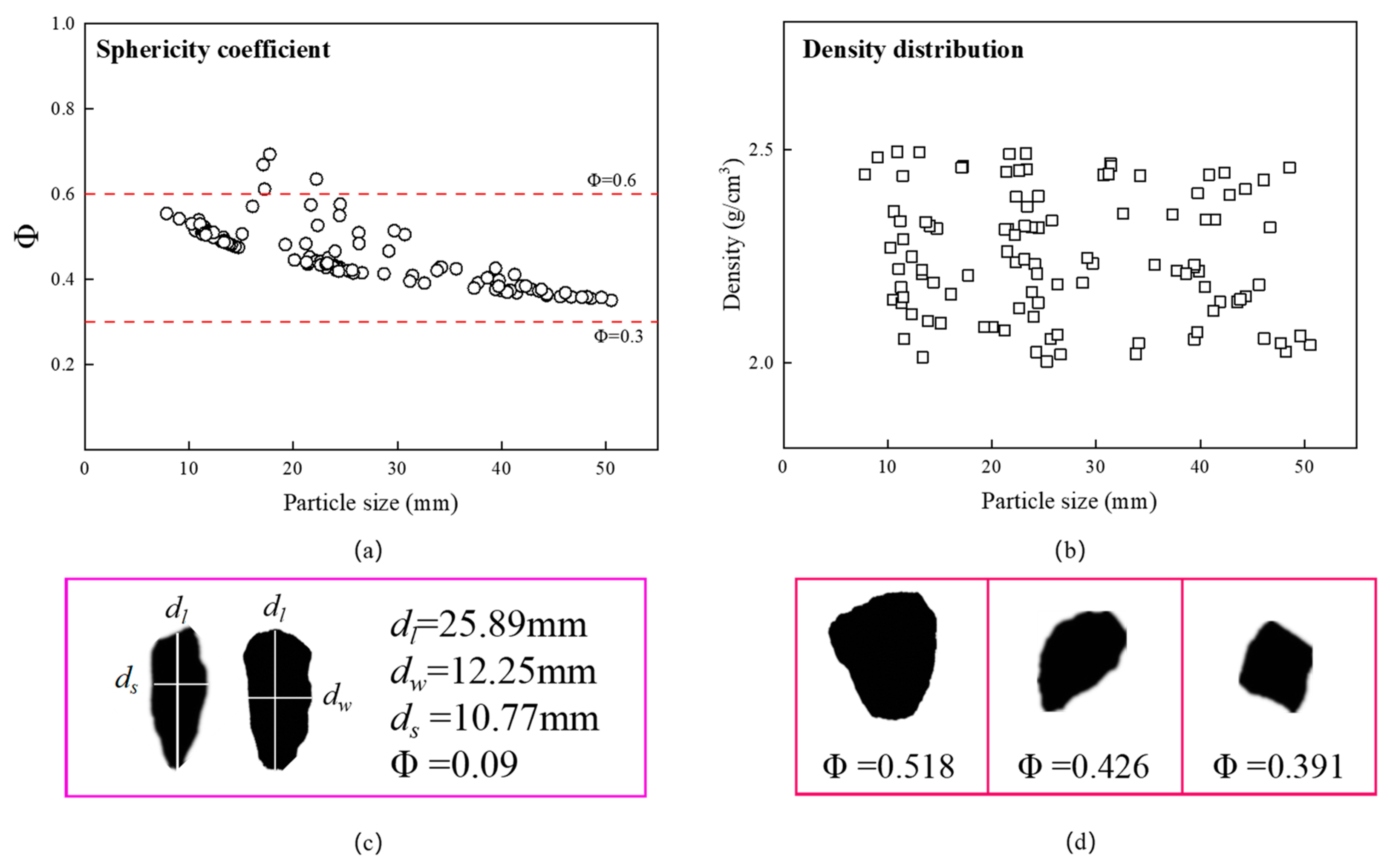
2.2. Properties of Dense Medium
2.3. Properties of Feeding Particles
2.3.1. Sphericity Coefficient
2.3.2. Properties of Simulated Particles
2.3.3. Properties of Selected Feeding Coal Particles
3. Theoretical Analysis of Single Feeding Particle Movement Behavior
3.1. Terminal Sinking Velocity
3.2. Theoretical Analysis of Single Feeding Particle Separation Behavior
4. Results and Discussion
4.1. Movement Behavior of Non-Spherical Single Feeding Particles in the Gas–Solid Separation Fluidized Bed
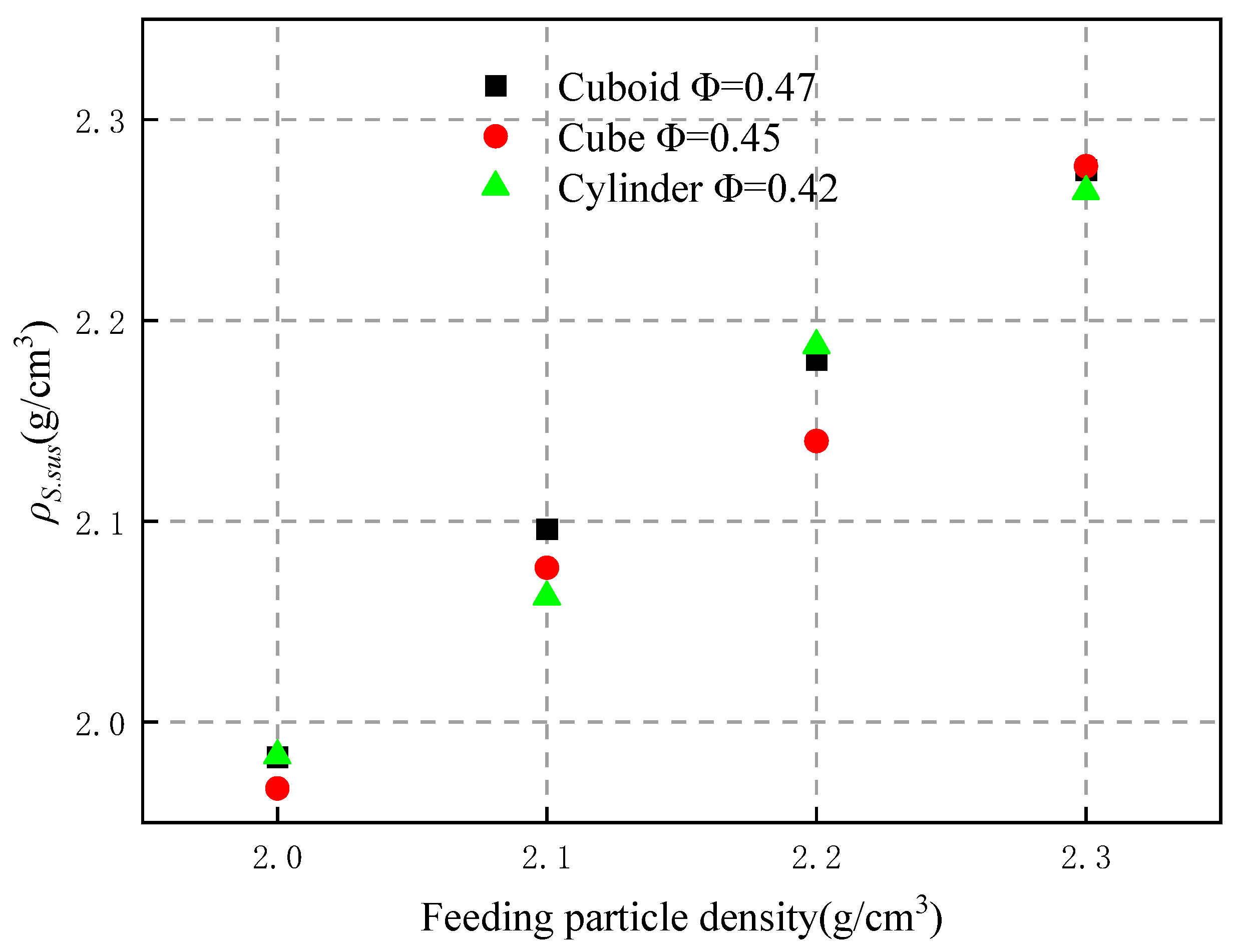
4.1.1. Relationship Between ρS.sus and Feeding Particle Density
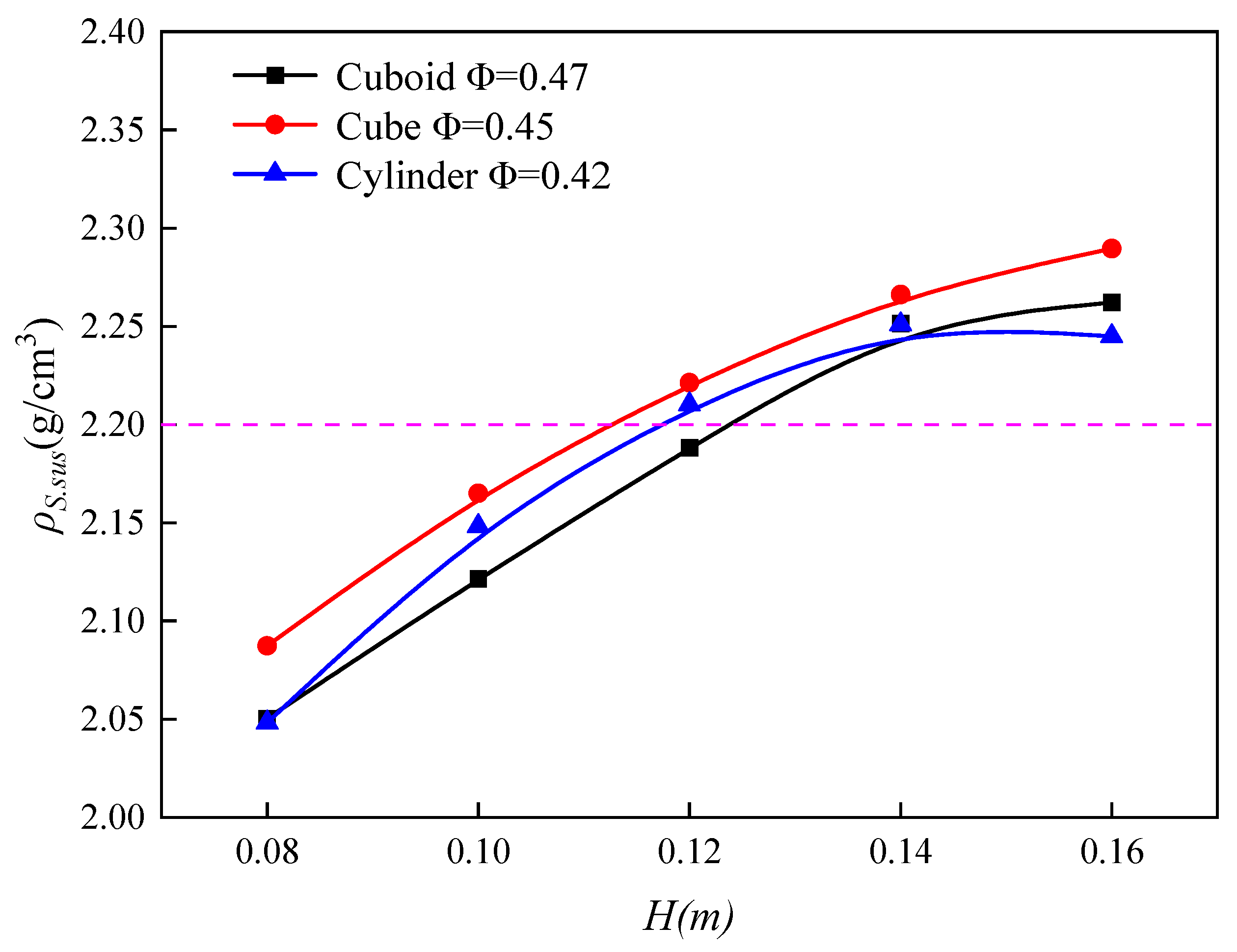
4.1.2. Relationship Between ρS.sus and Bed Height
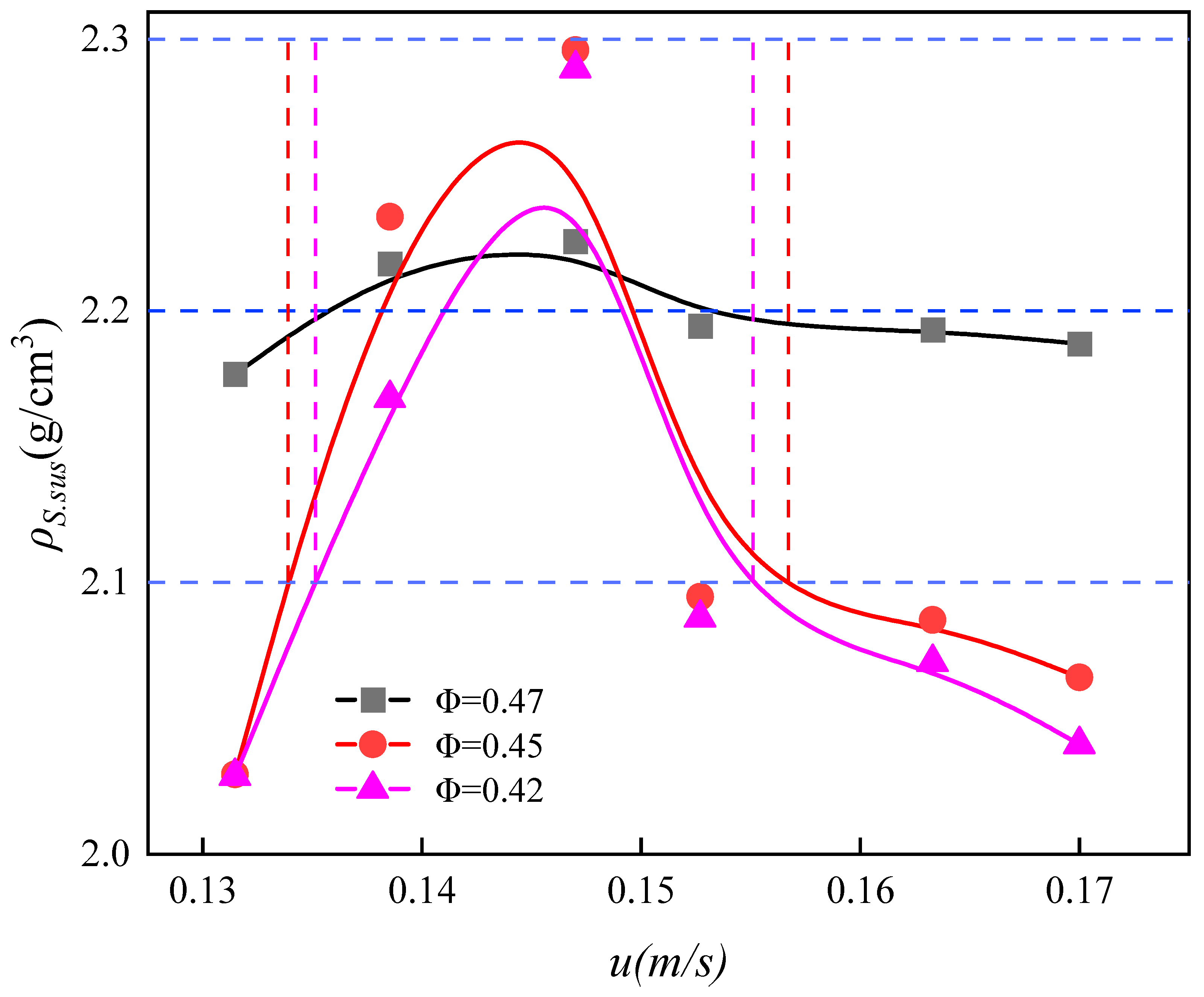
4.1.3. Relationship Between ρS.sus and Gas Velocity
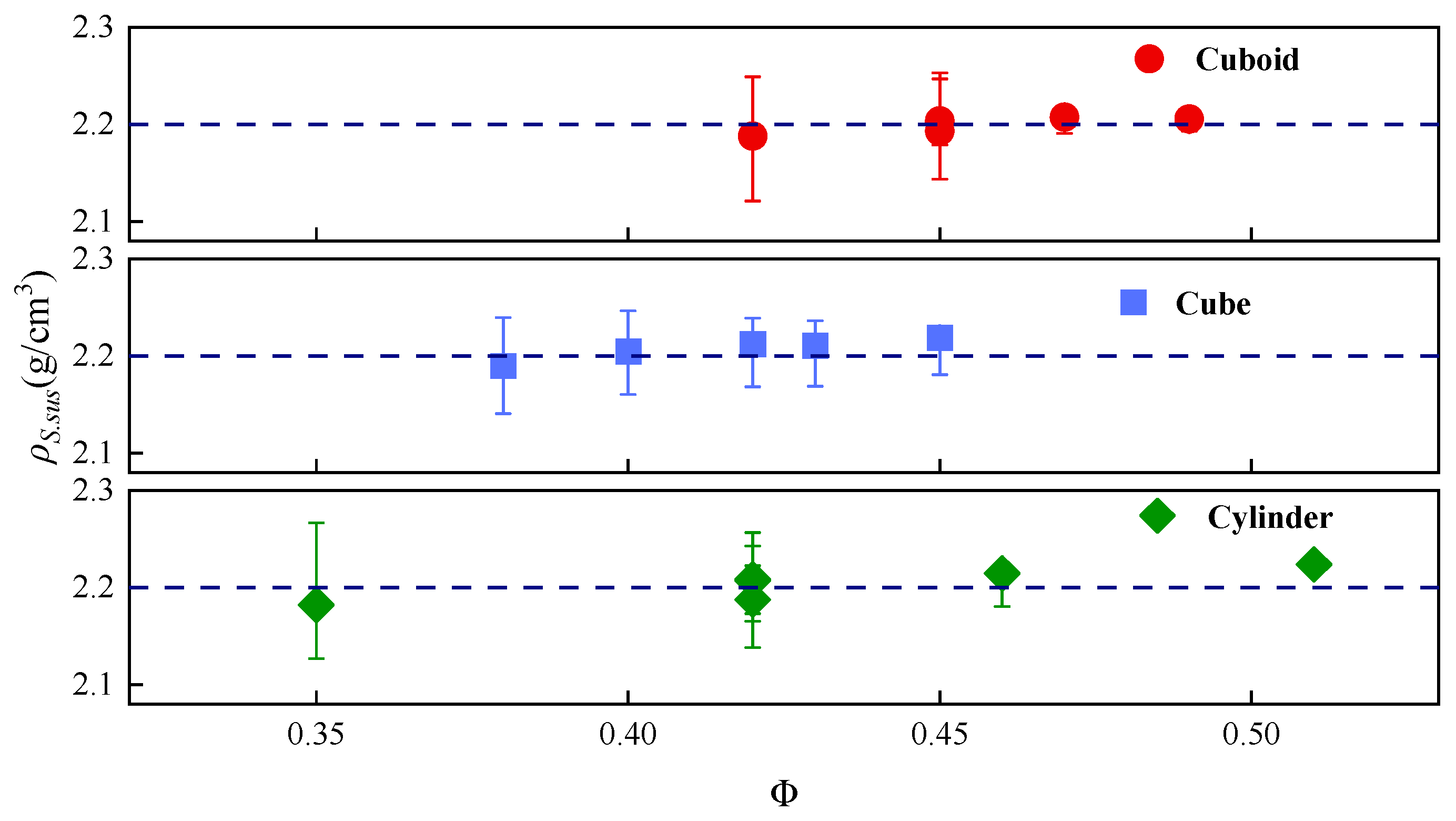
4.1.4. Relationship Between ρS.sus and Sphericity Coefficient
4.2. Movement Behavior Prediction Model and Error Analysis of Non-Spherical Single Feeding Particles in the Gas–Solid Separation Fluidized Bed
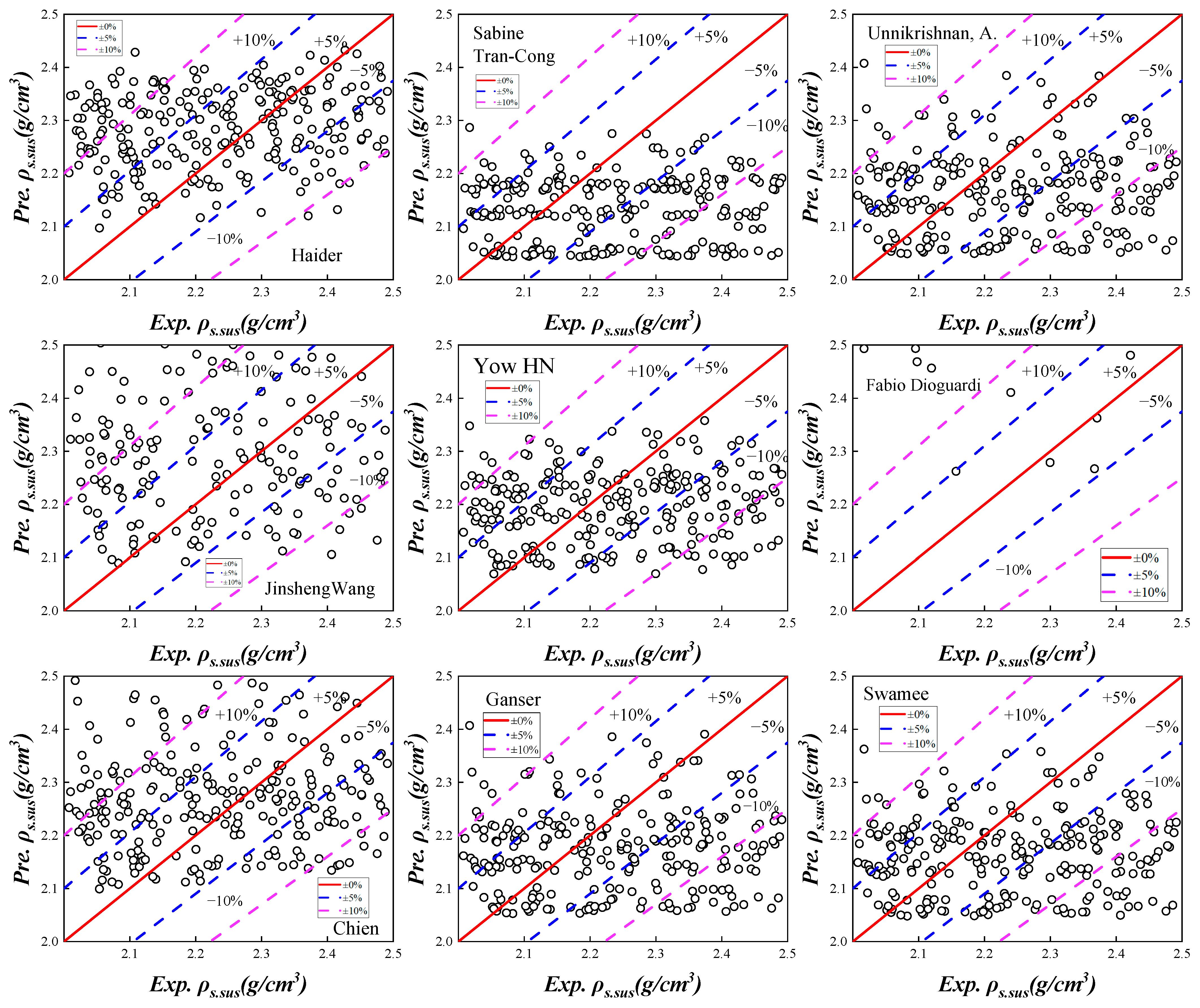
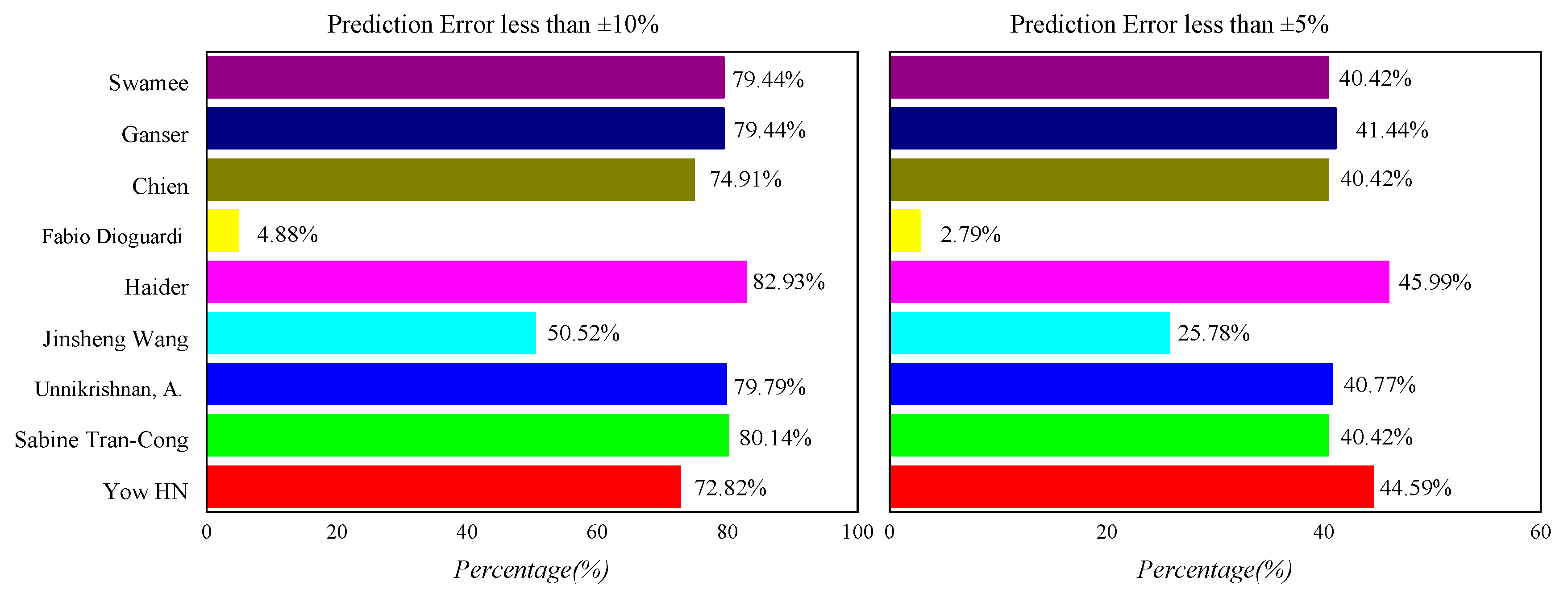
4.2.1. Relationship Between ρS.sus and Drag Coefficient
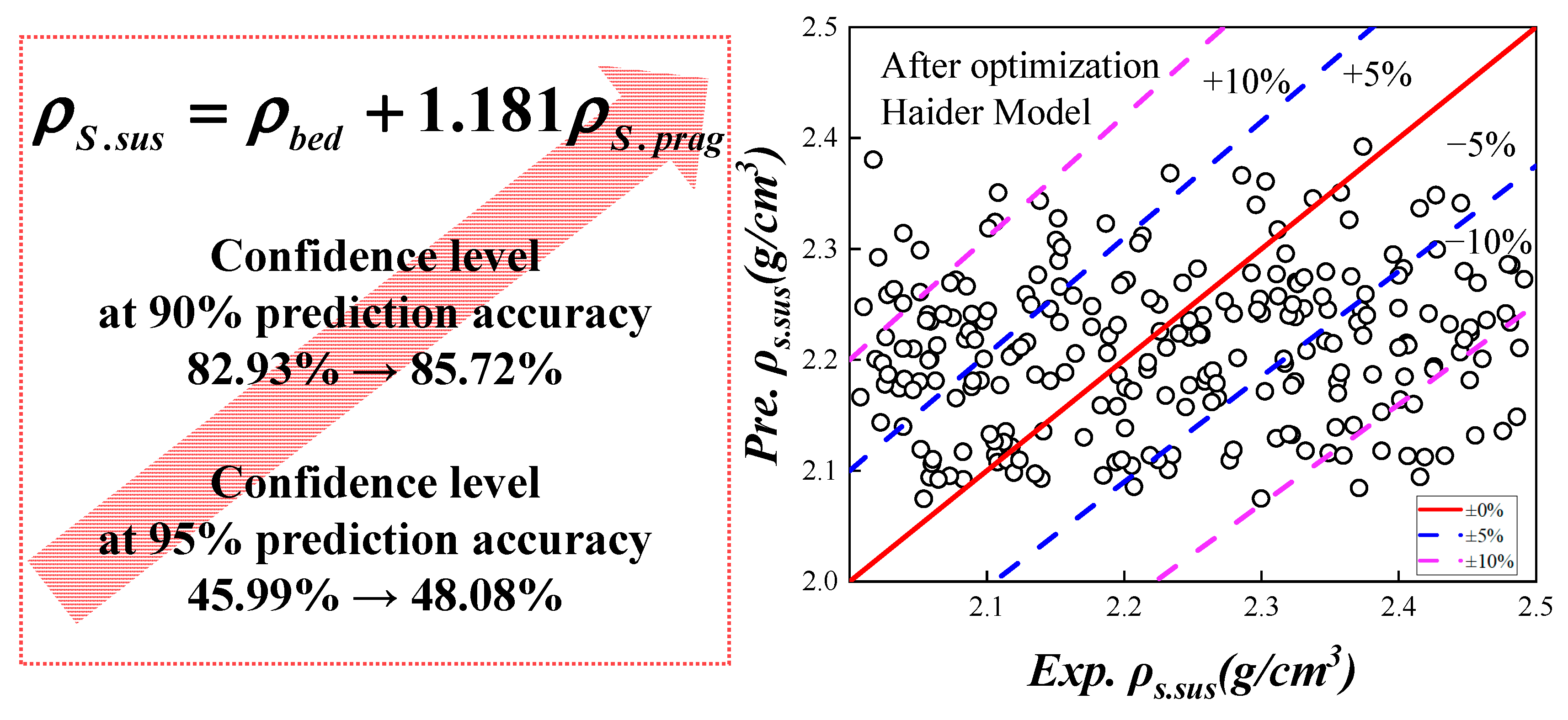
4.2.2. Optimization of the ρS.sus Prediction Model
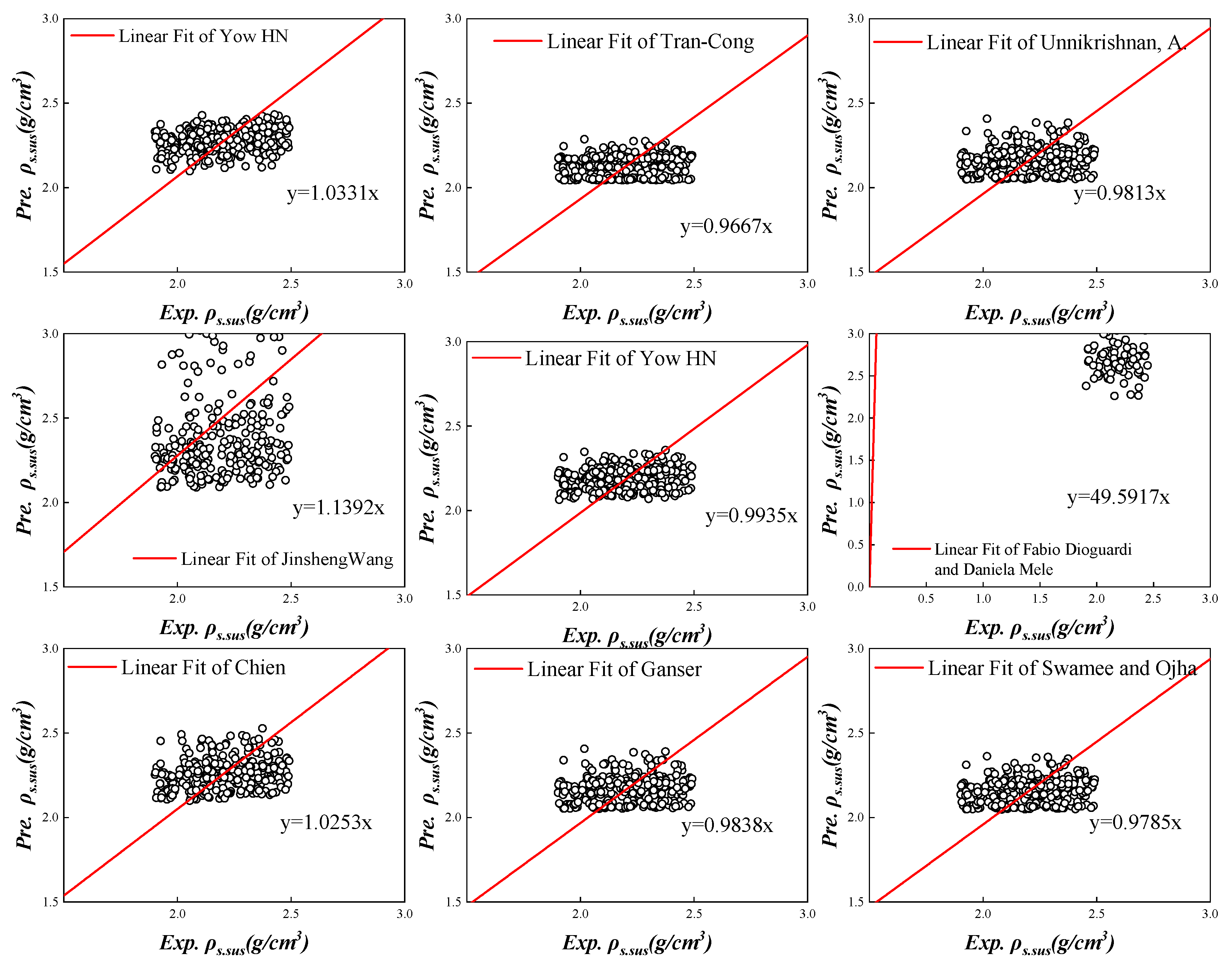
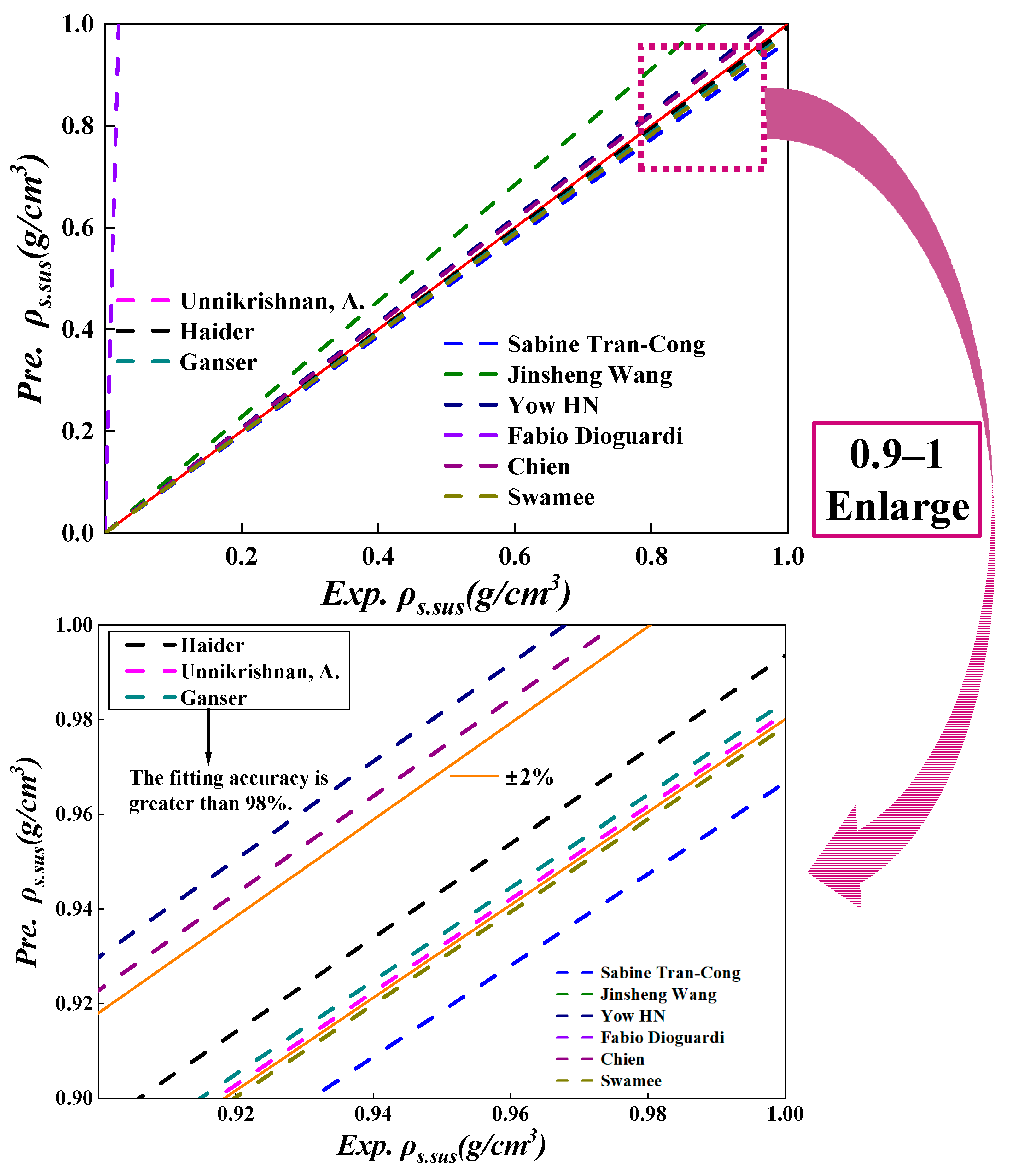
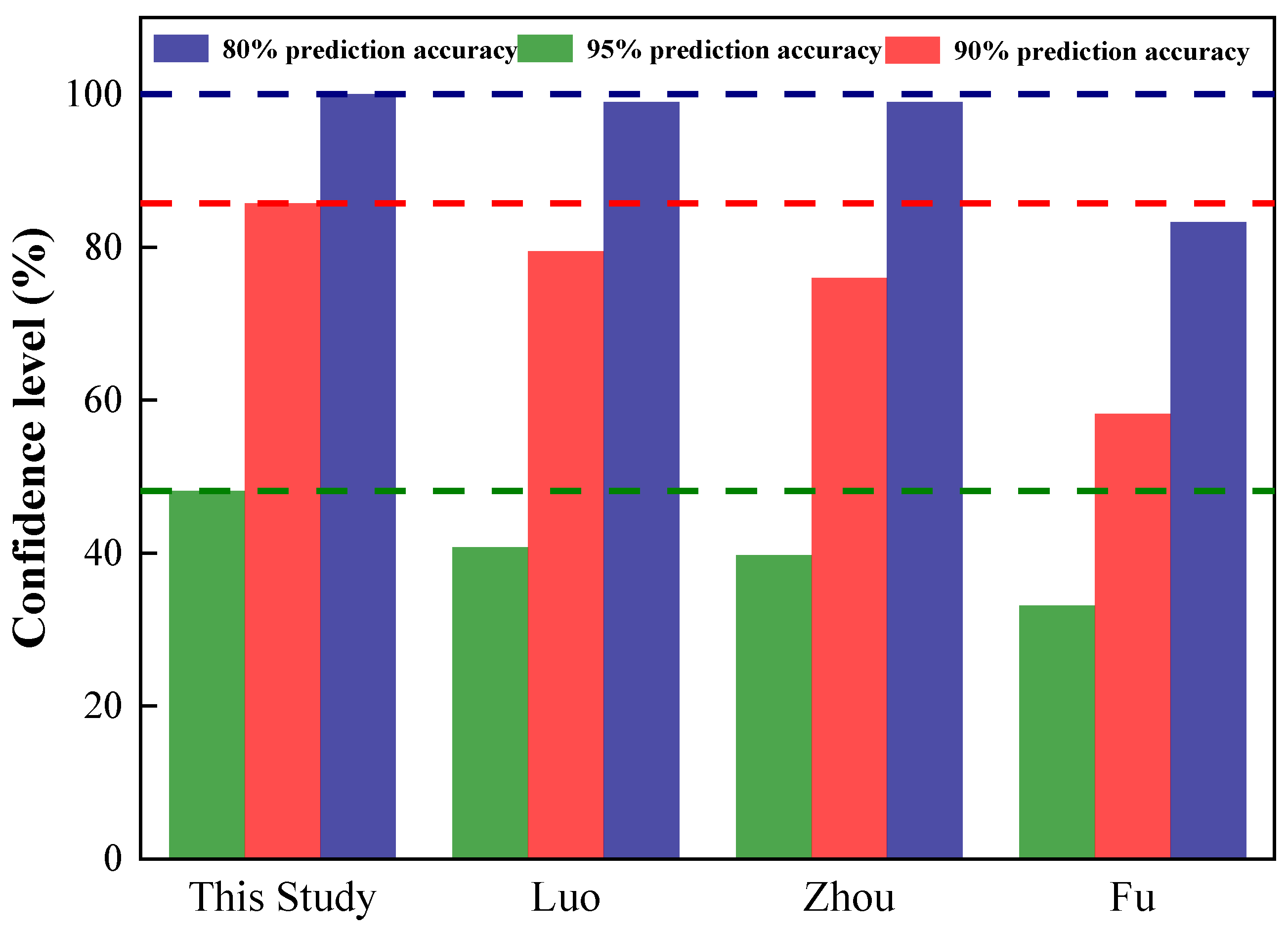
4.2.3. Model Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dindarloo, S.R.; Hood, M.M.; Bagherieh, A.; Hower, J.C. A statistical assessment of carbon monoxide emissions from the Truman Shepherd coal fire, Floyd County, Kentucky. Int. J. Coal Geol. 2015, 144, 88–97. [Google Scholar] [CrossRef]
- van Breugel, Y.; Cowan, A.K.; Tsikos, H. Geochemical Study of Weathered Coal, a Co-Substrate for Bioremediation of South African Coal Discard Dumps. Minerals 2019, 9, 772. [Google Scholar] [CrossRef]
- Wang, C.B.; Liu, H.M.; Zhang, Y.; Zou, C.; Anthony, E.J. Review of arsenic behavior during coal combustion: Volatilization, transformation, emission and removal technologies. Prog. Energy Combust. Sci. 2018, 68, 1–28. [Google Scholar] [CrossRef]
- Zhou, C.; Zhao, Y.; Liu, C.; Li, Y.; Gao, Z.; Fan, X.; Aleksandrova, T.; Duan, C. Fluidization expansion of novel generation dense medium and flow regime transition in gas-solid separation fluidized bed. Fundam. Res. 2023. [Google Scholar] [CrossRef]
- Yang, Y.W.; Yan, F.Y.; Yang, Y.H.; Chen, Y. Evaluating provincial carbon emission characteristics under China’s carbon peaking and carbon neutrality goals. Ecol. Indic. 2023, 156, 13. [Google Scholar] [CrossRef]
- Du, X.W. Thoughts on strategies and paths to achieve carbon peaking and carbon neutrality in China. Front. Energy 2023, 17, 324–331. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Wang, Z.G. Recent progress and emerging strategies for carbon peak and carbon neutrality in China. Greenh. Gases 2023, 13, 732–759. [Google Scholar] [CrossRef]
- Lu, Y.W.; Chen, S.L. Exploring the realization pathway of carbon peak and carbon neutrality in the provinces around the Yangtze river of China. J. Clean Prod. 2024, 466, 12. [Google Scholar] [CrossRef]
- Wei, Y.M.; Chen, K.Y.; Kang, J.N.; Chen, W.M.; Zhang, X.Y.; Wang, X.Y. Policy and Management of Carbon Peaking and Carbon Neutrality: A Literature Review. Engineering 2022, 14, 52–63. [Google Scholar] [CrossRef]
- China National Coal Association. 2023 Annual Report on the Development of the Coal Industry; China National Coal Association: Beijing, China, 2024. [Google Scholar]
- Zhao, Y.; Li, G.; Luo, Z.; Zhang, B.; Dong, L.; Liang, C.; Duan, C. Industrial Application of a Modularized Dry-Coal-Beneficiation Technique Based on a Novel Air Dense Medium Fluidized Bed. Int. J. Coal Prep. Util. 2017, 37, 44–57. [Google Scholar] [CrossRef]
- Firdaus, M.; O’Shea, J.P.; Oshitani, J.; Franks, G.V. Beneficiation of Coarse Coal Ore in an Air-Fluidized Bed Dry Dense-Medium Separator. Int. J. Coal Prep. Util. 2012, 32, 276–289. [Google Scholar] [CrossRef]
- Liu, C.G.; Zhou, C.Y.; Sun, Z.E.; Duan, C.L.; Zhu, J.; Zhao, Y.M. Geldart A-particles: Hydrodynamics of Geldart A magnetite powder with modulation by ultrafine coal particles in Gas-solid Fluidized Bed Coal Beneficiator (GFBCB). Powder Technol. 2022, 408, 10. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Liu, X.B.; Zhao, Y.M.; Yang, X.L.; Li, Y.J.; Dong, L.; Duan, C.L.; Rao, Z.H. Recent progress and potential challenges in coal upgrading via gravity dry separation technologies. Fuel 2021, 305, 28. [Google Scholar] [CrossRef]
- Fan, X.; Zhou, C.; Zhao, Y.; Duan, C.; Liu, Q. Flow pattern transition and coal beneficiation in gas solid fluidized bed with novel secondary distributor. Adv. Powder Technol. 2018, 29, 1255–1264. [Google Scholar] [CrossRef]
- Fan, X.; Zhou, C.; Dong, L.; Zhao, Y.; Duan, C.; Zhang, B. Novel method of air distributor design for enhancing bed stability and reducing impurities in gas-solid fluidized bed system. Part. Sci. Technol. 2019, 37, 652–664. [Google Scholar] [CrossRef]
- Fan, X.; Zhou, C. Estimation of Bed Expansion and Separation Density of Gas-Solid Separation Fluidized Beds Using a Micron-Sized-Particle-Dense Medium. Separations 2021, 8, 242. [Google Scholar] [CrossRef]
- Dong, L.; Zhao, Y.; Luo, Z.; Duan, C.; Wang, Y.; Yang, X.; Zhang, B. A model for predicting bubble rise velocity in a pulsed gas solid fluidized bed. Int. J. Min. Sci. Technol. 2013, 23, 227–230. [Google Scholar] [CrossRef]
- Luo, Z.F.; Zhao, Y.M.; Lv, B.; Fu, Y.H.; Xu, X.; Chen, C.S. Dry coal beneficiation technique in the gas-solid fluidized bed: A review. Int. J. Coal Prep. Util. 2022, 42, 986–1014. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Y.; Xu, J.; Wang, J.W.; Duan, C.L.; Ge, W.; Zhao, Y.M. CFD intensification of coal beneficiation process in gas-solid fluidized beds. Chem. Eng. Process. 2020, 148, 6. [Google Scholar] [CrossRef]
- Wang, Q.G.; Feng, Y.Q.; Lu, J.F.; Yin, W.D.; Yang, H.R.; Witt, P.J.; Zhang, M. Numerical study of particle segregation in a coal beneficiation fluidized bed by a TFM-DEM hybrid model: Influence of coal particle size and density. Chem. Eng. J. 2015, 260, 240–257. [Google Scholar] [CrossRef]
- Prusti, P.; Sahu, A.K.; Biswal, S.K. Prediction of the position of coal particles in an air dense medium fluidized bed system. Int. J. Min. Sci. Technol. 2015, 25, 421–427. [Google Scholar] [CrossRef]
- Luo, Z.; Zhao, Y. Separation Theory of Fluidization; China University of Mining and Technology Press: Xuzhou, China, 2002. [Google Scholar]
- Tran-Cong, S.; Gay, M.; Michaelides, E.E. Drag coefficients of irregularly shaped particles. Powder Technol. 2004, 139, 21–32. [Google Scholar] [CrossRef]
- Yow, H.N.; Pitt, M.J.; Salman, A.D. Drag correlations for particles of regular shape. Adv. Powder Technol. 2005, 16, 363–372. [Google Scholar] [CrossRef]
- Unnikrishnan, A.; Chhabra, R.P. An experimental study of motion of cylinders in newtonian fluids: Wall effects and drag coefficient. Can. J. Chem. Eng. 1991, 69, 729–735. [Google Scholar] [CrossRef]
- Wang, J.; Qi, H.; You, C. Experimental study of sedimentation characteristics of spheroidal particles. Particuology 2009, 7, 264–268. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Dioguardi, F.; Mele, D. A new shape dependent drag correlation formula for non-spherical rough particles. Experiments and results. Powder Technol. 2015, 277, 222–230. [Google Scholar] [CrossRef]
- Chien, S.-F. Settling Velocity of Irregularly Shaped Particles. SPE Drill. Complet. 1994, 9, 281–289. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Hatami, M.; Hosseinzadeh, K.; Domairry, G. Non-spherical particles sedimentation in an incompressible Newtonian medium by Padé approximation. Powder Technol. 2015, 278, 248–256. [Google Scholar] [CrossRef]
- Swamee Prabhata, K.; Ojha Chandra Shakhar, P. Drag Coefficient and Fall Velocity of nonspherical particles. J. Hydraul. Eng. 1991, 117, 660–667. [Google Scholar] [CrossRef]
- Karlsson, T.; Liu, X.M.; Pallarès, D.; Johnsson, F. Solids circulation in circulating fluidized beds with low riser aspect ratio and varying total solids inventory. Powder Technol. 2017, 316, 670–676. [Google Scholar] [CrossRef]
- Jiang, K.J.; Kong, Y.Q.; Xu, C.; Ge, Z.H.; Du, X.Z. Experimental performance of gas-solid countercurrent fluidized bed particle solar receiver with high-density suspension. Appl. Therm. Eng. 2022, 213, 14. [Google Scholar] [CrossRef]
- Geldart, D. Types of gas fluidization. Powder Technol. 1973, 7, 285–292. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Liu, C.G.; Yuan, Y.; Fu, Z.J.; Zhu, J.S.; Duan, C.L. Separation density prediction of geldart A- dense medium in gas-solid fluidized bed coal beneficiators. Particuology 2024, 92, 251–262. [Google Scholar] [CrossRef]
- Wei, L.P.; Lu, Y.J.; Wei, J.J. Flow separation from a spherical particle in supercritical water. Chem. Eng. Res. Des. 2014, 92, 2273–2282. [Google Scholar] [CrossRef]
- Fan, X.; Ren, Y.; Dong, L.; Zhou, C.; Zhao, Y. Optimization of coal size for beneficiation efficiency promotion in gas–solid fluidized bed. Part. Sci. Technol. 2023, 41, 151–162. [Google Scholar] [CrossRef]
- Dellino, P.; Mele, D.; Bonasia, R.; Braia, G.; La Volpe, L.; Sulpizio, R. The analysis of the influence of pumice shape on its terminal velocity. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Swanson, V.F. Free and hindered settling. Min. Metall. Explor. 1989, 6, 190–196. [Google Scholar] [CrossRef]
- Swanson, V.F. Settling equation for minerals and process applications. Min. Metall. Explor. 1999, 16, 8–13. [Google Scholar] [CrossRef]
- Zigrang, D.J.; Sylvester, N.D. An explicit equation for particle settling velocities in solid-liquid systems. AIChE J. 1981, 27, 1043–1044. [Google Scholar] [CrossRef]
- Fu, Z.J.; Zhu, J.S. Characterization of the Effective Density for the Separation of Immersed Objects in the Gas-Solid Fluidized Bed Coal Beneficiator. Ind. Eng. Chem. Res. 2023, 62, 17236–17242. [Google Scholar] [CrossRef]

| Shape | Length (mm) | Width (mm) | Height (mm) | Dp (mm) | Φ | Density (g/cm3) |
|---|---|---|---|---|---|---|
| Cuboid | 45 | 15 | 22 | 30.50 | 0.45 | 2.0–2.3 |
| 22 | 12 | 15 | 19.63 | 0.47 | ||
| 25 | 18 | 21 | 26.23 | 0.42 | ||
| 39 | 14 | 16 | 25.55 | 0.49 | ||
| 30 | 12 | 23 | 25.10 | 0.45 | ||
| 48 | 29 | 40 | 47.38 | 0.36 | ||
| Cube | 15 | 15 | 15 | 18.61 | 0.45 | 2.0–2.3 |
| 20 | 20 | 20 | 24.81 | 0.42 | ||
| 23 | 23 | 23 | 28.54 | 0.40 | ||
| 39 | 39 | 39 | 48.39 | 0.35 | ||
| 30 | 30 | 30 | 37.22 | 0.38 | ||
| 18 | 18 | 18 | 22.33 | 0.43 | ||
| Cylinder | 45 | 39 | 45 | 49.11 | 0.35 | 2.0–2.3 |
| 44 | 44 | 44 | 50.37 | 0.34 | ||
| 29 | 20 | 20 | 25.91 | 0.42 | ||
| 47 | 16 | 16 | 26.23 | 0.51 | ||
| 20 | 19 | 20 | 22.51 | 0.42 | ||
| 24 | 17 | 24 | 24.49 | 0.42 | ||
| 45 | 14 | 14 | 23.65 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Fu, Y.; He, Y.; Sun, L. Study on Separation Kinetics of Non-Spherical Single Feeding Particle in the Gas–Solid Separation Fluidized Bed. Separations 2024, 11, 341. https://doi.org/10.3390/separations11120341
Fan X, Fu Y, He Y, Sun L. Study on Separation Kinetics of Non-Spherical Single Feeding Particle in the Gas–Solid Separation Fluidized Bed. Separations. 2024; 11(12):341. https://doi.org/10.3390/separations11120341
Chicago/Turabian StyleFan, Xuchen, Yuping Fu, Yongliang He, and Liying Sun. 2024. "Study on Separation Kinetics of Non-Spherical Single Feeding Particle in the Gas–Solid Separation Fluidized Bed" Separations 11, no. 12: 341. https://doi.org/10.3390/separations11120341
APA StyleFan, X., Fu, Y., He, Y., & Sun, L. (2024). Study on Separation Kinetics of Non-Spherical Single Feeding Particle in the Gas–Solid Separation Fluidized Bed. Separations, 11(12), 341. https://doi.org/10.3390/separations11120341






