Hydrogen–Water Isotope Catalytic Exchange Process Analysis by Simulation
Abstract
:1. Introduction
2. Process Modeling
2.1. Pure Component Properties
2.2. Reaction Equations
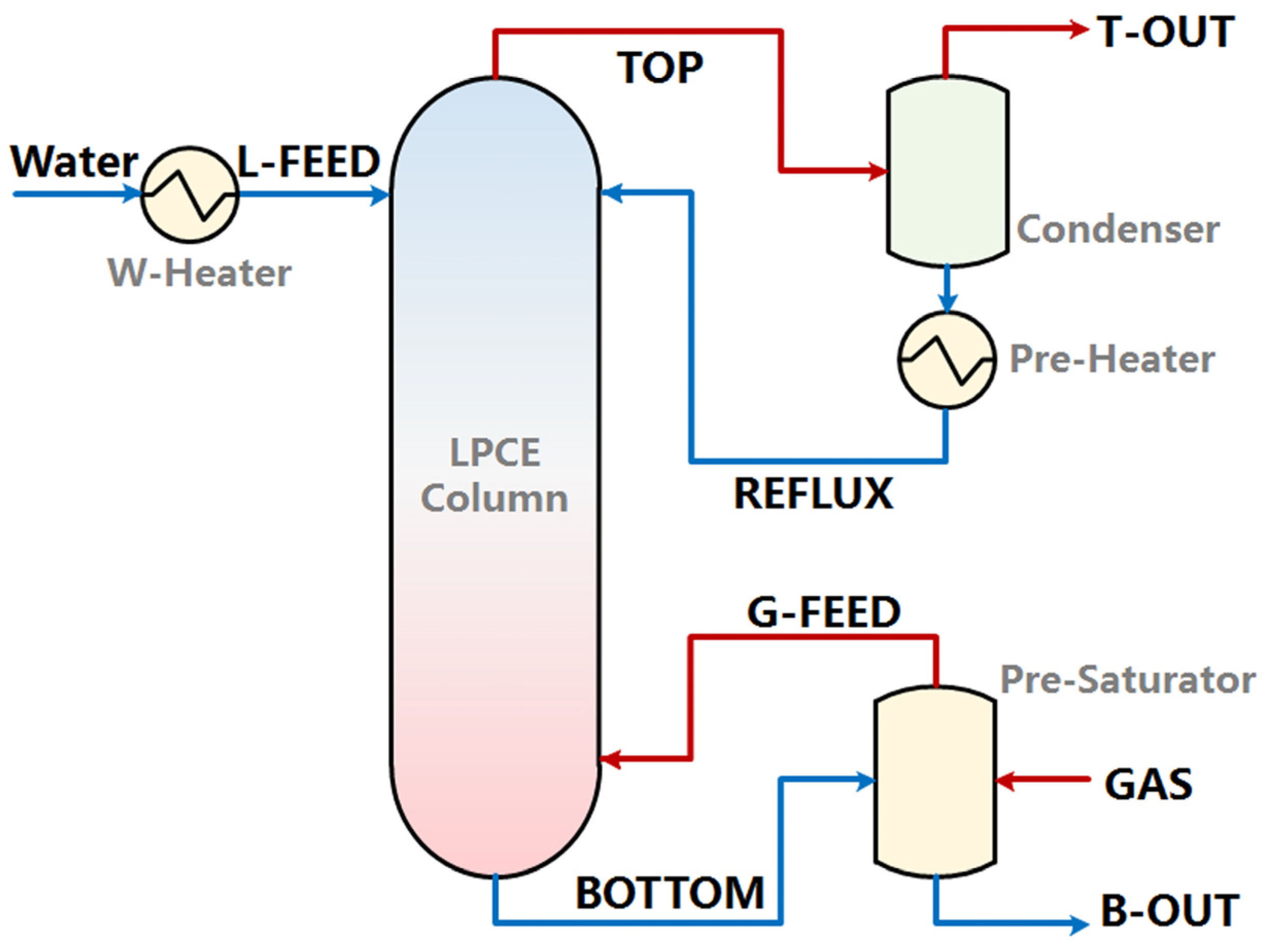
2.3. Simulation Process
3. Result and Discussion
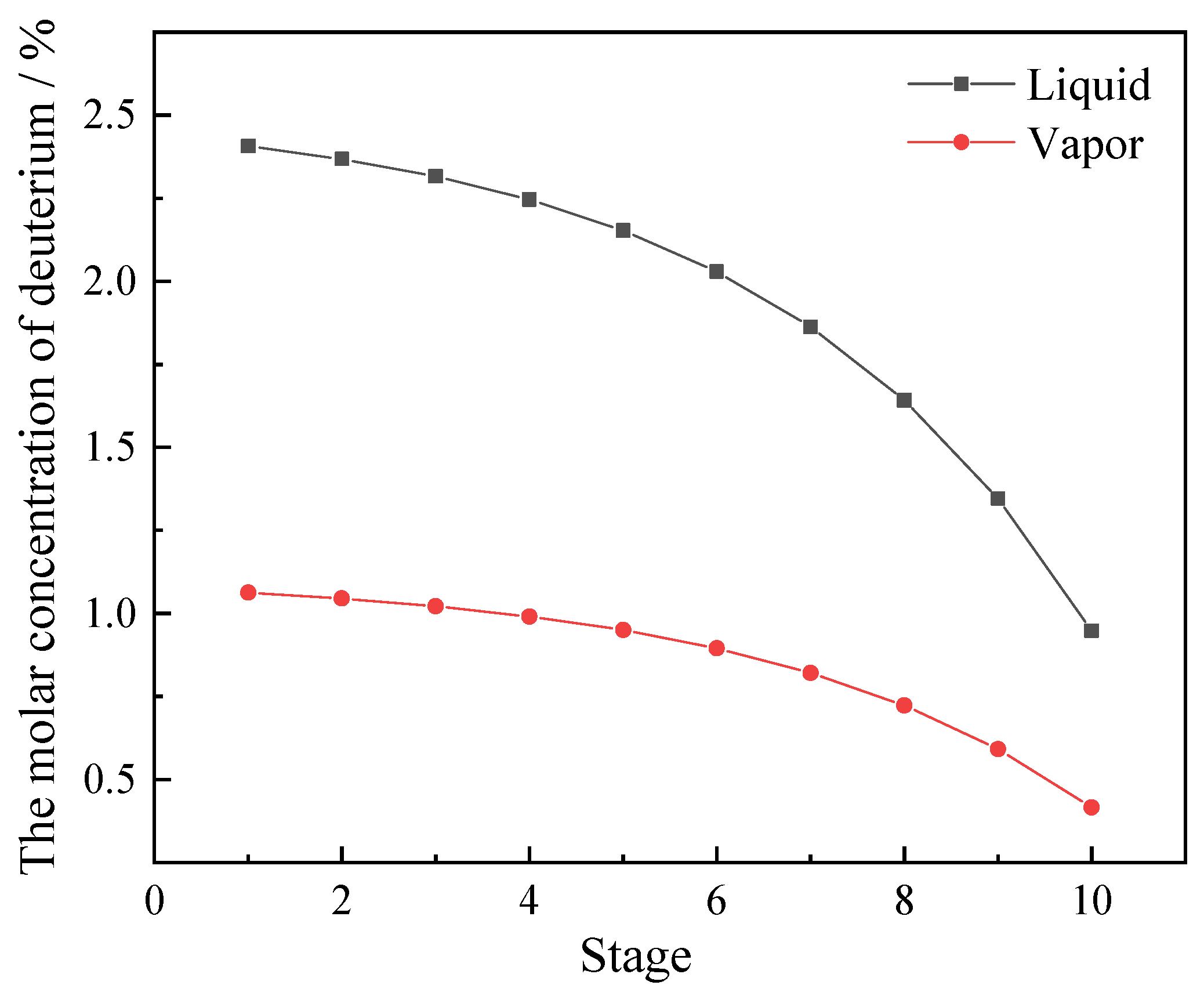
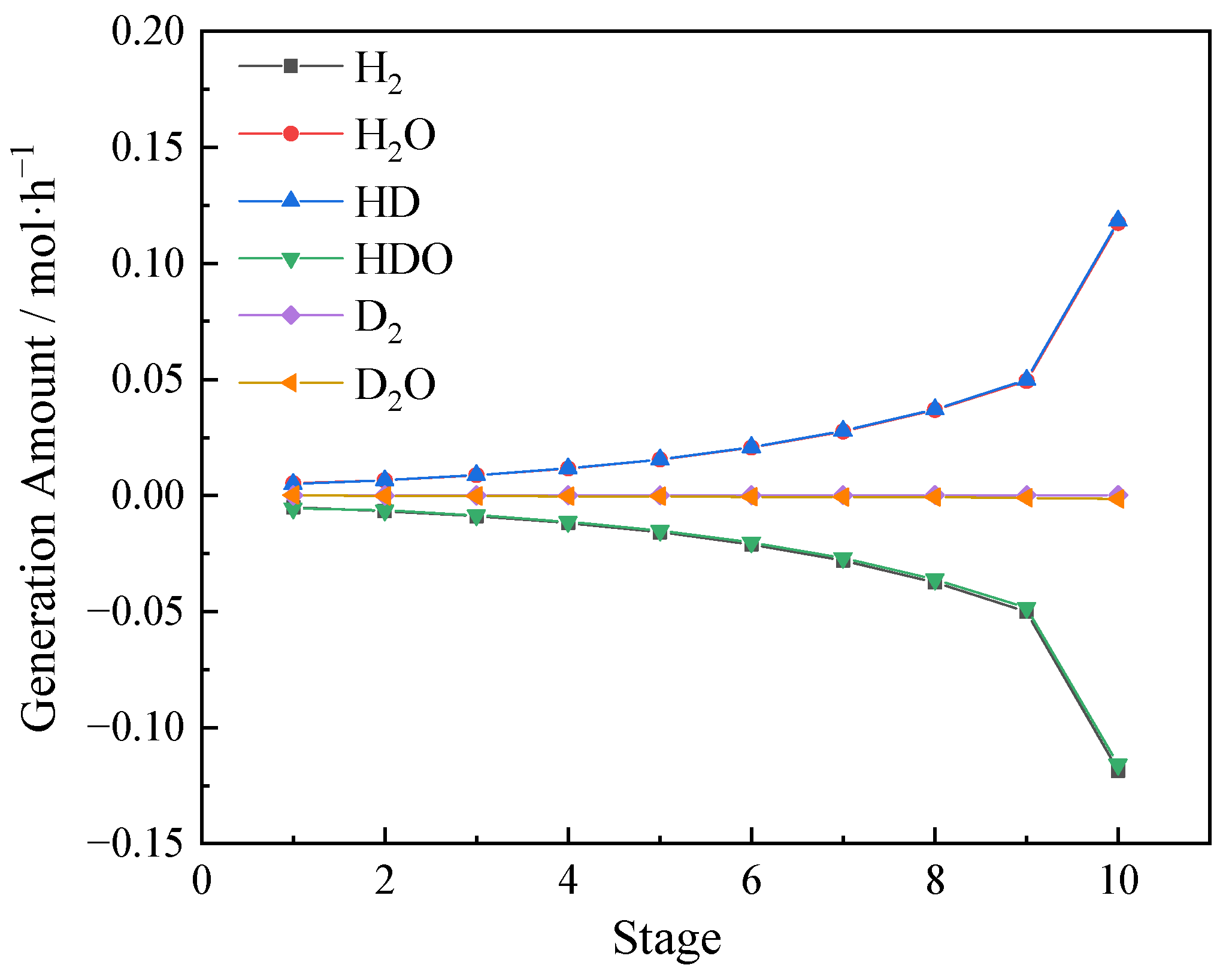
3.1. Reaction Process Analysis
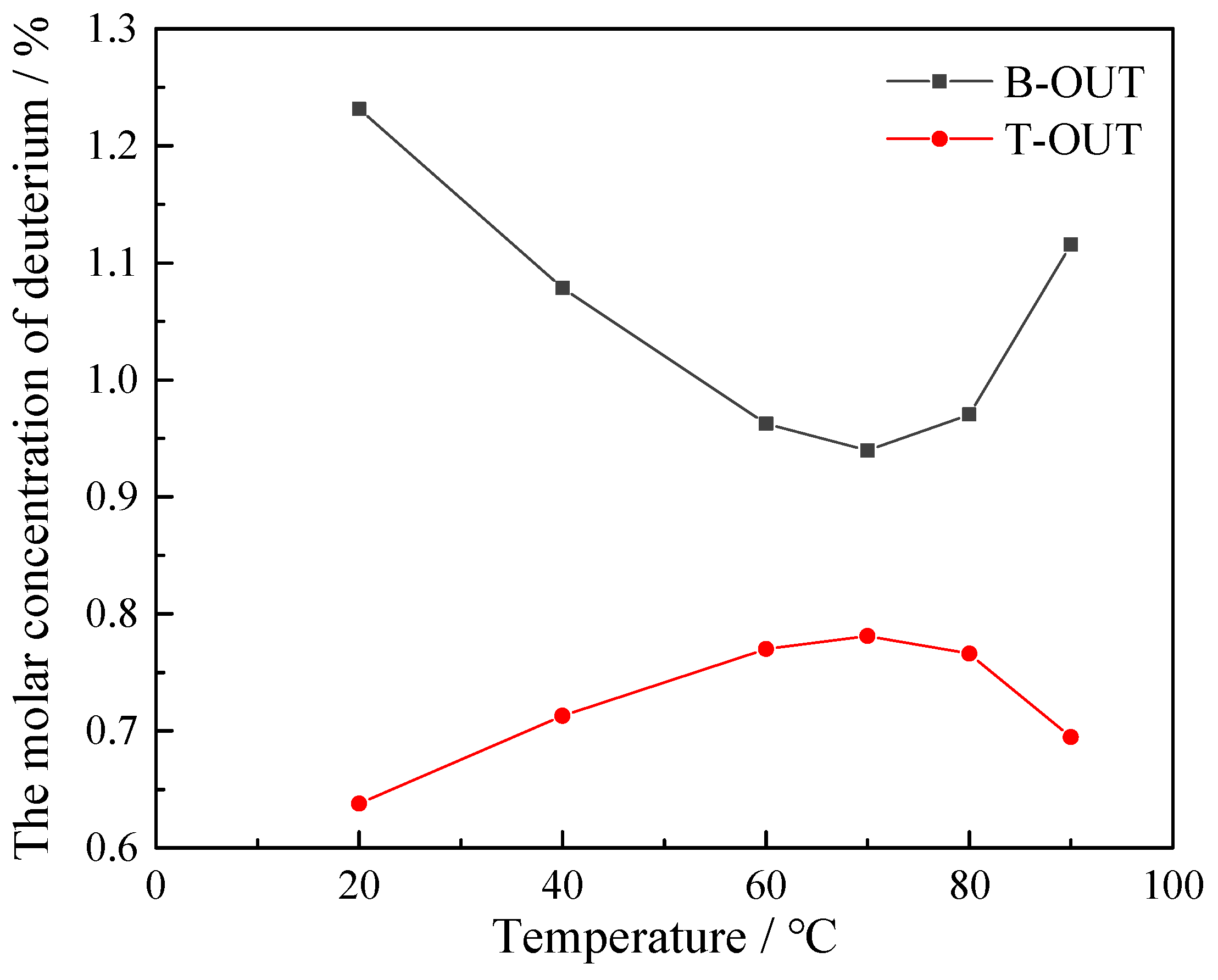
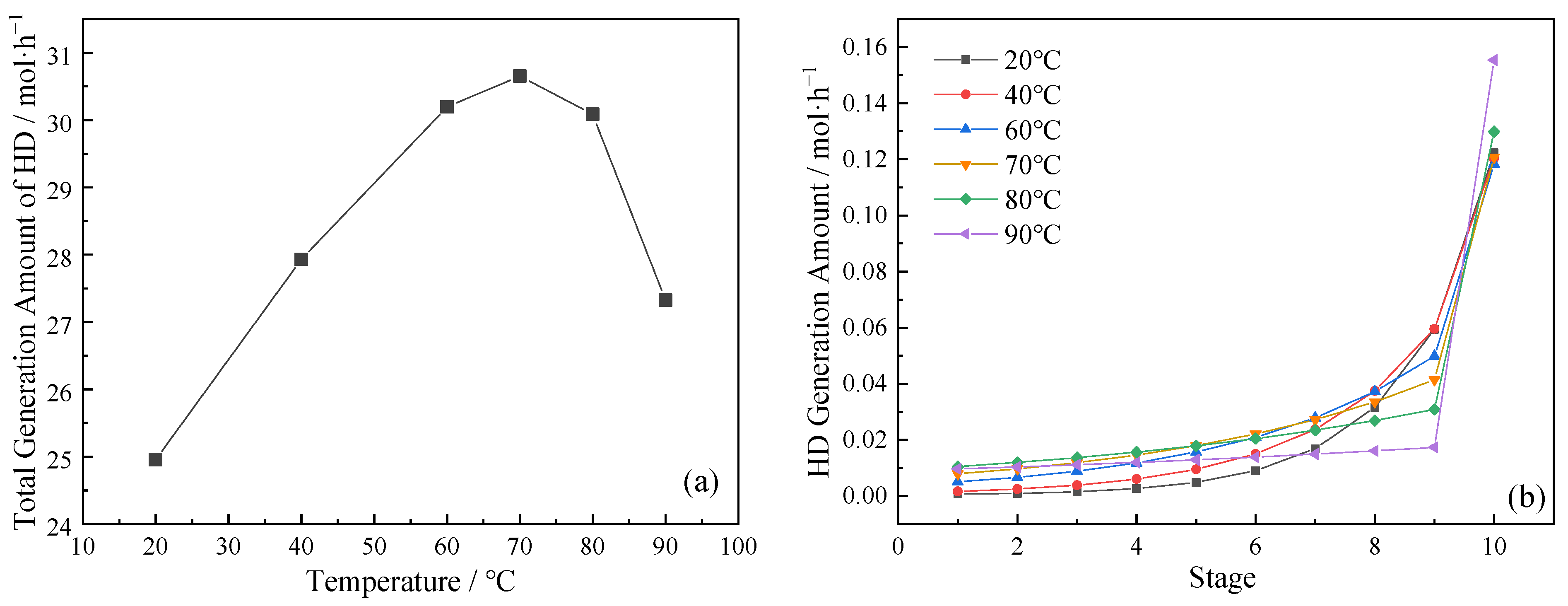
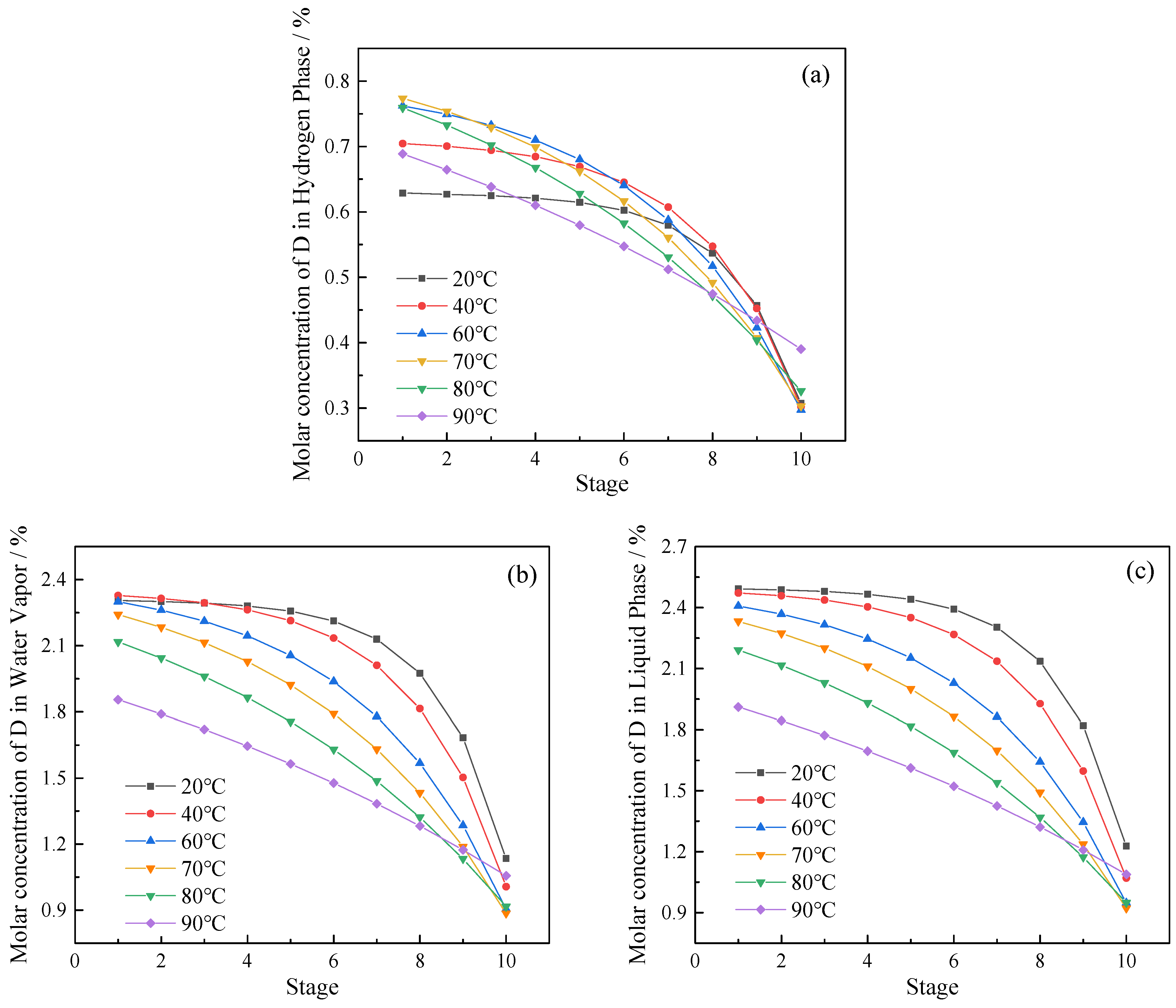
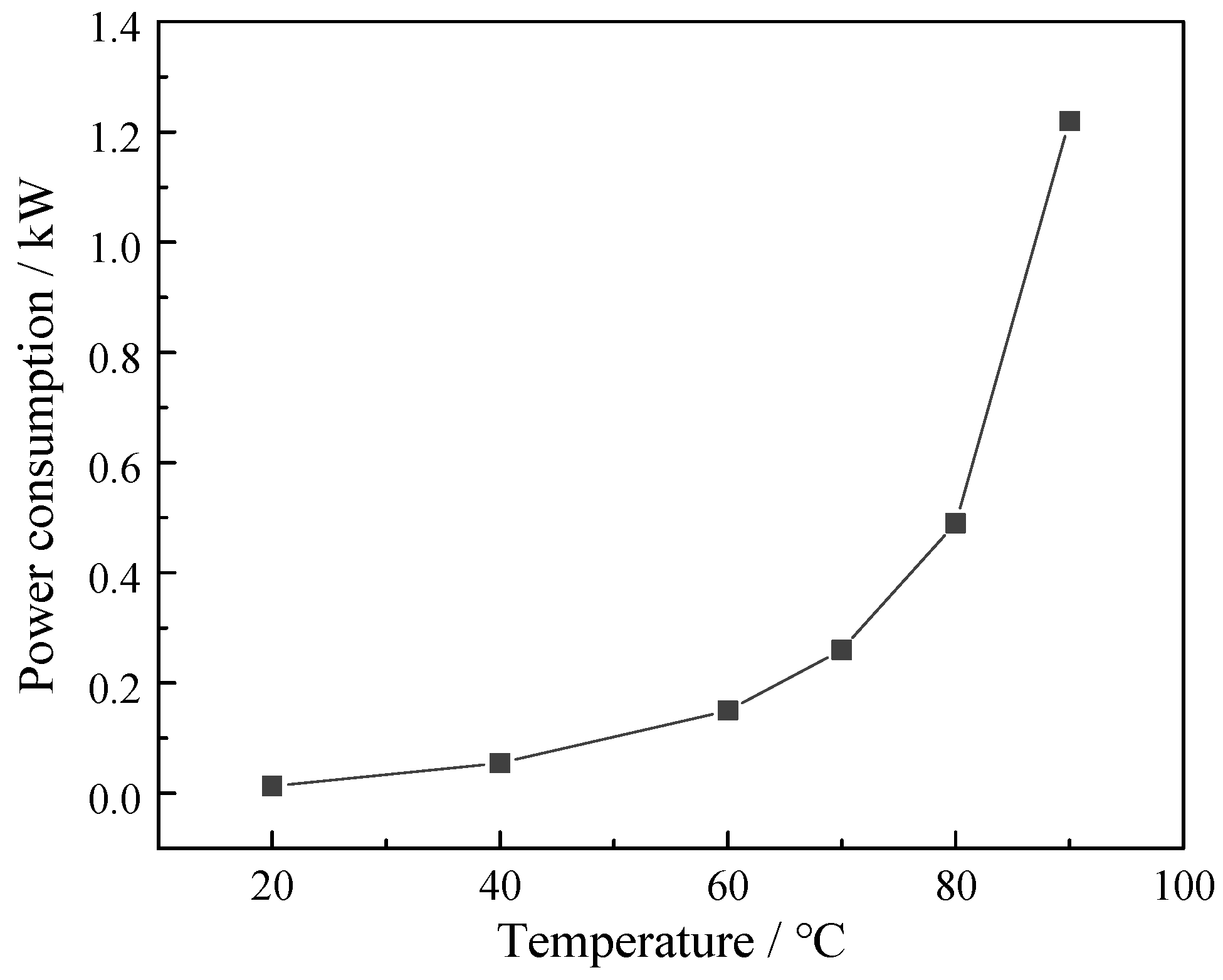
3.2. Effect of Operating Temperature
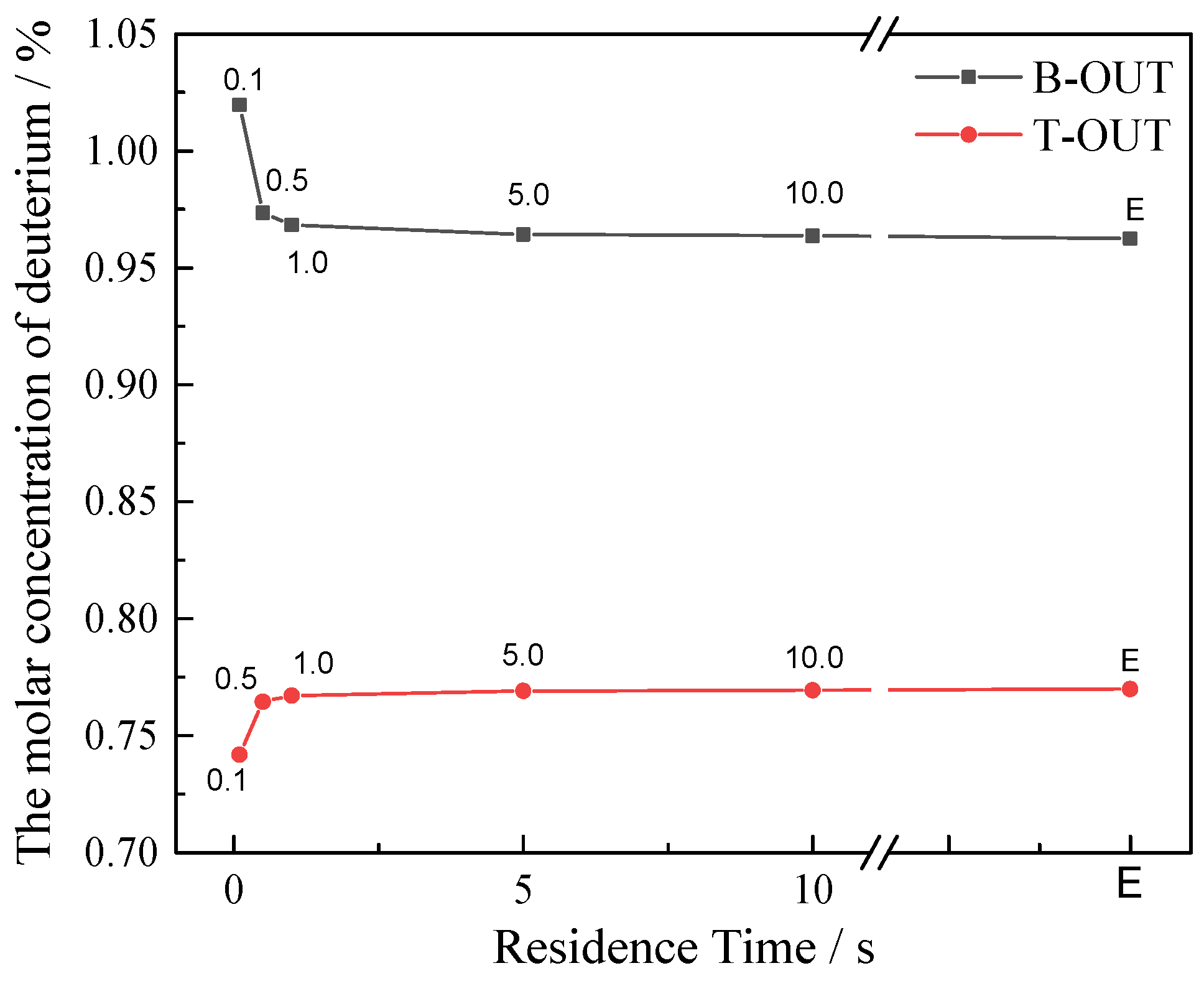
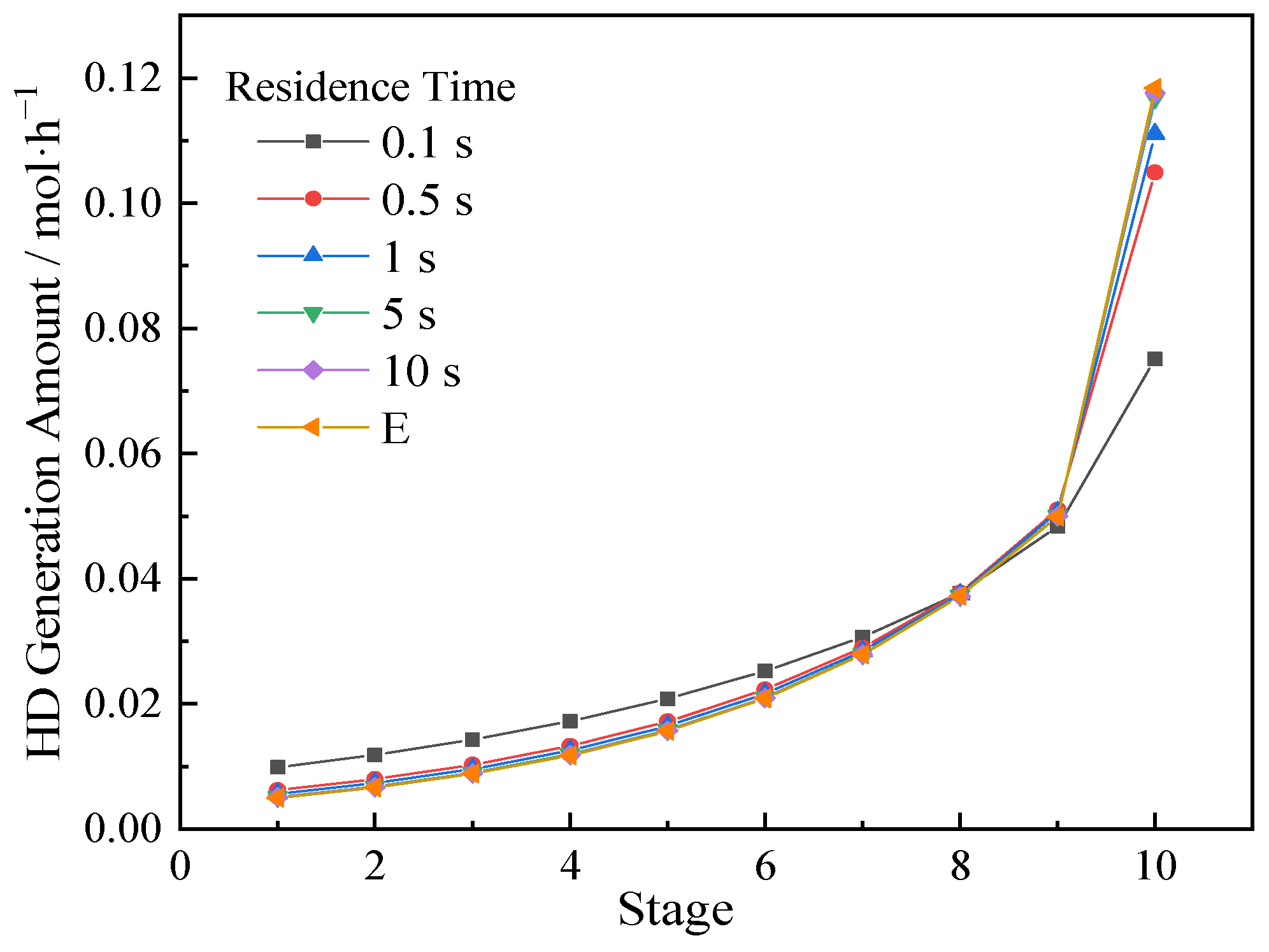
3.3. Effect of Reaction Kinetic Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bukin, A.N.; Marunich, S.; Pak, Y.; Rastunova, I.; Rozenkevich, M.; Chebotov, A.Y. Specific features and current status of processes for tritium removal from water: A critical review. Fusion Sci. Technol. 2022, 78, 595–606. [Google Scholar] [CrossRef]
- Galley, M.R. Future Trends in Heavy Water Production; Atomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1983. [Google Scholar]
- Ridzuan, N.D.M.; Ayodele, B.V.; Talib, N.N.A.; Shaharun, M.S.; Shariff, A.M.; Ahmad, K.N. Synthesis and characterization of hydrophobic nickel catalyst supported on different oxides for continuous liquid phase catalytic exchange reaction. J. Ind. Eng. Chem. 2024, in press. [Google Scholar] [CrossRef]
- Bondarenko, S.D.; Alekseev, I.A.; Fedorchenko, O.A.; Konoplev, K.A.; Vasyanina, T.V. Conceptual design of multi-purpose heavy water detritiation plant. Fusion Sci. Technol. 2017, 71, 605–609. [Google Scholar] [CrossRef]
- Butler, J.P. Hydrogen isotope separation by catalyzed exchange between hydrogen and liquid water. Sep. Sci. Technol. 1980, 15, 371–396. [Google Scholar] [CrossRef]
- Rae, H.K. Selecting heavy water processes. In The Separation of Hydrogen Isotopes; Rae, H.K., Ed.; American Chemical Society: Washington, DC, USA, 1978; Volume 68, pp. 1–26. ISBN 9780841204201. [Google Scholar]
- Ye, L.; Luo, D.; Tang, T.; Yang, W.; Yang, Y. Hydrogen isotope separation in hydrophobic catalysts between hydrogen and liquid water. Fusion Eng. Des. 2015, 100, 576–580. [Google Scholar] [CrossRef]
- Shi, Z.; Xiong, Y.; Wu, H. Preparation and hydrogen sorption performance of Ti-based hydrogen-absorbing materials without activation. Chin. J. Rare Met. 2022, 46, 1567–1572. [Google Scholar]
- Song, K.M.; Sohn, S.H.; Kang, D.W.; Paek, S.W.; Ahn, D.H. Installation of liquid phase catalytic exchange columns for the Wolsong tritium removal facility. Fusion Eng. Des. 2007, 82, 2264–2268. [Google Scholar] [CrossRef]
- Bondarenko, S.D.; Alekseev, I.A.; Fedorchenko, O.A.; Vasyanina, T.V. The current status of the heavy water detritiation facility at the NRC (Kurchatov Institute)–PNPI. Fusion Sci. Technol. 2020, 76, 690–695. [Google Scholar] [CrossRef]
- Wan, C.; Zhou, L.; Xu, S.; Jin, B.; Ge, X.; Qian, X.; Cheng, D.G. Defect engineered mesoporous graphitic carbon nitride modified with AgPd nanoparticles for enhanced photocatalytic hydrogen evolution from formic acid. Chem. Eng. J. 2022, 429, 132388. [Google Scholar] [CrossRef]
- Miller, A.I. Heavy water: A manufacturer’s guide for the hydrogen century. Can. Nucl. Soc. Bull. 2001, 22, 1–14. [Google Scholar]
- Lu, Z.; Li, J.; Fu, X.; Hou, J.; Ran, G.; Xiao, C.; Wang, X. Superhydrophobic Pt@SBA-15 catalyst for hydrogen water isotope exchange reactions. Int. J. Hydrogen Energy 2022, 47, 18080–18087. [Google Scholar] [CrossRef]
- Fedorchenko, O.A.; Alekseev, I.A.; Bondarenko, S.D.; Vasyanina, T.V. Recent progress in the experimental study of LPCE process on “eVIO” pilot plant. Fusion Sci. Technol. 2017, 71, 432–437. [Google Scholar] [CrossRef]
- Bornea, A.M.; Zamfirache, M.V. The influence of the extraction of gas/liquid samples on the isotopic separation regime of the CECE process. Fusion Eng. Des. 2024, 201, 114293. [Google Scholar] [CrossRef]
- Mistry, K.A.; Shenoy, N.S.; Bhanja, K.; Kohli, D.K.; Shenoy, K.T. Modeling and experimental investigation for development of Combined Electrolysis and Catalytic Exchange process for hydrogen isotope separation. Chem. Eng. Res. Des. 2023, 192, 487–499. [Google Scholar] [CrossRef]
- Ye, L.; Luo, D.; Tang, T.; Yang, W.; Zhao, P. Process simulation for hydrogen/deuterium exchange in a packed column. Int. J. Hydrogen Energy 2014, 39, 6604–6609. [Google Scholar] [CrossRef]
- Busigin, A.; Sood, S. FLOSHEET-A computer program for simulating hydrogen isotope separation systems. Fusion Technol. 1988, 14, 529–535. [Google Scholar] [CrossRef]
- Bornea, A.; Petrutiu, C.; Zamfirache, M. Complex software dedicated for design and simulation of LPCE process for heavy water detritiation. Fusion Sci. Technol. 2015, 67, 270–273. [Google Scholar] [CrossRef]
- Fedorchenko, O.A.; Alekseev, I.A.; Bondarenko, S.D.; Vasyanina, T.V. Experimental results and experience with the LPCE process. Fusion Sci. Technol. 2020, 76, 341–346. [Google Scholar] [CrossRef]
- Yang, B.; Wu, J.; Zhao, G.; Wang, H.; Lu, S. Multiplicity analysis in reactive distillation column using ASPEN PLUS. Chin. J. Chem. Eng. 2006, 14, 301–308. [Google Scholar] [CrossRef]
- Meng, W.X.; Banerjee, S.; Zhang, X.; Agarwal, R.K. Process simulation of multi-stage chemical-looping combustion using Aspen Plus. Energy 2015, 90, 1869–1877. [Google Scholar] [CrossRef]
- Noh, J.; Fulgueras, A.M.; Sebastian, L.J.; Lee, H.G.; Kim, D.S.; Cho, J. Estimation of thermodynamic properties of hydrogen isotopes and modeling of hydrogen isotope systems using Aspen Plus simulator. J. Ind. Eng. Chem. 2017, 46, 1–8. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, Q.; Shi, W.; Chen, H. Hydrogen isotope inventory evaluation of hydrogen isotopes separation system of CFETR using Aspen Plus simulator. Fusion Eng. Des. 2022, 177, 113078. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Aldehani, M.; Alzahrani, F.; An tSaoir, M.N. Kinetics and reactive stripping modelling of hydrogen isotopic exchange of deuterated waters. Chem. Eng. Process. Process Intensif. 2016, 108, 58–73. [Google Scholar] [CrossRef]
- Yamanishi, T.; Okuno, K. A Computer Code Simulating Multistage Chemical Exchange Column under Wide Range of Operating Conditions; JAERI-DATA/CODE-96-028; Japan Atomic Energy Research Institute: Tokyo, Japan, 1996. [Google Scholar]
- Butler, J.P.; Rolston, J.H.; Stevens, W.H. Novel Catalysts for Isotopic Exchange between Hydrogen and Liquid Water. In The Separation of Hydrogen Isotopes; Rae, H.K., Ed.; American Chemical Society: Washington, DC, USA, 1978; Volume 68, pp. 93–109. ISBN 9780841204201. [Google Scholar]
- Bornea, A.; Ana, G.; Balteanu, O.; Bidica, N.; Bucur, C.; Ionita, G.; Zamfirache, M. New catalytic packing performance: Theoretical and experimental characterization for LPCE process. Fusion Eng. Des. 2019, 146, 2384–2388. [Google Scholar] [CrossRef]
- Li, P.; Guo, L.; Xiong, R.; Luo, J.; Wen, M.; Yao, Y.; Zhang, Z.; Song, J.; Shi, Y.; Tang, T. Separation process study of liquid phase catalytic exchange reaction based on the Pt/C/PTFE catalysts. Chin. J. Chem. Eng. 2019, 27, 1837–1845. [Google Scholar] [CrossRef]
- Iwai, Y.; Misaki, Y.; Hayashi, T.; Yamanishi, T.; Konishi, S.; Nishi, M.; Ninomiya, R.; Yanagimachi, S.; Senrui, S.; Yoshida, H. The water detritiation system of the ITER tritium plant. Fusion Sci. Technol. 2002, 41, 1126–1130. [Google Scholar] [CrossRef]
- Alekseev, I.; Bondarenko, S.; Fedorchenko, O.; Konoplev, K.A.; Vasyanina, T.V.; Arkhipov, E.A.; Uborsky, V.V. Development of a heavy water detritiation plant for PIK reactor. Fusion Sci. Technol. 2005, 48, 286–289. [Google Scholar] [CrossRef]

| Parameters | Unit | H2 | H2O | HD | HDO | D2 | D2O |
|---|---|---|---|---|---|---|---|
| Vaporization Enthalpy | kJ/mol | 0.90 | 40.69 | 1.04 | 40.68 | 1.19 | 41.45 |
| Freeze Point | °C | −259.20 | 0.00 | −256.55 | 1.91 | −254.42 | 3.81 |
| Dipole Moment | debye | 0.00 | 1.85 | 0.00 | 1.82 | 0.00 | 1.78 |
| Molecular Weight | 2.02 | 18.02 | 3.02 | 19.02 | 4.03 | 20.03 | |
| Omega | −0.22 | 0.34 | −0.18 | 0.36 | −0.14 | 0.37 | |
| Critical Pressure | kPa | 1313.0 | 22,064.0 | 1484.0 | 21,867.5 | 1661.7 | 21,671.0 |
| Standard Specific Gravity | 0.30 | 1.00 | 0.30 | 1.05 | 0.30 | 1.11 | |
| Boiling Point | K | 20.39 | 373.15 | 22.29 | 374.00 | 23.65 | 374.57 |
| Critical Temperature | K | 33.19 | 647.10 | 35.91 | 645.64 | 38.35 | 643.89 |
| Triple Point Temperature | °C | −259.20 | 0.01 | −256.55 | 1.92 | −254.42 | 3.82 |
| Liquid Molar Volume at Boiling Point | cm3/mol | 28.57 | 18.83 | 26.84 | 18.84 | 25.11 | 18.85 |
| Critical Volume | cm3/mol | 64.15 | 55.95 | 62.00 | 56.12 | 60.26 | 56.30 |
| Standard Liquid Molar Volume | cm3/mol | 53.56 | 18.05 | 53.56 | 18.05 | 53.56 | 18.13 |
| Critical Compressibility Factor | 0.31 | 0.23 | 0.31 | 0.23 | 0.31 | 0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Li, J.; Xiao, C.; Wang, H.; Peng, S. Hydrogen–Water Isotope Catalytic Exchange Process Analysis by Simulation. Separations 2024, 11, 219. https://doi.org/10.3390/separations11070219
Hou J, Li J, Xiao C, Wang H, Peng S. Hydrogen–Water Isotope Catalytic Exchange Process Analysis by Simulation. Separations. 2024; 11(7):219. https://doi.org/10.3390/separations11070219
Chicago/Turabian StyleHou, Jingwei, Jiamao Li, Chengjian Xiao, Heyi Wang, and Shuming Peng. 2024. "Hydrogen–Water Isotope Catalytic Exchange Process Analysis by Simulation" Separations 11, no. 7: 219. https://doi.org/10.3390/separations11070219
APA StyleHou, J., Li, J., Xiao, C., Wang, H., & Peng, S. (2024). Hydrogen–Water Isotope Catalytic Exchange Process Analysis by Simulation. Separations, 11(7), 219. https://doi.org/10.3390/separations11070219





