Influence of Feed Rate on the Performance of Hydrocyclone Flow Field
Abstract
1. Introduction
2. Numerical Simulation Method
2.1. Modeling
2.2. Boundary Conditions
2.3. Independence Verification of Model and Grid
3. Simulation Results and Discussion
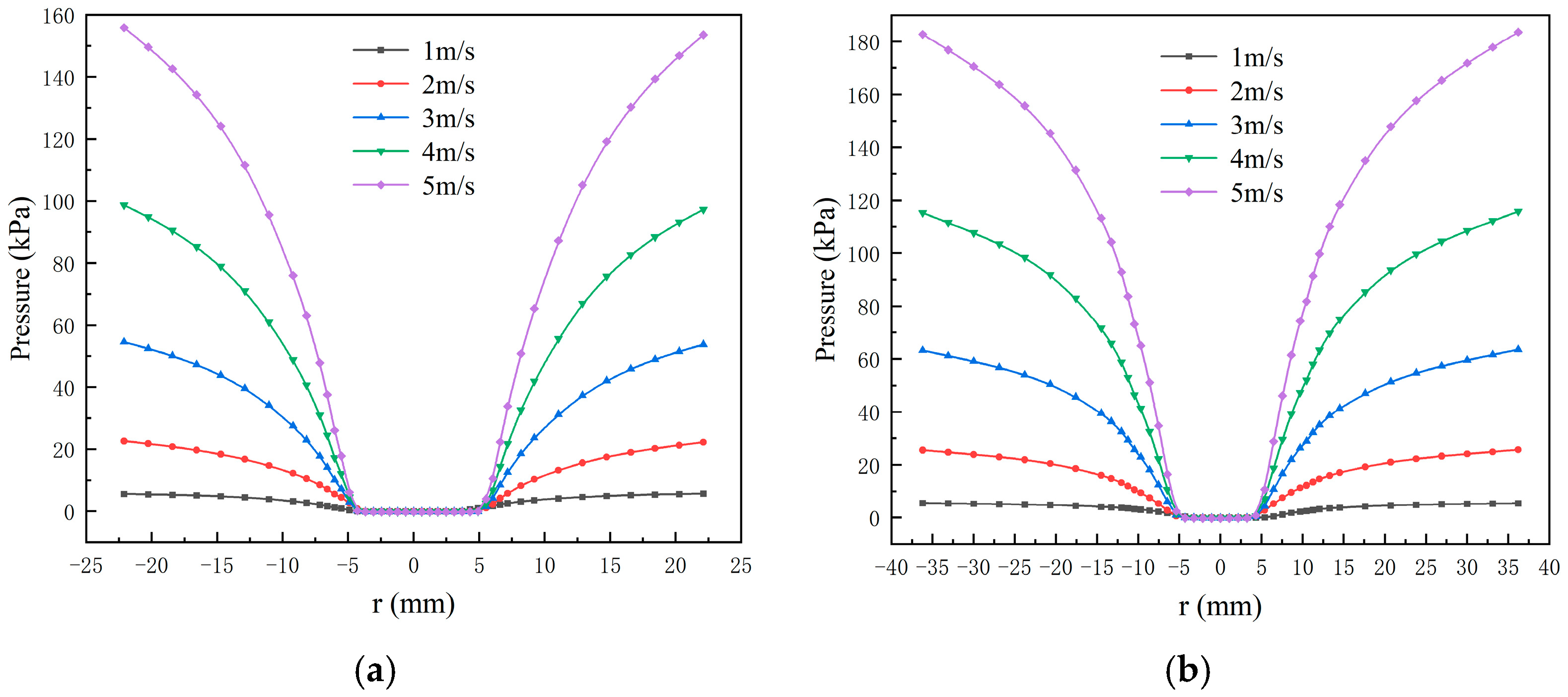
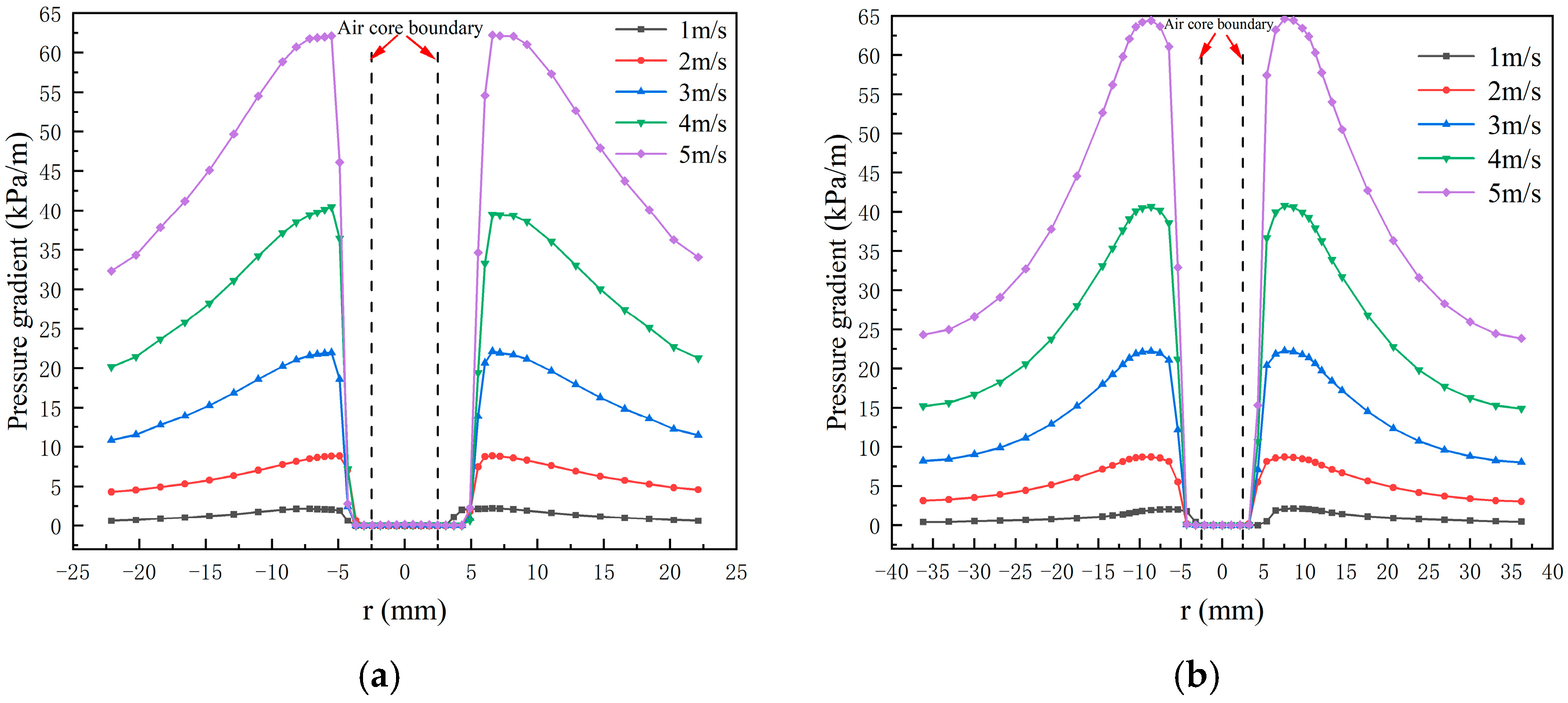
3.1. Static Pressure Distribution
3.2. Velocity Distribution
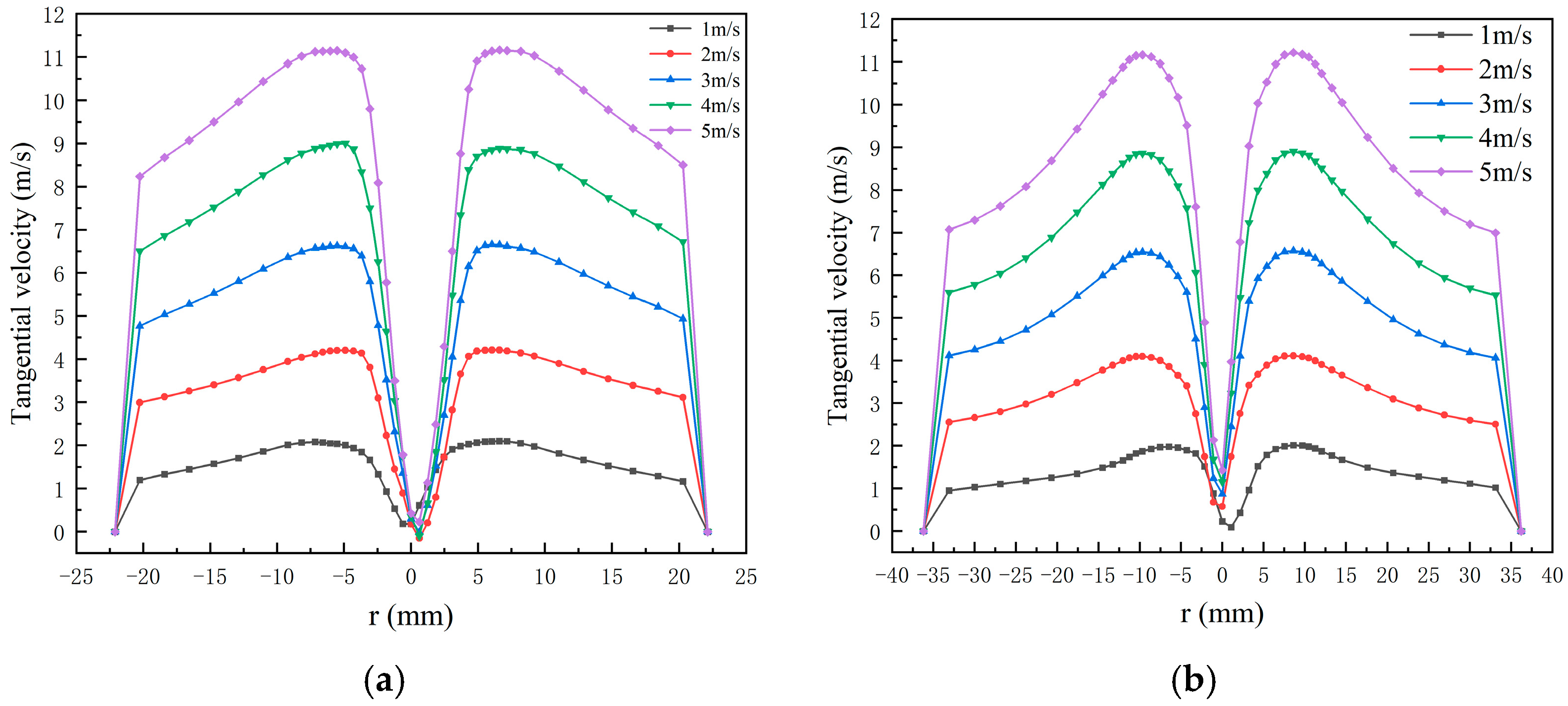
3.2.1. Distribution of Tangential Velocity
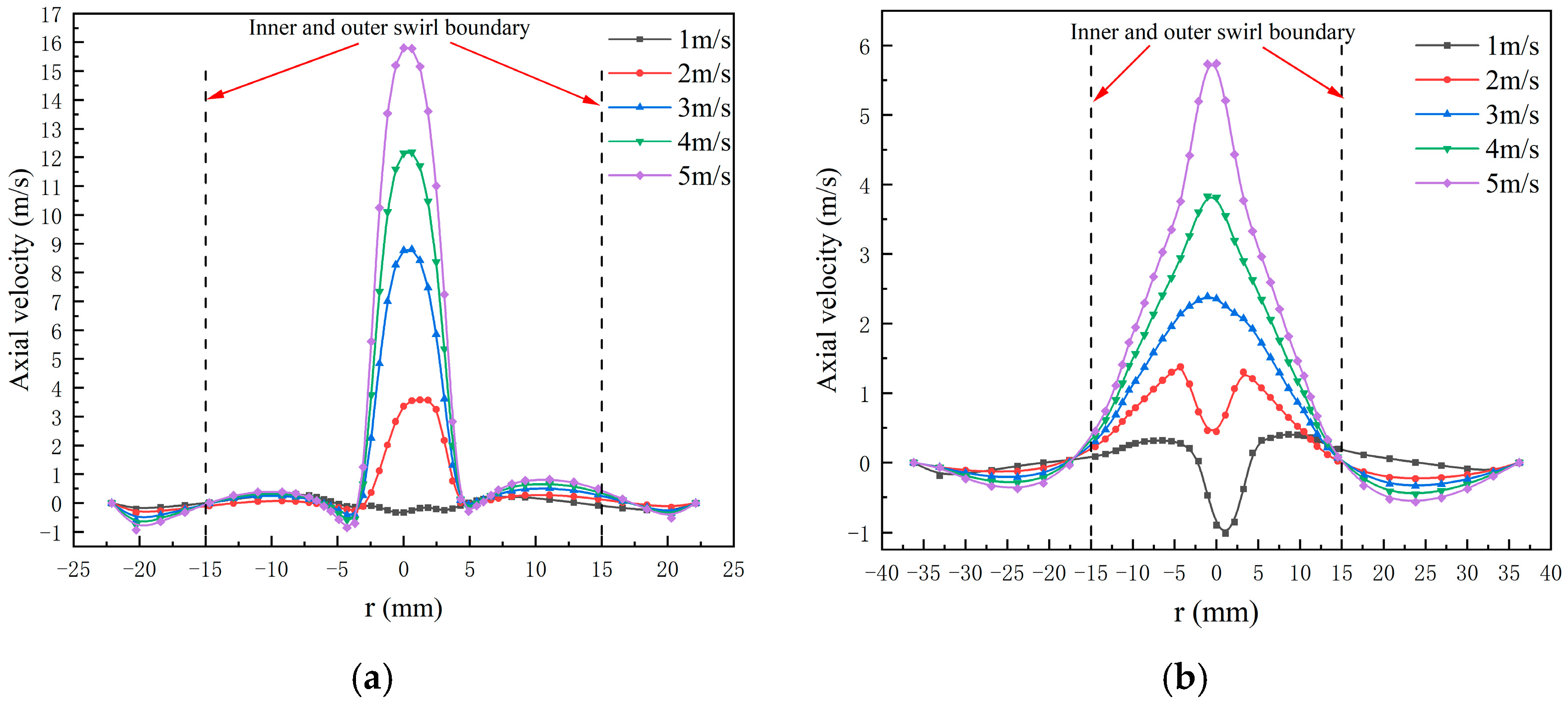
3.2.2. Distribution of Axial Velocity
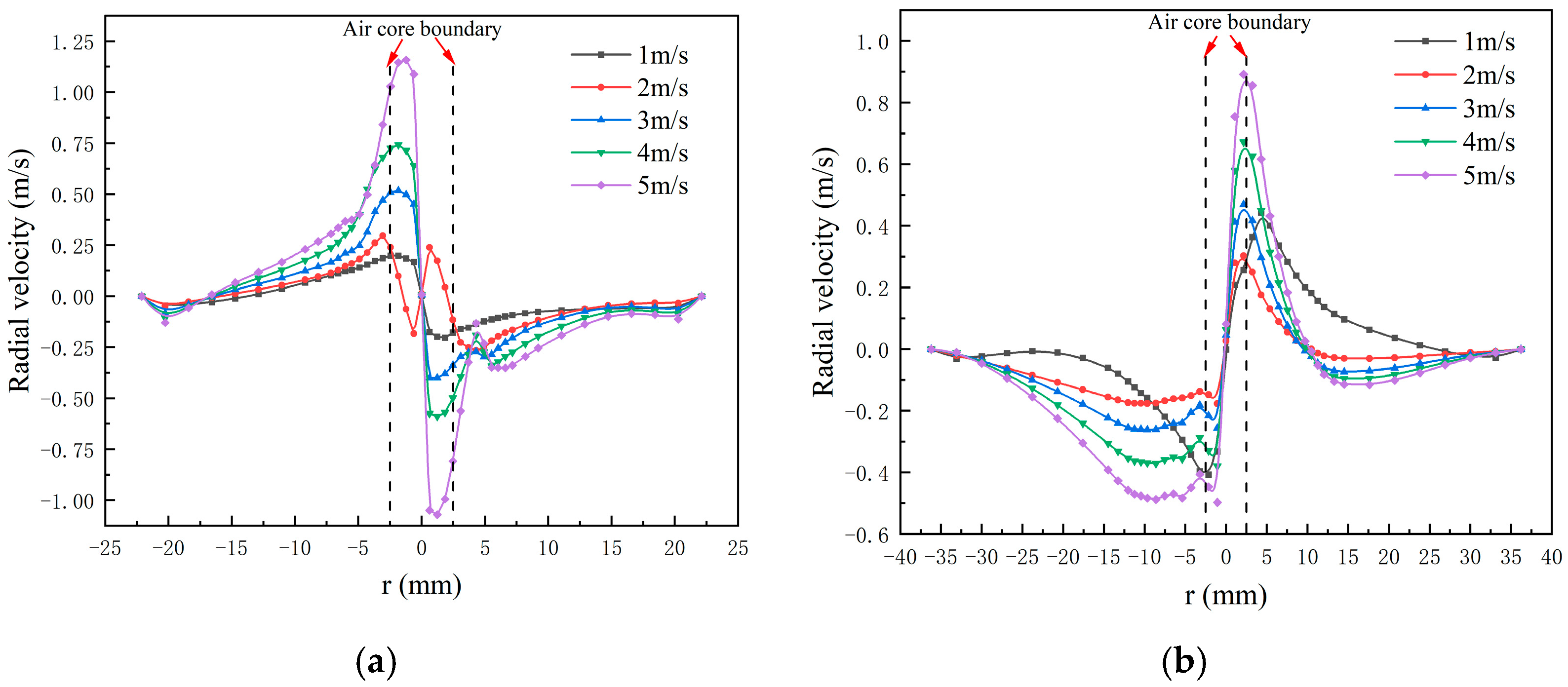
3.2.3. Distribution of Radial Velocity
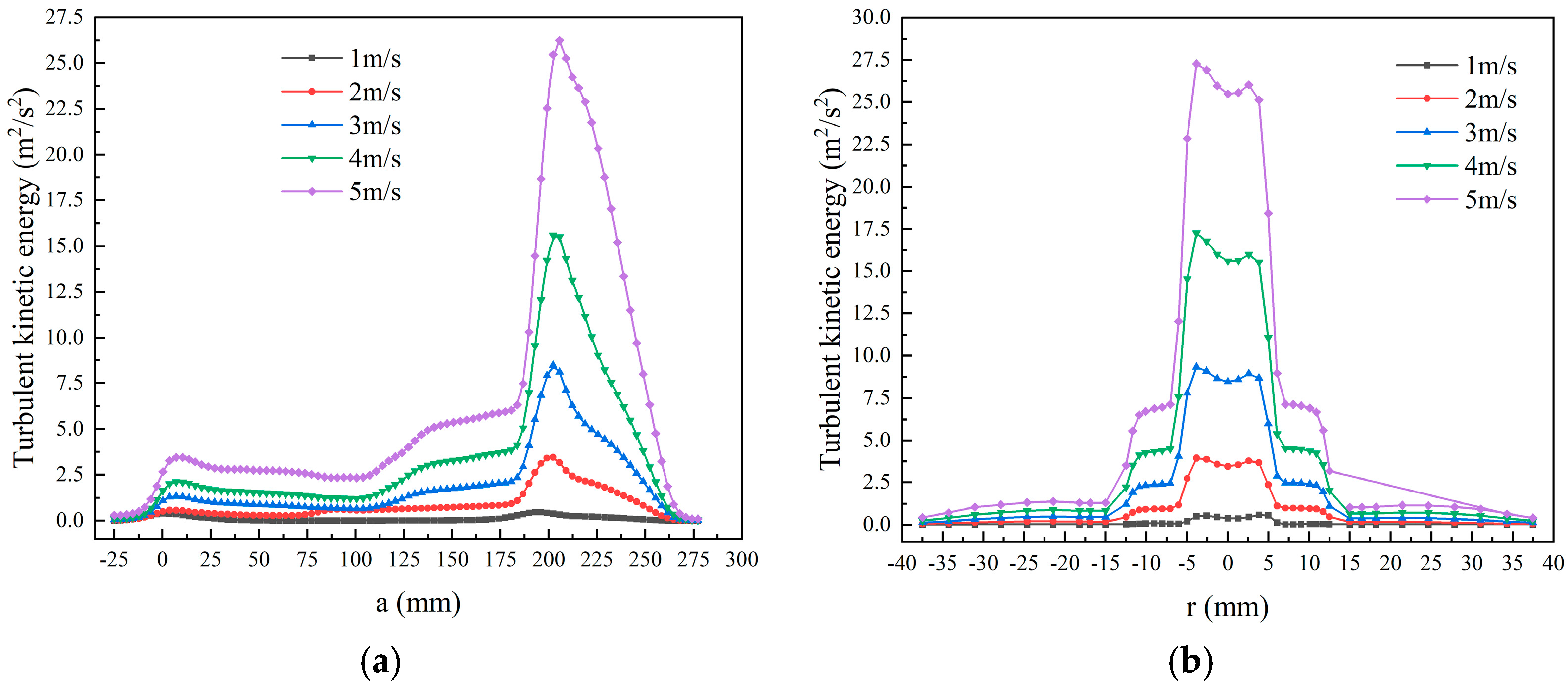
3.3. Turbulent Kinetic Energy
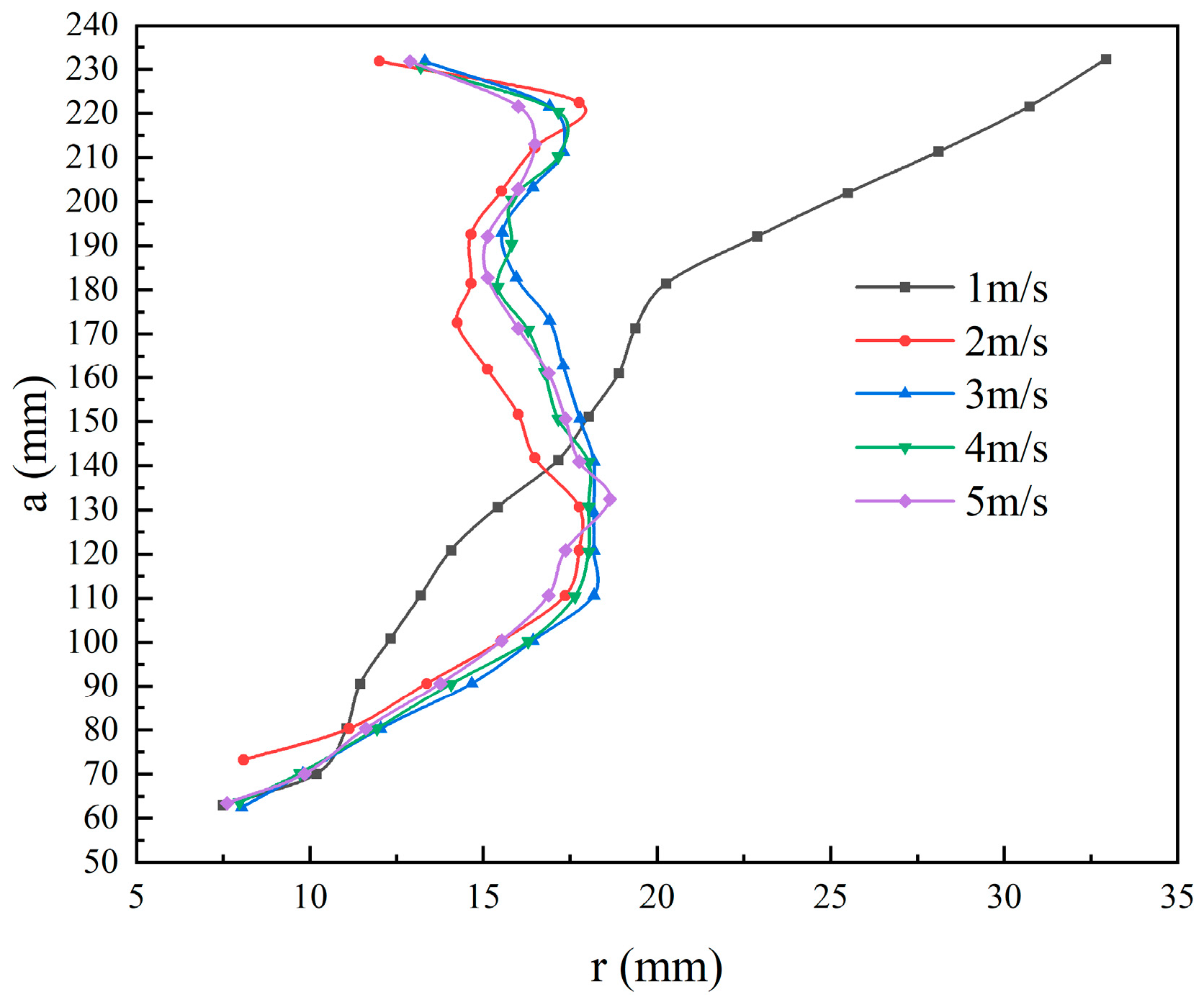
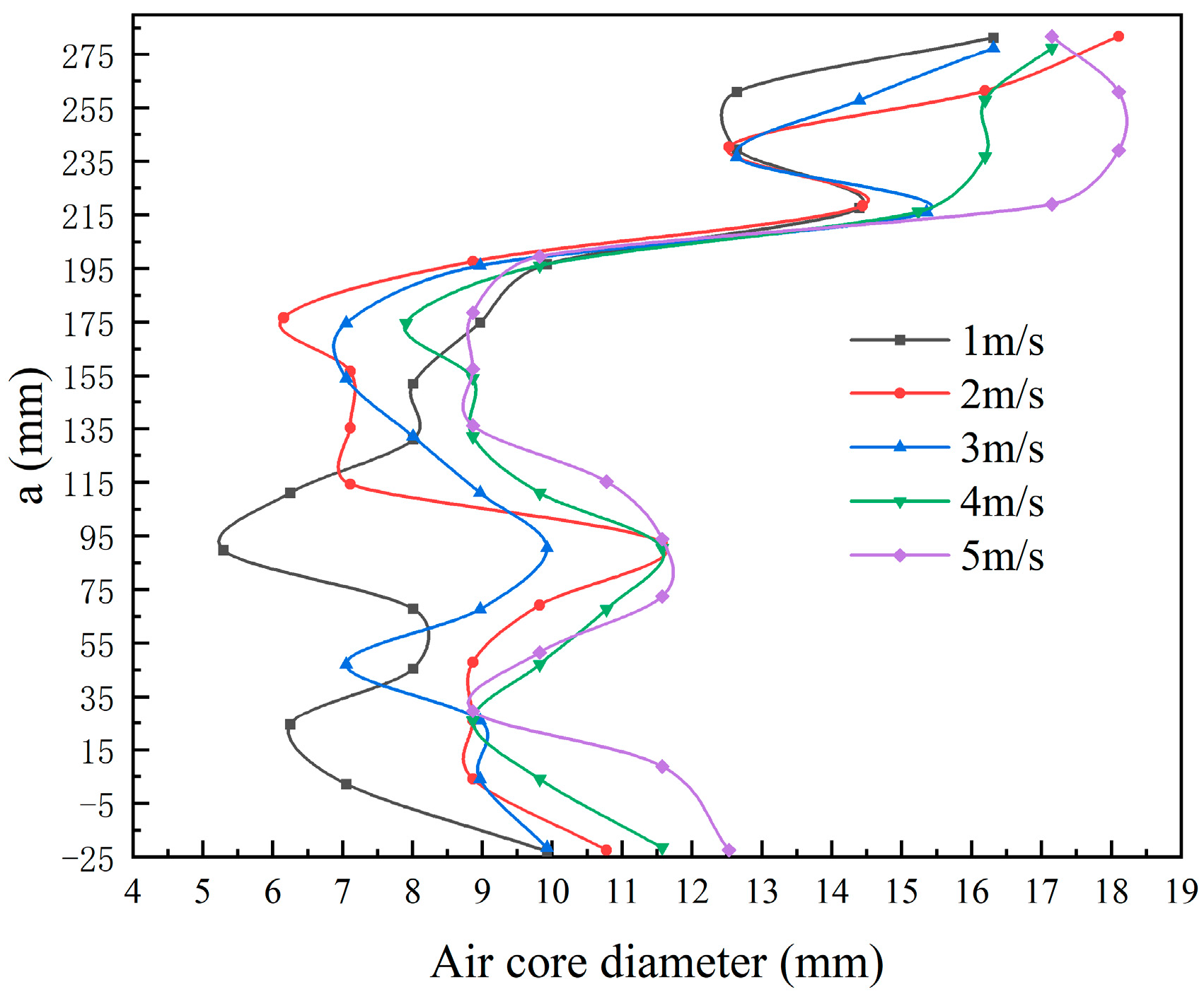
3.4. Effects of the Feed Rate at Inlet on the Air Column
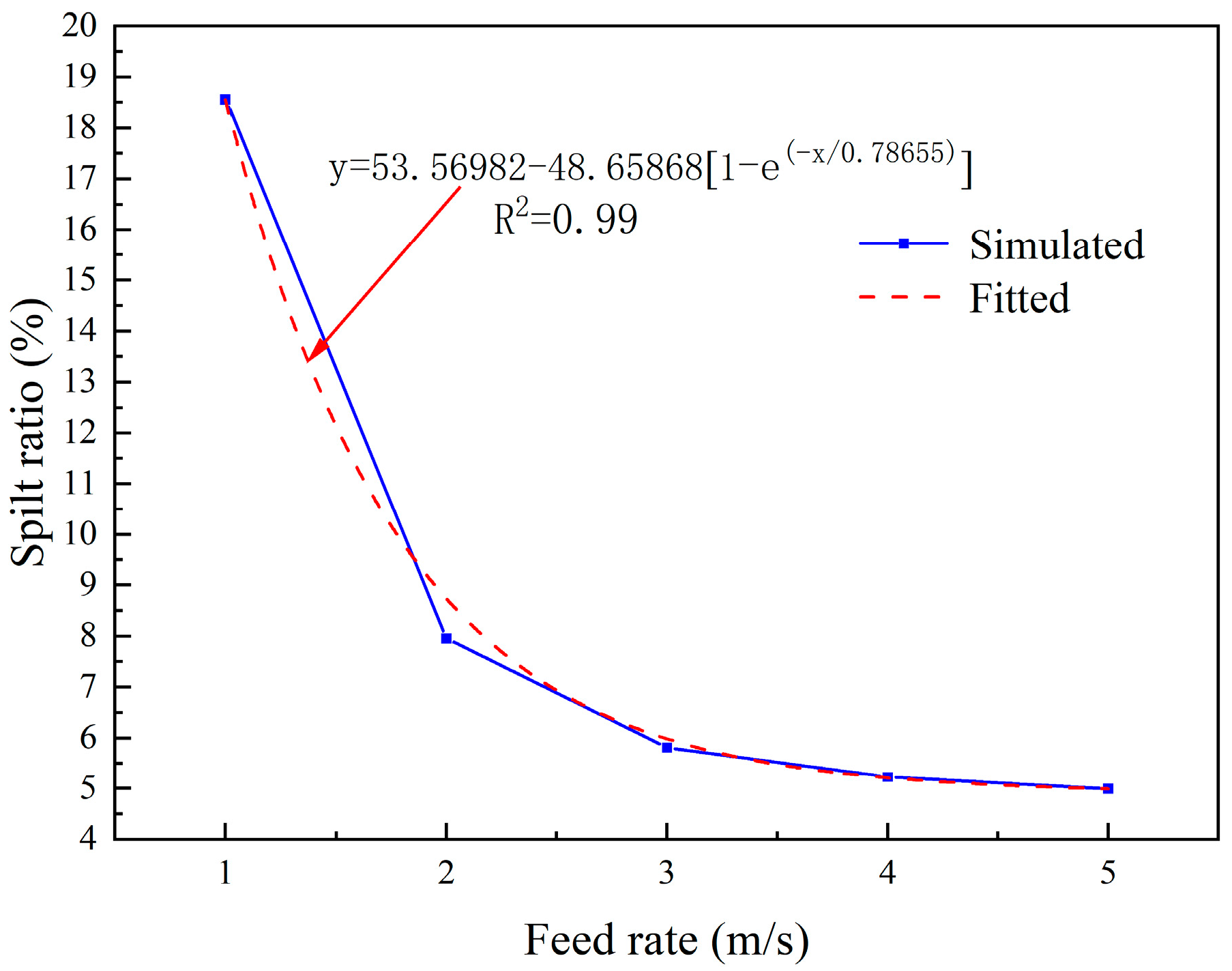
3.5. Effects of the Feed Rate at Inlet on the Split Ratio
4. Conclusions
- (1)
- Increasing the feed rate led to increased static pressure, radial pressure gradient, tangential velocity and radial velocity, and reduced the split ratio in the swirl field, which was beneficial to the separation of the two solid-liquid phases in the hydrocyclone. This was beneficial in improving the separation accuracy of the hydrocyclone.
- (2)
- Increasing the feed rate led to reduced fluctuations of the air column and the LZVV, as well as reduced the formation time of the air column, which was beneficial to the stability of the flow field in the hydrocyclone.
- (3)
- Increasing the feed rate led to increased axial velocity and turbulent kinetic energy, resulting in a negative impact on the separation accuracy and energy consumption of the hydrocyclone.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, H.Y.; Sun, R.; Ren, X.J.; You, Z.C.; Liu, Y.H.; Feng, D.X.; Chen, L.Z. Development of a novel fluidized hydrocyclone concentrator for mineral separation. Sep. Purif. Technol. 2020, 248, 116960. [Google Scholar] [CrossRef]
- Zhao, S.; Sun, J.P.; Wang, S.L.; Sun, Z.H. Modeling and Numerical Simulation of the Inlet Velocity on Oil-Water Two-Phase Vapor Separation Efficiency by the Hydrocyclone. Energies 2022, 15, 4900. [Google Scholar] [CrossRef]
- Lv, X.F.; Du, Y.H.; Du, S.J.; Xiang, L. Graded Preparation and Industrial Applications of Large-Ball Polyolefin Catalyst Carriers. Catalysts 2022, 12, 117. [Google Scholar] [CrossRef]
- Kuang, S.B.; Chu, K.W.; Yu, A.B.; Vince, A. Numerical study of liquid-gas-solid flow in classifying hydrocyclones: Effect of feed solids concentration. Miner. Eng. 2012, 31, 17–31. [Google Scholar] [CrossRef]
- Hou, D.X.; Zhao, Q.; Cui, B.Y.; Wei, D.Z.; Song, Z.G.; Feng, Y.Q. Geometrical configuration of hydrocyclone for improving the separation performance. Adv. Powder Technol. 2022, 33, 103419. [Google Scholar] [CrossRef]
- Liu, B.; Wang, H.J.; Li, L.C.; Zhao, Z.J.; Xu, L.P.; Xue, J.L. Study of GLR and Inlet Velocity on Hydrocyclone for Fracturing Flow-Back Fluids. J. Math. Probl. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Guo, D.; Jiang, X.Y.; Guo, M.Z.; Zeng, M.; Wu, N.; Hao, L.L.; Wang, C. Role of hydrocyclone separator on the formation and separation of aerobic granular sludge: Evaluating granulation efficiency and simulating hydrodynamic behavior. Sep. Purif. Technol. 2022, 283, 120231. [Google Scholar] [CrossRef]
- Yuan, H.X.; Fang, Y.; Fu, S.C.; Ye, J.; Fang, Y. Analysis of the classification performance of micron particles with hydrocyclones. Chem. Ind. Eng. Prog. 2017, 36, 4371–4377. [Google Scholar] [CrossRef]
- Zhu, G.F.; Liow, J.L.; Neely, A. Computational study of the flow characteristics and separation efficiency in a mini-hydrocyclone. Chem. Eng. Res. Des. 2012, 90, 2135–2147. [Google Scholar] [CrossRef]
- Murthy, Y.R.; Bhaskar, K.U. Parametric CFD studies on hydrocyclone. Powder Technol. 2012, 230, 36–47. [Google Scholar] [CrossRef]
- Razmi, H.; Goharrizi, A.S.; Mohebbi, A. CFD simulation of an industrial hydrocyclone based on multiphase particle in cell (MPPIC) method. Sep. Purif. Technol. 2018, 209, 851–862. [Google Scholar] [CrossRef]
- Abdollahzadeh, L.; Habibian, M.; Etezazian, R.; Naseri, S. Study of particle’s shape factor, inlet velocity and feed concentration on mini-hydrocyclone classification and fishhook effect. Power Technol. 2015, 283, 294–301. [Google Scholar] [CrossRef]
- Wu, S.E.; Hwang, K.J.; Cheng, T.W.; Hung, T.C.; Tung, K.L. Effectiveness of a hydrocyclone in separating particles suspended in power law fluids. Powder Technol. 2017, 320, 546–554. [Google Scholar] [CrossRef]
- Bagdi, P.; Bhardwaj, P.; Sen, A.K. Analysis and Simulation of a Micro Hydrocyclone Device for Particle Liquid Separation. J. Fluids Eng. 2012, 134, 021105. [Google Scholar] [CrossRef]
- Qiu, S.Z.; Wang, G.R.; Wang, L.Z.; Fang, X. A Downhole Hydrocyclone for the Recovery of Natural Gas Hydrates and Desanding: The CFD Simulation of the Flow Field and Separation Performance. Energies 2019, 12, 3257. [Google Scholar] [CrossRef]
- Dong, H.; Wu, K.S.; Kuang, Y.C.; Dai, M.L. Study on separation law of hydrate slurry in hydrocyclone based on CFD-DEM. J. Zhejiang Univ. (Eng. Sci.) 2018, 52, 1811–1820. [Google Scholar] [CrossRef]
- Im, I.T.; Gwak, G.D.; Kim, S.M.; Park, Y.K. A Numerical Study of the Flow Characteristics and Separation Efficiency of a Hydrocyclone. KSCE J. Civ. Eng. 2018, 22, 4272–4281. [Google Scholar] [CrossRef]
- Tang, B.; Xu, Y.X.; Song, X.F.; Sun, Z.; Yu, J.G. Effect of inlet configuration on hydrocyclone performance. Trans. Nonferrous Met. Soc. China 2017, 7, 1645–1655. [Google Scholar] [CrossRef]
- Li, F.; Liu, P.K.; Yang, X.H.; Zhang, Y.K.; Zhao, Y.Q. Effects of inlet concentration on the hydrocyclone separation performance with different inlet velocity. Powder Technol. 2020, 375, 337–351. [Google Scholar] [CrossRef]
- Zhu, G.F.; Liow, J.L. Experimental study of particle separation and the fishhook effect in a mini-hydrocyclone. Chem. Eng. Sci. 2014, 111, 94–105. [Google Scholar] [CrossRef]
- Su, T.L.; Zhang, Y.F. Effect of the Vortex Finder and Feed Parameters on the Short-Circuit Flow and Separation Performance of a Hydrocyclone. Processes 2022, 10, 771. [Google Scholar] [CrossRef]
- Junkratuek, A.; Srudhiprom, J.; Srinophakun, T. Computational fluid dynamics of a horizontal hydrocyclone for freezing desalination. Asia-Pac. J. Chem. Eng. 2017, 12, 765–774. [Google Scholar] [CrossRef]
- Jiang, L.Y.; Liu, P.K.; Zhang, Y.K.; Yang, X.H.; Wang, H. The Effect of Inlet Velocity on the Separation Performance of a Two-Stage Hydrocyclone. Minerals 2019, 9, 209. [Google Scholar] [CrossRef]
- Jiang, J.; Ying, R.; Feng, J.A.; Wang, W.B. Computational and Experimental Study of the Effect of Operating Parameters on Classification Performance of Compound Hydrocyclone. Math. Probl. Eng. 2018, 2018, 7596490. [Google Scholar] [CrossRef]
- Xu, Y.X.; Tang, B.; Song, X.F.; Li, S.M.; Sun, Z.; Yu, J.G. Computational study and PIV validation of flow field in a hydrocyclone. J. East China Univ. Sci. Technol. (Nat. Sci. Ed.) 2013, 39, 52–56. [Google Scholar] [CrossRef]
- Shapiro, E.; Drikakis, D. Artificial compressibility, characteristics-based schemes for variable density, incompressible, multi-species flows. Part I. Derivation of different formulations and constant density limit. J. Comput. Phys. 2005, 210, 584–607. [Google Scholar] [CrossRef]
- Liu, P.K.; Fu, W.X.; Jiang, L.Y.; Zhang, Y.K.; Li, X.Y.; Yang, X.H.; Chen, B. Effect of back pressure on the separation performance of a hydrocyclone. Powder Technol. 2022, 409, 117823. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Cai, P.; Jiang, F.H.; Dong, K.J.; Jiang, Y.C.; Wang, B. Understanding the separation of particles in a hydrocyclone by force analysis. Powder Technol. 2017, 322, 471–489. [Google Scholar] [CrossRef]
- Hao, M.X.; Zhang, Y.H.; Huang, Y.; Wang, H.L.; Li, H.; Du, J.Q.; Lv, W.J.; Li, J.P.; Fu, P.B.; Wu, J.W. Effect of particle self-rotation on separation efficiency in mini-hydrocyclones. Powder Technol. 2022, 399, 117165. [Google Scholar] [CrossRef]
- Thornber, B.J.R.; Drikakis, D. Numerical dissipation of upwind schemes in low Mach flow. Int. J. Numer. Methods Fluids 2008, 56, 1535–1541. [Google Scholar] [CrossRef]
- Xu, Y.X.; Song, X.F.; Sun, Z.; Tang, B.; Li, P.; Yu, J.G. Numerical Investigation of the Effect of the Ratio of the Vortex-Finder Diameter to the Spigot Diameter on the Steady State of the Air Core in a Hydrocyclone. Ind. Eng. Chem. Res. 2013, 52, 5470–5478. [Google Scholar] [CrossRef]
- Karimi, M.; Akdogan, G.; Dellimore, K.H.; Bradshaw, S.M. Quantification of numerical uncertainty in computational fluid dynamics modelling of hydrocyclones. Comput. Chem. Eng. 2012, 43, 45–54. [Google Scholar] [CrossRef]
- Schwarz, M.P.; Song, T.; Yang, T.H.; Zhou, J.W.; Wang, Q.K. Reconciliation of empirical correlations and CFD results for hydrocyclone performance for application in process modelling. Powder Technol. 2019, 144, 106028. [Google Scholar]
- Hsieh, K.T.; Rajamani, K. Phenomenological model of the hydrocyclone: Model development and verification for single-phase flow. Int. J. Miner. Process. 1988, 22, 223–237. [Google Scholar] [CrossRef]
- Feng, J.A.; Tang, X.Q.; Wang, W.B.; Ying, R.; Zhang, T. Reliability verification method of numerical simulation based on grid independence and time independence. J. Shihezi Univ. Nat. Sci. 2017, 35, 52–56. [Google Scholar] [CrossRef]
- Xu, Y.X.; Song, X.F.; Sun, Z.; Tang, B.; Yu, J.G. Steady-State Distribution of Air-Core in a Hydrocyclone. Can. J. Chem. Eng. 2017, 95, 757–766. [Google Scholar] [CrossRef]
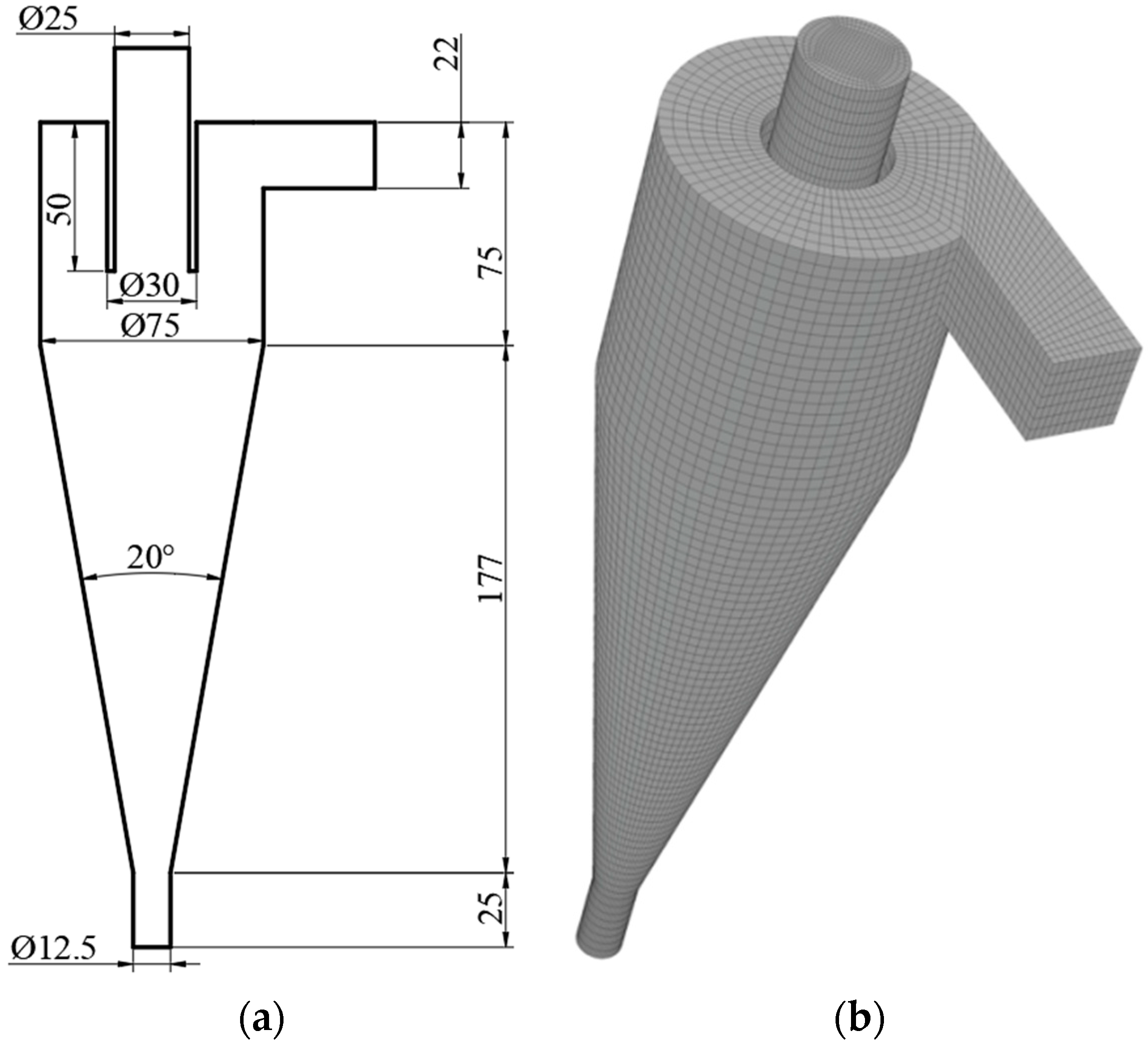





| Structural Parameters | Value |
|---|---|
| Cylinder diameter/mm | 75 |
| Import equivalent diameter/mm | 24.99 |
| Overflow outlet diameter/mm | 25 |
| Underflow outlet diameter/mm | 12.5 |
| Overflow pipe insertion depth/mm | 50 |
| Cone angle/(°) | 20 |
| Cylinder height/mm | 75 |
| Cone height/mm | 177 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, M.; Duan, Y.; Yang, X.; Yang, J.; Tang, X. Influence of Feed Rate on the Performance of Hydrocyclone Flow Field. Separations 2022, 9, 349. https://doi.org/10.3390/separations9110349
Zhang Y, Xu M, Duan Y, Yang X, Yang J, Tang X. Influence of Feed Rate on the Performance of Hydrocyclone Flow Field. Separations. 2022; 9(11):349. https://doi.org/10.3390/separations9110349
Chicago/Turabian StyleZhang, Yuekan, Mingyuan Xu, Yaoxu Duan, Xinghua Yang, Junru Yang, and Xiangcheng Tang. 2022. "Influence of Feed Rate on the Performance of Hydrocyclone Flow Field" Separations 9, no. 11: 349. https://doi.org/10.3390/separations9110349
APA StyleZhang, Y., Xu, M., Duan, Y., Yang, X., Yang, J., & Tang, X. (2022). Influence of Feed Rate on the Performance of Hydrocyclone Flow Field. Separations, 9(11), 349. https://doi.org/10.3390/separations9110349






