Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface
Abstract
:1. Introduction
2. Formulation of the Problem
Physical Quantities of Interest
3. Solution by HAM
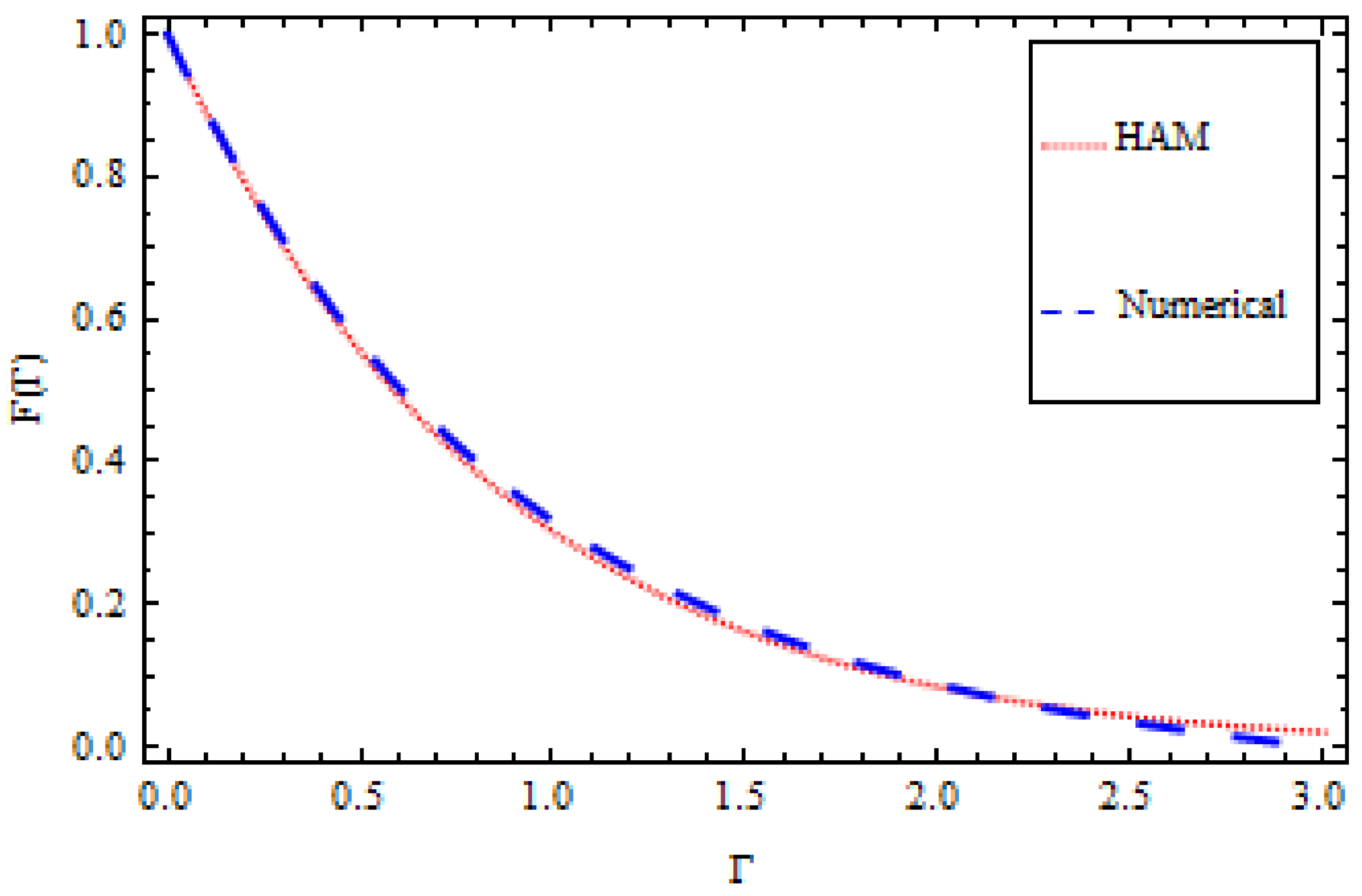
4. HAM Solution Convergence
5. Results and Discussion
Table Discussion
6. Conclusions
- The amplitude of the velocity decreased with an increase in and porosity , while it increased with an increase in the dimensionless fluid parameters and
- The temperature increased with an increase in , the radiation parameter , and the heat source/sink , while it decreased with an increase in the Prandtl number and the ratio of the oscillation frequency of the sheet to its stretching rate .
- The local Nusselt number increased with an increase in the Prandtl number , the heat source/sink , the dimensionless fluid parameter and radiation parameter , while it decreased with an increase in the porosity and the dimensionless fluid parameter .
Author Contributions
Conflicts of Interest
Nomenclature
| pressure (Pa) | |
| c | constant |
| X,Y | topological space |
| x,y | coordinates |
| , | velocity components |
| specific heat | |
| , | fluid materials |
| heat source/sink | |
| thermal conductivity () | |
| radiative heat flux | |
| absorption coefficient | |
| fluid parameter | |
| ratio of the oscillation frequency | |
| radiation parameter | |
| Prandtl number | |
| skin fraction coefficient | |
| local Nusselt number | |
| Greek Letters | |
| dynamic viscosity | |
| constant | |
| kinematic viscosity (m2/s) | |
| density (kg/m3) | |
| Stefan–Boltzmann constant | |
| porosity term | |
| heat source/sink | |
References
- Sakiadis, B.C. Boundary Layer Behavior on Continuous Solid Surfaces: II Boundary Layer on a Continuous Flat Surface. AIChE J. 1961, 7, 221–225. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Anderson, H.I.; Hansen, O.R.; Olmedal, B. Diffusion of chemically reactive species from a stretching sheet. Int. J. Heat Mass Transf. 1994, 37, 659–664. [Google Scholar] [CrossRef]
- Pop, I.; Na, T.Y. Unsteady flow past a stretching sheet. Mech. Res. Commun. 1996, 23, 413–422. [Google Scholar] [CrossRef]
- Cortell, R. A note on flow and heat transfer of viscoelastic fluid over a stretching sheet. Int. J. Non-Lin. Mech. 2006, 41, 78–85. [Google Scholar] [CrossRef]
- Ariel, P.D. Axismmetric flow of a second grade fluid past a stretching sheet. Int. J. Eng. Sci. 2001, 39, 529–553. [Google Scholar] [CrossRef]
- Rashdi, M.M.; Ali, M.E.S.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Rashdi, S.; Esfahani, A.J.; Ellahi, R. Convective heat transfer and particle motion in an obstructed duct with two side-by-side obstacles by means of DPM model. Appl. Sci. 2017, 7, 431. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. Heat and mass transfer analysis on the flow of second grade fluid in the presence of chemical reaction. Phys. Lett. A 2008, 372, 2400–2408. [Google Scholar] [CrossRef]
- Hayat, T.; Sajid, M. Analytic solution for axisymmetric flow and heat transfer flow of a second grade fluid past a stretching sheet. Int. J. Heat Mass Transf. 2007, 50, 75–84. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Radiation effects on the flow of Powell–Eyring fluid past an unsteady inclined stretching sheet with Non-uniform heat source/sink. PLoS ONE 2014, 9, e103214. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Awais, M.; Asghar, S. Radiative effects in a three-dimensional flow of MHD Eyring–Powell fluid. J. Egypt. Math. Soc. 2013, 21, 379–384. [Google Scholar] [CrossRef]
- Powell, R.E.; Eyring, H. Mechanism for the Relaxation Theory of Viscosity. Nature 1944, 154, 427–428. [Google Scholar] [CrossRef]
- Prasad, K.V.; Datti, P.S.; Raju, B.T. Momentum and Heat Transfer of a Non-Newtonian Eyring–Powell Fluid over a Non-Isothermal Stretching Sheet. Int. J. Math. Arch. 2013, 4, 230–241. [Google Scholar]
- Noreen, S.; Qasim, M. Peristaltic Flow of MHD Eyring–Powell Fluid in a Channel. Eur. Phys. J. Plus 2013, 128, 91–103. [Google Scholar] [CrossRef]
- Ellahi, R. Numerical study of magnetohydrodynamics generalized Couette flow of Eyring–Powell fluid with heat transfer and slip condition. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1433–1445. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of spherical and nonspherical nanoparticles in mixed convection flow over a vertical stretching permeable sheet. J. Mech. Adv. Mater. Struct. 2017, 24, 1231–1238. [Google Scholar] [CrossRef]
- Mahmoudi, M.A.A.; Ahmad, M.; Megahed, M. Slip flow of Powell–Eyring liquid film due to an unsteady stretching sheet with heat. Braz. J. Phys. 2016, 3, 299–307. [Google Scholar] [CrossRef]
- Zaman, H.; Shah, M.A.; Ibrahim, M. Unsteady incompressible coquette flow problem for the Eyring–Powell Model with porous walls. Am. J. Comput. Math. 2013, 3, 313–325. [Google Scholar] [CrossRef]
- Hayat, T.; Tanveer, A.; Yasmin, H.; Alsaedi, A. Effects of convective conditions and chemical reaction on peristaltic flow of Erying–Powell fluid. Appl. Bionics Biomech. 2014, 11, 221–233. [Google Scholar] [CrossRef]
- Javed, T.; Ali, N.; Abbas, Z.; Sajid, M. Flow of an Eyring–Powell non-Newtonian over a stretching sheet. Chem. Eng. Commun. 2012, 200, 327–336. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Effects of homogeneous-heterogeneous reactions in flow of Powell–Eyring fluid. J. Cent. South. Univ. Technol. 2015, 22, 3211–3216. [Google Scholar] [CrossRef]
- Khan, N.A.; Sultan, F. On the double diffusive convection flow of Eyring–Powell fluid due to cone through a porous medium with Soret and Dufour effects. AIP ADVANCES 2015, 5, 057140. [Google Scholar] [CrossRef]
- Panigrahi, S.; Reza, M.; Mishra, A.K. Mixed convective flow of a Powell–Eyring fluid over non-linear stretching surface with thermal diffusion and diffusion thermo. Procedia Eng. 2015, 127, 645–651. [Google Scholar] [CrossRef]
- Tawadem, L.M.; Gmetri, P.; Koti, A. Thin film flow and heat transfer over an unsteady stretching sheet with thermal radiation, internal heating in presence of external magnetic field. Int. J. Adv. Appl. Math. Mech. 2016, 3, 29–40. [Google Scholar]
- Ellahi, R.; Tariq, M.H.; Hassan, M.; Vafai, K. On boundary layer magnetic flow of nano-Ferroliquid under the influence of low oscillating over stretchable rotating disk. J. Mol. Liq. 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liq. 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Maqbool, M.; Sohail, A.; Naeema, M.; Ellahi, R. Hall effect on Falkner-Skan boundary layer flow of FENE-P fluid over a stretching sheet. Commun. Theor. Phys. 2016, 66, 547–554. [Google Scholar] [CrossRef]
- Shirvan, M.K.; Ellahi, R.; Mirzakhanlar, S.; Mamourian, M. Enhancement of Heat Transfer and Heat Exchanger Effectiveness in a Double Pipe Heat Exchanger Filled with Porous Media: Numerical Simulation and Sensitivity Analysis of Turbulent Fluid Flow. Appl. Therm. Eng. 2016, 109, 761–774. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Prasannakumara, B.C.; Gireesha, B.J.; Rashidi, M.M. Casson Fluid Flow near the Stagnation Point over a Stretching Sheet with Variable Thickness and Radiation. J. Appl. Fluid Mech. 2016, 9, 1115–1122. [Google Scholar] [CrossRef]
- Krishnamurthy, M.R.; Gireesha, B.J.; Prasannakumara, B.C.; Gorla, R.S.R. Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet. Nonlinear Eng. 2016, 5, 147–159. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Gireesha, B.J.; Gorla, R.S.R.; Krishnamurthy, M.R. Effect of multiple slips and thermal radiation on MHD flow of Jeffery nanofluid with heat transfer. J. Nanofluids 2016, 5, 82–93. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Gireesha, B.J.; Gorla, R.S.R.; Krishnamurthy, M.R. Non-Linear Thermal Radiation and Slip Effect on Boundary Layer Flow and Heat Transfer of Suspended Nanoparticles over a Stretching Sheet Embedded in Porous Medium with Convective Boundary Conditions. J. Nanofluids 2016, 5, 522–530. [Google Scholar]
- Bakier, A.Y. Thermal radiation effect on mixed convection from vertical surface in saturated porous media. Int. Commun. Heat Mass Transf. 2001, 28, 119–126. [Google Scholar] [CrossRef]
- Moradi, A.; Ahmadikia, H.; Hayat, T.; Alsaedi, A. On mixed convection-radiation interaction about an inclined plate through a porous medium. Int. J. Therm. Sci. 2013, 64, 129–136. [Google Scholar] [CrossRef]
- Chaudhary, S.; Singh, S.; Chaudhary, S. Thermal radiation effects on MHD Boundary layer flow over an exponentially stretching surface. Sci. Res. Publ. Appl. Math. 2015, 6, 295–303. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Method for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. An Explicit, Totally Analytic Approximate Solution for Blasius Viscous Flow Problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall, CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Rashidi, M.M.; Siddiqui, A.M.; Asadi, M. Application of homotopy analysis method to the unsteady squeezing flow of a second grade fluid between circular plates. Math. Probl. Eng. Art. 2010. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Pour, S.A.M. Analytic approximate solutions for unsteady boundary-layer flow and heat transfer due to a stretching sheet by homotopy analysis method. Nonlinear Anal. Model. Control 2010, 15, 83–95. [Google Scholar]
- Abbasbandy, S. Homotopy analysis method for heat radiation, equations. Int. Commun. Heat Mass Transf. 2007, 34, 380–388. [Google Scholar] [CrossRef]
- Nadeem, S.; Awais, M. Thin film flow of an unsteady shrinking sheet through porous medium with variable viscosity. Phys. Lett. A 2008, 372, 4965–4972. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, N.; Abas, Z. Hydromagnetic Flow and Heat Transfer of Eyring–Powell Fluid over an Oscillatory Stretching Sheet with Thermal Radiation. Appl. Appl. Math. 2015, 10, 893–908. [Google Scholar]
- Shah, Z.; Gul, T.; Khan, A.M.; Ali, I.; Islam, S. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, 280–296. [Google Scholar]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018. [Google Scholar] [CrossRef]
- Hammed, H.; Haneef, M.; Shah, Z.; Islam, S.; Khan, W.; Muhammad, S. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Muhammad, S.; Ali, G.; Shah, Z.; Islam, S.; Hussain, A. The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption. Appl. Sci. 2018, 8, 482. [Google Scholar] [CrossRef]














| 0.5 | - | - | −1.29447 |
| 0.7 | - | - | −1.39927 |
| 0.9 | - | - | −1.50053 |
| 1.1 | 1.0 | - | −1.59913 |
| - | 1.3 | - | −1.68426 |
| - | 1.5 | - | −1.73747 |
| - | 1.7 | 0.5 | −1.78810 |
| - | - | 0.6 | −1.81316 |
| - | - | 0.7 | −1.84069 |
| 1.0 | - | - | 1.82770 |
| 1.2 | - | - | 1.80574 |
| 1.4 | - | - | 1.78404 |
| 1.6 | 2.5 | - | 1.76259 |
| - | 2.6 | - | 1.79740 |
| - | 2.7 | - | 1.83133 |
| - | 2.8 | 0.3 | 1.85965 |
| - | - | 0.4 | 1.97571 |
| - | - | 0.5 | 2.08693 |
| HAM Solution | Numerical Solution | Absolute Error AE | |
|---|---|---|---|
| 0.0 | 1.12757 × 10−17 | 0.000000 | 1.12757 × 10−17 |
| 0.5 | 0.378563 | 0.381439 | 0.002876 |
| 1.0 | 0.586888 | 0.596535 | 0.009647 |
| 1.5 | 0.699341 | 0.715829 | 0.016488 |
| 2.0 | 0.758826 | 0.779103 | 0.020276 |
| 2.5 | 0.789566 | 0.808656 | 0.019089 |
| 3.0 | 0.804988 | 0.816817 | 0.011828 |
| 3.5 | 0.812414 | 0.866641 | 0.054227 |
| 4.0 | 0.815772 | 0.873029 | 0.057257 |
| 4.5 | 0.817129 | 0.875971 | 0.058842 |
| 5.0 | 0.817552 | 0.876772 | 0.059220 |
| HAM Solution | Numerical Solution | Absolute Error AE | |
|---|---|---|---|
| 0 | 1.000000 | 1.000000 | 0.000000 |
| 1.0 | 0.513778 | 0.543757 | 0.029978 |
| 2.0 | 0.266242 | 0.288424 | 0.022182 |
| 3.0 | 0.133781 | 0.152038 | 0.018257 |
| 4.0 | 0.065247 | 0.080017 | 0.014769 |
| 5.0 | 0.030998 | 0.042041 | 0.011042 |
| 6.0 | 0.014391 | 0.021973 | 0.007582 |
| 7.0 | 0.006548 | 0.011297 | 0.004748 |
| 8.0 | 0.002927 | 0.005503 | 0.002575 |
| 9.0 | 0.001288 | 0.002181 | 0.000892 |
| 10.0 | 0.000559 | 2.093 × 10−6 | 0.000557 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dawar, A.; Shah, Z.; Idrees, M.; Khan, W.; Islam, S.; Gul, T. Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface. Math. Comput. Appl. 2018, 23, 20. https://doi.org/10.3390/mca23020020
Dawar A, Shah Z, Idrees M, Khan W, Islam S, Gul T. Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface. Mathematical and Computational Applications. 2018; 23(2):20. https://doi.org/10.3390/mca23020020
Chicago/Turabian StyleDawar, Abdullah, Zahir Shah, Muhammad Idrees, Waris Khan, Saeed Islam, and Taza Gul. 2018. "Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface" Mathematical and Computational Applications 23, no. 2: 20. https://doi.org/10.3390/mca23020020
APA StyleDawar, A., Shah, Z., Idrees, M., Khan, W., Islam, S., & Gul, T. (2018). Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface. Mathematical and Computational Applications, 23(2), 20. https://doi.org/10.3390/mca23020020





