An Analytical Expression for Magnet Shape Optimization in Surface-Mounted Permanent Magnet Machines

Abstract

Surface-mounted permanent magnet machines are widely used in low and medium speed applications. Pulsating torque components is the most crucial challenge, especially in low-speed applications. Magnet pole shape optimization can be used to mitigate these components. In this research, an analytical model is proposed to calculate the magnetic vector potential in surface-mounted permanent magnet machines. A mathematical expression is also derived for optimal the magnet shape to reduce the cogging torque and electromagnetic torque components. The presented model is based on the resolution of the Laplace’s and Poisson’s equations in polar coordinates by using the subdomain method and applying hyperbolic functions. The proposed method is applied to the performance computation of a surface-mounted permanent magnet machine, i.e., a 3-phase 12S-10P motor. The analytical results are validated through the finite element analysis (FEA) method.

1. Introduction

Surface-mounted permanent magnet machines are interested in high-performance applications because of their high efficiency and power density. However, the noise and vibration caused by pulsating torque components seriously affect the machine performance. Pulsating torque is greatly affected by the distribution of the magnetic field and the configuration of the permanent magnets. Therefore, pulsating torque mitigation can be performed using magnet shape optimization to obtain a better magnetic field waveform and also to reduce the cogging torque and electromagnetic torque, effectively.

An extensive variety of techniques such as magnet skewing [1,2,3,4], magnet-arc optimization [5,6,7,8,9], magnet shape optimization [10], and magnet displacing [2,3,4,7,8,9] for minimizing cogging torque in permanent magnet motors is documented in the literature.

A variety of techniques including analytical and numerical methods have been conducted to evaluate the pulsating torque components in electrical machines. Numerical methods like the finite element method (FEA) give accurate results and are time-consuming especially in the first step of the design stage. Semi-analytical methods including conformal mapping [11,12,13,14] and Magnetic Equivalent Circuit (MEC) [15,16,17], and analytical methods including the subdomain model [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] are reported to model electrical machines and are useful in the design optimization stage. The subdomain model is more accurate than the other analytical models [15].

Indeed, the global or local saturation effect influences the electromagnetic performances, e.g., on the ripple/cogging torque [34]. To overcome that issue, recently, a new technique to account for finite soft-magnetic material permeabilities in the subdomain technique was developed by applying the superposition principle in both directions in polar or Cartesian coordinates [35,36]. According to Reference [37], the Dubas’ superposition technique [35,36] is very interesting since it enables the magnetic field calculation in the material of slotted geometries. This technique has been implemented in radial-flux electrical machines considering finite soft-magnetic material permeability [34]. The Dubas’s superposition technique could have been used to develop a new model with the consideration of the saturation effect. In References [38,39,40,41], an analytical model has been introduced to compute electric machine performance by using the subdomain method.

However, no analytical expression was found at present to calculate the optimal magnet pole shape in surface-mounted permanent magnet machines in order to minimize the pulsating torque components.

The focus of this paper is to derive an analytical expression for the optimal magnet pole shape in surface-mounted permanent magnet machines to reduce pulsating torque components. An analytical model is presented based on the resolution of the Laplace’s and Poisson’s equations in surface-mounted permanent magnet machines by using the subdomain method whilst considering pole shape optimization. It is shown that the developed model can effectively estimate the magnetic field, cogging torque, electromagnetic torque, back electromotive force and self/mutual inductance. This model is applied to the performance calculation of a surface-mounted permanent magnet motor, i.e., a 3-phase 12S-10P motor. It is shown that the results of the analytical model are in close agreement with the results of the FEA method.

2. Subdomain Definition

The schematic representation of the investigated machines is shown in Figure 1. The machine model is divided into four subdomains. The stator which has two subdomains including the $Q_1$ slot regions (domain $j$), the $Q_1$ slot opening regions (domain $i$) and the airgap subdomain (region $II$) are shown in Figure 2. The rotor has one subdomain including the permanent magnet regions (domain $I$), as shown in Figure 3.

Figure 1. The geometrical representation of the investigated machines with (a) uniform rotor shape, (b) non-uniform rotor shape.

Figure 2. The stator subdomains including the $j$ and $i$ regions.

Figure 3. The rotor permanent magnet subdomain. (a) Uniform rotor, (b) non-uniform rotor.

The angular position of the $j$-th stator slot and $i$-th stator slot opening are defined as (1) and (2), respectively.

$${\theta }_j=-\frac{\beta }{2}+\frac{2j\pi }{Q_1} with 1\le j\le Q_1$$

(1)

$${\theta }_i=-\frac{\alpha }{2}+\frac{2i\pi }{Q_1} with 1\le i\le Q_1$$

(2)

3. Magnetic Vector Potential Computation

The general solution to Laplace’s or Poisson’s equations in each subdomain is developed in this section. The Laplace equation can be described in the polar form as

$$\frac{{\partial }^2{A}_z}{\partial r^2}+\frac{1}{r}\frac{\partial A_z}{\partial r}+\frac{1}{r^2}\frac{{\partial }^2{A}_z}{\partial {\theta }^2}=0 for \{\begin{array}{c}{R}_1\le r\le R_2\\ {\theta }_1\le \theta \le {\theta }_2\end{array}$$

(3)

By replacing $r$ by $R_1{e}^{-t}$, one obtains

$$\frac{{\partial }^2{A}_z}{\partial t^2}+\frac{{\partial }^2{A}_z}{\partial {\theta }^2}=0 for \{\begin{array}{c}ln(\frac{R_1}{R_2})\le t\le 0\\ {\theta }_1\le \theta \le {\theta }_2\end{array}$$

(4)

The 2D analytical model in quasi-Cartesian coordinates is formulated with the following assumptions:

• The end effects are neglected (i.e., the machine is infinitely long: the magnetic variables are independent of z).
• The stator is assumed to be infinitely permeable (i.e., the saturation effect is neglected) with zero electrical conductivity.
• The relative magnetic permeability and electrical conductivity of the solid rotor and shaft are assumed to be constant.
• The current density in the slots has only one component along the z-axis.

3.1. Magnetic Vector Potential in the Stator Slot Subdomain (Region j)

The Poisson equation in the stator slot subdomain is given by

$$\frac{{\partial }^2{A}_{zj}}{\partial t^2}+\frac{{\partial }^2{A}_{zj}}{\partial {\theta }^2}=-{\mu }_0{J}_{zj}{R}_4^2{e}^{-2t} for \{\begin{array}{c}{t}_1\le t\le t_2\\ {\theta }_j\le \theta \le {\theta }_j+\beta \end{array}$$

(5)

where $t_1=ln\left(\frac{R_4}{R_5}\right)$, $t_2=0$ and $J_{zj}$ is the slot current density.

The Neumann boundary conditions at the bottom and at each side of the slot are obtained as

$${\frac{\partial A_{zj}}{\partial \theta }|}_{\theta ={\theta }_j}=0 and {\frac{\partial A_{zj}}{\partial \theta }|}_{\theta ={\theta }_j+\beta }=0$$

(6)

$${\frac{\partial A_{zj}}{\partial t}|}_{t=t_1}=0$$

(7)

The general solution of Equation (5) using the separation of variables method is given by

$$\begin{array}{ll}{A}_{zj}\left(t,\theta \right)=a_0{}^j-& \frac{1}{2}{\mu }_0{J}_{zj}{R}_5^2\left(e^{-2t_1}t+\frac{1}{2}{e}^{-2t+2t_1}\right)\\ & +{\displaystyle {\displaystyle \sum }_{h=1}^{\infty }}\left(a_h{}^j\frac{\beta }{h\pi }\frac{Cosh\left(\frac{h\pi }{\beta }\left(t-t_1\right)\right)}{Sinh\left(\frac{h\pi }{\beta }\left(t_2-t_1\right)\right)}\right)Cos\left(\frac{h\pi }{\beta }\left(\theta -{\theta }_j\right)\right)\end{array}$$

(8)

where $h$ is a positive integer and the coefficients $a_0{}^j$ and $a_h{}^j$ are determined based on the continuity and interface conditions.

The continuity of the magnetic vector potential between the subdomain $j$ and the region $i$ leads to

$${\frac{\partial A_{zj}}{\partial t}|}_{t=t_2}=f\left(\theta \right)=\{\begin{array}{c}{\frac{\partial A_{zi}}{\partial t}|}_{t=t_3}for {\theta }_i\le \theta \le {\theta }_i+\alpha \\ 0 elsewhere\end{array}$$

(9)

The interface condition (9) gives

$${\mu }_0{J}_{zj}Sinh\left(t_1\right)=\frac{1}{\beta }{{\displaystyle \int }}_{{\theta }_j}^{{\theta }_j+\beta }f\left(\theta \right)d\theta$$

(10)

$$a_h{}^j=\frac{2}{\beta }{{\displaystyle \int }}_{{\theta }_j}^{{\theta }_j+\beta }f\left(\theta \right)Cos\left(\frac{h\pi }{\beta }\left(\theta -{\theta }_j\right)\right)d\theta$$

(11)

3.2. Magnetic Vector Potential in the Stator Slot Opening Subdomain (Region i)

The Laplace equation in the stator second inner slot opening subdomain is given by

$$\frac{{\partial }^2{A}_{zi}}{\partial t^2}+\frac{{\partial }^2{A}_{zi}}{\partial {\theta }^2}=0 for \{\begin{array}{c}{t}_3\le t\le t_4\\ {\theta }_i\le \theta \le {\theta }_i+\alpha \end{array}$$

(12)

where $t_3=ln\left(\frac{R_3}{R_4}\right)$ and $t_4=0$.

The Neumann boundary conditions at the bottom and at each side of the slot are obtained as

$${\frac{\partial A_{zi}}{\partial \theta }|}_{\theta ={\theta }_i}=0 and {\frac{\partial A_{zi}}{\partial \theta }|}_{\theta ={\theta }_i+\alpha }=0$$

(13)

The general solution of Equation (12) using the separation of variables method is given by

$$\begin{array}{l}{A}_{zi}\left(t,\theta \right)=a_0{}^i+b_0{}^{i}t\\ +{\displaystyle {\displaystyle \sum }_{k=1}^{\infty }}\left(\frac{Sinh\left(\frac{k\pi }{\alpha }\left(t-t_4\right)\right)}{Sinh\left(\frac{k\pi }{\alpha }\left(t_3-t_4\right)\right)}{a}_k{}^i+\frac{Sinh\left(\frac{k\pi }{\alpha }\left(t-t_3\right)\right)}{Sinh\left(\frac{k\pi }{\alpha }\left(t_4-t_3\right)\right)}{b}_k{}^i\right)Cos\left(\frac{k\pi }{\alpha }\left(\theta -{\theta }_i\right)\right)\end{array}$$

(14)

where $k$ is a positive integer and the coefficients, $a_0{}^i$, $b_0{}^i$, $a_k{}^i$ and $b_k{}^i$ are determined based on the continuity and interface conditions.

The continuity of the magnetic vector potential between the subdomain $l$ and the regions $i$ and $II$ leads to

$$Azi\left(t_4,\theta \right)=AzII\left(t_5,\theta \right) for {\theta }_i\le \theta \le {\theta }_i+\alpha$$

(15)

$$Azi\left(t_3,\theta \right)=Azj\left(t_4,\theta \right) for {\theta }_i\le \theta \le {\theta }_i+\alpha$$

(16)

The interface condition (15) gives

$$a_0{}^i=\frac{1}{\alpha }{{\displaystyle \int }}_{{\theta }_l}^{{\theta }_i+\alpha }AII\left(t_5,\theta \right)d\theta$$

(17)

$$b_k{}^i=\frac{2}{\alpha }{{\displaystyle \int }}_{{\theta }_i}^{{\theta }_i+\alpha }AII\left(t_5,\theta \right)Cos\left(\frac{h\pi }{\alpha }\left(\theta -{\theta }_i\right)\right)d\theta$$

(18)

The interface condition (16) gives

$$a_0{}^i+ln\left(\frac{R_3}{R_4}\right)b_0{}^i=\frac{1}{\alpha }{{\displaystyle \int }}_{{\theta }_i}^{{\theta }_i+\alpha }Azj\left(t_4,\theta \right)d\theta$$

(19)

$$a_k{}^i=\frac{2}{\alpha }{{\displaystyle \int }}_{{\theta }_i}^{{\theta }_i+\alpha }Azj\left(t_4,\theta \right)Cos\left(\frac{k\pi }{\alpha }\left(\theta -{\theta }_i\right)\right)d\theta$$

(20)

3.3. Magnetic Vector Potential in the Air-Gap Subdomain (Region II)

The Laplace equation in the air-gap subdomain is given by

$$\frac{{\partial }^2{A}_{zII}}{\partial t^2}+\frac{{\partial }^2{A}_{zII}}{\partial {\theta }^2}=0 for \{\begin{array}{c}{t}_5\le t\le t_6\\ 0\le \theta \le 2\pi \end{array}$$

(21)

where $t_5=ln\left(\frac{R_2}{R_3}\right)$ and $t_6=0$.

The general solution of Equation (21), considering the periodicity boundary conditions is obtained as

$$\begin{array}{l}{A}_{zII}\left(\mathrm{t},\theta \right)={\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\left(\frac{1}{n}\frac{Cosh\left(n\left(\mathrm{t}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_n{}^{II}+\frac{1}{n}\frac{Cosh\left(n\left(\mathrm{t}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{b}_n{}^{II}\right)Cos\left(n\theta \right)\\ +{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\left(\frac{1}{n}\frac{Cosh\left(n\left(\mathrm{t}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{c}_n{}^{II}+\frac{1}{n}\frac{Cosh\left(n\left(\mathrm{t}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{d}_n{}^{II}\right)Sin\left(n\theta \right)\end{array}$$

(22)

where $n$ is a positive integer.

The coefficients $a_n{}^{II}$, $b_n{}^{II}$, $c_n{}^{II}$ and $d_n{}^{II}$ are determined by considering the continuity of the magnetic vector potential between the internal airgap subdomain II and the region i using a Fourier series expansion of interface condition (23) and (24) over the airgap interval.

The continuity of the magnetic vector potential between the internal airgap subdomain $II$ and the regions $i$ and leads to

$${\frac{\partial A_{zII}}{\partial t}|}_{t={\mathrm{t}}_5}=g\left(\theta \right)=\{\begin{array}{c}{\frac{\partial A_{zi}}{\partial t}|}_{t=t_4} for {\theta }_i\le \theta \le {\theta }_i+\alpha \\ 0 elsewhere\end{array}$$

(23)

$${\frac{\partial A_{zII}}{\partial t}|}_{t={\mathrm{t}}_6}=h\left(\theta \right)=\{\begin{array}{c}{\frac{\partial A_{zI}}{\partial t}|}_{t=t_7} for {\theta }_k\le \theta \le {\theta }_k+\gamma \\ 0 elsewhere\end{array}$$

(24)

The interface condition (23) gives

$$a_n{}^{II}=\frac{2}{2\pi }{{\displaystyle \int }}_{{\theta }_i}^{{\theta }_i+\alpha }g\left(\theta \right)Cos\left(n\theta \right)d\theta$$

(25)

$$c_n{}^{II}=\frac{2}{2\pi }{{\displaystyle \int }}_{{\theta }_i}^{{\theta }_i+\alpha }g\left(\theta \right)Sin\left(n\theta \right)d\theta$$

(26)

The interface condition (24) gives

$$b_n{}^{II}=\frac{2}{2\pi }{{\displaystyle \int }}_{{\theta }_k}^{{\theta }_k+\gamma }h\left(\theta \right)Cos\left(n\theta \right)d\theta$$

(27)

$$d_n{}^{II}=\frac{2}{2\pi }{{\displaystyle \int }}_{{\theta }_k}^{{\theta }_k+\gamma }h\left(\theta \right)Sin\left(n\theta \right)d\theta$$

(28)

3.4. Magnetic Vector Potential in the Rotor Permanent Magnet Subdomain (Region I)

The Poisson equation in the rotor permanent magnet subdomain is given by

$$\frac{{\partial }^2{A}_{zI}}{\partial t^2}+\frac{{\partial }^2{A}_{zI}}{\partial {\theta }^2}=-{\mu }_0{R}_1{e}^{-t}\left(M_{\theta }-\frac{\partial M_r}{\partial \theta }\right) for \{\begin{array}{c}{t}_7\le t\le t_8\\ 0\le \theta \le 2\pi \end{array}$$

(29)

where $t_7=ln\left(\frac{R_1}{R_2}\right)$ and $t_8=0$, $M_{\theta }$ and $M_r$ are the tangential and radial components of magnetization.

3.4.1. Radial Magnetization

The radial and tangential components of radial magnetization for the surface-mounted design can be expressed as

$$M_{rn}=\frac{4B_r}{{\mu }_{0}n\pi }Sin\left(\frac{n\pi {\alpha }_p}{2}\right)$$

(30)

$$M_{\theta n}=0$$

(31)

where ${\alpha }_p$ is the magnet pole width to magnet pitch ratio.

3.4.2. Parallel Magnetization

The radial and tangential components of the parallel magnetization for the surface-mounted design can be expressed as

$$M_{rn}=\frac{B_r}{{\mu }_0}{\alpha }_p\left[A_{1n}\left({\alpha }_p\right)+A_{2n}\left({\alpha }_p\right)\right]$$

(32)

$$M_{\theta n}=\frac{B_r}{{\mu }_0}{\alpha }_p\left[A_{1n}\left({\alpha }_p\right)-A_{2n}\left({\alpha }_p\right)\right]$$

(33)

where

$$A_{1n}\left({\alpha }_p\right)=\frac{Sin(\left(np+1\right)\frac{\pi {\alpha }_p}{2p})}{\left(np+1\right)\frac{\pi {\alpha }_p}{2p}}$$

(34)

$$A_{2n}\left({\alpha }_p\right)=\{\begin{array}{c}\frac{Sin(\left(np-1\right)\frac{\pi {\alpha }_p}{2p})}{\left(np-1\right)\frac{\pi {\alpha }_p}{2p}} for np\ne 1\\ 1 for np=1\end{array}$$

(35)

For a surface-mounted design, the Neumann boundary conditions at the bottom of the permanent magnet are obtained as

$${\frac{\partial A_{zI}}{\partial t}|}_{t=t_8}=0$$

(36)

The general solution of Equation (29) using the separation of variables method is given by

$$\begin{array}{c}{A}_{zI}\left(t,\theta \right)={\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\left(\begin{array}{c}{a}_n^I\frac{\cosh \left(n\left(t-t_8\right)\right)}{\cosh \left(n\left(t_7-t_8\right)\right)}\\ +X_n\left(t\right)Cos\left(\frac{n\pi {\alpha }_p}{2{\alpha }_r}\right)\end{array}\right)Cos\left(n\theta \right)\\ +{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\left(\begin{array}{c}{c}_n^I\frac{\cosh \left(n\left(t-t_8\right)\right)}{\cosh \left(n\left(t_7-t_8\right)\right)}\\ +X_n\left(t\right)Sin\left(\frac{n\pi {\alpha }_p}{2{\alpha }_r}\right)\end{array}\right)Sin\left(n\theta \right)\end{array}$$

(37)

$$X_n\left(t\right)=\left(1+\frac{1}{n}{e}^{\left(n+1\right)t}\right)f_n\left(t\right)-\frac{\mathrm{Cos}\mathrm{h}\left(n\left(t-t_8\right)\right)}{\mathrm{Cos}\mathrm{h}\left(n\left(t_7-t_8\right)\right)}\left(1+\frac{1}{n}{e}^{\left(n+1\right)t_7}\right)f_n\left(t_7\right)$$

(38)

$$f_n\left(t\right)=\{\begin{array}{c}{\mu }_0\frac{np{M}_{rn}+M_{\theta n}}{1-n{p}^2}{R}_1{e}^{-t} if np\ne 1 \\ -{\mu }_0\frac{M_{rn}+M_{\theta n}}{2}{R}_1{e}^{-t}ln\left(R_1{e}^{-t}\right) if np=1\end{array}$$

(39)

where $n$ is a positive integer and the coefficients $a_n{}^I$ and $c_n{}^I$ are determined based on the continuity and interface conditions.

The continuity of the magnetic vector potential between the subdomain $I$ and the regions $II$ leads to

$$A_{zI}\left(t_7,\theta \right)=A_{zII}\left(t_6\theta \right)$$

(40)

The interface condition (40) gives

$$a_n^I=\frac{2}{2\pi }{{\displaystyle \int }}_0^{2\pi }{A}_{zII}\left(t_6,\theta \right)Cos\left(n\theta \right)d\theta$$

(41)

$$c_n^I=\frac{2}{2\pi }{{\displaystyle \int }}_0^{2\pi }{A}_{zII}\left(t_6,\theta \right)Sin\left(n\theta \right)d\theta$$

(42)

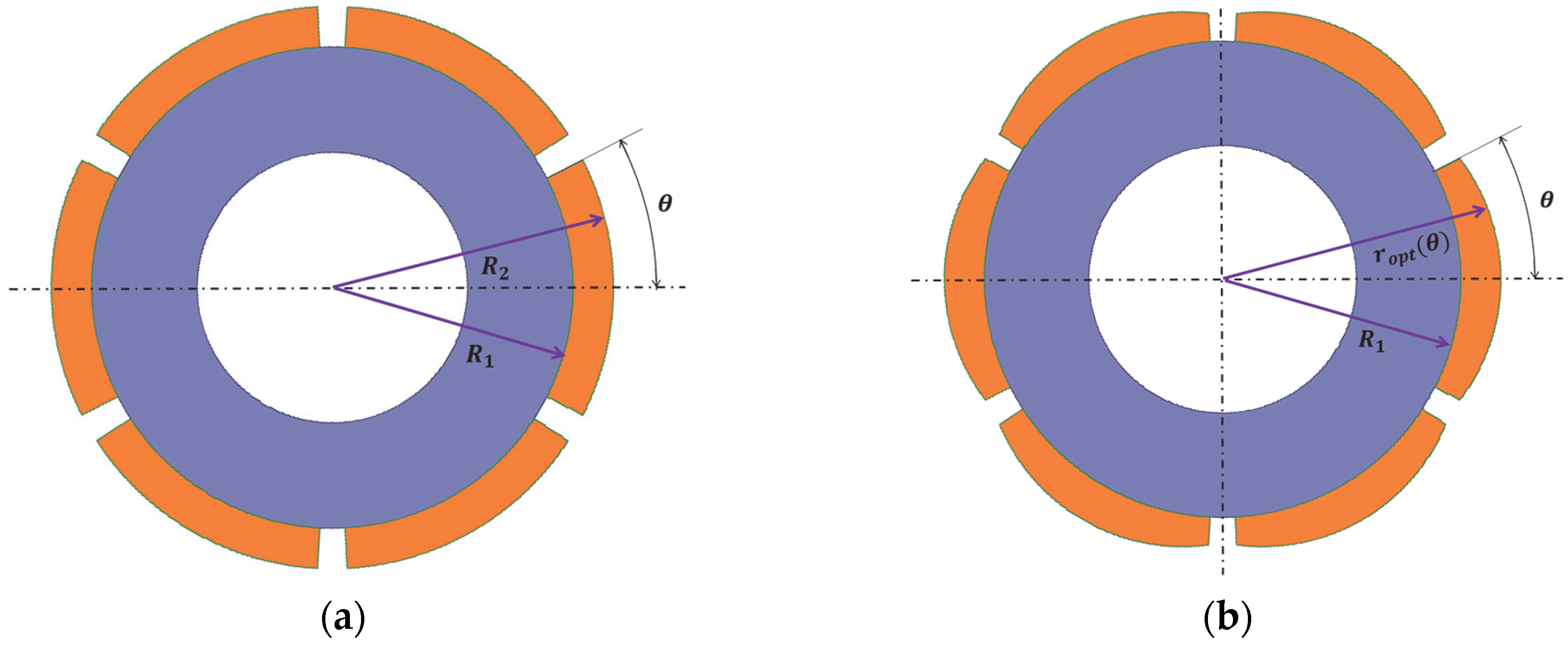
4. Magnet Pole Shape Optimization

The general solution for the magnetic potential distribution in the air-gap subdomain is

$$A_{zII}\left(\mathrm{t}.\theta \right)={\displaystyle \sum }_{n=1}^{\infty }\left(\frac{1}{n}\frac{Cosh\left(n\left(\mathrm{t}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_n{}^{II}+\frac{1}{n}\frac{Cosh\left(n\left(\mathrm{t}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{b}_n{}^{II}\right)Cos\left(n\theta \right)$$

(43)

The normal flux density $B_r$ is defined as

$$B_r=-{\mu }_0\frac{\partial A_{zII}}{\partial r}=-{\mu }_0\frac{e^{{\mathrm{t}}_5}}{R_2}\frac{\partial A_{zII}}{\partial t}$$

(44)

As the permeability of the stator/rotor iron core is much larger than that of air, the following boundary conditions are employed

• The scalar magnetic potential is expressed as $A_{II}=0$ in the inner stator surface

  $$A_{zII}\left(t_5,0\right)=0$$

  (45)

  or

  $${\displaystyle \sum }_{n=1}^{\infty }(\frac{1}{n}\frac{Cosh\left(n\left({\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5\right)\right)}{a}_n{}^{II}-\frac{1}{n}\frac{1}{Sinh\left(n\left({\mathrm{t}}_5\right)\right)}{b}_n{}^{II})=0$$

  (46)
• The normal flux density waveforms is sinusoidal in the inner stator surface and expressed as $B_r=B_{max}\cos \left(\theta \right)$. Therefore,

  $$-{\mu }_0\frac{e^{{\mathrm{t}}_5}}{R_2}\frac{\partial A_{zII}\left(t_5,\theta \right)}{\partial t}=B_{max}$$

  (47)

  or

  $$-{\mu }_0\frac{e^{{\mathrm{t}}_5}}{R_2}\left(\frac{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_n{}^{II}+\frac{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{b}_n{}^{II}\right)=B_{max}$$

  (48)

From the boundary conditions (46) and (48), we can get

$$b_1{}^{II}=Cosh\left(\left({\mathrm{t}}_5\right)\right)a_1{}^{II}$$

(49)

$$\{\begin{array}{c}\begin{array}{c}{a}_1{}^{II}=-\frac{B_{max}{R}_3}{{\mu }_0} n=1\\ b_1{}^{II}=-\frac{B_{max}{R}_3}{{\mu }_0}Cosh\left(\left({\mathrm{t}}_5\right)\right) n=1\end{array}\\ \begin{array}{c}{a}_n{}^{II}=0 n=3,5,7\\ b_n{}^{II}=0 n=3,5,7\end{array}\end{array}$$

(50)

At the position of $\theta =0$, the magnetic potential is expressed as

$$B_r{}_{II}\left({\mathrm{t}}_6,0\right)=-\frac{{\mu }_0}{R_2}\left(\frac{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_1{}^{II}-\frac{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{b}_1{}^{II}\right)$$

(51)

or

$$B_r{}_{II}\left({\mathrm{t}}_6,0\right)=-\frac{{\mu }_0}{R_2}{b}_1{}^{II}=\frac{{\mu }_0}{R_2}\frac{B_{max}{R}_3}{{\mu }_0}Cosh\left(\left({\mathrm{t}}_5\right)\right)$$

(52)

In the outer surface of the rotor, the magnetic potential can be derived as

$$B_r{}_{II}\left({\mathrm{t}}_6,0\right)=B_r{}_{II}\left(t,0\right)$$

(53)

or

$$B_r{{}_{II}}^2\left({\mathrm{t}}_6,0\right)= B_r{{}_{II}}^2\left(\mathrm{t},\theta \right)$$

(54)

or

$${\left(\frac{{\mu }_0}{R_2}\frac{B_{max}{R}_3}{{\mu }_0}Cosh\left(\left({\mathrm{t}}_5\right)\right)\right)}^2={\left(-\frac{{\mu }_0}{R_2}\left(\begin{array}{c}\frac{Sinh\left(n\left(\mathrm{t}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_1{}^{II}\\ -\frac{Sinh\left(n\left(\mathrm{t}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{b}_1{}^{II}\end{array}\right)Cos\left(\theta \right)\right)}^2$$

(55)

or

$$t_{opt}\left(\theta \right)=Cos{h}^{-1}\left\{\frac{Cosh\left(t_5\right)}{Cos \left(\theta \right)}\right\}+t_5$$

(56)

Therefore, the optimum magnet radii can be expressed as

$$r_{opt}=\frac{R_1}{exp\left(Cos{h}^{-1}\left\{\frac{Cosh\left(t_5\right)}{Cos \left(\theta \right)}\right\}+t_5\right)}$$

(57)

5. Performance Calculation

The electromagnetic torque is obtained using the Maxwell stress tensor and expressed as

$$T_e=\frac{L_s}{{\mu }_0}{{\displaystyle \int }}_0^{2\pi }BI{I}_r\left(t_e,\theta \right)BI{I}_{\theta }\left(t_e,\theta \right)d\theta$$

(58)

where $L_s$ is the axial length of the motor and $t_e$ is calculated by

$$\begin{array}{l}{t}_e=ln\left(\frac{R_2}{R_e}\right)\\ R_e=\left(R_2+R_3\right)/2\end{array}$$

(59)

The final expression of the electromagnetic torque can be expressed as

$$T_e=\frac{\pi L_s}{{\mu }_0}{\displaystyle \sum }_{n=1}^{\infty }\left(M_n{N}_n+O_n{P}_n\right)$$

where,

$$\begin{array}{l}{M}_n=-\frac{1}{R_e}\frac{Cosh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_n{}^{II}-\frac{1}{R_e}\frac{Cosh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{b}_n{}^{II}\\ N_n=-\frac{1}{R_e}\frac{Sinh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{c}_n{}^{II}-\frac{1}{R_e}\frac{Sinh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{d}_n{}^{II}\\ O_n=\frac{1}{R_e}\frac{Cosh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{c}_n{}^{II}+\frac{1}{R_e}\frac{Cosh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{d}_n{}^{II}\\ P_n=-\frac{1}{R_e}\frac{Sinh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_6\right)\right)}{Sinh\left(n\left({\mathrm{t}}_5-{\mathrm{t}}_6\right)\right)}{a}_n{}^{II}-\frac{1}{R_e}\frac{Sinh\left(n\left({\mathrm{t}}_{\mathrm{e}}-{\mathrm{t}}_5\right)\right)}{Sinh\left(n\left({\mathrm{t}}_6-{\mathrm{t}}_5\right)\right)}{b}_n{}^{II}\end{array}$$

For single layer winding, the phase flux vector is calculated by

$$\left[\begin{array}{c}{\psi }_a\\ {\psi }_b\\ {\psi }_c\end{array}\right]=N_c{C}^T\left[\begin{array}{ccc}\begin{array}{ccc}{\phi }_1& {\phi }_2& {\phi }_3\end{array}& \dots & {\phi }_{Q_2}\end{array}\right]$$

(60)

where $N_c$ is the number of conductors in the stator slot, C is a matrix connection between the stator slots and phase connections, and $\phi$ is the slot flux.

For the stator slots, $\phi$ is given by

$${\phi }_i=-\frac{L_s{R}_4{}^2}{k_{f}S}{{\displaystyle \int }}_0^{\beta }{{\displaystyle \int }}_0^{t_8}{A}_m{}_i\left(t,\theta \right)e^{-2t}dtd\theta$$

(61)

where $k_f$ is the stator fill factor and is the area of the stator slot.

For double-layer winding, the phase flux vector is calculated by

$$\left[\begin{array}{c}{\psi }_a\\ {\psi }_b\\ {\psi }_c\end{array}\right]=\left[\begin{array}{c}\psi 1_a\\ \psi 1_b\\ \psi 1_c\end{array}\right]+\left[\begin{array}{c}\psi 2_a\\ \psi 2_b\\ \psi 2_c\end{array}\right]$$

(62)

where

$$\left[\begin{array}{c}\psi 1_a\\ \psi 1_b\\ \psi 1_c\end{array}\right]=\frac{N_c}{2}{C}_1^T\left[\begin{array}{ccc}\begin{array}{ccc}{\phi }_{11}& {\phi }_{12}& {\phi }_{13}\end{array}& \dots & {\phi }_{1Q_2}\end{array}\right]$$

(63)

and

$$\left[\begin{array}{c}\psi 2_a\\ \psi 2_b\\ \psi 2_c\end{array}\right]=\frac{N_c}{2}{C}_2^T\left[\begin{array}{ccc}\begin{array}{ccc}{\phi }_{21}& {\phi }_{22}& {\phi }_{23}\end{array}& \dots & {\phi }_{2Q_2}\end{array}\right]$$

(64)

For the stator slots, $\phi$ is given by

$${\phi }_{1i}=-\frac{2L_s{R}_4{}^2}{k_{f}S}{{\displaystyle \int }}_0^{\frac{\beta }{2}}{{\displaystyle \int }}_0^{t_8}{A}_m{}_i\left(t,\theta \right)e^{-2t}dtd\theta$$

(65)

$${\phi }_{2i}=-\frac{2L_s{R}_4{}^2}{k_{f}S}{{\displaystyle \int }}_{\frac{\beta }{2}}^{\beta }{{\displaystyle \int }}_0^{t_8}{A}_m{}_i\left(t,\theta \right)e^{-2t}dtd\theta$$

(66)

The back-EMF of phase A is given by

$$E_a=\omega \frac{d{\psi }_a}{d{\theta }_r}$$

(67)

where $\omega$ is the rotor angular speed and ${\psi }_a$ is the flux linkage per phase A.

The stator inductance (self-inductance) of phase A is given by

$$L=\frac{{\psi }_a}{I_A}$$

(68)

where $I_A$ is the peak current in phase A.

The mutual inductance of phase A and phase B is given by

$$M=\frac{N{\phi }_{AB}}{I_B}$$

(69)

where $N$ is the number of phase turns, ${\phi }_{AB}$ is magnetic flux in phase A, and $I_B$ is the peak current in phase B.

6. Model Evaluation

In this section, the presented analytical model is used to study the magnetic flux density, electromagnetic torque, and back-electromotive force of a 12S-10P motor. The results of the analytical method are then verified by the results of the finite element method. A 2D model of the studied brushless permanent magnet motor is shown in Figure 4 and the motor parameters are given in Table 1. The PM magnetization is radial. The slot contains two coils as shown in Figure 4a. In order to have a good precision in the analytical evaluation, the number of harmonic terms used in the computations is equal to 50 (air-gap and PM subdomains) and 30 (slots and slot-opening subdomain).

Figure 4. The cross-sections of the studied motor. (a) with the uniform rotor; (b) uniform rotor, (c) with the optimal rotor, (d) optimal rotor.

Table 1. The specification of the investigated motors.

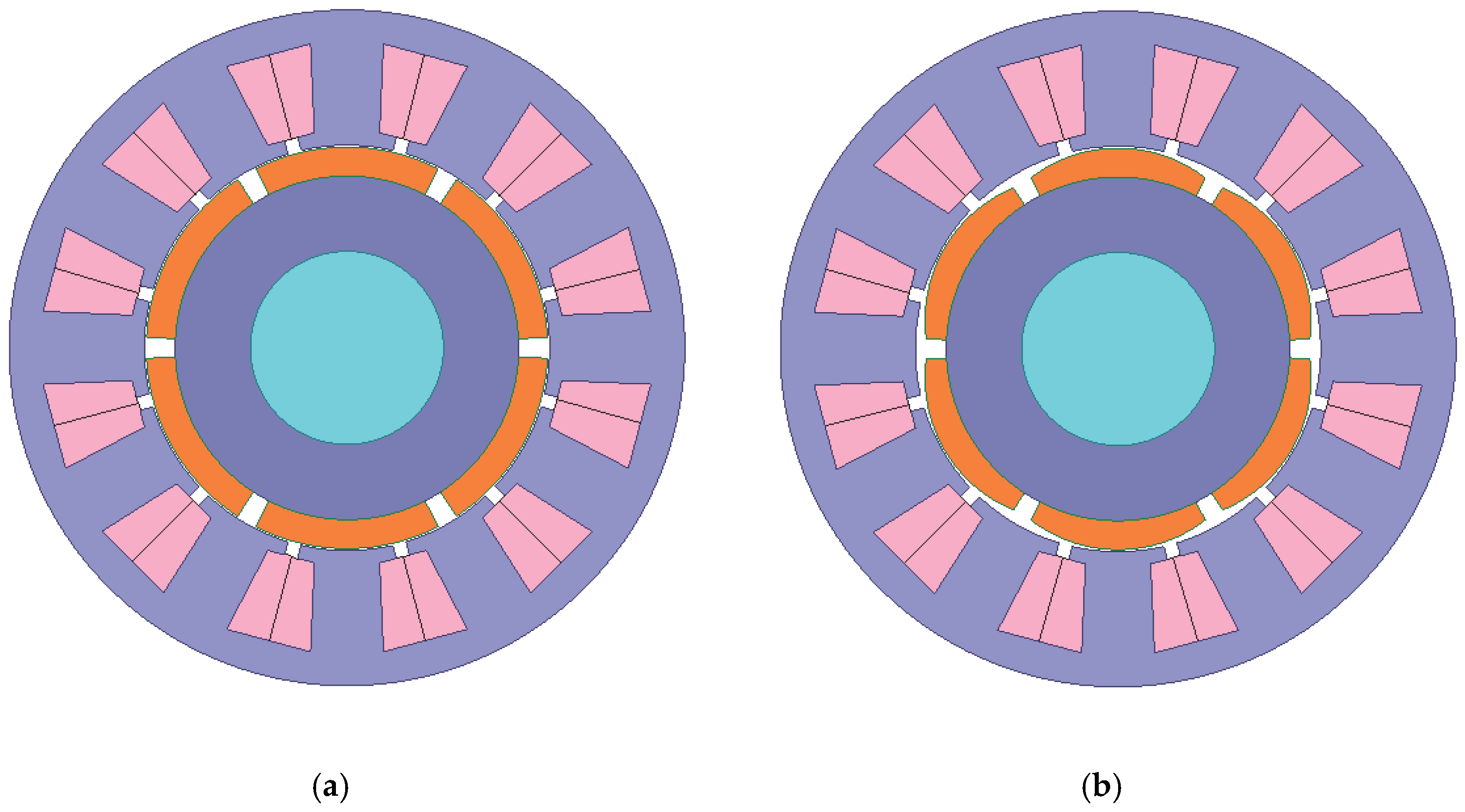
Parameter	Value
Rotor Outer Diameter	208 mm
Rotor Inner Diameter	130 mm
Number of poles	10
Pole Arc	35°
Pole Thickness	20 mm
Magnet material	NEO-39SH
Stator Outer Diameter	350 mm
Stator Inner Diameter	210 mm
Number of Slots	12
Stator Tooth Width	30 mm
Stator Yoke Width	26 mm
Slot Open	7 mm
Tip Thickness	2.5 mm
Slot Skew	0°
Stator Length	100 mm
Lamination material	M 19–0.5 mm

We have to solve a system of linear equations with the same number of unknowns (i.e., 12). The matrix connection between the stator slots and phase connections of each layer for the investigated motor are given by

$$\begin{array}{l}{C}_1=\left[\begin{array}{cccccccccccc}1& -1& 0& 0& 0& 0& -1& 1& 0& 0& 0& 0\\ 0& 0& -1& 1& 0& 0& 0& 0& 1& -1& 0& 0\\ 0& 0& 0& 0& 1& -1& 0& 0& 0& 0& -1& 1\end{array}\right]\\ C_2=\left[\begin{array}{cccccccccccc}0& -1& 1& 1& 0& 0& 0& 1& -1& 0& 0& 0\\ 0& 0& 0& 1& -1& 1& 0& 0& 0& -1& 1& 0\\ -1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 1\end{array}\right]\end{array}$$

The 2D finite element method is applied to the performance calculation of the motor with uniform and non-uniform rotor shapes. The magnetic field distribution in the studied motors is represented in Figure 5. Open circuit analytical and numerical comparisons of the cogging torque for both motors with initial and optimal magnet shapes are shown in Figure 6. The on-load comparison of the back electromotive force of the investigate motors with the initial and optimal magnet shapes is carried out analytically and numerically as shown in Figure 7. An analytical and numerical comparison of the radial flux density for the 12S-10P motor in an open circuit and on-load condition is shown in Figure 8. An analytical and numerical comparison of tangential flux density for the 12S-10P motor in open circuit and on-load condition is shown in Figure 9. An on-load comparison of the electromagnetic torque of the 12S-10P motor with the initial and optimal magnet shapes is shown in Figure 10.

Figure 5. The magnetic field distribution in the 12S-10P motor. (a) Initial magnet shape; (b) Optimal magnet shape.

Figure 6. An open circuit analytical and numerical comparison of the cogging torque.

Figure 7. An on-load analytical and numerical comparison of Back-EMF.

Figure 8. An analytical and numerical comparison of radial flux density for the 12S-10P motor. (a) Open circuit condition; (b) On-load condition.

Figure 9. An analytical and numerical comparison of the tangential flux density for the 12S-10P motor. (a) Open circuit condition; (b) On-load condition.

Figure 10. An on-load analytical and numerical comparison of the electromagnetic torque for the 12S-10P motor.

7. Conclusions

A mathematical expression for the optimal magnet shape in surface mounted permanent magnet machines was considered in this paper. The Fourier analysis method based on the subdomain method using hyperbolic functions is applied to derive the analytical expressions for the calculation of magnetic vector potential, magnetic flux density, cogging torque, electromagnetic torque and back-electromotive force in surface-mounted permanent magnet machines. This model is applied for the performance computation of a 12S-10P surface-mounted permanent magnet motor. The results of the proposed model have been verified thanks to the FEA results. In future work, the iron permeability for global saturation can be considered in the analytical model by Dubas’ superposition technique [35,36].