Abstract
The Ambartsumian delay equation is used in the theory of surface brightness in the Milky way. The Adomian decomposition method (ADM) is applied in this paper to solve this equation. Two canonical forms are implemented to obtain two types of the approximate solutions. The first solution is provided in the form of a power series which agrees with the solution in the literature, while the second expresses the solution in terms of exponential functions which is viewed as a new solution. A rapid rate of convergence has been achieved and displayed in several graphs. Furthermore, only a few terms of the new approximate solution (expressed in terms of exponential functions) are sufficient to achieve extremely accurate numerical results when compared with a large number of terms of the first solution in the literature. In addition, the residual error using a few terms approaches zero as the delay parameter increases, hence, this confirms the effectiveness of the present approach over the solution in the literature.
1. Introduction
In astronomy, Ambartsumian [1] derived a delay differential equation (DE) for the surface brightness in the Milky Way. The standard form of this equation is given as [2],
where q is a constant for the given model and Equation (1) is subjected to
where is also a constant. Existence and uniqueness has been proved and discussed by Kato and McLeod [3]. It is of great importance to search for accurate solution for Equations (1) and (2) due to its application in astronomy. Very recently, Patade and Bhalekar [2] have obtained a power series solution for this system by applying the Daftardar-Gejji and Jafari Method [4]. They have discussed the convergence for all , however, their solution is not valid in the whole domain as will be shown in this paper. In order to overcome such drawback, a new series solution shall be deduced by using the Adomian decomposition method (ADM) which possesses more accuracy and validity.
The ADM was applied to solving algebraic/transcendental/matrix equations [5,6,7,8,9], besides nonlinear integral/differential equations and both IVPs/BVPs, even for irregular boundary contours [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The solution of this method is an infinite series which converges when choosing an appropriate canonical form. Hence, a few terms achieve good accuracy for the model under consideration.
A very good analysis for delayed differential equations has been presented by [25,26]. In addition, theoretical analysis for the convergence of Adomian’s method to differential equations has been discussed earlier by Abbaoui and Cherruault [27]. We remark that a significant advantage of the ADM for solution of differential equations is that it neither invokes the fixed-point theorem to prove convergence nor is the Adomian solution algorithm developed in accordance with its premise. Also, the speed of convergence and the general error estimation of the series solution using the standard ADM have been previously reported by Cherruault and Adomian [28]. Moreover, Rach [29] has introduced an extensive bibliography of the theory, technique, and applications of the Adomian decomposition method.
The objective of this work is to reinvestigate the Ambartsumian delay equation by using the ADM. Two different canonical forms will be constructed. It will be shown that our first solution agrees with the power series solution [2], while the second series solution is expressed in terms of the exponential functions and this can be viewed as a new type of solution for the current problem. Also, it will be demonstrated that the sequence of the approximate solutions of the second type (expressed in terms of the exponential functions) converges faster than the solution in the literatures.
2. Application of the ADM
2.1. Power Series Solution
Therefore
Hence
and this is the same closed form solution obtained by Patade and Bhalekar [2]. Therefore, the m-term approximate solution of the power series (7) is given by
2.2. Approximate Solution in Terms of Exponential Functions
Equation (1) can be rewritten in the following canonical form
On using (4) into (9), we obtain the following recurrence scheme
and hence,
and so on. The n-term approximation for Ambartsumian equation is
In the following section, it will be illustrated that the sequence of the approximate solutions in (12) is convergent in a wider range than those in the literature at . Moreover, the present approximate numerical results will be validated by calculating the absolute residual error defined by
In addition, the advantage and the effectiveness of the present low-order approximate analytic solutions for the Ambartsumian delay equation over the existing method in the literature will be proved for certain higher values of the parameter q.
3. Discussion
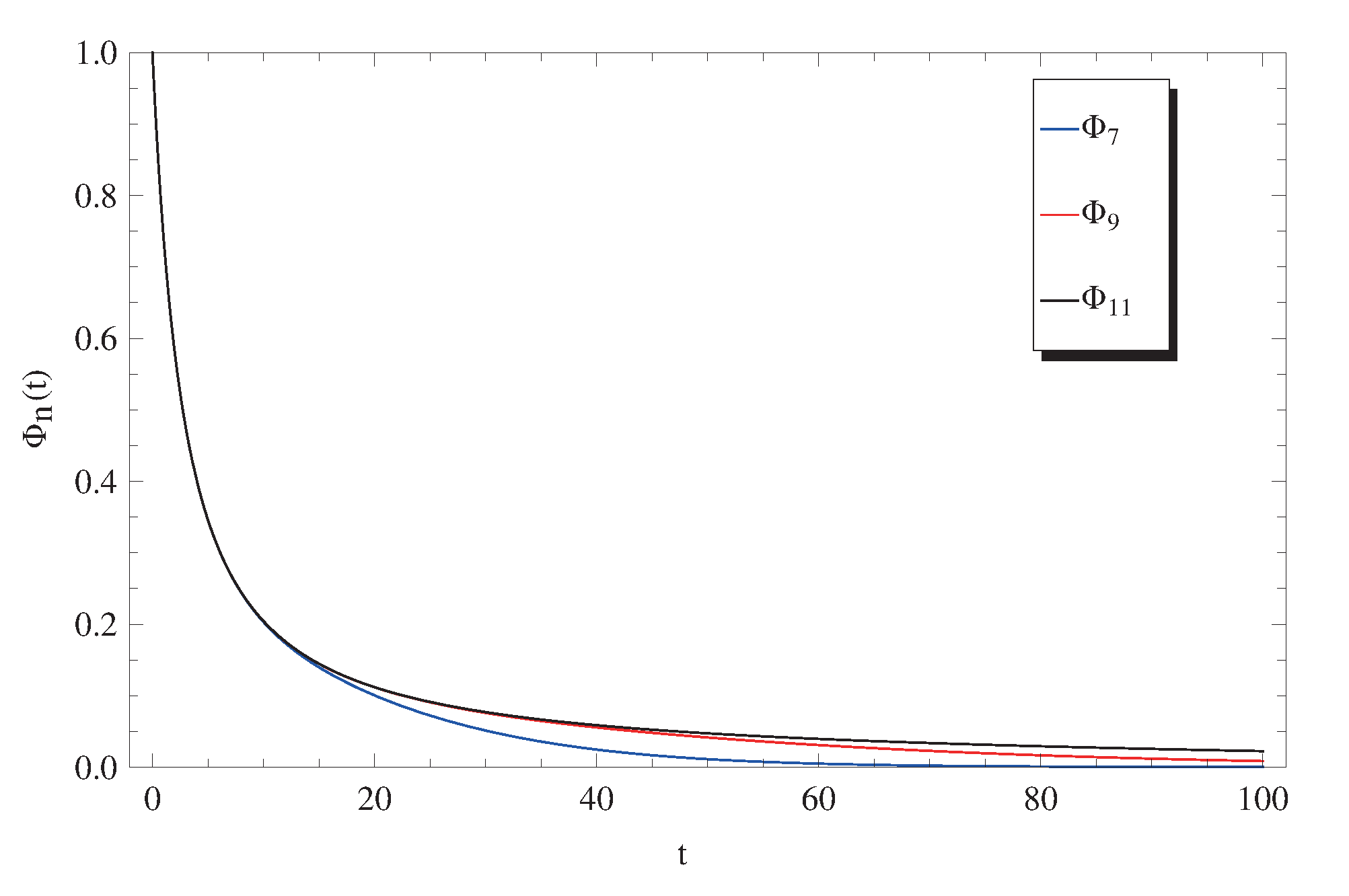
In the previous section, the ADM was applied to obtain two types of approximate solutions for the system (1) and (2). These two types are investigated in this discussion to stand on their domains of applicability and validity. Usually, we begin by graphically demonstrating the convergence of the approximate solutions in Equation (12). In Figure 1, Figure 2 and Figure 3, , , and are plotted at a fixed value of and different values for q, where (Figure 1), (Figure 2), and (Figure 3). A rapid convergence is observed from these figures using only a few terms of the Adomian approximate solutions of exponential terms (11). The main notice here is that the rate of convergence is increased for higher values of q, where at the 7-term, 9-term, and 11-term are nearly identical. Hence, of the decomposition method is sufficient to provide a remarkably accurate solution as will be shown later by discussing the absolute residuals , , and , while at the lower values of q in the domain , a higher-order approximate solution such as for is required to achieve a similar high accuracy.
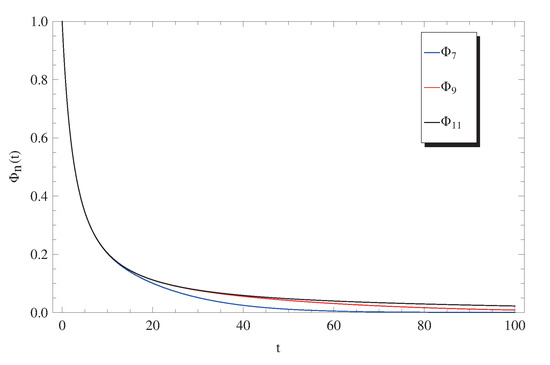
Figure 1.
Plots of approximate solutions (12) at and .
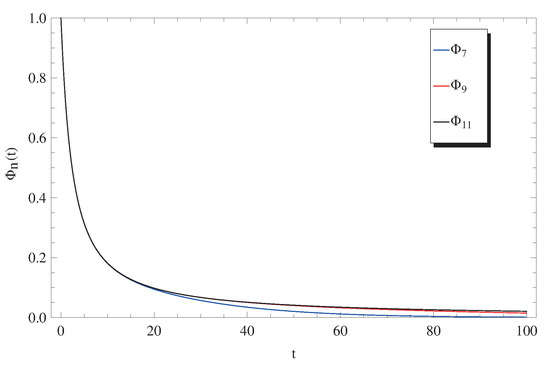
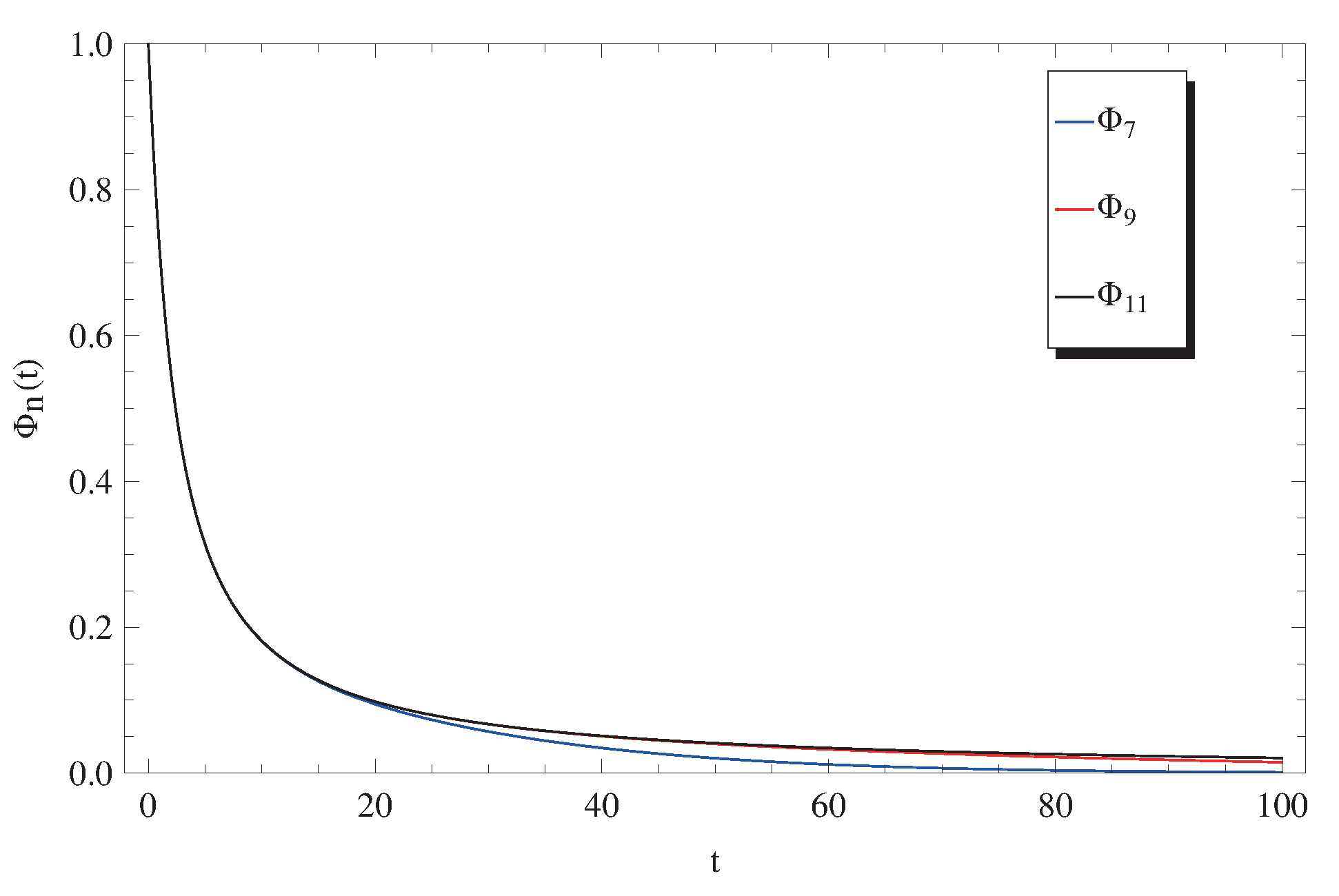
Figure 2.
Plots of approximate solutions (12) at and .
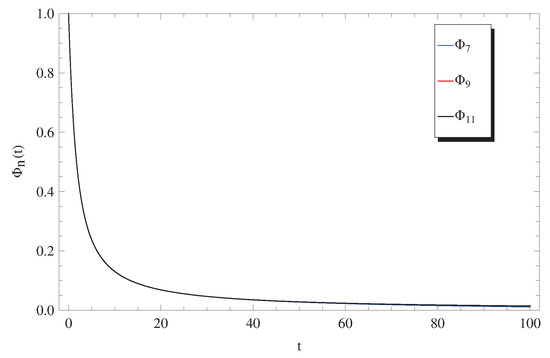
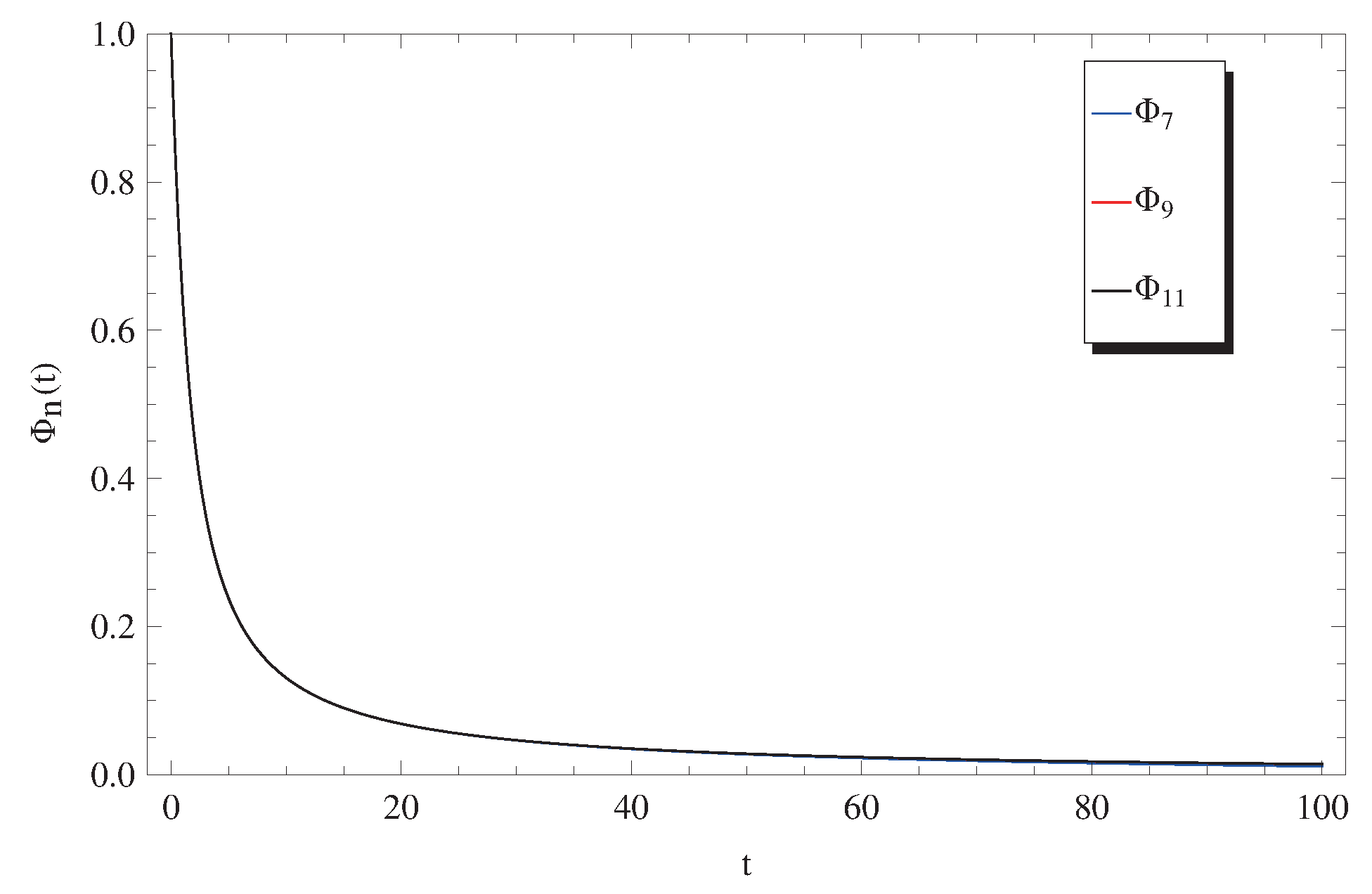
Figure 3.
Plots of approximate solutions (12) at and .
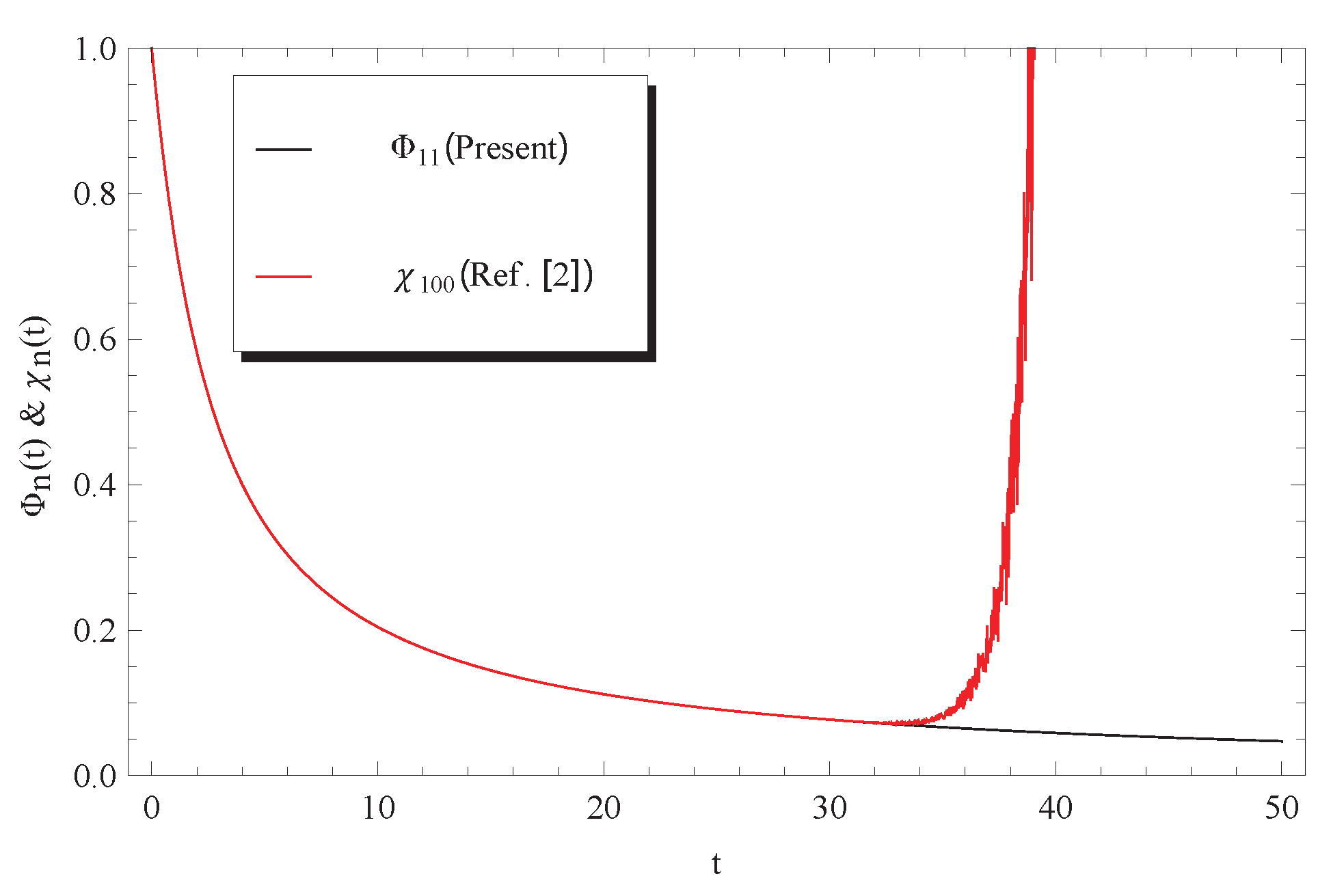
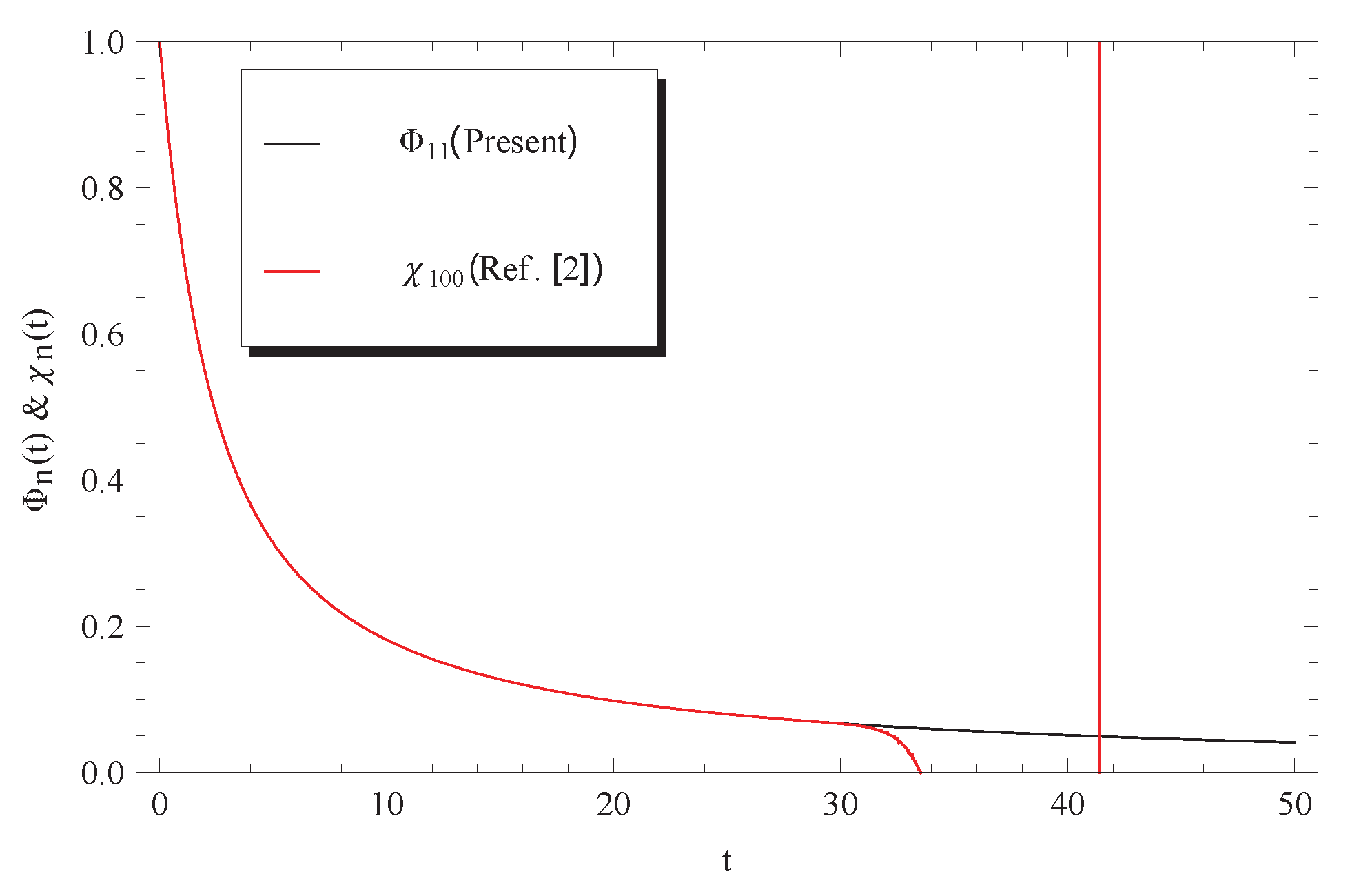
In addition, the approximate solutions , , and of the second type (exponential) are valid in the whole domain of . However, the approximate solution of the first type (power series) is only valid in sub-domains as shown from Figure 4, Figure 5 and Figure 6. The comparisons between the two types of the Adomian approximate solutions reveal that the second type posses some advantages over the first type that was expressed as power series. Moreover, a few terms of the second type is sufficient to achieve accurate numerical results in a wider range when compared with the 100-term of the power series solution (8).
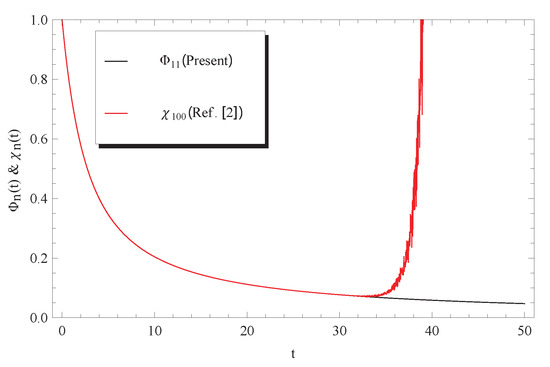
Figure 4.
Comparison between approximate solutions (12) and Ref. [2] at and .
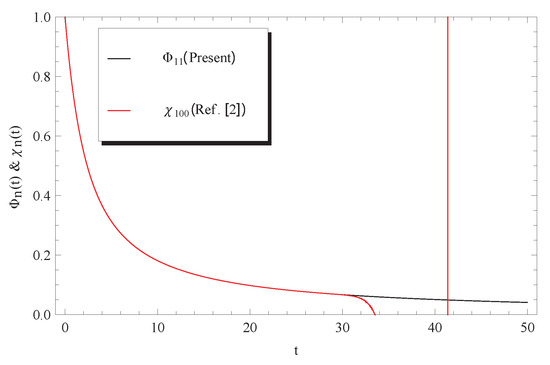
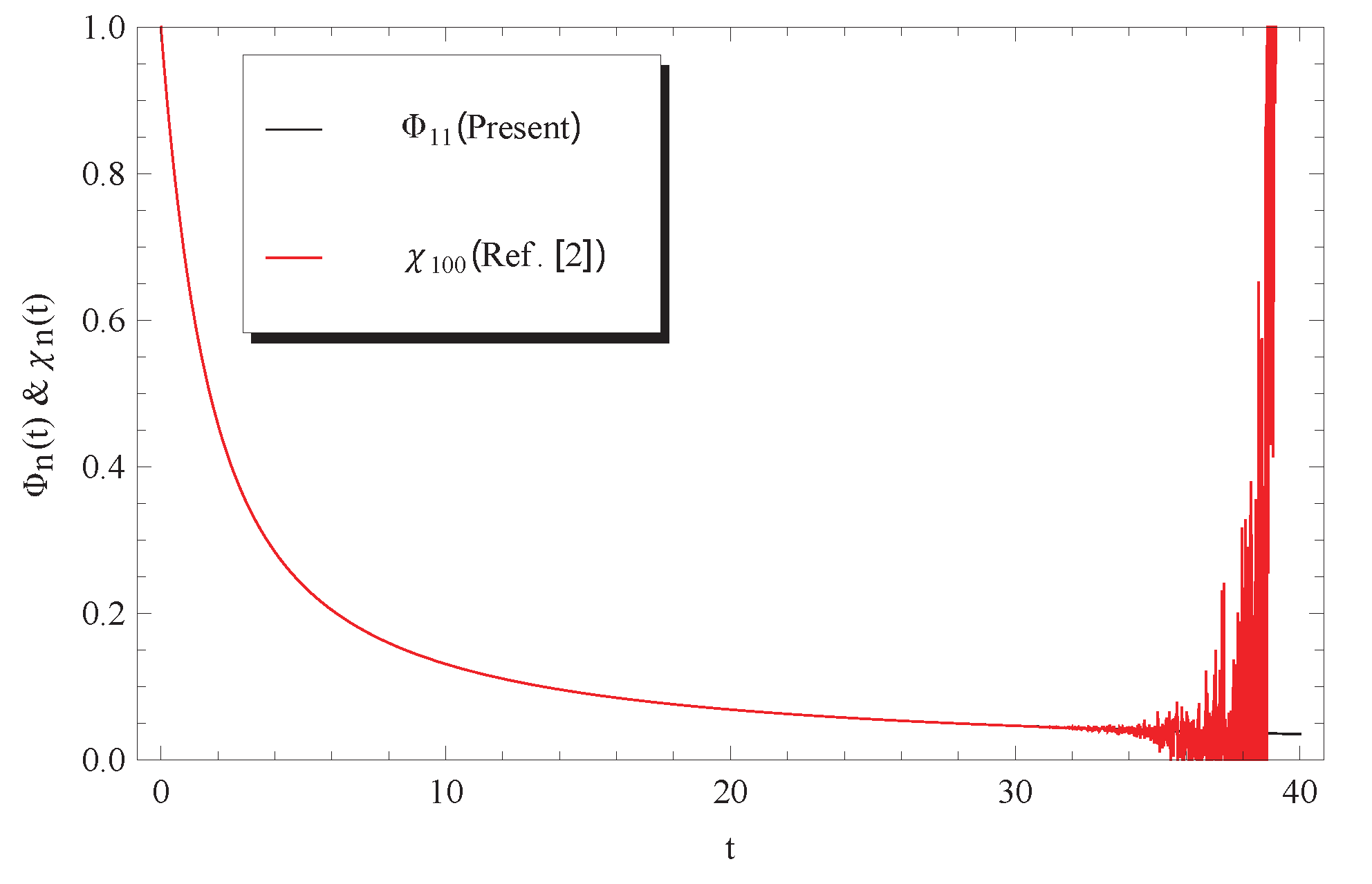
Figure 5.
Comparison between approximate solutions (12) and Ref. [2] at and .
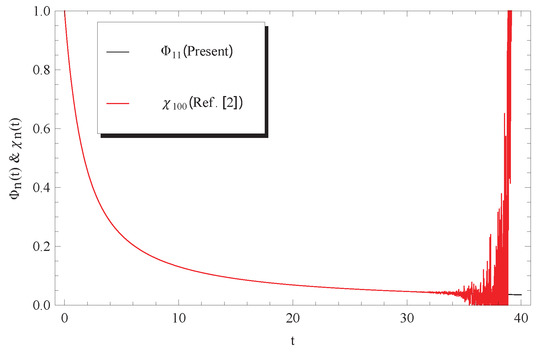
Figure 6.
Comparison between approximate solutions (12) and Ref. [2] at and .
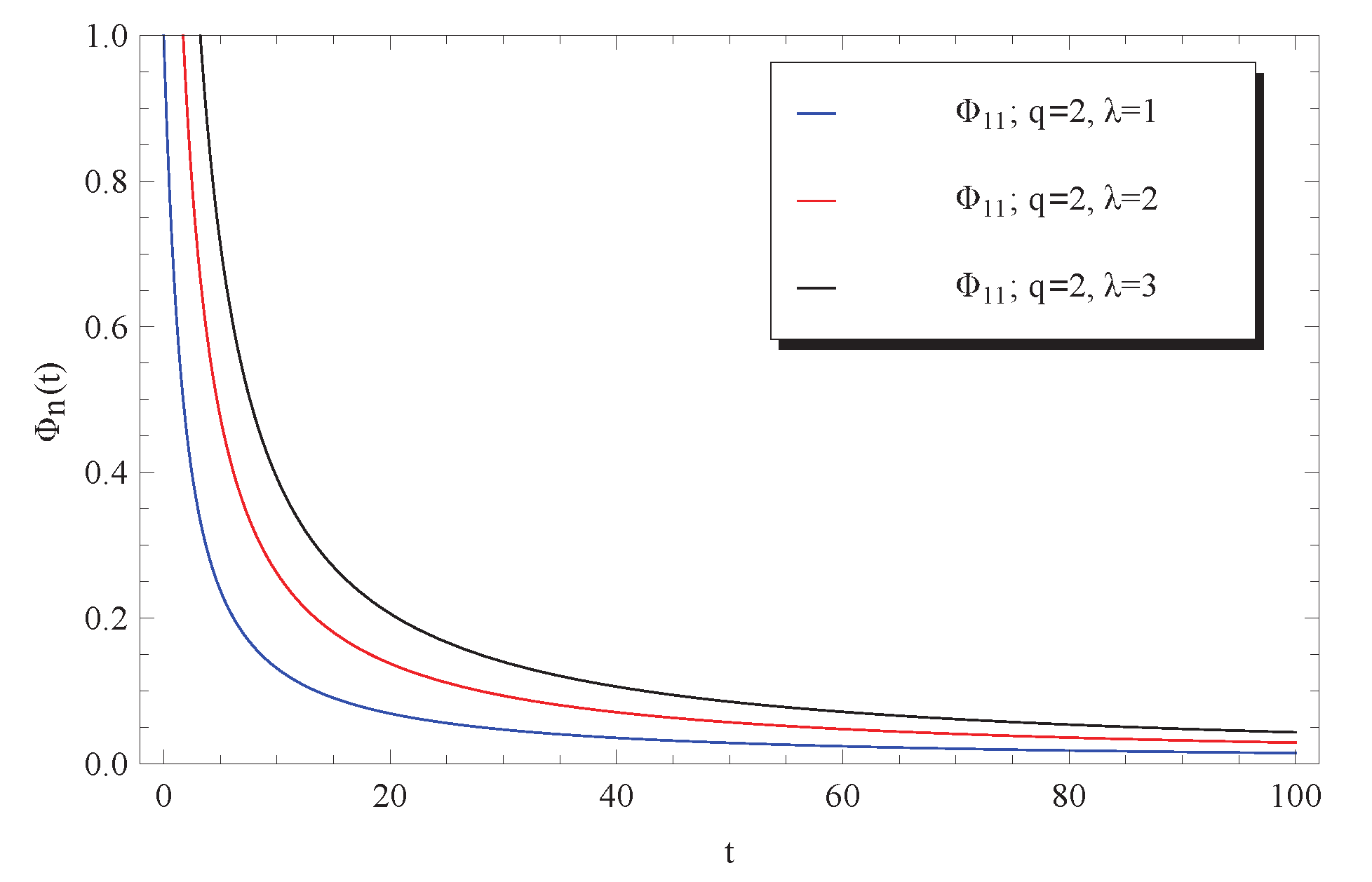
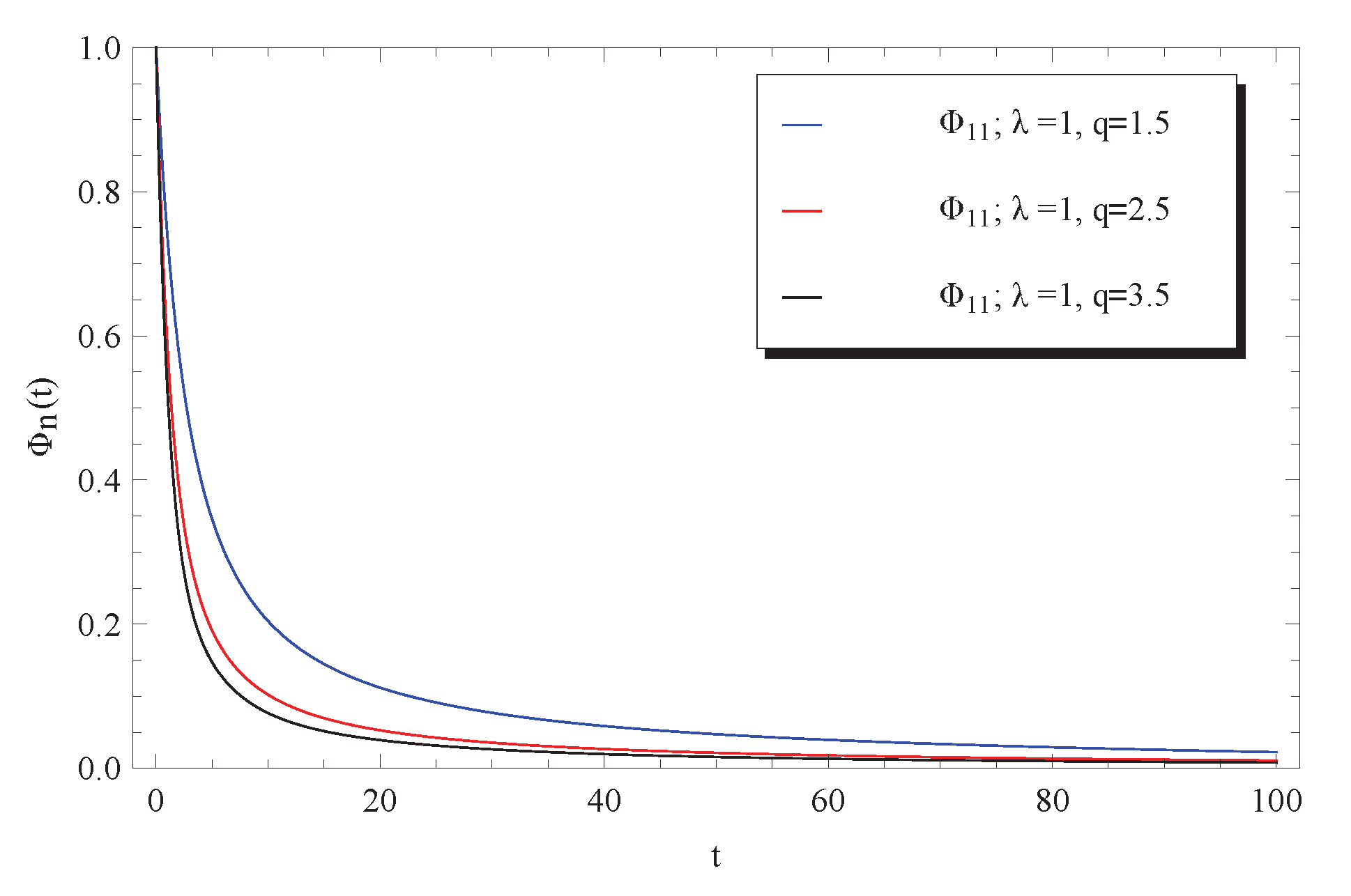
The impacts of the initial condition and the delay parameter q on the approximation for the fluctuations of the surface brightness are respectively depicted in Figure 7 and Figure 8. It can be seen from Figure 7 that the surface brightness is increased by increasing the given initial condition . However, a rapid decrease in the surface brightness has been remarked by increasing the delay parameter q. This latest notice reveals that the curves of tend faster to zero at higher values of q. Moreover, as we have from Equation (11) that
and accordingly,
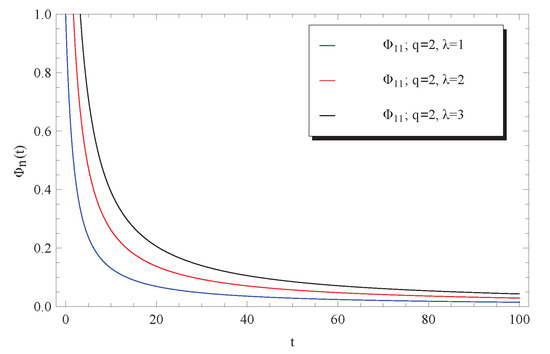
Figure 7.
Impact of on approximate solution (12) at .
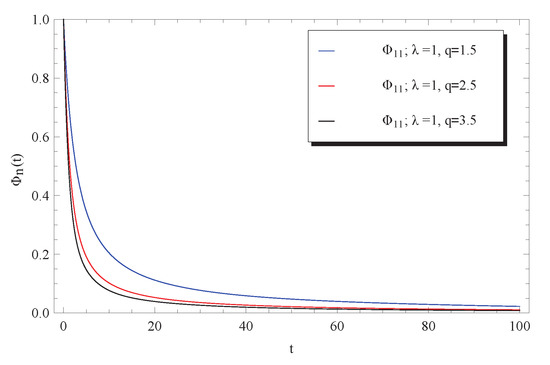
Figure 8.
Impact of q on approximate solution (12) at .
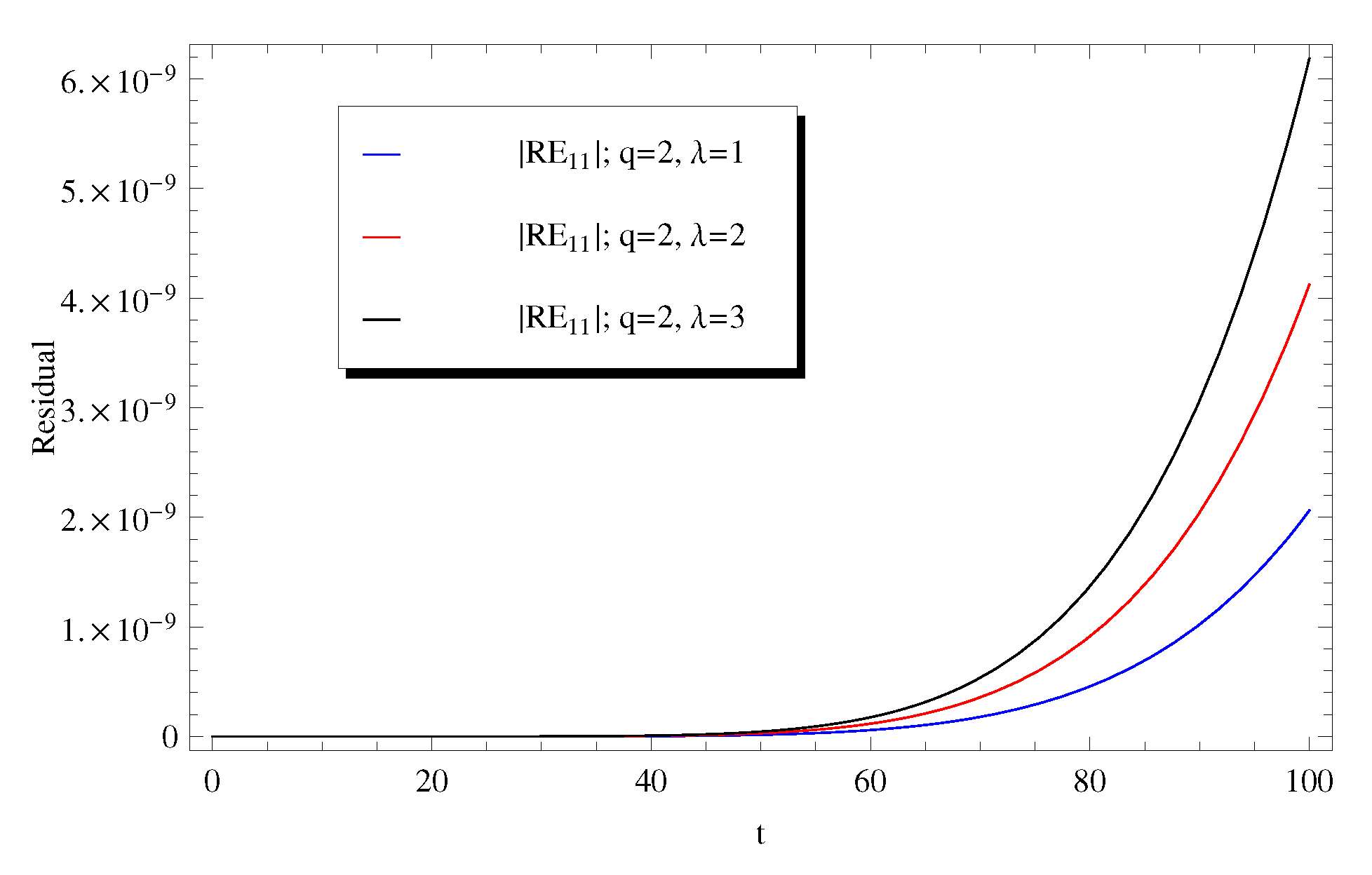
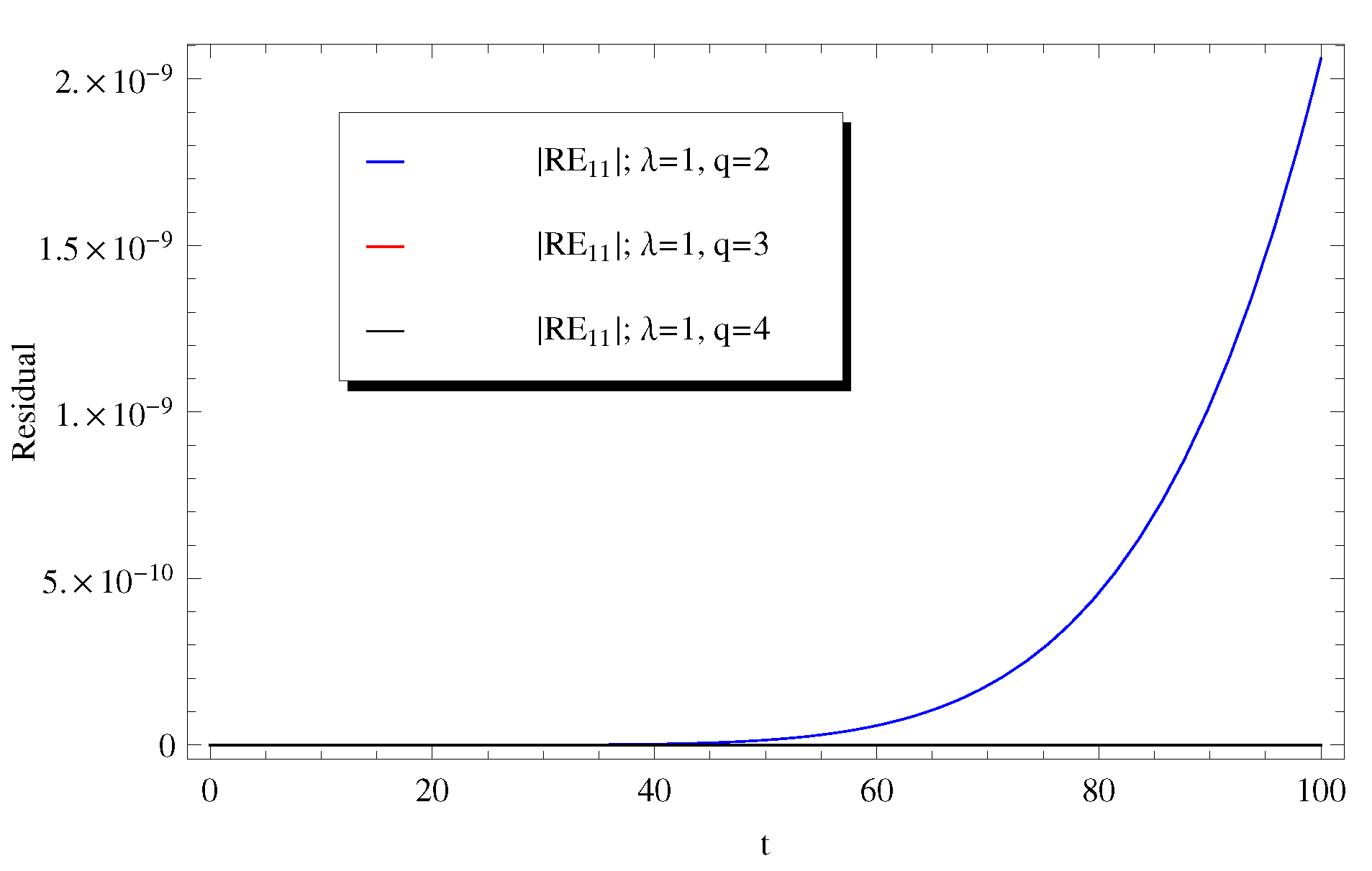
For a further validation of the current numerical results, two additional plots for the absolute residual error versus t at different values of () and at different values of q () in Figure 9 and Figure 10, respectively.
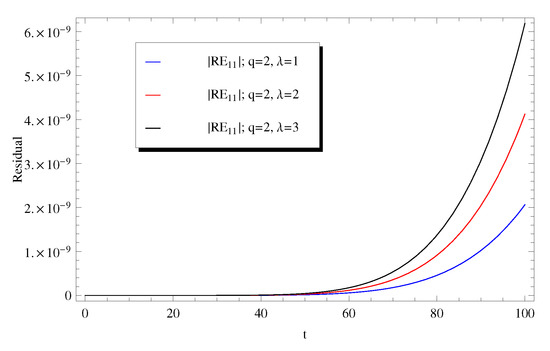
Figure 9.
Impact of on the absolute remainder error at .
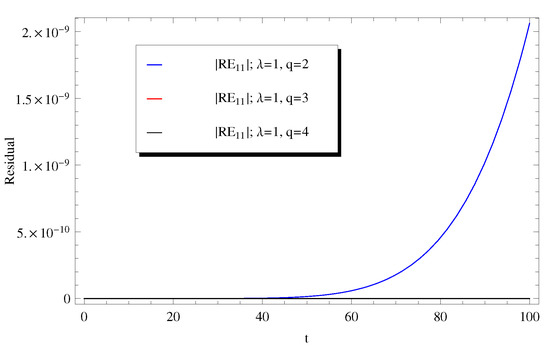
Figure 10.
Impact of q on the absolute remainder error at .
The results obtained from these two figures reveal that the approximate solution using only eleven terms of the Adomian’s series of exponential orders is highly accurate. Moreover, the absolute residual error approaches zero even at higher values of the delay parameter q. This proves the several remarkable advantages of Adomian’s method over the existing power series method in the literature [2]. The preceding discussion shows that the ADM can be effectively used to solve similar delay equations. In a future work, some delay equations of higher-orders will be also solved by applying the ADM to prove the effectiveness of this method.
4. Conclusions
In this paper, the Ambartsumian delay equation for the fluctuations of the surface brightness in the Milky way has been analytically solved by using the Adomian decomposition method (ADM). The obtained approximate solutions were of two types. The first was expressed as a power series solution which agreed with a previous solution in the literatures, while the second was expressed in terms of exponential functions. Unfortunately, the solution in the literatures was only effective in sub-domains while our second type solution was valid in the whole domain. Besides, very small absolute residual errors have been achieved using only eleven terms of the Adomian decomposition series. It was also found that the absolute residual errors tend to zero for higher values of the delay parameter q.
Author Contributions
Conceptualization, A.E. and A.A.-E.; Methodology, A.E.; Software, A.E.; Validation, B.Z.A.; Formal Analysis, A.E.; Investigation, A.E. and A.A.-E.; Data Curation, M.D.A. and B.Z.A.; Writing—Original Draft Preparation, A.A.-E. and M.D.A.; Writing—Review & Editing, A.A.-E.; Supervision, A.E.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ambartsumian, V.A. On the fluctuation of the brightness of the milky way. Doklady Akad Nauk USSR 1994, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On Analytical Solution of Ambartsumian Equation. Natl. Acad. Sci. Lett. 2017. [Google Scholar] [CrossRef]
- Kato, T.; McLeod, J.B. The functional-differential equation y′(x) = ay(λx) + by(x). Bull. Am. Math. Soc. 1971, 77, 891–935. [Google Scholar]
- Daftardar-Gejji, V.; Bhalekar, S. Solving fractional diffusion- wave equations using the new iterative method. Fract. Calc. Appl. Anal. 2008, 11, 193–202. [Google Scholar]
- Adomian, G.; Rach, R. On the solution of algebraic equations by the decomposition method. J. Math. Anal. Appl. 1985, 105, 141–166. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Algebraic equations with exponential terms. J. Math. Anal. Appl. 1985, 112, 136–140. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Algebraic computation and the decomposition method. Kybernetes 1986, 15, 33–37. [Google Scholar] [CrossRef]
- Fatoorehchi, H.; Abolghasemi, H. Finding all real roots of a polynomial by matrix algebra and the Adomian decomposition method. J. Egypt. Math. Soc. 2014, 22, 524–528. [Google Scholar] [CrossRef]
- Alshaery, A.; Ebaid, A. Accurate analytical periodic solution of the elliptical Kepler equation using the Adomian decomposition method. Acta Astronaut. 2017, 140, 27–33. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Acad: Boston, MA, USA, 1994. [Google Scholar]
- Wazwaz, A.M. Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput. 2005, 166, 652–663. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The combined Laplace transform-Adomian decomposition method for handling nonlinear Volterra integro-differential equations. Appl. Math. Comput. 2010, 216, 1304–1309. [Google Scholar] [CrossRef]
- Ebaid, A. Approximate analytical solution of a nonlinear boundary value problem and its application in fluid mechanics. Z. Naturforschung A. 2011, 66, 423–426. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Ebaid, A. A new analytical and numerical treatment for singular two-point boundary value problems via the Adomian decomposition method. J. Comput. Appl. Math. 2011, 235, 1914–1924. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Rach, R.; Duan, J.S. Adomian decomposition method for solving the Volterra integral form of the Lane-Emden equations with initial values and boundary conditions. Appl. Math. Comput. 2013, 219, 5004–5019. [Google Scholar] [CrossRef]
- Ali, E.H.; Ebaid, A.; Rach, R. Advances in the Adomian decomposition method for solving two-point nonlinear boundary value problems with Neumann boundary conditions. Comput. Math. Appl. 2012, 63, 1056–1065. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Ashorynejad, H.R. Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol. 2013, 239, 259–265. [Google Scholar] [CrossRef]
- Chun, C.; Ebaid, A.; Lee, M.; Aly, E.H. An approach for solving singular two point boundary value problems: analytical and numerical treatment. ANZIAM J. 2012, 53, 21–43. [Google Scholar] [CrossRef]
- Kashkari, B.S.; Bakodah, H.O. New Modification Of Laplace Decomposition Method for Seventh Order KdV Equation. Appl. Math. Inf. Sci. 2015, 9, 2507–2512. [Google Scholar]
- Ebaid, A.; Aljoufi, M.D.; Wazwaz, A.-M. An advanced study on the solution of nanofluid flow problems via Adomian’s method. Appl. Math. Lett. 2015, 46, 117–122. [Google Scholar] [CrossRef]
- Bhalekar, S.; Patade, J. An analytical solution of fishers equation using decomposition method. Am. J. Comput. Appl. Math. 2016, 6, 123–127. [Google Scholar]
- Bakodah, H.O.; Al-Zaid, N.A.; Mirzazadeh, M.; Zhou, Q. Decomposition method for Solving Burgers’ Equation with Dirichlet and Neumann boundary conditions. Optik 2017, 130, 1339–1346. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. The Adomian decomposition method for the slip flowand heat transfer of nanofluids over astretching/shrinking sheet. Rom. Rep. Phys. 2018, in press. [Google Scholar]
- Diblík, J.; Kúdelcíková, M. Two classes of asymptotically different positive solutions of the equation (t) = −f(t,yt). Nonlinear Anal. 2009, 70, 3702–3714. [Google Scholar] [CrossRef]
- Diblík, J.; Kúdelcíková, M. Two classes of positive solutions of first order functional differential equations of delayed type. Nonlinear Anal. 2012, 75, 4807–4820. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to nonlinear equations. Math. Comput. Model. 1994, 20, 69–73. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G. Decompostion Methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Rach, R. A bibliography of the theory and applications of the Adomian decomposition method, 1961–2011. Kybernetes 2012, 41, 1087–1148. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).