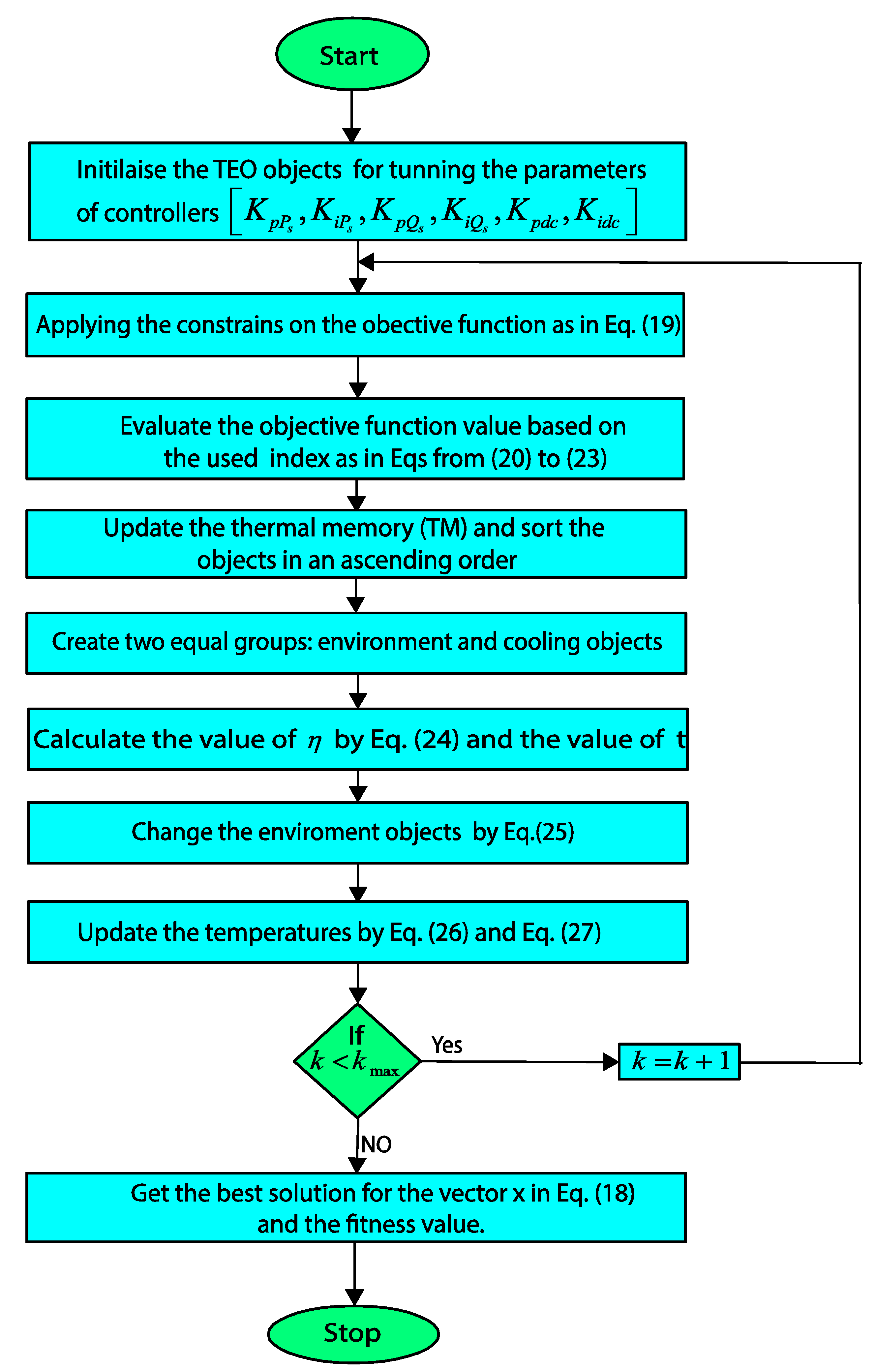
6.1. Execution of the Metaheuristic Algorithms
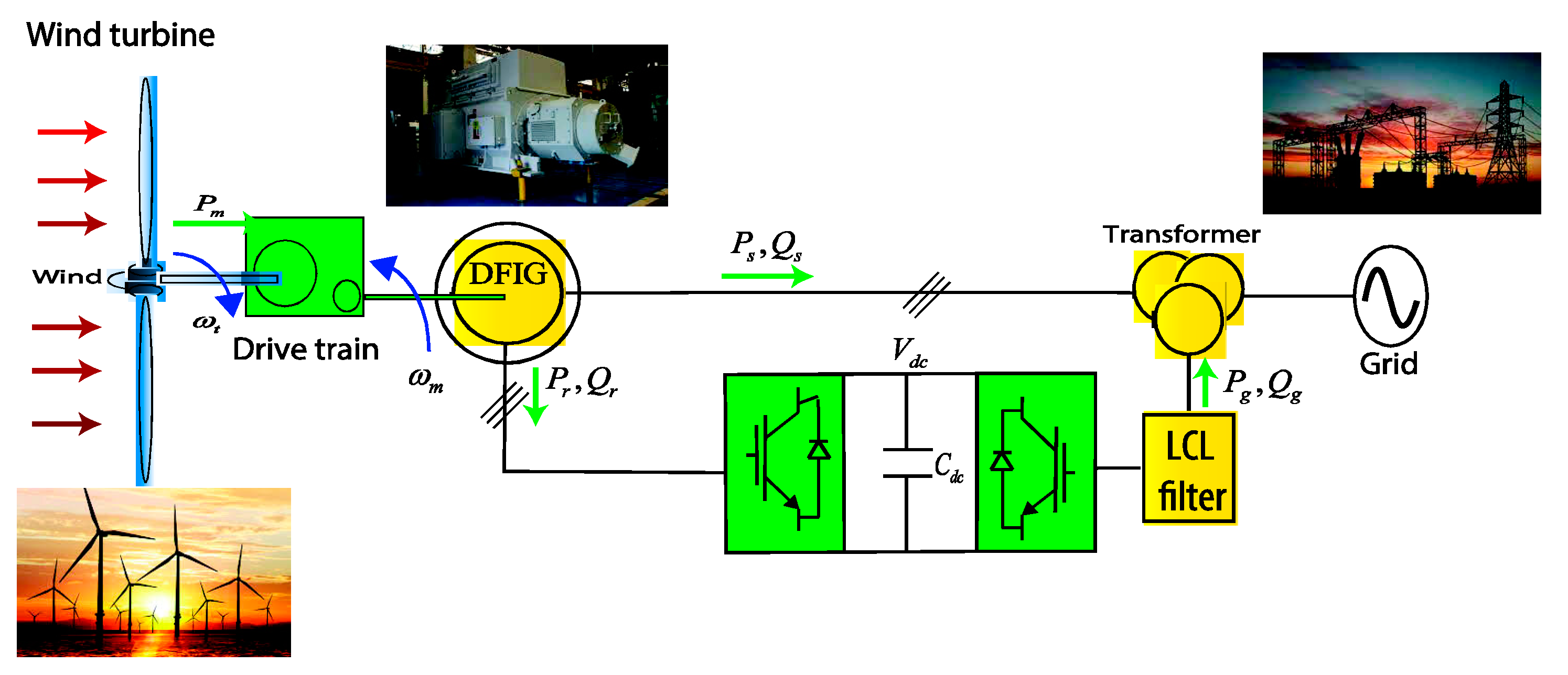
The proposed metaheuristics-based direct power control of the studied DFIG-based WECS is built using the MATLAB/Simulink environment. The respective nominal parameters of the DFIG, power converters at both sides, L-filter and LCL-filter are presented in
Table 1. Specifically, this work deals with the PI controllers tuning for the active and reactive powers loops in the RSC circuit, as well as it treats with the PI controller optimization-based selection of the DC-link voltage loop in the GSC component. It is worth indicating that the inner current loops in the RSC and GSC are tuned according to the pole assignment method. Since the grid current closed-loop of the LCL-filter is unstable, the passive damping method is applied as a solution to ensure the stability of such current dynamics. To investigate the effectiveness and superiority of the proposed TEO method, the well-known global algorithms GA, PSO, HSA, WCA and GOA are considered for comparison purposes.
All reported algorithms are independently run 10 times. The termination criterion is set as a maximum number of iteration reached
for a population size of the thermal agents equal to
. All the values of the used common parameters are kept equal. All algorithms have been executed on a PC computer with Core TM i5-7200U CPU and 2.5 GHz/8.00 GB RAM. The specific control parameters of the reported algorithms are listed in
Table 2.
The optimization problem (19) is minimized for various performance criteria, i.e., IAE, ISE, ITAE and Integral Time-weighted Square Error (ITSE), and under time-domain operational constraints. These performance indexes are calculated within two conditions, which are considered as follows:
- -
14.3% step change in the reference of DC-link voltage at time ;
- -
step change in the reference stator reactive power at time .
To find the accurate values of the decision variables , the bounded search domain is initially set to . Several runs of the algorithm are performed within this initial limitation. The results indicated that the search space could be reduced to . Therefore, the TEO algorithm explores within a smaller search domain for the next runs and more precise solution output vector is achievable.
Table 3 gives the statistical results attained by the introduced algorithms under minimizing the cost functions described in Equations (20)–(23). The worst, average, best values and the standard deviation (STD) experimental results are summarized in the
Table 3, where the optimal mean value of each index is highlighted in bold and underlined. In addition, the Elapsed Time (ET) is also listed, which is defined as the time that any algorithm requires finding the best solution. It can be clearly observed that the proposed TEO produces very competitive solutions with the reported algorithms.
Appendix A summarizes the obtained gains of the PI controllers for each proposed optimization method. Indeed, these tuned PI controllers’ gains lead to the best transient and steady state responses of the entire reported algorithms.
In addition,
Figure 7 shows the convergence histories of the mean objective function values of IAE, ISE, ITAE and ITSE criteria, respectively. Indeed, it is shown that the proposed TEO metaheuristic for both IAE and ISE indices outperforms the other reported methods in terms of the fastness and non-premature convergence as well as the solutions’ quality. The TEO-based method for ITAE and ITSE criteria gives the best solution as a second order after the GA one. From these results, the superiority of the TEO metaheuristic is still shown in terms of exploitation and exploration capabilities for local and global searches. This further justifies the use of such a global metaheuristic to systematic and easy design of the direct power control of the DFIG-based WECS. The Box-and-Whisker plots of the mean objective function values are shown in
Figure 8. From these results, one can observe that the boxplots of the TEO algorithm for all given performance criteria are generally lower and narrower than other algorithms. This confirms the high reproductivity of the TEO algorithm toward finding the optimal values of the solution.
In the remainder of the results, the obtained gains of the optimized PI controllers are used to assess the frequency-and time-domains performances of the outer-loops at the RSC and GSC power components. Moreover, comparisons with the classical pole placement [
8,
15], frequency response [
5] symmetrical optimum [
27], Ziegler–Nichols [
28] and Tyreus–Luyben [
29] tuning methods are made for the DC-link voltage dynamics as shown in
Table 4 and
Figure 9. The closed-loop response of the DC-link voltage dynamics is investigated under variable voltage profile. The DC-link voltage reference is varied up and down at various step levels.
Figure 9 describes such a response around the final set-point value for different tuned PI controllers. Although, in real systems, the DC-link voltage is required to be constant. This scenario is proposed to check the capability of the proposed TEO algorithm under different circumstances. The aim is to show the difference between the classical tuning methods and the proposed optimization-based one. Referring to this result, the ITAE-based TEO algorithm can regulate the DC-link voltage dynamics with higher performance compared to the other algorithms.
The voltage tracking is achieved with best performance in terms of response precision and fastness, i.e., the steady-state error and rise/settling time metrics are minimal as depicted in
Table 4. The performance in terms of response damping is acceptable for the proposed TEO-tuned PI control as shown in
Figure 9. Referring to the numerical results in
Table 4, one can clearly observe that the proposed TEO algorithm showed the best rise/settling times and steady-state error except the overshoot index, which the Tyreus–Luyben method gained the minimum overshoot. Since several runs were executed to obtain the PI controllers’ gains with the classical Ziegler–Nichols and Tyreus–Luyben methods, the tuning process becomes a tedious and time-consuming task. These minor degradations of the overshoot performance do not influence the effectiveness of the proposed TEO-based tuning method with respect to the systematization of the synthesis procedure, the simplicity of implementation and the superiority in other performance indices. The proposed TEO algorithm found the optimal gains of the PI controllers within a reduced computation time and under operational constraints compared to the reported trials-errors based tuning procedures which generally give local solutions for the formulated control problem.
Regarding to the grid current dynamics, the same tuning methods with adding the technical optimum instead of the symmetrical ones are used to select and adjust the PI controllers’ gains. All obtained results are reported in
Table 5.
The control performance of the introduced tuning methods is investigated by supposing that there is a step change in the q-axis grid current reference at time
. The reference q-axis grid current is changed from zero to −0.2 pu. However, the
q-axis reference grid current is usually set at zero to achieve a unity power factor.
Figure 10 shows the quadrature grid current response under step changes. It can be observed that the Tyreus–Luyben method gives superior performance in comparison with the other reported methods. Here, it is important to mention that the gains of the PI controllers for the inner current loops at both RSC and GSC are selected thanks to the classical methods and not with the proposed optimization algorithms. Since the plant models of the inner loops are available, the use of the pole-placement, Tyreus–Luyben and Ziegler–Nichols methods is well adapted instead of metaheuristics-based methods which do not require models of systems to be controlled. The Bode plot of the grid current loop is presented in
Figure 11.
The quality of the three phase grid currents is investigated through measuring the THD of the AC grid currents. As depicted in
Figure 12. It is obviously shown that the use of the LCL-filter achieves a better attenuation with a THD value about 4.05% for which the IEEE519-1992 standard limits are respected. Further analysis can be made to compare the THD of the AC grid currents in the case of using an L-filter based structure. According to the results of
Figure 12, it is clear that the THD for adopting the LCL-filer is smaller than that using the L-filer type at the same value of inductance.
Referring to the RSC control results, the stator active and reactive powers can be regulated by controlling the q-axis rotor current. The reference value of stator active power is generated from a Maximum Power Point Tracking (MPPT) strategy to extract the maximum power from the wind. In addition, the value of reference reactive power is set at different step levels to check the performance of the proposed PI controllers. As shown in
Figure 13, both active and reactive powers track effectively their reference values with good performance in terms of speed and damping dynamics. In addition, the decoupling between the active and reactive powers is perfectly assured and the DFIG extracts the maximum available power, which is approximately about 1.5 MW.
Figure 14 demonstrates the control performance of the PI controller for the reactive power loop around its final set-point value based on different tuned PI methods. The aim is to show the difference between the optimization tuning-based methods. On the other hand, both left and right sides of
Figure 15 show the tracking performance of the direct and quadrature rotor currents, respectively. Such tracking dynamics are perfectly performed and improved thanks to the proposed TEO-based tuning and control method.
6.2. Statistical Analysis and Comparison
In this part, the mean execution values related to the different optimization criteria are sorted to assess the best operating one according to its average objective function performance. Moreover, a statistical comparison based on the nonparametric Friedman and Bonferroni–Dunn is carried out by using these mean performances [
30,
31]. The average ranks for all the proposed methods based on the four performances indices are provided in
Table 6. One can note that the proposed TEO metaheuristic has worthily attained the lowest average ranks compared to the remaining methods. A statistical analysis has been performed to highlight the importance of the TEO-based tuning method over other algorithms [
32].
The Friedman test for six competitor algorithms (
) and four indices (
) provides the computed value
of the
-distribution. The critical value of such a distribution with degrees of freedom
and at confidence level
is equal to
. Since the above computed score is greater than this statistical value, the null hypothesis is declined. Moreover, for the Iman–Davenport test [
30,
31], the statistic is distributed with
and
degrees of freedom. For this test, the null hypothesis is also rejected as the calculated value
is greater than the critical value
at the same significant level of confidence. All these statistical results indicate that there are significant differences among the performances of the reported algorithms for the optimization problem (19). Thus, the proposed TEO is found to be the most effective one having the best average Friedman ranking as given in
Table 6. However, a Bonferroni–Dunn post-hoc test is called to investigate whether or not the proposed TEO algorithm is significantly better than another algorithm at the above considered level of confidence [
32]. The corresponding Critical Differences (CD) of the reported algorithms at the confidence levels
(95% significance level) and
(90% significance level) are computed as
and
, respectively.
Figure 16 illustrates the graphical representation of the Bonferroni–Dunn test considering the TEO as the control algorithm [
32,
33].
The bar of the TEO algorithm is the lowest high among the reported algorithms and the heights of the bars corresponding to the PSO algorithm. The GOA method violates the horizontal lines of significant levels. This reveals that the TEO algorithm performs at least significantly better than these two algorithms over the solutions equality.