1. Introduction
Intracranial head organs have been known to be the most sensitive organs involved in life-threatening injuries caused by impact incidents and blast waves [
1,
2,
3]. Due to the complex mechanical and physical reactions of the head and brain under impact and explosion waves, the mechanism of traumatic brain injuries (TBI) is not well understood [
4]. Finite element (FE) simulations provide a convincing framework for determining biomechanical responses of the head exposed to those high rated loads [
5]. These numerical models have been introduced to predict brain deformation for different applied loads and study intracranial organ behavior under TBI conditions [
6,
7,
8,
9,
10,
11,
12,
13]. The biofidelity of such computational simulations is strictly related to the accuracy of the material properties used to model these tissues.
Mechanical properties of brain tissue are a fundamental subject of biomechanics and have been extensively studied in the last few decades [
3,
14,
15]. It has been shown that the mechanical behavior of the brain is dominated by the loading rate and varies nonlinearly with any change in strain, as well as with its strain rate [
16,
17,
18,
19,
20]. Typically, soft biological materials such as brain and brainstem present complex mechanical responses characterized by large strains, load history, and rate sensitivity [
21,
22,
23,
24,
25,
26]. Since brain and brainstem tissues are rate-dependent materials, great care should be taken in selecting proper material properties from corresponding strain rates in different scenarios.
Dura mater (a surrounding membrane of brain) and skull, which hold and protect the brain, have significant roles in the analysis of the TBI incidents. Therefore, determining the material properties of the dura and cranial bone was the subject of earlier research in biomechanics [
27,
28,
29]. Both theoretical and experimental studies have shown that the dura and cranial bone present rate-dependent material properties [
30,
31,
32,
33,
34]. Although linear and hyperelastic models can approximate the behavior of dura and skull very well at each rate [
31,
35,
36], they behave differently under various speeds of loading. For instance, Persson et al. [
31] tested dura mater under uniaxial tension at three various strain rates of 0.01, 0.1, and 1.0 s
−1. They postulated the mechanical responses of dura is rate-dependent; however, they fitted their results to the rate-independent hyperelastic Ogden model. Additionally, experimental tensile results indicated the Young’s modulus of the cranial bone varies from 8 to 19.5 GPa for quasistatic to dynamic rates [
37]. Therefore, to have a correct result at each FE simulation, the right material properties corresponding to the rate of that application should be selected.
The majority of biomechanical characterizations for human head organs have been performed within experiments in relatively low strain rates. Recently, De Kegel et al. [
35] conducted some experiments for human dura specimens within a strain rate of 1.0 s
−1. They have obtained a highly nonlinear behavior for dura and characterized its mechanical response using three different hyperelastic material models. Franceschini et al. [
38] have experimentally studied the mechanical behavior of human brain tissue at strain rates ranging between 0.0055 and 0.0093 s
−1. Although their results are valid to be employed for studies in quasistatic loading, those material properties have been used in many computational simulations of TBI at dynamic loads [
39,
40]. It was confirmed [
16,
41] that, in addition to selecting an appropriate constitutive model, using the material constants derived from a mismatched strain rate may considerably affect the validity of the results. Farid et al. [
16] showed that hyper-viscoelastic material models, which are optimized for various low strain rates, will result in considerable errors when predicting brain behavior at higher strain rates. Therefore, it is crucial to know the range of strain rates at dynamic loading conditions and characterize the material properties of head organs at those rates.
Finding the ranges of strain rate for brain, brainstem, dura, and skull in TBI through simulations can help in determining and using the material properties at the right rate. The strain rates of different incidents cannot be measured in vivo, and therefore, a computational finite element analysis of the human head was conducted to predict the strain rates for loading scenarios associated with brain injury [
12]. In this paper, impact and blast assault simulations are conducted on a developed FE human head model to predict the range of strain rates. In this paper, it was assumed that the brain will experience minor injuries by blunt impact [
1] and an effective (mild to severe) brain injury caused by blast [
42]. This approach came from the fact that impact and blast load types are inherently different and cannot be directly compared to each other. The findings provide a ground basis for determining more relevant material properties for the strain rates corresponding to impact and blast cases.
3. Results
FE simulations of the head impacted by a golf ball are performed for different impact directions and ball speeds as stated in
Table 4. Moreover, the mentioned blast scenarios presented in
Table 5 were implemented in the head model. In this study, the resultant linear acceleration of the skull was assumed to be the same as human head acceleration [
58]. Therefore, this acceleration for three cases of impact and four scenarios of the blast are measured and shown in
Figure 4a,b. Instead of measuring the acceleration at one point or element, the whole skull geometry is considered as one body, and the averaged acceleration of this part was evaluated by LS-Dyna.
Figure 5 presents the blast wave propagation and intracranial pressure (ICP) distribution in the brain which is necessary to predict brain behavior during the blast. As can be seen, for this case (backward
heavy blast), the ICP in brain exceeds 300 kPa, and therefore, a severe TBI should be expected [
1]. Furthermore, in comparison to Rezaei et al.’s study [
56], it proves that the selection of HE masses and its distance from the head was adequate to create such a condition.
The strain rate distributions for all elements in the brain, brainstem, skull, and dura were examined. Similar to other mechanical parameters, such as ICP, strain or stress, the strain rate has a non-uniform distribution. For instance, in the brain, the maximum strain rate occurs only in a relatively small zone (some elements) which takes place in different locations for each case, and the rest of the brain observes a moderate regime of rates.
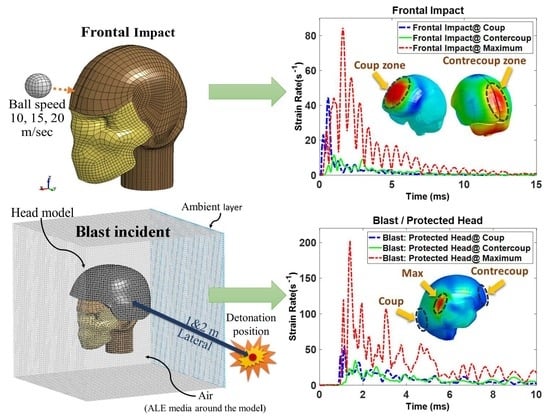
Figure 6a,b illustrates the history of 1st principal strain rate in three different locations of the brain for the head impacted by a golf ball. For the case where the ball hit the front of the head with 15 m/s of speed, the maximum strain rate does not happen in coup nor contrecoup. However, it was found that for lateral impacts, the highest rate happens at the coup zone. This shows the location of the maximum rate can occur in every area of the brain and varies for several impact scenarios. Similarly,
Figure 6c,d depicts the brain strain rates by the same measure (1st principal) for the protected and unprotected heads under
heavy blast conditions. As shown in
Figure 6c,d, for the heavy-blast scenario, the highest estimated strain rates of the protected and unprotected head are close to each other, although due to inherent high nonlinearity of blast analysis, it is difficult to find a rational explanation for this, and it seems the helmet in this scenario has a minor effect on the strain-rate measure. One probable reason for this can be the severe explosion happening in a very short distance from the head, which leads to the helmet not being effective in serving as a deep protective tool here. For blunt impact cases, the elements of the skull, which are located at the impact side, are observed to have the highest strain rates. Additionally, for all blast simulations (lateral and backside), the maximum rates occur at the temporal bone, which has the lowest cranial thickness.
In this study, the maximum shear strain rate was determined for brainstem since it has been shown to be the dominant cause of injury at brainstem occurring due to shear strain [
55].
Figure 7a–d demonstrates the histories of the strain rate at regions with highest values of rate in brain, brainstem, skull, and dura under three directions of impact. In addition, the computed strain rates at points with maximum rates in these head parts under four scenarios of blast are plotted and shown in
Figure 8a–d. Finally, the maximum linear acceleration of the head and highest calculated strain rate in the brain, brainstem, skull, and dura for all impact and blast cases are demonstrated in
Table 6 and
Table 7, respectively. Since the values of the acceleration in all impact scenarios are less than 90 g [
1], the damage level can be considered minor or close to the mild TBI. Head accelerations in some blast cases exceed 90 g, so severe brain injuries are expected under those circumstances.
4. Discussion
Evaluating mechanical properties of the human head organs is fundamental in understanding intracranial brain deformation under different loading conditions. It is known that the brain has a rate-dependent behavior and gets stiffer by increasing the loading rate [
16,
59]. That is why, in literature, it is common to conduct in vitro tests with certain strain rates to capture the wider properties of the brain [
18,
19,
60]. Similar approaches have been applied to identify the material parameters of brainstem, dura, and other rate-dependent biological tissue [
31,
61]. Cranial bone was found to behave differently at various rates [
30]. It was reported that the bone tissue for the skull at high rates (150 s
−1) can become up to 200% stiffer as skull in quasistatic rates [
37]. Therefore, to simulate these rate-dependent materials in dynamical studies such as TBI cases, the validated properties over the desired range of strain rates must be employed. In this regard, the findings of this paper propose a measure for the range of the rates needed for conducting the in vitro test and also selecting material properties from the right strain rates.
The time duration of a general head impacts is in the order of milliseconds, while in the case of a high-speed load such as a blast wave less than one millisecond. Regardless of the strain value, it was found that brain injury caused by impact happens with a brain strain rate of 23 to 140 s
−1 with an average of 84 s
−1 [
62,
63]. Using a validated FE head model is a very feasible approach for determining the strain rates of the brain and skull under loading. Clinical studies of reconstructed head impact simulations which led to mild TBI for 58 football players proposed a range of 35–97 s
−1 for the brain strain rate [
64]. Viano et al. [
5] analyzed 28 cases of NFL impacts involving 22 concussions by FEM, and they found the brain strain rates for those incidents were in the range of 19–162 s
−1. To the best of the authors’ knowledge, there is no reported study in the literature pointing out the range of the strain rate from experimental measurement of an in vivo or cadaver test.
In this paper, some impact and blast scenarios were modeled on a validated head model. Results (
Table 6 and
Table 7) showed that under these dynamic loads, the response of brain and brainstem were in the range of 36 to 241 and 15 to 412 s
−1, respectively. Meanwhile, the estimated strain rates of the dura and skull during such impact and blast loads were respectively in the range of 8 to 149 and 14 to 182 s
−1. Significant correlations of strain rates with linear head acceleration for brain, brainstem, dura, and skull were found and are presented in
Figure 9a–d. These linear regressions were independent of the effects of direction and speed of impactor, as well as the HE mass, distance, direction, and head condition (protection) under blast [
65]. The proposed strain rates of brain, brainstem, dura, and skull are, respectively, 1.9 (
R = 0.8,
p < 0.01), 0.7 (
R = 0.9,
p < 0.01), 1.18 (
R = 0.9,
p < 0.001) and 0.7 (
R = 0.6,
p < 0.01) times of resulting head acceleration by impact. In addition, under blast incidents, the brain, brainstem, dura, and skull behaved with a strain rate of 0.86 (
R = 0.96,
p < 0.001), 1.25 (
R = 0.9,
p < 0.001), 0.52 (
R = 0.95,
p < 0.001) and 0.43 (
R = 0.9,
p < 0.001) times of acceleration, respectively.
Figure 9 shows that for the equivalent linear acceleration of head, the strain rates induced by impact for the brain, dura, and skull are higher in comparison to the blast one.
As the first limitation of this study, the result was not based on a general impact or blast conditions. Numerous cases of other simulations for various scenarios of blunt impact and blast are required instead of the chosen limited representative cases. Therefore, it should be mentioned that the estimated range of rates in this study is more expected for a blunt impact causing mild TBI, and blast cases generating concussion or brain injury [
1,
63]. In this research, we did not study the effect of element size on the strain rate. We have used a validated head model that has been used in many computational studies of human head under similar dynamical loads. Therefore, we did not change the mesh size, and of course, once we had changed the element sizes, we needed to validate the new head model again. As another limitation, the FE simulations were done with one set of material properties, and we used a simple elastic material model for the cranial bone and dura mater. The most accurate material properties for this kind of simulation would be the nonhomogeneous anisotropic visco-hyperelastic materials. However, first, we could not find these properties for human head tissues in the current literature, and second, our head model was not developed for utilizing such material models. Among material properties available in the literature, those which were determined at the highest dynamic rates were selected. However, the findings of this study still suggest that there is a necessity to characterize those material properties at even higher ranges. Thus, the results of this paper can be considered as the first step in having the true estimation of selecting the right material properties in dynamical simulations.
5. Conclusions
Cranial bone, and particularly brain, brainstem, and dura are highly rate-dependent materials and will behave differently in various strain rates. In order to study the biomechanics of traumatic brain injury (TBI) through FE methods, it is necessary to implement correct properties associated with anticipated application rates. However, to calculate the material properties of the brain, brainstem, dura, and skull related to TBI cases, we need to know for which range of strain rates they are required to be examined. In this study, FE simulation was performed to estimate the strain rate ranges in impact and blast. It was found that the brain and skull experience strain rates in the range of 36 to 241 and 14 to 182 s−1 for impact and blast incidents, respectively. Additionally, in such dynamical simulations, the brainstem and dura behave at strain rates of 15 to 412 and 8 to 149 s−1, respectively. Knowing these ranges provides a good measurement for the more accurate characterization of these materials. Additionally, representing the rates based on head acceleration helps to get a better idea of selecting material properties in advance. It was shown in the impact incidents that the strain rates of the brain, brainstem, dura, and skull were approximately 1.9, 0.7, 1.18, and 0.7 times the resulting head acceleration. Furthermore, under blast loadings, the strain rates for those head organs were around 0.86, 1.25, 0.52, and 0.43 times head acceleration.